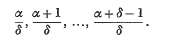Published online by Cambridge University Press: 24 October 2008
The object of this paper is to evaluate some integrals involving the product of Gauss's hypergeometric function and Meijer's G-function by expressing the G-function as a Mellin–Barnes type integral and interchanging the order of integrations. The integrals are important because on specializing the parameters they lead to many results for MacRobert's E-function, Bessel, Legendre, Whittaker functions and other related functions. In what follows δ is a positive integer and Δ(δ, α) represents the set of parameters