Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T21:24:41.916Z Has data issue: false hasContentIssue false
  • English
  • Français

The Hooley–Huxley contour method, for problems in number fields II: factorization and divisibility

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  26 February 2010

M. D. Coleman
M. D. Coleman
Affiliation:
Mathematics Department, UMIST, P.O. Box 88, Manchester M60 1QD
Get access

Extract

Let L be a Galois extension of the number field K. Set n = nK = deg K/ℚ, nL = deg L/ℚ and nL/K = deg L/K. Let I = IL/K denote the group of fractional ideals of K whose prime decomposition contains no prime ideals that ramify in L, and let P = {(α)ΣI: αΣK*, α>0}. Following Hecke [9}, let (λ1, λ2, …, λn − 1) be a basis for the torsion-free characters on P that satisfy λi(α) = 1 (1≤i≤n − 1) for all units α>0 in 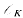, the ring of integers of K. Fixing an extension of each λi to a character on I, then λi,(α) (1 ≤i≤n − 1) are defined for all ideals α of K that do not ramify in L. So, for such ideals, we can define . Then the small region of K referred to above is

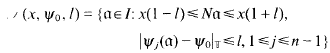
for 0<l<½ and with the notation that, for any α ∈ ℝ, we set 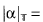β. where β is the unique real satisyfing .

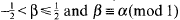MSC classification

Secondary: 11R47: Other analytic theory
Type
Research Article
Information
Mathematika , Volume 49 , Issue 1-2 , June 2002 , pp. 201 - 225
Copyright
Copyright © University College London 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Coleman, M. D.. The distribution of points at which binary quadratic forms are prime. Proc. London Math. Soc. (3), 61 (1990), 433–456.CrossRefGoogle Scholar
2.Coleman, M. D.. A zero-density region for the Hecke L.-functions. Mathematika 37 (1990), 287–304.CrossRefGoogle Scholar
3.Coleman, M. D.. The Rosser-Iwaniec sieve in number fields with an application. Ada Arith. 65 (1993), 53–83.CrossRefGoogle Scholar
4.Coleman, M. D.. Relative norms of prime ideals in small regions. Mathematika 43 (1996), 40–62.CrossRefGoogle Scholar
5.Coleman, M. D.. The Hooley-Huxley contour method for problems in number fields I: Arithmetic Functions. J. Number Theory, 74 (1999), 250–277.CrossRefGoogle Scholar
6.Delange, H.. Sur des formules de Alte Selberg, Ada Arith.. 19 (1971), 105–146.CrossRefGoogle Scholar
7.Delange, H.. Sur un theoreme de Renyi III, Ada Arith., 23 (1973), 153–182.CrossRefGoogle Scholar
8.Fogels, E.. On prime representable by a binary quadratic form. Latvijas PSR Zinatnu Akad. Vestis Fiz. Tehn. Zinatnu Ser., 1 (1966), 71–79.Google Scholar
9.Hecke, E.. Eine neue Art von Zeta Functionen und ihre Beziehungen zur Verteilung der Primzahlen, I, II. Math. Z., 1 (1918), 357–376; 6 (1920), II 51.CrossRefGoogle Scholar
10.Huxley, M. N.. On the difference between consecutive primes. Invent. Math.. 15 (1972). 164–170.CrossRefGoogle Scholar
11.Janusz, G. J., Algebraic number fields. Academic Press (1973).Google Scholar
12.Kaczorowski, J.. Some remarks on factorization in algebraic number fields. Ada Arith. 43 (1983), 53–68.CrossRefGoogle Scholar
13.Kátai, I.. A remark on a paper of K. Ramachandra. Lecture Notes in Math.. 1122 (1985). 147–152.CrossRefGoogle Scholar
14.Kubilius, J. P.. On some problems of the geometry of prime numbers. Mat. Sb. (N.S.), 31 (1952), 791–794.Google Scholar
15.Kubilius, J. P.. On a problem in the n-dimensional analytic theory of numbers. Viliniaus Vaht. Univ. Mokslo dardai Fiz. Chem. Moksly Ser., 4 (1955), 5–43.Google Scholar
16.Lagarias, J. C. and Odlyzko, A. M.. Effective versions of the Chebotarev density theorem. Algebraic Number Fields (ed. Frolich, A.). Academic Press (1977).Google Scholar
17.Landau, E.. Handbuch der Lehrc der Primzahlverteilung, Bd. 2, S. 643, Tenbner, Leipzig (1909).Google Scholar
18.Lang, S.. Algebraic Number Theory (2nd ed.). Springer-Verlag (1994).CrossRefGoogle Scholar
19.Narkiewicz, W.. Elementary and Analytic Theory of Algebraic Numbers, PWN Warszawa (1974).Google Scholar
20.Odoni, R. W. K.. The Farey density of norms of subgroups of global fields (1). Mathematika, 20 (1973), 155–169.CrossRefGoogle Scholar
21.Odoni, R. W. K.. Some global norm density results obtained from an extended Cebotarev density theorem. Algebraic Number Fields (ed. Frolich, A.). Academic Press (1977).Google Scholar
22.Ramachandra, K.. Some problems of analytic number theory. Ada Arith., 34 (1976), 313–324.CrossRefGoogle Scholar
23.Rémond, J. P.. Evaluations asymptotiques dans partitions certaines semi-groupes. C.R. Acad. Set. Paris. 260 (1965), 2250–2251; 262 (1966), A271–A273.Google Scholar
24.Serre, J.-P.. Divisibility de certaines fonctions arithmétiques. L'Enseignement Math (II) XXII (3/4) (1976). 227–260.Google Scholar
25.Sokolovskii, A. V.. A theorem on the zeros of Dedekind's zeta-function and the distance between “neighboring” prime ideals. Ada Arith., 13 (1967/1968), 321–334.Google Scholar
26.Tenenbaum, G.. Introduction to Analytic and Probabilistic Number Theory. Cambridge University Press (1995).Google Scholar
27.Wolke, D.. On a problem of A. Rényi. Mh. Math., Ill (1991), 323–330.CrossRefGoogle Scholar
28.Wu, J.Sur un probleme de Rényi. Mh. Math., 117 (1994), 303–322.CrossRefGoogle Scholar
29.Wu, J.. A sharpening of effective formulas of Selberg–Delange type for some arithmetic functions on the semigroup GK. J. Number Theory, 59 (1996), 1–19.CrossRefGoogle Scholar