Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-14T05:25:48.852Z Has data issue: false hasContentIssue false
  • English
  • Français

Erratum

Published online by Cambridge University Press:  28 September 2005

Uri Admon ,
David Donohue ,
Helmut Aigner ,
Gabriele Tamborini ,
Olivier Bildstein  and
Maria Betti
Uri Admon
Affiliation:
Physics, Chemistry, and Instrumentation Laboratory, International Atomic Energy Agency (IAEA), P.O. Box 100, A-1400 Vienna (Seibersdorf), Austria
David Donohue
Affiliation:
Safeguards Analytical Laboratory, International Atomic Energy Agency (IAEA), P.O. Box 100, A-1400 Vienna (Seibersdorf), Austria
Helmut Aigner
Affiliation:
Safeguards Analytical Laboratory, International Atomic Energy Agency (IAEA), P.O. Box 100, A-1400 Vienna (Seibersdorf), Austria
Gabriele Tamborini
Affiliation:
European Commission, Joint Research Centre, Institute for Transuranium Elements (ITU), P.O. Box 2340, 76125 Karlsruhe, Germany
Olivier Bildstein
Affiliation:
European Commission, Joint Research Centre, Institute for Transuranium Elements (ITU), P.O. Box 2340, 76125 Karlsruhe, Germany
Maria Betti
Affiliation:
European Commission, Joint Research Centre, Institute for Transuranium Elements (ITU), P.O. Box 2340, 76125 Karlsruhe, Germany

Extract

The following shows the correction to Equation (3) that appeared on page 356 of Microscopy and Microanalysis, 11:4, August 2005, in the article by Admon et al. The lines, highlighted with gray screen, were inadvertently left out.

Type
Erratum
Information
Microscopy and Microanalysis , Volume 11 , Issue 5 , October 2005 , pp. 477
Copyright
© 2005 Microscopy Society of America

The Two-Points Algorithm

In certain cases (e.g., in SEM-to-LM experiments) the sample plane is perpendicular to the viewing direction (z) in both the source and the target instruments. In such cases the dimensions measured on the sample do not require tilt-distortion correction, an inherent feature of the three-point algorithm. Hence, two reference marks, A and B, are sufficient for relocating any particle, P, in the sample plane (Fig. 2). If (x,y) are coordinates measured in the source instrument and (u,v) in the target instrument, then

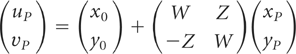
where

In the two-point case the sample plane is perpendicular to the viewing direction (z); hence the transformation from the source to the target instrument reduces to two-dimensional shift and rotation.

The Editor and Cambridge University Press regret the inconvenience that this inadvertent error may have caused.

Figure 0

In the two-point case the sample plane is perpendicular to the viewing direction (z); hence the transformation from the source to the target instrument reduces to two-dimensional shift and rotation.