Introduction
The interaction of light and matter has underpinned some of the most successful experimental techniques and technological advances in the modern era. These discoveries have been acknowledged by several Nobel Prizes, including the 2012 Physics Award to Wineland and Haroche for optical measurement and manipulation of individual quantum systems. The great progress in the study of quantum mechanics and engineering quantum systems has relied heavily on the experimental accessibility of studying the interaction between optical fields and atoms or atom-like systems. Atoms are a natural system for this research due to the restricted degrees of freedom afforded by such a simple system, and optical photons are a convenient probe as they match the typical energy scale of atomic transitions.
However, in order for applications based on atom-light interactions to become widespread, they need to be compatible with today’s highly developed large-scale fabrication processes used in, for example, microelectronics. Working with atoms in the gas phase has its limitations. In many cases, vacuum systems must be employed, and scaling these systems down to the nanoscale remains an open challenge. This has prompted a new line of research into what are coined “artificial atoms” in the solid state. These systems, including nonlinear superconducting circuitsReference You and Nori 1 and localized electrons in semiconductors,Reference Ladd, Jelezko, Laflamme, Nakamura, Monroe and O’Brien 2 exhibit the quantum mechanical properties of single atoms but are embedded in solids that can be processed using modern-day fabrication techniques.
In this issue of MRS Bulletin, we highlight progress toward applications based on one such solid-state “artificial atom”—the nitrogen-vacancy (NV) center in diamond. The NV center consists of a vacancy, or missing carbon atom, in the diamond lattice lying next to a nitrogen atom, which has substituted for one of the carbon atoms. They can form naturally during diamond growth or artificially using a variety of implantation and annealing techniques. Many of the properties of the NV center can be described by treating it as a system of two unpaired electrons exhibiting trigonal C3v symmetry.Reference Maze, Gali, Togan, Chu, Trifonov, Kaxiras and Lukin 3 Figure 1 shows a visualization of the NV electronic wave function. The center’s atom-like properties include a paramagnetic triplet ground state, which interacts strongly with both microwave and optical fields. Further, the diamond lattice is an ideal host for such an artificial atom, as its unique thermal and mechanical properties, biocompatibility, and nearly nuclear spin-free environment are highly favorable for applications in materials and biological engineering. Later we describe how the quantum mechanical properties of NV centers are being exploited for applications in quantum information science and electromagnetic sensing.

Figure 1. Visualization of the nitrogen-vacancy (NV) electronic wave function (iso-probabilistic spin-density surface). The spin density is highly localized on the three carbon atoms near the vacancy (cyan balls), while it is nearly negligible on the nitrogen atom and completely vanishes just a few lattice sites away. Figure courtesy of A. Gali, using ab initio techniques described in Reference Reference Gali, Fyta and Kaxiras29.
Quantum mechanical coherence and its applications
One of the key concepts in quantum mechanics is that a particle can simultaneously exist in an arbitrary superposition of discrete quantum states. For example, suppose the atom is in a state described by the wave function ψ = a|0〉 + b|1〉, where |0〉 and |1〉 refer to discrete energy levels (eigenstates) of the atomic system. Such a two-level system is referred to as a qubit—a quantum analog of a classical Boolean bit. The complex coefficients a and b hold an enormous amount of information, as they can vary continuously, constrained only by the normalization convention a 2 + b 2 = 1. If the qubit is entangled with other qubits, then any individual qubit can no longer be described by the simple expression for ψ; in this case, the number of degrees of freedom the system exhibits grows exponentially with the number of qubits. If these degrees of freedom can be manipulated by quantum engineers, then they can be used to process information using far fewer resources than with ordinary classical bits.Reference Nielsen and Chuang 4 This concept is the foundation of quantum information science.
Furthermore, a and b change in a predictable manner in the presence of tiny perturbations in the energies of |0〉 and |1〉. Consequently, the atoms serve as sensitive probes of external perturbations of the atomic states. If quantum metrologists can prepare and measure the coefficients, then these coefficients can be used to study variations in, for example, the local electromagnetic environment.
Information can only be stored and extracted with adequate fidelity if the atomic wave function remains coherent—loosely defined here as the coefficients a and b changing in a continuous, time-reversible manner. Maintaining coherence over a long time scale is essential in quantum metrology because noise is generated by the measurement process itself—a consequence of Heisenberg’s uncertainty principle. The highest precision is obtained by letting the coefficients evolve coherently under the influence of the external field for as long as the coherence time permits and performing a single measurement rather than averaging many repeated measurements over the same time interval.
Maintaining coherence for a longer time requires that the atom be isolated from uncontrolled perturbations, such as electromagnetic noise, which destroy atomic coherence and escape detection. Coherence can also be destroyed merely by vacuum fluctuations through a process known as spontaneous emission, so appropriate metastable or ground states for |0〉 and |1〉 must be selected. Suitable states include those connected by weak electronic transitions or ground-state spin transitions.
History of the diamond NV center
In recent years, it has come to light that the ground-state spin levels of the NV center satisfy all of the previously mentioned criteria even at room temperature. These spin states provide convenient qubits that can easily be manipulated with either magnetic or optical interactions. Optical readout of the NV electron spin is also possible, which places the NV into a special category of condensed matter systems exhibiting optically detected magnetic resonance (ODMR). Such systems are of great interest because they exhibit detectable magnetic resonance signals at much lower concentrations than is possible using a conventional electron spin resonance induction coil.
The optical and spin properties of the NV center were first discovered 35 years ago,Reference Davies and Hamer 5 , Reference Loubser and van Wyk 6 though the observation of ODMR did not occur until 10 years later.Reference Reddy, Manson and Krausz 7 , Reference van Oort, Manson and Glasbeek 8 Soon after the advent of single molecule spectroscopyReference Köhler, Disselhorst, Donckers, Groenen, Schmidt and Moerner 9 , Reference Wrachtrup, von Borczyskowski, Bernard, Orritt and Brown 10 in condensed matter (ca. 1993), ODMR on single NV centers was observed.Reference Gruber, Dräbenstedt, Tietz, Fleury, Wrachtrup and von Borczyskowski 11 This single NV ODMR study was done at room temperature. The ability to see a single NV soon led to its investigation as a potential alternative to trapped ions for quantum information applications (see the Childress and Hanson, Toyli et al., and Wrachtrup et al. articles in this issue) and eventually for precision magnetometry (see the Hong et al. and Hall et al. articles in this issue). Although it was not known in advance, the NV was eventually shown to have a nearly ideal excited-state level structure for this application, at least at cryogenic temperatures up to 10 K.Reference Santori, Tamarat, Neumann, Wrachtrup, Fattal, Beausoleil, Rabeau, Olivero, Greentree, Prawer, Jelezko and Hemmer 12 , Reference Batalov, Jacques, Kaiser, Siyushev, Neumann, Rogers, McMurtrie, Manson, Jelezko and Wrachtrup 13 The energy levels and associated optical transitions at low temperature are illustrated in Figure 2 . Furthermore, working with a solid-state host has also afforded the scalable fabrication of diamond optical networks, enabling efficient coupling of NV spins and optical photons (see the article by Loncar and Faraon).
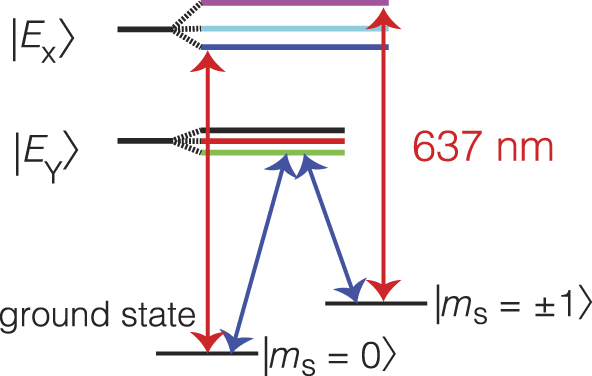
Figure 2. Energy level diagram of the nitrogen-vacancy (NV) center at low temperature. Two spin sublevels in the ground state form the qubit basis |m s = 0〉 and one of the |m s = ±1〉 levels. The excited state consists of two orbital levels (Ex and Ey ), which split under the presence of strain or electric field, and three spin sublevels within each orbital. Optical transitions (∼637 nm) to excited sublevels with m s = 0 spin projections do not alter the spin state (except in special cases) and consequently can be used to read out the qubit state. For certain values of strain, the levels in the lower branch become nearly degenerate. In this case, spin projection is not conserved, and Raman transitions are possible.Reference Santori, Tamarat, Neumann, Wrachtrup, Fattal, Beausoleil, Rabeau, Olivero, Greentree, Prawer, Jelezko and Hemmer 12 Raman transitions also occur near zero strain in the upper branch. See the Toyli et al., Wrachtrup et al., and Childress and Hanson articles for more details.
With advances in material purity, it was discovered that the NV electron spin coherence lifetime T 2 could be extended into the millisecond range. This was accomplished by removing nuclear and electronic spins, which act as sources of decoherence, using low-defect-density, isotopically enriched Reference Santori, Tamarat, Neumann, Wrachtrup, Fattal, Beausoleil, Rabeau, Olivero, Greentree, Prawer, Jelezko and Hemmer 12 C diamond. A long T 2, while routine for nuclear spins, was unprecedented for an electron spin system at room temperature, as electron spins are ∼1000 times more sensitive to magnetic perturbations than nuclear spins. Combining millisecond coherence lifetime with the rapid spin excitation rates (∼1 GHz) that can be achieved using microwave microstructuresReference Fuchs, Dobrovitski, Toyli, Heremans and Awschalom 14 gives up to 1 million single qubit operations per coherence time. This compares favorably with other quantum-computing systems, such as trapped ions, especially taking into account the much longer NV electron spin lifetimes available at moderately low temperature.Reference Jarmola, Acosta, Jensen, Chemerisov and Budker 15 Even at room temperature, exceptionally long spin coherence times (>1 s) can be achieved by storing the NV information in nearby nuclear spins, as recently demonstrated.Reference Maurer, Kucsko, Latta, Jiang, Yao, Bennett, Pastawski, Hunger, Chisholm, Markham, Twitchen, Cirac and Lukin 16 The long coherence time has also motivated the use of NV centers in precision magnetometry; a timeline of critical developments is depicted in Figure 3 .
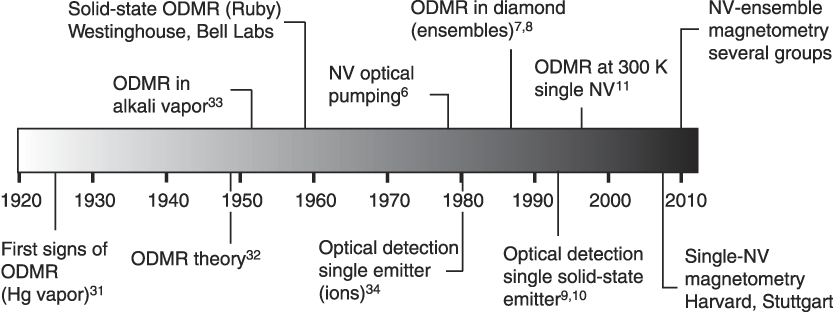
Figure 3. Timeline of critical developments leading to the use of nitrogen-vacancy (NV) centers in ultrasensitive magnetometry. ODMR, optically detected magnetic resonance.
Hybrid devices: Coupling NVs to novel solid-state quantum systems
The strong optical coupling afforded by the NV center makes it of great interest as a potential interface between photons and other solid-state quantum computers. One example is the use of ensembles of NV centers to store the coherence created in a superconducting qubit via microwave photons.Reference Kubo, Ong, Bertet, Vion, Jacques, Zheng, Dréau, Roch, Auffeves, Jelezko, Wrachtrup, Barthe, Bergonzo and Esteve 17 Such a hybrid system could combine the best of both worlds: the highly controllable superconducting qubits could serve as fast quantum processors, while the long-lived, optically active spin qubits could serve as quantum memory as well as transducers to upconvert microwave photons to the optical domain. While other electron spin systemsReference Duty 18 can also accomplish this task, the NV is of special interest, partly because of its exceptionally long storage time—several orders of magnitude longer than the lifetime of typical superconducting qubits—and partly because single NVs can be addressed and probed optically. This latter capability opens the possibility of eventually coupling single NV centers with individual superconducting qubits. However, thus far, ensembles of NVs have been required to overcome the relatively weak magnetic-dipole coupling via the √N enhancement of coupling strength for an ensemble of size N. It has been shown that a superconducting qubit can read out the state of a NV ensemble with high fidelity.Reference Zhu, Saito, Kemp, Kakuyanagi, Karimoto, Nakano, Munro, Tokura, Everitt, Nemoto, Kasu, Mizuochi and Semba 19
The NV has also shown recent promise in the context of nanomechanical resonators.Reference Arcizet, Jacques, Siria, Poncharal, Vincent and Seidelin 20 Here the motion of a single NV in an external magnetic field gradient can be used to measure the position of a macroscopic mechanical oscillator with much higher precision than is possible by optical means alone.Reference Shin, Kim, Kolesov, Balasubramanian, Jelezko, Wrachtrup and Hemmer 21 The significance of using a single NV for this purpose is that quantum mechanical interactions between a spin qubit and a macromechanical qubit could eventually be used to construct a hybrid quantum processor. Compared to a superconducting qubit, a mechanical oscillator may have the potential to work without cryogenics via optical cooling as in trapped ion methods. In fact, recent results show that the NV center can measure Brownian motion of a room temperature cantilever.Reference Kolkowitz, Bleszynski Jayich, Unterreithmeier, Bennett, Rabl, Harris and Lukin 22 Unlike trapped ions, the relatively large mass of a mechanical resonator makes it more sensitive to the environment and therefore opens potential new sensor applications.
Ultrasensitive diamond magnetometers
Aside from coupling to superconducting qubits, ensembles of NVs have also been explored for magnetic-sensor applications. So far, these investigations have fit into two main classes. One is the use of 2D NV ensembles where the NVs are confined to a thin layer, from a few nanometers up to a few microns, usually near the diamond surface. Here, biological, electronic circuit, and superconducting phase transition studies have been performed (see the articles by Hong et al. and Hall et al.).
The use of three-dimensional ensembles of NVs for magnetic sensing applications has also been investigated.Reference Acosta, Bauch, Ledbetter, Santori, Fu, Barclay, Beausoleil, Linget, Roch, Treussart, Chemerisov, Gawlik and Budker 23 Here, there is strong competition with atomic vapor magnetometers, especially in light of recently developed super coatings for the glass cells housing the vapor that give minute-long coherence times.Reference Balabas, Karaulanov, Ledbetter and Budker 24 However, vapor-cell magnetometers are typically limited by decoherence due to interatomic collisions,Reference Allred, Lyman, Kornack and Romalis 25 which become problematic for smaller cell sizes. On the other hand, NV ensembles require substantial light intensity for optical polarization, which translates into the need for high optical power as the ensemble size increases. This suggests a crossover sensor dimension of ∼100 μm, below which NV ensembles appear favorable. Additionally, the NV centers are encased in an inert diamond host and hence can operate over a very wide temperature range and in extremely harsh environments.
A remaining challenge is in efficient probing of the NV spin. The Faraday rotation employed in atomic vapor-cell sensors is negligible for NV centers at room temperature, but recent advances in diamond collection optics have enabled high fluorescence collection efficiency (see the Hong et al. article). Another route, enabled by an improved understanding of the NV energy-level structure,Reference Rogers, Armstrong, Sellars and Manson 26 , Reference Acosta, Jarmola, Zipp and Budker 27 is in the use of infrared-absorption probes, which now make diamond magnetometry at the picotesla scale feasible.Reference Acosta, Bauch, Jarmola, Zipp, Ledbetter and Budker 28
Summary
In just a short time, the diamond nitrogen-vacancy (NV) center has become one of the most widely studied solid-state defects, in large part due to its impressive performance at room temperature. This has led to rapid progress in realizing many of its envisioned applications, especially in quantum information and nanoscale biomagnetic sensing, as described throughout this issue. Hence the future looks especially bright for NV diamond, but there are still a few remaining challenges that require materials science solutions. These include the fabrication of pure, single-crystal, large-area diamond wafers and thin diamond films, and the reliable doping of high-quality NV centers very near the diamond surface. Looking forward, it may be possible to further improve the NV performance through a better understanding of its energy level structure, or to engineer a new super magneto-optical color center in another material. To this end, paramagnetic color centers in SiC have recently been demonstrated at room temperature (see the Toyli et al. article in this issue). Ultimately, the quest for the perfect solid-state artificial atom will benefit from a global collaboration among scientists from a variety of materials-related fields.
Acknowledgments
The authors thank C. Santori and D. Budker for countless valuable conversations.






