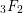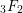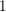Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
ASAKURA, MASANORI
and
OTSUBO, NORIYUKI
2019.
A FUNCTIONAL LOGARITHMIC FORMULA FOR THE HYPERGEOMETRIC FUNCTION.
Nagoya Mathematical Journal,
Vol. 236,
Issue. ,
p.
29.
Chen, Kwang-Wu
2021.
Explicit Formulas for Some Infinite 3F2(1)-Series.
Axioms,
Vol. 10,
Issue. 2,
p.
125.
CHEN, MARTA NA
and
CHU, WENCHANG
2023.
EVALUATION OF CERTAIN EXOTIC (1)-SERIES.
Nagoya Mathematical Journal,
Vol. 249,
Issue. ,
p.
107.
Chen, Marta Na
and
Chu, Wenchang
2024.
Yabu's formulae for hypergeometric $ _3F_2 $-series through Whipple's quadratic transformations.
AIMS Mathematics,
Vol. 9,
Issue. 8,
p.
21799.
Chen, Marta Na
and
Chu, Wenchang
2024.
Bisection Series Approach for Exotic 3F2(1)-Series.
Mathematics,
Vol. 12,
Issue. 12,
p.
1915.