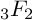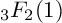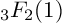1 Introduction and motivation
For an indeterminate x and an integer
![]() $n\in \mathbb {Z}$
, the shifted factorial (also called Pochhammer symbol) is defined as
$n\in \mathbb {Z}$
, the shifted factorial (also called Pochhammer symbol) is defined as
![]() $(x)_0\equiv 1$
and
$(x)_0\equiv 1$
and
 $$\begin{align*}(x)_n=\begin{cases} x(x+1)\cdots(x+n-1),&n>0,\\[2mm] \dfrac{1}{(x-1)(x-2)\cdots(x+n)},&n<0, \end{cases}\end{align*}$$
$$\begin{align*}(x)_n=\begin{cases} x(x+1)\cdots(x+n-1),&n>0,\\[2mm] \dfrac{1}{(x-1)(x-2)\cdots(x+n)},&n<0, \end{cases}\end{align*}$$
whose multiparameter form is abbreviated compactly to

The shifted factorial can also be expressed as a
![]() $\Gamma $
-function quotient
$\Gamma $
-function quotient
 $$\begin{align*}(x)_n=\frac{\Gamma(x+n)}{\Gamma(x)}, \quad\text{where}\quad \Gamma(x)=\int_{0}^{\infty} \tau^{x-1}e^{-\tau}d\tau.\end{align*}$$
$$\begin{align*}(x)_n=\frac{\Gamma(x+n)}{\Gamma(x)}, \quad\text{where}\quad \Gamma(x)=\int_{0}^{\infty} \tau^{x-1}e^{-\tau}d\tau.\end{align*}$$
There are several useful properties of the
![]() $\Gamma $
-function (see [Reference Rainville15, §17]). One of them is the reflection formula
$\Gamma $
-function (see [Reference Rainville15, §17]). One of them is the reflection formula
Following [Reference Bailey3], the classical hypergeometric series reads as

This series is always convergent for
![]() $|z|<1$
. However, for
$|z|<1$
. However, for
![]() $z=1$
, the series converges only when the real part of the sum of the numerator parameters is less than that of the denominator parameters.
$z=1$
, the series converges only when the real part of the sum of the numerator parameters is less than that of the denominator parameters.
There exist numerous summation identities of hypergeometric series in the literature (see, e.g., [Reference Chu7], [Reference Chu8], [Reference Chu10]–[Reference Gessel13]). Recently, Asakura et al. [Reference Asakura, Otsubo and Terasoma1] examined the following exotic
![]() $_3F_2$
-series:
$_3F_2$
-series:

Assuming further that
and
where
![]() $\{x\}$
denotes the fractional part of
$\{x\}$
denotes the fractional part of
![]() $x\in \mathbb {R}$
, they showed that
$x\in \mathbb {R}$
, they showed that
Here,
![]() $\bar {\mathbb {Q}}+\bar {\mathbb {Q}}\log \bar {\mathbb {Q}}^\times $
denotes the
$\bar {\mathbb {Q}}+\bar {\mathbb {Q}}\log \bar {\mathbb {Q}}^\times $
denotes the
![]() $\bar {\mathbb {Q}}$
-linear subspace spanned by
$\bar {\mathbb {Q}}$
-linear subspace spanned by
![]() $1,2\pi \mathbf {i}$
and
$1,2\pi \mathbf {i}$
and
![]() $\log \alpha $
for all
$\log \alpha $
for all
![]() $\alpha \in \bar {\mathbb {Q}}^\times $
. This result characterizes the
$\alpha \in \bar {\mathbb {Q}}^\times $
. This result characterizes the
![]() $\mathcal {F}(a,b,x)$
values in quality, but not in quantity, that is, it does not contribute to find explicit formulae for the
$\mathcal {F}(a,b,x)$
values in quality, but not in quantity, that is, it does not contribute to find explicit formulae for the
![]() $\mathcal {F}(a,b,x)$
values.
$\mathcal {F}(a,b,x)$
values.
Some of the
![]() $\mathcal {F}(a,b,x)$
values were subsequently determined by Asakura and Yabu [Reference Asakura and Yabu2], who listed without proofs the
$\mathcal {F}(a,b,x)$
values were subsequently determined by Asakura and Yabu [Reference Asakura and Yabu2], who listed without proofs the
![]() $\mathcal {F}(\frac 16,\frac 56,x)$
-values for all the irreducible proper rational numbers x with denominators in
$\mathcal {F}(\frac 16,\frac 56,x)$
-values for all the irreducible proper rational numbers x with denominators in
![]() $\{2,3,4,6\}$
. In particular, they provide a lengthy proof of five pages and half to the following elegant formula:
$\{2,3,4,6\}$
. In particular, they provide a lengthy proof of five pages and half to the following elegant formula:

Chen [Reference Chen5] examined further the series
![]() $\mathcal {F}(\frac 16,\frac 56,x+n)$
with
$\mathcal {F}(\frac 16,\frac 56,x+n)$
with
![]() $n\in \mathbb {Z}$
and succeeded in expressing this series explicitly as a linear combination of
$n\in \mathbb {Z}$
and succeeded in expressing this series explicitly as a linear combination of
![]() $\pi ^{-1}$
and
$\pi ^{-1}$
and
![]() $\mathcal {F}(\frac 16,\frac 56,x)$
with rational coefficients.
$\mathcal {F}(\frac 16,\frac 56,x)$
with rational coefficients.
The objective of this paper is twofold. First, we derive an integral representation for the
![]() $\mathcal {F}(\alpha ,1-\alpha ,\frac 12)$
-series, which enables us to provide relatively easy proofs for the closed formulae of
$\mathcal {F}(\alpha ,1-\alpha ,\frac 12)$
-series, which enables us to provide relatively easy proofs for the closed formulae of
![]() $\mathcal {F}(\alpha ,1-\alpha ,\frac 12)$
when
$\mathcal {F}(\alpha ,1-\alpha ,\frac 12)$
when
![]() $\alpha $
is one of the irreducible proper rational numbers with denominators belonging to
$\alpha $
is one of the irreducible proper rational numbers with denominators belonging to
![]() $\{2,3,4,5,6,8,10,12\}$
.
$\{2,3,4,5,6,8,10,12\}$
.
Second, we extend Chen’s series by considering the following
![]() $_3F_2$
-series:
$_3F_2$
-series:

By means of the linearization method (cf. [Reference Chen and Chu6], [Reference Chu9], [Reference Li and Chu14]), we show that this series is always evaluable as a linear function of
![]() $\mathcal {F}(\alpha ,1-\alpha ,x)$
with the coefficients being two sums of finite terms. In particular, when
$\mathcal {F}(\alpha ,1-\alpha ,x)$
with the coefficients being two sums of finite terms. In particular, when
![]() $x=\frac 12$
, several explicit formulae for the above
$x=\frac 12$
, several explicit formulae for the above
![]() $_3F_2$
-series are presented as consequences.
$_3F_2$
-series are presented as consequences.
2 Integral representation of
 $\mathcal {F}(\alpha ,1-\alpha ,\frac 12)$
$\mathcal {F}(\alpha ,1-\alpha ,\frac 12)$
Recalling the Beta function (see [Reference Rainville15, §16])
 $$\begin{align*}B(a,b)=\int_0^1x^{a-1}(1-x)^{b-1}dx =\frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}, \quad\text{where}\quad a,b>0,\end{align*}$$
$$\begin{align*}B(a,b)=\int_0^1x^{a-1}(1-x)^{b-1}dx =\frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}, \quad\text{where}\quad a,b>0,\end{align*}$$
we have the equalities
 $$ \begin{align*}B(\alpha+k,1-\alpha+k) &=\frac{(\alpha)_k(1-\alpha)_k}{(2k)!}B(\alpha,1-\alpha)\\ &=\frac{\pi}{\sin(\pi\alpha)}\times\frac{(\alpha)_k(1-\alpha)_k}{(2k)!}.\end{align*} $$
$$ \begin{align*}B(\alpha+k,1-\alpha+k) &=\frac{(\alpha)_k(1-\alpha)_k}{(2k)!}B(\alpha,1-\alpha)\\ &=\frac{\pi}{\sin(\pi\alpha)}\times\frac{(\alpha)_k(1-\alpha)_k}{(2k)!}.\end{align*} $$
Then we can rewrite the
![]() $\mathcal {F}(\alpha ,1-\alpha ,\frac 12)$
-series as
$\mathcal {F}(\alpha ,1-\alpha ,\frac 12)$
-series as
 $$ \begin{align*}\mathcal{F}(\alpha,1-\alpha,\tfrac12) &=\sum_{k=0}^{\infty}\frac{(\alpha)_k(1-\alpha)_k}{(2k+1)~(k!)^2}\\ &=\frac{\sin(\pi\alpha)}{\pi} \sum_{k=0}^{\infty}\binom{2k}{k} \frac{B(\alpha+k,1-\alpha+k)}{2k+1}\\ &=\frac{\sin(\pi\alpha)}{\pi} \sum_{k=0}^{\infty}\binom{2k}{k} \int_0^1\frac{x^{k-1+\alpha}(1-x)^{k-\alpha}}{2k+1}dx\\ &=\frac{\sin(\pi\alpha)}{\pi} \int_0^1x^{\alpha-1}(1-x)^{-\alpha} \sum_{k=0}^{\infty}\binom{2k}{k} \frac{x^{k}(1-x)^{k}}{2k+1}dx,\end{align*} $$
$$ \begin{align*}\mathcal{F}(\alpha,1-\alpha,\tfrac12) &=\sum_{k=0}^{\infty}\frac{(\alpha)_k(1-\alpha)_k}{(2k+1)~(k!)^2}\\ &=\frac{\sin(\pi\alpha)}{\pi} \sum_{k=0}^{\infty}\binom{2k}{k} \frac{B(\alpha+k,1-\alpha+k)}{2k+1}\\ &=\frac{\sin(\pi\alpha)}{\pi} \sum_{k=0}^{\infty}\binom{2k}{k} \int_0^1\frac{x^{k-1+\alpha}(1-x)^{k-\alpha}}{2k+1}dx\\ &=\frac{\sin(\pi\alpha)}{\pi} \int_0^1x^{\alpha-1}(1-x)^{-\alpha} \sum_{k=0}^{\infty}\binom{2k}{k} \frac{x^{k}(1-x)^{k}}{2k+1}dx,\end{align*} $$
where the interchanging between summation and integral is justified by Lebesgue’s monotone convergence theorem.
Taking into account the Maclaurin series
 $$\begin{align*}\arcsin{y}=\sum_{k=0}^{\infty} \binom{2k}{k}\frac{y^{2k+1}}{4^k(2k+1)},\end{align*}$$
$$\begin{align*}\arcsin{y}=\sum_{k=0}^{\infty} \binom{2k}{k}\frac{y^{2k+1}}{4^k(2k+1)},\end{align*}$$
we can evaluate, in closed forms,
 $$\begin{align*}\sum_{k=0}^{\infty}\binom{2k}{k} \frac{x^{k}(1-x)^{k}}{2k+1} =\frac{\arcsin\big(2\sqrt{x(1-x)}\big)}{2\sqrt{x(1-x)}}.\end{align*}$$
$$\begin{align*}\sum_{k=0}^{\infty}\binom{2k}{k} \frac{x^{k}(1-x)^{k}}{2k+1} =\frac{\arcsin\big(2\sqrt{x(1-x)}\big)}{2\sqrt{x(1-x)}}.\end{align*}$$
By substitution, we get the following integral expression
 $$ \begin{align} \mathcal{F}(\alpha,1-\alpha,\tfrac12) =\frac{\sin(\pi\alpha)}{2\pi} \int_0^1\frac{\arcsin\big(2\sqrt{x(1-x)}\big)} {x^{\frac32-\alpha}(1-x)^{\frac12+\alpha}}dx.\end{align} $$
$$ \begin{align} \mathcal{F}(\alpha,1-\alpha,\tfrac12) =\frac{\sin(\pi\alpha)}{2\pi} \int_0^1\frac{\arcsin\big(2\sqrt{x(1-x)}\big)} {x^{\frac32-\alpha}(1-x)^{\frac12+\alpha}}dx.\end{align} $$
According to
![]() $[0,1]=[0,\frac 12]\cup [\frac 12,1]$
, splitting the above integral into two and then making changes of variables
$[0,1]=[0,\frac 12]\cup [\frac 12,1]$
, splitting the above integral into two and then making changes of variables
![]() $x=\sin ^2\theta $
and
$x=\sin ^2\theta $
and
![]() $x=\cos ^2\theta $
, respectively, we can state the resulting expression as
$x=\cos ^2\theta $
, respectively, we can state the resulting expression as
 $$ \begin{align*}\mathcal{F}(\alpha,1-\alpha,\tfrac12) &=\frac{2\sin(\pi\alpha)}{\pi}\Big\{I(\alpha)+I(1-\alpha)\Big\},\\ \text{where }\quad I(\alpha)&=\int_0^{\frac{\pi}4}\frac{\theta} {\sin^{2\alpha}\theta\cos^{2-2\alpha}\theta}d\theta.\end{align*} $$
$$ \begin{align*}\mathcal{F}(\alpha,1-\alpha,\tfrac12) &=\frac{2\sin(\pi\alpha)}{\pi}\Big\{I(\alpha)+I(1-\alpha)\Big\},\\ \text{where }\quad I(\alpha)&=\int_0^{\frac{\pi}4}\frac{\theta} {\sin^{2\alpha}\theta\cos^{2-2\alpha}\theta}d\theta.\end{align*} $$
Making further change of variables
![]() $\theta =\arctan y$
, we deduce the next expression:
$\theta =\arctan y$
, we deduce the next expression:
 $$\begin{align*}I(\alpha)=\int_0^1\frac{\arctan y}{y^{2\alpha}}dy.\end{align*}$$
$$\begin{align*}I(\alpha)=\int_0^1\frac{\arctan y}{y^{2\alpha}}dy.\end{align*}$$
When
![]() $\alpha =\frac 12$
, we come across the Catalan constant G (cf. [16]):
$\alpha =\frac 12$
, we come across the Catalan constant G (cf. [16]):
 $$\begin{align*}I(\tfrac12)=\int_0^1\frac{\arctan y}{y}dy =\sum_{n=0}^{\infty}\frac{(-1)^n}{2n+1}\int_0^1y^{2n}dy =\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)^2}=G.\end{align*}$$
$$\begin{align*}I(\tfrac12)=\int_0^1\frac{\arctan y}{y}dy =\sum_{n=0}^{\infty}\frac{(-1)^n}{2n+1}\int_0^1y^{2n}dy =\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)^2}=G.\end{align*}$$
From this, we recover the following remarkable evaluation formula due to Ramanujan (cf. [Reference Berndt4, (29.3)]):
By means of the integration by parts, we can further reformulate
 $$ \begin{align*}I(\alpha)+I(1-\alpha) &=\int_0^1\bigg\{\frac{\arctan y}{y^{2\alpha}}+\frac{\arctan y}{y^{2-2\alpha}}\bigg\}dy\\[5pt] &=\arctan y\times\bigg\{\frac{y^{1-2\alpha}}{1-2\alpha}-\frac{y^{2\alpha-1}}{1-2\alpha}\bigg\}_0^1\\[5pt] & \quad +\frac1{1-2\alpha}\int_0^1\frac{y^{2\alpha-1}-y^{1-2\alpha}}{1+y^2}dy.\end{align*} $$
$$ \begin{align*}I(\alpha)+I(1-\alpha) &=\int_0^1\bigg\{\frac{\arctan y}{y^{2\alpha}}+\frac{\arctan y}{y^{2-2\alpha}}\bigg\}dy\\[5pt] &=\arctan y\times\bigg\{\frac{y^{1-2\alpha}}{1-2\alpha}-\frac{y^{2\alpha-1}}{1-2\alpha}\bigg\}_0^1\\[5pt] & \quad +\frac1{1-2\alpha}\int_0^1\frac{y^{2\alpha-1}-y^{1-2\alpha}}{1+y^2}dy.\end{align*} $$
Keeping in mind that
![]() $0<\alpha <1$
with
$0<\alpha <1$
with
![]() $\alpha \ne \frac 12$
, we can check that the expression in the middle line vanishes. By making the substitution
$\alpha \ne \frac 12$
, we can check that the expression in the middle line vanishes. By making the substitution
![]() $y\to \sqrt {y}$
in the last integral, we get a slightly reduced one
$y\to \sqrt {y}$
in the last integral, we get a slightly reduced one
 $$\begin{align*}I(\alpha)+I(1-\alpha) =\frac1{2-4\alpha}\int_0^1\frac{y^{\alpha-1}-y^{-\alpha}}{1+y}dy.\end{align*}$$
$$\begin{align*}I(\alpha)+I(1-\alpha) =\frac1{2-4\alpha}\int_0^1\frac{y^{\alpha-1}-y^{-\alpha}}{1+y}dy.\end{align*}$$
Therefore, we finally arrive at an integral expression as in the theorem below.
Theorem 1. Let
![]() $\alpha $
be a real number with
$\alpha $
be a real number with
![]() $0<\alpha <1$
and
$0<\alpha <1$
and
![]() $\alpha \ne \frac 12$
. The following formula holds:
$\alpha \ne \frac 12$
. The following formula holds:
 $$\begin{align*}\mathcal{F}(\alpha,1-\alpha,\tfrac12) =\frac{\sin(\pi\alpha)}{\pi(1-2\alpha)} \int_0^1\frac{y^{\alpha-1}-y^{-\alpha}}{1+y}dy.\end{align*}$$
$$\begin{align*}\mathcal{F}(\alpha,1-\alpha,\tfrac12) =\frac{\sin(\pi\alpha)}{\pi(1-2\alpha)} \int_0^1\frac{y^{\alpha-1}-y^{-\alpha}}{1+y}dy.\end{align*}$$
When
![]() $\alpha $
is a rational number, the above integral can be transformed into that about rational functions. By assigning
$\alpha $
is a rational number, the above integral can be transformed into that about rational functions. By assigning
![]() $\alpha $
to small rational numbers, we can compute, by means of this theorem, the exact values of the corresponding
$\alpha $
to small rational numbers, we can compute, by means of this theorem, the exact values of the corresponding
![]() $\mathcal {F}(\alpha ,1-\alpha ,\tfrac 12)$
-series. The first values are highlighted in the following proposition.
$\mathcal {F}(\alpha ,1-\alpha ,\tfrac 12)$
-series. The first values are highlighted in the following proposition.
Proposition 2. (Evaluation formulae for series
 $\mathcal {F}(\alpha ,1-\alpha ,\tfrac 12)$
)
$\mathcal {F}(\alpha ,1-\alpha ,\tfrac 12)$
)
 $$ \begin{align*}\mathrm{(a)}~\mathcal{F}(\tfrac12,\tfrac12,\tfrac12) &=\frac4{\pi}G,\\[3pt] \mathrm{(b)}~\mathcal{F}(\tfrac13,\tfrac23,\tfrac12) &=\frac{3\sqrt3}{\pi}\ln2,\\[3pt] \mathrm{(c)}~\mathcal{F}(\tfrac14,\tfrac34,\tfrac12) &=\frac{4}{\pi}\ln(1+\sqrt2),\\[3pt] \mathrm{(d)}~\mathcal{F}(\tfrac16,\tfrac56,\tfrac12) &=\frac{3\sqrt3}{2\pi}\ln(2+\sqrt3).\end{align*} $$
$$ \begin{align*}\mathrm{(a)}~\mathcal{F}(\tfrac12,\tfrac12,\tfrac12) &=\frac4{\pi}G,\\[3pt] \mathrm{(b)}~\mathcal{F}(\tfrac13,\tfrac23,\tfrac12) &=\frac{3\sqrt3}{\pi}\ln2,\\[3pt] \mathrm{(c)}~\mathcal{F}(\tfrac14,\tfrac34,\tfrac12) &=\frac{4}{\pi}\ln(1+\sqrt2),\\[3pt] \mathrm{(d)}~\mathcal{F}(\tfrac16,\tfrac56,\tfrac12) &=\frac{3\sqrt3}{2\pi}\ln(2+\sqrt3).\end{align*} $$
Among these four values, the first one (a) is already determined.
Proof of (b)
By making the substitution
![]() $y\to x^3$
, we can rewrite
$y\to x^3$
, we can rewrite
 $$\begin{align*}\mathcal{F}(\tfrac13,\tfrac23,\tfrac12) =\frac{3\sin\frac{\pi}3}{\pi} \int_{0}^{1}\frac{y^{-\frac{2}{3}}-y^{-\frac{1}{3}}}{1+y}dy =\frac{9\sqrt3}{2\pi}\int_{0}^{1}\frac{1-x}{1+x^3}dx.\end{align*}$$
$$\begin{align*}\mathcal{F}(\tfrac13,\tfrac23,\tfrac12) =\frac{3\sin\frac{\pi}3}{\pi} \int_{0}^{1}\frac{y^{-\frac{2}{3}}-y^{-\frac{1}{3}}}{1+y}dy =\frac{9\sqrt3}{2\pi}\int_{0}^{1}\frac{1-x}{1+x^3}dx.\end{align*}$$
According to the partial fraction decomposition
 $$\begin{align*}\frac{1-x}{1+x^3} =\frac{2}{3(1+x)}+\frac{1-2x}{3(1-x+x^2)},\end{align*}$$
$$\begin{align*}\frac{1-x}{1+x^3} =\frac{2}{3(1+x)}+\frac{1-2x}{3(1-x+x^2)},\end{align*}$$
the integral can be evaluated as follows:
 $$ \begin{align*}\mathcal{F}(\tfrac13,\tfrac23,\tfrac12) &=\frac{3\sqrt3}{2\pi}\int_{0}^{1} \bigg\{\frac{2}{1+x}+\frac{1-2x}{1-x+x^2}\bigg\}dx\\[4pt] &=\frac{3\sqrt3}{2\pi}\Big(2\ln2+0\Big) =\frac{3\sqrt3}{\pi}\ln2.\end{align*} $$
$$ \begin{align*}\mathcal{F}(\tfrac13,\tfrac23,\tfrac12) &=\frac{3\sqrt3}{2\pi}\int_{0}^{1} \bigg\{\frac{2}{1+x}+\frac{1-2x}{1-x+x^2}\bigg\}dx\\[4pt] &=\frac{3\sqrt3}{2\pi}\Big(2\ln2+0\Big) =\frac{3\sqrt3}{\pi}\ln2.\end{align*} $$
This confirms the value given in (b).
Proof of (c)
By making the substitution
![]() $y\to x^4$
, we can rewrite
$y\to x^4$
, we can rewrite
 $$\begin{align*}\mathcal{F}(\tfrac14,\tfrac34,\tfrac12) =\frac{2\sin\frac\pi4}{\pi} \int_{0}^{1}\frac{y^{-\frac34}-y^{-\frac14}}{1+y}dy =\frac{4\sqrt2}{\pi}\int_{0}^{1}\frac{1-x^2}{1+x^4}dx.\end{align*}$$
$$\begin{align*}\mathcal{F}(\tfrac14,\tfrac34,\tfrac12) =\frac{2\sin\frac\pi4}{\pi} \int_{0}^{1}\frac{y^{-\frac34}-y^{-\frac14}}{1+y}dy =\frac{4\sqrt2}{\pi}\int_{0}^{1}\frac{1-x^2}{1+x^4}dx.\end{align*}$$
According to the partial fraction decomposition
 $$\begin{align*}\frac{1-x^2}{1+x^4}=\frac{1}{2\sqrt2} \bigg\{\frac{2x+\sqrt2}{x^2+\sqrt{2}x+1} -\frac{2x-\sqrt2}{x^2-\sqrt{2}x+1}\bigg\},\end{align*}$$
$$\begin{align*}\frac{1-x^2}{1+x^4}=\frac{1}{2\sqrt2} \bigg\{\frac{2x+\sqrt2}{x^2+\sqrt{2}x+1} -\frac{2x-\sqrt2}{x^2-\sqrt{2}x+1}\bigg\},\end{align*}$$
the integral can be evaluated as follows:
 $$ \begin{align*}\mathcal{F}(\tfrac14,\tfrac34,\tfrac12) &=\frac{2}{\pi}\int_{0}^{1} \bigg\{\frac{2x+\sqrt2}{x^2+\sqrt{2}x+1} -\frac{2x-\sqrt2}{x^2-\sqrt{2}x+1}\bigg\}dx\\[4pt] &=\frac{2}{\pi}\Big\{\ln(2+\sqrt2)-\ln(2-\sqrt2)\Big\} =\frac{4}{\pi}\ln(1+\sqrt2).\end{align*} $$
$$ \begin{align*}\mathcal{F}(\tfrac14,\tfrac34,\tfrac12) &=\frac{2}{\pi}\int_{0}^{1} \bigg\{\frac{2x+\sqrt2}{x^2+\sqrt{2}x+1} -\frac{2x-\sqrt2}{x^2-\sqrt{2}x+1}\bigg\}dx\\[4pt] &=\frac{2}{\pi}\Big\{\ln(2+\sqrt2)-\ln(2-\sqrt2)\Big\} =\frac{4}{\pi}\ln(1+\sqrt2).\end{align*} $$
This confirms the value given in (c).
Proof of (d)
By making the substitution
![]() $y\to x^6$
, we can rewrite
$y\to x^6$
, we can rewrite
 $$\begin{align*}\mathcal{F}(\tfrac16,\tfrac56,\tfrac12) =\frac{3\sin\frac{\pi}{6}}{2\pi} \int_{0}^{1}\frac{y^{-\frac56}-y^{-\frac16}}{1+y}dy =\frac{9}{2\pi}\int_{0}^{1}\frac{1-x^4}{1+x^6}dx.\end{align*}$$
$$\begin{align*}\mathcal{F}(\tfrac16,\tfrac56,\tfrac12) =\frac{3\sin\frac{\pi}{6}}{2\pi} \int_{0}^{1}\frac{y^{-\frac56}-y^{-\frac16}}{1+y}dy =\frac{9}{2\pi}\int_{0}^{1}\frac{1-x^4}{1+x^6}dx.\end{align*}$$
According to the partial fraction decomposition
 $$\begin{align*}\frac{1-x^4}{1+x^6}=\frac{\sqrt3}{6} \bigg\{\frac{2x+\sqrt3}{x^2+\sqrt{3}x+1} -\frac{2x-\sqrt3}{x^2-\sqrt{3}x+1}\bigg\},\end{align*}$$
$$\begin{align*}\frac{1-x^4}{1+x^6}=\frac{\sqrt3}{6} \bigg\{\frac{2x+\sqrt3}{x^2+\sqrt{3}x+1} -\frac{2x-\sqrt3}{x^2-\sqrt{3}x+1}\bigg\},\end{align*}$$
the integral can be evaluated as follows:
 $$ \begin{align*}\mathcal{F}(\tfrac16,\tfrac56,\tfrac12) &=\frac{3\sqrt3}{4\pi}\int_{0}^{1} \bigg\{\frac{2x+\sqrt3}{x^2+\sqrt{3}x+1} -\frac{2x-\sqrt3}{x^2-\sqrt{3}x+1}\bigg\}dx\\ &=\frac{3\sqrt3}{4\pi}\Big\{\ln(2+\sqrt3) -\ln(2-\sqrt3)\Big\}=\frac{3\sqrt3}{2\pi}\ln(2+\sqrt3).\end{align*} $$
$$ \begin{align*}\mathcal{F}(\tfrac16,\tfrac56,\tfrac12) &=\frac{3\sqrt3}{4\pi}\int_{0}^{1} \bigg\{\frac{2x+\sqrt3}{x^2+\sqrt{3}x+1} -\frac{2x-\sqrt3}{x^2-\sqrt{3}x+1}\bigg\}dx\\ &=\frac{3\sqrt3}{4\pi}\Big\{\ln(2+\sqrt3) -\ln(2-\sqrt3)\Big\}=\frac{3\sqrt3}{2\pi}\ln(2+\sqrt3).\end{align*} $$
This confirms the value given in (d).
By carrying out the same procedure, we can further evaluate, in closed forms, the following series by expressing their values in terms of radicals:
 $$ \begin{align*}\mathcal{F}(\tfrac15,\tfrac45,\tfrac12) &=\frac{5\sqrt{5-\sqrt5}}{6\pi\sqrt2} \bigg\{\sqrt5\ln\frac{\sqrt{5}+1}{\sqrt{5}-1}+2\ln2\bigg\},\\[2pt] \mathcal{F}(\tfrac25,\tfrac35,\tfrac12) &=\frac{5\sqrt{5+\sqrt5}}{2\pi\sqrt2} \bigg\{\sqrt5\ln\frac{\sqrt{5}+1}{\sqrt{5}-1}-2\ln2\bigg\};\\[2pt] \mathcal{F}(\tfrac18,\tfrac78,\tfrac12) &=\frac{2\sqrt2}{3\pi}\ln\frac{2+\sqrt{2+\sqrt2}}{2-\sqrt{2+\sqrt2}} +\frac{2(2-\sqrt2)}{3\pi}\ln\frac{2+\sqrt{2-\sqrt2}}{2-\sqrt{2-\sqrt2}},\\ [2pt] \mathcal{F}(\tfrac38,\tfrac58,\tfrac12) &=\frac{2\sqrt2}{\pi}\ln\frac{2+\sqrt{2+\sqrt2}}{2-\sqrt{2+\sqrt2}} -\frac{2(2+\sqrt2)}{\pi}\ln\frac{2+\sqrt{2-\sqrt2}}{2-\sqrt{2-\sqrt2}};\\[2pt] \mathcal{F}(\tfrac{1}{10},\tfrac{9}{10},\tfrac12) &=\frac{5\sqrt{10-2\sqrt5}}{16\pi} \ln\frac{2\sqrt{5-\sqrt5}+\sqrt{10}}{2\sqrt{5-\sqrt5}-\sqrt{10}}\\[2pt] & \quad +\frac{5\sqrt{5-2\sqrt5}}{8\pi} \ln\frac{2\sqrt{5+\sqrt5}+\sqrt{10}}{2\sqrt{5+\sqrt5}-\sqrt{10}},\\[2pt] \mathcal{F}(\tfrac{3}{10},\tfrac{7}{10},\tfrac12) &=\frac{5\sqrt{10+2\sqrt5}}{8\pi} \ln\frac{2\sqrt{5-\sqrt5}+\sqrt{10}}{2\sqrt{5-\sqrt5}-\sqrt{10}}\\[2pt] & \quad -\frac{5\sqrt{5+2\sqrt5}}{4\pi} \ln\frac{2\sqrt{5+\sqrt5}+\sqrt{10}}{2\sqrt{5+\sqrt5}-\sqrt{10}};\\[2pt] \mathcal{F}(\tfrac{1}{12},\tfrac{11}{12},\tfrac12) &=\frac{24\ln(1+\sqrt2)}{5\pi(1+\sqrt3)} +\frac{3\sqrt3}{5\pi(1+\sqrt3)} \ln\frac{5+2\sqrt6}{5-2\sqrt6},\\[2pt] \mathcal{F}(\tfrac{5}{12},\tfrac{7}{12},\tfrac12) &=\frac{24\ln(1+\sqrt2)}{\pi(1-\sqrt3)} -\frac{3\sqrt3}{\pi(1-\sqrt3)} \ln\frac{5+2\sqrt6}{5-2\sqrt6}.\end{align*} $$
$$ \begin{align*}\mathcal{F}(\tfrac15,\tfrac45,\tfrac12) &=\frac{5\sqrt{5-\sqrt5}}{6\pi\sqrt2} \bigg\{\sqrt5\ln\frac{\sqrt{5}+1}{\sqrt{5}-1}+2\ln2\bigg\},\\[2pt] \mathcal{F}(\tfrac25,\tfrac35,\tfrac12) &=\frac{5\sqrt{5+\sqrt5}}{2\pi\sqrt2} \bigg\{\sqrt5\ln\frac{\sqrt{5}+1}{\sqrt{5}-1}-2\ln2\bigg\};\\[2pt] \mathcal{F}(\tfrac18,\tfrac78,\tfrac12) &=\frac{2\sqrt2}{3\pi}\ln\frac{2+\sqrt{2+\sqrt2}}{2-\sqrt{2+\sqrt2}} +\frac{2(2-\sqrt2)}{3\pi}\ln\frac{2+\sqrt{2-\sqrt2}}{2-\sqrt{2-\sqrt2}},\\ [2pt] \mathcal{F}(\tfrac38,\tfrac58,\tfrac12) &=\frac{2\sqrt2}{\pi}\ln\frac{2+\sqrt{2+\sqrt2}}{2-\sqrt{2+\sqrt2}} -\frac{2(2+\sqrt2)}{\pi}\ln\frac{2+\sqrt{2-\sqrt2}}{2-\sqrt{2-\sqrt2}};\\[2pt] \mathcal{F}(\tfrac{1}{10},\tfrac{9}{10},\tfrac12) &=\frac{5\sqrt{10-2\sqrt5}}{16\pi} \ln\frac{2\sqrt{5-\sqrt5}+\sqrt{10}}{2\sqrt{5-\sqrt5}-\sqrt{10}}\\[2pt] & \quad +\frac{5\sqrt{5-2\sqrt5}}{8\pi} \ln\frac{2\sqrt{5+\sqrt5}+\sqrt{10}}{2\sqrt{5+\sqrt5}-\sqrt{10}},\\[2pt] \mathcal{F}(\tfrac{3}{10},\tfrac{7}{10},\tfrac12) &=\frac{5\sqrt{10+2\sqrt5}}{8\pi} \ln\frac{2\sqrt{5-\sqrt5}+\sqrt{10}}{2\sqrt{5-\sqrt5}-\sqrt{10}}\\[2pt] & \quad -\frac{5\sqrt{5+2\sqrt5}}{4\pi} \ln\frac{2\sqrt{5+\sqrt5}+\sqrt{10}}{2\sqrt{5+\sqrt5}-\sqrt{10}};\\[2pt] \mathcal{F}(\tfrac{1}{12},\tfrac{11}{12},\tfrac12) &=\frac{24\ln(1+\sqrt2)}{5\pi(1+\sqrt3)} +\frac{3\sqrt3}{5\pi(1+\sqrt3)} \ln\frac{5+2\sqrt6}{5-2\sqrt6},\\[2pt] \mathcal{F}(\tfrac{5}{12},\tfrac{7}{12},\tfrac12) &=\frac{24\ln(1+\sqrt2)}{\pi(1-\sqrt3)} -\frac{3\sqrt3}{\pi(1-\sqrt3)} \ln\frac{5+2\sqrt6}{5-2\sqrt6}.\end{align*} $$
3 Extension by integer parameters m and n
In this section, we examine the series

By means of the linearization method (cf. [Reference Chen and Chu6], [Reference Chu9], [Reference Li and Chu14]), a surprising formula (see Theorem 5) is shown, which expresses the above series on the left as a linear function of
![]() $\mathcal {F}(\alpha ,1-\alpha ,x)$
with the coefficients being two finite sums.
$\mathcal {F}(\alpha ,1-\alpha ,x)$
with the coefficients being two finite sums.
We begin with the following recurrence relation.
Lemma 3. (Recurrence relation)
 $$\begin{align*}\mathcal{F}(\alpha,1-\alpha,x) =\frac{(x+\alpha)(1+x-\alpha)}{x(1+x)} \mathcal{F}(\alpha,1-\alpha,x+1) -\frac{\sin{(\pi\alpha)}}{\pi x}.\end{align*}$$
$$\begin{align*}\mathcal{F}(\alpha,1-\alpha,x) =\frac{(x+\alpha)(1+x-\alpha)}{x(1+x)} \mathcal{F}(\alpha,1-\alpha,x+1) -\frac{\sin{(\pi\alpha)}}{\pi x}.\end{align*}$$
Proof. As done by Chen [Reference Chen5], by putting the initial term aside, we can write
 $$ \begin{align*}\mathcal{F}(\alpha,1-\alpha,x) &=1+\sum_{k=1}^{\infty} \frac{(\alpha)_{k}(1-\alpha)_{k}(x)_{k}} {(k!)^2(1+x)_{k}} \qquad\boxed{k\to k+1}\\ &=1+\sum_{k=0}^{\infty} \frac{(\alpha)_{k}(1-\alpha)_{k}}{(k!)^2} \bigg\{\frac{(\alpha+k)(1-\alpha+k)x}{(k+1)^2(1+x+k)}\bigg\}.\end{align*} $$
$$ \begin{align*}\mathcal{F}(\alpha,1-\alpha,x) &=1+\sum_{k=1}^{\infty} \frac{(\alpha)_{k}(1-\alpha)_{k}(x)_{k}} {(k!)^2(1+x)_{k}} \qquad\boxed{k\to k+1}\\ &=1+\sum_{k=0}^{\infty} \frac{(\alpha)_{k}(1-\alpha)_{k}}{(k!)^2} \bigg\{\frac{(\alpha+k)(1-\alpha+k)x}{(k+1)^2(1+x+k)}\bigg\}.\end{align*} $$
According to the partial fractions
 $$\begin{align*}\frac{(\alpha+k)(1-\alpha+k)x}{(k+1)^2(1+x+k)} =\frac{\alpha-\alpha^2+x+x^2}{(1+x+k)x} +\frac{\alpha-\alpha^2}{(k+1)^2} -\frac{\alpha-\alpha^2+x}{(k+1)x},\end{align*}$$
$$\begin{align*}\frac{(\alpha+k)(1-\alpha+k)x}{(k+1)^2(1+x+k)} =\frac{\alpha-\alpha^2+x+x^2}{(1+x+k)x} +\frac{\alpha-\alpha^2}{(k+1)^2} -\frac{\alpha-\alpha^2+x}{(k+1)x},\end{align*}$$
we can evaluate, by making use of the Gauss summation theorem [Reference Bailey3, §1.3]

the three corresponding sums

Putting them together and making some simplifications, we find that

This proves the recurrence relation in Lemma 3.
Iterating n times the equation in Lemma 3 gives rise to the following general one:

Proposition 4. (
 $n\in \mathbb {N}_0$
)
$n\in \mathbb {N}_0$
)

It should be pointed out that when
![]() $\alpha =\frac 16$
, the corresponding transformation formulae in Proposition 4 were previously obtained by Chen [Reference Chen5].
$\alpha =\frac 16$
, the corresponding transformation formulae in Proposition 4 were previously obtained by Chen [Reference Chen5].
Proof. The first formula (a) is obtained by inverting (3).
To prove the second one (b), making the replacement
![]() $x\to x-n$
in (3), we have the following two equalities:
$x\to x-n$
in (3), we have the following two equalities:

Then the resulting identity under the replacement
![]() $k\to n-k$
becomes (b). This completes the proof of Proposition 4.
$k\to n-k$
becomes (b). This completes the proof of Proposition 4.
Observing further that

we can unify, for
![]() $m\in \mathbb {Z}$
, the two formulae in Proposition 4 to a single one
$m\in \mathbb {Z}$
, the two formulae in Proposition 4 to a single one

where sgn(k) and
![]() $\sigma (m)$
are given, respectively, by
$\sigma (m)$
are given, respectively, by
 $$\begin{align*}\text{sgn}(k)=\begin{cases} 1,&k>0,\\ 0,&k=0,\\ -1,&k<0, \end{cases} \quad\text{and}\quad \sigma(m)=[0,m)\cup[m,0) =\begin{cases} [0,m),&m>0,\\ [m,0),&m<0. \end{cases}\end{align*}$$
$$\begin{align*}\text{sgn}(k)=\begin{cases} 1,&k>0,\\ 0,&k=0,\\ -1,&k<0, \end{cases} \quad\text{and}\quad \sigma(m)=[0,m)\cup[m,0) =\begin{cases} [0,m),&m>0,\\ [m,0),&m<0. \end{cases}\end{align*}$$
Now, we are ready to prove the following general theorem.
Theorem 5. (
 $m,n\in \mathbb {Z}$
with
$m,n\in \mathbb {Z}$
with
 $m\le n$
)
$m\le n$
)

The importance of the above theorem lies in the fact that for any pair
![]() $m,n\in \mathbb {Z}$
with
$m,n\in \mathbb {Z}$
with
![]() $m\le n$
, the
$m\le n$
, the
![]() $_3F_2$
-series on the left results always in a linear function of
$_3F_2$
-series on the left results always in a linear function of
![]() $\mathcal {F}(\alpha ,1-\alpha ,x)$
with the coefficients being two sums of finite terms. Therefore, for any specific integers
$\mathcal {F}(\alpha ,1-\alpha ,x)$
with the coefficients being two sums of finite terms. Therefore, for any specific integers
![]() $m,n$
and an irreducible rational number x considered in the last section, we can explicitly compute, by means of this theorem, the corresponding
$m,n$
and an irreducible rational number x considered in the last section, we can explicitly compute, by means of this theorem, the corresponding
![]() $_3F_2$
-series in closed forms.
$_3F_2$
-series in closed forms.
Proof. Recall the Chu–Vandermonde convolution formula
 $$\begin{align*}1=\sum_{k=m}^n\binom{-x-m-i}{k-m}\binom{x+n+i}{n-k}.\end{align*}$$
$$\begin{align*}1=\sum_{k=m}^n\binom{-x-m-i}{k-m}\binom{x+n+i}{n-k}.\end{align*}$$
By putting the above relation inside the
![]() $_3F_2$
-series and then applying the equations
$_3F_2$
-series and then applying the equations
 $$ \begin{align*}\binom{-x-m-i}{k-m} &=\binom{-x-m}{k-m}\frac{(x+k)_i}{(x+m)_i},\\[4pt] \binom{x+n+i}{n-k} &=\binom{x+n}{n-k}\frac{(1+x+n)_i}{(1+x+k)_i},\end{align*} $$
$$ \begin{align*}\binom{-x-m-i}{k-m} &=\binom{-x-m}{k-m}\frac{(x+k)_i}{(x+m)_i},\\[4pt] \binom{x+n+i}{n-k} &=\binom{x+n}{n-k}\frac{(1+x+n)_i}{(1+x+k)_i},\end{align*} $$
we can manipulate the double sum as follows:

The resulting equality can be stated as

Now, replacing the rightmost series
![]() $\mathcal {F}(\alpha ,1-\alpha ,x+k)$
by (4), we arrive at the formula displayed in Theorem 5.
$\mathcal {F}(\alpha ,1-\alpha ,x+k)$
by (4), we arrive at the formula displayed in Theorem 5.
By specifying
![]() $x=\frac 12$
and
$x=\frac 12$
and
![]() $\alpha \in \big \{\frac 12,\frac 13,\frac 14,\frac 16\big \}$
in Theorem 5, we exhibit below several concrete infinite series identities in conjunction with Proposition 2.
$\alpha \in \big \{\frac 12,\frac 13,\frac 14,\frac 16\big \}$
in Theorem 5, we exhibit below several concrete infinite series identities in conjunction with Proposition 2.
Corollary 6. Twenty formulae for
![]() $\boldsymbol {{}_3F_2}={_3F_2}\Big [\genfrac {}{}{0mm}{1}{\frac 12,\frac 12,\frac 12+m}{\quad 1,\frac 32+n~}\Big ]$
with
$\boldsymbol {{}_3F_2}={_3F_2}\Big [\genfrac {}{}{0mm}{1}{\frac 12,\frac 12,\frac 12+m}{\quad 1,\frac 32+n~}\Big ]$
with
![]() $\mathcal {A}=\frac {4G}{\pi }$
:
$\mathcal {A}=\frac {4G}{\pi }$
:
 $$ \begin{align*} \begin{array}{||c|c|c||c|c|c||}\hline\hline m&n&\boldsymbol{{}_3F_2}&m&n&\boldsymbol{{}_3F_2}\\ \hline\hline \rule[-2mm]{0mm}{6mm}0 & 0 & \mathcal{A} & -3 & -3 & \frac{178}{45 \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 1 & \frac{9 \mathcal{A}}{8}-\frac{3}{4 \pi } & -3 & -2 & \frac{12}{5 \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 2 & \frac{615 \mathcal{A}}{512}-\frac{285}{256 \pi } & -3 & -1 & \frac{16}{15 \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 3 & \frac{5,145 \mathcal{A}}{4,096}-\frac{24,955}{18,432 \pi } & -2 & -2 & \frac{10}{3 \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 1 & \frac{3 \mathcal{A}}{4}+\frac{3}{2 \pi } & -2 & -1 & \frac{4}{3 \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 2 & \frac{105 \mathcal{A}}{128}+\frac{45}{64 \pi } & -2 & 0 & \frac{3 \mathcal{A}}{8}+\frac{13}{12 \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 3 & \frac{1,785 \mathcal{A}}{2,048}+\frac{1,015}{3,072 \pi } & -2 & 1 & \frac{33 \mathcal{A}}{64}+\frac{79}{96 \pi } \\\hline \rule[-2mm]{0mm}{6mm}2 & 2 & \frac{45 \mathcal{A}}{64}+\frac{65}{32 \pi } & -1 & -1 & \frac{2}{\pi } \\\hline \rule[-2mm]{0mm}{6mm}2 & 3 & \frac{385 \mathcal{A}}{512}+\frac{2765}{2,304 \pi } & -1 & 0 & \frac{\mathcal{A}}{2}+\frac{1}{\pi } \\\hline \rule[-2mm]{0mm}{6mm}3 & 3 & \frac{175 \mathcal{A}}{256}+\frac{2,723}{1,152 \pi } & -1 & 1 & \frac{21 \mathcal{A}}{32}+\frac{9}{16 \pi } \\\hline\hline \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{||c|c|c||c|c|c||}\hline\hline m&n&\boldsymbol{{}_3F_2}&m&n&\boldsymbol{{}_3F_2}\\ \hline\hline \rule[-2mm]{0mm}{6mm}0 & 0 & \mathcal{A} & -3 & -3 & \frac{178}{45 \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 1 & \frac{9 \mathcal{A}}{8}-\frac{3}{4 \pi } & -3 & -2 & \frac{12}{5 \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 2 & \frac{615 \mathcal{A}}{512}-\frac{285}{256 \pi } & -3 & -1 & \frac{16}{15 \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 3 & \frac{5,145 \mathcal{A}}{4,096}-\frac{24,955}{18,432 \pi } & -2 & -2 & \frac{10}{3 \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 1 & \frac{3 \mathcal{A}}{4}+\frac{3}{2 \pi } & -2 & -1 & \frac{4}{3 \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 2 & \frac{105 \mathcal{A}}{128}+\frac{45}{64 \pi } & -2 & 0 & \frac{3 \mathcal{A}}{8}+\frac{13}{12 \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 3 & \frac{1,785 \mathcal{A}}{2,048}+\frac{1,015}{3,072 \pi } & -2 & 1 & \frac{33 \mathcal{A}}{64}+\frac{79}{96 \pi } \\\hline \rule[-2mm]{0mm}{6mm}2 & 2 & \frac{45 \mathcal{A}}{64}+\frac{65}{32 \pi } & -1 & -1 & \frac{2}{\pi } \\\hline \rule[-2mm]{0mm}{6mm}2 & 3 & \frac{385 \mathcal{A}}{512}+\frac{2765}{2,304 \pi } & -1 & 0 & \frac{\mathcal{A}}{2}+\frac{1}{\pi } \\\hline \rule[-2mm]{0mm}{6mm}3 & 3 & \frac{175 \mathcal{A}}{256}+\frac{2,723}{1,152 \pi } & -1 & 1 & \frac{21 \mathcal{A}}{32}+\frac{9}{16 \pi } \\\hline\hline \end{array} \end{align*} $$
Corollary 7. Twenty formulae for
![]() $\boldsymbol {{}_3F_2}={_3F_2}\Big [\genfrac {}{}{0mm}{1}{\frac 13,\frac 23,\frac 12+m}{\quad 1,\frac 32+n~}\Big ]$
with
$\boldsymbol {{}_3F_2}={_3F_2}\Big [\genfrac {}{}{0mm}{1}{\frac 13,\frac 23,\frac 12+m}{\quad 1,\frac 32+n~}\Big ]$
with
![]() $\mathcal {B}=\frac {3\sqrt 3}{\pi }\ln 2$
:
$\mathcal {B}=\frac {3\sqrt 3}{\pi }\ln 2$
:
 $$ \begin{align*} \begin{array}{||c|c|c||c|c|c||}\hline\hline m&n&\boldsymbol{{}_3F_2}&m&n&\boldsymbol{{}_3F_2}\\\hline\hline \rule[-2mm]{0mm}{6mm}0 & 0 &\mathcal{B} & -3 & -3 & \frac{1,001\mathcal{B}}{6,561}+\frac{7,021}{1,215 \sqrt{3} \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 1 & \frac{39\mathcal{B}}{35}-\frac{27 \sqrt{3}}{70 \pi } & -3 & -2 & \frac{287\mathcal{B}}{2,187}+\frac{2,879}{810 \sqrt{3} \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 2 & \frac{1,185\mathcal{B}}{1,001}-\frac{2,295 \sqrt{3}}{4,004 \pi } & -3 & -1 & \frac{187\mathcal{B}}{2,187}+\frac{2,723}{1,620 \sqrt{3} \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 3 & \frac{56,993\mathcal{B}}{46,189}-\frac{128,853 \sqrt{3}}{184,756 \pi } & -2 & -2 & \frac{35\mathcal{B}}{243}+\frac{44}{9 \sqrt{3} \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 1 & \frac{27\mathcal{B}}{35}+\frac{27 \sqrt{3}}{35 \pi } & -2 & -1 & \frac{23\mathcal{B}}{243}+\frac{37}{18 \sqrt{3} \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 2 & \frac{837\mathcal{B}}{1,001}+\frac{729 \sqrt{3}}{2,002 \pi } & -2 & 0 & \frac{107\mathcal{B}}{243}+\frac{59}{36 \sqrt{3} \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 3 & \frac{40,797\mathcal{B}}{46,189}+\frac{31,833 \sqrt{3}}{184,756 \pi } & -1 & -1 & \frac{\mathcal{B}}{9}+\frac{\sqrt{3}}{\pi } \\\hline \rule[-2mm]{0mm}{6mm}2 & 2 & \frac{729\mathcal{B}}{1,001}+\frac{1,044 \sqrt{3}}{1,001 \pi } & -1 & 0 & \frac{5\mathcal{B}}{9}+\frac{\sqrt{3}}{2 \pi } \\\hline \rule[-2mm]{0mm}{6mm}2 & 3 & \frac{35,721\mathcal{B}}{46,189}+\frac{57,267 \sqrt{3}}{92,378 \pi } & -1 & 1 & \frac{73\mathcal{B}}{105}+\frac{39 \sqrt{3}}{140 \pi } \\\hline \rule[-2mm]{0mm}{6mm}3 & 3 & \frac{32,805\mathcal{B}}{46,189}+\frac{55,989 \sqrt{3}}{46,189 \pi }& -1 & 2 & \frac{6,997\mathcal{B}}{9,009}+\frac{547 \sqrt{3}}{4,004 \pi } \\\hline\hline \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{||c|c|c||c|c|c||}\hline\hline m&n&\boldsymbol{{}_3F_2}&m&n&\boldsymbol{{}_3F_2}\\\hline\hline \rule[-2mm]{0mm}{6mm}0 & 0 &\mathcal{B} & -3 & -3 & \frac{1,001\mathcal{B}}{6,561}+\frac{7,021}{1,215 \sqrt{3} \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 1 & \frac{39\mathcal{B}}{35}-\frac{27 \sqrt{3}}{70 \pi } & -3 & -2 & \frac{287\mathcal{B}}{2,187}+\frac{2,879}{810 \sqrt{3} \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 2 & \frac{1,185\mathcal{B}}{1,001}-\frac{2,295 \sqrt{3}}{4,004 \pi } & -3 & -1 & \frac{187\mathcal{B}}{2,187}+\frac{2,723}{1,620 \sqrt{3} \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 3 & \frac{56,993\mathcal{B}}{46,189}-\frac{128,853 \sqrt{3}}{184,756 \pi } & -2 & -2 & \frac{35\mathcal{B}}{243}+\frac{44}{9 \sqrt{3} \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 1 & \frac{27\mathcal{B}}{35}+\frac{27 \sqrt{3}}{35 \pi } & -2 & -1 & \frac{23\mathcal{B}}{243}+\frac{37}{18 \sqrt{3} \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 2 & \frac{837\mathcal{B}}{1,001}+\frac{729 \sqrt{3}}{2,002 \pi } & -2 & 0 & \frac{107\mathcal{B}}{243}+\frac{59}{36 \sqrt{3} \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 3 & \frac{40,797\mathcal{B}}{46,189}+\frac{31,833 \sqrt{3}}{184,756 \pi } & -1 & -1 & \frac{\mathcal{B}}{9}+\frac{\sqrt{3}}{\pi } \\\hline \rule[-2mm]{0mm}{6mm}2 & 2 & \frac{729\mathcal{B}}{1,001}+\frac{1,044 \sqrt{3}}{1,001 \pi } & -1 & 0 & \frac{5\mathcal{B}}{9}+\frac{\sqrt{3}}{2 \pi } \\\hline \rule[-2mm]{0mm}{6mm}2 & 3 & \frac{35,721\mathcal{B}}{46,189}+\frac{57,267 \sqrt{3}}{92,378 \pi } & -1 & 1 & \frac{73\mathcal{B}}{105}+\frac{39 \sqrt{3}}{140 \pi } \\\hline \rule[-2mm]{0mm}{6mm}3 & 3 & \frac{32,805\mathcal{B}}{46,189}+\frac{55,989 \sqrt{3}}{46,189 \pi }& -1 & 2 & \frac{6,997\mathcal{B}}{9,009}+\frac{547 \sqrt{3}}{4,004 \pi } \\\hline\hline \end{array} \end{align*} $$
Corollary 8. Twenty formulae for
![]() $\boldsymbol {{}_3F_2}={_3F_2}\Big [\genfrac {}{}{0mm}{1}{\frac 14,\frac 34,\frac 12+m}{\quad 1,\frac 32+n~}\Big ]$
with
$\boldsymbol {{}_3F_2}={_3F_2}\Big [\genfrac {}{}{0mm}{1}{\frac 14,\frac 34,\frac 12+m}{\quad 1,\frac 32+n~}\Big ]$
with
![]() $\mathcal {C}=\frac {4}{\pi }\ln (1+\sqrt 2)$
:
$\mathcal {C}=\frac {4}{\pi }\ln (1+\sqrt 2)$
:
 $$ \begin{align*} \begin{array}{||c|c|c||c|c|c||}\hline\hline m&n&\boldsymbol{{}_3F_2}&m&n&\boldsymbol{{}_3F_2}\\\hline\hline \rule[-2mm]{0mm}{6mm}0 & 0 &\mathcal{C} & -3 & -3 & \frac{21\mathcal{C}}{64}+\frac{149}{40 \sqrt{2} \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 1 & \frac{11\mathcal{C}}{10}-\frac{2 \sqrt{2}}{5 \pi } & -3 & -2 & \frac{37\mathcal{C}}{128}+\frac{559}{240 \sqrt{2} \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 2 & \frac{65\mathcal{C}}{56}-\frac{25}{21 \sqrt{2} \pi } & -3 & -1 & \frac{103\mathcal{C}}{512}+\frac{1,141}{960 \sqrt{2} \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 3 & \frac{8,267\mathcal{C}}{6,864}-\frac{287}{198 \sqrt{2} \pi } & -2 & -2 & \frac{5\mathcal{C}}{16}+\frac{19}{6 \sqrt{2} \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 1 & \frac{4\mathcal{C}}{5}+\frac{4 \sqrt{2}}{5 \pi } & -2 & -1 & \frac{7\mathcal{C}}{32}+\frac{17}{12 \sqrt{2} \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 2 & \frac{6\mathcal{C}}{7}+\frac{8 \sqrt{2}}{21 \pi } & -2 & 0 & \frac{67\mathcal{C}}{128}+\frac{53}{48 \sqrt{2} \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 3 & \frac{257\mathcal{C}}{286}+\frac{2 \sqrt{2}}{11 \pi } & -2 & 1 & \frac{811\mathcal{C}}{1,280}+\frac{397}{480 \sqrt{2} \pi } \\\hline \rule[-2mm]{0mm}{6mm}2 & 2 & \frac{16\mathcal{C}}{21}+\frac{68 \sqrt{2}}{63 \pi } & -1 & -1 & \frac{\mathcal{C}}{4}+\frac{\sqrt{2}}{\pi } \\\hline \rule[-2mm]{0mm}{6mm}2 & 3 & \frac{344\mathcal{C}}{429}+\frac{64 \sqrt{2}}{99 \pi } & -1 & 0 & \frac{5\mathcal{C}}{8}+\frac{1}{\sqrt{2} \pi } \\\hline \rule[-2mm]{0mm}{6mm}3 & 3 & \frac{320\mathcal{C}}{429}+\frac{124 \sqrt{2}}{99 \pi } & -1 & 1 & \frac{119\mathcal{C}}{160}+\frac{11}{20 \sqrt{2} \pi } \\\hline\hline \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{||c|c|c||c|c|c||}\hline\hline m&n&\boldsymbol{{}_3F_2}&m&n&\boldsymbol{{}_3F_2}\\\hline\hline \rule[-2mm]{0mm}{6mm}0 & 0 &\mathcal{C} & -3 & -3 & \frac{21\mathcal{C}}{64}+\frac{149}{40 \sqrt{2} \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 1 & \frac{11\mathcal{C}}{10}-\frac{2 \sqrt{2}}{5 \pi } & -3 & -2 & \frac{37\mathcal{C}}{128}+\frac{559}{240 \sqrt{2} \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 2 & \frac{65\mathcal{C}}{56}-\frac{25}{21 \sqrt{2} \pi } & -3 & -1 & \frac{103\mathcal{C}}{512}+\frac{1,141}{960 \sqrt{2} \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 3 & \frac{8,267\mathcal{C}}{6,864}-\frac{287}{198 \sqrt{2} \pi } & -2 & -2 & \frac{5\mathcal{C}}{16}+\frac{19}{6 \sqrt{2} \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 1 & \frac{4\mathcal{C}}{5}+\frac{4 \sqrt{2}}{5 \pi } & -2 & -1 & \frac{7\mathcal{C}}{32}+\frac{17}{12 \sqrt{2} \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 2 & \frac{6\mathcal{C}}{7}+\frac{8 \sqrt{2}}{21 \pi } & -2 & 0 & \frac{67\mathcal{C}}{128}+\frac{53}{48 \sqrt{2} \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 3 & \frac{257\mathcal{C}}{286}+\frac{2 \sqrt{2}}{11 \pi } & -2 & 1 & \frac{811\mathcal{C}}{1,280}+\frac{397}{480 \sqrt{2} \pi } \\\hline \rule[-2mm]{0mm}{6mm}2 & 2 & \frac{16\mathcal{C}}{21}+\frac{68 \sqrt{2}}{63 \pi } & -1 & -1 & \frac{\mathcal{C}}{4}+\frac{\sqrt{2}}{\pi } \\\hline \rule[-2mm]{0mm}{6mm}2 & 3 & \frac{344\mathcal{C}}{429}+\frac{64 \sqrt{2}}{99 \pi } & -1 & 0 & \frac{5\mathcal{C}}{8}+\frac{1}{\sqrt{2} \pi } \\\hline \rule[-2mm]{0mm}{6mm}3 & 3 & \frac{320\mathcal{C}}{429}+\frac{124 \sqrt{2}}{99 \pi } & -1 & 1 & \frac{119\mathcal{C}}{160}+\frac{11}{20 \sqrt{2} \pi } \\\hline\hline \end{array} \end{align*} $$
Corollary 9. Twenty formulae for
![]() $\boldsymbol {{}_3F_2}={_3F_2}\Big [\genfrac {}{}{0mm}{1}{\frac 16,\frac 56,\frac 12+m}{\quad 1,\frac 32+n~}\Big ]$
with
$\boldsymbol {{}_3F_2}={_3F_2}\Big [\genfrac {}{}{0mm}{1}{\frac 16,\frac 56,\frac 12+m}{\quad 1,\frac 32+n~}\Big ]$
with
![]() $\mathcal {D}=\frac {3\sqrt 3}{2\pi }\ln (2+\sqrt 3)$
:
$\mathcal {D}=\frac {3\sqrt 3}{2\pi }\ln (2+\sqrt 3)$
:
 $$ \begin{align*} \begin{array}{||c|c|c||c|c|c||}\hline\hline m&n&\boldsymbol{{}_3F_2}&m&n&\boldsymbol{{}_3F_2}\\\hline\hline \rule[-2mm]{0mm}{6mm}0 & 0 &\mathcal{D} & -3 & -3 & \frac{3,584\mathcal{D}}{6,561}+\frac{6,469}{3,645 \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 1 & \frac{69\mathcal{D}}{64}-\frac{27}{64 \pi } & -3 & -2 & \frac{1,088\mathcal{D}}{2,187}+\frac{1,378}{1,215 \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 2 & \frac{8,067\mathcal{D}}{7,168}-\frac{4,509}{7,168 \pi } & -3 & -1 & \frac{1,661\mathcal{D}}{4,374}+\frac{1,561}{2,430 \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 3 & \frac{151,963\mathcal{D}}{131,072}-\frac{100,485}{131,072 \pi } & -2 & -2 & \frac{128\mathcal{D}}{243}+\frac{41}{27 \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 1 & \frac{27\mathcal{D}}{32}+\frac{27}{32 \pi } & -2 & -1 & \frac{98\mathcal{D}}{243}+\frac{20}{27 \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 2 & \frac{1,593\mathcal{D}}{1,792}+\frac{729}{1,792 \pi } & -2 & 0 & \frac{1,249\mathcal{D}}{1,944}+\frac{121}{216 \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 3 & \frac{60,399\mathcal{D}}{65,536}+\frac{12,879}{65,536 \pi } & -2 & 1 & \frac{90,431\mathcal{D}}{124,416}+\frac{5,735}{13,824 \pi } \\\hline \rule[-2mm]{0mm}{6mm}2 & 2 & \frac{729\mathcal{D}}{896}+\frac{1,017}{896 \pi } & -1 & -1 & \frac{4\mathcal{D}}{9}+\frac{1}{\pi } \\\hline \rule[-2mm]{0mm}{6mm}2 & 3 & \frac{13,851\mathcal{D}}{16,384}+\frac{11,259}{16,384 \pi } & -1 & 0 & \frac{13\mathcal{D}}{18}+\frac{1}{2 \pi } \\\hline \rule[-2mm]{0mm}{6mm}3 & 3 & \frac{6,561\mathcal{D}}{8,192}+\frac{53,829}{40,960 \pi } & -1 & 1 & \frac{623\mathcal{D}}{768}+\frac{69}{256 \pi } \\\hline \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{||c|c|c||c|c|c||}\hline\hline m&n&\boldsymbol{{}_3F_2}&m&n&\boldsymbol{{}_3F_2}\\\hline\hline \rule[-2mm]{0mm}{6mm}0 & 0 &\mathcal{D} & -3 & -3 & \frac{3,584\mathcal{D}}{6,561}+\frac{6,469}{3,645 \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 1 & \frac{69\mathcal{D}}{64}-\frac{27}{64 \pi } & -3 & -2 & \frac{1,088\mathcal{D}}{2,187}+\frac{1,378}{1,215 \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 2 & \frac{8,067\mathcal{D}}{7,168}-\frac{4,509}{7,168 \pi } & -3 & -1 & \frac{1,661\mathcal{D}}{4,374}+\frac{1,561}{2,430 \pi } \\\hline \rule[-2mm]{0mm}{6mm}0 & 3 & \frac{151,963\mathcal{D}}{131,072}-\frac{100,485}{131,072 \pi } & -2 & -2 & \frac{128\mathcal{D}}{243}+\frac{41}{27 \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 1 & \frac{27\mathcal{D}}{32}+\frac{27}{32 \pi } & -2 & -1 & \frac{98\mathcal{D}}{243}+\frac{20}{27 \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 2 & \frac{1,593\mathcal{D}}{1,792}+\frac{729}{1,792 \pi } & -2 & 0 & \frac{1,249\mathcal{D}}{1,944}+\frac{121}{216 \pi } \\\hline \rule[-2mm]{0mm}{6mm}1 & 3 & \frac{60,399\mathcal{D}}{65,536}+\frac{12,879}{65,536 \pi } & -2 & 1 & \frac{90,431\mathcal{D}}{124,416}+\frac{5,735}{13,824 \pi } \\\hline \rule[-2mm]{0mm}{6mm}2 & 2 & \frac{729\mathcal{D}}{896}+\frac{1,017}{896 \pi } & -1 & -1 & \frac{4\mathcal{D}}{9}+\frac{1}{\pi } \\\hline \rule[-2mm]{0mm}{6mm}2 & 3 & \frac{13,851\mathcal{D}}{16,384}+\frac{11,259}{16,384 \pi } & -1 & 0 & \frac{13\mathcal{D}}{18}+\frac{1}{2 \pi } \\\hline \rule[-2mm]{0mm}{6mm}3 & 3 & \frac{6,561\mathcal{D}}{8,192}+\frac{53,829}{40,960 \pi } & -1 & 1 & \frac{623\mathcal{D}}{768}+\frac{69}{256 \pi } \\\hline \end{array} \end{align*} $$
Acknowledgment
The authors are sincerely grateful to the anonymous reviewer for the careful reading, critical comments, and valuable suggestions that contribute significantly to improving the manuscript during the revision.