Published online by Cambridge University Press: 16 March 2018
Let 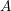 $A$ be an expansive dilation on
$A$ be an expansive dilation on 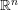 $\mathbb{R}^{n}$ and
$\mathbb{R}^{n}$ and 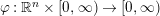 $\unicode[STIX]{x1D711}:\mathbb{R}^{n}\times [0,\infty )\rightarrow [0,\infty )$ an anisotropic growth function. In this article, the authors introduce the anisotropic weak Musielak–Orlicz Hardy space
$\unicode[STIX]{x1D711}:\mathbb{R}^{n}\times [0,\infty )\rightarrow [0,\infty )$ an anisotropic growth function. In this article, the authors introduce the anisotropic weak Musielak–Orlicz Hardy space 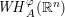 $\mathit{WH}_{A}^{\unicode[STIX]{x1D711}}(\mathbb{R}^{n})$ via the nontangential grand maximal function and then obtain its Littlewood–Paley characterizations in terms of the anisotropic Lusin-area function,
$\mathit{WH}_{A}^{\unicode[STIX]{x1D711}}(\mathbb{R}^{n})$ via the nontangential grand maximal function and then obtain its Littlewood–Paley characterizations in terms of the anisotropic Lusin-area function, 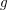 $g$-function or
$g$-function or 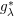 $g_{\unicode[STIX]{x1D706}}^{\ast }$-function, respectively. All these characterizations for anisotropic weak Hardy spaces
$g_{\unicode[STIX]{x1D706}}^{\ast }$-function, respectively. All these characterizations for anisotropic weak Hardy spaces 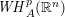 $\mathit{WH}_{A}^{p}(\mathbb{R}^{n})$ (namely,
$\mathit{WH}_{A}^{p}(\mathbb{R}^{n})$ (namely, 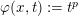 $\unicode[STIX]{x1D711}(x,t):=t^{p}$ for all
$\unicode[STIX]{x1D711}(x,t):=t^{p}$ for all 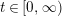 $t\in [0,\infty )$ and
$t\in [0,\infty )$ and 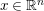 $x\in \mathbb{R}^{n}$ with
$x\in \mathbb{R}^{n}$ with 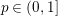 $p\in (0,1]$) are new. Moreover, the range of
$p\in (0,1]$) are new. Moreover, the range of 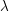 $\unicode[STIX]{x1D706}$ in the anisotropic
$\unicode[STIX]{x1D706}$ in the anisotropic 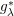 $g_{\unicode[STIX]{x1D706}}^{\ast }$-function characterization of
$g_{\unicode[STIX]{x1D706}}^{\ast }$-function characterization of 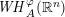 $\mathit{WH}_{A}^{\unicode[STIX]{x1D711}}(\mathbb{R}^{n})$ coincides with the best known range of the
$\mathit{WH}_{A}^{\unicode[STIX]{x1D711}}(\mathbb{R}^{n})$ coincides with the best known range of the 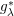 $g_{\unicode[STIX]{x1D706}}^{\ast }$-function characterization of classical Hardy space
$g_{\unicode[STIX]{x1D706}}^{\ast }$-function characterization of classical Hardy space 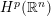 $H^{p}(\mathbb{R}^{n})$ or its weighted variants, where
$H^{p}(\mathbb{R}^{n})$ or its weighted variants, where 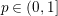 $p\in (0,1]$.
$p\in (0,1]$.
This project is partially supported by the National Natural Science Foundation of China (Grant Nos. 11461065 and 11661075).