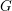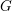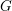ON EXISTENCE OF CANONICAL $G$-BASES

Abstract

We describe a general method for expanding a truncated $G$-iterative Hasse–Schmidt derivation, where $G$ is an algebraic group. We give examples of algebraic groups for which our method works.

1 Introduction

Our motivation for this paper is [3, 14], where some nice model-theoretic properties are obtained for fields equipped with HS-derivations satisfying the standard iterativity rule. Analyzing the reasoning in [3, 14], we deduce that one of the most important properties of an iterative Hasse–Schmidt derivation is Matsumura’s strong integrability (a notion from [4], see: Definition 2.15). Thus we are especially interested in it.

Briefly, strong integrability means that a truncated iterative HS-derivation can be expanded to a not-truncated one, satisfying the same iterativity conditions. We prove (Theorem 3.8) that the existence of a canonical basis (Definition 3.6) implies strong integrability for an arbitrary iterativity condition. However, the converse is not true in general (see Remark 3.9), which is related to the problem of the existence of canonical basis in a given field.

Finding a canonical basis is not an easy task. Matsumura in [4] proved the existence of canonical basis for $\mathbb{G}_{a}$ (the standard iterativity). Afterward Tyc in [9] did the same for $\mathbb{G}_{m}$ and one-dimensional formal groups over algebraically closed fields. Ziegler showed existence of canonical bases for powers of $\mathbb{G}_{a}$ proving the quantifier elimination for the theory of separably closed fields in [13, 14] (see Example 3.7). Before this paper only products of $\mathbb{G}_{a}$ and $\mathbb{G}_{m}$ were considered. We cover the case of commutative, connected, unipotent groups of dimension $2$ over an algebraically closed field. This leads us to Theorem 4.17, stating that, over an algebraically closed field, linear algebraic groups that are connected and commutative have canonical basis if unipotent elements form a subgroup of dimension ${\leqslant}2$ . This theorem includes all the previous results (mentioned above).

Kowalski and I in [2] are treating iterative HS-derivations in a much more abstract way. Many proofs from [2] would be obvious if canonical bases exist for the HS-derivations considered there (a similar sentence was noted at the end of [3, Section 2]). Moreover, [2, Section 6] suggests possible generalizations for the notion of canonical basis.

2 Basic notions about $F$ -derivations

2.1 HS-derivations

All the rings considered in this paper are commutative and with unity. Fix a field $k$ of the characteristic $p>0$ , $e\in \mathbb{N}_{{>}0}$ and $m\in \mathbb{N}_{{>}0}\cup \{\infty \}$ . Let $R$ be any $k$ -algebra. In this subsection we recall some definitions and well-known facts about HS-derivations.

Definition 2.1. We say that $\mathbb{D}=(D_{\mathbf{i}}:R\rightarrow R)_{\mathbf{i}\in \mathbb{N}^{e}}$ is an $e$ -dimensional HS-derivation over $k$ if the map

$$\begin{eqnarray}\mathbb{D}:R\rightarrow R\unicode[STIX]{x27E6}\bar{X}\unicode[STIX]{x27E7},\qquad r\mapsto \mathop{\sum }_{\mathbf{i}\in \mathbb{N}^{e}}D_{\mathbf{i}}(r)\bar{X}^{\mathbf{i}},\end{eqnarray}$$

where $\bar{X}^{\mathbf{i}}=X_{1}^{i_{1}}\cdot \ldots \cdot X_{e}^{i_{e}}$ for $\mathbf{i}=(i_{1},\ldots ,i_{e})$ , is a $k$ -algebra homomorphism and $D_{\mathbf{0}}=\operatorname{id}_{R}$ .

We introduce $R[\bar{v}]:=R[\bar{X}]/(X_{1}^{p^{m}},\ldots ,X_{e}^{p^{m}})$ , so $v_{i}=X_{i}+ (\!X_{1}^{p^{m}},\ldots ,X_{e}^{p^{m}}\! )$ and $\bar{v}=(v_{1},\ldots ,v_{e})$ (for $m=\infty$ we set $v_{i}=X_{i}$ , $R[\bar{v}]=R\unicode[STIX]{x27E6}\bar{X}\unicode[STIX]{x27E7}$ ). After composing $\mathbb{D}$ with the natural mapping $R[\bar{X}]\rightarrow R[\bar{v}]$ we obtain a truncation of $\mathbb{D}$ , denoted by $\mathbb{D}[m]=(D_{\mathbf{i}}:R\rightarrow R)_{\mathbf{i}\in [p^{m}]^{e}}$ . This lead us to the following:

Definition 2.2. A collection $\mathbb{D}=(D_{\mathbf{i}}:R\rightarrow R)_{\mathbf{i}\in [p^{m}]^{e}}$ is called an $m$ -truncated $e$ -dimensional HS-derivation over $k$ if the map

$$\begin{eqnarray}\mathbb{D}:R\rightarrow R[\bar{v}],\qquad r\mapsto \mathop{\sum }_{\mathbf{i}\in [p^{m}]^{e}}D_{\mathbf{i}}(r)\bar{v}^{\mathbf{i}},\end{eqnarray}$$

where $\bar{v}^{\mathbf{i}}=v_{1}^{i_{1}}\cdot \ldots \cdot v_{e}^{i_{e}}$ for $\mathbf{i}=(i_{1},\ldots ,i_{e})$ , is a $k$ -algebra homomorphism and $D_{\mathbf{0}}=\operatorname{id}_{R}$ .

Clearly, any $\infty$ -truncated HS-derivation is just an HS-derivation. We have seen that it is easy to obtain from an HS-derivation an $m$ -truncated one. For a field $R=K$ the converse is also true.

Theorem 2.3. Let $R$ be a smooth $k$ -algebra,  $\mathbb{D}=(D_{\mathbf{i}}:R\rightarrow R)_{\mathbf{i}\in [p^{m}]^{e}}$ an $m$ -truncated $e$ -dimensional HS-derivation over $k$ . There exists an $e$ -dimensional HS-derivation $\mathbb{D}^{\prime }=(D_{\mathbf{i}}^{\prime }:R\rightarrow R)_{\mathbf{i}\in \mathbb{N}^{e}}$ over $k$ such that for every $\mathbf{i}\in [p^{m}]^{e}$ we have $D_{\mathbf{i}}^{\prime }=D_{\mathbf{i}}$ .

Proof. We recursively construct $\mathbb{D}^{\prime }$ as was done at [4, page 236], but using the following diagram

where $\unicode[STIX]{x1D711}(x):=\sum _{\mathbf{i}\in [p^{n}]^{e}}D_{\mathbf{i}}(x)\bar{X}^{\mathbf{i}}+(X_{1}^{p^{n}},\ldots ,X_{e}^{p^{n}})$ and $\unicode[STIX]{x1D70B}$ is the quotient map.◻

Remark 2.4. Theorem 2.3 is a generalization of [4, Theorem 6]. Note that the best possible situation is for a $k$ -algebra $R$ which is étale over $k$ . In such a case there exists a unique expansion of every $m$ -truncated $e$ -dimensional HS-derivation.

By [5, Theorem 26.9], separability implies smoothness, so Theorem 2.3 works in particular for a separable fields extension $k\subseteq K$ . Because so far we do not demand anything from $k$ we can take $k=\mathbb{F}_{p}$ , hence the assumption about a separable extension $k\subseteq K$ is negligible in the following way:

Corollary 2.5. Every $m$ -truncated $e$ -dimensional HS-derivation on a field $K$ has an extension to an $e$ -dimensional HS-derivation.

We call an $m$ -truncated $e$ -dimensional HS-derivation $\mathbb{D}$ on $R$ integrable if there exists $e$ -dimensional HS-derivation $\mathbb{D}^{\prime }$ on $R$ such that $D_{\mathbf{i}}^{\prime }=D_{\mathbf{i}}$ for every $\mathbf{i}\in [p^{m}]^{e}$ . Corollary 2.5 says that truncated HS-derivations on a field are always integrable, but it is not true for arbitrary rings [4, Example 3]. Moreover, the described situation dramatically changes after adding some iterativity conditions. Before considering iterative HS-derivations, we state more well-known facts about general HS-derivations, which will be needed in the remainder of this article.

Lemma 2.6. Assume that $R\xrightarrow[{}]{f}S$ is a homomorphism of $k$ -algebras. Let $\mathbb{D}$ be an $m$ -truncated $e$ -dimensional HS-derivation on $R$ over $k$ .

1. (i) If $S$ is smooth over $R$ , then there exists an $m$ -truncated $e$ -dimensional HS-derivation $\mathbb{D}^{\prime }$ on $S$ over $k$ such that for every $i_{1},\ldots ,i_{e}<p^{m}$

   (1) $$\begin{eqnarray}fD_{(i_{1},\ldots ,i_{e})}=D_{(i_{1},\ldots ,i_{e})}^{\prime }f.\end{eqnarray}$$

2. (ii) If $S$ is unramified over $R$ , then there exists at most one $m$ -truncated $e$ -dimensional HS-derivation $\mathbb{D}^{\prime }$ on $S$ over $k$ such that for every $i_{1},\ldots ,i_{e}<p^{m}$

   $$\begin{eqnarray}fD_{(i_{1},\ldots ,i_{e})}=D_{(i_{1},\ldots ,i_{e})}^{\prime }f.\end{eqnarray}$$

Proof. The lemma just reformulates [2, Proposition 3.3]. ◻

Fact 2.7. For every $m$ -truncated $e$ -dimensional HS-derivation and every $x\in R$ the following holds

$$\begin{eqnarray}D_{(i_{1},\ldots ,i_{e})}(x^{p})=\left\{\begin{array}{@{}ll@{}}\displaystyle D_{(i_{1}/p,\ldots ,i_{e}/p)}(x)^{p}\quad & \displaystyle \text{if }p|i_{1},\ldots ,i_{e},\\ \displaystyle 0\quad & \displaystyle \text{otherwise.}\end{array}\right.\end{eqnarray}$$

Proof. It follows from the definition (see e.g. [6, Lemma 1.1]). ◻

2.2 Iterative HS-derivations

In this subsection we deal with iterative HS-derivations. The main purpose is to provide basic properties. Let $F(\bar{v},\bar{w})=(F_{1}(\bar{v},\bar{w}),\ldots ,F_{e}(\bar{v},\bar{w}))\in (k[\bar{v},\bar{w}])^{e}$ (still $k[\bar{v},\bar{w}]=k\unicode[STIX]{x27E6}\bar{X},\bar{Y}\unicode[STIX]{x27E7}$ for $m=\infty$ ) and let $\mathbb{D}$ be an $m$ -truncated $e$ -dimensional HS-derivation on $R$ over $k$ . Sometimes we need to distinguish between $\mathbb{D}:R\rightarrow R[\bar{v}]$ and $\mathbb{D}:R\rightarrow R[\bar{w}]$ ; Therefore, they will be denoted by $\mathbb{D}_{\bar{v}}$ and $\mathbb{D}_{\bar{w}}$ respectively.

Definition 2.8. We call $\mathbb{D}~F$ -iterative if the following diagram commutes

where $\mathbb{D}_{\bar{w}}[\bar{v}](\sum _{\mathbf{i}}r_{\mathbf{i}}\bar{v}^{\mathbf{i}}):=\sum _{\mathbf{i}}\mathbb{D}_{\bar{w}}(r_{\mathbf{i}})\bar{v}^{\mathbf{i}}$ . We write shortly $F$ -derivation for an $F$ -iterative $m$ -truncated $e$ -dimensional HS-derivation over $k$ .

Example 2.9. For $m=\infty$ and $e=1$ we can take $F=\mathbb{G}_{a}=X+Y$ . It encodes the classical iterativity rule

$$\begin{eqnarray}D_{i}\circ D_{j}=\binom{i+j}{i}D_{i+j}.\end{eqnarray}$$

An example of a $\mathbb{G}_{a}$ -derivation is the following collection of functions on $k[X]$ :

$$\begin{eqnarray}D_{n}\biggl(\mathop{\sum }_{i=0}^{k}\unicode[STIX]{x1D6FC}_{i}X^{i}\biggr)=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \displaystyle \text{if }n>k,\\ \displaystyle \mathop{\sum }_{i=n}^{k}\unicode[STIX]{x1D6FC}_{i}\binom{i}{n}X^{i-n}\quad & \displaystyle \text{if }n\leqslant k,\end{array}\right.\end{eqnarray}$$

where $n\in \mathbb{N}$ . For the formal group law $F=\mathbb{G}_{m}=X+Y+XY$ above formulas are more complicated (see [1, Example 3.6]).

Example 2.10. For every formal group law $F(\bar{X},\bar{Y})\in (k\unicode[STIX]{x27E6}\bar{X},\bar{Y}\unicode[STIX]{x27E7})^{e}$ we have canonical $F$ -derivation

$$\begin{eqnarray}\mathbb{D}^{F}:=\operatorname{ev}_{F(\bar{X},\bar{Y})}:k\unicode[STIX]{x27E6}\bar{X}\unicode[STIX]{x27E7}\rightarrow k\unicode[STIX]{x27E6}\bar{X}\unicode[STIX]{x27E7}\unicode[STIX]{x27E6}\bar{Y}\unicode[STIX]{x27E7}.\end{eqnarray}$$

Compare with [2, Example 3.25].

Example 2.11. For actions of finite group schemes, which underlying Hopf algebra is defined on $k[\bar{v}]$ , we have a natural correspondence with the truncated $F$ -derivations for an appropriate $F$ (see [2, Section 3]). Therefore, we are especially interested in group scheme actions of $k$ -group schemes of the form $\mathfrak{g}=\operatorname{Spec}k[\bar{v}]$ on the scheme $\operatorname{Spec}R$ . By [2, Remark 3.9], such a group scheme action corresponds to an $F$ -derivation on $R$ , where $F$ is the Hopf algebra comultiplication given by $\mathfrak{g}$ .

Assume that $R$ is a $k$ -algebra with an $F$ -derivation $\mathbb{D}$ . The pair $(R,\mathbb{D})$ will be called an $F$ -ring. If $K$ is a field and $(K,\mathbb{D})$ is an $F$ -ring, then $(K,\mathbb{D})$ will be called an $F$ -field. Let $(R,\mathbb{D})$ be an $F$ -ring, similarly $(S,\mathbb{D}^{\prime })$ . A morphism of $k$ -algebras $f:R\rightarrow S$ is an $F$ -morphism if for every $\mathbf{i}$ , $fD_{\mathbf{i}}=D_{\mathbf{i}}^{\prime }f$ . Moreover, if such $f$ is injective, $R$ is $F$ -subring of $S$ (similarly $F$ -subfield for $F$ -fields).

Example 2.12. Let $G$ be an algebraic group over $k$ , we denote by ${\mathcal{O}}_{G}$ the local ring of $G$ at the identity (it is a regular local ring) and by $\bar{x}=(x_{1},\ldots ,x_{e})$ a choice of its local parameters. For $F={\hat{G}}$ we have $F(\bar{x},\bar{Y})\in {\mathcal{O}}_{G}\unicode[STIX]{x27E6}\bar{Y}\unicode[STIX]{x27E7}$ , so $({\mathcal{O}}_{G},\mathbb{D}^{F}|_{{\mathcal{O}}_{G}})$ is an $F$ -subring of $(k\unicode[STIX]{x27E6}\bar{X}\unicode[STIX]{x27E7},\mathbb{D}^{F})$ . Hence $k(G)$ is equipped with a natural ${\hat{G}}$ -derivation, which will be denoted by $\mathbb{D}^{G}$ and called canonical $G$ -derivation. It depends on the choice of local parameters, but we prefer the adjective “canonical”. For more details check [2, Example 3.27].

For an $F$ -ring $(R,\mathbb{D})$ and $\mathbf{i}\in [p^{m}]^{e}$ we introduce $C_{\mathbf{i}}:=\ker D_{\mathbf{i}}$ , and two more sets:

$$\begin{eqnarray}C_{R}:=C_{(1,0\ldots ,0)}\cap \cdots \cap C_{(0,\ldots ,0,1)}\quad \text{ (the ring of constants)},\end{eqnarray}$$

and

$$\begin{eqnarray}C_{R}^{\text{abs}}:=\mathop{\bigcap }_{\mathbf{i}\not =\mathbf{0}}C_{\mathbf{i}}\quad \text{(the ring of absolute constants)}.\end{eqnarray}$$

Both, $C_{R}$ and $C_{R}^{\text{abs}}$ , are subrings of $R$ (see Remark 3.1).

Lemma 2.13. Assume that $R\xrightarrow[{}]{f}S$ is a homomorphism of $k$ -algebras. Let $\mathbb{D}$ be an $F$ -derivation on $R$ .

1. (i) If $S$ is étale (smooth and unramified) over $R$ , then there exists a unique $F$ -derivation $\mathbb{D}^{\prime }$ on $S$ such that for every $i_{1},\ldots ,i_{e}<p^{m}$

   $$\begin{eqnarray}fD_{(i_{1},\ldots ,i_{e})}=D_{(i_{1},\ldots ,i_{e})}^{\prime }f.\end{eqnarray}$$

2. (ii) If $S$ is unramified over $R$ , then there exists at most one $F$ -derivation $\mathbb{D}^{\prime }$ on $S$ such that for every $i_{1},\ldots ,i_{e}<p^{m}$

   $$\begin{eqnarray}fD_{(i_{1},\ldots ,i_{e})}=D_{(i_{1},\ldots ,i_{e})}^{\prime }f.\end{eqnarray}$$

Proof. Compare to [2, Proposition 3.18]. Part (ii) is, by Lemma 2.6(ii), true even without the iterativity assumption. For the proof of part (i), it is enough to show that an HS-derivation $\mathbb{D}^{\prime }$ from Lemma 2.6 is $F$ -iterative, that is, the following diagram is commutative

It is similar to the proof of [5, Theorem 27.2] and we leave it to the reader. ◻

Let $F(\bar{v},\bar{w})\in (k[\bar{v},\bar{w}])^{e}$ , $m^{\prime }\leqslant m$ and let $\bar{v^{\prime }}$ , $\bar{w^{\prime }}$ denote the $m^{\prime }$ -truncated variables ( $k[\bar{v^{\prime }},\bar{w^{\prime }}]=k[\bar{X},\bar{Y}]/(X_{1}^{p^{m^{\prime }}},\ldots ,X_{e}^{p^{m^{\prime }}},Y_{1}^{p^{m^{\prime }}},\ldots ,Y_{e}^{p^{m^{\prime }}})$ ). By $F[m^{\prime }]$ we denote the $m^{\prime }$ -truncation of $F$ which is equal to $\operatorname{ev}_{(\bar{v^{\prime }},\bar{w^{\prime }})}F(\bar{v},\bar{w})$ (the image of $F$ in the ring of truncated polynomials $(k[\bar{v^{\prime }},\bar{w^{\prime }}])^{e}$ ). If $\mathbb{D}$ is $F$ -iterative, then $\mathbb{D}[m^{\prime }]$ is $F[m^{\prime }]$ -iterative as well (for the notion of $\mathbb{D}[m]$ , check the first lines after Definition 2.1).

Example 2.14. For every $m\in \mathbb{N}_{{>}0}$ we get a ${\hat{G}}[m]$ -field structure on $k(G)$ –just consider $\mathbb{D}^{G}[m]$ .

Definition 2.15. Let $F(\bar{X},\bar{Y})\in (k\unicode[STIX]{x27E6}\bar{X},\bar{Y}\unicode[STIX]{x27E7})^{e}$ and let $\mathbb{D}$ be an $F[m]$ -derivation on a $k$ -algebra $R$ . We call $\mathbb{D}$ strongly integrable if there exists an $F$ -derivation $\mathbb{D}^{\prime }$ on $R$ such that $\mathbb{D}^{\prime }[m]=\mathbb{D}$ .

In the next few facts we give simple properties of $F$ -derivations on a $k$ -algebra $R$ . Those facts were intended for a formal group law $F$ , but it is enough to demand that $F(\bar{v},\bar{w})\in (k[\bar{v},\bar{w}])^{e}$ , $F(\bar{v},\bar{0})=\bar{v}$ and $F(\bar{0},\bar{w})=\bar{w}$ . However, we do not consider $F$ -derivations in the case when $F$ is not a formal group law, even the existence for such (nontrivial) derivations is not clear in general.

Fact 2.16. For every $\mathbf{i}$ and $\mathbf{j}$ there exists $\mathbf{r}(D_{\mathbf{j}^{\prime }})_{0<|\mathbf{j}^{\prime }|<|\mathbf{i}+\mathbf{j}|}$ , a $k$ -linear combination of $D_{\mathbf{j}^{\prime }}$ , where $0<|\mathbf{j}^{\prime }|<|\mathbf{i}+\mathbf{j}|$ , such that

$$\begin{eqnarray}D_{\mathbf{j}}D_{\mathbf{i}}=\binom{i_{1}+j_{1}}{i_{1}}\cdots \binom{i_{e}+j_{e}}{i_{e}}D_{\mathbf{i}+\mathbf{j}}+\mathbf{r}(D_{\mathbf{j}^{\prime }})_{0<|\mathbf{j}^{\prime }|<|\mathbf{i}+\mathbf{j}|}.\end{eqnarray}$$

Proof. It is clear for $\mathbf{i}=\mathbf{0}$ or $\mathbf{j}=\mathbf{0}$ , so assume that both $\mathbf{i}$ and $\mathbf{j}$ differ from $\mathbf{0}$ . Since $F(\bar{v},0)=\bar{v}$ , $F(0,\bar{w})=\bar{w}$ , we have $F(\bar{v},\bar{w})=(v_{1}+w_{1}+S_{1},\ldots ,v_{e}+w_{e}+S_{e})$ for some $S_{1},\ldots ,S_{e}$ belonging to the ideal $(v_{i}w_{j})_{i,j\leqslant e}$ . Therefore, for every $r\in R$

$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{j_{1},\ldots ,j_{e},i_{1},\ldots ,i_{e}}D_{(j_{1},\ldots ,j_{e})}D_{(i_{1},\ldots ,i_{e})}(r)v_{1}^{i_{1}}\cdot \ldots \cdot v_{e}^{i_{e}}\cdot w_{1}^{j_{1}}\cdot \ldots \cdot w_{e}^{j_{e}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{k_{1},\ldots ,k_{e}}D_{(k_{1},\ldots ,k_{e})}(r)(v_{1}+w_{1}+S_{1})^{k_{1}}\cdot \ldots \cdot (v_{e}+w_{e}+S_{e})^{k_{e}}.\nonumber\end{eqnarray}$$

We are interested in the coefficients at $A:=v_{1}^{i_{1}}\cdot \ldots \cdot v_{e}^{i_{e}}\cdot w_{1}^{j_{1}}\cdot \ldots \cdot w_{e}^{j_{e}}$ on the right side of the above equation. First of all, note that $v_{i}+w_{i}+S_{i}$ , $i\leqslant e$ , is an element of the maximal ideal $(v_{1},\ldots ,v_{e},w_{1},\ldots ,w_{e})$ , hence it is of the form

$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{1}v_{1}+\cdots +\unicode[STIX]{x1D6FC}_{e}v_{e}+\unicode[STIX]{x1D6FD}_{1}w_{1}+\cdots +\unicode[STIX]{x1D6FD}_{e}w_{e},\end{eqnarray}$$

for some $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{e},\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{e}\in k[\bar{v},\bar{w}]$ . Each component of the above sum has total degree at least $1$ , so the total degree of each summand of $(v_{i}+w_{i}+S_{i})^{k_{i}}$ is at least $k_{i}$ . Therefore, the total degree of

$$\begin{eqnarray}(v_{1}+w_{1}+S_{1})^{k_{1}}\cdot \ldots \cdot (v_{e}+w_{e}+S_{e})^{k_{e}}\end{eqnarray}$$

is at least equal to $k_{1}+\cdots +k_{e}$ . On the other hand, the total degree of $A$ is equal to $|\mathbf{i}+\mathbf{j}|$ . After comparing degrees, we see that if $k_{1}+\cdots +k_{e}>|\mathbf{i}+\mathbf{j}|$ then there is no chance to find a component of

$$\begin{eqnarray}D_{(k_{1},\ldots ,k_{e})}(r)(v_{1}+w_{1}+S_{1})^{k_{1}}\cdot \ldots \cdot (v_{e}+w_{e}+S_{e})^{k_{e}}\end{eqnarray}$$

equal to $A$ multiplied by some element of $R$ .

Let $k_{1}+\cdots +k_{e}=|\mathbf{i}+\mathbf{j}|$ . Since $S_{1},\ldots ,S_{e}\in (v_{i}w_{j})_{i,j\leqslant e}$ , each summand of $S_{i}$ , $i\leqslant e$ , has total degree at least $2$ . The only component of

$$\begin{eqnarray}D_{(k_{1},\ldots ,k_{e})}(r)(v_{1}+w_{1}+S_{1})^{k_{1}}\cdot \ldots \cdot (v_{e}+w_{e}+S_{e})^{k_{e}}\end{eqnarray}$$

for which the total degree will be equal to $|\mathbf{i}+\mathbf{j}|$ “omits” $S_{1},\ldots ,S_{e}$ . Therefore, we are looking for the coefficient of

$$\begin{eqnarray}D_{(k_{1},\ldots ,k_{e})}(r)(v_{1}+w_{1})^{k_{1}}\cdot \ldots \cdot (v_{e}+w_{e})^{k_{e}},\end{eqnarray}$$

which is divisible by $A$ .◻

Fact 2.17. Assume that also $\mathbb{D}^{\prime }$ is an $F$ -derivation on $R$ . If for all $l\leqslant e$ and $i<m$ we have $D_{(0,\ldots ,0,\underset{l\text{th place}}{p^{i}},0,\ldots ,0)}=D_{(0,\ldots ,0,\underset{l\text{th place}}{p^{i}},0,\ldots ,0)}^{\prime }$ then $\mathbb{D}=\mathbb{D}^{\prime }$ .

Proof. Induction on $|\mathbf{j}|$ . Clearly, $D_{(0,\ldots ,0)}=\operatorname{id}_{R}=D_{(0,\ldots ,0)}^{\prime }$ . Take $\mathbf{j}=(j_{1},\ldots ,j_{e})\neq (0,\ldots ,0)$ and assume that $D_{\mathbf{j}^{\prime }}=D_{\mathbf{j}^{\prime }}^{\prime }$ for every $\mathbf{j}^{\prime }$ such that $|\mathbf{j}^{\prime }|<|\mathbf{j}|$ . Without loss of generality, we set $j_{1}\neq 0$ . Let $j_{1}=\unicode[STIX]{x1D6FE}_{0}+\unicode[STIX]{x1D6FE}_{1}p+\cdots +\unicode[STIX]{x1D6FE}_{s}p^{s}$ , where $\unicode[STIX]{x1D6FE}_{0},\ldots ,\unicode[STIX]{x1D6FE}_{s}<p$ and $\unicode[STIX]{x1D6FE}_{s}\neq 0$ . Fact 2.16 implies that

$$\begin{eqnarray}\displaystyle & \displaystyle D_{(p^{s},0,\ldots ,0)}D_{(j_{1}-p^{s},j_{2},\ldots ,j_{e})}=\unicode[STIX]{x1D6FE}_{s}D_{\mathbf{j}}+\mathbf{r}(D_{\mathbf{j}^{\prime }})_{0<|\mathbf{j}^{\prime }|<|\mathbf{j}|}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle D_{(p^{s},0,\ldots ,0)}^{\prime }D_{(j_{1}-p^{s},j_{2},\ldots ,j_{e})}^{\prime }=\unicode[STIX]{x1D6FE}_{s}D_{\mathbf{j}}^{\prime }+\mathbf{r}(D_{\mathbf{j}^{\prime }}^{\prime })_{0<|\mathbf{j}^{\prime }|<|\mathbf{j}|}. & \displaystyle \nonumber\end{eqnarray}$$

A $k$ -linear combination $\mathbf{r}(D_{\mathbf{j}^{\prime }})_{0<|\mathbf{j}^{\prime }|<|\mathbf{j}|}$ is unique for $F$ (what can be deduced from the proof of Fact 2.16), hence, by the inductive assumption, it is equal to $\mathbf{r}(D_{\mathbf{j}^{\prime }}^{\prime })_{0<|\mathbf{j}^{\prime }|<|\mathbf{j}|}$ . Moreover, it follows from the inductive assumption that

$$\begin{eqnarray}D_{(p^{s},0,\ldots ,0)}D_{(j_{1}-p^{s},j_{2},\ldots ,j_{e})}=D_{(p^{s},0,\ldots ,0)}^{\prime }D_{(j_{1}-p^{s},j_{2},\ldots ,j_{e})}^{\prime },\end{eqnarray}$$

so $D_{\mathbf{j}}=D_{\mathbf{j}}^{\prime }$ .◻

Lemma 2.18. Let $(K,\mathbb{D})$ be an $F$ -field and let $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{p^{e}}$ be all different elements of $\{D_{(i_{0},\ldots ,i_{e})}\mid i_{0},\ldots ,i_{e}<p\}$ . Take any $x_{1},\ldots ,x_{n}\in K$ . Elements $x_{1},\ldots ,x_{n}$ are linearly dependent over $C_{K}$ if and only if the rank of the matrix $(\unicode[STIX]{x2202}_{i}(x_{j}))_{i\leqslant p^{e},j\leqslant n}$ is smaller than $n$ .

Proof. The proof of [2, Proposition 3.20] works well for the above, more general lemma. ◻

Corollary 2.19. For every $F$ -field extension $K\subseteq L$ , $K$ and $C_{L}$ are linearly disjoint over $C_{K}$ .

Definition 2.20. We call an $F$ -field $(K,\mathbb{D})$ strict if $C_{K}=K^{p}$ .

Remark 2.21. Let $K\subseteq L$ be an $F$ -field extension. If $K$ is strict, then $K\subseteq L$ is separable.

Proof. By Corollary 2.19, $K$ and $L^{p}\subseteq C_{L}$ are linearly disjoint over $K^{p}=C_{K}$ , so by [5, Theorem 26.4] $L$ is separable over $K$ .◻

Lemma 2.22. For any $F$ -field $(K,\mathbb{D})$ we have $[K:C_{K}]\leqslant p^{e}$ .

Proof. It follows from Lemma 2.18. ◻

2.3 Commutative HS-derivations

In this subsection we deal with formulas for $D_{\mathbf{i}}^{(p)}$ (the $p$ th composition) in the case of an $F$ -derivation $\mathbb{D}=(D_{\mathbf{i}})_{\mathbf{i}\in [p^{m}]^{e}}$ for a commutative $F$ (i.e.,  $F(\bar{v},\bar{w})=F(\bar{w},\bar{v})$ ). The main idea follows [1, Section 3.3], but improves the reasoning of [1, Proposition 3.11] and [1, Remark 3.12.(4)]. The idea to focus on the ring of symmetric polynomials comes from Kowalski. We assume only that $F(\bar{v},\bar{w})\in (k[\bar{v},\bar{w}])^{e}$ is commutative and that $(R,\mathbb{D})$ is an $F$ -ring. Obviously:

Fact 2.23. We have the following

$$\begin{eqnarray}D_{\mathbf{j}}\circ D_{\mathbf{i}}=D_{\mathbf{i}}\circ D_{\mathbf{j}}.\end{eqnarray}$$

For every $N\geqslant 1$ we introduce the following $k$ -algebra homomorphism

$$\begin{eqnarray}\displaystyle & \displaystyle E_{N}:R[\bar{v}_{1},\ldots ,\bar{v}_{N-1}]\rightarrow R[\bar{v}_{1},\ldots ,\bar{v}_{N}], & \displaystyle \nonumber\\ \displaystyle & \displaystyle E_{N}=\mathbb{D}_{\bar{v}_{N}}[\bar{v}_{1},\ldots ,\bar{v}_{N-1}], & \displaystyle \nonumber\end{eqnarray}$$

where $\bar{v}_{1},\ldots ,\bar{v}_{N}$ are $e$ -tuples of $m$ -truncated variables and

$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{D}_{\bar{v}_{N}}[\bar{v}_{1},\ldots ,\bar{v}_{N-1}]\biggl(\mathop{\sum }_{\mathbf{i}_{1},\ldots ,\mathbf{i}_{N-1}}\unicode[STIX]{x1D6FC}_{\mathbf{i}_{1},\ldots ,\mathbf{i}_{N-1}}\bar{v}_{1}^{\mathbf{i}_{1}}\cdot \ldots \cdot \bar{v}_{N-1}^{\mathbf{i}_{N-1}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\mathbf{i}_{1},\ldots ,\mathbf{i}_{N}}D_{\mathbf{i}_{N}}(\unicode[STIX]{x1D6FC}_{\mathbf{i}_{1},\ldots ,\mathbf{i}_{N-1}})\bar{v}_{1}^{\mathbf{i}_{1}}\cdot \ldots \cdot \bar{v}_{N}^{\mathbf{i}_{N}}.\nonumber\end{eqnarray}$$

For $N\geqslant 1$ we define inductively

$$\begin{eqnarray}\displaystyle & \displaystyle F_{1}(\bar{v}_{1}):=\bar{v}_{1}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle F_{N+1}(\bar{v}_{1},\ldots ,\bar{v}_{N+1}):=F_{N}(\bar{v}_{1},\ldots ,\bar{v}_{N-1},F(\bar{v}_{N},\bar{v}_{N+1})). & \displaystyle \nonumber\end{eqnarray}$$

Lemma 2.24. For every $N\geqslant 1$ the following diagram commutes

Proof. It is clear for $N=1$ , so assume for the induction step that the last diagram is commutative. Consider

Left part is commutative by the inductive assumption. For commutativity of the right side, just apply the functor

$$\begin{eqnarray}R\rightarrow R[\bar{v}_{1},\ldots ,\bar{v}_{N-1}]\end{eqnarray}$$

to the diagram from the $F$ -iterativity definition and change $\bar{v}$ , $\bar{w}$ to $\bar{v}_{N}$ , $\bar{v}_{N+1}$ . Finally

$$\begin{eqnarray}\operatorname{ev}_{(\bar{v}_{1},\ldots ,\bar{v}_{N-1},F(\bar{v}_{N},\bar{v}_{N+1}))}\circ \operatorname{ev}_{F_{N}}=\operatorname{ev}_{F_{N+1}\!}.\square\end{eqnarray}$$

Note that the following composition of mappings

$$\begin{eqnarray}R\xrightarrow[{}]{E_{1}}R[\bar{v}_{1}]\xrightarrow[{}]{E_{2}}R[\bar{v}_{1},\bar{v}_{2}]\rightarrow \cdots \xrightarrow[{}]{E_{p}}R[\bar{v}_{1},\ldots ,\bar{v}_{p}]\end{eqnarray}$$

is a $k$ -algebra homomorphism such that $\operatorname{im}(E_{p}\circ \cdots \circ E_{1})$ is, by Fact 2.23, a subset of the ring of symmetric polynomials in $\bar{v}_{1},\ldots ,\bar{v}_{p}$ , that is, elements of $R[\bar{v}_{1},\ldots ,\bar{v}_{p}]$ invariant under the action of $S_{p}$ ,

$$\begin{eqnarray}\unicode[STIX]{x1D70E}:\bar{v}_{i}=(v_{i,1},\ldots ,v_{i,e})\mapsto \bar{v}_{\unicode[STIX]{x1D70E}(i)}=(v_{\unicode[STIX]{x1D70E}(i),1},\ldots ,v_{\unicode[STIX]{x1D70E}(i),e}),\end{eqnarray}$$

for $\unicode[STIX]{x1D70E}\in S_{p}$ and $i\leqslant p$ . In other words the map $E_{p}\circ \cdots \circ E_{1}$ factors as in following the diagram

For $\unicode[STIX]{x1D711}:R[\bar{v}_{1},\ldots ,\bar{v}_{p}]^{S_{p}}\rightarrow R[\bar{v}_{1}^{1/p}]$ , given by $v_{i,j}\mapsto v_{1,j}^{1/p}$ , where $i\leqslant p$ and $j\leqslant e$ , also the map $\unicode[STIX]{x1D711}$ factors as in the following diagram

Therefore, $\unicode[STIX]{x1D711}:\operatorname{im}(E_{p}\circ \cdots \circ E_{1})\rightarrow R[\bar{v}_{1}]$ , defined is a well-defined $k$ -algebra homomorphism.

For any $N\geqslant 1$ we define inductively the “multiplication by $N$ map”:

$$\begin{eqnarray}\displaystyle & \displaystyle [1]_{F}:=\bar{v}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle [N+1]_{F}:=F(\bar{v},[N]_{F}). & \displaystyle \nonumber\end{eqnarray}$$

For example $[2]_{F}=F(\bar{v},\bar{v})$ .

Corollary 2.25. For any $r\in R$ we have

$$\begin{eqnarray}\mathop{\sum }_{\mathbf{i}}D_{\mathbf{i}}^{(p)}(r)\bar{v}^{\mathbf{i}}=\operatorname{ev}_{[p]_{F}(\bar{v}^{1/p})}\biggl(\mathop{\sum }_{\mathbf{i}}D_{\mathbf{i}}(r)\bar{v}^{\mathbf{i}}\biggr).\end{eqnarray}$$

Proof. By Lemma 2.24 we know that

$$\begin{eqnarray}E_{p}\circ \cdots \circ E_{1}(r)=\operatorname{ev}_{F_{p}}\circ E_{1}(r),\end{eqnarray}$$

so

$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\mathbf{i}}D_{\mathbf{i}}^{(p)}(r)\bar{v}_{1}^{\mathbf{i}} & = & \displaystyle \unicode[STIX]{x1D711}\circ E_{p}\circ \cdots \circ E_{1}(r)=\unicode[STIX]{x1D711}\circ \operatorname{ev}_{F_{p}}\circ E_{1}(r)\nonumber\\ \displaystyle & = & \displaystyle \operatorname{ev}_{[p]_{F}(\bar{v}_{1}^{1/p})}\biggl(\mathop{\sum }_{\mathbf{i}}D_{\mathbf{i}}(r)\bar{v}_{1}^{\mathbf{i}}\biggr).\nonumber\end{eqnarray}$$

The first equality is similar to [1, Lemma 3.7], the last follows from definitions of $[p]_{F}$ , $F_{p}$ and $\unicode[STIX]{x1D711}$ . For example let $p=2$ :

$$\begin{eqnarray}\unicode[STIX]{x1D711}\circ \operatorname{ev}_{F_{2}(\bar{v}_{1},\bar{v}_{2})}=\operatorname{ev}_{F_{2}(\bar{v}_{1}^{1/p},\bar{v}_{1}^{1/p})}=\operatorname{ev}_{[2]_{F}(\bar{v}_{1}^{1/p})\!}.\square\end{eqnarray}$$

3 Canonical $G$ -bases and the integrability

The results of this section focus on proving the integrability for a field equipped with an iterative HS-derivation and endowed with a $p$ -basis of a special kind. For the notion of $p$ -independence, $p$ -basis and their basic properties, the reader is referred to [5, page 202]. Recall that $k$ is a perfect field. Assume that $G$ is an algebraic group over $k$ of dimension $e$ (perhaps not commutative). We write $G[m]$ -derivation, $G[m]$ -ring, $G[m]$ -field, $\ldots$ instead of ${\hat{G}}[m]$ -derivation, ${\hat{G}}[m]$ -ring, ${\hat{G}}[m]$ -field, $\ldots$

Let $(K,\mathbb{D})$ be a $G[m]$ -field. For every $s\in \{0,\ldots ,m-1\}$ we introduce

$$\begin{eqnarray}F_{s}:=\mathop{\bigcap }_{j=0}^{s}C_{(p^{j},0,\ldots ,0)}\cap C_{(0,p^{j},0,\ldots ,0)}\cap \cdots \cap C_{(0,\ldots ,0,p^{j})},\quad F_{-1}:=K.\end{eqnarray}$$

Remark 3.1. Sets $F_{s}$ are, due to Fact 2.17, subfields of $K$ . In fact $F_{s}$ is equal to the field of constants of order $s$ (the absolute constants of $\mathbb{D}[s+1]$ ).

For the clarity of the following proofs, we note an obvious fact:

Fact 3.2. Let $L\subseteq L^{\prime }$ be an extension of fields. If $y\in L^{1/p}\backslash L\subseteq L^{\prime }$ , then $[L(y):L]=p$ .

Lemma 3.3. Let $z_{1},\ldots ,z_{e}\in K$ form a $p$ -basis of (or equivalently, by Lemma 2.22, “are $p$ -independent in”) $K$ over $C_{K}=F_{0}$ . For every $s\in \{0,\ldots ,m-1\}$ we have

$$\begin{eqnarray}[F_{s-1}:F_{s}]=p^{e},\qquad F_{s-1}=F_{s}(z_{1}^{p^{s}},\ldots ,z_{e}^{p^{s}}).\end{eqnarray}$$

Proof. Being a $p$ -basis for $K$ over $F_{0}$ , due to $K^{p}\subseteq F_{0}$ , means that $K=F_{0}(z_{1},\ldots ,z_{e})$ and that $[F_{0}(z_{1},\ldots ,z_{e}):F_{0}]=p^{e}$ . Notice that, by [2, Lemma 3.31] and Lemma 2.22,

$$\begin{eqnarray}[F_{s}(z_{1}^{p^{s}},\ldots ,z_{e}^{p^{s}}):F_{s}]\leqslant [F_{s-1}:F_{s}]\leqslant p^{e}.\end{eqnarray}$$

It is enough to show that $[F_{s}(z_{1}^{p^{s}},\ldots ,z_{e}^{p^{s}}):F_{s}]=p^{e}$ . We know that $\{z_{1}^{i_{1}}\cdot \ldots \cdot z_{e}^{i_{e}}\mid 0\leqslant i_{1},\ldots ,i_{e}<p\}$ is $F_{0}$ -linearly independent, thus $\{z_{1}^{i_{1}p^{s}}\cdot \ldots \cdot z_{e}^{i_{e}p^{s}}\mid 0\leqslant i_{1},\ldots ,i_{e}<p\}$ is $F_{0}^{p^{s}}$ -linearly independent. Consider

$$\begin{eqnarray}(K^{p^{s}},\mathbb{D}[s+1]|_{K^{p^{s}}})\subseteq (F_{s-1},\mathbb{D}[s+1]|_{F_{s-1}}).\end{eqnarray}$$

By [2, Lemma 3.31], it is an extension of $G[1]^{\operatorname{Fr}^{p^{s}}}$ -fields. Therefore, by Corollary 2.19, $K^{p^{s}}$ is linearly disjoint from constants of $\mathbb{D}[s+1]|_{F_{s-1}}$ over constants of $\mathbb{D}[s+1]|_{K^{p^{s}}}$ . So $F_{0}^{p^{s}}$ -linear independence of $\{z_{1}^{i_{1}p^{s}}\cdot \ldots \cdot z_{e}^{i_{e}p^{s}}\mid 0\leqslant i_{1},\ldots ,i_{e}<p\}$ implies its $F_{s}$ -linear independence. Hence $[F_{s}(z_{1}^{p^{s}},\ldots ,z_{e}^{p^{s}}):F_{s}]=p^{e}$ .◻

Remark 3.4. The equality

$$\begin{eqnarray}[F_{s-1}:F_{s}]=p^{e},\end{eqnarray}$$

where $s\in \{0,\ldots ,m-1\}$ , does not depend on the choice of a $p$ -basis. Therefore, it is true if $[K:C_{K}]=p^{e}$ .

Proposition 3.5. Let $z_{1},\ldots ,z_{e}\in K$ form a $p$ -basis of (or equivalently “are $p$ -independent in”) $K$ over $C_{K}=F_{0}$ . Then there exists a subset ${\mathcal{B}}_{0}\subseteq C_{K}^{\text{abs}}=F_{m-1}$ , for which ${\mathcal{B}}:={\mathcal{B}}_{0}\cup \{z_{1},\ldots ,z_{e}\}$ is a $p$ -basis for $K$ over $k$ .

Proof. In particular, Lemma 3.3 implies that the set $\{z_{1}^{p^{m}},\ldots z_{e}^{p^{m}}\}$ is $p$ -independent over $k$ in $F_{m-1}$ . Let ${\mathcal{B}}^{\prime }$ be a $p$ -basis ${\mathcal{B}}^{\prime }$ of the field $F_{m-1}$ over $k$ of the form We show that ${\mathcal{B}}:={\mathcal{B}}_{0}\cup \{z_{1},\ldots ,z_{e}\}$ is a $p$ -basis of $K$ over $k$ . Since for $s=m$ , ${\mathcal{B}}_{0}\cup \{z_{1}^{p^{m}},\ldots ,z_{e}^{p^{m}}\}={\mathcal{B}}^{\prime }$ is, as above, a $p$ -basis for $F_{m-1}$ over $k$ , it is enough to show the following induction step

$$\begin{eqnarray}\displaystyle & \displaystyle \text{if }{\mathcal{B}}_{0}\cup \{z_{1}^{p^{s}},\ldots ,z_{e}^{p^{s}}\}\text{is }p\text{-basis for }F_{s-1}\text{ over }k, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{then }{\mathcal{B}}_{0}\cup \{z_{1}^{p^{s-1}},\ldots ,z_{e}^{p^{s-1}}\}\text{is }p\text{-basis for }F_{s-2}\text{ over }k, & \displaystyle \nonumber\end{eqnarray}$$

where $s$ descends from $m$ to $1$ .

Firstly, we argue for the $p$ -independence of ${\mathcal{B}}_{0}$ in $F_{s-2}$ . For any $n\in \mathbb{N}$ and pairwise distinct $x_{1},\ldots ,x_{n}\in {\mathcal{B}}_{0}$ , by Lemma 3.3, we have

$$\begin{eqnarray}[F_{s-2}^{p}(x_{1},\ldots ,x_{n}):F_{s-1}^{p}]=[F_{s-1}^{p}(z_{1}^{p^{s}},\ldots ,z_{e}^{p^{s}},x_{1},\ldots ,x_{n}):F_{s-1}^{p}]=p^{n+e},\end{eqnarray}$$

using Lemma 3.3 again, we get

$$\begin{eqnarray}\displaystyle p^{n+e} & = & \displaystyle [F_{s-2}^{p}(x_{1},\ldots ,x_{n}):F_{s-2}^{p}]\cdot [F_{s-1}^{p}(z_{1}^{p^{s}},\ldots ,z_{e}^{p^{s}}):F_{s-1}^{p}]\nonumber\\ \displaystyle & = & \displaystyle [F_{s-2}^{p}(x_{1},\ldots ,x_{n}):F_{s-2}^{p}]\cdot p^{e}.\nonumber\end{eqnarray}$$

Elements $x_{1},\ldots ,x_{n}$ were chosen arbitrary, so indeed ${\mathcal{B}}_{0}$ is $p$ -independent over $k$ in $F_{s-2}$ .

We show now the $p$ -independence of ${\mathcal{B}}_{0}\cup \{z_{1}^{p^{s-1}},\ldots ,z_{e}^{p^{s-1}}\}$ in $F_{s-2}$ . For any $n\in \mathbb{N}$ , pairwise distinct $x_{1},\ldots ,x_{n}\in {\mathcal{B}}_{0}$ ,

$$\begin{eqnarray}\displaystyle & & \displaystyle [F_{s-2}^{p}(z_{1}^{p^{s-1}},\ldots ,z_{e}^{p^{s-1}},x_{1},\ldots ,x_{n}):F_{s-2}^{p}]\nonumber\\ \displaystyle & & \displaystyle \quad =[F_{s-2}^{p}(z_{1}^{p^{s-1}},\ldots ,z_{e}^{p^{s-1}},x_{1},\ldots ,x_{n}):F_{s-2}^{p}(x_{1},\ldots ,x_{n})]\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,[F_{s-2}^{p}(x_{1},\ldots ,x_{n}):F_{s-2}^{p}].\nonumber\end{eqnarray}$$

To show the $p$ -independence of ${\mathcal{B}}_{0}\cup \{z_{1}^{p^{s-1}},\ldots ,z_{e}^{p^{s-1}}\}$ over $k$ in $F_{s-2}$ we need only to prove

$$\begin{eqnarray}[F_{s-2}^{p}(z_{1}^{p^{s-1}},\ldots ,z_{e}^{p^{s-1}},x_{1},\ldots ,x_{n}):F_{s-2}^{p}(x_{1},\ldots ,x_{n})]=p^{e}.\end{eqnarray}$$

By Fact 3.2 it reduces to show that for each $i\leqslant e$ we have

$$\begin{eqnarray}z_{i}^{p^{s-1}}\not \in F_{s-2}^{p}(z_{i+1}^{p^{s-1}},\ldots ,z_{e}^{p^{s-1}},x_{1},\ldots ,x_{n})\end{eqnarray}$$

(clearly $z_{i}^{p^{s}}\in F_{s-2}^{p}$ ). It holds due to Lemma 3.3 and

$$\begin{eqnarray}F_{s-2}^{p}(z_{i+1}^{p^{s-1}},\ldots ,z_{e}^{p^{s-1}},x_{1},\ldots ,x_{n})\subseteq F_{s-1}(z_{i+1}^{p^{s-1}},\ldots ,z_{e}^{p^{s-1}}).\end{eqnarray}$$

Finally, we see that

$$\begin{eqnarray}\displaystyle F_{s-2} & = & \displaystyle F_{s-1}(z_{1}^{p^{s-1}},\ldots ,z_{e}^{p^{s-1}})\nonumber\\ \displaystyle & = & \displaystyle F_{s-1}^{p}({\mathcal{B}}_{0}\cup \{z_{1}^{p^{s}},\ldots ,z_{e}^{p^{s}}\})(z_{1}^{p^{s-1}},\ldots ,z^{p^{s-1}})\nonumber\\ \displaystyle & = & \displaystyle F_{s-1}^{p}(z_{1}^{p^{s}},\ldots ,z_{e}^{p^{s}})({\mathcal{B}}_{0}\cup \{z_{1}^{p^{s-1}},\ldots ,z^{p^{s-1}}\})\nonumber\\ \displaystyle & = & \displaystyle F_{s-2}^{p}({\mathcal{B}}_{0}\cup \{z_{1}^{p^{s-1}},\ldots ,z^{p^{s-1}}\}),\nonumber\end{eqnarray}$$

and that ends proof of the induction, after last step we obtain that ${\mathcal{B}}_{0}\cup \{z_{1},\ldots z_{e}\}$ is a $p$ -basis for $F_{1-2}=K$ over $k$ .◻

In the spirit of [2, Definition 6.1] we introduce the following term:

Definition 3.6. Let $(K,\mathbb{D}[m])$ be a $G[m]$ -field. A subset $B\subseteq K$ is called a canonical $G$ -basis if:

• ∙ $|B|=e$ ;

• ∙ $B$ is $p$ -independent in $K$ over $C_{K}$ ;

• ∙ there is an embedding of $G[m]$ -fields $(k(G),\mathbb{D}^{G}[m])\rightarrow (K,\mathbb{D}[m])$ (see Example 2.12) such that $B$ is the image of the set of canonical parameters of $G$ corresponding to the canonical $G$ -derivation.

Example 3.7. Let us take $G=\mathbb{G}_{a}^{e}$ . By [5, Theorem 27.3] and Lemma 4.15 if $[K:C_{K}]=p^{e}$ then $(K,\mathbb{D}[m])$ has a canonical $\mathbb{G}_{a}^{e}$ -basis. This fact was used in [14], to obtain the quantifier elimination for the theory of separably closed strict $\mathbb{G}_{a}^{e}$ -fields, satisfying $[K:C_{K}]=p^{e}$ .

Theorem 3.8. Assume that a $G[m]$ -field $(K,\mathbb{D}[m])$ has a canonical $G$ -basis, then $\mathbb{D}[m]$ is strongly integrable.

Proof. Let $B=\{z_{1},\ldots ,z_{e}\}$ be a canonical $G$ -basis of $(K,\mathbb{D}[m])$ and let $\bar{X}$ be an $e$ -tuple of variables. By a choice of local parameters of $G$ at the identity we get an embedding $k(\bar{X})\subseteq k(G)$ . Proposition 3.5 assures the existence of a set $B_{0}\subseteq C_{K}^{\text{abs}}$ such that $B_{0}\cup B$ is a $p$ -basis of $K$ over $k$ . Let $K^{\prime }:=k(B_{0})$ . Because $B_{0}\cup B$ is algebraically independent over $k$ , $B_{0}$ is algebraically independent over $k(B)$ . Moreover, $k(B)\cong k(\bar{X})\subset k(G)$ is an algebraic extension, thus $B_{0}$ is algebraically independent over $k(G)$ . Therefore, $K^{\prime }$ and $k(G)$ are linearly disjoint over $k$ , so the “multiplication” map $\unicode[STIX]{x1D707}:k(G)\otimes _{k}K^{\prime }\rightarrow K$ is an injection, and therefore it extends to $\tilde{\unicode[STIX]{x1D707}}:(k(G)\otimes _{k}K^{\prime })_{0}\rightarrow K$ .

By [5, Theorem 26.8], $K^{\prime }(B)$ is purely transcendental over $K^{\prime }$ and $K^{\prime }(B)\subseteq K$ is $0$ -étale. Hence we have $K^{\prime }(B)\cong K^{\prime }(\bar{X})\cong (k(\bar{X})\otimes _{k}K^{\prime })_{0}\subseteq (k(G)\otimes _{k}K^{\prime })_{0}$ ( $k(G)\otimes _{k}K^{\prime }$ is a domain as a subring of $K$ ). Therefore, we have a natural mapping $K^{\prime }(B)\rightarrow (k(G)\otimes _{k}K^{\prime })_{0}=:K^{\prime }(G)$ .

Note that the following diagram commutes

The extension of fields $K^{\prime }(B)\subseteq K$ is smooth, and by [5, Theorem 26.9] it is also separable. In particular, $K^{\prime }(G)$ is separable over $K^{\prime }(B)$ . The algebraicity of the extension $k(B)\subseteq k(G)$ implies the algebraicity of the extension $K^{\prime }(B)\subseteq K^{\prime }(G)$ , and that, due to [5, Theorem 26.1], means that $K^{\prime }(B)\subseteq K^{\prime }(G)$ is $0$ -étale. Therefore, also $\tilde{\unicode[STIX]{x1D707}}:K^{\prime }(G)\rightarrow K$ is $0$ -étale. We have the following tower of $k$ -algebras

$$\begin{eqnarray}k(G)\otimes _{k}K^{\prime }\subseteq (k(G)\otimes _{k}K^{\prime })_{0}=K^{\prime }(G)\xrightarrow[{}]{\tilde{\unicode[STIX]{x1D707}}}K,\end{eqnarray}$$

where both extensions are $0$ -étale. By [5, Theorem 26.7] $k(G)\otimes _{k}K^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D707}}K$ is $0$ -étale.

Now we are going to define a $G$ -ring structure on $R:=k(G)\otimes _{k}K^{\prime }$ . For every $\mathbf{i}\in \mathbb{N}^{e}$ , $v\in k(G)$ and $w\in K^{\prime }$ we define

$$\begin{eqnarray}D_{\mathbf{i}}^{\prime }(v\otimes w):=D_{\boldsymbol{ i}}^{G}(v)\otimes w.\end{eqnarray}$$

Note that for every $\mathbf{i}\in [p^{m}]^{e}$ , we have $\unicode[STIX]{x1D707}\circ D_{\mathbf{i}}^{\prime }=D_{\mathbf{i}}\circ \unicode[STIX]{x1D707}$ . Thus $(R,\mathbb{D}^{\prime }[m])\xrightarrow[{}]{\unicode[STIX]{x1D707}}(K,\mathbb{D})$ is a $G[m]$ -morphism. By Lemma 2.13 for $(R,\mathbb{D})$ , there exists a unique $G$ -derivation $\tilde{\mathbb{D}}$ on $K$ . Since both $\mathbb{D}$ and $\tilde{\mathbb{D}}[m]$ extend $\mathbb{D}^{\prime }[m]$ , by Lemma 2.13 for every $\mathbf{i}\in [p^{m}]^{e}$ we have $D_{\mathbf{i}}=\tilde{D}_{\mathbf{i}}$ .◻

Remark 3.9. The converse to Theorem 3.8 is not true in general. First of all, we need enough “space” to have a canonical $G$ -basis, so we assume

(2) $$\begin{eqnarray}[K:C_{K}]=p^{e}\end{eqnarray}$$

for an integrable $G[m]$ -field $(K,\mathbb{D})$ . For example $D_{\mathbf{i}}=0$ , for all $\mathbf{i}\neq \mathbf{0}$ , is integrable, but $[K:C_{K}]=1$ and there are not enough $p$ -independent elements to form a $G$ -basis. Equality (2) in dimension $e=1$ means that $D_{1}\neq 0$ and such an assumption is needed in [5, Theorem 27.3(ii)] to obtain the existence of a one-element canonical basis. Hence it is morally justified to assume (2) in the next Section, where we find a canonical $G$ -basis for a special algebraic group $G$ . Perhaps there are no general reasons for the converse theorem to hold and finding a canonical $G$ -basis is the only possibility for proving the existence of such a basis for a given algebraic group $G$ .

4 New examples of groups with canonical $G$ -bases

4.1 Unipotent groups of dimension two

In this subsection, we are going to find a canonical $G$ -basis for an algebraic group $G$ of a special type. Firstly we provide a well-known fact about derivations, then define $G$ and its group law. After this we specify which tuples satisfy the canonical $G$ -basis condition in this case and prove the existence of such basis for a $G[m]$ -field $(K,\mathbb{D})$ satisfying $[K:C_{K}]=p^{e}$ .

Fact 4.1. Let $L$ be a field, $\unicode[STIX]{x2202}\in \operatorname{Der}_{C}(L)$ , $\ker \unicode[STIX]{x2202}=C\neq L$ , $\unicode[STIX]{x2202}^{(p)}=0$ , then:

1. (i) there exists an element $z\in L$ such that $\unicode[STIX]{x2202}(z)=1$ , and $1,z,z^{2},\ldots ,z^{p-1}$ form a basis of $L$ over $C$ ;

2. (ii) $\ker \unicode[STIX]{x2202}^{(p-1)}=\operatorname{im}\unicode[STIX]{x2202}$ .

Proof. The first item is contained in [5, Theorem 27.3]. The second item is in [13, Lemma 3.], but for reader’s convenience, we include a short proof. The derivation $\unicode[STIX]{x2202}$ is a $C$ -linear map, after computing $\unicode[STIX]{x2202}$ on $1,z,z^{2},\ldots ,z^{p-1}$ we see that $\dim _{C}\ker \unicode[STIX]{x2202}=1$ . Therefore, $\dim _{C}\operatorname{im}\unicode[STIX]{x2202}=p-1$ , moreover $\dim _{C}\ker \unicode[STIX]{x2202}^{(p-1)}\leqslant p-1$ . The condition $\unicode[STIX]{x2202}^{(p)}=0$ implies that $\operatorname{im}\unicode[STIX]{x2202}\subseteq \ker \unicode[STIX]{x2202}^{(p-1)}$ , but $\dim _{C}\ker \unicode[STIX]{x2202}^{(p-1)}\leqslant \dim _{C}\operatorname{im}\unicode[STIX]{x2202}$ .◻

For $i\leqslant p$ let $\unicode[STIX]{x1D706}_{i}:=(p-1)!/(p-i)!i!\hspace{0.6em}{\rm mod}\hspace{0.2em}p$ , which is equal to the image of $(1/p)\binom{p}{i}$ in $\mathbb{F}_{p}$ . Following the [7, page 171], we define

$$\begin{eqnarray}\displaystyle & & \displaystyle H_{n}(X_{2},Y_{2}):=\biggl[\frac{1}{p}((X_{2}+Y_{2})^{p}-X_{2}^{p}-Y_{2}^{p})\biggr]^{p^{n}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{p}((X_{2}^{p^{n}}+Y_{2}^{p^{n}})^{p}-X_{2}^{p^{n+1}}-Y_{2}^{p^{n+1}})\in \mathbb{F}_{p}[X_{2},Y_{2}],\nonumber\end{eqnarray}$$

$$\begin{eqnarray}H_{n}(X_{2},Y_{2})=\mathop{\sum }_{i=1}^{p-1}\unicode[STIX]{x1D706}_{i}X_{2}^{ip^{n}}Y_{2}^{(p-i)p^{n}}.\end{eqnarray}$$

Consider the extension of commutative algebraic groups

$$\begin{eqnarray}0\rightarrow \mathbb{G}_{a}\rightarrow G\rightarrow \mathbb{G}_{a}\rightarrow 0,\end{eqnarray}$$

where the group operation $\ast$ on $G$ is given by

$$\begin{eqnarray}\displaystyle (X_{1},X_{2})\ast (Y_{1},Y_{2}) & = & \displaystyle F(X_{1},X_{2},Y_{1},Y_{2})\nonumber\\ \displaystyle & := & \displaystyle \biggl(X_{1}+Y_{1}+\mathop{\sum }_{n=0}^{M}\unicode[STIX]{x1D6FC}_{n}H_{n}(X_{2},Y_{2}),X_{2}+Y_{2}\biggr),\nonumber\end{eqnarray}$$

for a fixed $M\in \mathbb{N}$ and $\unicode[STIX]{x1D6FC}_{i}\in k$ for $i\leqslant M$ . We are interested in the following $m$ -truncation

$$\begin{eqnarray}F[m](v_{1},v_{2},w_{1},w_{2})=\biggl(v_{1}+w_{1}+\mathop{\sum }_{n=0}^{N}\unicode[STIX]{x1D6FC}_{n}H_{n}(v_{2},w_{2}),v_{2}+w_{2}\biggr),\end{eqnarray}$$

where $v_{1}$ , $v_{2}$ , $w_{1}$ and $w_{2}$ are $m$ -truncated variables and $N:=\min \{M,m-1\}$ . Without loss of generality we assume that $N=m-1$ . Let $(K,\mathbb{D})$ be a $G[m]$ -field (i.e.,  $(K,\mathbb{D})$ is a ${\hat{G}}[m]$ -field, but ${\hat{G}}=\hat{F}=F$ , so we consider just an $F[m]$ -field), such that $[K:C_{K}]=p^{2}$ .

Lemma 4.2. We have the following:

1. (i) $D_{(i,j)}=D_{(i,0)}D_{(0,j)}=D_{(0,j)}D_{(i,0)}$ ;

2. (ii) $D_{(i_{2},0)}\circ D_{(i_{1},0)}=\binom{i_{1}+i_{2}}{i_{1}}D_{(i_{1}+i_{2},0)}$ ;

3. (iii) $[p]_{F[m]}(v_{1},v_{2})=(-\!\sum _{n=0}^{N}\unicode[STIX]{x1D6FC}_{n}v_{2}^{p^{n+1}},0)$ ;

4. (iv) $D_{(i,j)}^{(p)}=0$ for every $i,j\leqslant p^{m-1}$ such that $i\neq 0$ ;

5. (v) if $j<m$ then

   $$\begin{eqnarray}D_{(0,p^{j})}^{(p)}=-\unicode[STIX]{x1D6FC}_{j}D_{(1,0)}+\mathop{\sum }_{n=p}^{p^{j}}\unicode[STIX]{x1D6FD}_{n}D_{(n,0)},\end{eqnarray}$$
   for some $\unicode[STIX]{x1D6FD}_{n}\in k$ .

Proof. The first two items are easy. For the proof of third item it is sufficient to prove inductively the following

$$\begin{eqnarray}[l]_{F}(v_{1},v_{2})=\biggl(lv_{1}+\mathop{\sum }_{n=0}^{N}\unicode[STIX]{x1D6FC}_{n}\biggl[\biggl(\frac{1}{p}(l^{p}-l)\biggr)v_{2}^{p}\biggr]^{p^{n}},lv_{2}\biggr).\end{eqnarray}$$

The fourth and the fifth item use the third part and Corollary 2.25. Specifically, one needs to show

$$\begin{eqnarray}\displaystyle D_{(0,j)}^{(p)} & = & \displaystyle \mathop{\sum }_{i_{0}+i_{1}p+\cdots +i_{N}p^{N}=j}(-1)^{i_{0}+\cdots +i_{N}}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\frac{(i_{0}+\cdots +i_{N})!}{i_{0}!\cdot \ldots \cdot i_{N}!}\quad \unicode[STIX]{x1D6FC}_{0}^{i_{0}}\cdot \ldots \cdot \unicode[STIX]{x1D6FC}_{N}^{i_{N}}D_{(i_{0}+\cdots +i_{N},0)},\nonumber\end{eqnarray}$$

for every $j\leqslant p^{m-1}$ . We leave it to the reader.◻

Let us consider the canonical $F$ -derivation from Example 2.10:

$$\begin{eqnarray}\operatorname{ev}_{F}:k\unicode[STIX]{x27E6}X_{1},X_{2}\unicode[STIX]{x27E7}\rightarrow (k\unicode[STIX]{x27E6}X_{1},X_{2}\unicode[STIX]{x27E7})\unicode[STIX]{x27E6}Y_{1},Y_{2}\unicode[STIX]{x27E7},\end{eqnarray}$$

where

$$\begin{eqnarray}\displaystyle & \displaystyle X_{1}\mapsto X_{1}+Y_{1}+\mathop{\sum }_{n=0}^{N}\unicode[STIX]{x1D6FC}_{n}\mathop{\sum }_{i=1}^{p-1}\unicode[STIX]{x1D706}_{i}X_{2}^{ip^{n}}Y_{2}^{(p-i)p^{n}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle X_{2}\mapsto X_{2}+Y_{2}. & \displaystyle \nonumber\end{eqnarray}$$

As in Example 2.12, the above $F$ -derivation could be considered as a $G$ -derivation on $k(G)$ (because $F={\hat{G}}$ ). In this situation $k(G)=k(X_{1},X_{2})$ , so we need to find an embedding $\unicode[STIX]{x1D711}$ of $(k(X_{1},X_{2}),\mathbb{D}^{G}[m])$ in $(K,\mathbb{D})$ such that for $x=\unicode[STIX]{x1D711}(X_{1})$ and $y=\unicode[STIX]{x1D711}(X_{2})$ we have:

1. (i) $[C_{K}(x,y):C_{K}]=p^{2}$ ;

2. (ii) $\sum _{i,j=0}^{p^{m}-1}D_{(i,j)}(x)v_{1}^{i}v_{2}^{j}=x+v_{1}+\sum _{n=0}^{N}\unicode[STIX]{x1D6FC}_{n}\sum _{i=1}^{p-1}\unicode[STIX]{x1D706}_{i}y^{ip^{n}}v_{2}^{(p-i)p^{n}}$ ;

3. (iii) $\sum _{i,j=0}^{p^{m}-1}D_{(i,j)}(y)v_{1}^{i}v_{2}^{j}=y+v_{2}.$

The conditions (i), (ii) and (iii) above are equivalent to

$$\begin{eqnarray}\displaystyle & \displaystyle D_{(1,0)}(x)=1,\quad D_{(0,1)}(x)=\unicode[STIX]{x1D6FC}_{0}\unicode[STIX]{x1D706}_{1}y^{p-1},\ldots , & \displaystyle \nonumber\\ \displaystyle & \displaystyle D_{(p^{n},0)}(x)=0,\quad D_{(0,p^{n})}(x)=\unicode[STIX]{x1D6FC}_{n}\unicode[STIX]{x1D706}_{1}y^{(p-1)p^{n}},\ldots & \displaystyle \nonumber\\ \displaystyle & \displaystyle D_{(1,0)}(y)=0,\quad ,D_{(0,1)}(y)=1,\quad D_{(p,0)}(y)=0,\quad D_{(0,p)}(y)=0,\ldots & \displaystyle \nonumber\end{eqnarray}$$

(since $D_{(1,0)}(x)=1$ , $D_{(1,0)}(y)=0$ and $D_{(0,1)}(y)=1$ imply, by Fact 3.2, that $[C_{K}(x,y):C_{K}]=p^{2}$ ). We are concerned now only with the terms of the form $D_{(p^{i},0)}$ and $D_{(0,p^{j})}$ . It will turn out later that it is enough to consider such terms to obtain expected $G$ -basis. Recall that $G$ is commutative, so each subset of constants is preserved, that is,

$$\begin{eqnarray}D_{(i,j)}(C_{(i^{\prime },j^{\prime })})\subseteq C_{(i^{\prime },j^{\prime })},\end{eqnarray}$$

for every $i,j,i^{\prime },j^{\prime }<p^{m}$ .

Recall also that $[F_{s-1}:F_{s}]=p^{2}$ for every $s\in \{0,\ldots ,m-1\}$ (Remark 3.4).

Fact 4.3. There exists $x,y\in K$ such that $D_{(1,0)}(x)=1$ , $D_{(1,0)}(y)=0$ and $D_{(0,1)}(y)=1$ .

Proof. Note that $D_{(1,0)}\in \operatorname{Der}_{C_{(1,0)}}(F_{-1})$ and $D_{(1,0)}^{(p)}=0$ , so we can use Lemma 2.22 and obtain $[F_{-1}:C_{(1,0)}]\leqslant p$ (Lemma 2.22 works for iterative HS-derivations, but by [5, Theorem 27.4], $D_{(1,0)}^{(p)}=0$ implies $\mathbb{G}_{a}$ -iterativity). Moreover, from Lemma 4.2,

$$\begin{eqnarray}D_{(0,1)}^{(p)}|_{C_{(1,0)}}=-\unicode[STIX]{x1D6FC}_{0}D_{(1,0)}|_{C_{(1,0)}}=0,\end{eqnarray}$$

so similarly $[C_{(1,0)}:F_{0}]\leqslant p$ . Since $[F_{-1}:F_{0}]=[K:C_{K}]=p^{2}$ , both $D_{(1,0)}\in \operatorname{Der}_{C_{(1,0)}}(F_{-1})$ and $D_{(0,1)}|_{C_{(1,0)}}\in \operatorname{Der}_{F_{0}}(C_{(1,0)})$ are nonzero, so they satisfy assumptions of Fact 4.1(i).◻

Lemma 4.4. Let $n\geqslant 0$ and $i,j<p^{n+1}$ , be such that $(i,j)\neq (0,0)$ . Then we have $F_{n}\subseteq C_{(i,j)}$ .

Proof. We argue inductively on $l=i+j$ to show that $D_{(i,j)}|_{F_{n}}=0$ for $i,j<p^{n+1}$ such that $(i,j)\neq (0,0)$ . For $l=1$ it is clear. Assume that $i,j<p^{n+1}$ , $(i,j)\neq (0,0)$ and for every $i^{\prime }+j^{\prime }<i+j$ such that $(i^{\prime },j^{\prime })\neq (0,0)$ we have $D_{(i^{\prime },j^{\prime })}|_{F_{n}}=0$ . If $i=\unicode[STIX]{x1D6FE}_{0}+\cdots +\unicode[STIX]{x1D6FE}_{r}p^{r}$ , $j=\unicode[STIX]{x1D6FD}_{0}+\cdots +\unicode[STIX]{x1D6FD}_{s}p^{s}$ , $r,s\leqslant n$ , $0\leqslant \unicode[STIX]{x1D6FE}_{0},\ldots ,\unicode[STIX]{x1D6FE}_{r},\unicode[STIX]{x1D6FD}_{0},\ldots ,\unicode[STIX]{x1D6FD}_{s}<p$ , and $\unicode[STIX]{x1D6FE}_{r},\unicode[STIX]{x1D6FD}_{s}\neq 0$ , then from Fact 2.16

$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{r}\unicode[STIX]{x1D6FD}_{s}D_{(i,j)}=D_{(i-p^{r},j-p^{s})}\circ D_{(p^{r},p^{s})}-\mathbf{r}(D_{(i^{\prime },j^{\prime })})_{0<i^{\prime }+j^{\prime }<i+j}.\end{eqnarray}$$

By Lemma 4.2  $F_{n}\subseteq \ker D_{(p^{r},0)}\subseteq \ker D_{(p^{r},p^{s})}$ .◻

Lemma 4.5. For each $n\geqslant -1$ sets $F_{n}$ and $F_{n}\cap C_{(p^{n+1},0)}$  are subfields of  $K$ .

Proof. By Remark 3.1  $F_{n}$ is a subfield. Using Lemma 4.4, we get that $D_{(p^{n+1},0)}|_{F_{n}}\in \operatorname{Der}(F_{n})$ and therefore $\ker D_{(p^{n+1},0)}|_{F_{n}}$ , equal to $F_{n}\cap C_{(p^{n+1},0)}$ , also is a subfield.◻

4.1.1 Finding $y$

Fact 4.6. There exists an element $y\in K$ such that:

1. (i) $D_{(1,0)}(y)=0$ and $D_{(0,1)}(y)=1$ ;

2. (ii) for every $0<n<m$ we have $D_{(p^{n},0)}(y)=D_{(0,p^{n})}(y)=0$ .

Proof. For the proof of (i) consider the element $y\in K$ from Fact 4.3. For the proof of (ii) we inductively correct $y$ . Take the maximal $0<l<m$ such that for every $0<l^{\prime }<l$

$$\begin{eqnarray}D_{(p^{l^{\prime }},0)}(y)=D_{(0,p^{l^{\prime }})}(y)=0.\end{eqnarray}$$

Assume that $D_{(p^{l},0)}(y)\neq 0$ or $D_{(0,p^{l})}(y)\neq 0$ , otherwise we have nothing to do.

Let $D_{(p^{l},0)}(y)\neq 0$ , clearly $D_{(p^{l},0)}(y)\in F_{l-1}$ , so $D_{(p^{l},0)}(y)\in \ker D_{(p^{l},0)}|_{F_{l-1}}^{(p-1)}$ equal, due to Fact 4.1, to the image of $D_{(p^{l},0)}|_{F_{l-1}}$ . There exists $z\in F_{l-1}$ such that $D_{(p^{l},0)}(y)=D_{(p^{l},0)}(z)$ . We exchange $y$ with $y-z$ .

Now let $D_{(p^{l},0)}(y)=0$ and $D_{(0,p^{l})}(y)\neq 0$ . We have $D_{(0,p^{l})}(y)\in F_{l-1}\cap C_{(p^{l},0)}$ and as before $D_{(0,p^{l})}(y)\in \ker D_{(0,p^{l})}|_{F_{l-1}\cap C_{(p^{l},0)\!}}^{(p-1)}$ . Again, we would like to use Fact 4.1, so it is enough to check that $D_{(0,p^{l})}|_{F_{l-1}\cap C_{(p^{l},0)}}^{(p)}=0$ , which follows from Lemmas 4.2 and 4.4.◻

For the rest of this subsection we fix $y\in K$ as in the fact above.

Remark 4.7. If $p^{q}\leqslant n<p^{q+1}$ and $D_{(p^{q},0)}(a)=0$ , then also $D_{(n,0)}(a)=0$ .

Proof. It is a property of the standard iterativity rule. ◻

The values of $D_{(p^{n},0)}$ and $D_{(0,p^{n})}$ ( $n<m$ ) at the element $y$ determine the value of $D_{(i,j)}$ (for every $(i,j)$ ) at $y$ , which we show below. Moreover, the proposition below assures us that $y$ fulfills the canonical $G$ -basis conditions.

Proposition 4.8. We have the following:

1. (i) for all $n>0$ $D_{(n,0)}(y)=0$ ;

2. (ii) $D_{(n,0)}(y^{s})=0$ for all $n>0$ and $1\leqslant s\leqslant p-1$ ;

3. (iii) for all $n>1$ $D_{(0,n)}(y)=0$ ;

4. (iv) $D_{(0,p^{n})}(y^{s})=0$ for all $n>1$ and $1\leqslant s\leqslant p-1$ ;

5. (v)

   $$\begin{eqnarray}D_{(i,j)}(y)=\left\{\begin{array}{@{}ll@{}}\displaystyle y\quad & \displaystyle \text{if }(i,j)=(0,0),\\ \displaystyle 1\quad & \displaystyle \text{if }(i,j)=(0,1),\\ \displaystyle 0\quad & \displaystyle \text{otherwise.}\end{array}\right.\end{eqnarray}$$

Proof. The item (i) follows from Remark 4.7. The item (ii) is a consequence of the equality $D_{(n,0)}(y^{s})=yD_{(n,0)}(y^{s-1})$ . Our iterativity rule forces (by Fact 2.16) that

(3) $$\begin{eqnarray}D_{(0,j_{2})}D_{(0,j_{1})}=\binom{j_{1}+j_{2}}{j_{1}}D_{(0,j_{1}+j_{2})}+\mathbf{r}(D_{(i,j)})_{\substack{ 0<i+j<j_{1}+j_{2} \\ i\neq 0}}.\end{eqnarray}$$

For the proof of item (iii) we use the equation above in an induction argument. If $p=2$ , then $D_{(0,2)}(y)=0$ . For $p>2$ we have

$$\begin{eqnarray}0=D_{(0,1)}D_{(0,1)}(y)=2D_{(0,2)}(y)+\mathbf{r}(D_{(0,j)}D_{(i,0)})_{i\neq 0}(y)=2D_{(0,2)}(y).\end{eqnarray}$$

Assume that $n\geqslant 2$ and $D_{(0,2)}(y)=\cdots =D_{(0,n)}(y)=0$ . Take $n+1=\unicode[STIX]{x1D6FE}_{0}+\unicode[STIX]{x1D6FE}_{1}p+\cdots +\unicode[STIX]{x1D6FE}_{s}p^{s}$ , where $\unicode[STIX]{x1D6FE}_{0},\ldots ,\unicode[STIX]{x1D6FE}_{s}<p$ , $\unicode[STIX]{x1D6FE}_{s}\neq 0$ .

$$\begin{eqnarray}\displaystyle D_{(0,n+1-p^{s})}D_{(0,p^{s})}(y) & = & \displaystyle \unicode[STIX]{x1D6FE}_{s}D_{(0,n+1)}(y)+\mathbf{r}(D_{(0,j)}D_{(i,0)})_{i\neq 0}(y)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FE}_{s}D_{(0,n+1)}(y).\nonumber\end{eqnarray}$$

If $s=0$ , then the left-hand side of the last expression is equal to $D_{(0,n)}D_{(0,1)}(y)=0$ , if $s\neq 0$ we proceed similarly due to the equation $D_{(0,p^{s})}(y)=0$ . The proof of the item (iv) uses the equation

$$\begin{eqnarray}D_{(0,l)}(y^{s})=yD_{(0,l)}(y^{s-1})+D_{(0,l-1)}(y^{s-1})\end{eqnarray}$$

and it is a simple induction on $s$ . The item (v) follows from Lemma 4.2(i).◻

4.1.2 Finding $x$

Fact 4.9. There exists an element $w\in K$ such that:

1. (i) $D_{(1,0)}(w)=1$ and $D_{(0,1)}(w)=0$ ;

2. (ii) for every $0<n<m$ we have $D_{(p^{n},0)}(w)=D_{(0,p^{n})}(w)=0$ .

Proof. We define $D_{(0,1)}^{\ast }:=D_{(0,1)}|_{C_{(1,0)}}$ , note that $D_{(0,1)}^{\ast (p)}=0$ and $D_{(0,1)}^{\ast }\neq 0$ . We start with an element $x$ from the statement of Fact 4.3, for which we have $D_{(0,1)}(x)\in C_{(1,0)}$ . Naturally $D_{(0,1)}(x)\in \ker D_{(0,1)}^{\ast (p-1)}=\operatorname{im}D_{(0,1)}^{\ast }$ . Hence there exists an element $z\in C_{(1,0)}$ such that $D_{(0,1)}(x)=D_{(0,1)}(z)$ . Taking $w=x-z$ give us the first part. The second part follows as in the proof of Fact 4.6.◻

Lemma 4.10. There exists an element $x\in K$ satisfying:

1. (i) $D_{(1,0)}(x)=1,\;\;D_{(0,1)}(x)=\unicode[STIX]{x1D6FC}_{0}y^{p-1}$ ;

2. (ii) $D_{(p^{n},0)}(x)=0$ and $D_{(0,p^{n})}(x)=\unicode[STIX]{x1D6FC}_{n}y^{(p-1)p^{n}}$ for each $0<n\leqslant N$ ;

3. (iii) $D_{(p^{n},0)}(x)=D_{(0,p^{n})}(x)=0$ for each $N<n<m$ .

Proof. The proof of item (ii) is more complicated, but reasoning is similar to the proof of the point (i).

(i) We start with $x\in K$ from Fact 4.3. If $\unicode[STIX]{x1D6FC}_{0}=0$ , we proceed like in the proof of Fact 4.6. Assume $\unicode[STIX]{x1D6FC}_{0}\neq 0$ , we need $x^{\prime }\in C_{(1,0)}$ such that $D_{(0,1)}(x+x^{\prime })=\unicode[STIX]{x1D6FC}_{0}y^{p-1}$ . We have

$$\begin{eqnarray}D_{(1,0)}(\unicode[STIX]{x1D6FC}_{0}y^{p-1}-D_{(0,1)}(x))=\unicode[STIX]{x1D6FC}_{0}D_{(1,0)}(y^{p-1})=0,\end{eqnarray}$$

therefore $\unicode[STIX]{x1D6FC}_{0}y^{p-1}-D_{(0,1)}(x)\in \ker D_{(1,0)}\subseteq \ker D_{(1,0)}^{(p-1)}=\operatorname{im}D_{(1,0)}$ . So there exists $z\in K$ such that

$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{0}y^{p-1}-D_{(0,1)}(x)=D_{(1,0)}(z)=-\frac{1}{\unicode[STIX]{x1D6FC}_{0}}D_{(0,1)}^{(p)}(z).\end{eqnarray}$$

The last equality comes from Lemma 4.2, since $D_{(0,1)}^{(p)}=-\unicode[STIX]{x1D6FC}_{0}D_{(1,0)}$ . Then we can take $x^{\prime }=-(1/\unicode[STIX]{x1D6FC}_{0})D_{(0,1)}^{(p-1)}(z)$ , since:

$$\begin{eqnarray}D_{(1,0)}\biggl(x-\frac{1}{\unicode[STIX]{x1D6FC}_{0}}D_{(0,1)}^{(p-1)}(z)\biggr)=1-\frac{1}{\unicode[STIX]{x1D6FC}_{0}}D_{(0,1)}^{(p-1)}(D_{(1,0)}(z)),\end{eqnarray}$$

but

(4) $$\begin{eqnarray}\displaystyle D_{(0,1)}^{(p-1)}(D_{(1,0)}(z)) & = & \displaystyle D_{(0,1)}^{(p-1)}(\unicode[STIX]{x1D6FC}_{0}y^{p-1}-D_{(0,1)}(x))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FC}_{0}D_{(0,1)}^{(p-1)}(y^{p-1})-D_{(0,1)}^{(p)}(x)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FC}_{0}(p-1)!+\unicode[STIX]{x1D6FC}_{0}D_{(1,0)}(x)=\unicode[STIX]{x1D6FC}_{0}((p-1)!+1)\end{eqnarray}$$

and by Wilson’s theorem it is equal to $0$ .

(ii) As in the proof of 4.6, we take the maximal $0<l\leqslant N$ such that for every $0<l^{\prime }<l$

$$\begin{eqnarray}D_{(p^{l^{\prime }},0)}(x)=0,\qquad D_{(0,p^{l^{\prime }})}(x)=\unicode[STIX]{x1D6FC}_{l^{\prime }}y^{(p-1)p^{l^{\prime }}}.\end{eqnarray}$$

Case 1. $D_{(p^{l},0)}(x)\neq 0$ .

Clearly, $D_{(p^{l},0)}(x)\in C_{(p^{l^{\prime }},0)}$ for every $0\leqslant l^{\prime }<l$ . Moreover, for every $0\leqslant l^{\prime }<l$

(5) $$\begin{eqnarray}\displaystyle D_{(0,p^{l^{\prime }})}D_{(p^{l},0)}(x) & = & \displaystyle D_{(p^{l},0)}D_{(0,p^{l^{\prime }})}(x)\nonumber\\ \displaystyle & = & \displaystyle D_{(p^{l},0)}(\unicode[STIX]{x1D6FC}_{l^{\prime }}y^{(p-1)p^{l^{\prime }}})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FC}_{l^{\prime }}D_{(p^{l-l^{\prime }},0)}(y^{p-1})^{p^{l^{\prime }}}=0,\end{eqnarray}$$

by Proposition 4.8(ii) where the last equation follows. This means that $D_{(p^{l},0)}(x)\in F_{l-1}$ and furthermore $D_{(p^{l},0)}(x)\in \ker D_{(p^{l},0)}|_{F_{l-1}}^{(p-1)}=\operatorname{im}D_{(p^{l},0)}|_{F_{l-1}}$ . Hence there exists $z\in F_{l-1}$ such that $D_{(p^{l},0)}(x)=D_{(p^{l},0)}(z)$ and we replace $x$ with $x-z$ .

Case 2. $D_{(p^{l},0)}(x)=0$ and $D_{(0,p^{l})}(x)\neq \unicode[STIX]{x1D6FC}_{l}y^{(p-1)p^{l}}$ .

If $\unicode[STIX]{x1D6FC}_{l}=0$ we argue similarly as many times before (compare also with the proof of item (iii)), so let $\unicode[STIX]{x1D6FC}_{l}\neq 0$ . The aim of this part is to find an element $x^{\prime }\in F_{l-1}\cap C_{(p^{l},0)}$ such that

$$\begin{eqnarray}D_{(0,p^{l})}(x+x^{\prime })=\unicode[STIX]{x1D6FC}_{l}y^{(p-1)p^{l}}.\end{eqnarray}$$

We introduce

$$\begin{eqnarray}W:=C_{(0,1)}\cap C_{(p^{l},0)}\cap \mathop{\bigcap }_{1\leqslant l^{\prime }<l}C_{(p^{l^{\prime }},0)}\cap C_{(0,p^{l^{\prime }})}.\end{eqnarray}$$

Note that the element $w$ from Fact 4.9 satisfies $w\in W\backslash \ker D_{(1,0)}^{\ast }$ , where $D_{(1,0)}^{\ast }:=D_{(1,0)}|_{W}$ .

Claim. $\ker D_{(1,0)}^{\ast }\subseteq \operatorname{im}D_{(1,0)}^{\ast }$ .

Proof of the Claim.

Note that $W_{0}:=W\cap C_{(1,0)}=F_{l-1}\cap C_{(p^{l},0)}=\ker D_{(1,0)}^{\ast }$ is a subfield of $K$ (by Lemma 4.5). Using Lemma 4.4 we obtain that $W$ is a vector space over $W_{0}$ . Now take $a\in W$ such that $D_{(1,0)}^{\ast }(a)=0$ , that means $a\in W_{0}$ . The element $a\cdot w$ belongs to $W$ and moreover $D_{(1,0)}^{\ast }(aw)=aD_{(1,0)}^{\ast }(w)=a$ , so $a\in \operatorname{im}D_{(1,0)}^{\ast }$ .◻

It is not to hard to see that

$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{l}y^{(p-1)p^{l}}-D_{(0,p^{l})}(x)\in F_{l-1}.\end{eqnarray}$$

Moreover, since $D_{(1,0)}(y)=0$ , we have

$$\begin{eqnarray}D_{(p^{l},0)}(\unicode[STIX]{x1D6FC}_{l}y^{(p-1)p^{l}})=\unicode[STIX]{x1D6FC}_{l}D_{(1,0)}(y^{(p-1)})^{p^{l}}=\unicode[STIX]{x1D6FC}_{l}(p-1)(y^{p-2}D_{(1,0)}(y))^{p^{l}}=0.\end{eqnarray}$$

We conclude that

$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{l}y^{(p-1)p^{l}}-D_{(0,p^{l})}(x)\in F_{l-1}\cap C_{(p^{l},0)}=W\cap C_{(1,0)}.\end{eqnarray}$$

In other words $\unicode[STIX]{x1D6FC}_{l}y^{(p-1)p^{l}}-D_{(0,p^{l})}(x)\in \ker D_{(1,0)}^{\ast }\subseteq \operatorname{im}D_{(1,0)}^{\ast }$ , and there is $z\in W$ such that

$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{l}y^{(p-1)p^{l}}-D_{(0,p^{l})}(x)=D_{(1,0)}(z).\end{eqnarray}$$

From Lemma 4.2 we know that

$$\begin{eqnarray}D_{(0,p^{l})}^{(p)}=-\unicode[STIX]{x1D6FC}_{l}D_{(1,0)}+\mathop{\sum }_{n=p}^{p^{l}}\unicode[STIX]{x1D6FD}_{n}D_{(n,0)},\end{eqnarray}$$

for some $\unicode[STIX]{x1D6FD}_{n}\in k$ . By Remark 4.7 for every $p\leqslant i\leqslant p^{l}$ $D_{(i,0)}|_{W}=0$ , consequently $D_{(1,0)}(z)=-(1/\unicode[STIX]{x1D6FC}_{l})D_{(0,p^{l})}^{(p)}(z)$ . For $x^{\prime }$ take $-(1/\unicode[STIX]{x1D6FC}_{l})D_{(0,p^{l})}^{(p-1)}(z)$ , only an argument for $D_{(0,p^{l})}^{(p-1)}(z)\in C_{(1,0)}$ is missing, and it is straightforward modification of the equation (4).

(iii) It follows the proof of Fact 4.6, we need to check only that $D_{(p^{l},0)}(x),D_{(0,p^{l})}(x)\in F_{l-1}$ for $l>N$ . Obviously, $D_{(p^{l},0)}(x),D_{(0,p^{l})}(x)\in \bigcap _{l^{\prime }=0}^{l-1}C_{(p^{l^{\prime }},0)}\cap \bigcap _{l^{\prime }=N+1}^{l-1}C_{(0,p^{l^{\prime }})}$ . Let $0\leqslant l^{\prime }\leqslant N$ , then

$$\begin{eqnarray}D_{(p^{l},0)}D_{(0,p^{l^{\prime }})}(x)=D_{(p^{l},0)}(\unicode[STIX]{x1D6FC}_{l^{\prime }}y^{(p-1)p^{l^{\prime }}})=\unicode[STIX]{x1D6FC}_{l^{\prime }}D_{(p^{l-l^{\prime }},0)}(y^{p-1})^{p^{l^{\prime }}}=0,\end{eqnarray}$$

as in (5). Furthermore,

$$\begin{eqnarray}D_{(0,p^{l})}D_{(0,p^{l^{\prime }})}(x)=D_{(0,p^{l})}(\unicode[STIX]{x1D6FC}_{l^{\prime }}y^{(p-1)p^{l^{\prime }}})=\unicode[STIX]{x1D6FC}_{l^{\prime }}D_{(0,p^{l-l^{\prime }})}(y^{p-1})^{p^{l^{\prime }}},\end{eqnarray}$$

so we are done if $D_{(0,p^{l-l^{\prime }})}(y^{p-1})=0$ , which is a part of Proposition 4.8.◻

We fix $x\in K$ as in the above fact.

Lemma 4.11. We have the following:

1. (i) for all $n>1$ $D_{(n,0)}(x)=0$ ;

2. (ii) for all $n>0$

   $$\begin{eqnarray}D_{(0,n)}(x)=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D6FC}_{l}\unicode[STIX]{x1D706}_{i}y^{(p-i)p^{l}}\quad & \displaystyle \text{if }0\leqslant l\leqslant N,1\leqslant i<p,n=ip^{l},\\ \displaystyle 0\quad & \displaystyle \text{otherwise.}\end{array}\right.\end{eqnarray}$$

Proof. The item (i) for $n\geqslant p$ follows from Remark 4.7, and for $1<n<p$ from Lemma 4.2 and $D_{(1,0)}(x)=1$ . To prove the item (ii) we argue inductively. Note that $\unicode[STIX]{x1D706}_{1}=1$ , so for $n=1$ it is clear. Assume that for every $n^{\prime }<n$ our thesis is true. Let $n=\unicode[STIX]{x1D6FE}_{0}+\unicode[STIX]{x1D6FE}_{1}p+\cdots +\unicode[STIX]{x1D6FE}_{s}p^{s}$ , where $\unicode[STIX]{x1D6FE}_{0},\ldots ,\unicode[STIX]{x1D6FE}_{s}<p$ and $\unicode[STIX]{x1D6FE}_{s}\neq 0$ .

Claim 1.

(6) $$\begin{eqnarray}\displaystyle & \displaystyle D_{(0,n-p^{s})}D_{(0,p^{s})}(x)=\unicode[STIX]{x1D6FE}_{s}D_{(0,n)}(x), & \displaystyle\end{eqnarray}$$

(7) $$\begin{eqnarray}\displaystyle & \displaystyle D_{(0,n-\unicode[STIX]{x1D6FE}_{s}p^{s})}D_{(0,\unicode[STIX]{x1D6FE}_{s}p^{s})}(x)=D_{(0,n)}(x). & \displaystyle\end{eqnarray}$$

Proof of the Claim 1.

Both equations have similar proofs, so we consider only the first one. We start with the equation (3) for $j_{1}=p^{s}$ and $j_{s}=n-p^{s}$ :

$$\begin{eqnarray}D_{(0,n-p^{s})}D_{(0,p^{s})}=\unicode[STIX]{x1D6FE}_{s}D_{(0,n)}+\mathbf{r}(D_{(i,j)})_{\substack{ 0<i+j<n \\ i\neq 0}}.\end{eqnarray}$$

Our aim is to show that $D_{(i,j)}(x)=0$ for $0<i+j<n$ , $i\neq 0$ . The component with $D_{(1,0)}$ ( $i=1$ and $j=0$ ) does not occur. To see this, we compare the sides of the equation from the iterativity definition for our chosen iterativity rule, where on the left-hand side we focus on $D_{(0,n-p^{s})}D_{(0,p^{s})}$ . A nonzero component with $D_{(1,0)}$ implies that $n=p^{s+1}$ and this is impossible. Let us assume that $i=1$ and $j>0$ . Because of $j<n$ , $D_{(0,j)}(x)$ is, due to the inductive assumption, equal to $\unicode[STIX]{x1D6FD}y^{r}$ for some $\unicode[STIX]{x1D6FD}\in k$ and $r>0$ , and then  $D_{(1,0)}D_{(0,j)}(x)=D_{(1,0)}(\unicode[STIX]{x1D6FD}y^{r})=0$ . If $i>1$ , then $D_{(i,j)}(x)=D_{(0,j)}D_{(i,0)}(x)=0$ .◻

Claim 2. For every $0\leqslant l\leqslant N$ and $0<i<p$ we have $D_{(0,ip^{l})}(x)=\unicode[STIX]{x1D6FC}_{l}\unicode[STIX]{x1D706}_{i}y^{(p-i)p^{l}}$ .

Proof of the Claim 2.

It is quite an obvious induction, using Claim 1:

$$\begin{eqnarray}\displaystyle D_{(0,(1+i)p^{l})}(x) & = & \displaystyle \frac{1}{i+1}D_{(0,p^{l})}D_{(0,ip^{l})}(x)=\frac{1}{i+1}D_{(0,p^{l})}(\unicode[STIX]{x1D6FC}_{l}\unicode[STIX]{x1D706}_{i}y^{(p-i)p^{l}})\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D6FC}_{l}\unicode[STIX]{x1D706}_{i}}{i+1}D_{(0,1)}(y^{p-i})^{p^{l}}=\frac{\unicode[STIX]{x1D6FC}_{l}\unicode[STIX]{x1D706}_{i}}{i+1}(p-i)y^{(p-i-1)p^{l}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FC}_{l}\unicode[STIX]{x1D706}_{i+1}y^{(p-i-1)p^{l}}.\square\nonumber\end{eqnarray}$$

Now we are going to the proof of the main induction step. We deal with several cases. If $s>N$ , then $D_{(0,p^{s})}(x)=0$ and the equation (6) implies that $D_{(0,n)}(x)=0$ . We can assume that $s\leqslant N$ and $n-\unicode[STIX]{x1D6FE}_{s}p^{s}\neq 0$ (otherwise we apply claim 2),

$$\begin{eqnarray}D_{(0,n)}(x)=D_{(0,n-\unicode[STIX]{x1D6FE}_{s}p^{s})}D_{(0,\unicode[STIX]{x1D6FE}_{s}p^{s})}(x)=\unicode[STIX]{x1D6FC}_{s}\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}_{s}}D_{(0,n-\unicode[STIX]{x1D6FE}_{s}p^{s})}((y^{p-\unicode[STIX]{x1D6FE}_{s}})^{p^{s}}).\end{eqnarray}$$

Recall that for every $a\in K$ the element $a^{p^{s}}$ belongs to $F_{s-1}$ , thus by Lemma 4.4  $D_{(0,n-\unicode[STIX]{x1D6FE}_{s}p^{s})}(a^{p^{s}})=0$ .◻

We show below that fixed element $x$ satisfies the required properties.

Proposition 4.12.

$$\begin{eqnarray}D_{(i,j)}(x)=\left\{\begin{array}{@{}ll@{}}\displaystyle x\quad & \displaystyle \text{if }(i,j)=(0,0),\\ \displaystyle 1\quad & \displaystyle \text{if }(i,j)=(1,0),\\ \displaystyle \unicode[STIX]{x1D6FC}_{l}\unicode[STIX]{x1D706}_{i}y^{(p-i)p^{l}}\quad & \displaystyle \text{if }(i,j)=(0,ip^{l}),0\leqslant l\leqslant N,1\leqslant i<p,\\ \displaystyle 0\quad & \displaystyle \text{otherwise.}\end{array}\right.\end{eqnarray}$$

Proof. By Lemma 4.2(i) we decompose $D_{(i,j)}$ into $D_{(0,j)}D_{(i,0)}$ . For $i\geqslant p$ Remark 4.7 and $D_{(p^{n},0)}(x)=0$ , where $0<n<m$ , ensure us that $D_{(i,0)}(x)=0$ , thus also $D_{(i,j)}(x)=0$ . For $1<i<p$ Remark 4.7(ii) used in an inductive argument give $D_{(i,0)}(x)=0$ . If $i=1$ , then $D_{(i,j)}(x)=D_{(j,0)}(1)$ . Hence $D_{(i,j)}(x)\neq 0$ if and only if $j=0$ . The case with $i=0$ is exactly Lemma 4.11.◻

By Propositions 4.8 and 4.12 the pair $\{x,y\}$ is a canonical $G$ -basis (see the beginning of Section 4.1). Thus we end with the following:

Corollary 4.13. For $G$ as defined above, any $m\in \mathbb{N}_{{>}0}$ and any $G[m]$ -field $(K,D[m])$ such that $[K:C_{K}]=p^{2}$ , there is a canonical $G$ -basis in $K$ .

4.2 Canonical $G$ -bases for commutative and connected groups

In the previous subsection we showed the existence of a canonical $G$ -basis for every $G[m]$ -field $(K,\mathbb{D})$ such that $[K:C_{K}]=p^{e}$ , where $G$ was very specific. Now we are going to apply those results to a more general class of algebraic groups.

Definition 4.14. Let $G$ be an algebraic group over $k$

1. (1) We call $G$ integrable if for any $m\in \mathbb{N}_{{>}0}$ , every $G[m]$ -derivation on a field $K$ such that $[K:C_{K}]=p^{\dim G}$ is strongly integrable.

2. (2) If for any $m\in \mathbb{N}_{{>}0}$ , every $G[m]$ -field $K$ such that $[K:C_{K}]=p^{\dim G}$ has a canonical $G$ -basis, we call $G$ canonically integrable.

By Theorem 3.8 each canonically integrable algebraic group is integrable.

Lemma 4.15. Let $G$ and $H$ be algebraic groups over $k$ . If both are canonically integrable, then also $G\times H$ is canonically integrable.

Proof. Introduce $A:=G\times H$ , $e_{1}:\dim G$ , $e_{2}:=\dim H$ and let $(K,\mathbb{D})$ be an $A[m]$ -field such that $[K:C_{K}]=p^{e_{1}+e_{2}}$ . We define

$$\begin{eqnarray}\displaystyle & \displaystyle \mathbb{D}^{\prime }:=(D_{(j_{1},\ldots ,j_{e_{1}})}^{\prime }:=D_{(j_{1},\ldots ,j_{e_{1}},\underbrace{0,\ldots ,0}_{e_{2}\text{ times}})})_{j_{1},\ldots ,j_{e_{1}}<p^{m}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbb{D}^{\prime \prime }:=(D_{(j_{e_{1}+1},\ldots ,j_{e_{1}+e_{2}})}^{\prime \prime }:=D_{(\underbrace{0,\ldots ,0}_{e_{1}\text{ times}},j_{e_{1}+1},\ldots ,j_{e_{1}+e_{2}})})_{j_{e_{1}+1},\ldots ,j_{e_{1}+e_{2}}<p^{m}}. & \displaystyle \nonumber\end{eqnarray}$$

From the $A[m]$ -iterativity diagram (see Definition 2.8) it follows that

$$\begin{eqnarray}D_{(j_{1},\ldots ,j_{e_{1}+e_{2}})}=D_{(j_{1},\ldots ,j_{e_{1}})}^{\prime }D_{(j_{e_{1}+1},\ldots ,j_{e_{1}+e_{2}})}^{\prime \prime },\end{eqnarray}$$

$\mathbb{D}^{\prime }$ is $G[m]$ -iterative and the second one, $\mathbb{D}^{\prime \prime }$ is $H[m]$ -iterative.

Taking any $p$ -basis of $K$ over $C_{K}$ and using Remark 3.4 assures us that for every $s<m\;[F_{s-1}:F_{s}]=p^{e_{1}+e_{2}}$ . Thus $[K:C_{K}^{\text{abs}}]=p^{m(e_{1}+e_{2})}$ . For $s<m$ we introduce

$$\begin{eqnarray}\displaystyle & \displaystyle F_{s}^{\prime }:=\mathop{\bigcap }_{j=0}^{s}C_{(p^{j},0,\ldots ,0)}\cap \cdots \cap C_{(0,\ldots ,0,p^{j},\underbrace{0,\ldots ,0}_{e_{2}\text{ times}})},\qquad F_{-1}^{\prime }:=K, & \displaystyle \nonumber\\ \displaystyle & \displaystyle F_{s}^{\prime \prime }:=\mathop{\bigcap }_{j=0}^{s}C_{(\underbrace{0,\ldots ,0}_{e_{1}\text{ times}},p^{j},0\ldots ,0)}\cap \cdots \cap C_{(0,\ldots ,0,p^{j})},\qquad F_{-1}^{\prime \prime }:=K. & \displaystyle \nonumber\end{eqnarray}$$

Consider the following tower of subfields

$$\begin{eqnarray}K\supseteq F_{0}^{\prime }\supseteq F_{1}^{\prime }\supseteq \cdots \supseteq F_{m-1}^{\prime }\supseteq F_{m-1}^{\prime }\cap F_{0}^{\prime \prime }\supseteq F_{m-1}^{\prime }\cap F_{1}^{\prime \prime }\supseteq \cdots F_{m-1}^{\prime }\cap F_{m-1}^{\prime \prime }.\end{eqnarray}$$

For every $s<m$ , due to Lemma 2.22 and $[K:C_{K}^{\text{abs}}]=p^{m(e_{1}+e_{2})}$ , we have

$$\begin{eqnarray}[F_{s-1}^{\prime }:F_{s}^{\prime }]=p^{e_{1}},\qquad [F_{m-1}^{\prime }\cap F_{s-1}^{\prime \prime }:F_{m-1}^{\prime }\cap F_{s}^{\prime \prime }]=p^{e_{2}}.\end{eqnarray}$$

In particular

$$\begin{eqnarray}[F_{m-1}^{\prime }:F_{m-1}^{\prime }\cap F_{0}^{\prime \prime }]=p^{e_{2}},\end{eqnarray}$$

so there exists a canonical $H[m]$ -basis $\{\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{e_{2}}\}$ of $(F_{m-1}^{\prime },\mathbb{D}^{\prime \prime })$ . Analogously, there exists a canonical $G[m]$ -basis $\{b_{1},\ldots ,b_{e_{1}}\}$ of $(F_{m-1}^{\prime \prime },\mathbb{D}^{\prime })$ . Elements $\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{e_{2}}$ are $p$ -independent in $F_{m-1}^{\prime }$ over $F_{m-1}^{\prime }\cap F_{0}^{\prime \prime }$ . By Corollary 2.19, they are also $p$ -independent in $K$ over $F_{0}^{\prime \prime }$ . Similarly for elements $b_{1},\ldots ,b_{e_{1}}$ , Corollary 2.19 implies that they are $p$ -independent in $F_{0}^{\prime \prime }$ over $F_{0}^{\prime \prime }\cap F_{0}^{\prime }$ . We have

$$\begin{eqnarray}[F_{0}^{\prime \prime }:F_{0}^{\prime \prime }\cap F_{0}^{\prime }]\leqslant p^{e_{1}},\end{eqnarray}$$

hence $F_{0}(b_{1},\ldots ,b_{e_{1}})=F_{0}^{\prime \prime }$ (note that $C_{K}=F_{0}=F_{0}^{\prime \prime }\cap F_{0}^{\prime }$ ). Now we have all the ingredients to state that $B:=\{b_{1},\ldots ,b_{e_{1}},\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{e_{2}}\}$ is a $p$ -basis of $K$ over $C_{K}$ . Verification that $B$ is also a canonical $A$ -basis is not hard and left to the reader.◻

We note the obvious fact:

Fact 4.16. Let $G$ and $H$ be isomorphic algebraic groups over $k$ . If $G$ is canonically integrable, then also $H$ is canonically integrable.

We can prove now the main theorem of this paper.

Theorem 4.17. Let $G$ be a commutative and connected linear algebraic group over an algebraically closed field $k$ . If maximal unipotent subgroup of $G$ has dimension at most 2, then $G$ is integrable.

Proof. Due to “Jordan decomposition” (last theorem on [10, page 70]), $G$ decomposes as $G_{U}\times G_{S}$ , where $G_{U}$ consists of unipotent elements and $G_{S}$ of semisimple elements. If the dimension of $G_{U}$ is equal to 2 we know by [7, Proposition 8, page 171] that $G_{U}$ is isomorphic to the group defined at the beginning of the previous subsection, so it is canonically integrable. If $\dim G_{U}=1$ , then by [8, Theorem 3.4.9] it is isomorphic to $\mathbb{G}_{a}$ , so canonically integrable by [1, Proposition 4.5]. We focus now on the semisimple part. By [8, Lemma 2.4.2(ii)], $G_{S}$ is diagonalizable, and by [8, Corollary 3.2.7(ii)] it is a torus. Proposition 4.10 from [1] states that also $\mathbb{G}_{m}$ is canonically integrable, so our group $G$ is isomorphic to the product of canonically integrable groups. Finally, we use Lemma 4.15, Fact 4.16 and Theorem 3.8.◻

In most cases of applications of the model theory to the differential algebra, we are dealing with an algebraic group $G$ over a field $k$ , which is assumed only to be perfect. One may wonder if Theorem 4.17 can be used for such $G[m]$ -fields, that is, for models of $G[m]-\operatorname{DCF}$  [2]. The answer is positive, because separable closure of $k$ , which is also algebraic closure, is contained in the absolute constants for models of $G[m]-\operatorname{DCF}$ (for an argument check e.g. proof of [12, Theorem 10]).

4.3 Possible generalizations

The desired generalization is to drop, in the assumptions of Theorem 4.17, the condition for the dimension of the unipotent component of group $G$ . Unfortunately, the ideas from the above proof do not work in the case of unipotent groups of dimension higher than $2$ . There are several reasons for that, which will be explained below.

First of all, we are using in Section 4.1 formulas for the group law of our group $G$ . Commutative, connected unipotent groups of dimension $2$ are characterized by [7, Proposition 8, page 171], so the explicit formulas for the group law are known. For the unipotent groups of dimension $3$ or greater, the best known to the author results coincide with [7, Theorem 1, page 176] and [7, Theorem 2, page 177]. It is unknown how the condition “being a subgroup” translates to the case of iterative derivations, hence the last reference does not help in finding a canonical basis. However, there is a hope to use [7, Theorem 1, page 176]. We sketch this idea and reveal difficulties in extending our technique to this context.

Assume that $G$ is isogenous to $W_{n}$ (the Witt group of dimension $n$ ). We should give a modification of [1, Lemma 2.6], from which we would conclude that $G$ is integrable if and only if $W_{n}$ is integrable. If this can be done, then we need to check whether $W_{n}$ is integrable. Unluckily, the whole procedure from Section 4.1 cannot be extended to show the existence of a canonical basis for $W_{n}$ . Even in the case $p=2$ and $n=3$ , some issues appear. If we translate the group law of $W_{3}$ (given by e.g. the formulas (a) and (b) in [11, page 128]) for $p=2$ into the conditions for a canonical basis:

1. (i) $[C_{K}(x,y,z):C_{K}]=2^{3}$ ;

2. (ii) $\sum _{i,j,l=0}^{2^{m}-1}D_{(i,j,l)}(x)v_{1}^{i}v_{2}^{j}v_{3}^{l}=x+v_{1}-yv_{2}+yzv_{3}+zv_{2}v_{3}-zv_{3}^{3}-z^{3}v_{3}$ ;

3. (iii) $\sum _{i,j,l=0}^{2^{m}-1}D_{(i,j,l)}(y)v_{1}^{i}v_{2}^{j}v_{3}^{l}=y+v_{2}-zv_{3}$ ;

4. (iv) $\sum _{i,j,l=0}^{2^{m}-1}D_{(i,j,l)}(z)v_{1}^{i}v_{2}^{j}v_{3}^{l}=z+v_{3}$ ;

we can notice occurrence of equations of a new kind:

$$\begin{eqnarray}D_{(0,1,1)}(x)=z.\end{eqnarray}$$

Proofs from Section 4.1 involve only “one-dimensional differential equations” and the above equation is not of such a form. The “one-dimensional differential equations” appear, because after diminishing the dimension by $1$ , at the induction step, we deal with one-dimensional subgroup, what is the case for two-dimensional group $G$ .

To summarize, generalizations of Theorem 4.17 to the higher dimensional unipotent component case need to involve new proofs. It is also possible that such a generalization cannot be done without some additional assumptions, or even cannot be done at all.