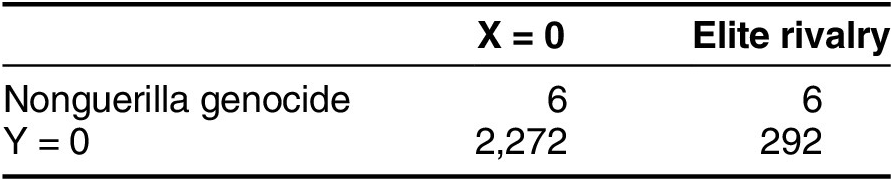In this article, we outline and seek to codify an emerging research practice that, following Fortna (Reference Fortna2004), we call “Large-N Qualitative Analysis” or LNQA. Among its distinctive features are a focus on regularities rather than average treatment effects, an effort to conduct within-case causal inference with respect to all cases falling within stipulated scope conditions, and the weight that the case analysis plays in causal inference. Not all exemplars of the approach that we identify fulfill these desiderata in full; the approach is emergent. Yet research of this sort is visible in both international relations and comparative politics, and also includes a multimethod variant (M-LNQA) that combines statistical and serial case work.
A particular advantage of LNQA is its approach to case selection. Gerring (Reference Gerring2006, 37) has argued that the case study approach to research “is most usefully defined as an intensive study of a single unit or small number of units (the cases), for the purpose of understanding a larger class of similar units (a population of cases)” (see also Beach and Pedersen Reference Beach and Pedersen2016). Because only a few cases are selected from a population, the qualitative methods literature has focused substantial attention on case selection to assure either representativeness or variation on the independent or dependent variables (Gerring Reference Gerring2017, pt. II; Goertz Reference Goertz2017, chap. 3). By seeking to select all cases, or at least very significant samples, LNQA increases our confidence that generalizations across the population—the share of cases that do and do not comport with the postulated causal relationship—reflect causal processes.
Dale Copeland’s (Reference Copeland2015) Economic Interdependence and War self-consciously adopts a methodological approach of this sort and thus nicely illustrates core features of LNQA.
-
• Copeland hypothesizes that the effects of interdependence on conflict operate not through the level of current transactions but through expectations of future trade and capital flows. If key decision makers think the status quo will continue—regardless of the current level of exchange—then peace continues. If political leaders anticipate future disruptions, including through the imposition of controls or sanctions, great powers take offensive and defensive measures that increase risks and can lead to conflict and war. Copeland’s theory is an example of a causal sufficiency hypothesis: if expectations are of future interdependence, then crises will be averted.
-
• Copeland then defines a class of cases that constitutes the scope for the proposed generalization, “the onset of essentially all the significant great power crises and wars from 1790 to 1991” (76). There are 40 of these.
-
• The findings are offered in the form of a regularity across this scope. The book does not undertake statistical analysis of the effect of X on Y, the outcome of the crises. Rather, it seeks to offer a summary of the percentage of the 40 great-power conflicts in which Copeland’s postulated causal mechanism—expectations about future interdependence—was present and operated as hypothesized. He concludes that “in thirty of the forty case periods, or 75 percent, economic interdependence played a moderate to strong causal role in shaping the events” (93).
-
• The causal force of the argument does not rest on this regularity, however, which could well be spurious. Rather, it rests on within-case causal inference across all cases falling in the stipulated scope. Copeland considers each case, looking not only at the influence of his favored causal variable but at competing theories and possible confounds. He pays particular attention to complex beliefs held by leaders, drawing widely on both primary and secondary sources. It is this within-case examination of the 40 cases that confirms that Copeland’s observed regularity is a causal generalization.
Copeland’s book generated significant debate, including with respect to his choice of major power crises and wars and whether his causal inferences were warranted (see Büthe Reference Büthe2017; Snyder Reference Snyder2015/16). However, he illustrates how LNQA combines existing methodological tools into a distinctive mix. He postulates a sufficient-conditions hypothesis about interdependence and conflict. He does not seek to identify the average treatment effect of X on Y. Rather, he seeks to confirm that a simple regularity is causal. He does so through case studies—within-case causal inference—on an entire population and uses those findings to reach a causal generalization about interdependence and conflict.
Copeland is among the more methodologically self-conscious examples of LNQA, but variants of the method have a much wider footprint in political science and sociology than might be thought. A full history of the emergence of LNQA is beyond the scope of this article, in part because it is hard to identify with any single theoretical or research tradition. Some classics of comparative historical analysis approximate the purely qualitative variant of the method (for example, Luebbert Reference Luebbert1991). Boolean approaches associated with Qualitative Comparative Analysis (QCA) also bear a family resemblance to LNQA. Yet with a handful of notable exceptions (for example, Mahoney Reference Mahoney2010), QCA has generally eschewed case studies on the entire population under scrutiny. Copeland (Reference Copeland2015) is exemplary of a much longer tradition of qualitative security studies that have adopted LNQA techniques, looking at rare events such as major-power wars, the rise and decline of great powers, or the acquisition or diplomatic use of nuclear weapons. In comparative politics, examples can be found in qualitative and multimethod studies that seek to generalize across all countries in a region—Latin America, Africa, Western and Eastern Europe—drawing on case studies of most or all the countries under consideration.
But LNQA is by no means limited to purely qualitative research. Around 2010, a wave of LNQA studies began to appear that were disconfirmatory in their approach (Goertz Reference Goertz2017, chap. 7). These studies took an existing theory, including quantitative empirical results, and subjected them to scrutiny through a consideration of a population of cases. Subsequently we find confirmatory multimethod LNQA studies in which sophisticated econometric designs and even game theory are coupled with case analysis of an entire population; we walk through examples of both of these combinations in more detail below (Carnegie and Carson Reference Carnegie and Carson2019; Sechser and Fuhrmann Reference Sechser and Fuhrmann2017).
To confirm that LNQA was in fact a more-or-less coherent research practice, we conducted a structured survey of all books in comparative politics and international relations with imprints from 2015–20 from Cornell (83), Princeton (42), and Cambridge (530) university presses. The selection procedures and links to exercises are included in the appendix. The appendix provides an annotated discussion—by no means exhaustive—of over 50 prominent examples covering a wide array of topics in the discipline.
What is striking about this diverse body of work is that almost none of it—with exceptions such as Copeland and a handful of others—justified their research designs with recourse to any methodological literature. Rather, authors felt their way, drawing on the particular mix of tools that we identify: hypothesized causal mechanisms; particular attention to scope conditions; an effort to establish regularities or generalizations rather than average treatment effects; and an approach to within-case causal inference that considers a very large sample of a population and ideally all cases. Not all this work comports with the method we outline in all regards. Yet we will make the case that norms with respect to LNQA are emergent and can be identified and codified.
We proceed in three steps. Part I provides an outline of the method and then discuses each of its core elements, linking them to relevant discussions in the case study and multimethod research literature. Part II provides examples of LNQA analyses of different types, starting with simple generalizations and moving to more complex ones. Part III describes the multimethod variant of the approach (M-LNQA), which we also illustrate with examples.
Part I: The Method Outlined
What Is LNQA?
What, exactly, is LNQA? We identify two variants, one that combines regularities and within-case causal inference (which we will refer to simply as LNQA); and multimethod LNQA (M-LNQA), which includes a statistical as well as case study component. Figure 1 offers a schematic description of the former. The approach starts with a theory and hypotheses along with a proposed causal mechanism concerning the relationship between X and Y. The stipulation of a precise causal mechanism is quite central to the method, because the mechanism structures the case research that is the inferential core of LNQA.

Figure 1 What Is LNQA?
The method does not focus on probabilistic average treatment effects that structure statistical work. Rather, it focuses on regularity causal claims. Necessary-conditions causal claims take the form of an expectation that if we see the outcome (Y = 1) we should also see the postulated treatment (X = 1). The scope of the empirical regularity is, therefore, all cases where Y = 1 and we call these Y generalizations. X generalizations take the form of an expectation that if we see the postulated treatment X, it will be followed by the outcome Y. We return to how scope conditions for these claims are established in more detail below. But what makes LNQA a plausible strategy is that the total number of X = 1 or Y = 1 cases is of limited enough size that within-case inference on all of them is feasible.
As a wide array of meanings are attached to the terms “regularity” and “generalization,” as well as cognate concepts such as “external validity,” it is worth clarifying what we—and those doing LNQA—mean. Going back to Hume, a proposed regularity or generalization is an expectation that there is a “constant conjunction” between a treatment X and a dependent variable Y. The regularity is typically expressed as a share of the cases that comport with the expectation, falling in a range from 0.0 to 1.0. For example, Pearl and Mackenzie (Reference Pearl and MacKenzie2018) report that a British research team considered a sample of 649 lung cancer patients and found that all but two were smokers, a 0.99 Y regularity. A classic example from international relations is that democratic states do not fight each other. This can be expressed as an extremely strong—indeed lawlike—X regularity: if democratic dyad, then not war.
As we will show, regularities or generalizations of this sort are quite different from statistical correlations. Correlations or average treatment effects focus on a particular relationship between X and Y, holding other factors constant through experimental or quasi-experimental designs or appropriate controls.
As with statistical analysis, LNQA is also interested in establishing that regularities and generalizations are causal. The crucial step in the analysis is within-case causal inference to establish that the postulated causal mechanism is present, operates as expected and has the predicted causal effect. Causal inference does not arise from comparative or cross-case causal analysis, as is the case both in statistical work and QCA. In LNQA, it is the within-case causal mechanism analyses that drives causal inference.
In sum, it is the combination of diverse methodological and evidential approaches—proposing mechanistic accounts, establishing scope conditions and regularities, and conducting within-case causal inference—that allows LNQA to generate valid causal generalizations. In what follows we seek to explain how the approach and the evidence it requires has been used to make causal claims and strengthen inference.
Causal Mechanisms and Theory
As discussed above and illustrated in figure 1, a proposed causal mechanism is central to LNQA because it structures the within-case causal analysis. Within-case causal inference through process tracing or causal process observation depends heavily on the stipulation of a clear causal mechanism. That mechanism may be more or less complex and can range from macrohistorical phenomena such as war and state building to microlevel processes and even psychological factors. However, they are best represented by a causal mechanism figure, including those that take the shape of a formal model.
Philosophers have debated the definition of a causal mechanism, and disagreements persist on some points (see Glennan, Illari, and Weber Reference Glennan, Illari and Weber2022 for a survey). However, the key feature of a causal mechanism is that it explains how the cause leads to the effect: how the outcome is actually produced. An influential definition, coming out of an analysis of the biomedical sciences, is that “mechanisms are entities and activities organized such that they are productive of regular changes from start or set-up to finish or termination conditions” (Machamer, Darden, and Craver Reference Machamer, Darden and Craver2000, 3). Although there is debate whether causal mechanisms can be seen as intervening variables, they are more typically seen as complex systems. Moreover, they are closely tied to regularities. For example, Glennan (Reference Glennan2002, S344) defines a mechanism for a behavior as “a complex system that produces that behavior by the interaction of a number of parts, where the interactions between parts can be characterized by direct, invariant, change-relating generalizations” (see also Crasnow Reference Crasnow2017). Whether coming from the natural or social sciences, it is common for mechanisms to be portrayed, represented, or modeled by figures, which provide a framework for the case analysis.
Rather than summarizing the large literature on mechanisms, it is more useful to see how mechanistic accounts and causal figures are deployed in prominent LNQA work. In their recent book Revolution and Dictatorship: The Violent Origins of Durable Authoritarianism, Levitsky and Way (Reference Levitsky and Way2022) present their argument through a clear causal mechanism figure (figure 2). The proposed regularity is that social revolution leads to durable authoritarianism. They identify 20 cases of social revolution, and report that durable authoritarianism follows in 15 of those cases, with the remainder largely accounted for by social revolutions that are of short duration and are subsequently reversed. However, as the figure shows, this is not a simple or linear process: rather, social revolutions influence subsequent regime type through a complex causal process involving the creation of a new army (which provides a loyal coercive apparatus) and a counterrevolutionary conflict that increases the cohesiveness of the incumbent elite while weakening alternative centers of power. The book is given over to cases demonstrating how this causal process worked, tracing the process from the start-up condition (a revolutionary seizure of power) to the production of the outcome (durable authoritarianism).

Figure 2 Causal Mechanism in Levitsky and Way’s Revolution and Dictatorship
Source: Based on Levitsky and Way (Reference Levitsky and Way2022).
Establishing Scope Conditions
Establishing scope conditions for the purpose of doing LNQA involves a set of pragmatic considerations about the types of phenomena that are most appropriate for the method. A distinctive feature of LNQA is that it seeks to minimize concerns about case selection by testing for the presence of regularities across a clearly defined population. As we discuss below, the scope is typically defined using Y or X. A generalization about the casual effect of a treatment defines the scope as all X = 1 cases; a generalization about the antecedents of an outcome will define the scope as all Y = 1 cases. Since all cases in the scope are subject to scrutiny, concerns about the representativeness of any given case are mitigated; the approach thus addresses a central concern of the entire literature on case selection.
The LNQA approach to establishing scope conditions is thus quite different from the approach in statistical studies. In Sechser and Fuhrmann’s (Reference Sechser and Fuhrmann2017) analysis of nuclear compellence, which we discuss in more detail below, the statistical analysis includes models of country dyads with an N that exceeds 100,000 observations (the vast majority of which are coded as zeroes on the outcome variable). But it is not the total number of observations in the dataset that is germane for LNQA purposes. Scope conditions for LNQA focus on the number of cases that satisfy the requirements of the proposed causal generalization, in this case of nuclear compellence. Depending on definitions there are less than two dozen such cases.
As the example suggests, the type of phenomenon that are most appropriate for LNQA are those that are relatively rare events. However, a brief tour of possibilities suggests that the range of such topics is surprisingly wide and intersects with a number of core disciplinary concerns. In international relations, rare events of interest include wars, civil wars, state failure, genocides, and episodes of ethnic cleansing. The emergence of global hegemonies or empires, megacities, and international financial centers are rarer still. The acquisition of nuclear weapons is a relatively rare event that has elicited an enormous literature, as has the use of those weapons for deterrence and compellence purposes.
Famines and pandemics are rare events, as are a host of phenomena of interest to comparativists: revolutions, regime changes, coups, constitutional choices, and critical realignments. Comparative political economy has focused on episodes of rapid growth as well as financial crises; both are relatively rare. It should be noted that rare events are not necessarily big or macrohistorical in scope. Politically salient examples of micro events that are nonetheless rare include terrorist suicide attacks, political assassinations and kidnappings, and mass shootings. In short, any time Y = 1 is rare, LNQA becomes a tractable methodological approach.
Although these topics might be dependent variables of interest, they are also explored for their causal effect, as treatments. For example, we might be interested in the social consequences of famines or the effect of civil wars on the rule of law. The rise and decline of major powers are rare events that have a variety of causal effects, and we see an important cluster of LNQA work on this topic that we survey briefly below and in the appendix. LNQA can also be used to analyze rare treatments, for example, X = 1 cases, or even narrower sets of cases in which interactions are presumed to operate (X1 = 1 AND X2 = 1).
Defining scope conditions that are amenable to treatment through LNQA in terms of rare events is intuitively appealing. But on reflection there is no such thing as an intrinsically rare event. All events are ultimately constructed through the definition of concepts. How is this done? One common strategy we found in surveying LNQA work is by considering the tail or tails of some distribution. This approach is virtually canonical in security studies where the overwhelming emphasis is on the major powers, which lie in the tail of the distribution of all states. Great-power wars—which absorb substantial scholarly attention—are clearly a subset of all wars. There are large literatures on advanced economies or newly industrializing countries, both of which are small subsets of all countries.
Erica De Bruin’s (Reference De Bruin2020) analysis of coup-proofing shows how scope can be appropriately defined for LNQA purposes by considering the tail of a distribution. It also illustrates how LNQA can focus on rare treatments. Table 1 is modified from her book. Her theory postulates a relationship between coups and the presence and extent of what she calls counterweights: actors or institutions capable of checking the power of other political contenders. Put most simply, her hypothesis is that the more counterweights, the less likely that coups will be successful. She identifies a total of 266 coup attempts in her sample, a very large number for conducting within-case analysis. However, if we move to the tail of X (number of counterweights) we arrive at a sufficient-conditions generalization that is highly amenable to serial case analysis: “if a high number of counterweights then coup failure.” At this extreme there are only 29 coup attempts, of which 21 (72%) failed.
Table 1 Moving to the Tail: De Bruin’s How to Prevent Coups d’Etat

Source: Based on De Bruin (Reference De Bruin2020), table 2.2.
Levitsky and Way (Reference Levitsky and Way2022) provide a recent example of a second way qualitative researchers establish tractable samples: through what we call “conceptual engineering” or narrowing. As we have seen, their purpose is to explain durable authoritarianism. The core causal factor they advance in the book is “social revolution,” which has four defining features:
First, they occur from below, in that they are led by mass-based movements that emerge outside the state and regime.… Second, social revolutions involve the violent overthrow of the old regime. This may take the form of a civil war (Mexico, Rwanda), a guerrilla struggle (China, Cuba, Eritrea, Mozambique), or a rapid and violent seizure of power (Russia, Bolivia in 1952, Iran). Third, social revolutions produce a fundamental transformation of the state. State transformation initially involves the collapse or crippling of the preexisting coercive apparatus. Military chains of command are shattered by mutinies or widespread desertion, preventing the security forces from functioning as coherent organizations. In many cases, preexisting coercive structures simply dissolve (e.g., Mexico, Cuba, Cambodia, Nicaragua, Russia) or, in anticolonial revolutions (e.g., Algeria, Mozambique, Vietnam), are withdrawn. Upon seizing power, revolutionary forces usually dismantle remaining coercive agencies and build new armies, police forces, and bureaucracies—often from scratch. Fourth, social revolutions involve the initiation of radical socioeconomic or cultural change. (Levitsky and Way Reference Levitsky and Way2022, 5–6)
They go on to explicitly exclude situations like the color revolutions, the Arab Spring, and other regimes that emerge out of social violence but do not initiate radical social transformations. Their conceptual narrowing is theoretically justified, and produces a scope of 20 cases, each of which is considered in some detail.
Finally, it is worth bringing attention to a third way that scope conditions are narrowed that is quite common in comparative politics: by confining the scope of a claim to a particular region of the world or to subnational jurisdictions within a country. With the regional or subnational jurisdiction strategy, Y = 1 and Y = 0 cases might well both be rare. In a well-crafted study of civil conflict in Africa, for example, Lewis (Reference Lewis2020) explores all proto-rebel groups in Uganda, an N of 16.
In sum, establishing scope conditions plays a crucial role in LNQA and it has both a formal and practical component. Formally, scope conditions define the population over which the proposed causal generalization is expected to operate. But establishing scope conditions also rests on a pragmatic foundation of identifying phenomena for which the method is tractable. LNQA is typically deployed to analyze rare events and treatments; these are ultimately constructed by considering tails of distributions, by conceptual engineering, or by choosing samples not on X or Y but on other parameters—such as region or status as a subnational jurisdiction—that limit the number of cases.
Regularities
LNQA can be seen as a regularity methodology and in that regard follows in the footsteps of regularity approaches to causation that date to Hume. Philosophical surveys of causation continue to note the significance of the approach. Probably the most influential post-1945 account is Mackie (Reference Mackie1974), who introduced the concept of INUS conditions and used necessary- and sufficient-conditions causal concepts. Such approaches can be grounded in mathematical logic or Boolean algebra and those approaches have filtered into the social sciences. QCA is a particularly prominent methodology focusing on necessary and sufficient conditions (Oana, Schneider, and Thomann Reference Oana, Schneider and Thomann2021; Ragin Reference Ragin1987), although it has not typically pursued the extensive within-case analysis that LNQA requires.
Empirical regularities have played a much more significant role in defining research programs in the social sciences than is often recognized. Some proposed regularities are well known, such as Lipset (Reference Lipset1959) on the relationship between level of development and democracy and Drèze and Sen (Reference Drèze and Sen1991) on democracy and famine. Barrington Moore’s (Reference Moore1966) famous dictum—“no bourgeoisie, no democracy”—is a classic causal regularity. The initial regularity that launched the democratic peace literature was posed as “democratic states do not fight wars with each other.” But these well-used examples are hardly alone. Goertz (Reference Goertz and Kincaid2012) provides a catalogue of examples and the LNQA work we cite in the appendix all rests on the identification of some empirical regularity.
Although there are many different types of regularities that we will explore in the examples provided below, they come in two basic forms, what we call “Y generalizations” and “X generalizations.” Y = 1 regularities are the more common of the two in the LNQA work we surveyed. A simple one is given in table 2, which shows all possible outcomes in the context of two dichotomous or discrete variables. The Y generalization or causal claim selects on the dependent variable. But it involves looking not only at the confirming cases (the [1,1] cell) but at both cells in the Y = 1 row. If the percentage of cases where “if Y = 1 then X = 1” approaches or equals 1.0, we have a strong empirical regularity. Note that there is nothing intrinsically “qualitative” about such regularities, and they can be based on quantitative data or through the simple coding of cases, and frequently are.
Table 2 Y Generalizations

Although much LNQA work focuses on the presence of Y = 1 outcomes, the logic of table 2 demonstrates that it is possible to have a Y = 0 generalization: a proposition about when Y does not occur. However, it is often the case that Y = 0 is extremely common—as in the Sechser and Fuhrmann example cited above—and LNQA testing of a Y = 0 proposition is infeasible. But where the total N for the two-way table is relatively small, Y = 0 generalizations may be of significant interest—for example, because of their identification of a constraint causal mechanism (Goertz Reference Goertz2017, 98–100).
X generalizations are formulated in terms of one or more X or causal variables. Table 3 illustrates a simple X generalization. Research designs focused on Y select on the presence or absence of the outcome. Those studies proposing X generalizations are focused on whether the treatment has the postulated effect. The theory therefore is about how the treatment produces the outcome, so it is natural to select the X = 1 cases for particular attention.
Table 3 X Generalizations

Table 3 is analogous to table 2 but for an X = 1 regularity: that X = 1 is expected to be followed by Y = 1. However, table 3 differs from table 2 in some important ways. The (1,0) cell contains the nonconforming cases—cases in which the presence of X did not generate the Y. These cases can be seen as falsifying in the standard Popperian sense; they refute the regularity claim. However, it should also be stressed that just as Y-focused LNQA might generate multiple necessary-conditions claims, so X-focused LNQA can yield multiple sufficiency claims as well.
As with Y = 0 regularities, it is sometimes possible to investigate X = 0 regularities. This is often not practical where the number of Y = 0, X = 0 cases is large, and not associated with a clear causal mechanism.
Tables 2 and 3 provide examples of simple regularities. Regularities can involve multiple Xs or Ys, however. In his recent book on transitions to democratic rule, for example, Miller (Reference Miller2021, 2, 7) offers a Y regularity and states his main conclusions in necessary-conditions terms: “I show that more than 9 in 10 democratic transitions since 1800 fit one of these two paths … democratization almost never happens without a country first experiencing a major violent shock (such as a coup or civil war) or having a ruling party capable of winning power in democracy.… Of 139 democratic transitions since 1800, more than 9 in 10 fit one of these two paths. Thus, they combine to make up a virtually necessary condition for democratization.” The scope of this generalization is Y = 1: all cases in which a democratic transition has occurred. The empirical regularity can be expressed as “if Y = 1 then (X1 = 1 OR X2 = 1).” We explore more examples of complex regularities below.
Before concluding, it is worth underlining the crucial difference between a regularity as we have defined it here and the statistical approach that focuses on average treatment effects in experimental, quasi-experimental, or observational studies. Note that while regularities draw on information in the X = 1 column or Y = 1 row, standard statistical analysis requires the complete set of data in the two-way table. To get at the distinction, it is worth considering table 4, which provides empirical data about the democratic peace drawing on Russett (Reference Russett1995, 174). The example is particularly compelling because of the strength of the regularity. As can be seen from the table, the number of wars among democratic dyads is precisely zero. This can be formulated either as an X = 1 regularity (“if democratic dyad [X = 1] then no war [Y = 1]”) or as a Y = 1 regularity (“if war then nondemocratic dyad”). A statistical analysis of the data in table 4 by contrast would typically involve a logit analysis—which uses the data in all cells—and would report the effect of democracy on the likelihood of war.
Table 4 Regularity or Correlation? The Democratic Peace

In sum, LNQA involves postulating regularities and identifying them empirically. These regularities can arise from systematic examination of many cases, descriptive analysis of datasets, game-theoretic models, comparative historical analyses with multiple dependent variables, and many other routes. Without a hypothesized regularity or causal generalization, however, LNQA cannot proceed because the regularity and mechanism determine the core aspects of the analysis: the stipulation of the scope and particularly the design of within-case causal inference.
Within-Case Causal Inference
Perhaps the most significant unifying feature of the LNQA work that we surveyed was the shared belief that causal inference was strengthened not simply by case studies, but by case studies of (ideally) all the relevant cases stipulated by the scope conditions, or at least some significant share of them. The purpose of these studies is straightforward: to reach a conclusion about whether the bulk of the evidence supports the proposed mechanistic account in the case, including with respect to its various component parts. Judgments typically conclude by claiming that the case is well explained by the evidence for the proposed model (for example, using criteria such as clearing hoop tests or the evidence being doubly decisive), or that it constitutes a falsifying or anomalous case in whole or part. Only once this work is done can findings from the individual cases be aggregated into causal generalizations.
Given that LNQA is rooted in serial testing of a hypothesis and stipulated mechanism across a scope of cases, the qualitative component of the method is its labor-intensive core. There are debates about the most appropriate way to conduct within-case causal inference, but we believe the method is compatible with a variety of different qualitative approaches. The examples we identified typically invoked mechanistic process-tracing methods such as those summarized by Beach and Pedersen (Reference Beach and Pedersen2016) and Waldner (Reference Waldner, Bennett and Checkel2014), and we focus on that approach here. But we can imagine accounts based on Bayesian approaches (e.g., Fairfield and Charman Reference Fairfield and Charman2022) as well as within-case counterfactual designs (e.g., Harvey Reference Harvey2011; Mahoney and Barrenechea Reference Mahoney and Barrenechea2019).
Waldner (Reference Waldner, Bennett and Checkel2014) provides a succinct summary of the process-tracing method that comports closely with our understanding of the field; we do little more here than summarize his characterization, with limited modifications. First, a process-tracing exercise is based on a causal mechanism figure—ultimately an argument—in which the nodes are connected in such a way that they provide the necessary and/or sufficient conditions for the outcome to occur. Second, this is typically rooted in an event-history map that demonstrates, typically in narrative form, the correspondence between those events and the nodes in the causal graph. Third, the causal mechanism claims link the nodes, and the evidence allows us to infer that “the events were in actuality generated by the relevant mechanisms.” (128). To this, Waldner adds that rival explanations should also be weighed and either rejected or taken into account—for example, as anomalous cases or those in which multiple causal factors were at work. Bayesian approaches, and particularly Fairfield and Charman (Reference Fairfield and Charman2022), strongly support this final injunction and, in fact, require the consideration of rival hypotheses for causal inference to be possible at all.
While the conduct of any case study poses challenges, the most important practical issue in doing LNQA is in managing trade-offs between breadth and depth. Fairfield’s (Reference Fairfield2015) study of the political economy of taxation identifies approximately 60 different proposals to increase revenues in three Latin American countries. Reiter’s (Reference Reiter1995) early LNQA contribution on preemptive war considers 67 cases. Haggard and Kaufman’s (Reference Haggard and Kaufman2016) study of transitions to democratic rule considers two (overlapping) populations of 73 and 79 cases depending on the dataset from which they were drawn. These examples probably sit at the outer limits of the what the method can bear.
Yet managing the depth versus breadth trade-off is not simply a function of the size of the scope. It is also a function of how complex is the theoretical claim being made. Reiter’s (Reference Reiter1995) disconfirmatory within-case analysis is limited to interrogating whether a war could be considered preemptive. He shows that the mechanisms associated with the preemptive war account do not pertain except in a very limited number of cases, and those are examined closely to show they did not conform precisely either. Haggard and Kaufman (Reference Haggard and Kaufman2016) consider the presence and operation of a relatively spare causal mechanism: distributive grievances, mass mobilization, and the overthrow or departure of incumbents because of such mobilization. Their qualitative appendix contains a discussion of each case, but the cases are limited to assessing whether a distributive conflict transition had occurred and typically run to no more than two pages.
Other LNQA studies entertain much more complex causal mechanisms—typically over fewer cases—and as a result rest on thicker evidence. A classic example is Elisabeth Wood’s (Reference Wood2000) treatment of transitions from labor-repressive regimes. Her book has subsequently been treated as a model of a complex—yet clearly articulated and tested—mechanistic account demonstrated through the consideration of a limited number of cases (for example, by Waldner Reference Waldner, Bennett and Checkel2014).
We have argued that the ability to establish regularities ideally involves a treatment of all the cases within the defined scope. The reasons are straightforward: without such treatment any conclusions are potentially biased. We find that this norm is the one most likely to be violated. Many studies broadly in the LNQA-style undertake most or many but not all the cases.
An important practical question is, therefore, how the breadth–depth trade-off can be managed. One way of increasing the tractability of the approach is to allow for greater asymmetry in the depth of analysis. We found a number of LNQA studies that conduct a smaller number of cases in significant depth to demonstrate the causal process in detail, but accompany them with shorter cases that are nonetheless adequate to demonstrate that the causal proposition holds beyond the cases selected for more intensive treatment. These shorter cases typically appear in penultimate or concluding chapters in which the author directly addresses the issue of generalizability across the population. For example, Ripsman’s (Reference Ripsman2016) study of enduring rivalries defines a population of nine such conflicts and does chapter-length case studies of three, but provides shorter case studies of the remaining six that permit some generalizing conclusions. Levitsky and Way’s (Reference Levitsky and Way2022) study of enduring authoritarianism establishes a scope of 20 cases, treats 13 in detail, and addresses the remaining seven in the concluding chapter. Even with shorter analyses, the objective remains the same: to assess whether the proposed causal mechanism provides a plausible account of the cases.
In closing our discussion of the within-causal inference component of LNQA, it is worth noting a practical innovation that we have seen not only in books but in articles as well: the use of qualitative appendices and datasets, including online ones. These can mitigate a key space constraint even in books and are a necessity for article-length studies. An example that we take up in more detail below is Carnegie and Carson’s (Reference Carnegie and Carson2019) study of nuclear intelligence sharing, but they are not alone (see Haggard and Kaufman Reference Haggard and Kaufman2016; Reference Haggard and Kaufman2021; Miller Reference Miller2021; Schenoni et al. Reference Schenoni, Goertz, Owsiak and Diehl2020).
Causal Generalizations
The goal of LNQA—as illustrated in figure 1—is to demonstrate that observed regularities constitute valid causal generalizations through within-case causal inference. It is important to underline that these causal generalizations rarely have the lawlike quality of democratic peace claims. Our survey found that LNQA researchers typically paid significant attention to anomalies and sought to identify the reasons why they did not comport with the postulated and observed regularity. In some cases, this closer scrutiny revealed measurement error; we take this up in more detail with our discussion of Sechser and Fuhrmann below. Another purpose of this intensive treatment is to explore the possibility of equifinality: that the nonconforming cases could be explained by some other causal mechanism, thus identifying alternative pathways and explaining a higher share of the total cases within the scope.
Because causal generalizations are not typically “iron laws,” we need to consider the bar for what we call a strong causal generalization. We started the article with the Copeland example where the causal generalization is in the 0.75 range. This standard seemed adequate to Copeland and even his critics take the finding seriously. QCA also happens to consider findings in the 0.75–0.80 range as the bar for a strong regularity. We take a pragmatic approach to this issue; as with p-values in statistical analysis, norms clearly evolve over time and we suspect they will with respect to LNQA as well.
Another consideration in determining whether a causal generalization is a strong one, however, is the number of cases. LNQA work has ranged from populations up to 50, and even above, down to a handful of cases. How strong can a causal generalization be if it is only based on five cases? Dion (Reference Dion1998), in an award-winning article focusing in particular on necessary conditions, found using a Bayesian analysis that regularities can be established with confidence with as few as five or six cases.
However, a more significant question is whether it is necessary to look at all the cases to establish a strong causal generalization. As noted, this was the one area where we saw the sharpest divergence from our norms. Studies would choose some “high” percentage of all cases based on various rationales. The question is basically whether LNQA could operate on the basis of some sampling procedure. One obvious choice would be a random sample from the population, but we did not find a single example of this approach. For now, the established norm seems to be to attempt all or near-all cases. But the question of sampling—which could extend LNQA to phenomena of much larger scopes—should be on the agenda for future research.
Part II: Examples
In this section, we take up examples of Y, X, and more complex generalizations drawing on our survey of LNQA work.
Y Generalizations
We take as our first example a Y generalization from Haggard and Kaufman (Reference Haggard and Kaufman2021) on the issue of democratic backsliding, illustrated in figure 3, revised from a similar figure in their book. As with most LNQA work, they propose a causal process involving several steps. As can be seen, these include polarization, the presence of an autocratic executive, compliant legislatures, and an incremental process of democratic regress. From this causal process we extract one of their core causal generalizations: they expect that polarization (X) is a necessary condition for backsliding (Y). This is not a hypothesis about the average treatment effect of polarization on backsliding, although it might be tested as such. Rather, it is a proposed regularity. They identify three specific causal mechanisms linking polarization to democratic regress, including the loss of trust in institutions as a result of stalemates over policy, increasing tolerance for autocratic behavior on the part of copartisans, and the emergence of extreme parties or extreme factions within existing parties. These expected causal mechanisms in turn structure the extensive case work, contained in an online appendix to the book.

Figure 3 Mechanisms and Generalizations: Polarization and Backsliding in Democracies
Source: Based on Haggard and Kaufman (Reference Haggard and Kaufman2021).
Haggard and Kaufman begin by selecting a complete population of backsliding cases (Y = 1) based on two sources of information: statistically significant erosion of Varieties of Democracy (V-Dem) liberal democracy scores in countries that had crossed a democracy threshold for some period; and triangulation with three other datasets to assure that the assessment using V-Dem data was not idiosyncratic. This yields a scope of 16 backsliding cases.
To establish the regularity with respect to polarization they use four V-Dem indicators and consider levels of polarization compared to regional benchmarks. They find that of the 16 cases, only one—the Dominican Republic—is not particularly polarized, yielding a strong regularity: 15 of 16 of the backsliding cases, or 94%, are relatively polarized when compared to benchmark cases.
However, the causal generalization is not established by the regularity alone. Rather, the causal work is done by the within-case analysis, which is organized around the particular causal mechanisms linking polarization to backsliding noted above. Some exemplary cases are discussed in the book, but an online appendix provides much more extended treatment of each of the 16 cases. Based on their within-case causal analysis, they find that in 14 there is clear evidence the polarization was, in fact, a cause of backsliding. They devote significant attention to two anomalous cases. In one, Greece, they raise questions of whether the case should be considered a backsliding case at all. In the Dominican Republic, they note alternative processes that might have been at work, as well as the fact that the relatively low level of polarization was also associated with a much milder and transient form of backsliding.
Much of the LNQA that we survey in the appendix involves Y generalizations of the sort just outlined, focusing on outcomes as a result. A few examples focusing on how scope conditions are set provide a flavor of the diversity of this work across both international relations and comparative politics. Social revolutions (Skocpol Reference Skocpol1979) and genocides (Power Reference Power2002) are natural foci for Y generalizations using LNQA because they are relatively rare events. Classic examples of scope conditions set by region include James Mahoney’s work on democracy in Central America (Reference Mahoney2001) and development in Latin America as a whole (Reference Mahoney2010), as well as more recent treatments of the region, such as Soifer (Reference Soifer2015) on state building and Cyr (Reference Cyr2017) on party collapse. In all this work, scope conditions were bounded by detailed consideration of a single region or subregion, permitting within-case inference of all, or a large share of all, countries in the region.
X Generalizations
To illustrate the logic of an X causal generalization, we use Sechser and Fuhrmann’s Nuclear Weapons and Coercive Diplomacy (2017). The Sechser and Fuhrmann study is a critique of what they call the coercionist school, which argues that states enjoy a diplomatic advantage as a result of having nuclear weapons or threatening—either explicitly or implicitly—their use. To put it most simply, Sechser and Fuhrmann argue nuclear coercion and compellence do not work: “if nuclear compellence attempt (X = 1) then no compliance behavior by the target state (Y = 1).” Hence, Y = 1 is compellence failure.
Sechser and Fuhrmann outline their postulated theory in a causal mechanism figure (figure 4, modified from their book). The core of their argument draws on two somewhat different theoretical traditions: those dealing with counterforce damage limitation and more standard treatments of competition in risk taking. They argue that nuclear compellent threats are not credible, in part because to carry through on them would generate a massive backlash. Both potential wielders of nuclear threats and their adversaries anticipate these dynamics. Their framework generates some additional subsidiary hypotheses, but is articulated sharply enough to allow them to verify on a case-by-case basis both whether threats failed (Y = 1) and the extent to which the postulated causal mechanisms—credibility concerns on the part of both initiators and targets—arose within the cases (X = 1).

Figure 4 Sechser and Fuhrmann on Nuclear Threats and the Failure of Compellence
Source: Based on figures 2.1 and 2.2 in Sechser and Fuhrmann (Reference Sechser and Fuhrmann2017).
Note: Italic type is Sechser and Fuhrmann’s (Reference Sechser and Fuhrmann2017) theory.
The next step is to constitute the scope. Sechser and Fuhrmann use the standard militarized interstate dispute dataset, which contains militarized disputes from 1816 forward, but naturally confine the scope of their analysis to the nuclear era. They select all cases in which nuclear compellence was attempted (X = 1), including in militarized diplomatic crises as well as in wars. This definition of the scope yields 19 total cases. The initial regularity is outlined in table 5. Recall that their expectation is that nuclear compellence does not work; the cases in which compellence does not work comport with the theory. Nonetheless, their initial finding is a relatively weak one; less than 50% (9 of 19) of the cases constitute failures of nuclear compellence.
Table 5 X Regularity, Nuclear Compellence Does Not Work

Source: Based on Sechser and Fuhrmann (Reference Sechser and Fuhrmann2017).
The crucial step, however, is to explore these 19 cases of nuclear compellence to see if the initial causal generalization is borne out by within-case causal inference. They start the case study portion of the book with the subsample of cases that are widely acknowledged as failed compellence cases. From the perspective of their theory, these are actually conforming cases because the model predicts failure. They argue via within-case causal analysis of these failures “that nuclear threats may be dismissed by targets as not credible even when challengers engage in potentially dangerous brinkmanship. Indeed, in all the crises analyzed above, states tried—and failed—to coerce their adversaries by raising the specter of nuclear attacks” (Sechser and Fuhrmann Reference Sechser and Fuhrmann2017, 172).
They turn next to the nonconforming cases, those in which compellence is coded to have worked in the large-N dataset (again, from the perspective of their theory, the [1,0] nonconforming cases). Although causal process observation is typically seen as focusing on the presence and operation of stipulated causal mechanisms, they also can uncover measurement problems. One is that a case that is coded in the large-N dataset as an example of attempted nuclear compellence is, in fact, a case of nuclear deterrence, which is easier to achieve. This means that it is not an X = 1 case but rather an X = 0 case and should be moved out of the nonconforming cell.
After undertaking within-case causal analysis of each of the 10 cases in the nonconforming cell—the X = 1 causal generalization column in table 6—Sechser and Fuhrmann (Reference Sechser and Fuhrmann2017, 231) conclude that cell, in fact, houses no cases: “The chapter critically assessed ten apparently successful cases of nuclear coercion [(1,0) cases from the perspective of their theory]. These cases should have provided the clearest evidence in favor of the view that nuclear blackmail works. However, none of them unequivocally supports the nuclear coercionist school.” Within-case analysis ends up reaching results given in table 6, which is, in fact, a LNQA causal generalization to which there are no exceptions. At least with respect to this scope of cases—which is arguably the whole universe—Sechser and Fuhrmann claim that nuclear compellence never works.
Table 6 X Causal Generalization, Nuclear Compellence Does Not Work

Source: Based on Sechser and Fuhrmann (Reference Sechser and Fuhrmann2017).
These findings are by no means accepted by all scholars working on the issue, and a significant debate ensued between Sechser and Fuhrmann and Matthew Kroenig on the issue, centered in large part on choices with respect to the coding of cases and the specification of the statistical models (Fuhrmann and Sechser Reference Fuhrmann and Sechser2013; Kroenig Reference Kroenig2013). We do not adjudicate that debate, but only note that a refutation of Sechser and Fuhrmann would not hinge solely on the statistical findings. It would have to engage the claims arising from the within-case causal inference: why that choice of cases and the evidence provided in them did not support their claims.
Our review of the LNQA literature in the appendix suggests that X generalizations are somewhat less common in the LNQA literature than Y generalizations, but there are some significant clusters. A particularly important one is the literature on responses to hegemonic decline, again a phenomenon with a clearly bounded set of cases. Graham Allison’s (Reference Allison2015) widely debated Atlantic article begins with a classic X generalization: “In 12 of the 16 cases in which a rising power has confronted a ruling power, the result was bloodshed.” More typically, this work combines hegemonic or major-power decline with other X variables to determine why states respond to it as they do. Other LNQA work in this vein has addressed not only the question of war but retrenchment (MacDonald and Parent Reference MacDonald and Parent2018), accommodation on the part of great powers (Goddard Reference Goddard2018), and on the strategies of rising powers (Shifrinson Reference Shifrinson2018). Each of these studies looks at a limited number of hegemonic declines—albeit coded somewhat differently—and casts findings in terms of regularities.
Complex Causal Generalizations
The Haggard and Kaufman example has already demonstrated that the method can accommodate Y generalizations in which the postulated causal factor arises from a complex causal mechanism. Here we explore such explanations in more detail by considering a particularly strong example of the method. Carnegie and Carson’s (Reference Carnegie and Carson2019) work on information sharing in international institutions is also of interest because it is based on a game-theoretic causal mechanism and shows how LNQA can be done in an article format using a qualitative appendix (see also Carnegie and Carson Reference Carnegie and Carson2020). Hence this example shows how a major research program includes multiple causal generalizations and ones that involve both complex Y and X generalizations.
The basic theory is an informational one: major powers with intelligence on proliferators will not share that intelligence with an international organization (IO)—in this case the International Atomic Energy Agency—if they believe that their sources would be compromised. Such information sharing and the downstream effects of it in the form of more effective nonproliferation efforts—their dependent variable—will only materialize when sources are protected (a necessity claim). This hypothesis permits a within-case design, with the treatment taking the form of an organizational reform that increases the integrity of information sharing.
Yet Carnegie and Carson also consider the problem of possible bias in the provision of information: that those having intelligence have a greater interest in enforcement actions against adversaries than allies. International institutions have to take this bias into account when assessing any information that is provided to them. Table 7 summarizes what their theory predicts for information sharing according to the values of the two core independent variables: whether the country in question is an ally and whether the IO protects sources.
Table 7 Carnegie and Carson on IO Reform, Alliances, and Intelligence Sharing I

Source: Based on Carnegie and Carson (Reference Carnegie and Carson2019), table 1).
Following the previous discussion, we can formulate their basic theory in terms of a complex generalization postulating one X claim and two Y ones. The X generalization takes the following form: “if the international organization protects information AND the country is not a US ally, then information will be provided.” The Y-generalizations claim is that there are two paths to the US not revealing information: when either of the two core necessary conditions are absent. This illustrates how one might think in terms of Y = 0 generalizations. Although they do not present their theory in this way, the 2 × 2 in table 7 describes the underlying logic of their argument.
Carnegie and Carson illustrate a crucial feature of LNQA: that examining all cases in the two-way table—including Y = 0 and Y = 1 cases—is sometimes tractable. Typically “rare events” means Y = 1 is rare, but Y = 0 is common, and often extremely common. Here the total N of the 2 × 2 table provides a tractable number of cases for within-case causal inference. This is even true despite the fact that a single country can—and often does—enter the 2 × 2 twice: prior to the treatment of the organizational reform and after it. By contrast, the independent variable “US ally,” X1, is relatively constant with only one case—Iran—shifting on this factor. This empirical setup permits a simple 2 × 2 table, but in the form of the allocation of all the cases across two X variables: (1) pre- and post-information-sharing reform; and (2) whether the country is a US ally or not.
Using their summary data, we can construct table 8, which shows more clearly not only their results but the strength of their causal generalizations. We have listed where each case goes according to the theory summarized in table 7. As can be seen in table 8, the X generalization holds over six cases. Carnegie and Carson provide detailed and clear criteria for assessing the extent to which cases do or do not conform with the model. To illustrate how the strength of generalizations can be coded in a more nuanced way, we assign “fully conforming” cases a weight of 1.0 and “moderately conforming” cases a weight of 0.5. The strength of the causal generalization is (4 + (0.5 × 2))/6 = 5/6 = 0.83 for this compound X causal generalization. Following our rule of thumb, this constitutes a strong causal generalization.
Table 8 Carnegie and Carson on IO reform, Alliance, and Intelligence Sharing II

Source: Based on Carnegie and Carson (Reference Carnegie and Carson2019, table 4).
Note: There are no nonconforming cases for any cell.
The Y = 0 generalization involves looking at the three cells in table 8 where Y = 0. These three cells have a total of 15 cases. There are 11 conforming cases, four moderately conforming, and no nonconforming ones. This yields 13/15 = 0.87 for these two Y = 0 causal generalizations, again a strong regularity.
In the article itself, Carnegie and Carson use North Korea to demonstrate their approach, drawing on an array of declassified sources. The case is a conforming one for the generalization and a moderately conforming one for the “pre-reform period and not-ally” configuration of the Y generalization. The Carnegie and Carson article constitutes a strong example of LNQA, however, because the appendix provides studies of all cases, and it is the case studies that allow table 4 in their article to report on all cases and for us to report their findings as regularities. In a study led by a game-theoretic model, the entire weight of inference is carried by the systematic within-case causal inference conducted on all cases.
Part III: Multimethod LNQA (M-LNQA)
The classic question regarding regularities is how to identify the conditions under which they may be considered causal. The same classic question applies to correlations with observational data or even in well-specified designs: is the relationship causal or not? While standard LNQA starts with a proposed and observed regularity, multimethod LNQA starts with a statistical relationship, using within-case causal inference across a range of cases to strengthen inference.
What Is M-LNQA?
Figure 5 provides an outline of the methodology that parallels figure 1 but with some important differences. As with LNQA, theory leads: the starting point is a causal expectation of a significant correlation or average treatment effect of X on Y. The scope for the statistical analysis necessarily draws on information from all four cells we identify in our discussion of X and Y generalizations.

Figure 5 Multimethod LNQA
However, the whole statistical dataset is not the scope for the case analysis. Although there are a number of competing criteria for selecting cases, multimethod LNQA typically focuses on the (1,1) cases: those in which X and Y are both present. Choosing these cases would seem a classic example of selecting on the dependent variable in a way that generates bias. However, this is not the case. If the statistical finding is robust, it is precisely the (1,1) cases that should exhibit the presence and operation of the causal mechanism. If within-case causal inference confirms the operation of the causal mechanism in the (1,1) cases, then LNQA strengthens confidence that the average treatment or correlation is causal. Conversely, if it does not then it casts doubt on the statistical findings, as some disconfirmatory LNQA has sought to do.
Analysis of the (1,1) cell—the causal mechanism cases—is also in line with standard practice in multimethod research that combines statistical analyses with cases from the (1,1) cell for intensive scrutiny. These cases are almost always chosen to support the theory and statistical findings and are often called illustrations; the load of causal inference is carried largely, if not entirely, by the statistical analysis. In M-LNQA, by contrast, the within-case analysis of the (1,1) cases is equally, if not more, important for causal inference. As opposed to using case studies to “explore” or “illustrate” causal mechanisms, examination of all occupants of the (1,1) cell tests for the presence and operation of the postulated cause across the entire population.
We identify two ways LNQA might complement statistical designs. Early multimethod LNQA took a disconfirmatory form, challenging a causal claim established via correlational analysis. The within-case evidence was held to disconfirm the causal interpretation of the correlational analyses. We also illustrate how doing multimethod LNQA can significantly strengthen statistical analysis in the context of a confirmatory study of a rare event. Confirmatory M-LNQA rests on the combination of a robust statistical finding and within-case causal mechanism evidence, typically of all the (1,1) cases.
Disconfirmatory M-LNQA
Disconfirmatory LNQA rests on a logic of looking at (1,1) cases in the context of a preexisting statistical finding. If the within-case analysis of most or all the (1,1) case reveals no causal impact of X on Y, the correlational findings are likely not causal and are disconfirmed.
An early example of disconfirming M-LNQA is Narang and Nelson’s (Reference Narang and Nelson2009) critical examination of the claims made by Mansfield and Snyder in their Reference Mansfield and Snyder2005 book Electing to Fight: Why Emerging Democracies Go to War. Mansfield and Snyder have a complex X generalization that rests on two causal factors: incomplete democratization (X1) and weak institutionalization (X2) makes countries more likely to go to war (Y). Their correlational analysis provides strong evidence for this claim, captured in the significant interaction term between the two independent variables. Countries with these properties are eight to ten times more likely to engage in conflict, a strikingly strong statistical finding.
M-LNQA is about seeing if the regularity from the correlational analysis is confirmed by within-case causal inference. In reconstructing Narang and Nelson’s critique, Goertz (Reference Goertz2017, 197) provides a table showing the distribution of possible cases. We reproduce it in table 9 because it captures some of the core features of multimethod LNQA. The total number of cases given by the dataset used in the econometric analysis—defined here as the country-year cells in the panel—is 2,530. But, as is typical in econometric tests of the causes or consequences of rare events, 2,271 cases fall in the (0,0) cell. War is a relatively rare event, occurring in 117 of the cases (4.6%).
Table 9 Disconfirmatory Multimethod LNQA: Weak Institutions and Democratic Transitions Produce War

The question for multimethod LNQA, however, is whether the crucial causal mechanism (1,1) cases comport with the theory. Narang and Nelson make two critical observations. First, they note that despite the strength of the statistical findings, there are only six cases that fall in the (1,1) cell. Second, they note that these all occurred before World War I and most involved the Ottoman Empire, calling into question the generalizability of the Mansfield and Snyder finding.
In the response by Mansfield and Snyder (Reference Mansfield and Snyder2009), they return to the cases, not only to the statistical findings. They make two rejoinders. First, they note that these pre-World War I Ottoman cases are, in fact, well explained by their theory (something not contested by Narang and Nelson). Narang and Nelson also raised the question of the external validity of their findings for interstate war after 1992 when their dataset ends. Drawing on other examples, Mansfield and Snyder claim that their findings do have external validity.
Again, we do not seek to adjudicate a fruitful debate, but rather to draw attention to how statistical and qualitative analysis can best be combined. Despite the strength of their statistical findings—resting on over 2,500 dataset observations—Mansfield and Snyder’s causal claims ultimately rest on a very small number of cases. When findings involve rare events such as war, demonstrating that the (1,1) cases fit the model is not incidental to inference, but crucial for it. This can be done either by demonstrating directly that the cases comport with the theory or by considering out-of-sample cases that show that the proposed regularity has external validity.
Confirmatory M-LNQA
The confirmatory version of M-LNQA uses the same basic methodology, but with the theoretical expectation that analysis of the (1,1) cells will generate support for the correlational analysis. Rather than considering examples of LNQA, we turn to two strong quantitative designs that could have profited from a consideration of cases. Maat’s (Reference Maat2020) study of mass indiscriminate violence, including genocide, and Meng and Paine’s (Reference Meng and Paine2022) consideration of the consequences of rebel groups’ seizure of power underlines points made with respect to the Mansfield and Snyder–Narang and Nelson discussion. Both illustrate how statistical findings can hinge on a very small number of cases and how consideration of those cases can be crucial to our confidence in the experimental, quasi-experimental, or observational findings.
Maat proposes a complex causal mechanism leading from elite rivalry to genocide, arguing that it serves the function of assisting authoritarian leaders to consolidate control over the regime, or what he calls “genocide consolidation.” Maat combines sophisticated econometric work and clear presentation of information on the distribution of cases. Table 10—taken directly from Maat—outlines the basis of his correlational findings on one form of such violence—non-counterguerilla genocide—and shows again how cases in multimethod LNQA designs are typically distributed. The total number of observations is large: 2,576 to be exact, about the size of the Mansfield and Snyder dataset. But the mass-violence genocide cases (Y = 1) total only 12.
Table 10 Multimethod LNQA with a Y Generalization: Elite Rivalry and Genocide

Source: Based on Maat (Reference Maat2020), table 3.
Maat deploys a wide range of sophisticated statistical techniques to argue that elite rivalry is an important cause of genocide consolidation, and they derive ultimately from the fact that the difference between X = 0 and X = 1 cases are significant. “While genocidal consolidation is extremely rare, the effects of elite rivalry are considerable.… For example, in any given year a median nondemocratic regime has essentially a 0 percent chance (CI 95%: 0.0%; 0.1%) of genocidal consolidation onset; during elite rivalry this percentage increases to 0.6 percent (CI 95%: 0.1%; 1.5%)” (Maat Reference Maat2020, 795). As with Mansfield and Snyder, these are strong average treatment effect claims.
As can be seen, however, Maat’s claims ultimately hinge on a very limited group of cases: the six cases in the (1,1) cell. While Maat makes only passing reference to these cases, a close examination of them would have substantially increased confidence in the theory and correlational findings.
Given that there are only 12 cases in the Y = 1 row, however, it would be even more informative to consider the nonconforming cases as well—that is, to conduct a standard LNQA analysis on all the cases in which Y = 1. This is particularly true given that a postulated Y regularity only holds for half of the cases. Maat is interested in an extremely rare event. If an intense analysis of the nonconforming cases finds there is a causal mechanism that explains the alternative causal path in those six cases, we would have a strong compound Y generalization that explains all the cases: if Y = 1, then X1 = 1 OR X2 = 1.
While Maat provides the opportunity for a Y generalization, Meng and Paine (Reference Meng and Paine2022) provide an example of a rare treatment or X generalization in a statistical design. Their study also suggests the high value-added from complementary case analysis. They are interested in the conditions under which rebel groups seize political power and can reform and control the military in ways that generate long-lasting authoritarian rule. They restrict their analysis to Africa—following our regional strategy with respect to setting scope conditions—and identify 21 cases. They note a very strong regularity: that 78% of postindependence rebel regimes in Africa are still in power today. Moreover, “in 19 of the 21 cases, rebel regimes either completely transformed and displaced the existing state military or occupied top positions in an integrated military” (Meng and Paine Reference Meng and Paine2022, 1). The limited number of X = 1 cases would make multimethod LNQA a strong complement to the statistical analysis, showing precisely how the conditions they outline contributed to the outcome.
In sum, in any econometric analysis where the number of cases in the (1,1) cell is small—no matter how well specified—the conclusions are likely to be fragile because they rest on so few cases. In such circumstances, LNQA—typically focusing on the (1,1) cases—not only provides an illustrative complement to the statistical analysis but increases confidence that the econometric findings are, in fact, causal.
Conclusions
Our main purpose in this essay was to outline an observed research practice—Large-N Qualitative Analysis—and to provide some practical methodological guidelines for doing it. LNQA combines a number of existing research practices, but in a distinctive mix. Of particular significance is its approach to defining scope conditions, the conduct of case studies of the entire population, and its focus on generating causal regularities.
LNQA is not necessarily appropriate for phenomena with a large number of observations that are best addressed through various statistical techniques. But we have attempted to show—including through our survey of the literature in the appendix—that the approach cuts across a variety of different theoretical and substantive preoccupations and provides particular advantages for the study of rare treatments or outcomes. Moreover, its multimethod variant is complementary to experimental, quasi-experimental, or observational designs, can significantly strengthen causal inference in them, and has already drawn attention from philosophers of social science (building on Russo and Williamson Reference Russo and Williamson2007; Williamson Reference Williamson2019; see, for example, Runhardt Reference Runhardt2022; Shan and Williamson Reference Shan and Williamson2023). Looking forward, we hope our treatment of the topic serves as an invitation: that a delineation of the approach will strengthen empirical work and further methodological innovation in case study and multimethod designs.
Supplementary Material
To view supplementary material for this article, please visit http://doi.org/10.1017/S1537592723002037.
Acknowledgments
Thanks to Sharon Crasnow, Jesse Driscoll, Emilie Hafner-Burton (and her class), Nancy Cartwright, Jack Goldstone, Evelyne Huber, Bob Kaufman, James Mahoney, Barry Naughton, Agustin Markarian, Charles Ragin, Philip Roeder, Kevin Rossillon, Rosa Runhardt, Jason Seawright, Jack Snyder, Jon Williamson, Kurt Weyland, and Elisabeth Wood for comments on earlier drafts. Kimberly Peh provided excellent assistance on many aspects of this project.