1 Introduction
Over the past decade, interest in causal mediation has rapidly grown in political science. Many scholars are no longer satisfied with merely establishing the presence of a causal effect between one variable and another; rather, they now seek to additionally identify causal mechanisms that explain such effects. Although the study of causal mediation often rests on strong and untestable assumptions (VanderWeele and Vansteelandt Reference VanderWeele and Vansteelandt2009, Imai et al. Reference Imai, Keele, Tingley and Yamamoto2011), these assumptions are relatively weak when we focus on a quantity called the controlled direct effect (CDE) (Pearl Reference Pearl, Breese and Koller2001, Robins Reference Robins, Green, Hjort and Richardson2003). The CDE measures the strength of the causal relationship between a treatment and outcome when a mediator is fixed at a given value for all units. A nonzero CDE implies that the causal effect of treatment on the outcome does not operate exclusively through the mediator of interest. The difference between the total effect and CDE can also be interpreted as the degree to which the mediator contributes to a causal mechanism that transmits the effect of treatment to the outcome (Acharya, Blackwell, and Sen Reference Acharya, Blackwell and Sen2016, Reference Acharya, Blackwell and Sen2018).
Identification of the CDE is not straightforward. Simply conditioning on the mediator (via stratification, matching, or regression adjustment) is insufficient because the effect of the mediator on the outcome may be confounded, possibly by posttreatment variables. For example, when assessing the CDE of media framing on support for immigration at a given level of anxiety (the mediator), posttreatment variables, such as beliefs about the economic or cultural impact of immigration, may affect both anxiety and support for immigration (Imai and Yamamoto Reference Imai and Yamamoto2013). Following Acharya, Blackwell, and Sen (Reference Acharya, Blackwell and Sen2016), we call these variables intermediate confounders. Intermediate confounders pose a dilemma for the identification and estimation of CDEs when they are affected by treatment. In this situation, omitting intermediate confounders would lead to bias in the estimated effects of the mediator on the outcome, and by extension, in estimates of the CDE. However, controlling for intermediate confounders using conventional regression or matching methods would also engender bias in estimates of the CDE because it would block causal pathways, and unblock noncausal pathways, from treatment to the outcome, which would also lead to bias in estimates of the CDE.
Fortunately, several approaches overcome this dilemma. First, we could estimate a model for the marginal mean of the potential outcomes under different levels of the treatment and mediator, known as a marginal structural model (MSM), using the method of inverse probability weighting (IPW) (Robins, Hernan, and Brumback Reference Robins, Hernan and Brumback2000, VanderWeele Reference VanderWeele2009). This approach performs best when both the treatment and mediator are binary. When the treatment and/or mediator are continuous, it performs poorly because the weights involve conditional density estimates that are typically unreliable. Second, to overcome these limitations, we could instead estimate a structural nested mean model (SNMM) for the conditional mean of the potential outcomes given a set of both pretreatment and intermediate confounders using the method of sequential g-estimation (Joffe and Greene Reference Joffe and Greene2009, Vansteelandt Reference Vansteelandt2009). This approach, however, is difficult to implement when there are “intermediate interactions,” that is, when the effect of the mediator on the outcome is moderated by an intermediate confounder. As Acharya, Blackwell, and Sen (Reference Acharya, Blackwell and Sen2016) note:
[I]f Assumption 2 [no intermediate interactions] is violated, it is still possible to estimate the ACDE in a second stage, but that requires (i) a model for the distribution of the intermediate covariates conditional on the treatment and (ii) the evaluation of the average of within-stratum ACDEs across the distribution of that model. The second part entails a high-dimensional integral that is computationally challenging, though Monte Carlo procedures have been developed (Robins Reference Robins1986, Reference Robins and Berkane1997).
Because of these complications, intermediate interactions are typically assumed away in applications of sequential g-estimation, but if this assumption is not met in practice, then estimates of the CDE may be biased.
In this letter, we introduce an alternative method, termed “regression-with-residuals” (RWR), for estimating the CDE. Compared with sequential g-estimation, it is relatively easy to implement, even in the presence of intermediate interactions. In the absence of such interactions, we show that RWR is algebraically equivalent to sequential g-estimation. We illustrate RWR by reanalyzing data from a survey experiment conducted by Brader, Valentino, and Suhay (Reference Brader, Valentino and Suhay2008) to estimate the CDE of negative media framing on support for immigration while controlling for the level of anxiety triggered by negative media cues.
2 Notation, Assumptions, and Sequential G-estimation
We use
![]() $A$
to denote treatment,
$A$
to denote treatment,
![]() $M$
to denote the mediator,
$M$
to denote the mediator,
![]() $Y$
to denote the observed outcome, and
$Y$
to denote the observed outcome, and
![]() $Y(a,m)$
to denote the potential outcome under treatment
$Y(a,m)$
to denote the potential outcome under treatment
![]() $a$
and mediator
$a$
and mediator
![]() $m$
. The CDE is defined as the average effect of changing treatment from
$m$
. The CDE is defined as the average effect of changing treatment from
![]() $a$
to
$a$
to
![]() $a^{\prime }$
while fixing the mediator at a given level
$a^{\prime }$
while fixing the mediator at a given level
![]() $m$
:
$m$
:
This quantity is identified under the assumption of sequential ignorability (Robins Reference Robins and Berkane1997, VanderWeele and Vansteelandt Reference VanderWeele and Vansteelandt2009), which can be formally expressed in two parts as follows:
(1)
 $Y(a,m)\bot \!\!\!\bot A|X,\forall a,m$
(i.e., no unmeasured treatment–outcome confounders).
$Y(a,m)\bot \!\!\!\bot A|X,\forall a,m$
(i.e., no unmeasured treatment–outcome confounders).(2)
 $Y(a,m)\bot \!\!\!\bot M|X,A,Z,\forall a,m$
(i.e., no unmeasured mediator–outcome confounders).
$Y(a,m)\bot \!\!\!\bot M|X,A,Z,\forall a,m$
(i.e., no unmeasured mediator–outcome confounders).
Here,
![]() $X$
denotes a vector of observed pretreatment confounders, while
$X$
denotes a vector of observed pretreatment confounders, while
![]() $Z$
denotes a vector of observed intermediate confounders that affect both the mediator and outcome and that may be affected by treatment. The sequential ignorability assumption is satisfied in Figure 1, which contains a directed acyclic graph summarizing a set of hypothesized causal relationships between the variables outlined previously. In this figure,
$Z$
denotes a vector of observed intermediate confounders that affect both the mediator and outcome and that may be affected by treatment. The sequential ignorability assumption is satisfied in Figure 1, which contains a directed acyclic graph summarizing a set of hypothesized causal relationships between the variables outlined previously. In this figure,
![]() $Z$
is affected by
$Z$
is affected by
![]() $A$
, and thus it is both an intermediate confounder and also a mediator. Because we focus on the CDE controlling for
$A$
, and thus it is both an intermediate confounder and also a mediator. Because we focus on the CDE controlling for
![]() $M$
only, we henceforth refer to
$M$
only, we henceforth refer to
![]() $Z$
exclusively as a confounder for clarity. Of course, it is possible to define a CDE controlling for
$Z$
exclusively as a confounder for clarity. Of course, it is possible to define a CDE controlling for
![]() $M$
and
$M$
and
![]() $Z$
jointly, which would illuminate the mediating role of both variables taken together. Estimands involving multiple mediators, however, are beyond the scope of this letter, although the methods we consider below can be generalized for more complex analyses of this type.
$Z$
jointly, which would illuminate the mediating role of both variables taken together. Estimands involving multiple mediators, however, are beyond the scope of this letter, although the methods we consider below can be generalized for more complex analyses of this type.
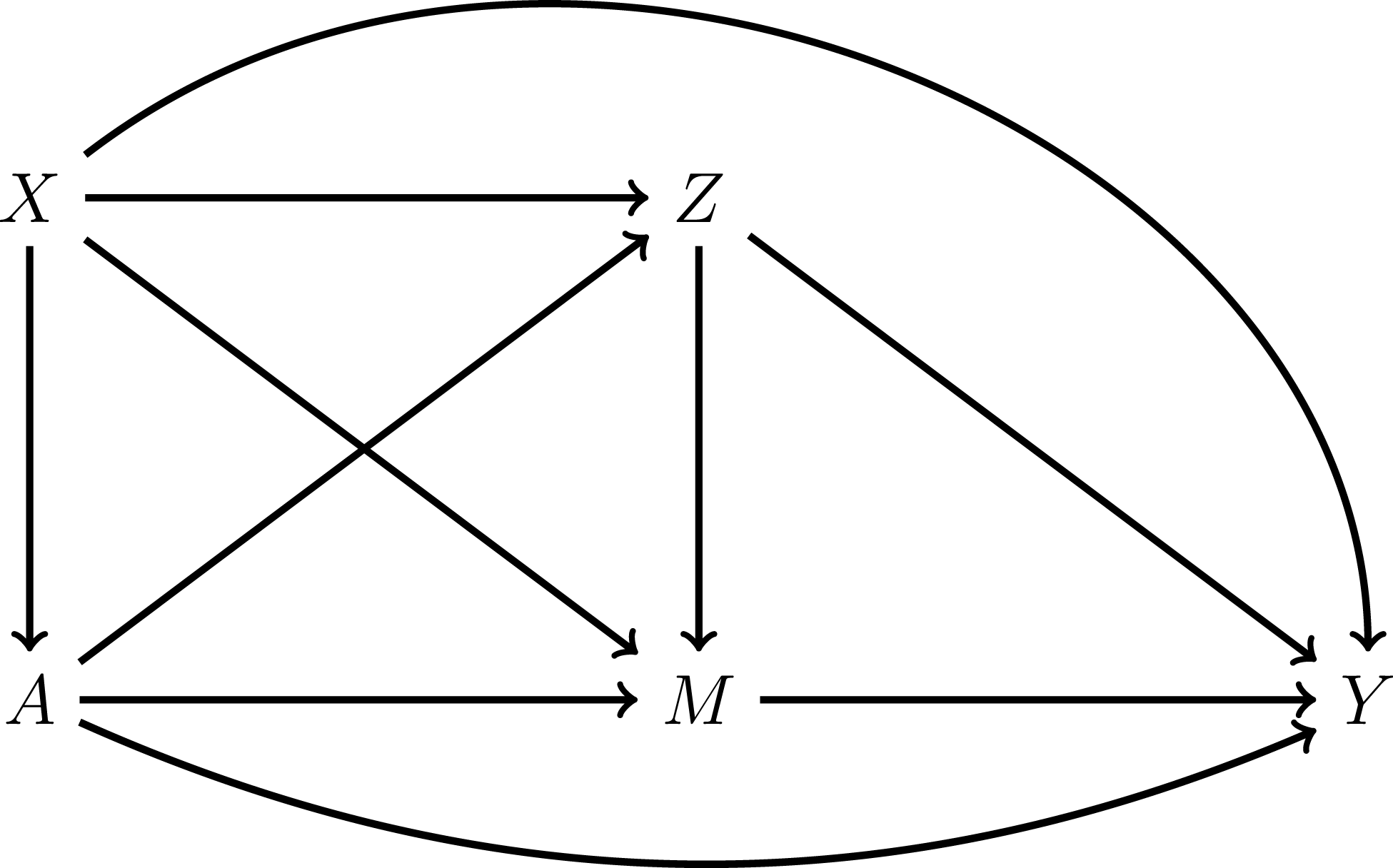
Figure 1. Causal Relationships under Sequential Ignorability Shown in a Direct Acyclic Graph. Note:
![]() $A$
denotes the treatment,
$A$
denotes the treatment,
![]() $M$
denotes the mediator,
$M$
denotes the mediator,
![]() $Y$
denotes the outcome,
$Y$
denotes the outcome,
![]() $X$
denotes the pretreatment confounders, and
$X$
denotes the pretreatment confounders, and
![]() $Z$
denotes the intermediate confounders.
$Z$
denotes the intermediate confounders.
The CDE is distinct from several other estimands considered in analyses of causal mediation. For example, it is distinct from the average direct effect (ADE) considered in Imai et al. (Reference Imai, Keele, Tingley and Yamamoto2011), which is defined as
where
![]() $M(a)$
denotes the potential outcome for the mediator under treatment
$M(a)$
denotes the potential outcome for the mediator under treatment
![]() $a$
. In contrast to the CDE, the ADE represents the average effect of changing treatment from
$a$
. In contrast to the CDE, the ADE represents the average effect of changing treatment from
![]() $a$
to
$a$
to
![]() $a^{\prime }$
while fixing the mediator for each unit at its value under treatment
$a^{\prime }$
while fixing the mediator for each unit at its value under treatment
![]() $a$
. The ADE is equal to the difference between the total effect and the average causal mediation effect (ACME), which is defined as
$a$
. The ADE is equal to the difference between the total effect and the average causal mediation effect (ACME), which is defined as
In general, the CDE differs from the ADE, and thus the difference between the total effect and CDE differs from the ACME, as long as the unit-level direct effect
![]() $Y(a,m)-Y(a^{\prime },m)$
depends on
$Y(a,m)-Y(a^{\prime },m)$
depends on
![]() $m$
for some units. We focus on the CDE because it is identified under much weaker assumptions than the ADE and ACME. In particular, the CDE can still be identified in the presence of intermediate confounders affected by treatment, unlike the ADE and ACME (VanderWeele and Vansteelandt Reference VanderWeele and Vansteelandt2009).
$m$
for some units. We focus on the CDE because it is identified under much weaker assumptions than the ADE and ACME. In particular, the CDE can still be identified in the presence of intermediate confounders affected by treatment, unlike the ADE and ACME (VanderWeele and Vansteelandt Reference VanderWeele and Vansteelandt2009).
Although the CDE is identified under sequential ignorability, additional modeling assumptions are needed to estimate the CDE in finite samples. Sequential g-estimation, for example, relies on a linear model for the conditional mean of the outcome given
![]() $A$
,
$A$
,
![]() $M$
,
$M$
,
![]() $X$
, and
$X$
, and
![]() $Z$
. Moreover, because sequential g-estimation is difficult to implement in the presence of intermediate interactions, its application in practice also typically relies on an additional simplifying assumption that the effect of the mediator on the outcome is not moderated by intermediate confounders, which can be formally expressed as follows:
$Z$
. Moreover, because sequential g-estimation is difficult to implement in the presence of intermediate interactions, its application in practice also typically relies on an additional simplifying assumption that the effect of the mediator on the outcome is not moderated by intermediate confounders, which can be formally expressed as follows:
In words, this assumption states that among the units exposed to treatment
![]() $a$
, the effect of the mediator on the outcome would not differ across the subgroups defined by the postreatment confounders within levels of the pretreatment confounders.
$a$
, the effect of the mediator on the outcome would not differ across the subgroups defined by the postreatment confounders within levels of the pretreatment confounders.
Under this assumption, Acharya, Blackwell, and Sen (Reference Acharya, Blackwell and Sen2016) illustrate sequential g-estimation of the CDE using the following model for the outcome:
With this model, sequential g-estimation proceeds in three steps:
(1) Compute least squares estimates for equation (1) and save
 $\hat{\unicode[STIX]{x1D6FE}}_{2}$
.
$\hat{\unicode[STIX]{x1D6FE}}_{2}$
.(2) Construct a “de-mediated” outcome defined as
 $Y_{d}=Y-M(\hat{\unicode[STIX]{x1D6FE}}_{0}+\hat{\unicode[STIX]{x1D6FE}}_{1}^{T}X+\hat{\unicode[STIX]{x1D6FE}}_{2}A)$
.
$Y_{d}=Y-M(\hat{\unicode[STIX]{x1D6FE}}_{0}+\hat{\unicode[STIX]{x1D6FE}}_{1}^{T}X+\hat{\unicode[STIX]{x1D6FE}}_{2}A)$
.(3) Compute least squares estimates for a linear regression of
 $Y_{d}$
on
$Y_{d}$
on
 $X$
and
$X$
and
 $A$
, which can be expressed as
$A$
, which can be expressed as
 ${\hat{Y}}_{d}=\hat{\unicode[STIX]{x1D705}}_{0}+\hat{\unicode[STIX]{x1D705}}_{1}^{T}X+\hat{\unicode[STIX]{x1D705}}_{2}A$
.
${\hat{Y}}_{d}=\hat{\unicode[STIX]{x1D705}}_{0}+\hat{\unicode[STIX]{x1D705}}_{1}^{T}X+\hat{\unicode[STIX]{x1D705}}_{2}A$
.
The sequential g-estimate of the CDE is then given by
This estimator is consistent under the assumptions of sequential ignorability and a correctly specified linear model for the outcome, which here requires that there must not be any effect moderation by the intermediate confounders. Standard errors can be obtained via the nonparametric bootstrap or a consistent variance estimator derived in Acharya, Blackwell, and Sen (Reference Acharya, Blackwell and Sen2016).
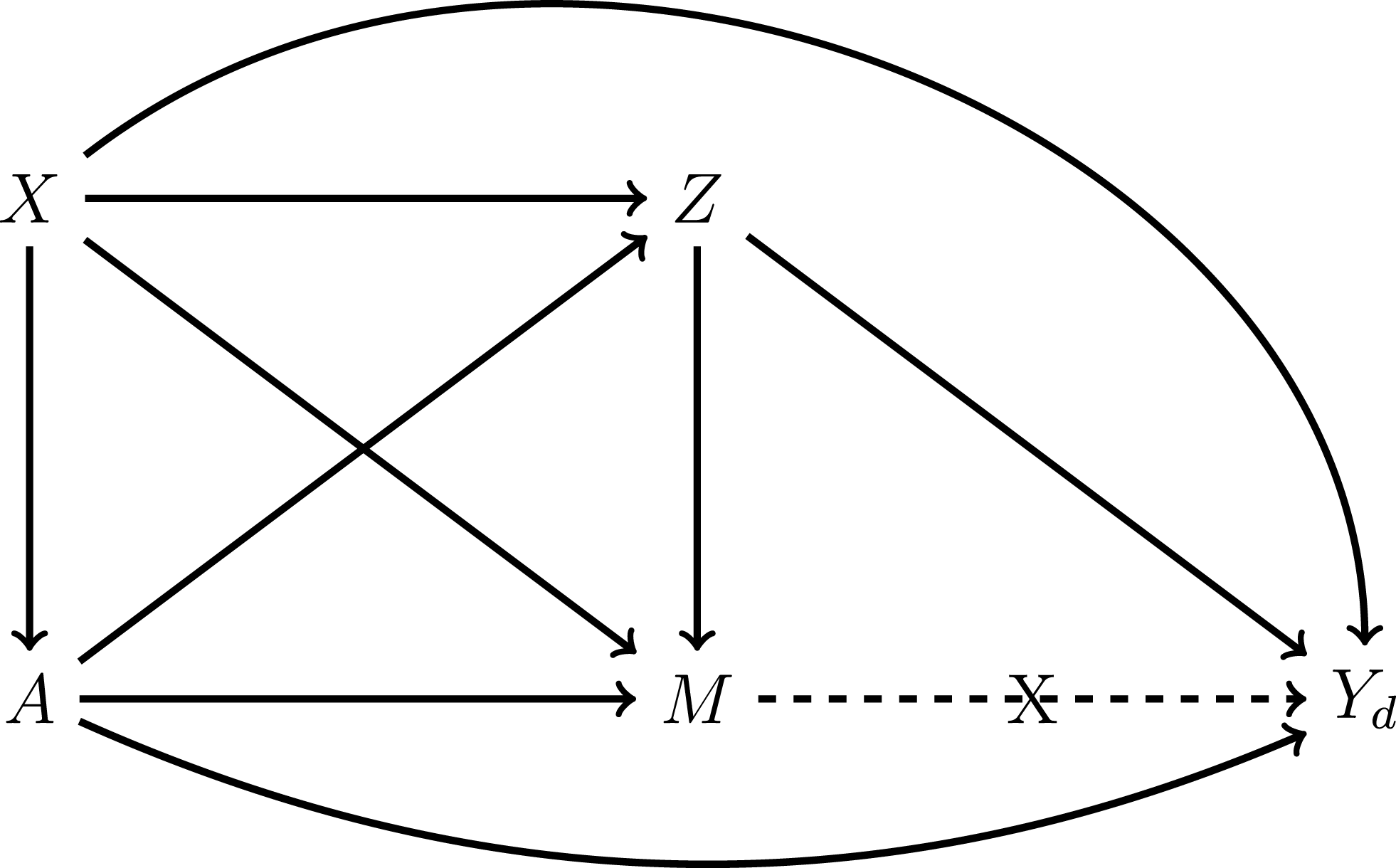
Figure 2. The Logic of Sequential G-estimation. Note:
![]() $A$
denotes the treatment,
$A$
denotes the treatment,
![]() $M$
denotes the mediator,
$M$
denotes the mediator,
![]() $Y$
denotes the outcome,
$Y$
denotes the outcome,
![]() $X$
denotes the pretreatment confounders, and
$X$
denotes the pretreatment confounders, and
![]() $Z$
denotes the intermediate confounders.
$Z$
denotes the intermediate confounders.
In Figure 2, we illustrate the logic of sequential g-estimation. First, under the identification and modeling assumptions outlined previously, the regression in step 1 identifies the causal effect of
![]() $M$
on
$M$
on
![]() $Y$
. Then, the “de-mediation” calculation in step 2 neutralizes the causal path from
$Y$
. Then, the “de-mediation” calculation in step 2 neutralizes the causal path from
![]() $M$
to
$M$
to
![]() $Y$
, while all other causal paths remain intact. Finally, the regression of the de-mediated outcome,
$Y$
, while all other causal paths remain intact. Finally, the regression of the de-mediated outcome,
![]() $Y_{d}$
, on
$Y_{d}$
, on
![]() $X$
and
$X$
and
![]() $A$
in step 3 identifies the controlled direct effect of
$A$
in step 3 identifies the controlled direct effect of
![]() $A$
when
$A$
when
![]() $M=0$
, and because
$M=0$
, and because
![]() $\hat{\unicode[STIX]{x1D6FE}}_{2}$
is a consistent estimate of the treatment–mediator interaction effect, the CDE when
$\hat{\unicode[STIX]{x1D6FE}}_{2}$
is a consistent estimate of the treatment–mediator interaction effect, the CDE when
![]() $M=m$
can be estimated with equation (2).
$M=m$
can be estimated with equation (2).
3 Regression-with-Residuals Estimation
RWR estimation was originally developed to assess how time-varying covariates moderate the effect of time-varying treatments (Almirall, Ten Have, and Murphy Reference Almirall, Ten Have and Murphy2010, Wodtke and Almirall Reference Wodtke and Almirall2017). In this section, we show how RWR can be adapted to estimate CDEs while properly adjusting for intermediate confounders. Specifically, RWR estimation of the CDE based on a model without intermediate interactions, such as equation (1), proceeds in two steps:
(1) For each of the intermediate confounders, compute least squares estimates for a linear regression of
 $Z$
on
$Z$
on
 $X$
and
$X$
and
 $A$
, and save the residuals, which we denote by
$A$
, and save the residuals, which we denote by
 $Z_{\bot }$
.
$Z_{\bot }$
.(2) Compute least squares estimates for a model similar to equation (1) but with
 $Z$
replaced by
$Z$
replaced by
 $Z_{\bot }$
, which can be expressed as
$Z_{\bot }$
, which can be expressed as
 ${\hat{Y}}=\tilde{\unicode[STIX]{x1D6FD}}_{0}+\tilde{\unicode[STIX]{x1D6FD}}_{1}^{T}X+\tilde{\unicode[STIX]{x1D6FD}}_{2}A+\tilde{\unicode[STIX]{x1D6FD}}_{3}^{T}Z_{\bot }+M(\tilde{\unicode[STIX]{x1D6FE}}_{0}+\tilde{\unicode[STIX]{x1D6FE}}_{1}^{T}X+\tilde{\unicode[STIX]{x1D6FE}}_{2}A)$
.
${\hat{Y}}=\tilde{\unicode[STIX]{x1D6FD}}_{0}+\tilde{\unicode[STIX]{x1D6FD}}_{1}^{T}X+\tilde{\unicode[STIX]{x1D6FD}}_{2}A+\tilde{\unicode[STIX]{x1D6FD}}_{3}^{T}Z_{\bot }+M(\tilde{\unicode[STIX]{x1D6FE}}_{0}+\tilde{\unicode[STIX]{x1D6FE}}_{1}^{T}X+\tilde{\unicode[STIX]{x1D6FE}}_{2}A)$
.
The RWR estimate of the CDE is then given by
As shown in Supplementary Material A, RWR and sequential g-estimation are algebraically equivalent (i.e.,
![]() $\hat{\unicode[STIX]{x1D705}}_{2}=\tilde{\unicode[STIX]{x1D6FD}}_{2}$
;
$\hat{\unicode[STIX]{x1D705}}_{2}=\tilde{\unicode[STIX]{x1D6FD}}_{2}$
;
![]() $\hat{\unicode[STIX]{x1D6FE}}_{2}=\tilde{\unicode[STIX]{x1D6FE}}_{2}$
) when there are no intermediate interactions. They rely on the same identification and modeling assumptions, and they share the same statistical properties.
$\hat{\unicode[STIX]{x1D6FE}}_{2}=\tilde{\unicode[STIX]{x1D6FE}}_{2}$
) when there are no intermediate interactions. They rely on the same identification and modeling assumptions, and they share the same statistical properties.
In Figure 3, we illustrate the logic of RWR. First, residualizing the intermediate confounders in step 1 neutralizes the causal paths emanating from
![]() $X$
and
$X$
and
![]() $A$
to
$A$
to
![]() $Z$
. Then, the residualized confounders can be included in an outcome regression to adjust for mediator–outcome confounding while avoiding the bias that normally results from conditioning on posttreatment variables. RWR estimation avoids posttreatment bias because
$Z$
. Then, the residualized confounders can be included in an outcome regression to adjust for mediator–outcome confounding while avoiding the bias that normally results from conditioning on posttreatment variables. RWR estimation avoids posttreatment bias because
![]() $Z_{\bot }$
is no longer a consequence of
$Z_{\bot }$
is no longer a consequence of
![]() $A$
, and it avoids omitted variable bias because all confounders have been appropriately controlled in a model for the outcome.
$A$
, and it avoids omitted variable bias because all confounders have been appropriately controlled in a model for the outcome.
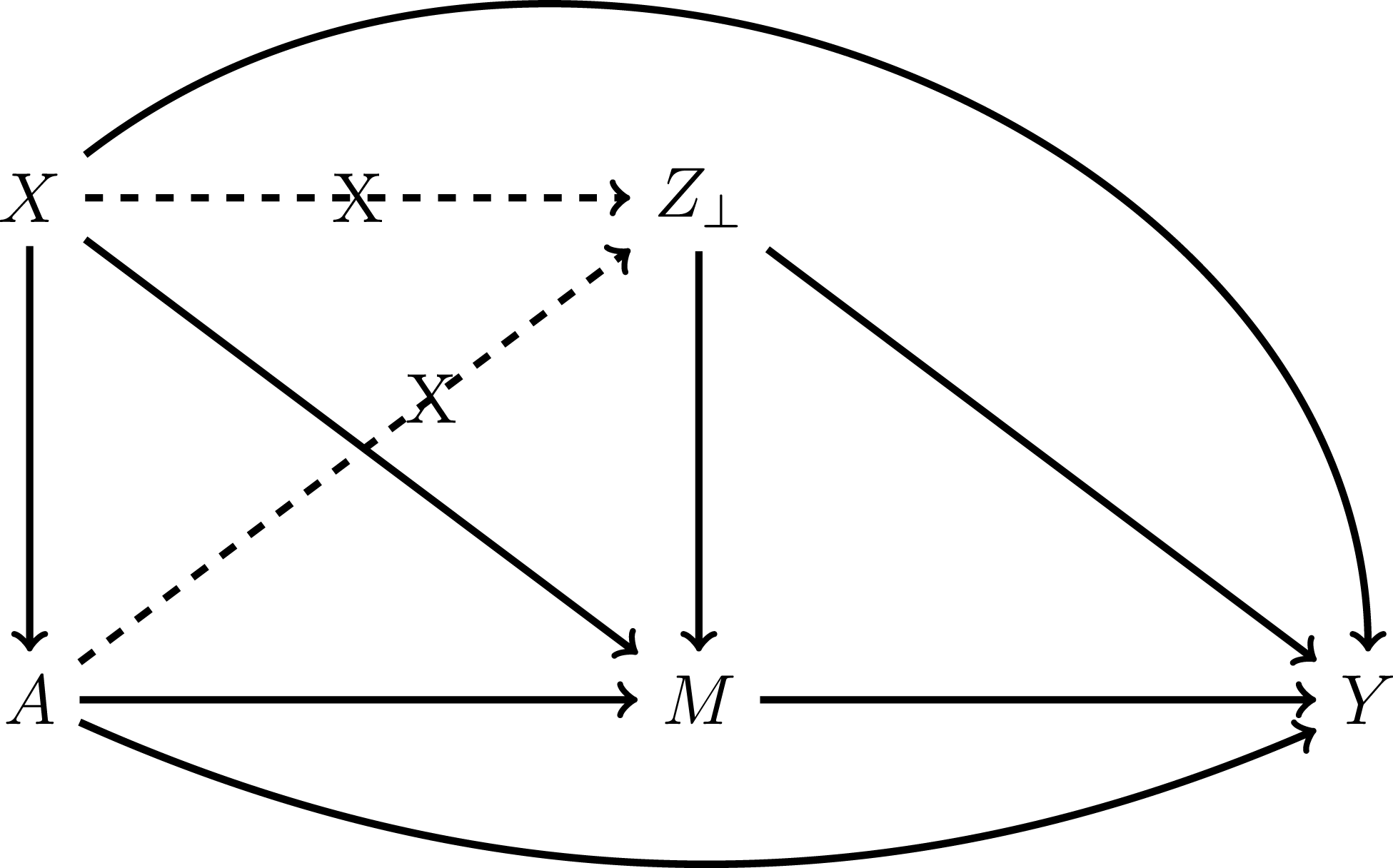
Figure 3. The Logic of Regression-with-residuals. Note:
![]() $A$
denotes the treatment,
$A$
denotes the treatment,
![]() $M$
denotes the mediator,
$M$
denotes the mediator,
![]() $Y$
denotes the outcome,
$Y$
denotes the outcome,
![]() $X$
denotes the pretreatment confounders, and
$X$
denotes the pretreatment confounders, and
![]() $Z$
denotes the intermediate confounders.
$Z$
denotes the intermediate confounders.
4 Intermediate Interactions
In the models considered previously, the effect of the mediator on the outcome is assumed to be invariant across all intermediate confounders. This is a strong and arguably implausible assumption in many social science applications. When it is not satisfied, estimates of the CDE may be biased and inconsistent. Thus, methods that accommodate, rather than naively assume away, intermediate interactions will make analyses of causal mediation more robust. The main advantage of RWR over sequential g-estimation is the ease with which RWR can accommodate intermediate interactions (Wodtke, Alaca, and Zhou Reference Wodtke, Alaca and Zhou2018). Consider the following model, which extends equation (1) by including an interaction term between
![]() $M$
and
$M$
and
![]() $Z$
:
$Z$
:
With this model, sequential g-estimation can still be used to estimate the CDE at
![]() $m=0$
. The only modification to the sequential g-estimator in this situation is that the de-mediated outcome,
$m=0$
. The only modification to the sequential g-estimator in this situation is that the de-mediated outcome,
![]() $Y_{d}$
, is obtained by subtracting
$Y_{d}$
, is obtained by subtracting
![]() $M(\hat{\unicode[STIX]{x1D6FE}}_{0}+\hat{\unicode[STIX]{x1D6FE}}_{1}^{T}X+\hat{\unicode[STIX]{x1D6FE}}_{2}A+\hat{\unicode[STIX]{x1D6FE}}_{3}^{T}Z)$
instead of
$M(\hat{\unicode[STIX]{x1D6FE}}_{0}+\hat{\unicode[STIX]{x1D6FE}}_{1}^{T}X+\hat{\unicode[STIX]{x1D6FE}}_{2}A+\hat{\unicode[STIX]{x1D6FE}}_{3}^{T}Z)$
instead of
![]() $M(\hat{\unicode[STIX]{x1D6FE}}_{0}+\hat{\unicode[STIX]{x1D6FE}}_{1}^{T}X+\hat{\unicode[STIX]{x1D6FE}}_{2}A)$
from the observed outcome. Then,
$M(\hat{\unicode[STIX]{x1D6FE}}_{0}+\hat{\unicode[STIX]{x1D6FE}}_{1}^{T}X+\hat{\unicode[STIX]{x1D6FE}}_{2}A)$
from the observed outcome. Then,
![]() $\widehat{\text{CDE}}_{\text{ SG}}(a,a^{\prime },0)=\hat{\unicode[STIX]{x1D705}}_{2}(a-a^{\prime })$
, where
$\widehat{\text{CDE}}_{\text{ SG}}(a,a^{\prime },0)=\hat{\unicode[STIX]{x1D705}}_{2}(a-a^{\prime })$
, where
![]() $\hat{\unicode[STIX]{x1D705}}_{2}$
is the coefficient on treatment from the regression of
$\hat{\unicode[STIX]{x1D705}}_{2}$
is the coefficient on treatment from the regression of
![]() $Y_{d}$
on
$Y_{d}$
on
![]() $X$
and
$X$
and
![]() $A$
.
$A$
.
Although sequential g-estimation can still be used to estimate the CDE at
![]() $m=0$
in the presence of intermediate interactions, we can no longer estimate the CDE at any general value of
$m=0$
in the presence of intermediate interactions, we can no longer estimate the CDE at any general value of
![]() $m$
using equation (2). This is because
$m$
using equation (2). This is because
![]() $\hat{\unicode[STIX]{x1D6FE}}_{2}m(a-a^{\prime })$
is no longer a consistent estimate of the treatment–mediator interaction effect, as the inclusion of the term
$\hat{\unicode[STIX]{x1D6FE}}_{2}m(a-a^{\prime })$
is no longer a consistent estimate of the treatment–mediator interaction effect, as the inclusion of the term
![]() $\unicode[STIX]{x1D6FE}_{3}^{T}z$
in equation (4) leads to posttreatment bias in
$\unicode[STIX]{x1D6FE}_{3}^{T}z$
in equation (4) leads to posttreatment bias in
![]() $\unicode[STIX]{x1D6FE}_{2}a$
. In other words, the de-mediation step only removes posttreatment bias in
$\unicode[STIX]{x1D6FE}_{2}a$
. In other words, the de-mediation step only removes posttreatment bias in
![]() $\unicode[STIX]{x1D6FD}_{2}a$
but not in
$\unicode[STIX]{x1D6FD}_{2}a$
but not in
![]() $\unicode[STIX]{x1D6FE}_{2}a$
.Footnote
1
$\unicode[STIX]{x1D6FE}_{2}a$
.Footnote
1
RWR estimation, by contrast, easily accommodates intermediate interactions, and its implementation in their presence remains almost exactly the same as before:
(1) For each of the intermediate confounders, compute least squares estimates for a linear regression of
 $Z$
on
$Z$
on
 $X$
and
$X$
and
 $A$
, and save the residuals, denoted by
$A$
, and save the residuals, denoted by
 $Z_{\bot }$
.
$Z_{\bot }$
.(2) Compute least squares estimates for a model similar to equation (4) but with
 $Z$
replaced by
$Z$
replaced by
 $Z_{\bot }$
, which can be expressed as
$Z_{\bot }$
, which can be expressed as  $$\begin{eqnarray}{\hat{Y}}=\tilde{\unicode[STIX]{x1D6FD}}_{0}+\tilde{\unicode[STIX]{x1D6FD}}_{1}^{T}X+\tilde{\unicode[STIX]{x1D6FD}}_{2}A+\tilde{\unicode[STIX]{x1D6FD}}_{3}^{T}Z_{\bot }+M(\tilde{\unicode[STIX]{x1D6FE}}_{0}+\tilde{\unicode[STIX]{x1D6FE}}_{1}^{T}X+\tilde{\unicode[STIX]{x1D6FE}}_{2}A+\tilde{\unicode[STIX]{x1D6FE}}_{3}^{T}Z_{\bot }).\end{eqnarray}$$
$$\begin{eqnarray}{\hat{Y}}=\tilde{\unicode[STIX]{x1D6FD}}_{0}+\tilde{\unicode[STIX]{x1D6FD}}_{1}^{T}X+\tilde{\unicode[STIX]{x1D6FD}}_{2}A+\tilde{\unicode[STIX]{x1D6FD}}_{3}^{T}Z_{\bot }+M(\tilde{\unicode[STIX]{x1D6FE}}_{0}+\tilde{\unicode[STIX]{x1D6FE}}_{1}^{T}X+\tilde{\unicode[STIX]{x1D6FE}}_{2}A+\tilde{\unicode[STIX]{x1D6FE}}_{3}^{T}Z_{\bot }).\end{eqnarray}$$
The RWR estimate of the CDE is then given by
where
![]() $\tilde{\unicode[STIX]{x1D6FE}}_{2}$
remains a consistent estimate of the treatment–mediator interaction effect.Footnote
2
$\tilde{\unicode[STIX]{x1D6FE}}_{2}$
remains a consistent estimate of the treatment–mediator interaction effect.Footnote
2
As shown in Supplementary Material B, equation (5) is a consistent estimator of the CDE under the assumptions of sequential ignorability and no model misspecification. RWR estimation remains consistent even in the presence of intermediate interactions because, by appropriately residualizing the intermediate confounders, it removes any posttreatment bias from the main effect of treatment and from the treatment–mediator interaction effect. RWR can also accommodate “baseline interactions” between treatment
![]() $A$
and the pretreatment confounders
$A$
and the pretreatment confounders
![]() $X$
. In this situation, we need only recenter the pretreatment confounders at their sample means and then include the appropriate interaction terms in the outcome regression. Standard errors can be computed using the nonparametric bootstrap.
$X$
. In this situation, we need only recenter the pretreatment confounders at their sample means and then include the appropriate interaction terms in the outcome regression. Standard errors can be computed using the nonparametric bootstrap.
5 The Effect of Media Framing on Support for Immigration
To illustrate RWR, we reanalyze data from Brader, Valentino, and Suhay (Reference Brader, Valentino and Suhay2008) to estimate the CDE of negative media framing on public support for immigration, controlling for respondent anxiety potentially triggered by negative media cues.Footnote
3
With a nationally representative sample of 354 white non-Hispanic adults, Brader, Valentino, and Suhay (Reference Brader, Valentino and Suhay2008) conducted a survey experiment in which respondents were asked to read a mock news report on immigration. In this report, both the ethnicity of the featured immigrant and the tone of the story were randomly manipulated using a
![]() $2\times 2$
design. Specifically, respondents were presented with a story that featured either a white European immigrant or a Latino immigrant and that focused on either the benefits or the costs of immigration. After reading the story, respondents were asked to report their beliefs about the harms of immigration, their feelings about increased immigration, and their support for immigration. With these data, Brader, Valentino, and Suhay (Reference Brader, Valentino and Suhay2008) found that stories featuring both a Latino immigrant and a negative frame emphasizing the costs of immigration had a large negative effect on support for immigration. They also reported that a substantial proportion of this effect is mediated by respondents’ anxiety about increased immigration and that beliefs about the harms of immigration, as opposed to negative emotions, do not play an important mediating role. However, Brader, Valentino, and Suhay (Reference Brader, Valentino and Suhay2008) assessed the mediating role of beliefs and emotions separately under the assumption that respondent anxiety is not affected by perceptions of the harms associated with immigration, which seems unlikely and appears to be inconsistent with their own data (Imai and Yamamoto Reference Imai and Yamamoto2013). Thus, we treat beliefs about the harm of immigration as an intermediate confounder and reassess the mediating role of respondent anxiety using RWR and, for comparative purposes, sequential g-estimation.
$2\times 2$
design. Specifically, respondents were presented with a story that featured either a white European immigrant or a Latino immigrant and that focused on either the benefits or the costs of immigration. After reading the story, respondents were asked to report their beliefs about the harms of immigration, their feelings about increased immigration, and their support for immigration. With these data, Brader, Valentino, and Suhay (Reference Brader, Valentino and Suhay2008) found that stories featuring both a Latino immigrant and a negative frame emphasizing the costs of immigration had a large negative effect on support for immigration. They also reported that a substantial proportion of this effect is mediated by respondents’ anxiety about increased immigration and that beliefs about the harms of immigration, as opposed to negative emotions, do not play an important mediating role. However, Brader, Valentino, and Suhay (Reference Brader, Valentino and Suhay2008) assessed the mediating role of beliefs and emotions separately under the assumption that respondent anxiety is not affected by perceptions of the harms associated with immigration, which seems unlikely and appears to be inconsistent with their own data (Imai and Yamamoto Reference Imai and Yamamoto2013). Thus, we treat beliefs about the harm of immigration as an intermediate confounder and reassess the mediating role of respondent anxiety using RWR and, for comparative purposes, sequential g-estimation.
Specifically, we estimate the CDE of negative media framing on support for immigration, controlling for respondent anxiety, using several variants of the following model:
where the outcome,
![]() $Y$
, is a measure of support for immigration on a five-point scale; the treatment,
$Y$
, is a measure of support for immigration on a five-point scale; the treatment,
![]() $A$
, denotes receipt of a news story featuring both a Latino immigrant and a negative frame emphasizing the costs of immigration; the mediator,
$A$
, denotes receipt of a news story featuring both a Latino immigrant and a negative frame emphasizing the costs of immigration; the mediator,
![]() $M$
, is the level of anxiety expressed by the respondent on a ten-point scale; the intermediate confounder,
$M$
, is the level of anxiety expressed by the respondent on a ten-point scale; the intermediate confounder,
![]() $Z$
, is a measure of the perceived harm of immigration on a seven-point scale; and finally, the vector of pretreatment covariates,
$Z$
, is a measure of the perceived harm of immigration on a seven-point scale; and finally, the vector of pretreatment covariates,
![]() $X$
, includes measures of gender, age, education, and income.Footnote
4
We control for a set of pretreatment covariates because, although treatment is randomly assigned, the mediator–outcome relationship may still be confounded by baseline factors in these data. To simplify interpretation, all variables except the treatment and outcome are centered at their sample means.
$X$
, includes measures of gender, age, education, and income.Footnote
4
We control for a set of pretreatment covariates because, although treatment is randomly assigned, the mediator–outcome relationship may still be confounded by baseline factors in these data. To simplify interpretation, all variables except the treatment and outcome are centered at their sample means.
Table 1. Estimated CDE of Media Framing on Support for Immigration using Sequential G-estimation, RWR, and RWR with Intermediate Interactions.
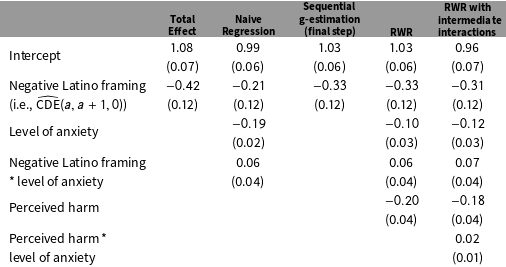
Note: Numbers in parentheses are bootstrapped standard errors (500 replications). For ease of interpretation, all predictors except the treatment are centered at their means. Coefficients of pretreatment covariates are omitted. Supplementary Material C presents the R code used to generate the results.
As a benchmark, the first two columns of Table 1 present an estimate of the total treatment effect from a regression of
![]() $Y$
on
$Y$
on
![]() $X$
and
$X$
and
![]() $A$
as well as a “naive” estimate of the CDE from a regression model similar to equation (6) but without adjustments for the intermediate confounder
$A$
as well as a “naive” estimate of the CDE from a regression model similar to equation (6) but without adjustments for the intermediate confounder
![]() $Z$
. Consistent with results reported by Brader, Valentino, and Suhay (Reference Brader, Valentino and Suhay2008), the estimated total effect indicates that negative media framing reduces support for immigration, and the naive estimate of the CDE suggests that about half of the total treatment effect is due to heightened anxiety.
$Z$
. Consistent with results reported by Brader, Valentino, and Suhay (Reference Brader, Valentino and Suhay2008), the estimated total effect indicates that negative media framing reduces support for immigration, and the naive estimate of the CDE suggests that about half of the total treatment effect is due to heightened anxiety.
The third and fourth columns of Table 1 present sequential g-estimates and RWR estimates, respectively, for the CDE based on model (6). As expected, the estimates given by these two methods are exactly the same (
![]() $-0.33$
) because there are no intermediate interactions in this model. Contrary to the naive estimate of the CDE discussed previously, these results suggest that less than one-quarter of the total treatment effect may be due to heightened respondent anxiety. This finding is consistent with estimates of the ADE reported by Imai and Yamamoto (Reference Imai and Yamamoto2013).
$-0.33$
) because there are no intermediate interactions in this model. Contrary to the naive estimate of the CDE discussed previously, these results suggest that less than one-quarter of the total treatment effect may be due to heightened respondent anxiety. This finding is consistent with estimates of the ADE reported by Imai and Yamamoto (Reference Imai and Yamamoto2013).
With sequential g-estimation, only the CDE at
![]() $m=0$
(i.e., when the level of respondent anxiety is set at its sample mean) is reported in the final step. To construct the CDE at other levels of the mediator, the analyst must extract the coefficient on the treatment–mediator interaction from the regression in step 1 of the procedure. With RWR, by contrast, all the coefficients required for constructing the CDE at any level of the mediator are reported in the single regression for the outcome. This allows an analyst to construct any CDE of interest directly from the results in Table 1. For example, when respondent anxiety is one standard deviation (2.77) above the sample mean, the CDE is estimated to be
$m=0$
(i.e., when the level of respondent anxiety is set at its sample mean) is reported in the final step. To construct the CDE at other levels of the mediator, the analyst must extract the coefficient on the treatment–mediator interaction from the regression in step 1 of the procedure. With RWR, by contrast, all the coefficients required for constructing the CDE at any level of the mediator are reported in the single regression for the outcome. This allows an analyst to construct any CDE of interest directly from the results in Table 1. For example, when respondent anxiety is one standard deviation (2.77) above the sample mean, the CDE is estimated to be
![]() $(-0.33+2.77\ast 0.064)=-0.15$
.
$(-0.33+2.77\ast 0.064)=-0.15$
.
Thus far, the effect of anxiety on support for immigration has been assumed to be invariant across levels of the intermediate confounder, but if this effect is in fact moderated by beliefs about the harms of immigration, then estimates reported previously may be biased. We now relax this assumption by additionally including an interaction term between the level of anxiety and the perceived harm of immigration when implementing RWR. Results from this analysis are shown in the last column of Table 1. The estimated CDE from this model at
![]() $m=0$
is
$m=0$
is
![]() $-0.31$
, which is similar to that obtained from the model without intermediate interactions. In this example, it appears that our findings are fairly robust to the exclusion of intermediate interactions. Nevertheless, it is the flexibility of RWR that allows us to easily assess the sensitivity of results to different specifications.
$-0.31$
, which is similar to that obtained from the model without intermediate interactions. In this example, it appears that our findings are fairly robust to the exclusion of intermediate interactions. Nevertheless, it is the flexibility of RWR that allows us to easily assess the sensitivity of results to different specifications.
6 Concluding Remarks
In this letter, we introduced RWR for estimating controlled direct effects. In the absence of intermediate interactions, RWR is algebraically equivalent to the sequential g-estimator. But unlike the sequential g-estimator, RWR can easily accommodate several different types of effect moderation, including intermediate interactions, which are likely common in the social sciences. In general, models with less stringent parametric constraints can be estimated more easily with RWR than with sequential g-estimation.
Nevertheless, RWR is still premised on a number of strong modeling assumptions. In particular, RWR requires a correctly specified linear model for the outcome. In applications with many confounders or complex patterns of effect heterogeneity, the modeling assumptions required of RWR may be difficult to satisfy, and when they are violated, RWR is biased. Moreover, in applications where a linear model may be inappropriate (e.g., in analyses with binary outcomes), RWR does not generalize in a straightforward manner for use with nonlinear models. Thus, semiparametric methods, such as IPW estimation of MSMs or certain types of sensitivity analysis (e.g., Imai and Yamamoto Reference Imai and Yamamoto2013), may be preferable in applications with a large number of confounders, complex effect heterogeneity, or categorical outcomes.
These limitations notwithstanding, simulation studies indicate that g- and RWR estimation can still outperform IPW estimation even when the outcome model is misspecified, especially in applications with continuous treatments and/or mediators (Vansteelandt Reference Vansteelandt2009, Wodtke Reference Wodtke2018). RWR estimation can also be combined with a sensitivity analysis to assess the robustness of estimates to different violations of its motivating assumptions. Given its simplicity, flexibility, and relative efficiency, we expect that RWR will be widely used in causal mediation analyses.
Supplementary material
For supplementary material accompanying this paper, please visithttps://doi.org/10.1017/pan.2018.53.






