No CrossRef data available.
Published online by Cambridge University Press: 20 January 2009
Theorem. If a point be taken on the radical axis of a coaxial system of circles, and from it tangents be drawn to any circle of the system, these tangents are cut in points on a conic, by the radical axis of the circle and a given fixed point. The two points are the foci of the conic. (Fig. 1.) Let W1W2 be the line of
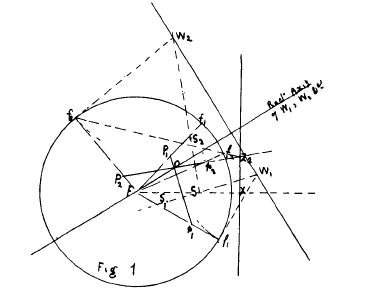
gives an ellipse as the locus of P1P2, &c, when, as in Fig, 1, S is internal to F. If S were an external point, we should have P1F-P1S = P1F - P1f1 = radius of F = constant, and the locus of P1, P2, &c., would be a hyperbola. When F is at infinity on the radical axis, P1S = P1f1, and P1f1 being at right angles to W1W2, the conic is a parabola, and the line of centres the directrix.