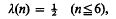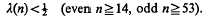Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Diananda, P. H.
1962.
Some Cyclic and Other Inequalities.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 58,
Issue. 2,
p.
425.
Diananda, P. H.
1962.
A Cyclic Inequality and an Extension of it. II.
Proceedings of the Edinburgh Mathematical Society,
Vol. 13,
Issue. 2,
p.
143.
Diananda, P. H.
1962.
A Cyclic Inequality and an Extension of It. I.
Proceedings of the Edinburgh Mathematical Society,
Vol. 13,
Issue. 1,
p.
79.
Djoković, D. Ž.
1963.
Sur une inégalité.
Proceedings of the Glasgow Mathematical Association,
Vol. 6,
Issue. 1,
p.
1.
Mitrinović, Dragoslav S.
1970.
Analytic Inequalities.
p.
27.
Drinfel'd, V. G.
1971.
A cyclic inequality.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 9,
Issue. 2,
p.
68.
Godunova, E. K.
and
Levin, V. I.
1973.
Sharpening certain cyclic inequalities.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 14,
Issue. 3,
p.
735.
Baston, V. J.
1974.
Some cyclic inequalities.
Proceedings of the Edinburgh Mathematical Society,
Vol. 19,
Issue. 2,
p.
115.
Troesch, B. A.
1989.
The validity of Shapiro’s cyclic inequality.
Mathematics of Computation,
Vol. 53,
Issue. 188,
p.
657.
Clausing, Achim
1992.
General Inequalities 6.
Vol. 103,
Issue. ,
p.
17.
Mitrinović, D. S.
Pečarić, J. E.
and
Fink, A. M.
1993.
Classical and New Inequalities in Analysis.
p.
407.
Fink, A. M.
1998.
Recent Progress in Inequalities.
p.
241.
Sadov, Sergey
2016.
Lower bound for cyclic sums of Diananda type.
Archiv der Mathematik,
Vol. 106,
Issue. 2,
p.
135.