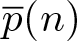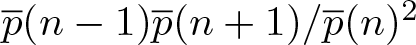Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mukherjee, Gargi
2024.
Asymptotic expansion for the Fourier coefficients associated with the inverse of the modular discriminant function $$\Delta $$.
Research in Number Theory,
Vol. 10,
Issue. 4,
Liu, Xin-Bei
and
Zhang, Zhong-Xue
2025.
The Briggs inequality for partitions and overpartitions.
The Ramanujan Journal,
Vol. 67,
Issue. 3,
Mukherjee, Gargi
2026.
Asymptotic growth of (−1)rΔrlogp‾(n)/nαn and the reverse higher order Turán inequalities for p‾(n)/nαn.
Journal of Mathematical Analysis and Applications,
Vol. 553,
Issue. 2,
p.
129884.