Article contents
The cyclicity of the period annulus of a reversible quadratic system
Published online by Cambridge University Press: 10 February 2021
Abstract
We prove that perturbing the periodic annulus of the reversible quadratic polynomial differential system 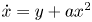 $\dot x=y+ax^2$,
$\dot x=y+ax^2$, 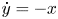 $\dot y=-x$ with a ≠ 0 inside the class of all quadratic polynomial differential systems we can obtain at most two limit cycles, including their multiplicities. Since the first integral of the unperturbed system contains an exponential function, the traditional methods cannot be applied, except in Figuerasa, Tucker and Villadelprat (2013, J. Diff. Equ., 254, 3647–3663) a computer-assisted method was used. In this paper, we provide a method for studying the problem. This is also the first purely mathematical proof of the conjecture formulated by Dumortier and Roussarie (2009, Discrete Contin. Dyn. Syst., 2, 723–781) for q ⩽ 2. The method may be used in other problems.
$\dot y=-x$ with a ≠ 0 inside the class of all quadratic polynomial differential systems we can obtain at most two limit cycles, including their multiplicities. Since the first integral of the unperturbed system contains an exponential function, the traditional methods cannot be applied, except in Figuerasa, Tucker and Villadelprat (2013, J. Diff. Equ., 254, 3647–3663) a computer-assisted method was used. In this paper, we provide a method for studying the problem. This is also the first purely mathematical proof of the conjecture formulated by Dumortier and Roussarie (2009, Discrete Contin. Dyn. Syst., 2, 723–781) for q ⩽ 2. The method may be used in other problems.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 2 , April 2022 , pp. 281 - 290
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 1
- Cited by



