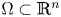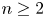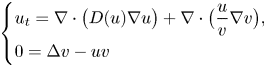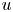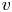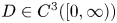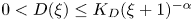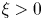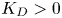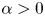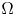Finite-time blow-up in a repulsive chemotaxis-consumption system

Abstract

In a ball $\Omega \subset \mathbb {R}^{n}$ with $n\ge 2$, the chemotaxis system

\[ \left\{ \begin{array}{@{}l} u_t = \nabla \cdot \big( D(u)\nabla u\big) + \nabla\cdot \big(\dfrac{u}{v} \nabla v\big), \\ 0=\Delta v - uv \end{array} \right. \]

is considered along with no-flux boundary conditions for $u$ and with prescribed constant positive Dirichlet boundary data for $v$. It is shown that if $D\in C^{3}([0,\infty ))$ is such that $0< D(\xi ) \le {K_D} (\xi +1)^{-\alpha }$ for all $\xi >0$ with some ${K_D}>0$ and $\alpha >0$, then for all initial data from a considerably large set of radial functions on $\Omega$, the corresponding initial-boundary value problem admits a solution blowing up in finite time.

1. Introduction

The analysis of chemotaxis-consumption systems has been stimulated to a significant extent by experimental observations witnessing an unexpectedly rich variety of facets in the collective behaviour of aerobic bacteria: in diverse particular settings, colonies of Bacillus subtilis have been seen to generate strikingly complex patterns during their search for oxygen [19, 25]. In their simplest shape, mathematical descriptions for such nutrient taxis processes reduce to cross-diffusion models of the form

(1.1)\begin{equation} \left\{ \begin{array}{@{}ll} u_t = \nabla \cdot \big( D(u,v)\nabla u\big) - \nabla\cdot \big(u S(u,v) \nabla v\big), \\ \tau v_t=\Delta v - uv, \end{array} \right. \end{equation}

for the unknown population density $u=u(x,t)$ and the signal concentration $v=v(x,t)$. Here a key feature is linked to the circumstance that according to its fundamental purpose, (1.1) presupposes the considered signal to be consumed, contrary to frameworks covered by classical Keller–Segel systems that typically address application contexts of self-enhancing aggregation mechanisms in which the directing cues are produced by individuals, and in which the corresponding second sub-problems then suitably generalize the production-diffusion equation $v_t=\Delta v - v + u$ [13].

At levels of rigorous mathematical analysis, this difference between (1.1) and such Keller–Segel production systems has been found to go along with substantial deviations with respect to core characteristics: while several representatives of the latter model class are well known to generate structures even in the extreme sense of spontaneous singularity formation [4, 8, 11, 20, 28], the literature concerned with solution behaviour in nutrient taxis systems related to (1.1) seems exclusively restricted to the identification of situations determined by relaxation towards spatial homogeneous states.

For instance, in its simplest fully parabolic version with $\tau =1$ and constant diffusivities $D$ and chemotactic sensitivities $S$, and posed under no-flux boundary conditions in bounded two-dimensional domains $\Omega$, (1.1) is known to admit global classical solutions for arbitrarily large initial data $(u_0,v_0)$, with each of these solutions approaching the respectively unique spatially constant equilibrium at the considered mass level, as given by $(\tfrac {1}{|\Omega |} \int _\Omega u_0,0)$ ([24, 35]; cf. also [18, 37]). Although for the corresponding three-dimensional analogue involving large data only certain weak solutions have been found to exist globally, while results on global classical solvability are until now limited to suitable small-data scenarios [22], for any of these solutions a similar statement concerning the large time behaviour has been derived [24]. A considerable stability of this trend towards homogeneity in (1.1) has been indicated by studies revealing comparably trivial asymptotics even in the presence of buoyancy-induced couplings to Navier–Stokes flows such as those being of relevance in the experimental framework addressed in [25] ([2, 6, 12, 29, 31]).

Beyond studies explicitly focusing on large time behaviour, the literature contains considerable additional evidence for relaxation, and especially also for blow-up prevention, in numerous further versions and relatives of (1.1). This becomes manifest in results on existence and regularity for systems involving nonlinear diffusion rates or nonconstant cross-diffusion rates, or both [14, 15, 17, 34, 36, 38], possibly in frameworks of small-data trajectories [1, 23, 27], and partially even in findings concerned with instantaneous regularization of singular initial distributions [16, 26].

Subtly accounting for directional effects. Main results.  Most of the precedents studies on (1.1) have either disregarded any directional information on chemotactic motion by simply estimating cross-diffusive effects in their absolute strength, hence leading to results irrespective of the sign of $S$, or explicitly concentrated on attractive taxis mechanisms by assuming $S$ to be nonnegative. In fact, at least in their simpler forms such chemoattraction-consumption systems have been found to possess some global dissipative structure, and an appropriate exploitation thereof has been underlying the derivation of regularity and stabilization features to a substantial extent (cf. e.g. [36] and [24]). It may be interpreted as evidence for more complex behaviour in systems differing from fully attractive ones that for the close relative thereof obtained on still letting $D\equiv const.>0$ but allowing $S$ in (1.1) to be tensor-valued, even in simple cases of constant $S$ only slightly deviating from positive multiples of the identity matrix the knowledge is yet much sparser: until now, only certain generalized and possibly quite irregular solutions have been found exist globally [30], with statements on eventual smoothness and large time stabilization limited to two-dimensional settings [32].

The intention of the present work will now be to indicate that chemotaxis-consumption systems of the form (1.1) may indeed generate strongly structured solution behaviour if cross-diffusion acts in an appropriately destabilizing direction. In fact, we shall see that when $S$ is a suitably chosen negative scalar function, hence modelling repulsive taxis, then solutions may even exhibit finite-time blow-up phenomena. Notably, this outcome will thereby considerably diverge from some previous findings on differences in solution behaviour induced by deviations from purely attractive taxis in classical Keller–Segel production systems: in such settings, namely, switching to tensor-type constant $S\not \equiv {\mathbf {1}}_{n\times n}$, or even to fully repulsive cross-diffusion, has been found to significantly reduce the respective tendency towards singularity formation [3, 7]. To specify the exemplary setting within which this will be studied, let us consider the no-flux/Dirichlet initial-boundary value problem associated with a parabolic-elliptic version of (1.1) given by

(1.2)\begin{equation} \left\{ \begin{array}{@{}ll} u_t = \nabla \cdot \big( D(u)\nabla u\big) + \nabla\cdot \left(\dfrac{u}{v} \nabla v\right), \quad & x\in\Omega, \ t>0, \\ 0=\Delta v - uv, \quad & x\in\Omega, \ t>0, \\ \big(D(u)\nabla u + \dfrac{u}{v} \nabla v\big)\cdot\nu=0, \quad v=1, \quad & x\in\partial\Omega, \ t>0, \\ u(x,0)=u_0(x), \quad & x\in\Omega, \end{array} \right. \end{equation}

where we will focus on the case when $\Omega$ is a ball in $\mathbb {R}^{n}$ with $n\ge 2$; here the particular choice of the so-called logarithmic sensitivity $0< v\mapsto \frac {1}{v}$, well consistent with classical approaches to account for the Weber–Fechner law of stimulus response [9, 21], ensures that upon replacing $v$ with $\frac {v}{M}$ if necessary, (1.2) can be seen to be equivalent to the corresponding variant in which $v|_{\partial \Omega }=M>0$.

Our main result now shows that whenever the diffusion mechanism herein is assumed to undergo any asymptotic damping effect of algebraic functional type [10], finite-time singularity formation occurs within a considerably large set of choices of the initial data $u_0$:

Theorem 1.1 Let $n\ge 2,$ $R>0$ and $\Omega =B_R(0)\subset \mathbb {R}^{n},$ and suppose that

(1.3)\begin{equation} D\in C^{3}([0,\infty))\text{ is such that }D(\xi)>0\text{ for all } \xi\ge 0, \end{equation}

and such that

(1.4)\begin{equation} D(\xi) \le {K_D} (\xi+1)^{-\alpha}\quad \text{ for all } \xi>0 \end{equation}

with some ${K_D}>0$ and $\alpha >0$. Then for each $R_0\in (0,R)$ and any $\theta \in (0,1)$ there exists $m_\star =m_\star (R,R_0,\theta )>0$ with the property that whenever

(1.5)\begin{equation} u_0\in W^{1,\infty}(\Omega) \text{ is radially symmetric and nonnegative} \end{equation}

and such that

(1.6)\begin{equation} \int_\Omega u_0 {\rm d}x \ge m_\star\text{ as well as }\int_{B_{R_0}} u_0 {\rm d}x \ge \theta \int_\Omega u_0 {\rm d}x, \end{equation}

the problem (1.2) admits a solution blowing up in finite time. More precisely, there exist ${T_{\max }}\in (0,\infty )$ and a uniquely determined pair of functions

(1.7)\begin{equation} \left\{ \begin{array}{@{}l} u\in \bigcup_{q>n} C^{0}([0,{T_{\max}});W^{1,q}(\Omega)) \cap C^{2,1}(\overline{\Omega}\times (0,{T_{\max}}))\ \text{ and} \\ v\in C^{2,0}(\overline{\Omega}\times (0,{T_{\max}})) \end{array} \right. \end{equation}

such that $u>0$ and $v>0$ in $\overline {\Omega }\times (0,{T_{\max }})$, that $(u,v)$ solves (1.2) in the classical sense in $\Omega \times (0,{T_{\max }})$, and that

(1.8)\begin{equation} \limsup_{t\nearrow{T_{\max}}} \|u({\cdot},t)\|_{L^{\infty}(\Omega)}=\infty. \end{equation}

Remark 1.2 A challenging question is how far results of the above flavour can be expected to carry over to the attraction-consumption counterpart of (1.2) obtained on replacing the first equation therein by an identity of the form $u_t=\nabla \cdot (D(u)\nabla u) - \nabla \cdot (\frac {u}{v}\nabla v)$; of particular interest in this context would then be a comparison of corresponding blow-up mechanisms and times. Examining this in detail would go beyond the scope of the present manuscript, however, as mainly through a positive sign of the taxis-related contribution to the key inequality (3.9) below, our analysis to be subsequently developed will quite crucially rely on the repulsive character of the cross-diffusive mechanism in (1.2).

2. Local existence and transformation to a scalar problem

To begin with, let us state an essentially straightforward extension of known results on local existence and extensibility to the present setting. For detailed reasonings in some closely related situations, we may refer to [33, lemma 2.1] and [5, theorem 1.3].

Lemma 2.1 Let $n\ge 2, R>0$ and $\Omega =B_R(0)\subset \mathbb {R}^{n},$ and suppose that (1.3) is valid. Then for any choice of initial data fulfilling (1.5) , one can find ${T_{\max }}\in (0,\infty ]$ and functions $u$ and $v$, uniquely determined by the inclusions in (1.7) , such that $u(\cdot,t)$ and $v(\cdot,t)$ are radially symmetric for all $t\in (0,{T_{\max }}),$ that $u>0$ and $v>0$ in $\overline {\Omega }\times (0,{T_{\max }}),$ that $(u,v)$ forms a classical solution of (1.2) in $\Omega \times (0,{T_{\max }}),$ and that

(2.1)\begin{equation} \text{if }{T_{\max}}<\infty, \text{ then }\limsup_{t\nearrow{T_{\max}}} \|u({\cdot},t)\|_{L^{\infty}(\Omega)}=\infty. \end{equation}

Moreover,

(2.2)\begin{equation} \int_\Omega u(x,t) {\rm d}x= \int_\Omega u_0(x) {\rm d}x\quad \mbox{ for all } t\in (0,{T_{\max}}). \end{equation}

Throughout the sequel, we suppose that $\Omega =B_R(0)\subset \mathbb {R}^{n}$ with some $n\ge 2$ and $R>0$, and whenever $D$ and $u_0$ fulfilling (1.3) and (1.5) have been fixed, we let ${T_{\max }}\in (0,\infty ]$ and $(u,v)$ be as obtained in lemma 2.1. Moreover, whenever this appears convenient we shall switch to standard radial notation, e.g. by writing $u(r,t)$ instead of $u(x,t)$ for $r=|x|\in [0,R]$ and $t\in (0,{T_{\max }})$.

By following a well-established reduction procedure [11], we can transform the accordingly relevant radial version of (1.2) to a scalar problem:

Lemma 2.2 Let $R>0,$ assume (1.3) and (1.5) , and let

(2.3)\begin{equation} w(s,t):=\int_0^{s^{{1}/{n}}} \rho^{n-1} u(\rho,t) {\rm d}\rho, \quad s\in [0,R^{n}],\ t\in [0,{T_{\max}}). \end{equation}

Then $w$ belongs to $C^{0}([0,{T_{\max }});C^{1}([0,R^{n}]) \cap C^{2,1}((0,R^{n}]\times (0,{T_{\max }}))$ and satisfies

(2.4)\begin{equation} w_s(s,t)=\frac{1}{n} u\big(s^{{1}/{n}},t\big)\quad \mbox{ for all }s\in [0,R^{n}]\text{ and } t\in [0,{T_{\max}}), \end{equation}

and we have

(2.5)\begin{align} w_t & = n^{2} s^{2-{2}/{n}} D(nw_s) w_{ss}\nonumber\\ & \quad + nw_s \cdot \big\{ r^{n-1} \partial_r \ln v \big\}\Big|_{r=s^{{1}/{n}}} \text{ for all }s\in (0,R^{n})\text{ and } t\in (0,{T_{\max}}) \end{align}

as well as

(2.6)\begin{equation} w(0,t)=0\text{ and } w(R^{n},t)=\frac{m}{n|B_1(0)|}\text{ for all } t\in [0,{T_{\max}}), \end{equation}

where $m:=\int _\Omega u_0 {\rm d}x$.

Proof. All these statements can be verified by straightforward computations on the basis of (1.2) and (2.3).

3. Basic evolution properties of $\phi (t)=\int _0^{R^{n}} s^{-\gamma } w(s,t) {\rm d}s$

The purpose of this section will be to derive a first statement on how the antagonistic effects of the diffusive and cross-diffusive contributions to (2.5) quantitatively influence the evolution of the moment-like quantities $[0,{T_{\max }})\ni t\mapsto \int _0^{R^{n}} s^{-\gamma } w(s,t) {\rm d}s$. A preparatory observation of key importance in this regard provides a pointwise bound for the taxis gradient acting in (1.2), the effect of which is estimated from below in terms of a nonlocal expression involving the function $w$ from (2.3):

Lemma 3.1 If $R>0$ and (1.3) as well as (1.5) hold, then

(3.1)\begin{equation} r^{n-1} \partial_r \ln v(r,t) \ge \frac{U(r,t)}{1+\int_0^{r} \rho^{1-n} U(\rho,t) {\rm d}\rho} \text{ for all }r\in (0,R)\text{ and } t\in (0,{T_{\max}}), \end{equation}

where with $w$ taken from (2.3) we have set

(3.2)\begin{equation} U(r,t):=w(r^{n},t) \equiv \int_0^{r} \rho^{n-1} u(\rho,t) {\rm d}\rho \text{ for }r\in [0,R]\text{ and } t\in [0,{T_{\max}}). \end{equation}

Proof. For fixed $t\in (0,{T_{\max }})$, we note that by positivity of $v(\cdot,t)$ in $\overline {\Omega }$ and the inclusion $v(\cdot,t)\in C^{2}(\overline {\Omega })$,

\[ y(r):=r^{n-1} \partial_r \ln v(r,t),\quad r\in [0,R], \]

defines a function $y\in C^{1}([0,R])$ which satisfies

\[ y(r) \le c_1 r^{n} \text{ for all } r\in [0,R] \]

with some $c_1=c_1(t)>0$, because $v_r(0,t)=0$. On the other hand, the strict positivity of $u(\cdot,t)$ in $\overline {\Omega }$ ensures the existence of $c_2=c_2(t)>0$ fulfilling

\[ U_r(r,t)=r^{n-1} u(r,t) \ge c_2 r^{n-1}\text{ for all } r\in [0,R]. \]

Therefore,

\[ r^{1-n} y^{2}(r) \le \frac{c_1^{2}}{c_2} \cdot r^{2} U_r(r,t)\text{ for all } r\in (0,R), \]

whence given any $\eta \in (0,1)$ we can pick $r_0(\eta )=r_0(\eta ;t)\in (0,R)$ such that

(3.3)\begin{equation} r^{1-n} y^{2}(r) \le \eta U_r(r,t)\text{ for all } r\in (0,r_0(\eta)]. \end{equation}

We now use the second equation in (1.2) to compute, partially suppressing arguments and especially the time $t$ yet fixed,

(3.4)\begin{align} y_r(r) & = \partial_r \Big( r^{n-1} \frac{v_r}{v}\Big) \nonumber\\ & =r^{n-1} \frac{v_{rr}}{v} + (n-1) r^{n-2} \frac{v_r}{v} - r^{n-1} \frac{v_r^{2}}{v^{2}} \nonumber\\ & =\frac{r^{n-1}}{v} \cdot \Big( v_{rr} + \frac{n-1}{r} v_r\Big) - r^{1-n} y^{2}(r) \nonumber\\ & =r^{n-1} u - r^{1-n} y^{2}(r) \nonumber\\ & =U_r - r^{1-n} y^{2}(r)\text{ for all } r\in (0,R). \end{align}

To make use of this in the course of a comparison argument, for $\eta >0$ we let $r_0(\eta )$ be as above and define

(3.5)\begin{equation} \zeta(r):=\bigg\{ \frac{1}{1-\eta} + \int_{r_0(\eta)}^{r} \rho^{1-n} U(\rho, t) {\rm d}\rho \bigg\}^{{-}1}, \quad r\in [r_0(\eta),R], \end{equation}

noting that then $\zeta$ solves $\zeta '(r)=-r^{1-n} U(r,t)\zeta ^{2}(r)$ for all $r\in (r_0(\eta ),R)$ with $\zeta (r_0(\eta ))=1-\eta$. Accordingly, using that hence especially $\zeta (r)\le 1$ on $[r_0(\eta ),R]$ we infer that

(3.6)\begin{equation} \underline{y}(r):=\zeta(r) U(r,t), \quad r\in [r_0(\eta),R], \end{equation}

satisfies

(3.7)\begin{align} & \underline{y}'(r) - U_r(r,t) + r^{1-n} \underline{y}^{2}(r)\nonumber\\ & \quad =\Big\{ \zeta(r)-1\Big\} \cdot U_r(r,t) + \Big\{ \zeta'(r) + r^{1-n} U(r,t) \zeta^{2}(r)\Big\} \cdot U(r,t) \nonumber\\ & \qquad\le 0\text{ for all } r\in (r_0(\eta),R) \end{align}

as well as $\underline {y}(r_0(\eta ))=(1-\eta ) U(r_0(\eta ),t)$. As (3.4) together with (3.3) implies that

\[ y_r(r) \ge (1-\eta) U_r(r,t)\text{ for all } r\in (0,r_0(\eta)) \]

and that thus, by direct integration based on the identity $y(0)=U(0,t)=0$,

(3.8)\begin{equation} y(r) \ge (1-\eta) U(r,t)\text{ for all } r\in [0,r_0(\eta)], \end{equation}

we particularly obtain that $y(r_0(\eta ))\ge \underline {y}(r_0(\eta ))$, so that we may combine (3.4) with (3.7) to infer upon an ODE comparison that $y(r)\ge \underline {y}(r)$ for all $r\in [r_0(\eta ),R]$. Since (3.5) and (3.6) therefore imply that

\[ y(r)\ge \underline{y}(r)\ge \frac{(1-\eta) U(r,t)}{1 + \int_0^{r} \rho^{1-n} U(\rho,t) {\rm d}\rho} \text{ for all } r\in [r_0(\eta),R], \]

and since (3.8) trivially entails that

\[ y(r)\ge \frac{(1-\eta) U(r,t)}{1 + \int_0^{r} \rho^{1-n} U(\rho,t) {\rm d}\rho} \text{ for all } r\in [0,r_0(\eta)], \]

on taking $\eta \searrow 0$ we can confirm (3.1).

As a result, the identity in (2.5) can be turned into an autonomous scalar parabolic inequality containing a nonlocal source term.

Lemma 3.2 Let $R>0,$ suppose that (1.3) and (1.5) hold, and let $w$ be as in (2.3). Then

(3.9)\begin{align} w_t & \ge n^{2} s^{2-{2}/{n}} D(nw_s) w_{ss}\nonumber\\ & \quad+ n\cdot \frac{ww_s}{1+\frac{1}{n} \int_0^{s} \sigma^{{2}/{n}-2} w(\sigma,t) {\rm d}\sigma} \text{ for all }s\in (0,R^{n})\text{ and } t\in (0,{T_{\max}}). \end{align}

Proof. In view of (3.2) and (2.3), we only need to insert (3.1) into (2.5), use the nonnegativity of $w_s$, and observe that

\[ \int_0^{r} \rho^{1-n} U(\rho,t) {\rm d}\rho = \frac{1}{n} \int_0^{s} \sigma^{{2}/{n}-2}w(\sigma,t) {\rm d}\sigma \]

for $t\in (0,{T_{\max }}), r\in (0,R)$ and $s=r^{n}$.

For the moment-type functional in question, this has the following fairly immediate consequence.

Lemma 3.3 Let $R>0,$ suppose that $D$ satisfies (1.3) as well as

(3.10)\begin{equation} D(\xi)\le {K_D} \xi^{-\alpha'}\text{ for all } \xi>0 \end{equation}

with some ${K_D}>0$ and $\alpha '\in (0,1),$ and assume (1.5). Then for any choice of $\gamma \in (-\infty,2-\frac {2}{n})$,

(3.11)\begin{equation} \phi(t):=\int_0^{R^{n}} s^{-\gamma} w(s,t) {\rm d}s,\quad t\in [0,{T_{\max}}), \end{equation}

defines a positive function $\phi \in C^{0}([0,{T_{\max }})) \cap C^{1}((0,{T_{\max }}))$ fulfilling

(3.12)\begin{align} \phi'(t) & \ge - \frac{n^{2-\alpha'} \cdot (2-\frac{2}{n}-\gamma){K_D}}{1-\alpha'} \int_0^{R^{n}} s^{1-{2}/{n}-\gamma} w_s^{1-\alpha'}(s,t) {\rm d}s \nonumber\\ & \quad+ n\int_0^{R^{n}} \frac{s^{-\gamma} w(s,t) w_s(s,t)}{1+\frac{1}{n} \int_0^{s} \sigma^{{2}/{n}-2} w(\sigma,t) {\rm d}\sigma} {\rm d}s \text{ for all } t\in (0,{T_{\max}}). \end{align}

Proof. Since $\gamma <2$, in view of the inclusions $u\in C^{0}(\overline {\Omega }\times [0,{T_{\max }}))$ and $u_t\in C^{0}(\overline {\Omega }\times (0,{T_{\max }}))$ asserted by (1.7) it follows from the dominated convergence theorem that $\phi$ has the claimed regularity properties and satisfies

(3.13)\begin{align} \phi'(t) & =\int_0^{R^{n}} s^{-\gamma} w_t(s,t) {\rm d}s \nonumber\\ & \ge n^{2} \int_0^{R^{n}} s^{2-{2}/{n}-\gamma} D\big(nw_s(s,t)\big) w_{ss}(s,t) {\rm d}s \nonumber\\ & \quad+ n\int_0^{R^{n}} \frac{s^{-\gamma} w(s,t) w_s(s,t)}{1+\frac{1}{n} \int_0^{s} \sigma^{{2}/{n}-2} w(\sigma,t) {\rm d}\sigma} {\rm d}s \text{ for all } t\in (0,{T_{\max}}). \end{align}

To estimate the second last integral, we note that according to (1.3) and (3.10), letting

\[ D_0(\xi):=\int_0^{\xi} D(\tau) {\rm d}\tau,\quad \xi\ge 0, \]

defines a nonnegative function from $C^{1}([0,\infty ))$ which satisfies $D_0(\xi )\le \frac {{K_D}}{1-\alpha '} \xi ^{1-\alpha '}$ for all $\xi \ge 0$, so that an integration by parts shows that for all $t\in (0,{T_{\max }})$ we have

(3.14)\begin{align} & n^{2} \int_0^{R^{n}} s^{2-{2}/{n}-\gamma} D\big(nw_s(s,t)\big) w_{ss}(s,t) {\rm d}s \nonumber\\ & \quad= n\int_0^{R^{n}} s^{2-{2}/{n}-\gamma} \partial_s D_0\big(nw_s(s,t)\big) {\rm d}s \nonumber\\ & \quad={-} n\Big(2-\frac{2}{n}-\gamma\Big) \int_0^{R^{n}} s^{1-{2}/{n}-\gamma} D_0\big(nw_s(s,t)\big) {\rm d}s \nonumber\\ & \qquad+ n R^{2n-2-n\gamma} D_0\big(nw_s(R^{n},t)\big) - \lim_{s\nearrow 0} \Big\{ ns^{2-{2}/{n}-\gamma} D_0\big(nw_s(s,t)\big)\Big\} \nonumber\\ & \quad\ge -n\Big(2-\frac{2}{n}-\gamma\Big) \int_0^{R^{n}} s^{1-{2}/{n}-\gamma} D_0\big(nw_s(s,t)\big) {\rm d}s \nonumber\\ & \quad\ge - \frac{n^{2-\alpha'} \cdot \left(2-\frac{2}{n}-\gamma\right) {K_D}}{1-\alpha'} \int_0^{R^{n}} s^{1-{2}/{n}-\gamma} w_s^{1-\alpha'}(s,t) {\rm d}s, \end{align}

because our assumption $\gamma <2-\frac {2}{n}$ ensures that for all $t\in (0,{T_{\max }})$,

\[ s^{2-{2}/{n}-\gamma} D_0\big(nw_s(s,t)\big) \to 0\text{ as } s\searrow 0. \]

Combining (3.14) with (3.13) establishes (3.12).

4. Turning (3.12) into an autonomous ODI for $\phi$. Proof of theorem 1.1

To see that for suitable choices of the free parameter $\gamma$ in (3.11) the resulting function $\phi$ indeed satisfies an appropriately forced autonomous ODI, we shall next relate the transport-driven and the diffusive part in (3.12) to $\phi$. Of technically crucial importance in this respect will be the observation that this can be achieved in quite a convenient manner if instead of $\phi$ itself, an intermediate quantity $\psi$, to be specified in (4.3), will be referred to in a preliminary step.

For suitably large values of $\gamma$, this function can be used to control the action of the nonlocal expression arising in the denominator of the rightmost summand from (3.12):

Lemma 4.1 Let $R>0,$ assume (1.3) , and let $\gamma \in (-\infty,2-\frac {2}{n})$ be such that

(4.1)\begin{equation} \gamma>2-\frac{4}{n}. \end{equation}

Then there exists $C(\gamma,R)>0$ such that whenever (1.5) holds,

(4.2)\begin{equation} \int_0^{s} \sigma^{{2}/{n}-2} w(\sigma,t) {\rm d}\sigma \le C(\gamma,R) \psi^{{1}/{2}}(t) \end{equation}

where we have set

(4.3)\begin{equation} \psi(t):=\int_0^{R^{n}} s^{-\gamma-1} w^{2}(s,t) {\rm d}s,\quad t\in (0,{T_{\max}}), \end{equation}

Proof. By nonnegativity of $w$ and the Cauchy–Schwarz inequality,

\begin{align*} \int_0^{s} \sigma^{{2}/{n}-2} w(\sigma,t) {\rm d}\sigma & \le \int_0^{R^{n}} \sigma^{{2}/{n}-2} w(\sigma,t) {\rm d}\sigma \\ & \le \bigg\{ \int_0^{R^{n}} \sigma^{-\gamma-1} w^{2}(\sigma,t) {\rm d}\sigma \bigg\}^{{1}/{2}}\\ & \quad\cdot \bigg\{ \int_0^{R^{n}} \sigma^{{4}/{n}-3+\gamma} {\rm d}\sigma \bigg\}^{{1}/{2}} \text{ for all } t\in (0,{T_{\max}}), \end{align*}

so that since (4.1) warrants that $\frac {4}{n}-3+\gamma >-1$, (4.2) results if, for instance, we let $C(\gamma,R):=(\frac {4}{n}-2+\gamma )^{-{1}/{2}} R^{2-n+{n\gamma }/{2}}$.

Actually for all $\gamma$ from the range addressed in lemma 3.3, in much the same manner also $\phi$ itself can be related to $\psi$:

Lemma 4.2 Suppose that $R>0$ and that (1.3) holds, and let $\gamma \in (-\infty,2-\tfrac {2}{n})$. Then one can find $C(\gamma,R)>0$ such that for any choice of $u_0$ fulfilling (1.5) , the functions $\phi$ an $\psi$ accordingly defined through (3.11) and (4.3) satisfy

(4.4)\begin{equation} \phi(t) \le C(\gamma,R)\psi^{{1}/{2}}(t)\text{ for all } t\in (0,{T_{\max}}). \end{equation}

Proof. Again using the Cauchy–Schwarz inequality, we see that

\[ \phi(t) \le \bigg\{ \int_0^{R^{n}} s^{-\gamma-1} w^{2}(s,t) {\rm d}s \bigg\}^{{1}/{2}} \cdot \bigg\{ \int_0^{R^{n}} s^{-\gamma+1} {\rm d}s \bigg\}^{{1}/{2}} \text{ for all } t\in (0,{T_{\max}}), \]

and that thus (4.4) is valid with $C(\gamma,R):=(2-\gamma )^{-{1}/{2}} R^{n-{n\gamma }/{2}}$.

In deriving the following estimate for the diffusion-related part from (3.12) in terms of $\psi$, we shall now make essential use of our assumption (3.10) on $D$.

Lemma 4.3 Suppose that $R>0,$ and assume that (1.3) and (3.10) hold with some ${K_D}>0$ and $\alpha '\in (0,1)$. Then for any $\gamma \in (-\infty,2-\tfrac {2}{n})$ which is such that

(4.5)\begin{equation} \gamma <\frac{2-\frac{4}{n}+2\alpha'}{1+\alpha'}, \end{equation}

one can fix $C(\gamma,R)>0$ in such a way that whenever (1.5) holds, with $\psi$ taken from (4.3) we have

(4.6)\begin{align} \int_0^{R^{n}} s^{1-{2}/{n}-\gamma} w_s^{1-\alpha'}(s,t) {\rm d}s& \le C(\gamma,R) \psi^{{(1-\alpha')}/{2}}(t)\nonumber\\ & \quad + C(\gamma,R) \cdot \bigg\{ \int_\Omega u_0 {\rm d}x \bigg\}^{1-\alpha'} \text{ for all } t\in (0,{T_{\max}}). \end{align}

Proof. Observing that our assumption (4.5) guarantees that

\[ \frac{-1+\frac{2}{n}+\gamma-\alpha'}{1-\alpha'} - \frac{\gamma}{2} = \frac{(1+\alpha')\gamma-2+\frac{4}{n}-2\alpha'}{2(1-\alpha')} { <} 0, \]

we can pick a positive number $\lambda =\lambda (\gamma )$ such that

(4.7)\begin{equation} \frac{-1+\frac{2}{n}+\gamma-\alpha'}{1-\alpha'} <\lambda < \frac{\gamma}{2}. \end{equation}

Assuming (1.5) with $m:=\int _\Omega u_0{\rm d}x$, for $t\in (0,{T_{\max }})$ we then particularly obtain from the right inequality in (4.7) that $\lambda <1$, and that thus $\int _0^{R^{n}} s^{-\lambda } w_s(s,t) {\rm d}s$ is finite and may be rewritten using an integration by parts according to

(4.8)\begin{equation} \int_0^{R^{n}} s^{-\lambda} w_s(s,t) {\rm d}s = \lambda \int_0^{R^{n}} s^{-\lambda-1} w(s,t) {\rm d}s + \frac{R^{{-}n\lambda} m}{n|B_1(0)|}, \end{equation}

because $s^{-\lambda } w(s,t) \to 0$ as $s\searrow 0$ and $w(R^{n},t)=\frac {m}{n|B_1(0)|}$ by (2.6). Here, again invoking the Cauchy–Schwarz inequality we can estimate

\[ \int_0^{R^{n}} s^{-\lambda-1} w(s,t) {\rm d}s \le \bigg\{ \int_0^{R^{n}} s^{-\gamma-1} w^{2}(s,t) {\rm d}s \bigg\}^{{1}/{2}} \cdot \bigg\{ \int_0^{R^{n}} s^{{-}2\lambda+\gamma-1} {\rm d}s \bigg\}^{{1}/{2}}, \]

whence making full use of the second restriction in (4.7) now we obtain that

(4.9)\begin{equation} \int_0^{R^{n}} s^{-\lambda} w_s(s,t) {\rm d}s \le c_1(\gamma,R) \psi^{{1}/{2}}(t) + c_2(\gamma,R) m \text{ for all } t\in (0,{T_{\max}}) \end{equation}

with $c_1(\gamma,R):=\lambda (\gamma -2\lambda )^{-{1}/{2}} R^{{n\gamma }/{2}-n\lambda }$ and $c_2(\gamma,R):=(n|B_1(0)| R^{n\lambda })^{-1}$.

In order to relate this to (4.6), we now rely on the positivity of $\alpha '$ in employing the Hölder inequality to see that

(4.10)\begin{align} & \int_0^{R^{n}} s^{1-{2}/{n}-\gamma} w_s^{1-\alpha'}(s,t) {\rm d}s \nonumber\\ & \quad=\int_0^{R^{n}} \Big\{ s^{-\lambda} w_s(s,t) \Big\}^{1-\alpha'} \cdot s^{1-{2}/{n}-\gamma+(1-\alpha')\lambda} {\rm d}s \nonumber\\ & \quad\le \bigg\{ \int_0^{R^{n}} s^{-\lambda} w_s(s,t) {\rm d}s \bigg\}^{1-\alpha'}\nonumber\\ & \qquad \cdot \bigg\{ \int_0^{R^{n}} s^{[1-{2}/{n}-\gamma+(1-\alpha')\lambda] \cdot ({1}/{\alpha'})} {\rm d}s \bigg\}^{\alpha'} \text{ for all } t\in (0,{T_{\max}}), \end{align}

where thanks to the lower estimate for $\lambda$ in (4.7), $\mu \equiv \mu (\gamma ):=[1-\frac {2}{n}-\gamma + (1-\alpha ')\lambda ] \cdot \frac {1}{\alpha '}$ satisfies

\[ \mu > \Big[ 1-\frac{2}{n}-\gamma + \Big({-}1+\frac{2}{n}+\gamma-\alpha'\Big)\Big] \cdot \frac{1}{\alpha'} ={-}1. \]

Therefore, writing $c_3(\gamma,R):=(\mu +1)^{-\alpha '} R^{n(\mu +1)\alpha '}$ we infer from (4.8) and (4.9) that since $(A+B)^{\alpha '} \le A^{\alpha '}+B^{\alpha '}$ for all $A\ge 0$ and $B\ge 0$,

\begin{align*} & \int_0^{R^{n}} s^{1-{2}/{n}-\gamma} w_s^{1-\alpha'}(s,t) {\rm d}s \nonumber\\ & \quad\le \Big\{ c_1(\gamma,R) \psi^{{1}/{2}}(t) + c_2(\gamma,R) m\Big\}^{1-\alpha'} \cdot c_3(\gamma,R) \nonumber\\ & \quad\le c_1^{1-\alpha'}(\gamma,R) c_3(\gamma,R) \psi^{(1-\alpha')}/{2}(t)\nonumber\\ & \qquad + c_2^{1-\alpha'}(\gamma,R) c_3(\gamma,R) m^{1-\alpha'} \text{ for all } t\in (0,{T_{\max}}), \end{align*}

and conclude as intended.

By suitably choosing the parameter $\gamma$ so as to become compatible with the requirements from both (4.1) and (4.5), we can collect the outcomes of lemmas 4.1, 4.2 and 4.3 to establish an autonomous ODI for $\phi$, here yet conditional in being asserted only throughout time intervals within which $\phi$ is a priori known to remain suitably large.

Lemma 4.4 Let $R>0,$ and suppose that (1.3) and (3.10) are valid with some ${{K_D}>0}$ and $\alpha '\in (0,1)$. Then there exist $\gamma \in (-\infty,2-\frac {2}{n}),$ $\Gamma (R)>0$ and $C(R)>0$ with the property that whenever (1.5) holds and $T\in (0,{T_{\max }}]$ is such that the function $\phi$ from (3.11) satisfies

(4.11)\begin{equation} \phi(t) \ge \Gamma(R)\text{ for all } t\in (0,T), \end{equation}

we have

(4.12)\begin{equation} \phi'(t) \ge \frac{1}{C(R)} \cdot \phi(t) - C(R)\cdot \bigg\{ \int_\Omega u_0{\rm d}x \bigg\}^{1-\alpha'}\text{ for all } t\in (0,T). \end{equation}

Proof. The positivity of $\alpha '$ warrants that

\[ \frac{2-\frac{4}{n}+2\alpha'}{1+\alpha'} - \Big(2-\frac{4}{n}\Big) = \frac{4\alpha'}{n(1+\alpha')}>0, \]

so that we can pick $\gamma \in (2-\frac {4}{n},1-\frac {2}{n})$ such that $\gamma <\frac {2-{4}/{n}+2\alpha '}{1+\alpha '}$. We may therefore employ lemma 4.3 to find $c_1(R)>0$ with the property that if (1.5) holds, then for all $t\in (0,{T_{\max }})$ we have

(4.13)\begin{align} & \frac{n^{2-\alpha'} \cdot (2-\frac{2}{n}-\gamma){K_D}}{1-\alpha'} \int_0^{R^{n}} s^{1-{2}/{n}-\gamma} w_s^{1-\alpha'}(s,t) {\rm d}s\nonumber\\ & \quad \le c_1(R) \psi^{{(1-\alpha')}/{2}}(t) + c_1(R) \cdot \bigg\{ \int_\Omega u_0 {\rm d}x \bigg\}^{1-\alpha'}, \end{align}

while lemmas 4.1 and 4.2 yield $c_2(R)>0$ and $c_3(R)>0$ such that for each $u_0$ fulfilling (1.5),

(4.14)\begin{equation} \frac{1}{n} \int_0^{s} \sigma^{{2}/{n}-2} w(\sigma,t) {\rm d}\sigma \le c_2(R) \psi^{{1}/{2}}(t) \text{ for all } t\in (0,{T_{\max}}) \end{equation}

and

(4.15)\begin{equation} \psi^{{1}/{2}}(t) \ge c_3(R) \phi(t)\text{ for all } t\in (0,{T_{\max}}). \end{equation}

We now choose $\Gamma (R)>0$ large enough fulfilling

(4.16)\begin{equation} c_1(R)\cdot \big\{ c_3(R) \Gamma(R)\big\}^{{-}1-\alpha'} + c_1(R) c_2(R) \cdot \big\{ c_3(R) \Gamma(R)\big\}^{-\alpha'}\le \frac{n\gamma}{4}, \end{equation}

and henceforth suppose that $u_0$ is such that (1.5) holds, and that (4.11) is satisfied with some $T\in (0,{T_{\max }}]$. Then thanks to (4.14), in the rightmost summand in (3.12) we can estimate

\begin{align*} & n\int_0^{R^{n}} \frac{s^{-\gamma} w(s,t) w_s(s,t)}{1+\frac{1}{n} \int_0^{s} \sigma^{{2}/{n}-2} w(\sigma,t) {\rm d}\sigma} {\rm d}s \\ & \quad\ge \frac{n}{1+c_2(R) \psi^{{1}/{2}}(t)} \cdot\int_0^{R^{n}} s^{-\gamma} w(s,t) w_s(s,t) {\rm d}s \\ & \quad= \frac{n}{1+c_2(R) \psi^{{1}/{2}}(t)} \cdot \bigg\{ \frac{\gamma}{2} \int_0^{R^{n}} s^{-\gamma-1} w^{2}(s,t) {\rm d}s + \frac{R^{{-}n\gamma} w^{2}(R^{n},t)}{2} \bigg\} \nonumber\\ & \quad\ge \frac{n\gamma}{2} \cdot \frac{\psi(t)}{1+c_2(R) \psi^{{1}/{2}}(t)} \text{ for all } t\in (0,{T_{\max}}) \end{align*}

because of (4.3) and the fact that since $\gamma <2$, we have $s^{-\gamma } w^{2}(s,t) \to 0$ as $s\searrow 0$ for all $t\in (0,{T_{\max }})$. Using (4.13), from (3.12) we thus infer that

(4.17)\begin{align} \phi'(t)& \ge \frac{n\gamma}{2} \cdot \frac{\psi(t)}{1+c_2(R)\psi^{{1}/{2}}(t)} - c_1(R) \psi^{{(1-\alpha')}/{2}}(t)\nonumber\\ & \quad - c_1(R)\cdot \bigg\{ \int_\Omega u_0 {\rm d}x \bigg\}^{1-\alpha'} \text{ for all } t\in (0,{T_{\max}}), \end{align}

where we note that due to (4.15), (4.11) and (4.16),

(4.18)\begin{align} \frac{c_1(R) \psi^{{(1-\alpha')}/{2}}(t)}{\frac{\psi(t)}{1+c_2(R)\psi^{{1}/{2}}(t)}} & = c_1(R) \cdot \big\{ 1+c_2(R)\psi^{{1}/{2}}(t)\big\} \cdot \psi^{-({(1+\alpha')}/{2})}(t) \nonumber\\ & =c_1(R) \psi^{-({(1+\alpha')}/{2})}(t) + c_1(R)c_2(R) \psi^{-({(\alpha')}/{2})}(t) \nonumber\\ & \le c_1(R) \cdot \big\{ c_3(R) \phi(t)\big\}^{{-}1-\alpha'} + c_1(R) c_2(R) \cdot \big\{ c_3(R) \phi(t)\big\}^{-\alpha'} \nonumber\\ & \le \frac{n\gamma}{4}\text{ for all } t\in (0,T). \end{align}

Furthermore, since both $0\le \xi \mapsto \frac {\xi }{1+c_2(R)\xi ^{{1}/{2}}}$ and $0\le \xi \mapsto \frac {\xi }{1+c_2(R)c_3(R)\xi }$ are nondecreasing, again relying on (4.15) and (4.11) we can estimate

\begin{align*} \frac{\psi(t)}{1+c_2(R)\psi^{{1}/{2}}(t)} & \ge \frac{c_3^{2}(R) \phi^{2}(t)}{1+c_2(R) c_3(R)\phi(t)} \\ & = \frac{c_3^{2}(R) \phi(t)}{1+c_2(R) c_3(R)\phi(t)} \cdot \phi(t) \\ & \ge \frac{c_3^{2}(R) \Gamma(R)}{1+c_2(R) c_3(R) \Gamma(R)} \cdot \phi(t)\text{ for all } t\in (0,T). \end{align*}

Combining this with (4.18) and (4.17) we thus obtain that

\begin{align*} \phi'(t) & \ge \frac{n\gamma}{4} \cdot \frac{\psi(t)}{1+c_2(R)\psi^{{1}/{2}}(t)} + \bigg\{ \frac{n\gamma}{4} \cdot \frac{\psi(t)}{1+c_2(R)\psi^{{1}/{2}}(t)} - c_1(R) \psi^{{(1-\alpha')}/{2}}(t)\bigg\}\nonumber\\ & \quad - c_1(R) \cdot \bigg\{ \int_\Omega u_0 {\rm d}x \bigg\}^{1-\alpha'} \\ & \ge \frac{n\gamma}{4} \cdot \frac{c_3^{2}(R) \Gamma(R)}{1+c_2(R) c_3(R)\Gamma(R)} \cdot \phi(t) - c_1(R) \cdot \bigg\{ \int_\Omega u_0 {\rm d}x \bigg\}^{1-\alpha'} \text{ for all } t\in (0,T), \end{align*}

whence letting

\[ C(R):=\max \bigg\{ \frac{4}{n\gamma} \cdot \frac{1-c_2(R) c_3(R) \Gamma(R)}{c_3^{2}(R)\Gamma(R)} , \, c_1(R) \bigg\}, \]

we arrive at (4.12).

It remains to make sure that at sufficiently large mass levels, not only the hypothesis in (4.11) can be guaranteed to hold throughout evolution, but also (4.12) can be turned into an absorption-free linear ODI describing exponential growth of $\phi$. The actual impossibility thereof on suitably large time intervals will lead us to our main result on the occurrence of finite-time blow-up in (1.2):

Proof of theorem 1.1. We take any $\alpha '\in (0,1)$ such that $\alpha '\le \alpha$, and noting that then (1.4) implies (3.10), we first apply lemma 4.4 to find $\gamma \in (-\infty,2-\frac {2}{n})$, ${c_1(R)>0}$ and $c_2(R)>0$ such that if (1.5) and (4.11) hold with $\phi$ as in (3.11) and some $T\in (0,{T_{\max }}]$, we have

(4.19)\begin{equation} \phi'(t) \ge c_1(R) \phi(t) - c_2(R)\cdot\bigg\{ \int_\Omega u_0 {\rm d}x \bigg\}^{1-\alpha'} \text{ for all } t\in (0,T). \end{equation}

Given $R_0\in (0,R)$ and $\theta \in (0,1)$, we thereupon fix $m_\star =m_\star (R,R_0,\theta )>0$ large enough such that abbreviating

(4.20)\begin{equation} c_3(R,R_0):=\frac{R^{n(1-\gamma)} -R_0^{n(1-\gamma)}}{n(1-\gamma)|B_1(0)|} \end{equation}

we have

(4.21)\begin{equation} c_3(R,R_0) \theta m_\star>\Gamma(R) \end{equation}

and

(4.22)\begin{equation} \frac{1}{2} c_1(R) c_3(R,R_0) \theta m_\star^{\alpha'} >c_2(R), \end{equation}

and henceforth assume that (1.5) and (1.6) hold.

With ${T_{\max }}\in (0,\infty ]$ and $w$ as accordingly defined in lemma 2.1 and (2.3), writing $m:=\int _\Omega u_0 {\rm d}x$ we then obtain from (2.3) and (1.6) that

\[ w(R_0^{n},0) = \int_0^{R_0} r^{n-1} u_0(r) {\rm d}r = \frac{1}{n|B_1(0)|} \int_{B_{R_0}(0)} u_0 {\rm d}x \ge \frac{\theta m}{n|B_1(0)|}, \]

so that since $w_s\ge 0$, from (3.11) and (4.20) it follows that

(4.23)\begin{align} \phi(0) & \ge \int_{R_0^{n}}^{R^{n}} s^{-\gamma} w(s,0) {\rm d}s \nonumber\\ & \ge \frac{\theta m}{n|B_1(0)|} \int_{R_0^{n}}^{R^{n}} s^{-\gamma} {\rm d}s \nonumber\\ & = c_3(R,R_0)\theta m. \end{align}

Since this $\phi (0)>\Gamma (R)$ by (4.21), and since (4.23) furthermore implies that

\begin{align*} & \frac{1}{2} c_1(R) \phi(0) - c_2(R) \cdot \bigg\{ \int_\Omega u_0 {\rm d}x \bigg\}^{1-\alpha'} \\ & \quad\ge \frac{1}{2} c_1(R) c_3(R,R_0) \theta m - c_2(R) \cdot \bigg\{ \int_\Omega u_0 {\rm d}x\bigg\}^{1-\alpha'} \\ & \quad= m^{1-\alpha'} \cdot \Big\{ \frac{1}{2} c_1(R) c_3(R,R_0) \theta m^{\alpha'} - c_2(R)\Big\} \\ & \quad> 0, \end{align*}

from (4.19) it readily follows that

\[ T:=\sup \bigg\{ T'\in (0,{T_{\max}}) \ \bigg| \ \phi>\Gamma(R) \mbox{ and } \phi'>\frac{c_1(R)}{2} \phi \mbox{ on } [0,T'] \bigg\} \]

is a well-defined element of $(0,{T_{\max }}] \subset (0,\infty ]$ and actually must have the property that $T={T_{\max }}$, because $\phi$ is nondecreasing on $[0,T)$ and therefore satisfies $\phi (t)>\phi (0)$ on $(0,T)$ and hence also

\begin{align*} \phi'(t) & \ge c_1(R) \phi(t) - c_2(R) \cdot \bigg\{ \int_\Omega u_0 {\rm d}x \bigg\}^{1-\alpha'} \\ & \ge \frac{1}{2} c_1(R) \phi(t) + \Bigg\{ \frac{1}{2} c_1(R) \phi(0) - c_2(R) \cdot \bigg\{ \int_\Omega u_0 {\rm d}x \bigg\}^{1-\alpha'} \Bigg\} \\ & > \frac{1}{2} c_1(R) \phi(t)\text{ for all } t\in (0,T) \end{align*}

by (4.19). Thus knowing that $\phi '>\frac {c_1(R)}{2} \phi$ throughout $(0,{T_{\max }})$, upon an integration thereof we infer that

\[ \frac{c_1(R)}{2} \cdot t < \ln \frac{\phi(t)}{\phi(0)} \text{ for all } t\in (0,{T_{\max}}), \]

and that thus

\[ \frac{c_1(R)}{2} \cdot {T_{\max}}\le \ln \frac{m R^{n(1-\gamma)}}{n(1-\gamma) |B_1(0)|\phi(0)} , \]

because

\[ \phi(t)\le \int_0^{R^{n}} s^{-\gamma} \cdot \frac{m}{n|B_1(0)|} {\rm d}s = \frac{m R^{n(1-\gamma)}}{n(1-\gamma)|B_1(0)|} \text{ for all } t\in (0,{T_{\max}}) \]

according to (3.11) and (2.6). As therefore ${T_{\max }}$ indeed is finite, in view of (2.1) we finally obtain that also (1.8) holds.