Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T08:35:42.786Z Has data issue: false hasContentIssue false
  • English
  • Français

A nonlinear pseudoparabolic equation

Published online by Cambridge University Press:  14 November 2011

Dang Dinh Ang  and
Tran Thanh
Dang Dinh Ang
Affiliation:
Department of Mathematics, Dai Hoc Tong Hop, Ho Chi Minh City University, Vietnam
Tran Thanh
Affiliation:
Department of Mathematics, Dai Hoc Tong Hop, Ho Chi Minh City University, Vietnam
Get access Rights & Permissions [Opens in a new window]

Synopsis

The authors prove results on uniqueness and global existence of initial and boundary value problems for the nonlinear pseudoparabolic equation

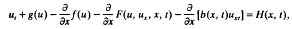
with nonhomogeneous boundary conditions. A salient feature of the paper is that F and its partial derivatives are allowed to be unbounded. In the special case b(x, t)= α2 (a positive constant), it is proved that the corresponding solution uα, under appropriate conditions on the data (which are satisfied, for example, by the Benjamin–Bona–Mahony equation), uα→ u0 the solution corresponding to β = 0, on sufficiently small time interval. A result on the asymptotic behaviour of the solution is given for t → ∞.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 114 , Issue 1-2 , 1990 , pp. 119 - 133
Copyright
Copyright © Royal Society of Edinburgh 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Arnold, D. N., Douglas, J. Jr and Thomee, V.. Superconvergence of a finite element approximation to the solution of a Sobolev equation in a single space variable. Math. Comp. 36 (1981), 53–63.CrossRefGoogle Scholar
2Beckenbach, E. F. and Bellman, R.. Inequalities (Berlin: Springer 1961).CrossRefGoogle Scholar
3Benjamin, T. B., Bona, J. L. and Mahony, J. J.. Model equations for long waves in nonlinear dispersive systems. Philos. Trans. Roy. Soc. London Ser. A 272 (1972), 47–78.Google Scholar
4Bona, J. L. and Dougalis, V. A.. An initial and boundary value problem for a model equation for propagation of long waves. J. Math. Anal. Appl. 75 (1980), 503–522.CrossRefGoogle Scholar
5Henry, D.. Geometric Theory of Semilinear Parabolic Equations, Lecture Notes in Math. 840 (Berlin: Springer, 1981).CrossRefGoogle Scholar
6Medeiros, L. A. and Miranda, M. M.. Weak solutions for a nonlinear dispersive equation. J. Math. Anal. Appl. 59 (1977), 432–441.CrossRefGoogle Scholar
7Quarteroni, A.. Fourier Spectral Methods for Pseudo-parabolic Equations (Pavia: Istituto di Anal. Num. del CNR, 1985).Google Scholar