Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T06:13:35.537Z Has data issue: false hasContentIssue false
  • English
  • Français

On the generalized Hardy-Rellich inequalities

Part of: Partial differential equations Linear function spaces and their duals

Published online by Cambridge University Press:  26 January 2019

T.V. Anoop ,
Ujjal Das  and
Abhishek Sarkar
T.V. Anoop
Affiliation:
Department of Mathematics, Indian Institute of Technology Madras, Chennai600036, India (anoop@iitm.ac.in)
Ujjal Das
Affiliation:
The Institute of Mathematical Sciences, Chennai600113, India (ujjaldas@imsc.res.in, ujjal.rupam.das@gmail.com)
Abhishek Sarkar
Affiliation:
NTIS, University of West Bohemia Technická 8, 306 14 Plzeň, Czech Republic (sarkara@ntis.zcu.cz)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we look for the weight functions (say g) that admit the following generalized Hardy-Rellich type inequality:

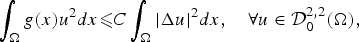$$\int_\Omega g (x)u^2 dx \les C\int_\Omega \vert \Delta u \vert ^2 dx,\quad \forall u\in {\rm {\cal D}}_0^{2,2} (\Omega ),$$
for some constant C > 0, where Ω is an open set in ℝN with N ⩾ 1. We find various classes of such weight functions, depending on the dimension N and the geometry of Ω. Firstly, we use the Muckenhoupt condition for the one-dimensional weighted Hardy inequalities and a symmetrization inequality to obtain admissible weights in certain Lorentz-Zygmund spaces. Secondly, using the fundamental theorem of integration we obtain the weight functions in certain weighted Lebesgue spaces. 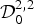As a consequence of our results, we obtain simple proofs for the embeddings of ${\cal D}_0^{2,2} $ into certain Lorentz-Zygmund spaces proved by Hansson and later by Brezis and Wainger.

Keywords

Generalized Hardy-Rellich inequalityMuckenhoupt conditionsymmetrizationLorentz spacesLorentz-Zygmund spacesexterior domains

MSC classification

Primary: 35A23: Inequalities involving derivatives and differential and integral operators, inequalities for integrals
Secondary: 46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.) 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 2 , April 2020 , pp. 897 - 919
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Adams, D.R.. A sharp inequality of J. Moser for higher order derivatives. Ann. of Math. (2) 128 (1988), 385–398.CrossRefGoogle Scholar
2Adimurthi, A. and Santra, S.. Generalized Hardy-Rellich inequalities in critical dimension and its applications. Commun. Contemp. Math. 11 (2009), 367–394.CrossRefGoogle Scholar
3Adimurthi, A., Chaudhuri, N. and Ramaswamy, M.. An improved Hardy-Sobolev inequality and its application. Proc. Amer. Math. Soc. 130 (2002), 489–505 (electronic).CrossRefGoogle Scholar
4Adimurthi, A., Grossi, M. and Santra, S.. Optimal Hardy-Rellich inequalities, maximum principle and related eigenvalue problem. J. Funct. Anal. 240 (2006), 36–83.CrossRefGoogle Scholar
5Allegretto, W.. Principal eigenvalues for indefinite-weight elliptic problems in ℝn. Proc. Amer. Math. Soc. 116 (1992), 701–706.Google Scholar
6Anoop, T.V.. A note on generalized Hardy-Sobolev inequalities. Int. J. Anal. 2013 (2013), 1–9.CrossRefGoogle Scholar
7Anoop, T.V., Lucia, M. and Ramaswamy, M.. Eigenvalue problems with weights in Lorentz spaces. Calc. Var. Partial Diff. Equ. 36 (2009), 355–376.CrossRefGoogle Scholar
8Bennett, C. and Rudnick, K.. On Lorentz-Zygmund spaces. Dissertationes Math. (Rozprawy Mat.) 175 (1980), 67.Google Scholar
9Bennett, C. and Sharpley, R.. Interpolation of operators, volume 129 of Pure and Applied Mathematics (Boston, MA: Academic Press, Inc., 1988).Google Scholar
10Brézis, H. and Vázquez, J.L.. Blow-up solutions of some nonlinear elliptic problems. Rev. Mat. Univ. Complut. Madrid 10 (1997), 443–469.Google Scholar
11Brézis, H. and Wainger, S.. A note on limiting cases of Sobolev embeddings and convolution inequalities. Comm. Partial Diff. Equ. 5 (1980), 773–789.CrossRefGoogle Scholar
12Cianchi, A.. Second-order derivatives and rearrangements. Duke Math. J. 105 (2000), 355–385.CrossRefGoogle Scholar
13Cianchi, A.. Symmetrization and second-order Sobolev inequalities. Ann. Mat. Pura Appl. (4) 183 (2004), 45–77.CrossRefGoogle Scholar
14Edelson, A.L. and Rumbos, A.J.. Linear and semilinear eigenvalue problems in ℝn. Comm. Partial Diff. Equ. 18 (1993), 215–240.CrossRefGoogle Scholar
15Edmunds, D.E. and Evans, W.D.. Hardy operators, function spaces and embeddings. Springer Monographs in Mathematics (Berlin: Springer-Verlag, 2004).CrossRefGoogle Scholar
16Edmunds, D.E. and Triebel, H.. Sharp Sobolev embeddings and related Hardy inequalities: the critical case. Math. Nachr. 207 (1999), 79–92.CrossRefGoogle Scholar
17Edmunds, D.E., Kerman, R. and Pick, L.. Optimal Sobolev imbeddings involving rearrangement-invariant quasinorms. J. Funct. Anal. 170 (2000), 307–355.CrossRefGoogle Scholar
18Filippas, S. and Tertikas, A.. Optimizing improved Hardy inequalities. J. Funct. Anal. 192 (2002), 186–233.CrossRefGoogle Scholar
19Ghoussoub, N. and Moradifam, A.. On the best possible remaining term in the Hardy inequality. Proc. Natl. Acad. Sci. USA 105 (2008), 13746–13751.CrossRefGoogle ScholarPubMed
20Ghoussoub, N. and Moradifam, A.. Bessel pairs and optimal Hardy and Hardy-Rellich inequalities. Math. Ann. 349 (2011), 1–57.CrossRefGoogle Scholar
21Ghoussoub, N. and Moradifam, A.. Functional inequalities: new perspectives and new applications, volume 187 of Mathematical Surveys and Monographs (Providence, RI: American Mathematical Society, 2013).Google Scholar
22Grafakos, L.. Classical Fourier analysis, 2nd edn, volume 249 of Graduate Texts in Mathematics (New York: Springer, 2008).Google Scholar
23Hansson, K.. Imbedding theorems of Sobolev type in potential theory. Math. Scand. 45 (1979), 77–102.CrossRefGoogle Scholar
24Hörmander, L. and Lions, J.L.. Sur la complétion par rapport à une intégrale de Dirichlet. Math. Scand. 4 (1956), 259–270.CrossRefGoogle Scholar
25Hunt, R.A.. On L(p, q) spaces. Enseignement Math. (2) 12 (1966), 249–276.Google Scholar
26Kufner, A., Maligranda, L. and Persson, L.-E.. The Hardy inequality. Vydavatelský Servis, Plzeň, 2007. About its history and some related results.Google Scholar
27Lorentz, G.G.. Some new functional spaces. Ann. of Math. (2) 51 (1950), 3–755.CrossRefGoogle Scholar
28Manes, A. and Micheletti, A.M.. Un'estensione della teoria variazionale classica degli autovalori per operatori ellittici del secondo ordine. Boll. Un. Mat. Ital. (4) 7 (1973), 285–301.Google Scholar
29Milman, M. and Pustylnik, E.. On sharp higher order Sobolev embeddings. Commun. Contemp. Math. 6 (2004), 495–511.CrossRefGoogle Scholar
30Muckenhoupt, B.. Hardy's inequality with weights. Studia Math. 44 (1972), 31–38. Collection of articles honoring the completion by Antoni Zygmund of 50 years of scientific activity, I.CrossRefGoogle Scholar
31O'Neil, R.. Convolution operators and L(p, q spaces. Duke Math. J. 30 (1963), 129–142.CrossRefGoogle Scholar
32Rellich, F.. Halbbeschränkte Differentialoperatoren höherer Ordnung. In Proceedings of the International Congress of Mathematicians, 1954 (ed. Erven, P. and Noordhoff, N.V.). Amsterdam, vol. III, pp. 243–250 (Amsterdam: Groningen; North-Holland Publishing Co., 1956).Google Scholar
33Stavrakakis, N.M. and Zographopoulos, N.. Global bifurcation results for a semilinear biharmonic equation on all of ℝN. Z. Anal. Anwendungen 18 (1999), 753–766.CrossRefGoogle Scholar
34Tarsi, C.. Adams' inequality and limiting Sobolev embeddings into Zygmund spaces. Potential Anal. 37 (2012), 353–385.CrossRefGoogle Scholar
35Tertikas, A. and Zographopoulos, N.B.. Best constants in the Hardy-Rellich inequalities and related improvements. Adv. Math. 209 (2007), 407–459.CrossRefGoogle Scholar
36Visciglia, N.. A note about the generalized Hardy-Sobolev inequality with potential in L p, d(ℝn). Calc. Var. Partial Diff. Equ. 24 (2005), 167–184.CrossRefGoogle Scholar