Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wang, J.
Ren, Y.
and
Zhang, E.
2023.
A weighted weak-type inequality for the one-sided maximal operators.
Ukrains’kyi Matematychnyi Zhurnal,
Vol. 75,
Issue. 5,
p.
712.
Wang, J.
Ren, Y.
and
Zhang, E.
2023.
A Weighted Weak-Type Inequality for One-Sided Maximal Operators.
Ukrainian Mathematical Journal,
Vol. 75,
Issue. 5,
p.
817.
Zhang, Erxin
and
Ren, Yanbo
2023.
A Unified Version of Weighted Weak Type Inequalities for One-Sided Maximal Function on $${\mathbb {R}}^2$$.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 46,
Issue. 4,
Zhang, Erxin
2024.
A Unified Version of Weighted Weak-Type Inequalities for the One-Sided Hardy–Littlewood Maximal Function in Orlicz Classes.
Mathematics,
Vol. 12,
Issue. 18,
p.
2814.
Ren, Yanbo
and
Wang, Jing
2024.
Criteria of a Four-Weight Weak Type Inequality for One-Sided Maximal Operators in Orlicz Classes.
Mediterranean Journal of Mathematics,
Vol. 21,
Issue. 2,


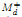 , smaller than the one-sided Hardy–Littlewood maximal operator
, smaller than the one-sided Hardy–Littlewood maximal operator 