Stable minimizers of functionals of the gradient

Abstract

Let Ω ⊂ ℝⁿ be a bounded Lipschitz domain. Let $L: {\mathbb R}^n\rightarrow \bar {\mathbb R}= {\mathbb R}\cup \{+\infty \}$ be a continuous function with superlinear growth at infinity, and consider the functional 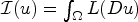$\mathcal {I}(u)=\int \nolimits _\Omega L(Du)$, u ∈ W^1,1(Ω). We provide necessary and sufficient conditions on L under which, for all f ∈ W^1,1(Ω) such that 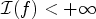$\mathcal {I}(f) < +\infty $, the problem of minimizing 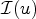$\mathcal {I}(u)$ with the boundary condition u_|∂Ω = f has a solution which is stable, or – alternatively – is such that all of its solutions are stable. By stability of 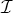$\mathcal {I}$ at u we mean that $u_k\rightharpoonup u$ weakly in W^1,1(Ω) together with 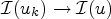$\mathcal {I}(u_k)\to \mathcal {I}(u)$ imply u_k → u strongly in W^1,1(Ω). This extends to general boundary data some results obtained by Cellina and Cellina and Zagatti. Furthermore, with respect to the preceding literature on existence results for scalar variational problems, we drop the assumption that the relaxed functional admits a continuous minimizer.