Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T19:33:40.104Z Has data issue: false hasContentIssue false
  • English
  • Français

The Tutte polynomial and toric Nakajima quiver varieties

Published online by Cambridge University Press:  27 October 2021

Tarig Abdelgadir ,
Anton Mellit  and
Fernando Rodriguez Villegas
Tarig Abdelgadir
Affiliation:
Mathematical Sciences, Loughborough University, Loughborough LE11 3TU, United Kingdom t.abdelgadir@lboro.ac.uk
Anton Mellit
Affiliation:
University of Vienna, Oskar-Morgenstern-Platz 1, Vienna 1090, Austria, anton.mellit@univie.ac.at
Fernando Rodriguez Villegas
Affiliation:
The Abdus Salam International Centre for Theoretical Physics, Stada Costiera 11, Trieste 34151, Italy villegas@ictp.it
Get access Rights & Permissions [Opens in a new window]

Abstract

For a quiver 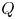$Q$ with underlying graph 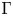$\Gamma$, we take 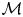$ {\mathcal {M}}$ an associated toric Nakajima quiver variety. In this article, we give a direct relation between a specialization of the Tutte polynomial of 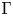$\Gamma$, the Kac polynomial of 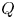$Q$ and the Poincaré polynomial of 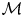$ {\mathcal {M}}$. We do this by giving a cell decomposition of 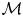$ {\mathcal {M}}$ indexed by spanning trees of 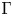$\Gamma$ and ‘geometrizing’ the deletion and contraction operators on graphs. These relations have been previously established in Hausel–Sturmfels [6] and Crawley-Boevey–Van den Bergh [3], however the methods here are more hands-on.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 5 , October 2022 , pp. 1323 - 1339
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Coutinho, G., A brief introduction to the Tutte polynomial, https://homepages.dcc.ufmg.br/~gabriel/seminars/coutinho_tuttepolynomial_seminar.pdf.Google Scholar
Craw, A., Quiver representations in toric geometry, arXiv:0807.2191 (2008).Google Scholar
Crawley-Boevey, W. and Van den Bergh, M.. Absolutely indecomposable representations and Kac-Moody Lie algebras. Invent. Math. 155 (2004), 537–559. With an appendix by Hiraku Nakajima. MR2038196.Google Scholar
Ginzburg, V., Lectures on Nakajima's quiver varieties, Geometric methods in representation theory. I, Sémin. Congr., vol. 24, Soc. Math. France, Paris, 2012, pp. 145–219. MR3202703.Google Scholar
Hausel, T., Letellier, E. and Rodriguez-Villegas, F., Locally free representations of quivers over commutative frobenius algebras, arXiv:1810.01818 (2018).Google Scholar
Hausel, T. and Sturmfels, B.. Toric hyperkähler varieties. Doc. Math. 7 (2002), 495–534. MR2015052.Google Scholar
Hoskins, V., Moduli problems and geometric invariant theory, https://userpage.fu-berlin.de/hoskins/M15_Lecture_notes.pdf.Google Scholar
King, A. D.. Moduli of representations of finite-dimensional algebras. Quart. J. Math. Oxford Ser. (2) 45 (1994), 515–530. MR1315461.CrossRefGoogle Scholar
Kuznetsov, A.. Quiver varieties and Hilbert schemes. Mosc. Math. J. 7 (2007), 673–697. MR2372209.CrossRefGoogle Scholar