Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T07:46:41.175Z Has data issue: false hasContentIssue false
  • English
  • Français

The breadth of the lattice of those varieties of inverse semigroups which contain the variety of groups

Published online by Cambridge University Press:  14 November 2011

Norman R. Reilly
Norman R. Reilly
Affiliation:
Department of Mathematics, Simon Fraser University, Burnaby, B.C., Canada
Get access Rights & Permissions [Opens in a new window]

Synopsis

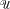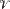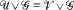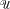The relations v1 and v2 defined on the lattice ℒ of varieties of inverse semigroups by v1 if and only if and v2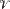 if and only if 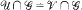, where denotes tie variety of groups, are both congruences on ℒ the class v1, is simply the lattice of varieties of grcups and is therefore known to have cardinality .

The class v2 is precisely the sublattice of ℒ consisting of those varieties containing . Each v1-class contains preciselyone element of v2. The main result of this paper establishes that the sublattice v2 of ℒ has breadth . From this it follows that the lattice ℒ/v1 also has breadth . Some consequences concerning varieties generated by fundamental inverse semigroups are also considered.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 93 , Issue 3-4 , 1983 , pp. 319 - 325
Copyright
Copyright © Royal Society of Edinburgh 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Adyan, S.. The Bumside problem and identities in groups. Ergebnisse der Mathematik (Berlin: Springer, 1979).CrossRefGoogle Scholar
2Howie, J. M.. An introduction to semigroup theory (London: Academic Press, 1976).Google Scholar
3Kleiman, E. I.. On the lattice of varieties of inverse semigroups. Izv. Vysš. Učeb. Zabend. Matematika 7 (1976), 106–109.Google Scholar
4Kleiman, E. I.. On bases of identities of Brandt semigroups. Semigroup Forum 13 (1977), 209–218.CrossRefGoogle Scholar
5Munn, W. D.. Fundamental inverse semigroups. Quart. J. Math. Oxford 21 (1970), 157–170.CrossRefGoogle Scholar
6Olshansky, A. U.. On the problem of finite basis of identities in groups. Izv. Akad.Nauk SSSR Ser. Mat. 34 (1970), 176–184. (In Russian).Google Scholar
7Reilly, N. R.. Varieties of completely semisimple inverse semigroups. J. Algebra 65 (1980), 427–444.CrossRefGoogle Scholar
8Reilly, N. R.. Modular sublattices of the lattice of varieties of inverse semigroups. Pacific J. Math. 89 (1980), 405–417.CrossRefGoogle Scholar