Article contents
Fractal dimension of potential singular points set in the Navier–Stokes equations under supercritical regularity
Published online by Cambridge University Press: 18 April 2023
Abstract
The main objective of this paper is to answer the questions posed by Robinson and Sadowski [22, p. 505, Commun. Math. Phys., 2010] for the Navier–Stokes equations. Firstly, we prove that the upper box dimension of the potential singular points set $\mathcal {S}$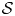 of suitable weak solution $u$
of suitable weak solution $u$ belonging to $L^{q}(0,T;L^{p}(\mathbb {R}^{3}))$
belonging to $L^{q}(0,T;L^{p}(\mathbb {R}^{3}))$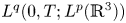 for $1\leq \frac {2}{q}+\frac {3}{p}\leq \frac 32$
for $1\leq \frac {2}{q}+\frac {3}{p}\leq \frac 32$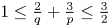 with $2\leq q<\infty$
with $2\leq q<\infty$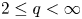 and $2< p<\infty$
and $2< p<\infty$ is at most $\max \{p,q\}(\frac {2}{q}+\frac {3}{p}-1)$
is at most $\max \{p,q\}(\frac {2}{q}+\frac {3}{p}-1)$ in this system. Secondly, it is shown that $1-2s$
in this system. Secondly, it is shown that $1-2s$ dimension Hausdorff measure of potential singular points set of suitable weak solutions satisfying $u\in L^{2}(0,T;\dot {H}^{s+1}(\mathbb {R}^{3}))$
dimension Hausdorff measure of potential singular points set of suitable weak solutions satisfying $u\in L^{2}(0,T;\dot {H}^{s+1}(\mathbb {R}^{3}))$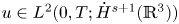 for $0\leq s\leq \frac 12$
for $0\leq s\leq \frac 12$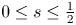 is zero, whose proof relies on Caffarelli–Silvestre's extension. Inspired by Barker–Wang's recent work [1], this further allows us to discuss the Hausdorff dimension of potential singular points set of suitable weak solutions if the gradient of the velocity is under some supercritical regularity.
is zero, whose proof relies on Caffarelli–Silvestre's extension. Inspired by Barker–Wang's recent work [1], this further allows us to discuss the Hausdorff dimension of potential singular points set of suitable weak solutions if the gradient of the velocity is under some supercritical regularity.
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 154 , Issue 3 , June 2024 , pp. 727 - 745
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 1
- Cited by


