Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T15:23:29.712Z Has data issue: false hasContentIssue false
  • English
  • Français

One-relator groups and algebras related to polyhedral products

Part of: Homotopy theory Algebraic combinatorics Homology and homotopy of topological groups and related structures Low-dimensional topology Special aspects of infinite or finite groups

Published online by Cambridge University Press:  15 January 2021

Jelena Grbić ,
George Simmons ,
Marina Ilyasova  and
Taras Panov Open the ORCID record for Taras Panov [Opens in a new window]
Jelena Grbić
Affiliation:
School of Mathematical Sciences, University of Southampton, UK (j.grbic@soton.ac.uk; g.j.h.simmons@soton.ac.uk)
George Simmons
Affiliation:
School of Mathematical Sciences, University of Southampton, UK (j.grbic@soton.ac.uk; g.j.h.simmons@soton.ac.uk)
Marina Ilyasova
Affiliation:
Department of Mathematics and Mechanics, Moscow State University, Russia (marina_ilyasova@bk.ru)
Taras Panov
Affiliation:
Department of Mathematics and Mechanics, Moscow State University, Moscow, Russia Institute for Information Transmission Problems, Russian Academy of Sciences, Moscow, Russia (tpanov@mech.math.msu.su)
Get access Rights & Permissions [Opens in a new window]

Abstract

We link distinct concepts of geometric group theory and homotopy theory through underlying combinatorics. For a flag simplicial complex 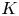$K$, we specify a necessary and sufficient combinatorial condition for the commutator subgroup 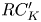$RC_K'$ of a right-angled Coxeter group, viewed as the fundamental group of the real moment-angle complex 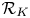$\mathcal {R}_K$, to be a one-relator group; and for the Pontryagin algebra 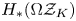$H_{*}(\Omega \mathcal {Z}_K)$ of the moment-angle complex to be a one-relator algebra. We also give a homological characterization of these properties. For 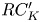$RC_K'$, it is given by a condition on the homology group 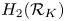$H_2(\mathcal {R}_K)$, whereas for 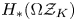$H_{*}(\Omega \mathcal {Z}_K)$ it is stated in terms of the bigrading of the homology groups of 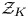$\mathcal {Z}_K$.

Keywords

one-relator groups and algebrascommutator subgroups of right-angled Coxeter groupsmoment-angle complexesflag complexes

MSC classification

Primary: 20F55: Reflection and Coxeter groups 20F65: Geometric group theory 55P15: Classification of homotopy type
Secondary: 05E45: Combinatorial aspects of simplicial complexes 57M07: Topological methods in group theory 57T30: Bar and cobar constructions
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 1 , February 2022 , pp. 128 - 147
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, J. F.. On the cobar construction. Proc. Nat. Acad. Sci. USA. 42 (1956), 409–412.CrossRefGoogle ScholarPubMed
Adams, J. F. and Hilton, P. J.. On the chain algebra of a loop space. Comment. Math. Helv. 30 (1956), 305–330.CrossRefGoogle Scholar
Amelotte, S. Connected sums of sphere products and minimally non-Golod complexes. Preprint. (2020) arXiv:2006.16320.Google Scholar
Beben, P. and Wu, J.. The homotopy type of a Poincaré duality complex after looping. Proc. Edinb. Math. Soc. 58 (2015), 581–616.10.1017/S0013091515000048CrossRefGoogle Scholar
Buchstaber, V. M. and Panov, T. E.. Toric topology. In Mathematical surveys and monographs, vol. 204 (Providence, RI: American Mathematical Society, 2015), xiv+518 pp.Google Scholar
Dyer, E. and Vasquez, A. T.. Some small aspherical spaces. J. Austral. Math. Soc. 16 (1973), 332–352.10.1017/S1446788700015147CrossRefGoogle Scholar
Grbić, J., Panov, T., Theriault, S. and Wu, J.. The homotopy types of moment-angle complexes for flag complexes. Trans. Amer. Math. Soc. 368 (2016), 6663–6682.CrossRefGoogle Scholar
Grbić, J. and Theriault, S.. The homotopy type of the complement of a coordinate subspace arrangement. Topology 46 (2007), 357–396.CrossRefGoogle Scholar
Hatcher, A.. Algebraic topology (Cambridge: Cambridge University Press, 2002).Google Scholar
Iriye, K. and Yano, T.. A Golod complex with non-suspension moment-angle complex. Topol. Appl. 225 (2017), 145–163.CrossRefGoogle Scholar
Limonchenko, I. Y.. Families of minimally non-Golod complexes and polyhedral products. Dal'nevost. Mat. Zh. 15 (2015), 222–237, (in Russian); arXiv:1509.04302.Google Scholar
Lyndon, R. C.. Cohomology theory of groups with a single defining relation. Ann. of Math. 52 (1950), 650–665.CrossRefGoogle Scholar
McGavran, D.. Adjacent connected sums and torus actions. Trans. Amer. Math. Soc. 251 (1979), 235–254.CrossRefGoogle Scholar
Panov, T. E. and Ray, N.. Categorical aspects of toric topology. Toric topology, contemporary mathematics, Harada, M. et al. , editors, vol. 460, pp. 293–322 (Providence, RI: American Mathematical Society, 2008).CrossRefGoogle Scholar
Panov, T. E. and Veryovkin, Y. A.. Polyhedral products and commutator subgroups of right-angled Artin and Coxeter groups. Sb. Math. 207 (2016), 1582–1600.CrossRefGoogle Scholar
Veryovkin, Y. A.. Pontryagin algebras of some moment-angle-complexes. Dal'nevost. Mat. Zh. 2016, 9–23, (in Russian); arXiv:1512.00283.Google Scholar