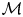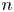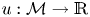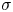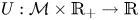1. Introduction
The Carleson measure $\nu$![]() on $\mathbb {R}^{n+1}_+$
on $\mathbb {R}^{n+1}_+$![]() , meaning that
, meaning that
as its name implies, was introduced by Carleson in the 1950s. This measure captures essential orthogonality properties and exploits properties of extension of a function on the upper half-space. There exists a natural and deep connection between Carleson measure and bounded mean oscillation function (BMO function for short); indeed, a measure derived from some function is Carleson if and only if the underlying function is in BMO. In his ground-breaking paper, Fefferman [Reference Fefferman14] announced that, a function $u$![]() belongs to BMO space if and only if its Poisson integral (also called harmonic extension) $U(x,\,t)=\mathrm {e}^{-t\sqrt {-\Delta }}u(x)$
belongs to BMO space if and only if its Poisson integral (also called harmonic extension) $U(x,\,t)=\mathrm {e}^{-t\sqrt {-\Delta }}u(x)$![]() satisfies the following Carleson measure condition
satisfies the following Carleson measure condition
where $\nabla _{(x,t)}=(\nabla _x,\,\partial _t)$![]() denotes the total gradient. This Poisson integral is effectively to solve the Dirichlet problem for the Laplace equation on $\mathbb {R}^{n+1}_+$
denotes the total gradient. This Poisson integral is effectively to solve the Dirichlet problem for the Laplace equation on $\mathbb {R}^{n+1}_+$![]() , i.e., one obtains $U(x,\,t)=\mathrm {e}^{-t\sqrt {-\Delta }}u(x)$
, i.e., one obtains $U(x,\,t)=\mathrm {e}^{-t\sqrt {-\Delta }}u(x)$![]() as the solution to
as the solution to

For more related works on BMO function and Carleson measure, we refer the reader to [Reference Chen5, Reference Chen, Duong, Li, Song and Yan6, Reference Ding, Lee and Lin10, Reference Duong, Yan and Zhang11, Reference Fabes and Neri13, Reference Hartzstein and Salinas20, Reference Jiang and Li22, Reference Jiang, Xiao and Yang24, Reference Lin and Liu27–Reference Song and Wu29, Reference Trong and Tung32, Reference Wang and Xiao33] and their references therein. On the other hand, to define the fractional powers of the Laplacian $(-\Delta )^\sigma$![]() in local form, $0<\sigma <1$
in local form, $0<\sigma <1$![]() , Caffarelli-Silvestre [Reference Caffarelli and Silvestre3] introduced the $\sigma$
, Caffarelli-Silvestre [Reference Caffarelli and Silvestre3] introduced the $\sigma$![]() -harmonic extension
-harmonic extension

They interpreted the function $U$![]() satisfying the equation above as the $\sigma$
satisfying the equation above as the $\sigma$![]() -harmonic extension of $u$
-harmonic extension of $u$![]() to a fractional dimension $2-2\sigma$
to a fractional dimension $2-2\sigma$![]() , and proved that, up to a multiplicative constant,
, and proved that, up to a multiplicative constant,
This means any fractional power of the Laplacian can be determined as an operator that maps a Dirichlet boundary condition to a Neumann-type condition via the above extension problem. Later on, Brazke–Schikorra–Sire [Reference Brazke, Schikorra and Sire2] considered the boundary behaviour of the $\sigma$![]() -harmonic extension. They characterised the BMO function $u : \mathcal {M} \to {\mathbb {R}}$
-harmonic extension. They characterised the BMO function $u : \mathcal {M} \to {\mathbb {R}}$![]() by a Carleson measure condition of its $\sigma$
by a Carleson measure condition of its $\sigma$![]() -harmonic extension $U:\mathcal {M}\times {\mathbb {R}}_+ \to {\mathbb {R}}$
-harmonic extension $U:\mathcal {M}\times {\mathbb {R}}_+ \to {\mathbb {R}}$![]() , where $\mathcal {M}$
, where $\mathcal {M}$![]() is a complete path connected and Ahlfors regular manifold without boundary, such that either the Ricci curvature is non-negative or the Ricci curvature is bounded from below together with a pointwise bound on the gradient of the heat kernel. However, since this pointwise bound fails already for the elliptic operators (see [Reference Coulhon, Jiang, Koskela and Sikora8, Reference Jiang and Lin23] for instance), a basic question arising from the above discussions motivates our work:
is a complete path connected and Ahlfors regular manifold without boundary, such that either the Ricci curvature is non-negative or the Ricci curvature is bounded from below together with a pointwise bound on the gradient of the heat kernel. However, since this pointwise bound fails already for the elliptic operators (see [Reference Coulhon, Jiang, Koskela and Sikora8, Reference Jiang and Lin23] for instance), a basic question arising from the above discussions motivates our work:
• Question : Can we remove the pointwise bound on the gradient of the heat kernel or the non-negative Ricci curvature condition on $\mathcal {M}$
 ?
?
In this paper, under a more general Dirichlet metric measure space setting, we will provide a positive answer to the above question; see Theorem 2.2. Moreover, we equip the solution $U$![]() and the trace $u$
and the trace $u$![]() with some limiting conditions to derive the relationship between vanishing Carleson measure and vanishing mean oscillation function (CMO function for short); see Theorem 6.1. It is remarkable that our method and technique in this paper are different from that of Brazke–Schikorra–Sire. Their proofs lean heavily on the Ricci curvature condition, the pointwise bound on the gradient of the heat kernel, the $T(b)$
with some limiting conditions to derive the relationship between vanishing Carleson measure and vanishing mean oscillation function (CMO function for short); see Theorem 6.1. It is remarkable that our method and technique in this paper are different from that of Brazke–Schikorra–Sire. Their proofs lean heavily on the Ricci curvature condition, the pointwise bound on the gradient of the heat kernel, the $T(b)$![]() -theorem proved by Hofmann–Mitrea–Mitrea–Morris, and so on. However our main tools are the space-time conversion technology (see Lemma 3.2), the spectral theory (see Proposition 4.1), and the theory of the tent space (see the proof of Theorem 5.4). Therefore, our conclusions can get rid of the Ricci curvature condition and the pointwise bound on the gradient of the heat kernel, and are suitable for the Dirichlet metric measure space setting; see the proof of Theorem 2.2 for more details.
-theorem proved by Hofmann–Mitrea–Mitrea–Morris, and so on. However our main tools are the space-time conversion technology (see Lemma 3.2), the spectral theory (see Proposition 4.1), and the theory of the tent space (see the proof of Theorem 5.4). Therefore, our conclusions can get rid of the Ricci curvature condition and the pointwise bound on the gradient of the heat kernel, and are suitable for the Dirichlet metric measure space setting; see the proof of Theorem 2.2 for more details.
The remainder of this paper will be as follows. In § 2, we collect some preliminaries, state the main result (namely Theorem 2.2) that the relationship between BMO and Carleson measure without the pointwise bound on the gradient of the heat kernel, and pose two open problems related to the main result. In § 3, we first establish the time derivative estimate of the $\sigma$![]() -Poisson kernel, and then control the spatial gradient of the $\sigma$
-Poisson kernel, and then control the spatial gradient of the $\sigma$![]() -harmonic function by the time derivative part. § 4 provides the $L^2$
-harmonic function by the time derivative part. § 4 provides the $L^2$![]() -estimate of the square function by applying the spectral theory, and § 5 will be devoted to the proof of Theorem 2.2. In § 6, we continue the line of § 5 to study the $\sigma$
-estimate of the square function by applying the spectral theory, and § 5 will be devoted to the proof of Theorem 2.2. In § 6, we continue the line of § 5 to study the $\sigma$![]() -harmonic function with CMO trace. Some remarks are then presented in the final section.
-harmonic function with CMO trace. Some remarks are then presented in the final section.
The letter $C$![]() (or $c$
(or $c$![]() ) will denote a positive constant that may vary from line to line but will remain independent of the main variables.
) will denote a positive constant that may vary from line to line but will remain independent of the main variables.
2. Main result
In this section, we first briefly describe our metric measure space settings; see [Reference Fukushima, Oshima and Takeda15, Reference Gyrya and Saloff-Coste19, Reference Sturm31] for more details, and then state the main result about BMO and Carleson measure; see Theorem 2.2. Finally, two open problems are considered.
2.1 Preliminaries
Suppose that $\mathcal {M}$![]() is a separable, connected, locally compact and metrisable space. Let $\mu$
is a separable, connected, locally compact and metrisable space. Let $\mu$![]() be a Borel measure that is strictly positive on non-empty open sets and finite on compact sets. We consider a strongly local, closed, and regular Dirichlet form $\mathscr {E}$
be a Borel measure that is strictly positive on non-empty open sets and finite on compact sets. We consider a strongly local, closed, and regular Dirichlet form $\mathscr {E}$![]() on $L^{2}(\mathcal {M},\, \mu )$
on $L^{2}(\mathcal {M},\, \mu )$![]() with dense domain $\mathscr {D} \subset L^{2}(\mathcal {M},\, \mu )$
with dense domain $\mathscr {D} \subset L^{2}(\mathcal {M},\, \mu )$![]() (see [Reference Fukushima, Oshima and Takeda15] or [Reference Gyrya and Saloff-Coste19] for an accurate definition). Suppose that $\mathscr {E}$
(see [Reference Fukushima, Oshima and Takeda15] or [Reference Gyrya and Saloff-Coste19] for an accurate definition). Suppose that $\mathscr {E}$![]() admits a ‘carré du champ’, which means that, for all $f,\, g \in \mathscr {D}$
admits a ‘carré du champ’, which means that, for all $f,\, g \in \mathscr {D}$![]() , the measure-valued non-negative and symmetric bilinear form $\Gamma (f,\, g)$
, the measure-valued non-negative and symmetric bilinear form $\Gamma (f,\, g)$![]() is absolutely continuous with respect to the measure $\mu$
is absolutely continuous with respect to the measure $\mu$![]() . In what follows, for simplicity of notation, let $\langle \nabla _{x} f,\, \nabla _{x} g\rangle$
. In what follows, for simplicity of notation, let $\langle \nabla _{x} f,\, \nabla _{x} g\rangle$![]() denote the energy density ${\mathrm {d} \Gamma (f,\, g)}/{\mathrm {d} \mu }$
denote the energy density ${\mathrm {d} \Gamma (f,\, g)}/{\mathrm {d} \mu }$![]() and $|\nabla _{x} f|$
and $|\nabla _{x} f|$![]() denote the square root of ${\mathrm {d} \Gamma (f,\, f)}/{\mathrm {d} \mu }$
denote the square root of ${\mathrm {d} \Gamma (f,\, f)}/{\mathrm {d} \mu }$![]() . Assume that $(\mathcal {M},\, \mu,\, \mathscr {E})$
. Assume that $(\mathcal {M},\, \mu,\, \mathscr {E})$![]() is endowed with the intrinsic (pseudo-)distance on $\mathcal {M}$
is endowed with the intrinsic (pseudo-)distance on $\mathcal {M}$![]() related to $\mathscr {E}$
related to $\mathscr {E}$![]() , which is defined by setting
, which is defined by setting
where $C(\mathcal {M})$![]() is the space of continuous functions on $\mathcal {M}$
is the space of continuous functions on $\mathcal {M}$![]() . Suppose $d$
. Suppose $d$![]() is indeed a distance and induces a topology equivalent to the original topology on $\mathcal {M}$
is indeed a distance and induces a topology equivalent to the original topology on $\mathcal {M}$![]() . As a summary of the above situation, we will say that $(\mathcal {M},\, d,\, \mu,\, \mathscr {E})$
. As a summary of the above situation, we will say that $(\mathcal {M},\, d,\, \mu,\, \mathscr {E})$![]() is a complete Dirichlet metric measure space.
is a complete Dirichlet metric measure space.
Corresponding to such a Dirichlet form $\mathscr {E}$![]() , there exists an operator denoted by $\Delta _\mathcal {M}$
, there exists an operator denoted by $\Delta _\mathcal {M}$![]() (similar to the Laplacian), acting on a dense domain $\mathscr {D}(\Delta _\mathcal {M})$
(similar to the Laplacian), acting on a dense domain $\mathscr {D}(\Delta _\mathcal {M})$![]() in $L^2(\mathcal {M},\,\mu )$
in $L^2(\mathcal {M},\,\mu )$![]() , $\mathscr {D}(\Delta _\mathcal {M})\subset W^{1,2}(\mathcal {M})$
, $\mathscr {D}(\Delta _\mathcal {M})\subset W^{1,2}(\mathcal {M})$![]() , such that for all $f\in \mathscr {D}(\Delta _\mathcal {M})$
, such that for all $f\in \mathscr {D}(\Delta _\mathcal {M})$![]() and each $g\in W^{1,2}(\mathcal {M})$
and each $g\in W^{1,2}(\mathcal {M})$![]() ,
,
where $W^{1,2}(\mathcal {M})$![]() is the Sobolev space equipped with the norm $([f]^{2}_{L^2}+\mathscr {E}(f,\, f))^{1/2}$
is the Sobolev space equipped with the norm $([f]^{2}_{L^2}+\mathscr {E}(f,\, f))^{1/2}$![]() on the domain $\mathscr {D}$
on the domain $\mathscr {D}$![]() . The ‘Laplacian’ $\Delta _\mathcal {M}$
. The ‘Laplacian’ $\Delta _\mathcal {M}$![]() is the infinitesimal generator of the heat semigroup $H_t=\mathrm {e}^{t\Delta _\mathcal {M}}$
is the infinitesimal generator of the heat semigroup $H_t=\mathrm {e}^{t\Delta _\mathcal {M}}$![]() , $t>0$
, $t>0$![]() . The heat semigroup $\{H_t\}_{t>0}$
. The heat semigroup $\{H_t\}_{t>0}$![]() has an integral kernel $h_t(x,\,y)$
has an integral kernel $h_t(x,\,y)$![]() (also called heat kernel), namely,
(also called heat kernel), namely,

which is a non-negative measureable function on ${\mathbb {R}}_+\times \mathcal {M}\times \mathcal {M}$![]() such that
such that
see [Reference Sturm31] for more details.
To state the main result, we impose some assumptions on the underlying space and the heat kernel, define the $\sigma$![]() -harmonic extension and introduce some function classes.
-harmonic extension and introduce some function classes.
Denote by $B(x,\, r)$![]() the open ball with centre $x$
the open ball with centre $x$![]() and radius $r$
and radius $r$![]() , by $V(x,\,r)$
, by $V(x,\,r)$![]() its volume $\mu (B(x,\,r))$
its volume $\mu (B(x,\,r))$![]() , and set $\lambda B(x,\, r)=B(x,\, \lambda r)$
, and set $\lambda B(x,\, r)=B(x,\, \lambda r)$![]() for each $\lambda >0$
for each $\lambda >0$![]() . We suppose that the measure $\mu$
. We suppose that the measure $\mu$![]() is doubling, i.e., there exists a constant $C_D >0$
is doubling, i.e., there exists a constant $C_D >0$![]() such that
such that
Note that the doubling property of $\mu$![]() implies there exists a constant $n\ge1$
implies there exists a constant $n\ge1$![]() such that
such that
and the reverse doubling property holds on a connected space (cf. [Reference Heinonen, Koskela, Shanmugalingam and Tyson21, Remark 8.1.15]), i.e., there exists a constant $0<\kappa \leq n$![]() such that
such that
Obviously, the Ahlfors regular measure is doubling with $n=\kappa$![]() .
.
Assume that the heat kernel $h_t(x,\,y)$![]() admits the so-called diagonal upper estimate
admits the so-called diagonal upper estimate
The conjunction of (2.1) and (2.3) is well understood: it is equivalent to a relative Faber–Krahn inequality
for all balls $B(x,\, r)$![]() in $\mathcal {M}$
in $\mathcal {M}$![]() and each open set $\Omega \subset B(x,\, r)$
and each open set $\Omega \subset B(x,\, r)$![]() , where $\lambda _1(\Omega )$
, where $\lambda _1(\Omega )$![]() is the smallest Dirichlet eigenvalue of $\Delta _\mathcal {M}$
is the smallest Dirichlet eigenvalue of $\Delta _\mathcal {M}$![]() in $\Omega$
in $\Omega$![]() ; see [Reference Grigor'yan18] for more details. Under the doubling conditon (2.1), the diagonal upper estimate (2.3) self-improves into a Gaussian upper bound
; see [Reference Grigor'yan18] for more details. Under the doubling conditon (2.1), the diagonal upper estimate (2.3) self-improves into a Gaussian upper bound
see [Reference Grigor'yan17, Theorem 1.1] for the Riemannian manifold case, and [Reference Coulhon and Sikora9, Section 4.2] for the metric measure space case. Due to some technical reasons, we also assume the heat kernel $h_t(x,\,y)$![]() satisfies the Hölder condition of order $\theta$
satisfies the Hölder condition of order $\theta$![]() ($0<\theta \le 1$
($0<\theta \le 1$![]() )
)
On the other hand, note that the doubling property (2.1) together with the $L^2$![]() -Poincaré inequality
-Poincaré inequality

where $f_B$![]() denotes the mean (or average) of $f$
denotes the mean (or average) of $f$![]() over $B$
over $B$![]() , implies that two sides Gaussian bounds for the heat kernel (also called Li-Yau's estimate), i.e., it holds
, implies that two sides Gaussian bounds for the heat kernel (also called Li-Yau's estimate), i.e., it holds
see [Reference Sturm31] for example. Moreover, the two-sided estimate above is equivalent to a parabolic Harnack inequality for positive solutions to the heat equation; see [Reference Sturm31]. Therefore, under the validity of (2.1) and (2.7), the heat kernel is Hölder continuous.
2.2 Relationship between BMO and Carleson measure
The $\sigma$![]() -harmonic extension is defined as follows.
-harmonic extension is defined as follows.
Definition 2.1 Let $(\mathcal {M},\,d,\,\mu,\,\mathscr {E})$![]() be a complete Dirichlet metric measure space. Given $0<\sigma <1$
be a complete Dirichlet metric measure space. Given $0<\sigma <1$![]() , for every $u\in L^1(\mathcal {M},\,{(1+d(x,\,x_0))^{-\varepsilon } V(x_0,\,1+d(x,\,x_0))^{-1}}\mathrm {d}\mu (x))$
, for every $u\in L^1(\mathcal {M},\,{(1+d(x,\,x_0))^{-\varepsilon } V(x_0,\,1+d(x,\,x_0))^{-1}}\mathrm {d}\mu (x))$![]() with some $x_0\in \mathcal {M}$
with some $x_0\in \mathcal {M}$![]() and $0<\varepsilon <\min \{2\sigma,\,\kappa /2\}$
and $0<\varepsilon <\min \{2\sigma,\,\kappa /2\}$![]() , its $\sigma$
, its $\sigma$![]() -harmonic extension $U : \mathcal {M}\times {\mathbb {R}}_+ \to {\mathbb {R}}$
-harmonic extension $U : \mathcal {M}\times {\mathbb {R}}_+ \to {\mathbb {R}}$![]() is the solution to
is the solution to

This solution is formally given by

and explicitly one has

where $P^\sigma _t$![]() is the $\sigma$
is the $\sigma$![]() -Poisson operator and $p^\sigma _t(x,\,y)$
-Poisson operator and $p^\sigma _t(x,\,y)$![]() is its integral kernel.
is its integral kernel.
The previous definition is not explicitly stated in [Reference Stinga and Torrea30] (see also [Reference Galé, Miana and Stinga16]) but it is easy to check that the semigroup approach automatically carries over to such a geometric setting under very weak assumptions on the metric measure space; see [Reference Baudoin, Lang and Sire1] for the Dirichlet case and [Reference Brazke, Schikorra and Sire2] for the manifold case. Moreover, Brazke–Schikorra–Sire [Reference Brazke, Schikorra and Sire2] assume the boundary value $u(x)$![]() is a smooth function with compact support to ensure that its $\sigma$
is a smooth function with compact support to ensure that its $\sigma$![]() -harmonic extension $U(x,\,t)$
-harmonic extension $U(x,\,t)$![]() is vanishing at infinity
is vanishing at infinity
However, via a more elaborate analysis, we can substitute the integrability of $u$![]() for the smoothness.
for the smoothness.
We define the following semi-norms. Denote the usual BMO norm as

Furthermore, let $U(x,\,t)$![]() be the $\sigma$
be the $\sigma$![]() -harmonic extension of a function $u(x)$
-harmonic extension of a function $u(x)$![]() to the upper half-space $\mathcal {M} \times {\mathbb {R}}_+$
to the upper half-space $\mathcal {M} \times {\mathbb {R}}_+$![]() , and we introduce a notion of the Carleson measure
, and we introduce a notion of the Carleson measure

Above the two supremum are taken over all balls $B$![]() in $\mathcal {M}$
in $\mathcal {M}$![]() .
.
The following Theorem 2.2 is the main result of this paper.
Theorem 2.2 Let $(\mathcal {M},\,d,\,\mu,\,\mathscr {E})$![]() be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$
be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$![]() admits the diagonal upper estimate (2.3) and the Hölder continuity (2.6). If $0<\sigma <1,$
admits the diagonal upper estimate (2.3) and the Hölder continuity (2.6). If $0<\sigma <1,$![]() then $u$
then $u$![]() is a BMO function if and only if $U$
is a BMO function if and only if $U$![]() is a Carleson measure. Moreover, it holds
is a Carleson measure. Moreover, it holds
Remark 2.3 In 2017, Carron [Reference Carron4, Theorem 2.4] established that, if a manifold satisfies a volume comparison condition, the relatively connected to an end condition, and the Ricci curvature has quadratic decay, then the manifold satisfies the doubling condition (2.1) and the heat kernel admits the diagonal upper estimate (2.3).
Remark 2.4 To the best of our knowledge, when $(\mathcal {M},\,d,\,\mu )=({{{\mathbb {R}}}^n},\,|\cdot |,\,\mathrm {d} x)$![]() , Theorem 2.2 is new even for the second-order elliptic operator $L=-\mathrm {div} A\nabla$
, Theorem 2.2 is new even for the second-order elliptic operator $L=-\mathrm {div} A\nabla$![]() , where $A=A(x)$
, where $A=A(x)$![]() is an $n\times n$
is an $n\times n$![]() matrix of real, symmetric, bounded measurable coefficients, defined on ${{{\mathbb {R}}}^n}$
matrix of real, symmetric, bounded measurable coefficients, defined on ${{{\mathbb {R}}}^n}$![]() , and satisfies the ellipticity condition, i.e., there exist constants $0<\lambda \le \Lambda <\infty$
, and satisfies the ellipticity condition, i.e., there exist constants $0<\lambda \le \Lambda <\infty$![]() such that, for all $\xi \in {{{\mathbb {R}}}^n}$
such that, for all $\xi \in {{{\mathbb {R}}}^n}$![]() ,
,
Moreover, as we do not need any curvature condition, our result can be applied to different settings, such as Euclidean space with Muckenhoupt weight, Lie group of polynomial growth, sub-Riemannian manifold; see [Reference Coulhon, Jiang, Koskela and Sikora8, Section 7] for more details.
2.3 Two open problems
We pose two open problems related to Theorem 2.2.
Problem 1: As stated in [Reference Fefferman14], Fefferman in advance assumed the harmonic function can represented as the Poisson integral of an initial value. Later on, Fabes–Johnson–Neri [Reference Fabes, Johnson and Neri12] found that the Carleson measure condition actually characterises all harmonic functions $U(x,\,t)$![]() on $\mathbb {R}^{n+1}_+$
on $\mathbb {R}^{n+1}_+$![]() with boundary value in BMO space. They proved that a harmonic function $U$
with boundary value in BMO space. They proved that a harmonic function $U$![]() satisfies the Carleson measure condition if and only if its trace $u$
satisfies the Carleson measure condition if and only if its trace $u$![]() is a BMO function.
is a BMO function.
Inspired by [Reference Fabes, Johnson and Neri12], rather than assuming $U=P^\sigma _tu$![]() in advance, can we seek the trace of the $\sigma$
in advance, can we seek the trace of the $\sigma$![]() -harmonic function $U$
-harmonic function $U$![]() ? At this point we believe that the underlying space $(\mathcal {M},\,d,\,\mu,\,\mathscr {E})$
? At this point we believe that the underlying space $(\mathcal {M},\,d,\,\mu,\,\mathscr {E})$![]() needs to satisfy the doubling condition (2.1) and support the Poincaré inequality (2.7) (which is equivalent to Li-Yau’ estimate (2.8)); see [Reference Coulhon, Jiang, Koskela and Sikora8] and [Reference Jiang and Li22] for example.
needs to satisfy the doubling condition (2.1) and support the Poincaré inequality (2.7) (which is equivalent to Li-Yau’ estimate (2.8)); see [Reference Coulhon, Jiang, Koskela and Sikora8] and [Reference Jiang and Li22] for example.
Based on the arguments above, we pose that
Conjecture 2.5 Let $(\mathcal {M},\,d,\,\mu,\,\mathscr {E})$![]() be a complete Dirichlet metric measure space satisfying the doubling condition (2.1) and supporting the Poincaré inequality (2.7). For every $0<\sigma <1$
be a complete Dirichlet metric measure space satisfying the doubling condition (2.1) and supporting the Poincaré inequality (2.7). For every $0<\sigma <1$![]() , a $\sigma$
, a $\sigma$![]() -harmonic function $U$
-harmonic function $U$![]() satisfies the Carleson measure condition if and only if its trace $u$
satisfies the Carleson measure condition if and only if its trace $u$![]() is a BMO function.
is a BMO function.
The proof of the necessity relies heavily on the structure of the elliptic equation and the Poincaré inequality. The main difficulty lies in that the $\sigma$![]() -harmonic function only satisfies a Hölder continuity condition (since $t^{1-2\sigma }$
-harmonic function only satisfies a Hölder continuity condition (since $t^{1-2\sigma }$![]() is a Muckenhoupt $A_2$
is a Muckenhoupt $A_2$![]() -weight) instead of smoothness or Lipschitz continuity. When $\sigma =1/2$
-weight) instead of smoothness or Lipschitz continuity. When $\sigma =1/2$![]() , we can prove that such harmonic function enjoys Lipschitz regularity in the time direction; see [Reference Jiang and Li22] and [Reference Jin, Li and Shen25] for example. This together with the Carleson measure condition enables us to derive suitable control of the growth of the harmonic function. Whereas $\sigma \neq 1/2$
, we can prove that such harmonic function enjoys Lipschitz regularity in the time direction; see [Reference Jiang and Li22] and [Reference Jin, Li and Shen25] for example. This together with the Carleson measure condition enables us to derive suitable control of the growth of the harmonic function. Whereas $\sigma \neq 1/2$![]() , we do not know that how to establish $L^\infty$
, we do not know that how to establish $L^\infty$![]() -estimate of $t\partial _tU(x,\,t)$
-estimate of $t\partial _tU(x,\,t)$![]() . We look forward to proving the estimate
. We look forward to proving the estimate

holds for all $x\in \mathcal {M}$![]() and $t>0$
and $t>0$![]() .
.
Problem 2: In paper [Reference Fabes and Neri13] (see also [Reference Jiang, Xiao and Yang24]), Fabes-Neri solved the Dirichlet problem for the heat equation
on the upper half-space. They characterised the caloric function (the solution to the heat equation) by a parabolic Carleson measure condition

More precisely, they showed that a caloric function $V$![]() satisfies the parabolic Carleson measure condition if and only if its trace $v$
satisfies the parabolic Carleson measure condition if and only if its trace $v$![]() is a BMO function.
is a BMO function.
In the setting of this paper, how to define the $\sigma$![]() -heat equation? Note that a $W^{1,2}$
-heat equation? Note that a $W^{1,2}$![]() -function $U : \mathcal {M}\times {\mathbb {R}}_+ \to {\mathbb {R}}$
-function $U : \mathcal {M}\times {\mathbb {R}}_+ \to {\mathbb {R}}$![]() is said to be $\sigma$
is said to be $\sigma$![]() -harmonic if it is the solution to the elliptic equation
-harmonic if it is the solution to the elliptic equation
in the weak sense, namely, it holds
for all Lipschitz functions $\Phi$![]() on $\mathcal {M} \times {\mathbb {R}}_+$
on $\mathcal {M} \times {\mathbb {R}}_+$![]() with compact support, where the classical product measure $\mathrm {d}\mu \mathrm {d} t$
with compact support, where the classical product measure $\mathrm {d}\mu \mathrm {d} t$![]() is replaced by the weighted measure $t^{1-2\sigma }\mathrm {d}\mu \mathrm {d} t$
is replaced by the weighted measure $t^{1-2\sigma }\mathrm {d}\mu \mathrm {d} t$![]() . Therefore the $\sigma$
. Therefore the $\sigma$![]() -caloric function (the solution to the $\sigma$
-caloric function (the solution to the $\sigma$![]() -heat equation) $V : \mathcal {M}\times {\mathbb {R}}_+ \to {\mathbb {R}}$
-heat equation) $V : \mathcal {M}\times {\mathbb {R}}_+ \to {\mathbb {R}}$![]() should be also understood in the weighted product measure $t^{1-2\sigma }\mathrm {d}\mu \mathrm {d} t$
should be also understood in the weighted product measure $t^{1-2\sigma }\mathrm {d}\mu \mathrm {d} t$![]() , namely, it holds
, namely, it holds
for all Lipschitz functions $\Psi$![]() on $\mathcal {M} \times {\mathbb {R}}_+$
on $\mathcal {M} \times {\mathbb {R}}_+$![]() with compact support.
with compact support.
Inspired by [Reference Fabes and Neri13], can we consider the Dirichlet problem for the $\sigma$![]() -heat equation
-heat equation
on the upper half-space, and study the relationship between the $\sigma$![]() -caloric function and its trace?
-caloric function and its trace?
Based on the above arguments, we pose a conjecture related to the $\sigma$![]() -heat equation as follows.
-heat equation as follows.
Conjecture 2.6 Let $(\mathcal {M},\,d,\,\mu,\,\mathscr {E})$![]() be a complete Dirichlet metric measure space satisfying the doubling condition (2.1) and supporting the Poincaré inequality (2.7). For every $0<\sigma <1$
be a complete Dirichlet metric measure space satisfying the doubling condition (2.1) and supporting the Poincaré inequality (2.7). For every $0<\sigma <1$![]() , a $\sigma$
, a $\sigma$![]() -caloric function $V$
-caloric function $V$![]() satisfies the parabolic Carleson measure condition
satisfies the parabolic Carleson measure condition

if and only if its trace $u$![]() is a BMO function.
is a BMO function.
The parabolic Carleson measure condition in Conjecture 2.6 is different from that in [Reference Fabes and Neri13]. When $(\mathcal {M},\,d,\,\mu )=({{{\mathbb {R}}}^n},\,|\cdot |,\,\mathrm {d} x)$![]() , these two parabolic Carleson measure conditions coincide with each other. The time derivative part $t\partial _tV$
, these two parabolic Carleson measure conditions coincide with each other. The time derivative part $t\partial _tV$![]() in our parabolic Carleson measure condition is essential due to the complex structure of the parabolic equation; see [Reference Li, Ma, Shen, Wu and Zhang26] for example.
in our parabolic Carleson measure condition is essential due to the complex structure of the parabolic equation; see [Reference Li, Ma, Shen, Wu and Zhang26] for example.
3. $\sigma$ -Poisson kernel estimates
-Poisson kernel estimates
In this section, we estimate the time derivative of the $\sigma$![]() -Poisson kernel, and the spatial gradient of the $\sigma$
-Poisson kernel, and the spatial gradient of the $\sigma$![]() -harmonic function.
-harmonic function.
Proposition 3.1 For each integer $k\ge 0,$![]() the $\sigma$
the $\sigma$![]() -Poisson kernel satisfies
-Poisson kernel satisfies
Proof. It follows from the $\sigma$![]() -Poisson formula that
-Poisson formula that
Differentiating both sides of the identity with respect to $t$![]() , using the basic inequality, and invoking the Gaussian upper bound (2.5), we deduce that
, using the basic inequality, and invoking the Gaussian upper bound (2.5), we deduce that

To estimate the local part $I_1$![]() , we conclude by the doubling condition (2.1) that
, we conclude by the doubling condition (2.1) that

For the global part $I_2$![]() , there holds by the doubling condition (2.1) again that
, there holds by the doubling condition (2.1) again that

Collecting the three inequalities above leads to the desired result.
Lemma 3.2 Given a $\sigma$![]() -harmonic function $U,$
-harmonic function $U,$![]() then for each ball $B=B(x_B,\,r_B) \subset \mathcal {M},$
then for each ball $B=B(x_B,\,r_B) \subset \mathcal {M},$![]() it holds that
it holds that
where $T(B)$![]() is the tent over the ball $B$
is the tent over the ball $B$![]() , namely, $T(B)=B\times (0,\,r_B)$
, namely, $T(B)=B\times (0,\,r_B)$![]() .
.
Proof. Take a Lipschitz function $\varphi$![]() on $\mathcal {M}$
on $\mathcal {M}$![]() with ${\rm {\,supp\,}}\varphi \subset 2B$
with ${\rm {\,supp\,}}\varphi \subset 2B$![]() such that $\varphi =1$
such that $\varphi =1$![]() on $B$
on $B$![]() and $|\nabla _x\varphi |\le C/{r_B}$
and $|\nabla _x\varphi |\le C/{r_B}$![]() , and for each $\epsilon \in (0,\,r_B)$
, and for each $\epsilon \in (0,\,r_B)$![]() , take a smooth function $\phi _\epsilon (t)$
, take a smooth function $\phi _\epsilon (t)$![]() on ${\mathbb {R}}$
on ${\mathbb {R}}$![]() such that ${\rm {\,supp\,}}\phi _\epsilon \subset (\epsilon,\,2r_B)$
such that ${\rm {\,supp\,}}\phi _\epsilon \subset (\epsilon,\,2r_B)$![]() , $\phi _\epsilon (t)=1$
, $\phi _\epsilon (t)=1$![]() on $(2\epsilon,\,r_B)$
on $(2\epsilon,\,r_B)$![]() , $|\partial _t\phi _\epsilon (t)|\le C/\epsilon$
, $|\partial _t\phi _\epsilon (t)|\le C/\epsilon$![]() for $t\in (\epsilon,\,2\epsilon )$
for $t\in (\epsilon,\,2\epsilon )$![]() , $|\partial _t\phi _\epsilon (t)|\le C/{r_B}$
, $|\partial _t\phi _\epsilon (t)|\le C/{r_B}$![]() for $t>r_B$
for $t>r_B$![]() . By repeating the Caccioppoli argument, we arrive at
. By repeating the Caccioppoli argument, we arrive at

Using the fact $|\nabla _x\varphi |\le C/{r_B}\le C/{t}$![]() and employing the mean value inequality lead to
and employing the mean value inequality lead to
This combined with the monotonic converges theorem tells us

which completes the proof.
4. Square function estimate
By applying the spectral theory, we give the $L^2$![]() -estimate of the square function in this section.
-estimate of the square function in this section.
Proposition 4.1 Let $U$![]() be a $\sigma$
be a $\sigma$![]() -harmonic function $U$
-harmonic function $U$![]() with trace $u$
with trace $u$![]() . Then it holds that
. Then it holds that

Proof. We only consider the spatial gradient part since the proof of the time part is similar. It follows from the $\sigma$![]() -Poisson formula and Minkowski's inequality that
-Poisson formula and Minkowski's inequality that

By the self-adjointness of the heat semigroup, and the spectral theory, we arrive at

Collecting the two inequalities above leads to the desired result.
5. BMO and Carleson measure: proof of Theorem 2.2
In this section, we give the proof of Theorem 2.2 stated in § 2.
5.1 From BMO to Carleson measure
Lemma 5.1 Let $(\mathcal {M},\,d,\,\mu,\,\mathscr {E})$![]() be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$
be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$![]() admits the diagonal upper estimate (2.3). For every $0<\sigma <1,$
admits the diagonal upper estimate (2.3). For every $0<\sigma <1,$![]() if $u$
if $u$![]() is a BMO function, then its $\sigma$
is a BMO function, then its $\sigma$![]() -harmonic extension $U : \mathcal {M}\times {\mathbb {R}}_+ \to {\mathbb {R}}$
-harmonic extension $U : \mathcal {M}\times {\mathbb {R}}_+ \to {\mathbb {R}}$![]() is well-defined.
is well-defined.
Proof. By the conservation property of the heat semigroup
the $\sigma$![]() -Poisson upper bound (Proposition 3.1), and Hölder's inequality, we arrive at
-Poisson upper bound (Proposition 3.1), and Hölder's inequality, we arrive at

which completes the proof.
Remark 5.2 From the argument used in the above lemma, we see that, if $u$![]() is a BMO function, then
is a BMO function, then
for all $x_0 \in \mathcal {M}$![]() and $\varepsilon >0$
and $\varepsilon >0$![]() .
.
Theorem 5.3 Let $(\mathcal {M},\,d,\,\mu,\,\mathscr {E})$![]() be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$
be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$![]() admits the diagonal upper estimate (2.3). For every $0<\sigma <1$
admits the diagonal upper estimate (2.3). For every $0<\sigma <1$![]() , if $u$
, if $u$![]() is a BMO function, then its $\sigma$
is a BMO function, then its $\sigma$![]() -harmonic extension $U$
-harmonic extension $U$![]() is a Carleson measure. Moreover, there exists a constant $C>0$
is a Carleson measure. Moreover, there exists a constant $C>0$![]() such that
such that
Proof. We follow the argument from [Reference Brazke, Schikorra and Sire2, Proposition 4.1] without the Ahlfors regular condition and the pointwise bound on the gradient of the heat kernel.
Fixed a ball $B\subset \mathcal {M}$![]() , we decompose
, we decompose
where $U_i$![]() is the $\sigma$
is the $\sigma$![]() -harmonic extension of $u_i$
-harmonic extension of $u_i$![]() , respectively, given as
, respectively, given as

It follows from the conservation property of the heat semigroup that
and thus $\nabla _{(x,t)}U_3=0$![]() .
.
In view of Proposition 4.1, we have

It remains to estimate $U_2$![]() . In view of Lemma 3.2, we arrive at
. In view of Lemma 3.2, we arrive at

Denote by $B_k$![]() , $k\in {\mathbb {N}}$
, $k\in {\mathbb {N}}$![]() , the ball concentric around $B$
, the ball concentric around $B$![]() but with radius $4^k$
but with radius $4^k$![]() times the radius of $B$
times the radius of $B$![]() . Since ${\rm {\,supp\,}} u_2\subset \mathcal {M}\setminus 4B$
. Since ${\rm {\,supp\,}} u_2\subset \mathcal {M}\setminus 4B$![]() , we deduce from the $\sigma$
, we deduce from the $\sigma$![]() -Poisson upper bound (Proposition 3.1) that, for all $x\in 2B$
-Poisson upper bound (Proposition 3.1) that, for all $x\in 2B$![]() ,
,

By the triangle inequality and a telescoping sum, it holds that

Using Hölder's inequality and the definition of BMO function, we have
Consequently one has

This implies

which, combined with the estimates of $U_1$![]() and $U_3$
and $U_3$![]() , concludes the proof of Theorem 5.3.
, concludes the proof of Theorem 5.3.
5.2 From Carleson measure to BMO
Theorem 5.4 Let $(\mathcal {M},\,d,\,\mu,\,\mathscr {E})$![]() be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$
be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$![]() admits the diagonal upper estimate (2.3) and the Hölder continuity (2.6). For every $0<\sigma <1,$
admits the diagonal upper estimate (2.3) and the Hölder continuity (2.6). For every $0<\sigma <1,$![]() if the $\sigma$
if the $\sigma$![]() -harmonic extension $U$
-harmonic extension $U$![]() is a Carleson measure, then its trace $u$
is a Carleson measure, then its trace $u$![]() is a BMO function. Moreover, there exists a constant $C>0$
is a BMO function. Moreover, there exists a constant $C>0$![]() such that
such that
To show Theorem 5.4, we need to introduce the definition of the $H^1$![]() -atom. An $L^\infty$
-atom. An $L^\infty$![]() -function $a(x)$
-function $a(x)$![]() is called a $H^1$
is called a $H^1$![]() -atom associated with a ball $B=B(x_B,\,r_B)\subset \mathcal {M}$
-atom associated with a ball $B=B(x_B,\,r_B)\subset \mathcal {M}$![]() , if it satisfies
, if it satisfies
(i) ${\rm {\,supp\,}} a \subset B$
 ;
;(ii) $[a]_{L^\infty } \leq V(x_B,\,r_B)^{-1 }$
 ;
;(iii) $\int _{\mathcal {M}} a \mathrm {d} \mu =0$
 .
.
The following lemma establishes the Calderón reproducing formula with respect to the $H^1$![]() -atom.
-atom.
Lemma 5.5 Let $U,\,A: \mathcal {M}\times {\mathbb {R}}_+\to {\mathbb {R}}$![]() be the $\sigma$
be the $\sigma$![]() -harmonic extension of $u$
-harmonic extension of $u$![]() and $a,$
and $a,$![]() respectively. Then it holds
respectively. Then it holds
Proof. We first claim
In fact, on the one hand, it follows from the $\sigma$![]() -Poisson formula that
-Poisson formula that

On the other hand, by the $\sigma$![]() -Poisson formula again, the definition of the $H^1$
-Poisson formula again, the definition of the $H^1$![]() -atom, and the reverse doubling property (2.2), we arrive at
-atom, and the reverse doubling property (2.2), we arrive at

Therefore, one has
and similarly
as claimed.
Below we verify the Calderón reproducing formula. Employing the integration by parts and using the above decay as $t\to \infty$![]() , we deduce that
, we deduce that

where the second line from the bottom is due to the extension problem for the fractional of $-\Delta _\mathcal {M}$![]() ; see [Reference Baudoin, Lang and Sire1] and [Reference Stinga and Torrea30] for example. One may use the above identity, the integration by parts again, the vanishing properties of $Ut\partial _tA$
; see [Reference Baudoin, Lang and Sire1] and [Reference Stinga and Torrea30] for example. One may use the above identity, the integration by parts again, the vanishing properties of $Ut\partial _tA$![]() and $At\partial _tU$
and $At\partial _tU$![]() at 0 and $\infty$
at 0 and $\infty$![]() , and the fact that $U$
, and the fact that $U$![]() and $A$
and $A$![]() are $\sigma$
are $\sigma$![]() -harmonic, to obtain
-harmonic, to obtain
see also [Reference Brazke, Schikorra and Sire2, Lemma 4.3]. This completes the proof.
Remark 5.6 It is worth noting the proof of the above lemma is analogous to that of [Reference Brazke, Schikorra and Sire2, Lemma 4.3]. However, based on some new observations, we can provide another proof. Indeed note that the structure of the elliptic equation. One obtains

and similarly
Therefore, we arrive at

as desired.
Proof of Theorem 5.4 Step 1. We verify that, if $a(x)$![]() is a $H^1$
is a $H^1$![]() -atom associated with a ball $B=B(x_B,\,r_B)\subset \mathcal {M}$
-atom associated with a ball $B=B(x_B,\,r_B)\subset \mathcal {M}$![]() , then its $\sigma$
, then its $\sigma$![]() -harmonic extension $A$
-harmonic extension $A$![]() satisfies
satisfies
One can write

For the term $I_2$![]() , it follows from Hölder's inequality, the square function estimate (Proposition 4.1) and the definition of the $H^1$
, it follows from Hölder's inequality, the square function estimate (Proposition 4.1) and the definition of the $H^1$![]() -atom that
-atom that

To estimate the term $I_k$![]() , one may invoke the space–time conversion technology (see the proof of Lemma 3.2) to obtain
, one may invoke the space–time conversion technology (see the proof of Lemma 3.2) to obtain

Below we claim that, for all $(x,\,t)\in T(2^{k+1}B)\setminus T(2^{k-2}B)$![]() with $k\ge 3$
with $k\ge 3$![]() ,
,
where $0<\theta \le 1$![]() as in (2.6). Indeed, from the $\sigma$
as in (2.6). Indeed, from the $\sigma$![]() -Poisson formula, it holds
-Poisson formula, it holds

If $d(y,\,x_B)<\sqrt {s}$![]() , then by the cancellation condition of $a(y)$
, then by the cancellation condition of $a(y)$![]()

where the last inequality is due to the Hölder continuity of the heat kernel (2.6). Otherwise $d(y,\,x_B)\ge \sqrt {s}$![]() , there holds from the Gaussian upper bound (2.5) that
, there holds from the Gaussian upper bound (2.5) that

Therefore an argument similar to the one used in Proposition 3.1 shows that

which, together with
provided $y\in B$![]() and $(x,\,t)\in T(2^{k+1}B)\setminus T(2^{k-2}B)$
and $(x,\,t)\in T(2^{k+1}B)\setminus T(2^{k-2}B)$![]() with $k\ge 3$
with $k\ge 3$![]() , implies
, implies

as claimed. By substituting this estimate into (5.1), we obtain

This combined with Hölder's inequality yields

Summing over $k$![]() , we arrive at
, we arrive at
Step 2. Let $f$![]() be a finite linear combinations of the $H^1$
be a finite linear combinations of the $H^1$![]() -atoms, namely,
-atoms, namely,

From the Calderón reproducing formula (Lemma 5.5) and the conclusion of Step 1, it follows that

By taking the infimum over all admissible decompositions of $f$![]() on the both sides of the above inequality, and invoking the fact that the vector space of all finite linear combinations of the $H^1$
on the both sides of the above inequality, and invoking the fact that the vector space of all finite linear combinations of the $H^1$![]() -atoms is dense in the Hardy space $H^1=H^1(\mathcal {M})$
-atoms is dense in the Hardy space $H^1=H^1(\mathcal {M})$![]() , we conclude that, for any $g \in H^1(\mathcal{M})$
, we conclude that, for any $g \in H^1(\mathcal{M})$![]() ,
,
From this and the $H^1$![]() -${\mathrm {BMO}}$
-${\mathrm {BMO}}$![]() dual theorem of Fefferman–Stein (see [Reference Coifman and Weiss7] for instance), it follows that
dual theorem of Fefferman–Stein (see [Reference Coifman and Weiss7] for instance), it follows that
which completes the proof.
6. Limiting behaviours of BMO and Carleson measure
In this section we set a fixed reference point $x_0$![]() in $\mathcal {M}$
in $\mathcal {M}$![]() .
.
Let us introduce the CMO function and the vanishing Carleson measure. A BMO function $u$![]() is said to be in $\mathrm {CMO}=\mathrm {CMO}(\mathcal {M})$
is said to be in $\mathrm {CMO}=\mathrm {CMO}(\mathcal {M})$![]() , the space of functions of vanishing mean oscillation, if $u$
, the space of functions of vanishing mean oscillation, if $u$![]() satisfies the limiting conditions
satisfies the limiting conditions
where

A $\sigma$![]() -harmonic function $U$
-harmonic function $U$![]() with trace $u$
with trace $u$![]() is said to satisfy the vanishing Carleson measure condition, if $U$
is said to satisfy the vanishing Carleson measure condition, if $U$![]() is a Carleson measure, and satisfies the limiting conditions
is a Carleson measure, and satisfies the limiting conditions
where

Roughly speaking, the CMO function and the vanishing Carleson measure are the BMO function and the Carleson measure, which satisfy the vanishing conditions, respectively.
Theorem 6.1 Let $(\mathcal {M},\,d,\,\mu,\,\mathscr {E})$![]() be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$
be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$![]() admits the diagonal upper estimate (2.3) and the Hölder continuity (2.6). If $0<\sigma <1,$
admits the diagonal upper estimate (2.3) and the Hölder continuity (2.6). If $0<\sigma <1,$![]() then $u$
then $u$![]() is a CMO function if and only if $U$
is a CMO function if and only if $U$![]() is a vanishing Carleson measure. Moreover, it holds
is a vanishing Carleson measure. Moreover, it holds
Remark 6.2
(i) Evidently, $\mathrm {CMO}(\mathcal {M})$
 is a proper subspace of $\mathrm {BMO}(\mathcal {M})$
is a proper subspace of $\mathrm {BMO}(\mathcal {M})$ since it is the predual of the Hardy space $H^1(\mathcal {M})$
since it is the predual of the Hardy space $H^1(\mathcal {M})$ ; see [Reference Coifman and Weiss7, Theorem 4.1].
; see [Reference Coifman and Weiss7, Theorem 4.1].(ii) When $(\mathcal {M},\,d,\,\mu )=({{{\mathbb {R}}}^n},\,|\cdot |,\,\mathrm {d} x)$
 , the space $\mathrm {CMO}({{{\mathbb {R}}}^n})$
, the space $\mathrm {CMO}({{{\mathbb {R}}}^n})$ is defined by the closure in the BMO norm of the smooth function with compact support.
is defined by the closure in the BMO norm of the smooth function with compact support.
6.1 From CMO to Carleson measure
Theorem 6.3 Let $(\mathcal {M},\,d,\,\mu,\,\mathscr {E})$![]() be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$
be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$![]() admits the diagonal upper estimate (2.3). For every $0<\sigma <1$
admits the diagonal upper estimate (2.3). For every $0<\sigma <1$![]() , if $u$
, if $u$![]() is a CMO function, then its $\sigma$
is a CMO function, then its $\sigma$![]() -harmonic extension $U$
-harmonic extension $U$![]() is a vanishing Carleson measure. Moreover, there exists a constant $C>0$
is a vanishing Carleson measure. Moreover, there exists a constant $C>0$![]() such that
such that
Proof. By Theorem 5.3, we know
It remains to verify that $U$![]() satisfies the three limiting conditions. We only consider the last one since the proofs of the other two cases are similar. Fixed a ball $B\subset \mathcal {M}$
satisfies the three limiting conditions. We only consider the last one since the proofs of the other two cases are similar. Fixed a ball $B\subset \mathcal {M}$![]() , by the proof of Theorem 5.3, we see that
, by the proof of Theorem 5.3, we see that

For any fixed integer $i$![]() , it follows from $\gamma _2(u)=\gamma _3(u)=0$
, it follows from $\gamma _2(u)=\gamma _3(u)=0$![]() that
that

as $a\to \infty$![]() , and from the definition of BMO that
, and from the definition of BMO that

Therefore, we have

where the constant $C$![]() is independent of $K$
is independent of $K$![]() . As the positive integer $K$
. As the positive integer $K$![]() is arbitrary, we derive that the last limiting condition $\beta _3(U)=0$
is arbitrary, we derive that the last limiting condition $\beta _3(U)=0$![]() holds by letting $K\to \infty$
holds by letting $K\to \infty$![]() . The proof is completed.
. The proof is completed.
6.2 From Carleson measure to CMO
Theorem 6.4 Let $(\mathcal {M},\,d,\,\mu,\,\mathscr {E})$![]() be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$
be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$![]() admits the diagonal upper estimate (2.3) and the Hölder continuity (2.6). For every $0<\sigma <1$
admits the diagonal upper estimate (2.3) and the Hölder continuity (2.6). For every $0<\sigma <1$![]() , if the $\sigma$
, if the $\sigma$![]() -harmonic extension $U$
-harmonic extension $U$![]() is a vanishing Carleson measure, then its trace $u$
is a vanishing Carleson measure, then its trace $u$![]() is a CMO function. Moreover, there exists a constant $C>0$
is a CMO function. Moreover, there exists a constant $C>0$![]() such that
such that
Proof. By Theorem 5.4, we know
It remains to verify that $u$![]() satisfies the three limiting conditions. Let $f$
satisfies the three limiting conditions. Let $f$![]() be a finite linear combinations of $H^1$
be a finite linear combinations of $H^1$![]() -atoms, namely,
-atoms, namely,

From the Calderón reproducing formula (Lemma 5.5), and the conclusion of Step 1 in Theorem 5.4, it follows that

By taking the infimum over all admissible decompositions of $f$![]() on the both sides of the above inequality, and invoking the fact that the vector space of all finite linear combinations of the $H^1$
on the both sides of the above inequality, and invoking the fact that the vector space of all finite linear combinations of the $H^1$![]() -atoms is dense in the Hardy space $H^1(\mathcal{M})$
-atoms is dense in the Hardy space $H^1(\mathcal{M})$![]() , we conclude that, for any $g \in H^1(\mathcal{M})$
, we conclude that, for any $g \in H^1(\mathcal{M})$![]() ,
,

This, combined with the $H^1$![]() -${\mathrm {BMO}}$
-${\mathrm {BMO}}$![]() dual theorem of Fefferman–Stein (see [Reference Coifman and Weiss7] for instance), tells us that
dual theorem of Fefferman–Stein (see [Reference Coifman and Weiss7] for instance), tells us that

Therefore an argument similar to the one used in Theorem 6.3 shows that the limiting conditions
hold, which completes the proof.
7. Final remarks
This paper will end by pointing out some further results. Since it is intended solely as a brief review and not as a rigorous development, the pertinent results are stated without proof.
For each $\alpha >0$![]() , a function $u$
, a function $u$![]() on $\mathcal {M}$
on $\mathcal {M}$![]() is said to be Lipschitz of order $\alpha$
is said to be Lipschitz of order $\alpha$![]() if it satisfies
if it satisfies
where the supremum is taken over all balls $B$![]() containing $x$
containing $x$![]() and $y$
and $y$![]() . In fact, our Theorem 2.2 is also valid for the Lipschitz function. To this end, let us introduce the corresponding $\alpha$
. In fact, our Theorem 2.2 is also valid for the Lipschitz function. To this end, let us introduce the corresponding $\alpha$![]() -Carleson measure of $U$
-Carleson measure of $U$![]() as follows:
as follows:

The following result is the Lipschitz version of Theorem 2.2.
Theorem 7.1 Let $(\mathcal {M},\,d,\,\mu,\,\mathscr {E})$![]() be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$
be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$![]() admits the diagonal upper estimate (2.3) and the Hölder continuity (2.6). If $0<\alpha <\theta /n$
admits the diagonal upper estimate (2.3) and the Hölder continuity (2.6). If $0<\alpha <\theta /n$![]() and $0<\sigma <1$
and $0<\sigma <1$![]() , then $u$
, then $u$![]() is a Lipschitz function of order $\alpha$
is a Lipschitz function of order $\alpha$![]() if and only if $U$
if and only if $U$![]() is an $\alpha$
is an $\alpha$![]() -Carleson measure. Moreover, it holds
-Carleson measure. Moreover, it holds
When $0<\alpha <\theta /n$![]() , the Lipschitz space ${\mathrm {Lip}(\alpha )}={\mathrm {Lip}(\alpha )}(\mathcal {M})$
, the Lipschitz space ${\mathrm {Lip}(\alpha )}={\mathrm {Lip}(\alpha )}(\mathcal {M})$![]() coincides with the Campanato space $\mathrm {Cam}(\alpha )=\mathrm {Cam}(\alpha )(\mathcal {M})$
coincides with the Campanato space $\mathrm {Cam}(\alpha )=\mathrm {Cam}(\alpha )(\mathcal {M})$![]() as follows:
as follows:

which is the dual of Hardy space $H^p(\mathcal {M})$![]() provided $\alpha =1/p-1$
provided $\alpha =1/p-1$![]() ; see [Reference Coifman and Weiss7] for example. Note that $\mathrm {Cam}(0)={\mathrm {BMO}}$
; see [Reference Coifman and Weiss7] for example. Note that $\mathrm {Cam}(0)={\mathrm {BMO}}$![]() . Therefore the Campanato norm $[\cdot ]_{\mathrm {Cam}(\alpha )}$
. Therefore the Campanato norm $[\cdot ]_{\mathrm {Cam}(\alpha )}$![]() unifies the BMO norm $[\cdot ]_{{\mathrm {BMO}}}$
unifies the BMO norm $[\cdot ]_{{\mathrm {BMO}}}$![]() and the Lipschitz norm $[\cdot ]_{\mathrm {Lip}(\alpha )}$
and the Lipschitz norm $[\cdot ]_{\mathrm {Lip}(\alpha )}$![]() by assigning different values to $\alpha$
by assigning different values to $\alpha$![]() . Similar to the definition of $\mathrm {CMO}$
. Similar to the definition of $\mathrm {CMO}$![]() in § 6, we can introduce the vanishing $\mathrm {BMO}(\alpha )$
in § 6, we can introduce the vanishing $\mathrm {BMO}(\alpha )$![]() function and the vanishing $\alpha$
function and the vanishing $\alpha$![]() -Carleson measure, respectively. The details will be omitted.
-Carleson measure, respectively. The details will be omitted.
The following result is the Campanato version of Theorems 2.2 and 6.1.
Theorem 7.2 Let $(\mathcal {M},\,d,\,\mu,\,\mathscr {E})$![]() be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$
be a complete Dirichlet metric measure space satisfying the doubling condition (2.1). Assume that the heat kernel $h_t(x,\,y)$![]() admits the diagonal upper estimate (2.3) and the Hölder continuity (2.6). If $0\le \alpha <\theta /n$
admits the diagonal upper estimate (2.3) and the Hölder continuity (2.6). If $0\le \alpha <\theta /n$![]() and $0<\sigma <1$
and $0<\sigma <1$![]() , then $u$
, then $u$![]() is a (vanishing) $\mathrm {Cam}(\alpha )$
is a (vanishing) $\mathrm {Cam}(\alpha )$![]() function if and only if $U$
function if and only if $U$![]() is a (vanishing) $\alpha$
is a (vanishing) $\alpha$![]() -Carleson measure. Moreover, it holds
-Carleson measure. Moreover, it holds
Acknowledgements
Bo Li thanks Denis Brazke for many helpful discussions during the preparation of this work. Bo Li is supported by NNSF of China (12201250) and NSF of Zhejiang Province (LQ23A010007). Jinxia Li is supported by NNSF of China (12101199), NSF of Henan Province (232300421142), and the Doctoral Fund of Henan Polytechnic University (B2021-54). Qingze Lin is supported by NNSF of China (11801094). Bolin Ma is supported by NNSF of China (11871452).