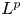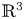Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Govindan Sheri, Aswin
2024.
$$L^2$$ Estimates for a Nikodym Maximal Function Associated to Space Curves.
Journal of Fourier Analysis and Applications,
Vol. 30,
Issue. 1,