XXIX.—On a Problem in Correlated Errors

Extract

The problem with which this paper is concerned arose in the discussion of a series of chronometric observations, but it is of more general application, and is capable of wide extension. Pairs of readings (x_i y_i) were taken at times t_i, i = 1, 2, …, n. These readings were known to be affected by respective errors (ξ_i η_i) from sources different but possessing some common part. It was important to have an estimate of the consequent correlation and to assess its precision. The assumptions made in the particular experiment were that x and y were both linear in t, representable by x = a₀ + a₁t, y = b₀ + b₁t, and that the distributions of error in x and y were normal. The parameters a₀ and a₁, b₀ and b₁ were therefore obtained from two separate sets of normal equations, and the unknown correlation was then estimated from the sum of products of corresponding residuals u_i, v_i, one from each set. In the corresponding situation in n samples (x_i,y_i) from a bivariate normal distribution the mean value of 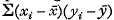is (n − 1) ρσ₁σ₂, where σ₁², σ₂² are the variances of x and y and ρσ₁σ₂ is their product moment. One might therefore anticipate, by analogy, that in the present case the mean value of Σu_iv_i would be (n − 2)ρσ₁σ₂. So indeed it proves to be, and the sampling variance of Σu_iv_i conforms likewise with standard results; but it is desirable, by an extension of the problem, both to see why this is so and to take notice of cases where the analogy fails to hold.