1 INTRODUCTION
The distance of an astronomical object plays an important role in deriving absolute magnitudes of stars and determining the three-dimensional structure of the Milky Way galaxy. The distance to a star can be evaluated by trigonometric or photometric parallaxes. Trigonometric parallaxes are available only for nearby stars where Hipparcos (ESA 1997) is the main supplier for the data. For stars at large distances, the use of photometric parallaxes is unavoidable. In other words, the study of the Galactic structure is strictly tied to the precise determination of absolute magnitudes.
Different methods can be used for absolute magnitude determination where most of them are devoted to dwarfs. The method used in the Strömgren’s uvby − β (Nissen & Schuster Reference Nissen and Schuster1991) and in the UBV (Laird, Carney, & Latham Reference Laird, Carney and Latham1988) photometry depends on the absolute magnitude offset from a standard main sequence. In recent years, the derivation of absolute magnitudes has been carried out by means of colour–absolute magnitude diagrams of some specific clusters whose metal abundances are generally adopted as the mean metal abundance of a Galactic population, such as thin, thick discs and halo. The studies of Phleps et al. (Reference Phleps, Meisenheimer, Fuchs and Wolf2000) and Chen et al. (Reference Chen2001) can be given as examples. A slightly different approach is that of Siegel et al. (Reference Siegel, Majewski, Reid and Thompson2002) where two relations, one for stars with solar-like abundances and another for metal-poor stars, were derived between MR and the colour index R − I, where MR is the absolute magnitude in the R filter of the Johnson system. For a star of given metallicity and colour, absolute magnitude can be estimated by the linear interpolation of two ridgelines and by means of linear extrapolation beyond the metal-poor ridgeline.
The most recent procedure used for absolute magnitude determination consists of finding the most likely values of the stellar parameters, given the measured atmospheric ones, and the time spent by a star in each region of the H–R diagram. In practice, researchers select the subset of isochrones with [M/H]±Δ[M/H], where Δ[M/H] is the estimated error on the metallicity, for each set of derived T eff, log g, and [M/H]. Then a Gaussian weight is associated with each point of the selected isochrones, which depends on the measured atmospheric parameters and the considered errors. This criterion allows the algorithm to select only the points whose values are closed by the pipeline of the corresponding survey such as the Radial Velocity Experiment (RAVE). For details of this procedure, we refer to the works of Breddels et al. (Reference Breddels2010) and Zwitter et al. (Reference Zwitter2010). This procedure is based on many parameters. Hence, it provides absolute magnitudes with high accuracy. Also, it can be applied to both dwarf and giant stars simultaneously.
In Karaali et al. (Reference Karaali, Karataş, Bilir, Ak and Hamzaoğlu2003), we presented a procedure for the photometric parallax estimation of dwarf stars which depends on the absolute magnitude offset from the main sequence of the Hyades cluster. Bilir et al. (Reference Bilir, Karaali, Ak, Yaz, Cabrera-Lavers and Coşkunoğlu2008) obtained the absolute magnitude calibrations of the thin disc main-sequence stars in the optical (MV ) and the near-infrared (MJ ) bands using the recent reduced Hipparcos astrometric data (van Leeuwen Reference van Leeuwen2007). Bilir et al. (Reference Bilir, Karaali, Ak, Coşkunoğlu, Yaz and Cabrera-Lavers2009) derived a new luminosity colour relation based on trigonometric parallaxes for the thin disc main-sequence stars with the Sloan Digital Sky Survey (SDSS) photometry. In Karaali et al. (Reference Karaali, Bilir and Yaz2012, hereafter Paper I), we used a similar procedure for the absolute magnitude estimation of red giants by using the V 0, (B − V)0 apparent magnitude–colour diagrams of Galactic clusters with different metallicities. Here, we will estimate absolute magnitudes for red giants with g 0, (g − r)0 colour–magnitude diagrams. Thus, we will give a chance to the researchers who work with the SDSS photometry (Fukugita et al. Reference Fukugita, Ichikawa, Gunn, Doi, Shimasaku and Schneider1996) for a direct estimation of the absolute magnitudes of the red giants. The outline of the paper is as follows. We present the data in Section 2. The procedure used for calibration is given in Section 3, and Section 4 is devoted to summary and discussion.
2 DATA
Six clusters with different metallicities, i.e. M92, M13, M3, M71, NGC 6791, and NGC 2158, were selected for our programme. The gʹ and rʹ magnitudes for the first five clusters were taken from Clem, Vanden Berg, & Stetson (Reference Clem, Berg and Stetson2008). They observed the clusters in the uʹgʹrʹiʹzʹ passbands with the MegaCam wide-field imager on the Canada–France–Hawaii Telescope. However, the g and r magnitudes for the cluster NGC 2158 were provided by the observation of the cluster on instrumental ugriz passbands (Smolinski et al. Reference Smolinski2011). The two sets of passbands are very similar, but not quite identical. We derived the following equations by the transformations of Rider et al. (Reference Rider, Tucker, Smith, Stoughton, Allam and Neilsen2004) and transformed the gʹ and gʹ − rʹ data of Chem et al. (Reference Clem, Berg and Stetson2008) to the g and g − r data. Thus, we obtained a homogeneous set of data for an absolute magnitude calibration:
The range of the metallicity of the clusters given in iron abundance is −2.15≤[Fe/H]≤+0.37 dex. The (g − Mg )0 true distance modulus, E(B − V) colour excess, and [Fe/H] iron abundance for M92, M13, M3, M71, and NGC 6791 are taken from the authors given in the second order of the reference list in Table 1, whereas those for NGC 2158 are those of Smolinski et al. (Reference Smolinski2011). The g and g − r data are presented in Table 2. We adopted R = AV /E(B − V) = 3.1 to convert the colour excess to the extinction. Although different numerical values appeared in the literature for specific regions of our Galaxy, a single value is applicable everywhere. Then, we used the equations Ag /AV = 1.199 and Ar /AV = 0.858, Ai /AV = 0.639 of Fan (Reference Fan1999) to evaluate the total extinctions in Ag , Ar , and Ai . Then, the equation for the selective extinction in SDSS is E(g − r)/AV = 0.341.
Table 1. Data for the Clusters Used in Our Work

References. (1) Chem et al. (Reference Clem, Berg and Stetson2008); (2) Gratton et al. (Reference Gratton, Pecci, Carretta, Clementini, Corsi and Lattanzi1997); (3) Harris (Reference Harris1996, Reference Harris2010); 4) Hodder et al. (Reference Hodder, Nemec, Richer and Fahlman1992); (5) Sandage, Lubin, & VandenBerg (Reference Sandage, Lubin and VandenBerg2003); (6) Smolinski et al. (Reference Smolinski2011).
Table 2. Original gʹ, gʹ − rʹ, rʹ − iʹ and the Transformed g 0, (g − r)0 Data for the Clusters M92, M13, M3, M71, and NGC 6791. The g Magnitudes and g − r Colours for the Cluster NGC 2158 Are Original

The uʹgʹrʹiʹzʹ magnitudes for the clusters in Chem et al. (Reference Clem, Berg and Stetson2008) were given in ridgelines. We plotted the transformed g 0, (g − r)0 sequences on a diagram for each cluster and identified the giants by means of their positions in the diagram. However, the fiducial red giant sequence of the cluster NGC 2158 given in Table 2, supplied by binning the transformed g magnitudes and g − r colours of 54 red giants in Smolinski et al. (Reference Smolinski2011). We then fitted the fiducial sequence of giants to high-degree polynomials. A fourth-degree polynomial was sufficient for the clusters NGC 6791 and NGC 2158, whereas a fifth-degree polynomial was necessary for a good correlation coefficient for the clusters M92, M13, M3, and M71. The calibration of g 0 is as follows:
The numerical values of the coefficients ai (i = 0, 1, 2, 3, 4, 5) are given in Table 3 and the corresponding diagrams are presented in Figure 1. The (g − r)0 interval in the second line of the table denotes the range of (g − r)0 available for each cluster.
Table 3. Numerical Values of the Coefficients ai (i = 0, 1, 2, 3, 4, 5)


Figure 1. g 0, (g − r)0 colour–apparent magnitude diagrams for six Galactic clusters used for the absolute magnitude calibration.
3 THE PROCEDURE
3.1 Absolute Magnitude as a Function of Metallicity
The procedure consists of a slight modification of the procedure in Paper I. There, we calibrated the absolute magnitude offsets from the fiducial red giant sequence of a standard cluster (M5) for a given colour index as a function of metallicity offsets. However, here we calibrated the absolute magnitudes directly to metallicities for a given (g − r)0 colour. Thus, one does not need to calculate an absolute magnitude offset from a standard cluster and then to add it to the corresponding absolute magnitude of the standard cluster for the final absolute magnitude estimation. Also, the new procedure decreased the number of columns in the final tables. We estimated the Mg absolute magnitudes for the (g − r)0 colours given in Table 4 for the cluster sample in Table 1 by combining the g 0 apparent magnitudes evaluated by Equation (2) and the true distance modulus (μ0) of the cluster in question, i.e.
Table 4. Mg Absolute Magnitudes Estimated for a Set of (g − r)0 Colours for Six Galactic Clusters Used in the Calibration

Then, we plotted the absolute magnitudes versus (g − r)0 colours. Figure 2 shows that the absolute magnitude is colour and metallicity dependent. It increases (algebraically) with increasing metallicity and decreasing colour.

Figure 2. Mg , (g − r)0 colour–absolute magnitude diagrams for six clusters used for the absolute magnitude calibration.
Now, we can fit the Mg absolute magnitudes to the corresponding [Fe/H] metallicity for a given (g − r)0 colour index and obtain the required calibration. This is carried out for the colour indices (g − r)0 = 0.60, 0.75, 0.95, 1.05, and 1.20 just for the exhibition of the procedure. The results are given in Table 5 and Figure 3. The absolute magnitudes in the colour indices (g − r)0 = 0.60, 0.75, 1.05, and 1.20 could be fitted to a second-degree polynomial with (squared) correlation coefficients R 2 ≥ 0.9993. The range of the metallicity for the colour index (g − r)0 = 0.95 is the highest, i.e. −2.15≤[Fe/H]≤0.37 dex. Hence, a third-degree polynomial was necessary for the high (squared) correlation coefficient R 2 = 0.9994. The high correlation coefficients indicate accurate absolute magnitude estimation.
Table 5. Mg Absolute Magnitudes and [Fe/H] Metallicities for Five (g − r)0 Intervals


Figure 3. Calibration of the absolute magnitude Mg as a function of metallicity [Fe/H] for five colour indices.
This procedure can be applied to any (g − r)0 colour interval for which the sample clusters are defined. The (g − r)0 domain of the clusters is different. Hence, we adopted this interval in our study as 0.45 ≤ (g − r)0 ≤ 1.30 where at least two clusters are defined, and we evaluated Mg absolute magnitudes for each colour. Then, we combined them with the corresponding [Fe/H] metallicities and obtained the final calibrations. The metallicities of the clusters M13 and M3 are close to each other, i.e. [Fe/H] −1.41 and −1.50 dex, respectively. Hence, we adopted the mean of the data of these clusters in the absolute magnitude calibration. The general form of the equation for the calibrations is as follows:
Note that Mg could be fitted in terms of metallicity by different degrees of polynomials. A cubic polynomial was necessary only for a limited interval, i.e. 0.85 ≤ (g − r)0 ≤ 0.96, for a high correlation coefficient. However, a quadratic or linear polynomial was sufficient for most of the colour indices, i.e. 0.45 ≤ (g − r)0 ≤ 0.84 and 0.97 ≤ (g − r)0 ≤ 1.30, for a high correlation coefficient. The degree of the polynomial depends mainly on the metallicity range considered. However, in spite of the large domain in metallicity, −2.15 ≤[Fe/H]≤ 0.37 dex, absolute magnitudes for the colour index interval 0.97 ≤ (g − r)0 ≤ 1.15 could be fitted by quadratic polynomials with high correlation coefficients. Then, one can say that the data presented for different clusters are homogeneous and our procedure promises accurate absolute magnitude estimation. The absolute magnitudes estimated via Equation (3) for 86 (g − r)0 colour indices and the corresponding bi (i = 0, 1, 2, 3) coefficients are given in Table 6. However, the diagrams for the calibrations are not given in the paper because of space constraints. One can use any data set taken from Table 6 depending on the desire for accuracy, and apply it to stars whose iron abundances are available.
Table 6. Mg Absolute Magnitudes Estimated for Six Galactic Clusters and the Numerical Values of bi (i = 0, 1, 2, 3) Coefficients in Equation (3)

Notes. The absolute magnitudes and metallicities of the clusters M13 and M3 were combined in the evaluation of bi coefficients. The last column gives the range of the metallicity [Fe/H] (dex) for the star whose absolute magnitude would be estimated. R 2 is the square of the correlation coefficient.
The calibration of Mg in terms of [Fe/H] is carried out for the colour interval 0.45 ≤ (g − r)0 ≤ 1.30 mag in steps of 0.01 mag. A small step is necessary to isolate an observational error on g − r plus an error due to reddening. The origin of the mentioned errors shows the trend of the red giant branch (RGB) sequence. As it is very steep, a small error in g − r implies a large change in the absolute magnitude.
Iron abundance, [Fe/H], is not the only parameter that determines the chemistry of the star but α enhancement, [α/Fe], is also equally important. However, as stated in Paper I, there is a correlation between two sets of abundances. Hence, we do not expect any considerable change in the numerical values of Mg in the case of addition of the α enhancement term in Equation (4).
3.2 Application of the Method
We applied the method to five clusters with different metallicities, i.e. M15, M53, M5, NGC 5466, and NGC 7006, as explained in the following. The reason of choosing clusters instead of individual field giants is that clusters provide absolute magnitudes for comparison with the ones estimated by our method. The distance modulus, colour excess, and metallicity of the clusters are given in Table 7, whereas the g magnitudes and g − r colours are presented in Table 8 and they are calibrated in Figure 4. The g and g − r data of the clusters are taken from An et al. (Reference An2008). Also, the colour excesses and the distance moduli of all clusters and the metallicities of M15 and M5 are taken from An et al. (Reference An2008). However, the metallicities of three clusters, M53, NGC 5466, and NGC 7006, are taken from the authors cited in Table 7. An et al. (Reference An2008) claimed [Fe/H] = −1.99 and −1.48 dex for the clusters M53 and NGC 7006, respectively. However, the metallicities in Santos & Piatti (Reference Santos and Piatti2004), i.e. [Fe/H] = −1.88 and −1.35 dex, provide more accurate absolute magnitudes. The metallicities cited by An et al. (Reference An2008) and Rosenberg et al. (Reference Rosenberg, Saviane, Piotto and Aparicio1999) for the cluster NGC 5466 are [Fe/H] = −2.22 and −2.13±0.36 dex, respectively. Here again, the metallicity in Rosenberg et al. (Reference Rosenberg, Saviane, Piotto and Aparicio1999) plus its error, i.e. [Fe/H] = −1.17 dex, provides more accurate absolute magnitudes.
Table 7. Data for the Clusters Used for the Application of the Method
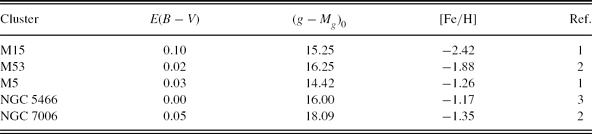
References. (1) An et al. (Reference An2008); (2) Santos & Piatti (Reference Santos and Piatti2004); (3) Rosenberg et al. (Reference Rosenberg, Saviane, Piotto and Aparicio1999).
Table 8. Fiducial Giant Sequences for the Galactic Clusters Used in the Application of the Procedure


Figure 4. g 0, (g − r)0 colour–apparent magnitude diagrams for the Galactic clusters used for the application of the procedure.
We evaluated the Mg absolute magnitude by Equation (4) for a set of (g − r)0 colour indices where the clusters are defined. The results are presented in Table 9. The columns refer to (1) (g − r)0 colour index; (2) (Mg )cl, absolute magnitude for a cluster estimated by its colour–magnitude diagram; (3) (Mg )ev, the absolute magnitude estimated by the procedure; and (4) ΔM, absolute magnitude residuals. Also, the metallicity for each cluster is indicated near the name of the cluster. The differences between the absolute magnitudes estimated by the procedure presented in this study and those evaluated via the colour magnitudes of the clusters (the residuals) lie between −0.28 and +0.43 mag. However, the range of 94% of the absolute magnitude residuals is shorter, i.e. 0.1 < Mg ≤ 0.4 mag. The mean and the standard deviation of the residuals are 〈ΔM〉 = 0.169 and σ = 0.140 mag, respectively. The distribution of the residuals is given in Table 10 and Figure 5.
Table 9. Absolute Magnitudes [(Mg )ev] and Residuals (ΔM) estimated by the Procedure Explained in Our Work. (Mg )cl Denotes the Absolute Magnitude Evaluated by Means of the Colour–Magnitude Diagram of the Cluster

Table 10. Distribution of the Residuals. N Denotes the Number of Stars
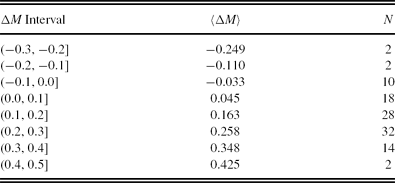

Figure 5. Histogram of the residuals.
The absolute magnitudes on the RGB at a given colour and metallicity do not change linearly or quadratically with age. Instead, the absolute magnitudes become rapidly fainter for young (and massive) stars with a certain g − r and [Fe/H], but shows virtually the same absolute magnitude for all old stars, i.e. t > 6 Gyr. That is, the gradient of the absolute magnitude with respect to a given colour and metallicity is greater for a young star than for an old one.
4 SUMMARY AND DISCUSSION
We presented an absolute magnitude calibration for giants based on the colour–magnitude diagrams of six Galactic clusters with different metallicities, i.e. M92, M13, M3, M71, NGC 6791, and NGC 2158. All the clusters were observed in the uʹgʹrʹiʹzʹ passbands by Chem et al. (Reference Clem, Berg and Stetson2008), except the cluster NGC 2158 which is observed in the ugriz passbands by Smolinski et al. (Reference Smolinski2011). We used the transformations of Rider et al. (Reference Rider, Tucker, Smith, Stoughton, Allam and Neilsen2004) and transformed the gʹ and gʹ − rʹ data in Chem et al. (Reference Clem, Berg and Stetson2008) to the g and g − r data. Thus, we obtained a homogeneous set of data in the SDSS system for absolute magnitude calibration. We combined the calibrations between g 0 and (g − r)0 for each cluster with their true distance modulus and evaluated a set of absolute magnitudes for the (g − r)0 range of each clusters. Then, we fitted the Mg absolute magnitudes in terms of iron metallicity, [Fe/H], by different degrees of polynomials for a given (g − r)0 colour index. Our absolute magnitude calibrations cover the range 0.45 ≤ (g − r)0 ≤ 1.30. However, not all the clusters could be considered for each (g − r)0 colour index in this interval due to different (g − r)0 domains of the clusters. The limited interval that all the clusters were considered is 0.85 ≤ (g − r)0 ≤ 0.96. Also, this interval is the unique interval where the highest degree (n = 3) of the polynomial was fitted. A linear or quadratic polynomial was sufficient for the colour intervals 0.45 ≤ (g − r)0 ≤0.84 and 0.97≤ (g − r)0 ≤ 1.30 for a high correlation coefficient.
We applied the procedure to another set of the Galactic cluster, i.e. M15, M53, M5, NGC 5466, and NGC 7006. The reason for this choice is that a cluster provides absolute magnitude for comparison with those estimated by our procedure. We used the equations of Fan (Reference Fan1999) for de-reddening of the colour and magnitudes, and the calibration in Equation (4) for the evaluation of a set ofMg absolute magnitudes for each cluster in their (g − r)0 domain.
We compared the absolute magnitudes estimated by this procedure with those evaluated via a combination of the fiducial g 0, (g − r)0 sequence and the true distance modulus for each cluster. The residuals lie between −0.28 and +0.43 mag. However, the range of 94% of them is smaller, i.e. 0.1 < Mg ≤ 0.4 mag. The mean and the standard deviation of all the residuals are 〈ΔM〉 = 0.169 and σ = 0.140 mag, respectively. The range of the residuals in Paper I was greater than the one in this study, i.e. −0.61 < ΔMV < +0.66 mag. Also, the mean and the standard deviation of the residuals in a smaller range, −0.4 ≤ ΔM ≤ +0.4, which consists of 91% of the residuals, were 〈ΔM〉 = 0.05 and σ = 0.19 mag, respectively. A comparison of the statistical results presented in two studies shows that there is a small improvement in the results of this study with respect to the former one. As claimed in Paper I, there was an improvement in the results therein with respect to those of Hog & Flynn (Reference Hog and Flynn1998). Hence, the same improvement holds for this study. The same improvement also holds for the work of Ljunggren & Oja (Reference Ljunggren and Oja1966).
Although age plays an important role in the trend of the fiducial sequence of the RGB, we have not used it as a parameter in the calibration of absolute magnitude. Another problem may originate from the red clump (RC) stars. These stars lie very close to the RGB but they present a completely different group of stars. Table 10 and Figure 5 summarise how reliable are our absolute magnitudes. If age and possibly the mix with RC stars would affect our results, this should show up, i.e. the range of the residuals would be greater and their distributions would be multimodal. However, in our study their range is small and the histogram of the residuals in Figure 5 is almost symmetric, resembling a Gaussian distribution. In addition, note that the fiducial sequences used in our study were properly selected as RGBs. However, researchers should identify and exclude the RC stars when they apply our calibrations to the field stars.
The accuracy of the estimated absolute magnitudes depends mainly on the accuracy of the metallicity. We altered the metallicity by [Fe/H]+Δ[Fe/H] in the evaluation of the absolute magnitudes by the procedure presented in our study and checked its effect on the absolute magnitude. We adopted [Fe/H] = −1.88, −1.26, −1.17, −1.35 dex and Δ[Fe/H] = 0.05, 0.10, 0.15, 0.20 dex and re-evaluated the absolute magnitudes for 14 (g − r)0 colour indices for this purpose. The differences between the absolute magnitudes evaluated in this way and the corresponding ones evaluated without Δ[Fe/H] increments are given in Table 11. The maximum difference in the absolute magnitude is ~0.3 mag corresponding to the metallicity increment Δ[Fe/H] = 0.20 dex. The mean error in metallicity for 42 globular and 33 open clusters in the catalogue of Santos & Piatti (Reference Santos and Piatti2004) is σ = 0.19 dex. If we assume the same error for the field stars, the probable error in Mg magnitudes would be less than 0.3 mag.
Table 11. Absolute Magnitudes Estimated by Altering the Metallicity as [Fe/H]+Δ[Fe/H]

Notes. The numerical values of [Fe/H] are indicated in the last column. The absolute magnitudes in column (1) are the original values taken from Table 9, whereas those in columns (2)–(5) correspond to the increments 0.05, 0.10, 0.15, and 0.20 dex. The differences between the original absolute magnitudes and those evaluated by means of the metallicity increments are given in columns (6)–(9).
The absolute magnitude could be calibrated as a function of ultraviolet excess, instead of metallicity. However, the ultraviolet magnitudes cannot be provided easily. However, metallicity can be derived by different methods, such as by means of atmospheric model parameters of a star, a procedure which is applied rather extensively in large surveys such as RAVE. In such cases, one needs to transform the calibration from SDSS to the system in question. The age is a secondary parameter for the old clusters and does not influence much the position of their RGBs. The youngest cluster in our paper is NGC 2158, with age 2 Gyr (Carraro, Girardi & Marigo Reference Carraro, Girardi and Marigo2002). However, the field stars may be much younger. Note that the derived relations are applicable to stars older than 2 Gyr. For clarification of this argument, let a star younger than 2 Gyr be with colour 0.55 < (g − r)0 < 0.86 mag. This star will be more metal-rich than the stars in the cluster NGC 2158 and, according to the positions of the colour–absolute magnitude diagrams of the clusters in Figure 2, it will be absolutely fainter than a star in the cluster NGC 2158 of the same colour. Then, one needs to extrapolate the corresponding absolute magnitude–metallicity diagram in Figure 3 for its absolute magnitude evaluation (one of the two panels at the top depending on its colour). However, extrapolation may result in erroneous absolute Mg magnitudes.
We conclude that the Mg absolute magnitudes of the red giants can be estimated with an accuracy of ΔM ≤ 0.3 mag, provided that their [Fe/H] metallicities are known.
ACKNOWLEDGMENTS
We thank to the anonymous reviewer for comments. This research has made use of NASA’s Astrophysics Data System and the SIMBAD database, operated at CDS, Strasbourg, France.



















