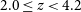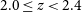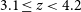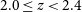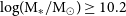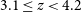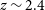1. Introduction
Galaxies are some of the most complex bodies in the universe. With different structural features such as bulges, arms, discs, bars, tidal tails and warps, the apparent ‘zoo’ of optical morphologies in the local universe has long motivated questions about how galaxies have evolved over cosmic time. The processes of galaxy formation and evolution appear to depend on the proximity of neighbouring galaxies, more commonly referred to as ‘environment’. Galaxy environments, such as groups and clusters, are some of the densest regions in the universe and represent an example of external processes responsible for accelerating galaxy evolution. Galaxies in overdense environments are generally thought to have their evolutions influenced by (1) large-scale galaxy-galaxy interactions like merger activity (e.g. Lin et al. Reference Lin2008, Reference Lin2010; Jian et al. Reference Jian2017) and harassment (e.g. Moore et al. Reference Moore, Katz, Lake, Dressler and Oemler1996; Moore, Lake, & Katz Reference Moore, Lake and Katz1998; Dutta et al. Reference Dutta, Begum, Bharadwaj and Chengalur2010), or (2) hydrodynamical interactions like ram pressure stripping (e.g. Gunn & Gott Reference Gunn and Gott1972; Abadi, Moore, & Bower Reference Abadi, Moore and Bower1999; Fujita Reference Fujita2001; Hester Reference Hester2006), viscous stripping (e.g. Nulsen Reference Nulsen1982) and other gas depleting processes (e.g. Bekki, Couch, & Shioya Reference Bekki, Couch and Shioya2002; Kawata & Mulchaey Reference Kawata and Mulchaey2008; Peng et al. Reference Peng, Maiolino and Cochrane2015; Maier et al. Reference Maier2016). Early galaxy environment studies (e.g. Oemler Reference Nulsen1974; Dressler 1980; Postman & Geller Reference Postman and Geller1984) found that elliptical or bulge-like morphologies dominate regions like dense cluster cores; a correlation now known as the morphology-density relation, while other work has argued that environment affects other galaxy properties like age (e.g. Deng &Wen Reference Deng and Wen2020) and star formation activity (e.g. Hashimoto et al. Reference Hashimoto, Oemler, Lin and Tucker1998; Cooper et al. Reference Cooper2007; Vulcani et al. Reference Vulcani2010; Rasmussen et al. Reference Rasmussen2012).
While galaxy environments in the low redshift universe have been studied extensively, the role that environment plays in high redshift galaxy evolution remains poorly understood. For example, there is strong evidence that quiescent or passive galaxies are preferentially found in dense environments towards lower redshifts (e.g.Wijesinghe et al. Reference Wijesinghe2012; Lin et al. Reference Lin2014; Damjanov et al. Reference Damjanov, Zahid, Geller and Hwang2015; Davies et al. Reference Davies2016; Allen et al. Reference Allen2016; Jian et al. Reference Jian2017), but at
![]() $z\sim1-1.5$
this trend appears to reverse (e.g. Lin et al. Reference Lin2016). This effect is known as the Butcher–Oemler effect (Butcher & Oemler Reference Butcher1978), which states that the fraction of blue, star-forming galaxies in overdense environments increases with redshift. However, some high redshift measurements (e.g. Allen et al. Reference Allen2016; Kawinwanichakij et al. Reference Kawinwanichakij2017) disagree, where comparisons between low- and high-density environments reveals the latter to host a larger fraction of red, passive galaxies.
$z\sim1-1.5$
this trend appears to reverse (e.g. Lin et al. Reference Lin2016). This effect is known as the Butcher–Oemler effect (Butcher & Oemler Reference Butcher1978), which states that the fraction of blue, star-forming galaxies in overdense environments increases with redshift. However, some high redshift measurements (e.g. Allen et al. Reference Allen2016; Kawinwanichakij et al. Reference Kawinwanichakij2017) disagree, where comparisons between low- and high-density environments reveals the latter to host a larger fraction of red, passive galaxies.
Furthermore, there is evidence to suggest that the relationship between passive galaxy fractions and environment is closely correlated with the relation between star formation rate (SFR) and density (e.g. Bolzonella et al. Reference Bolzonella2010; Peng et al. Reference Peng2010; Deng, Chen, & Jiang Reference Deng, Chen and Jiang2011; Lu et al. Reference Lu, Gilbank, McGee, Balogh and Gallagher2012), whereby an increase in passive galaxy fractions drives the suppression of star formation in dense environments in the local universe. Analogous to the work of Butcher & Oemler (Reference Butcher1978), some studies (e.g. Elbaz et al. Reference Elbaz2007; Cooper et al. Reference Cooper2007) have argued that
![]() $z\sim1$
represents a ‘transition point’, where regions of high density instead have enhanced star formation activity. In support of this picture, Patel et al. (Reference Patel, Kelson, Holden, Franx and Illingworth2011) find low star formation activity and high quiescent fractions in groups and a cluster at redshifts
$z\sim1$
represents a ‘transition point’, where regions of high density instead have enhanced star formation activity. In support of this picture, Patel et al. (Reference Patel, Kelson, Holden, Franx and Illingworth2011) find low star formation activity and high quiescent fractions in groups and a cluster at redshifts
![]() $0.6<z<0.9$
while at higher redshifts (e.g.
$0.6<z<0.9$
while at higher redshifts (e.g.
![]() $z\geq1.5$
; Tran et al. Reference Tran2010; Hayashi et al. Reference Hayashi2010, Reference Hayashi, Kodama, Koyama, Tadaki and Tanaka2011; Strazzullo et al. Reference Strazzullo2013; Santos et al. Reference Santos2015; Wang et al. Reference Wang2016), overdense environments tend to have enhanced star formation activity. This picture is not clear-cut though, with some work finding that
$z\geq1.5$
; Tran et al. Reference Tran2010; Hayashi et al. Reference Hayashi2010, Reference Hayashi, Kodama, Koyama, Tadaki and Tanaka2011; Strazzullo et al. Reference Strazzullo2013; Santos et al. Reference Santos2015; Wang et al. Reference Wang2016), overdense environments tend to have enhanced star formation activity. This picture is not clear-cut though, with some work finding that
![]() $z>1$
high-density environments consist of suppressed star formation activity when compared to lower density counterparts (e.g. Lidman et al. Reference Lidman2008; Grützbauch et al. Reference Grützbauch2011; Old et al. Reference Old2020). Other studies (e.g. Darvish et al. Reference Darvish2016) have even found that star formation activity does not significantly change between environments out to
$z>1$
high-density environments consist of suppressed star formation activity when compared to lower density counterparts (e.g. Lidman et al. Reference Lidman2008; Grützbauch et al. Reference Grützbauch2011; Old et al. Reference Old2020). Other studies (e.g. Darvish et al. Reference Darvish2016) have even found that star formation activity does not significantly change between environments out to
![]() $z\sim3$
, and that environmental quenching is strongest towards lower redshifts (i.e.
$z\sim3$
, and that environmental quenching is strongest towards lower redshifts (i.e.
![]() $z\leq1$
; also suggested by Kawinwanichakij et al. Reference Kawinwanichakij2017).
$z\leq1$
; also suggested by Kawinwanichakij et al. Reference Kawinwanichakij2017).
Finally, the
![]() $z\sim2-3$
regime is considered a key epoch, sometimes called ‘cosmic noon’ (Schreiber & Wuyts Reference Schreiber and Wuyts2020), where universal star formation peaked, galaxies formed approximately half of their stellar mass, the dusty star-forming population peaked (e.g. Simpson et al. Reference Simpson2014; Dudzevičiūt˙e et al. Reference Dudzevičiūt˙e2020) and AGN activity was the most prominent (Cowley et al. Reference Cowley2018). In addition, there is strong evidence that merger interactions were common in the early universe (e.g. Lin et al. Reference Lin2008; Tacconi et al. Reference Tacconi2008; Allen et al. Reference Allen2015; Li et al. Reference Li, Jiang, He, Guo and Wang2022), and that the apparent growth of stellar mass (e.g. Tomczak et al. Reference Tomczak2014) may be driven by these merger processes (e.g. Conselice et al. Reference Conselice, Bershady, Dickinson and Papovich2003; Naab, Johansson, & Ostriker Reference Naab, Johansson and Ostriker2009; van Dokkum et al. Reference van Dokkum2010). The ‘cosmic noon’ consequently encompasses some of the most significant stages of galaxy evolution.
$z\sim2-3$
regime is considered a key epoch, sometimes called ‘cosmic noon’ (Schreiber & Wuyts Reference Schreiber and Wuyts2020), where universal star formation peaked, galaxies formed approximately half of their stellar mass, the dusty star-forming population peaked (e.g. Simpson et al. Reference Simpson2014; Dudzevičiūt˙e et al. Reference Dudzevičiūt˙e2020) and AGN activity was the most prominent (Cowley et al. Reference Cowley2018). In addition, there is strong evidence that merger interactions were common in the early universe (e.g. Lin et al. Reference Lin2008; Tacconi et al. Reference Tacconi2008; Allen et al. Reference Allen2015; Li et al. Reference Li, Jiang, He, Guo and Wang2022), and that the apparent growth of stellar mass (e.g. Tomczak et al. Reference Tomczak2014) may be driven by these merger processes (e.g. Conselice et al. Reference Conselice, Bershady, Dickinson and Papovich2003; Naab, Johansson, & Ostriker Reference Naab, Johansson and Ostriker2009; van Dokkum et al. Reference van Dokkum2010). The ‘cosmic noon’ consequently encompasses some of the most significant stages of galaxy evolution.
To determine how the relationship between quiescent galaxy fraction, star formation activity, and environmental density evolves over cosmological redshift, we take advantage of the FourStar Galaxy Evolution (ZFOURGE) survey and study the properties of environment spanning redshifts of
![]() $2.0\leq z<4.2$
. This paper is structured as follows. In Section 2, we introduce the ZFOURGE catalogues and the parameters we employ for this study. In Section 3, we outline our methods for creating our subsamples, searching for overdense environments and defining low, intermediate and high environmental density. In Section 4, we present our comparative analysis of the environments and discuss the implications of the results in Section 5. We then summarise our main findings and provide concluding remarks in Section 6. The work in this study assumes a
$2.0\leq z<4.2$
. This paper is structured as follows. In Section 2, we introduce the ZFOURGE catalogues and the parameters we employ for this study. In Section 3, we outline our methods for creating our subsamples, searching for overdense environments and defining low, intermediate and high environmental density. In Section 4, we present our comparative analysis of the environments and discuss the implications of the results in Section 5. We then summarise our main findings and provide concluding remarks in Section 6. The work in this study assumes a
![]() $\Lambda$
CDM cosmology of
$\Lambda$
CDM cosmology of
![]() $H_{0}=70\,$
km s
$H_{0}=70\,$
km s
![]() $^{-1}$
Mpc
$^{-1}$
Mpc
![]() $^{-1}$
,
$^{-1}$
,
![]() $\Omega_{m}=0.3$
and
$\Omega_{m}=0.3$
and
![]() $\Omega_{\Lambda}=0.7$
.
$\Omega_{\Lambda}=0.7$
.
2. The samples
2.1. ZFOURGE catalogues
The parent sample of this work consists of galaxies from the 2017 release of the ZFOURGEFootnote a survey (Straatman et al. Reference Straatman2016). ZFOURGE consists of approximately
![]() $60000$
galaxies at
$60000$
galaxies at
![]() $z>0.1$
and was taken using the near-IR FourStar imager (Persson et al. Reference Persson2013), mounted on the
$z>0.1$
and was taken using the near-IR FourStar imager (Persson et al. Reference Persson2013), mounted on the
![]() $6.5$
-m Magellan Baade Telescope at the Las Campanas Observatory, Chile. The ZFOURGE survey covered three
$6.5$
-m Magellan Baade Telescope at the Las Campanas Observatory, Chile. The ZFOURGE survey covered three
![]() $11^{\prime} \times 11^{\prime}$
HST legacy fields, COSMOS (Scoville et al. Reference Scoville2007), CDFS (Giacconi et al. Reference Giacconi2002) and UDS (Lawrence et al. Reference Lawrence2007), and employed deep near-IR imaging in the
$11^{\prime} \times 11^{\prime}$
HST legacy fields, COSMOS (Scoville et al. Reference Scoville2007), CDFS (Giacconi et al. Reference Giacconi2002) and UDS (Lawrence et al. Reference Lawrence2007), and employed deep near-IR imaging in the
![]() $J_{1}$
,
$J_{1}$
,
![]() $J_{2}$
,
$J_{2}$
,
![]() $J_{3}$
,
$J_{3}$
,
![]() $H_{l}$
and
$H_{l}$
and
![]() $H_{s}$
medium-band filters and
$H_{s}$
medium-band filters and
![]() $K_{s}$
broad-band filter. The imaging of ZFOURGE, measured over
$K_{s}$
broad-band filter. The imaging of ZFOURGE, measured over
![]() $ 1.0-1.8\,\mu$
m, consists of a circular aperture of diameter
$ 1.0-1.8\,\mu$
m, consists of a circular aperture of diameter
![]() $D = 0.6^{\prime\prime}$
and reaches
$D = 0.6^{\prime\prime}$
and reaches
![]() $5\sigma$
point-source limited depths of
$5\sigma$
point-source limited depths of
![]() $26$
AB mag in the J medium-bands and
$26$
AB mag in the J medium-bands and
![]() $25$
AB mag in the H and
$25$
AB mag in the H and
![]() $K_{s}$
-bands (Spitler et al. Reference Spitler2012). For sources across
$K_{s}$
-bands (Spitler et al. Reference Spitler2012). For sources across
![]() $1<z<4$
, these filters result in well-constrained photometric redshifts with
$1<z<4$
, these filters result in well-constrained photometric redshifts with
![]() $\Delta z/(1+z) \simeq$
1–2% (Spitler et al. Reference Spitler2012) and better detection of quiescent and dusty star-forming sources. ZFOURGE is also supplemented with existing public data from the HST/WFC3 F160W and F125W imaging of the CANDELS (Grogin et al. Reference Grogin2011; Koekemoer et al. Reference Koekemoer2011) survey and also contains data from the Spitzer/Infrared Array Camera (IRAC) and Herschel/Photodetector Array Camera and Spectrometer (PACS). For a full description of the data and methods of ZFOURGE, see Straatman et al. (Reference Straatman2016).
$\Delta z/(1+z) \simeq$
1–2% (Spitler et al. Reference Spitler2012) and better detection of quiescent and dusty star-forming sources. ZFOURGE is also supplemented with existing public data from the HST/WFC3 F160W and F125W imaging of the CANDELS (Grogin et al. Reference Grogin2011; Koekemoer et al. Reference Koekemoer2011) survey and also contains data from the Spitzer/Infrared Array Camera (IRAC) and Herschel/Photodetector Array Camera and Spectrometer (PACS). For a full description of the data and methods of ZFOURGE, see Straatman et al. (Reference Straatman2016).
2.2. Photometric redshifts, UVJ rest-frame colour diagram, stellar mass, specific star formation rates and AGN candidates
In this study, we use the photometric redshifts, rest-frame colours, stellar masses and star formation rates of the COSMOS legacy field of ZFOURGE. Photometric redshifts are determined using EAZY (Brammer, van Dokkum, & Coppi Reference Brammer, van Dokkum and Coppi2008), which fits linear combinations of nine spectral templates to the 0.3–8
![]() $\mu$
m observed photometry of the galaxies. Five of the templates are from the library of PÉGASE stellar population synthesis models (Fioc & Rocca-Volmerange Reference Fioc and Rocca-Volmerange1997). The remaining four templates are that of young and dusty galaxies, old reddened galaxies, old dusty galaxies and galaxies with strong emission lines. The ZFOURGE collaboration also chose to include a template error function to account for wavelength-dependent uncertainties. Offsets in zeropoints, which may affect flux and therefore the photometric redshifts, are corrected for by iteratively fitting the EAZY templates to the SEDs of the ZFOURGE galaxies. During the fitting procedure, the ZFOURGE collaboration calculated the systematic offsets between the templates and data and modified the templates accordingly. This allows the templates to highlight fainter features of galaxies including dust absorption at
$\mu$
m observed photometry of the galaxies. Five of the templates are from the library of PÉGASE stellar population synthesis models (Fioc & Rocca-Volmerange Reference Fioc and Rocca-Volmerange1997). The remaining four templates are that of young and dusty galaxies, old reddened galaxies, old dusty galaxies and galaxies with strong emission lines. The ZFOURGE collaboration also chose to include a template error function to account for wavelength-dependent uncertainties. Offsets in zeropoints, which may affect flux and therefore the photometric redshifts, are corrected for by iteratively fitting the EAZY templates to the SEDs of the ZFOURGE galaxies. During the fitting procedure, the ZFOURGE collaboration calculated the systematic offsets between the templates and data and modified the templates accordingly. This allows the templates to highlight fainter features of galaxies including dust absorption at
![]() $2175$
Å. Zeropoint corrections are then calculated in the observed frame. This fitting process was repeated until the zeropoint corrections in the bands were
$2175$
Å. Zeropoint corrections are then calculated in the observed frame. This fitting process was repeated until the zeropoint corrections in the bands were
![]() $<$
1%, which was typically after three or four iterations. Lastly, the ZFOURGE photometric redshifts were compared to spectroscopic redshifts in the same fields provided by the 3D-HST survey (Skelton et al. Reference Skelton2014). The ZFOURGE collaboration used the Normalised Median Absolute Deviation (i.e.
$<$
1%, which was typically after three or four iterations. Lastly, the ZFOURGE photometric redshifts were compared to spectroscopic redshifts in the same fields provided by the 3D-HST survey (Skelton et al. Reference Skelton2014). The ZFOURGE collaboration used the Normalised Median Absolute Deviation (i.e.
![]() $\sigma_{z} = 1.48 \times median$
absolute value
$\sigma_{z} = 1.48 \times median$
absolute value
![]() $[\mid z_{phot}-z_{spec}\mid/(1+z_{spec})]$
) to quantify the errors and achieved excellent results (COSMOS
$[\mid z_{phot}-z_{spec}\mid/(1+z_{spec})]$
) to quantify the errors and achieved excellent results (COSMOS
![]() $\sigma_{z}=0.009$
). For more information on the photometric redshifts, refer to Section 5 of Straatman et al. (Reference Straatman2016).
$\sigma_{z}=0.009$
). For more information on the photometric redshifts, refer to Section 5 of Straatman et al. (Reference Straatman2016).
We use the UVJ rest-frame colour diagram to divide the galaxy populations into quiescent, star-forming, and dusty star-forming. Sources that reside in the upper-left region of the UVJ diagram are defined as being quiescent, given by the vertices
![]() $({\rm V}-{\rm J}$
,
$({\rm V}-{\rm J}$
,
![]() ${\rm U}-{\rm V})=({-}\infty,1.3),(0.85,1.3),(1.6,1.95),(1.6,+\infty)$
, while the vertical boundary of
${\rm U}-{\rm V})=({-}\infty,1.3),(0.85,1.3),(1.6,1.95),(1.6,+\infty)$
, while the vertical boundary of
![]() $({\rm V}-{\rm J})=1.2$
divides the star-forming and dusty star-forming populations (Spitler et al. Reference Spitler2014). The diagram has been shown to be an efficient way of separating the quiescent and star-forming populations (e.g.Wuyts et al. Reference Wuyts2007;Williams et al. Reference Williams, Quadri, Franx, van Dokkum and Labbe2009;Wild et al. Reference Wild2014).
$({\rm V}-{\rm J})=1.2$
divides the star-forming and dusty star-forming populations (Spitler et al. Reference Spitler2014). The diagram has been shown to be an efficient way of separating the quiescent and star-forming populations (e.g.Wuyts et al. Reference Wuyts2007;Williams et al. Reference Williams, Quadri, Franx, van Dokkum and Labbe2009;Wild et al. Reference Wild2014).
The stellar masses of ZFOURGE are determined by fitting the stellar population synthesis models of Bruzual & Charlot (Reference Bruzual and Charlot2003) using FAST (Kriek et al. Reference Kriek2009). The models assume solar metallicity, the
![]() $A_{v} = 0-4$
dust extinction law of Calzetti et al. (Reference Calzetti2000), IMF of Chabrier (Reference Chabrier2003), and an exponentially decreasing star formation history.
$A_{v} = 0-4$
dust extinction law of Calzetti et al. (Reference Calzetti2000), IMF of Chabrier (Reference Chabrier2003), and an exponentially decreasing star formation history.
The ZFOURGE SFRs consider the rest-frame UV emission from massive stars and the IR emission re-radiated from dust-obscured stars. SFRs are determined via methods detailed in Bell et al. (Reference Bell2005), scaled to the IMF of Chabrier (Reference Chabrier2003), and given by,
where
![]() $L_{UV}$
is the EAZY-derived rest-frame luminosity, integrated over
$L_{UV}$
is the EAZY-derived rest-frame luminosity, integrated over
![]() , and
, and
![]() $L_{IR}$
is the bolometric IR luminosity, integrated over 8–1000
$L_{IR}$
is the bolometric IR luminosity, integrated over 8–1000
![]() $\mu$
m and calculated via a luminosity-independent conversion (Wuyts et al. Reference Wuyts2008, Reference Wuyts2011) using Herschel/PACS and Spitzer/MIPS out to 160
$\mu$
m and calculated via a luminosity-independent conversion (Wuyts et al. Reference Wuyts2008, Reference Wuyts2011) using Herschel/PACS and Spitzer/MIPS out to 160
![]() $\mu$
m fluxes where available. The inclusion of IR emission results in more robust SFRs (Tomczak et al. Reference Tomczak2016). To eliminate the bias of stellar mass, we use the specific star formation rate (sSFR) parameter, which is a relative measure of the level of star formation activity within a galaxy. The sSFRs of ZFOURGE (in units of
$\mu$
m fluxes where available. The inclusion of IR emission results in more robust SFRs (Tomczak et al. Reference Tomczak2016). To eliminate the bias of stellar mass, we use the specific star formation rate (sSFR) parameter, which is a relative measure of the level of star formation activity within a galaxy. The sSFRs of ZFOURGE (in units of
![]() ${\rm Gyr^{-1}}$
) are calculated by dividing the SFRs by stellar mass.
${\rm Gyr^{-1}}$
) are calculated by dividing the SFRs by stellar mass.
Finally, we highlight that the ZFOURGE catalogues also include radio, IR and X-ray AGN data (Cowley et al. Reference Cowley2016). For our study, we use these three bands to generate a simple data set that indicates the AGN status of the galaxies, where positive AGN detection
![]() $= 1$
, no AGN detection
$= 1$
, no AGN detection
![]() $= 0$
. This new data is used to reduce contamination in the sSFRs (Section 4.4) and to highlight the on-sky positions of AGN-dominated galaxies in the results of Section 4.1. According to Cowley et al. (Reference Cowley2016), the ZFOURGE AGN candidates have minimal impact on the derived photometric redshifts, SFRs and UVJ colours. However, given that AGN galaxies are notorious for contaminating light from star formation activity (e.g. Juneau et al. Reference Juneau2013), we decided to take a cautious approach and omit the AGN candidates from our sSFR samples. The majority of the ZFOURGE AGN (
$= 0$
. This new data is used to reduce contamination in the sSFRs (Section 4.4) and to highlight the on-sky positions of AGN-dominated galaxies in the results of Section 4.1. According to Cowley et al. (Reference Cowley2016), the ZFOURGE AGN candidates have minimal impact on the derived photometric redshifts, SFRs and UVJ colours. However, given that AGN galaxies are notorious for contaminating light from star formation activity (e.g. Juneau et al. Reference Juneau2013), we decided to take a cautious approach and omit the AGN candidates from our sSFR samples. The majority of the ZFOURGE AGN (
![]() $\sim$
85%) have been selected via IR techniques and are classified as Type 2. This is because Type 2 sources are more readily detected via IR selection due to the presence of obscuring material.
$\sim$
85%) have been selected via IR techniques and are classified as Type 2. This is because Type 2 sources are more readily detected via IR selection due to the presence of obscuring material.
![]() $\sim$
90% of the AGN sources in this study exhibit characteristics which are consistent with Type 2 AGN. For more information on the ZFOURGE AGN classification methods, refer to Cowley et al. (Reference Cowley2016).
$\sim$
90% of the AGN sources in this study exhibit characteristics which are consistent with Type 2 AGN. For more information on the ZFOURGE AGN classification methods, refer to Cowley et al. (Reference Cowley2016).
3. Galaxy environment search
3.1. Mass-limited sample, redshift slices and 7NN algorithm
For our galaxy sample, we isolate COSMOS sources with use=1 flags that lie in
![]() $2.0\leq z< 4.2$
. The use flag provides a standard selection of galaxies that have been surveyed by all medium-band filters of ZFOURGE, and consist of good photometry (Straatman et al. Reference Straatman2016). The distribution of stellar masses within the ZFOURGE survey is not consistent, with lower mass galaxies (
$2.0\leq z< 4.2$
. The use flag provides a standard selection of galaxies that have been surveyed by all medium-band filters of ZFOURGE, and consist of good photometry (Straatman et al. Reference Straatman2016). The distribution of stellar masses within the ZFOURGE survey is not consistent, with lower mass galaxies (
![]() ${\rm log(M_{*}/M_{\odot})}<8$
) being more prominent towards
${\rm log(M_{*}/M_{\odot})}<8$
) being more prominent towards
![]() $z<1$
while higher redshifts consist of a bias towards larger stellar masses. To reduce this bias and obtain a more complete sample, we impose a stellar mass limit of
$z<1$
while higher redshifts consist of a bias towards larger stellar masses. To reduce this bias and obtain a more complete sample, we impose a stellar mass limit of
![]() ${\rm log(M_{*}/M_{\odot})}\geq9.5$
on our
${\rm log(M_{*}/M_{\odot})}\geq9.5$
on our
![]() $2.0\leq z< 4.2$
COSMOS sources. This mass cut is consistent with the 80% stellar mass completeness limits of Tomczak et al. (Reference Tomczak2014) and Papovich et al. (Reference Papovich2015).
$2.0\leq z< 4.2$
COSMOS sources. This mass cut is consistent with the 80% stellar mass completeness limits of Tomczak et al. (Reference Tomczak2014) and Papovich et al. (Reference Papovich2015).
We define eight redshift slices:
![]() $2.0\leq z<2.2$
$2.0\leq z<2.2$
![]() $(z_{1})$
,
$(z_{1})$
,
![]() $2.2\leq z<2.4$
$2.2\leq z<2.4$
![]() $(z_{2})$
,
$(z_{2})$
,
![]() $2.4\leq z<2.6$
$2.4\leq z<2.6$
![]() $(z_{3})$
,
$(z_{3})$
,
![]() $2.6\leq z<2.8$
$2.6\leq z<2.8$
![]() $(z_{4})$
,
$(z_{4})$
,
![]() $2.8\leq z<3.1$
$2.8\leq z<3.1$
![]() $(z_{5})$
,
$(z_{5})$
,
![]() $3.1\leq z<3.4$
$3.1\leq z<3.4$
![]() $(z_{6})$
,
$(z_{6})$
,
![]() $3.4\leq z<3.8$
$3.4\leq z<3.8$
![]() $(z_{7})$
and
$(z_{7})$
and
![]() $3.8\leq z<4.2$
$3.8\leq z<4.2$
![]() $(z_{8})$
. We tested the widths of our redshift slices by comparing comoving space densities in the form of
$(z_{8})$
. We tested the widths of our redshift slices by comparing comoving space densities in the form of
![]() $N/V_{C}$
, where N and
$N/V_{C}$
, where N and
![]() $V_{C}$
is the galaxy count and comoving volume of a given redshift slice, respectively. We find that the comoving space densities decrease as redshift increases, which in turn reflects the distribution of the COSMOS galaxies in ZFOURGE. We also tested larger redshift slice widths (i.e.
$V_{C}$
is the galaxy count and comoving volume of a given redshift slice, respectively. We find that the comoving space densities decrease as redshift increases, which in turn reflects the distribution of the COSMOS galaxies in ZFOURGE. We also tested larger redshift slice widths (i.e.
![]() $\delta z\leq0.6$
) and found that the qualitative result remains unchanged. Lastly, we examined the photometric redshift uncertainties of ZFOURGE and found that, across bins of
$\delta z\leq0.6$
) and found that the qualitative result remains unchanged. Lastly, we examined the photometric redshift uncertainties of ZFOURGE and found that, across bins of
![]() $2.0<z<3.0$
and
$2.0<z<3.0$
and
![]() $3.0<z<4.0$
, the average redshift errors are
$3.0<z<4.0$
, the average redshift errors are
![]() $\sim$
$\sim$
![]() $0.146$
and
$0.146$
and
![]() $\sim$
$\sim$
![]() $0.172$
, respectively. Our redshift slice selection, therefore, accommodates the uncertainties in the photometric redshifts.
$0.172$
, respectively. Our redshift slice selection, therefore, accommodates the uncertainties in the photometric redshifts.
We searched for high-density environments over the eight redshift slices by generating projected surface density maps using the seventh nearest neighbour (7NN) metric (Spitler et al. Reference Spitler2012). At each ‘pixel’ on the ZFOURGE COSMOS sky, we calculated the projected surface density by isolating the seventh closest galaxy and its distance, given by,
where
![]() $r_{N}$
is the on-sky distance to the
$r_{N}$
is the on-sky distance to the
![]() $n{\rm th}$
closest galaxy and
$n{\rm th}$
closest galaxy and
![]() $N=7$
. The pixels range from the minimum to maximum RA and Dec coordinates of the galaxies and have an adopted spacing of
$N=7$
. The pixels range from the minimum to maximum RA and Dec coordinates of the galaxies and have an adopted spacing of
![]() $0.000357$
deg
$0.000357$
deg
![]() $(\sim 1.29)$
". Finally, to quantify the statistical significance of the high-density environments, the 7NN densities of each redshift slice are averaged using the means and standard deviations of the adjacent redshift slices (e.g. for
$(\sim 1.29)$
". Finally, to quantify the statistical significance of the high-density environments, the 7NN densities of each redshift slice are averaged using the means and standard deviations of the adjacent redshift slices (e.g. for
![]() $z_{1}$
, adjacent slices are
$z_{1}$
, adjacent slices are
![]() $1.8\leq z<2.0$
and
$1.8\leq z<2.0$
and
![]() $2.2\leq z<2.4$
.). The 7NN density estimates for the adjacent redshift slices are evaluated only at the locations of the galaxies. To show contrast between colours, the 7NN densities are plotted via a logarithmic scale, over a 0.1-20 range. We selected redshift slices
$2.2\leq z<2.4$
.). The 7NN density estimates for the adjacent redshift slices are evaluated only at the locations of the galaxies. To show contrast between colours, the 7NN densities are plotted via a logarithmic scale, over a 0.1-20 range. We selected redshift slices
![]() $z_{1}$
,
$z_{1}$
,
![]() $z_{2}$
,
$z_{2}$
,
![]() $z_{6}$
, and
$z_{6}$
, and
![]() $z_{8}$
for our study, elaborate on this choice in Section 4.1 and show the 7NN projected surface density maps of these slices in Fig. 1.
$z_{8}$
for our study, elaborate on this choice in Section 4.1 and show the 7NN projected surface density maps of these slices in Fig. 1.

Figure 1. Projected surface density maps of COSMOS redshift slices
![]() $2.0\leq z<2.2$
(
$2.0\leq z<2.2$
(
![]() $z_{1}$
; upper-left),
$z_{1}$
; upper-left),
![]() $2.2\leq z<2.4$
(
$2.2\leq z<2.4$
(
![]() $z_{2}$
; upper-right),
$z_{2}$
; upper-right),
![]() $3.1\leq z<3.4$
(
$3.1\leq z<3.4$
(
![]() $z_{6}$
; lower-left), and
$z_{6}$
; lower-left), and
![]() $3.8\leq z<4.2$
(
$3.8\leq z<4.2$
(
![]() $z_{8}$
; lower-right). The general location of the high-density environments are shown by the apertures (black circles). The
$z_{8}$
; lower-right). The general location of the high-density environments are shown by the apertures (black circles). The
![]() $z_{1}$
,
$z_{1}$
,
![]() $z_{2}$
,
$z_{2}$
,
![]() $z_{6}$
, and
$z_{6}$
, and
![]() $z_{8}$
apertures are
$z_{8}$
apertures are
![]() $\sim$
30′′, 33′′, 33′′, and 45′′, respectively. The colour bar shows the statistical significance of the 7NN densities above the mean density averaged over adjacent redshift slices. H2 and H3 in
$\sim$
30′′, 33′′, 33′′, and 45′′, respectively. The colour bar shows the statistical significance of the 7NN densities above the mean density averaged over adjacent redshift slices. H2 and H3 in
![]() $z_{1}$
represent the original overdensities identified by Spitler et al. (Reference Spitler2012) and spectroscopically confirmed by Yuan et al. (Reference Yuan2014). Quiescent, star-forming and dusty star-forming sources are shown as red, blue and orange markers, respectively, while those that have an AGN according to the catalogues of Cowley et al. (Reference Cowley2016) are shown as star markers.
$z_{1}$
represent the original overdensities identified by Spitler et al. (Reference Spitler2012) and spectroscopically confirmed by Yuan et al. (Reference Yuan2014). Quiescent, star-forming and dusty star-forming sources are shown as red, blue and orange markers, respectively, while those that have an AGN according to the catalogues of Cowley et al. (Reference Cowley2016) are shown as star markers.
These algorithms usually require testing to ensure that true overdensities are being observed and not imperfect photometric redshift measurements. Spitler et al. (Reference Spitler2012) developed this 7NN metric and tested its reliability in two ways. First, they performed a bootstrap resampling of the photometric redshifts, shuffled the results of each iteration and produced new 7NN density maps. From this, it was found that only
![]() $3/1000$
resampled maps had one high-density environment. For the second check, Spitler et al. (Reference Spitler2012) generated 121 mock density maps using the light cone catalogues of the online laboratory Mock Galaxy Factory (Bernyk et al. Reference Bernyk2016) and found that the mock maps had a scatter which was consistent with that of the real density map. The above results indicate that the 7NN overdensities are not random associations and are therefore robust and reliable. Allen et al. (Reference Allen2015), who studied the
$3/1000$
resampled maps had one high-density environment. For the second check, Spitler et al. (Reference Spitler2012) generated 121 mock density maps using the light cone catalogues of the online laboratory Mock Galaxy Factory (Bernyk et al. Reference Bernyk2016) and found that the mock maps had a scatter which was consistent with that of the real density map. The above results indicate that the 7NN overdensities are not random associations and are therefore robust and reliable. Allen et al. (Reference Allen2015), who studied the
![]() $z_{1}$
H2 and H3 overdensities in detail, also carried out tests for the 7NN algorithm and achieved similar results. Different values of N (i.e.
$z_{1}$
H2 and H3 overdensities in detail, also carried out tests for the 7NN algorithm and achieved similar results. Different values of N (i.e.
![]() $N=5-9$
) in Equation (2) were tested by Spitler et al. (Reference Spitler2012), who confirmed that the results do not significantly change for the surface density maps.
$N=5-9$
) in Equation (2) were tested by Spitler et al. (Reference Spitler2012), who confirmed that the results do not significantly change for the surface density maps.
3.2. Environmental density definitions
Fig. 2 shows the distributions of the 7NN projected surface density pixels of
![]() $z_{1}$
,
$z_{1}$
,
![]() $z_{2}$
,
$z_{2}$
,
![]() $z_{6}$
, and
$z_{6}$
, and
![]() $z_{8}$
and includes the colour bar of Fig. 1 for comparison. The means, medians,
$z_{8}$
and includes the colour bar of Fig. 1 for comparison. The means, medians,
![]() $\pm\sigma$
,
$\pm\sigma$
,
![]() $\pm2\sigma$
and
$\pm2\sigma$
and
![]() $\pm3\sigma$
parameters are shown as the solid red, dashed red, and darkening blue dot-dashed lines, respectively. We chose a fixed threshold in
$\pm3\sigma$
parameters are shown as the solid red, dashed red, and darkening blue dot-dashed lines, respectively. We chose a fixed threshold in
![]() $\log(n_{7})$
below, between and above
$\log(n_{7})$
below, between and above
![]() $-0.5$
and
$-0.5$
and
![]() $+0.5$
to define low-, intermediate-, and high-density, respectively. We therefore selected the
$+0.5$
to define low-, intermediate-, and high-density, respectively. We therefore selected the
![]() $\sigma$
-valued boundaries of Table 1 to most closely approximate the
$\sigma$
-valued boundaries of Table 1 to most closely approximate the
![]() $\log(n_{7})$
environmental density threshold. We tested the
$\log(n_{7})$
environmental density threshold. We tested the
![]() $25{\rm th}$
and
$25{\rm th}$
and
![]() $75{\rm th}$
quartiles, but these parameters were not symmetrical around the non-Gaussian distributions and overestimated the low- and high-density environments due to the very uneven cuts. Different definitions using the
$75{\rm th}$
quartiles, but these parameters were not symmetrical around the non-Gaussian distributions and overestimated the low- and high-density environments due to the very uneven cuts. Different definitions using the
![]() $\sigma$
parameters were also tested, but we concluded that those of Table 1 divided the sources into low-, intermediate-, and high-density environments most consistently. Previous ZFOURGE environment papers that employed the same 7NN algorithm (e.g. Spitler et al. Reference Spitler2012; Allen et al. Reference Allen2015, Reference Allen2016) also referred to their overdensities in terms of
$\sigma$
parameters were also tested, but we concluded that those of Table 1 divided the sources into low-, intermediate-, and high-density environments most consistently. Previous ZFOURGE environment papers that employed the same 7NN algorithm (e.g. Spitler et al. Reference Spitler2012; Allen et al. Reference Allen2015, Reference Allen2016) also referred to their overdensities in terms of
![]() $\sigma$
. We provide the environment sample sizes of the redshift slices in Table 2.
$\sigma$
. We provide the environment sample sizes of the redshift slices in Table 2.

Figure 2. Distributions of the logarithmic-scaled 7NN surface density pixels of
![]() $2.0\leq z<2.2$
(
$2.0\leq z<2.2$
(
![]() $z_{1}$
; upper-left),
$z_{1}$
; upper-left),
![]() $2.2\leq z<2.4$
(
$2.2\leq z<2.4$
(
![]() $z_{2}$
; upper-right),
$z_{2}$
; upper-right),
![]() $3.1\leq z<3.4$
(
$3.1\leq z<3.4$
(
![]() $z_{6}$
; lower-left) and
$z_{6}$
; lower-left) and
![]() $3.8\leq z<4.2$
(
$3.8\leq z<4.2$
(
![]() $z_{8}$
; lower-right). The colour bar corresponds to that of Fig. 1. Means and medians of the densities are shown as solid and dashed red lines, respectively, while
$z_{8}$
; lower-right). The colour bar corresponds to that of Fig. 1. Means and medians of the densities are shown as solid and dashed red lines, respectively, while
![]() $\pm\sigma$
,
$\pm\sigma$
,
![]() $\pm2\sigma$
and
$\pm2\sigma$
and
![]() $\pm3\sigma$
are given by the darkening dot-dash blue lines.
$\pm3\sigma$
are given by the darkening dot-dash blue lines.
4. Results
4.1. Projected surface density maps
We discover new high-density environment candidates in the COSMOS legacy field within redshift slices
![]() $z_{1}$
,
$z_{1}$
,
![]() $z_{2}$
,
$z_{2}$
,
![]() $z_{6}$
, and
$z_{6}$
, and
![]() $z_{8}$
as shown by the apertures (black circles) in the 7NN projected surface density maps of Fig. 1.
$z_{8}$
as shown by the apertures (black circles) in the 7NN projected surface density maps of Fig. 1.
![]() $z_{1}$
apertures are
$z_{1}$
apertures are
![]() $\sim 30^{\prime\prime}$
,
$\sim 30^{\prime\prime}$
,
![]() $z_{2}$
and
$z_{2}$
and
![]() $z_{6}$
apertures are
$z_{6}$
apertures are
![]() $\sim 33^{\prime\prime}$
while the
$\sim 33^{\prime\prime}$
while the
![]() $z_{8}$
aperture is
$z_{8}$
aperture is
![]() $\sim 45^{\prime\prime}$
. The colour bar represents the statistical significance (in
$\sim 45^{\prime\prime}$
. The colour bar represents the statistical significance (in
![]() $\sigma$
) of the 7NN densities above the mean density, which is averaged over the adjacent redshift slices. In Fig. 1, H2 and H3 represent the overdensities found by Spitler et al. (Reference Spitler2012) and spectroscopically confirmed by Yuan et al. (Reference Yuan2014), while H1 appears to be a new high-density candidate for this slice. Redshift slices
$\sigma$
) of the 7NN densities above the mean density, which is averaged over the adjacent redshift slices. In Fig. 1, H2 and H3 represent the overdensities found by Spitler et al. (Reference Spitler2012) and spectroscopically confirmed by Yuan et al. (Reference Yuan2014), while H1 appears to be a new high-density candidate for this slice. Redshift slices
![]() $z_{2}$
,
$z_{2}$
,
![]() $z_{6}$
, and
$z_{6}$
, and
![]() $z_{8}$
have one newly detected high-density environment each. We did not identify any concentrated
$z_{8}$
have one newly detected high-density environment each. We did not identify any concentrated
![]() ${\rm log_{10}}(n_{7})\gtrsim+0.5$
high-density environments across
${\rm log_{10}}(n_{7})\gtrsim+0.5$
high-density environments across
![]() $z_{3}$
,
$z_{3}$
,
![]() $z_{4}$
,
$z_{4}$
,
![]() $z_{5}$
, and
$z_{5}$
, and
![]() $z_{7}$
, and so omit these redshift slices from this study.
$z_{7}$
, and so omit these redshift slices from this study.
4.2. Quiescent fractions
We compare the quiescent galaxy fractions as a function of environment and redshift. As described in Section 2.2, the quiescent classification is based on the UVJ rest-frame colour diagram. For the complete samples, the quiescent fraction for a given redshift slice is in the form of
![]() $f_{q}=N_{q}/N_{total}$
. For the environment samples, we find the count of a given galaxy population and divide this by the count of galaxies in that environment (e.g. low-density quiescent fraction is defined as
$f_{q}=N_{q}/N_{total}$
. For the environment samples, we find the count of a given galaxy population and divide this by the count of galaxies in that environment (e.g. low-density quiescent fraction is defined as
![]() $f_{q(L)}=N_{q(L)}/N_{total(L)}$
). Fig. 3 shows the quiescent fractions of the low- (blue squares), intermediate- (green circles) and high-density (red triangles) environments. Quiescent fractions of the complete samples (white diamonds) are also included for comparison. Errors shown are the
$f_{q(L)}=N_{q(L)}/N_{total(L)}$
). Fig. 3 shows the quiescent fractions of the low- (blue squares), intermediate- (green circles) and high-density (red triangles) environments. Quiescent fractions of the complete samples (white diamonds) are also included for comparison. Errors shown are the
![]() $1\sigma$
Clopper–Pearson binomial confidence intervals. Only one source was identified as being part of the
$1\sigma$
Clopper–Pearson binomial confidence intervals. Only one source was identified as being part of the
![]() $z_{6}$
low-density environment, and is therefore excluded from this analysis. Across all redshift slices, Fig. 3 reveals that the quiescent galaxy fraction tends to increase with environmental density and appears to be largest for
$z_{6}$
low-density environment, and is therefore excluded from this analysis. Across all redshift slices, Fig. 3 reveals that the quiescent galaxy fraction tends to increase with environmental density and appears to be largest for
![]() $z_{2}$
. We note that
$z_{2}$
. We note that
![]() $z_{6}$
and
$z_{6}$
and
![]() $z_{8}$
have significantly fewer quiescent sources than
$z_{8}$
have significantly fewer quiescent sources than
![]() $z_{1}$
and
$z_{1}$
and
![]() $z_{2}$
, and so caution is warranted with the results of Fig. 3 at
$z_{2}$
, and so caution is warranted with the results of Fig. 3 at
![]() $z\geq3.1$
. There is also some overlap in the uncertainties between the low- and high-density samples of
$z\geq3.1$
. There is also some overlap in the uncertainties between the low- and high-density samples of
![]() $z_{1}$
. Despite this, Fig. 3 shows evidence that quiescent galaxies are preferentially found in high-density environments across all redshifts probed in this study.
$z_{1}$
. Despite this, Fig. 3 shows evidence that quiescent galaxies are preferentially found in high-density environments across all redshifts probed in this study.
Table 1. Environmental density definitions of the four redshift slices, derived from the 7NN density distributions of Fig. 2. The low-density
![]() $\sigma$
-boundaries of
$\sigma$
-boundaries of
![]() $z_{1}$
,
$z_{1}$
,
![]() $z_{2}$
,
$z_{2}$
,
![]() $z_{6}$
, and
$z_{6}$
, and
![]() $z_{8}$
are
$z_{8}$
are
![]() $\sim$
$\sim$
![]() $-0.5$
,
$-0.5$
,
![]() $-0.2$
,
$-0.2$
,
![]() $-0.4$
, and
$-0.4$
, and
![]() $-0.3$
, respectively. The high-density
$-0.3$
, respectively. The high-density
![]() $\sigma$
-boundaries of
$\sigma$
-boundaries of
![]() $z_{1}$
,
$z_{1}$
,
![]() $z_{2}$
,
$z_{2}$
,
![]() $z_{6}$
, and
$z_{6}$
, and
![]() $z_{8}$
are
$z_{8}$
are
![]() $\sim$
$\sim$
![]() $0.5$
,
$0.5$
,
![]() $0.3$
,
$0.3$
,
![]() $0.6$
, and
$0.6$
, and
![]() $0.5$
, respectively.
$0.5$
, respectively.

Table 2. Environment sample sizes of the four redshift slices, according to the definitions of Table 1.

4.3. Stellar mass
Fig. 4 shows the average stellar mass as a function of environment and redshift. The stellar mass of the galaxy belonging to the
![]() $z_{6}$
low-density environment is also included. Errors shown indicate the
$z_{6}$
low-density environment is also included. Errors shown indicate the
![]() $\rm {68\%}$
confidence intervals evaluated via bootstrapping methods. For the bootstrapping analysis, we generated 9999 new samples from the original and calculated the average for each. All bootstrapped averages were then arranged in ascending order and the averages at the lower and upper percentiles were used to construct the lower and upper limits of the
$\rm {68\%}$
confidence intervals evaluated via bootstrapping methods. For the bootstrapping analysis, we generated 9999 new samples from the original and calculated the average for each. All bootstrapped averages were then arranged in ascending order and the averages at the lower and upper percentiles were used to construct the lower and upper limits of the
![]() $68 \%$
confidence intervals. Across all redshift slices, Fig. 4 reveals that the high-density environments tend to have the most massive galaxies compared to the complete, low- and intermediate-density samples. This is strongest for redshift slices
$68 \%$
confidence intervals. Across all redshift slices, Fig. 4 reveals that the high-density environments tend to have the most massive galaxies compared to the complete, low- and intermediate-density samples. This is strongest for redshift slices
![]() $z_{1}$
and
$z_{1}$
and
![]() $z_{2}$
, where the average stellar masses for the high-density environments were found to be
$z_{2}$
, where the average stellar masses for the high-density environments were found to be
![]() ${\rm log(M_{*}/M_{\odot})}\sim10.220\pm0.096$
and
${\rm log(M_{*}/M_{\odot})}\sim10.220\pm0.096$
and
![]() $\sim10.571^{+0.139}_{-0.136}$
, respectively. The average stellar masses of the
$\sim10.571^{+0.139}_{-0.136}$
, respectively. The average stellar masses of the
![]() $z_{6}$
and
$z_{6}$
and
![]() $z_{8}$
high-density environments, on the other hand, were found to be
$z_{8}$
high-density environments, on the other hand, were found to be
![]() ${\rm log(M_{*}/M_{\odot})}\sim 10.015^{+0.102}_{-0.104}$
and
${\rm log(M_{*}/M_{\odot})}\sim 10.015^{+0.102}_{-0.104}$
and
![]() $\sim 10.172^{+0.106}_{-0.108}$
, respectively.
$\sim 10.172^{+0.106}_{-0.108}$
, respectively.

Figure 3. Quiescent galaxy fractions of the environments and complete samples of
![]() $2.0\leq z<2.2$
$2.0\leq z<2.2$
![]() $(z_{1})$
,
$(z_{1})$
,
![]() $2.2\leq z<2.4$
$2.2\leq z<2.4$
![]() $(z_{2})$
,
$(z_{2})$
,
![]() $3.1\leq z<3.4$
$3.1\leq z<3.4$
![]() $(z_{6})$
and
$(z_{6})$
and
![]() $3.8\leq z<4.2$
$3.8\leq z<4.2$
![]() $(z_{8})$
. Low-, intermediate- and high-density environments are given by the blue square, green circle and red triangle markers, respectively, while the complete samples are represented by the white diamonds. Errors shown indicate
$(z_{8})$
. Low-, intermediate- and high-density environments are given by the blue square, green circle and red triangle markers, respectively, while the complete samples are represented by the white diamonds. Errors shown indicate
![]() $1\sigma$
Clopper–Pearson binomial confidence intervals. The quiescent fraction of the environments is given by
$1\sigma$
Clopper–Pearson binomial confidence intervals. The quiescent fraction of the environments is given by
![]() $N_{q(env)}/N_{total(env)}$
, while the quiescent fraction of the complete samples is in the form of
$N_{q(env)}/N_{total(env)}$
, while the quiescent fraction of the complete samples is in the form of
![]() $N_{q}/N_{total}$
. The low-density environment of
$N_{q}/N_{total}$
. The low-density environment of
![]() $z_{6}$
is omitted due to low numbers.
$z_{6}$
is omitted due to low numbers.

Figure 4. Average stellar mass,
![]() ${\rm log(M_{*}/M_\odot)}$
, of the environments and complete samples of
${\rm log(M_{*}/M_\odot)}$
, of the environments and complete samples of
![]() $2.0\leq z<2.2$
$2.0\leq z<2.2$
![]() $(z_{1})$
,
$(z_{1})$
,
![]() $2.2\leq z<2.4$
$2.2\leq z<2.4$
![]() $(z_{2})$
,
$(z_{2})$
,
![]() $3.1\leq z<3.4$
$3.1\leq z<3.4$
![]() $(z_{6})$
and
$(z_{6})$
and
![]() $3.8\leq z<4.2$
$3.8\leq z<4.2$
![]() $(z_{8})$
. Errors shown correspond to the
$(z_{8})$
. Errors shown correspond to the
![]() $\rm {68\%}$
confidence intervals calculated from a bootstrap analysis. The stellar mass of the low-density galaxy of
$\rm {68\%}$
confidence intervals calculated from a bootstrap analysis. The stellar mass of the low-density galaxy of
![]() $z_{6}$
is also included in the figure for completeness. Markers are as in Fig. 3.
$z_{6}$
is also included in the figure for completeness. Markers are as in Fig. 3.
We found the low-to-high density stellar mass offsets for redshift slices
![]() $z_{1}$
,
$z_{1}$
,
![]() $z_{2}$
, and
$z_{2}$
, and
![]() $z_{8}$
to be
$z_{8}$
to be
![]() $\Delta\rm log(M_{*})\sim0.247^{+0.142}_{-0.141}$
,
$\Delta\rm log(M_{*})\sim0.247^{+0.142}_{-0.141}$
,
![]() $\sim0.470^{+0.149}_{-0.147}$
and
$\sim0.470^{+0.149}_{-0.147}$
and
![]() $\sim0.318^{+0.154}_{-0.155}$
dex, respectively. For
$\sim0.318^{+0.154}_{-0.155}$
dex, respectively. For
![]() $z_{6}$
, we calculated the high-density complete sample offset which evaluated to
$z_{6}$
, we calculated the high-density complete sample offset which evaluated to
![]() $\Delta\rm log(M_{*})\sim0.104^{+0.105}_{-0.107}$
dex. Redshift slices
$\Delta\rm log(M_{*})\sim0.104^{+0.105}_{-0.107}$
dex. Redshift slices
![]() $z_{2}$
and
$z_{2}$
and
![]() $z_{8}$
, therefore, have the most significant and greatest elevation of stellar mass.
$z_{8}$
, therefore, have the most significant and greatest elevation of stellar mass.
4.4. Star formation activity
Fig. 5 shows the average sSFRs as a function of environment and redshift. Errors shown are the
![]() $\rm {68\%}$
confidence intervals evaluated via bootstrapping methods described in Section 4.3. We found that the sSFR ranges differed between the lower and higher redshift slices. Therefore, to better highlight the contrast in star formation activity, we pair
$\rm {68\%}$
confidence intervals evaluated via bootstrapping methods described in Section 4.3. We found that the sSFR ranges differed between the lower and higher redshift slices. Therefore, to better highlight the contrast in star formation activity, we pair
![]() $z_{1}$
and
$z_{1}$
and
![]() $z_{2}$
on one axis and
$z_{2}$
on one axis and
![]() $z_{6}$
and
$z_{6}$
and
![]() $z_{8}$
on another. As mentioned in Section 2.2, we remove the Cowley et al. (Reference Cowley2016) AGN candidates from the sSFR samples to reduce contamination. The low-density environment of
$z_{8}$
on another. As mentioned in Section 2.2, we remove the Cowley et al. (Reference Cowley2016) AGN candidates from the sSFR samples to reduce contamination. The low-density environment of
![]() $z_{6}$
lacks SFR data and so is excluded from this analysis. From Fig. 5, we find evidence that the high-density environments tend to have the lowest sSFRs across all redshift slices. This is particularly strong for
$z_{6}$
lacks SFR data and so is excluded from this analysis. From Fig. 5, we find evidence that the high-density environments tend to have the lowest sSFRs across all redshift slices. This is particularly strong for
![]() $z_{8}$
.
$z_{8}$
.
We find that from low to high density, the average sSFRs decrease by
![]() $\sim$
34%,
$\sim$
34%,
![]() $\sim$
60% and
$\sim$
60% and
![]() $\sim$
82% for redshift slices
$\sim$
82% for redshift slices
![]() $z_{1}$
,
$z_{1}$
,
![]() $z_{2}$
, and
$z_{2}$
, and
![]() $z_{8}$
, respectively. For
$z_{8}$
, respectively. For
![]() $z_{6}$
, we determined the percentage difference between the complete sample and high-density environment, which is
$z_{6}$
, we determined the percentage difference between the complete sample and high-density environment, which is
![]() $\sim$
15%. Therefore, we find that the drop in star formation activity is greatest across redshift slices
$\sim$
15%. Therefore, we find that the drop in star formation activity is greatest across redshift slices
![]() $z_{2}$
and
$z_{2}$
and
![]() $z_{8}$
.
$z_{8}$
.
5. Discussion
For the first time using ZFOURGE data, we have studied the influence of environment on galaxy evolution spanning redshifts of
![]() $2.0\leq z<4.2$
. With previous work debating the redshift at which the Butcher–Oemler effect reverses (and if it does at all), we compared the quiescent galaxy fractions and average stellar masses and sSFRs in regions of low-, intermediate- and high-density in the early universe. Predominately, it appears that high-density environments contain evolved, passive galaxies as far back as
$2.0\leq z<4.2$
. With previous work debating the redshift at which the Butcher–Oemler effect reverses (and if it does at all), we compared the quiescent galaxy fractions and average stellar masses and sSFRs in regions of low-, intermediate- and high-density in the early universe. Predominately, it appears that high-density environments contain evolved, passive galaxies as far back as
![]() $z\sim2.4$
and potentially to the much higher redshift of
$z\sim2.4$
and potentially to the much higher redshift of
![]() $z\sim 4$
.
$z\sim 4$
.
From Fig. 3, we find that the quiescent galaxy fraction tends to increase with environmental density across all redshift slices probed in this study. It should be noted, however, that the quiescent galaxy numbers naturally decrease as photometric redshift increases within the ZFOURGE catalogues, meaning that we may not have enough quiescent systems at
![]() $z\geq3.1$
to make a fair comparison between environments. Reinforcing our results, though, is that they are consistent with those of Strazzullo et al. (Reference Strazzullo2013), for example, who also found that a dense cluster core at
$z\geq3.1$
to make a fair comparison between environments. Reinforcing our results, though, is that they are consistent with those of Strazzullo et al. (Reference Strazzullo2013), for example, who also found that a dense cluster core at
![]() $z\sim2$
had an enhanced passive galaxy fraction. Work by Spitler et al. (Reference Spitler2012), who studied the photometrically identified H2 and H3 overdensities of
$z\sim2$
had an enhanced passive galaxy fraction. Work by Spitler et al. (Reference Spitler2012), who studied the photometrically identified H2 and H3 overdensities of
![]() $z_{1}$
, also highlighted that galaxies in these environments tended to be redder than the field or low-density population. The results of Fig. 3 appear to suggest that the positive correlation between passive galaxy fractions and environmental density in the low redshift universe (e.g.
$z_{1}$
, also highlighted that galaxies in these environments tended to be redder than the field or low-density population. The results of Fig. 3 appear to suggest that the positive correlation between passive galaxy fractions and environmental density in the low redshift universe (e.g.
![]() $z<2$
; Dressler 1980; Lidman et al. Reference Lidman2008; Damjanov et al. Reference Damjanov, Zahid, Geller and Hwang2015; Allen et al. Reference Allen2016; Davies et al. Reference Davies2016; Jian et al. Reference Jian2017; Kawinwanichakij et al. Reference Kawinwanichakij2017) extends into the higher redshift universe, to at least
$z<2$
; Dressler 1980; Lidman et al. Reference Lidman2008; Damjanov et al. Reference Damjanov, Zahid, Geller and Hwang2015; Allen et al. Reference Allen2016; Davies et al. Reference Davies2016; Jian et al. Reference Jian2017; Kawinwanichakij et al. Reference Kawinwanichakij2017) extends into the higher redshift universe, to at least
![]() $z\sim2.4$
.
$z\sim2.4$
.
Fig. 5 reveals that, across all redshift slices, the high-density environments have the lowest sSFRs. From low to high density, we found that the
![]() $z_{1}$
star formation activity decreased by
$z_{1}$
star formation activity decreased by
![]() $\sim$
34%, while in
$\sim$
34%, while in
![]() $z_{2}$
star formation activity dropped by
$z_{2}$
star formation activity dropped by
![]() $\sim$
60%. Coupled with our quiescent fraction findings, the suppressed sSFRs provide evidence to suggest that the SFR-density relation and Butcher–Oemler effect do not appear to reverse at higher redshifts. Our findings are in direct contrast to those of Wang et al. (Reference Wang2016), who found that a dense concentration of massive galaxies at
$\sim$
60%. Coupled with our quiescent fraction findings, the suppressed sSFRs provide evidence to suggest that the SFR-density relation and Butcher–Oemler effect do not appear to reverse at higher redshifts. Our findings are in direct contrast to those of Wang et al. (Reference Wang2016), who found that a dense concentration of massive galaxies at
![]() $z=2.506$
was dominated by star-forming sources and high SFRs of
$z=2.506$
was dominated by star-forming sources and high SFRs of
![]() $\sim$
$\sim$
![]() $3400$
$3400$
![]() ${\rm M_\odot yr^{-1}}$
as well as other high redshift studies (e.g.
${\rm M_\odot yr^{-1}}$
as well as other high redshift studies (e.g.
![]() $z\geq1.2$
; Tran et al. Reference Tran2010; Hayashi et al. Reference Hayashi, Kodama, Koyama, Tadaki and Tanaka2011; Alberts et al. Reference Alberts2014; Santos et al. Reference Santos2015) who find that their high-density environments experienced accelerated levels of star formation activity.
$z\geq1.2$
; Tran et al. Reference Tran2010; Hayashi et al. Reference Hayashi, Kodama, Koyama, Tadaki and Tanaka2011; Alberts et al. Reference Alberts2014; Santos et al. Reference Santos2015) who find that their high-density environments experienced accelerated levels of star formation activity.
The question now is why we observe well-evolved, passive sources in overdense environments across
![]() $2.0\leq z<2.4$
. With the fates of galaxies generally controlled by their stellar masses (e.g. Peng et al. Reference Peng2010; Rasmussen et al. Reference Rasmussen2012; Davies et al. Reference Davies2016; Old et al. Reference Old2020; Contini et al. Reference Contini2020), our results in Fig. 4 may provide more context. When comparing the average stellar masses of our environment samples, we highlighted in Section 4.3 that the
$2.0\leq z<2.4$
. With the fates of galaxies generally controlled by their stellar masses (e.g. Peng et al. Reference Peng2010; Rasmussen et al. Reference Rasmussen2012; Davies et al. Reference Davies2016; Old et al. Reference Old2020; Contini et al. Reference Contini2020), our results in Fig. 4 may provide more context. When comparing the average stellar masses of our environment samples, we highlighted in Section 4.3 that the
![]() $z_{1}$
and
$z_{1}$
and
![]() $z_{2}$
high-density environments contained, on average, massive
$z_{2}$
high-density environments contained, on average, massive
![]() ${\rm log(M_{*}/M_\odot)}\geq10.2$
galaxies. Taken at face value, the apparent build-up of stellar mass may indicate that merger interactions are present in
${\rm log(M_{*}/M_\odot)}\geq10.2$
galaxies. Taken at face value, the apparent build-up of stellar mass may indicate that merger interactions are present in
![]() $z_{1}$
and
$z_{1}$
and
![]() $z_{2}$
. This hypothesis is supported by Allen et al. (Reference Allen2015), who suggested star-forming cluster galaxies at
$z_{2}$
. This hypothesis is supported by Allen et al. (Reference Allen2015), who suggested star-forming cluster galaxies at
![]() $z\sim2.1$
may be experiencing growth via minor mergers, as well as other high redshift studies (e.g.
$z\sim2.1$
may be experiencing growth via minor mergers, as well as other high redshift studies (e.g.
![]() $z\leq3$
; Conselice et al. Reference Conselice, Bershady, Dickinson and Papovich2003; Conselice Reference Conselice2006; Lin et al. Reference Lin2008; Naab et al. Reference Naab, Johansson and Ostriker2009; van Dokkum et al. Reference van Dokkum2010) who argued that galaxy mergers were the most dominant interaction in the early universe.
$z\leq3$
; Conselice et al. Reference Conselice, Bershady, Dickinson and Papovich2003; Conselice Reference Conselice2006; Lin et al. Reference Lin2008; Naab et al. Reference Naab, Johansson and Ostriker2009; van Dokkum et al. Reference van Dokkum2010) who argued that galaxy mergers were the most dominant interaction in the early universe.
Because we are working with massive systems, however, we highlight that the apparent suppressed star formation activity and large quiescent fractions may be a result of stellar mass quenching and not necessarily environmental-based quenching. Kawinwanichakij et al. (Reference Kawinwanichakij2017), for example, find that galaxy quenching via environmental processes dominate for lower-mass galaxies (
![]() ${\rm log(M_{*}/M_\odot)}\leq9.5$
) towards lower redshifts (
${\rm log(M_{*}/M_\odot)}\leq9.5$
) towards lower redshifts (
![]() $z<1.5$
), while at higher redshifts (
$z<1.5$
), while at higher redshifts (
![]() $z<2$
) environmental and mass quenching processes are indistinguishable. It is plausible to suggest that at our redshifts, environmental and stellar mass quenching processes may have been operating closely, and that the high-density environments of
$z<2$
) environmental and mass quenching processes are indistinguishable. It is plausible to suggest that at our redshifts, environmental and stellar mass quenching processes may have been operating closely, and that the high-density environments of
![]() $z_{1}$
and
$z_{1}$
and
![]() $z_{2}$
built up stellar mass via merger interactions while mass quenching is more likely to be responsible for the quiescent and sSFR results of Figs. 3 and 5, respectively. Darvish et al. (Reference Darvish2016), who studied the effects of environment and stellar mass on
$z_{2}$
built up stellar mass via merger interactions while mass quenching is more likely to be responsible for the quiescent and sSFR results of Figs. 3 and 5, respectively. Darvish et al. (Reference Darvish2016), who studied the effects of environment and stellar mass on
![]() $z<3$
galaxy quenching suggest something similar, finding that while quiescent fractions are dependent on environment at
$z<3$
galaxy quenching suggest something similar, finding that while quiescent fractions are dependent on environment at
![]() $z\leq1$
, they become more dependent on stellar mass out to
$z\leq1$
, they become more dependent on stellar mass out to
![]() $z\sim3$
. Similarly, Grützbauch et al. (Reference Grützbauch2011) argued that very overdense environments tended to have suppressed star formation activity up to
$z\sim3$
. Similarly, Grützbauch et al. (Reference Grützbauch2011) argued that very overdense environments tended to have suppressed star formation activity up to
![]() $z\sim2$
, possibly due to merger activity (though it is worth noting that for the most part, they found that local environment appears to have very little effect on galaxy SFRs at
$z\sim2$
, possibly due to merger activity (though it is worth noting that for the most part, they found that local environment appears to have very little effect on galaxy SFRs at
![]() $z>1.5$
). The connection between quiescent galaxies, star formation activity, and the role of environmental and stellar mass quenching is clearly challenging to disentangle at higher redshifts. Given previous evidence, we cannot rule out the possibility of hidden stellar mass quenching processes in Figs. 3–5. In addition, we also need to carry out other tests to investigate whether galaxy mergers are present, which may be achieved by analysing dustiness (e.g. Tacconi et al. Reference Tacconi2008; Casey, Narayanan, & Cooray Reference Casey, Narayanan and Cooray2014), effective half-light radii (e.g. Allen et al. Reference Allen2015) and possibly gas tracing (e.g. Puglisi et al. Reference Puglisi2021).
$z>1.5$
). The connection between quiescent galaxies, star formation activity, and the role of environmental and stellar mass quenching is clearly challenging to disentangle at higher redshifts. Given previous evidence, we cannot rule out the possibility of hidden stellar mass quenching processes in Figs. 3–5. In addition, we also need to carry out other tests to investigate whether galaxy mergers are present, which may be achieved by analysing dustiness (e.g. Tacconi et al. Reference Tacconi2008; Casey, Narayanan, & Cooray Reference Casey, Narayanan and Cooray2014), effective half-light radii (e.g. Allen et al. Reference Allen2015) and possibly gas tracing (e.g. Puglisi et al. Reference Puglisi2021).
It is currently thought that massive galaxy clusters which pervade the local universe (e.g. Hernández-Fernández, Vílchez, &Iglesias-Páramo Reference Hernández-Fernández, Vlchez and Iglesias-Páramo2012) were assembled via merging of group structures (e.g. Press & Schechter Reference Press and Schechter1974; Fakhouri, Ma, & Boylan-Kolchin Reference Fakhouri, Ma and Boylan-Kolchin2010), according to the
![]() $\Lambda$
CDM hierarchical models. This means that prior to infall, some group galaxies have already experienced environmental interactions and star formation quenching, more commonly known as pre-processing (e.g. Fujita Reference Fujita2004; Wetzel et al. Reference Wetzel, Tinker, Conroy and van den Bosch2013; Bianconi et al. Reference Bianconi2018; Olave-Rojas et al. Reference Olave-Rojas2018). Because our study involves high redshift galaxies, we suspect that the high-density environments are still in early stages of development and that they will merge with other galaxies and small structures (e.g. Spitler et al. Reference Spitler2012) before settling into the large clusters that we observe in the low redshift universe. This means that the Butcher–Oemler effect and SFR-density relation may be difficult to pin down here, given that our high-density galaxies could undergo positive or negative growth mechanisms (e.g. cold gas accretion and tidal interactions, respectively) if they merge with other structures at later times.
$\Lambda$
CDM hierarchical models. This means that prior to infall, some group galaxies have already experienced environmental interactions and star formation quenching, more commonly known as pre-processing (e.g. Fujita Reference Fujita2004; Wetzel et al. Reference Wetzel, Tinker, Conroy and van den Bosch2013; Bianconi et al. Reference Bianconi2018; Olave-Rojas et al. Reference Olave-Rojas2018). Because our study involves high redshift galaxies, we suspect that the high-density environments are still in early stages of development and that they will merge with other galaxies and small structures (e.g. Spitler et al. Reference Spitler2012) before settling into the large clusters that we observe in the low redshift universe. This means that the Butcher–Oemler effect and SFR-density relation may be difficult to pin down here, given that our high-density galaxies could undergo positive or negative growth mechanisms (e.g. cold gas accretion and tidal interactions, respectively) if they merge with other structures at later times.
As addressed, the relationship we detect between galaxy evolution and environment appears to be strongest up to
![]() $z\sim2.4$
. At higher redshifts (
$z\sim2.4$
. At higher redshifts (
![]() $z>3.1$
), we suffer from small samples of quiescent sources and sSFR data and express caution with these results. Across our quiescent fraction, stellar mass and sSFR findings (Figs. 3, 4 and 5, respectively), we also encounter large errors and error overlap of some of the samples. Despite this, we established that the high-density environments of
$z>3.1$
), we suffer from small samples of quiescent sources and sSFR data and express caution with these results. Across our quiescent fraction, stellar mass and sSFR findings (Figs. 3, 4 and 5, respectively), we also encounter large errors and error overlap of some of the samples. Despite this, we established that the high-density environments of
![]() $z_{6}$
and
$z_{6}$
and
![]() $z_{8}$
have the largest stellar masses. Our data may suggest that we are detecting some environmental influence across
$z_{8}$
have the largest stellar masses. Our data may suggest that we are detecting some environmental influence across
![]() $z_{6}$
and
$z_{6}$
and
![]() $z_{8}$
, and that it may strengthen over time (as observed at
$z_{8}$
, and that it may strengthen over time (as observed at
![]() $z_{1}$
and
$z_{1}$
and
![]() $z_{2}$
), but a more complete sample is needed to confirm this result.
$z_{2}$
), but a more complete sample is needed to confirm this result.

Figure 5. Average specific star formation rate (sSFR) in
![]() $\rm {Gyr^{-1}}$
of the environments and complete samples of
$\rm {Gyr^{-1}}$
of the environments and complete samples of
![]() $2.0\leq z<2.2$
$2.0\leq z<2.2$
![]() $(z_{1})$
,
$(z_{1})$
,
![]() $2.2\leq z<2.4$
$2.2\leq z<2.4$
![]() $(z_{2})$
,
$(z_{2})$
,
![]() $3.1\leq z<3.4$
$3.1\leq z<3.4$
![]() $(z_{6})$
and
$(z_{6})$
and
![]() $3.8\leq z<4.2$
$3.8\leq z<4.2$
![]() $(z_{8})$
. Redshift slices
$(z_{8})$
. Redshift slices
![]() $z_{1}$
and
$z_{1}$
and
![]() $z_{2}$
share a horizontal axis, while
$z_{2}$
share a horizontal axis, while
![]() $z_{6}$
and
$z_{6}$
and
![]() $z_{8}$
share another. Errors shown correspond to the
$z_{8}$
share another. Errors shown correspond to the
![]() $\rm {68\%}$
confidence intervals calculated from a bootstrap analysis. The
$\rm {68\%}$
confidence intervals calculated from a bootstrap analysis. The
![]() $z_{6}$
low-density galaxy is omitted from the figure due to unavailable star formation data. AGN candidates of Cowley et al. (Reference Cowley2016) are also excluded from the sSFR samples. Markers are as in Fig. 3.
$z_{6}$
low-density galaxy is omitted from the figure due to unavailable star formation data. AGN candidates of Cowley et al. (Reference Cowley2016) are also excluded from the sSFR samples. Markers are as in Fig. 3.
We recognise that (excepting the H2 and H3 regions of
![]() $z_1$
; Yuan et al. Reference Yuan2014) the high-density environments of this study are photometric candidates and require spectroscopic confirmation for better characterisation, should they be studied in more detail. With deep near-IR imaging from its medium-band filters, the ZFOURGE survey has provided accurate samples of high redshift galaxies that has allowed us to explore the early universe (e.g. Spitler et al. Reference Spitler2012; Cowley et al. Reference Cowley2016, Reference Cowley2018; Kawinwanichakij et al. Reference Kawinwanichakij2016; Allen et al. Reference Allen2017; Papovich et al. Reference Papovich2018), but remains somewhat limited beyond
$z_1$
; Yuan et al. Reference Yuan2014) the high-density environments of this study are photometric candidates and require spectroscopic confirmation for better characterisation, should they be studied in more detail. With deep near-IR imaging from its medium-band filters, the ZFOURGE survey has provided accurate samples of high redshift galaxies that has allowed us to explore the early universe (e.g. Spitler et al. Reference Spitler2012; Cowley et al. Reference Cowley2016, Reference Cowley2018; Kawinwanichakij et al. Reference Kawinwanichakij2016; Allen et al. Reference Allen2017; Papovich et al. Reference Papovich2018), but remains somewhat limited beyond
![]() $z>3.1$
. To continue investigating early galaxy environments, we require larger datasets of high redshift sources which may be possible with the new Keck Wide-Field Imager and upcoming observations from the James Webb Space Telescope (JWST). Further investigation of the high-density environments probed in this work may be considered as one of the scientific goals of ZFOURGE 2, should a follow-up survey be conducted.
$z>3.1$
. To continue investigating early galaxy environments, we require larger datasets of high redshift sources which may be possible with the new Keck Wide-Field Imager and upcoming observations from the James Webb Space Telescope (JWST). Further investigation of the high-density environments probed in this work may be considered as one of the scientific goals of ZFOURGE 2, should a follow-up survey be conducted.
Finally, it is worth highlighting that we observed a very small volume of the universe through ZFOURGE and that cosmic variance may have an impact on our findings. While we detected environmental influence across
![]() $z_{1}$
,
$z_{1}$
,
![]() $z_{2}$
and potentially
$z_{2}$
and potentially
![]() $z_{6}$
and
$z_{6}$
and
![]() $z_{8}$
, we cannot say whether all overdense environments at these redshifts are accelerating galaxy evolution. Even though our results are supported by many previous studies, we acknowledge that any differences between our analyses and others is likely attributed to the phenomenon of cosmic variance, differences between galaxy surveys and environment detection and isolation techniques.
$z_{8}$
, we cannot say whether all overdense environments at these redshifts are accelerating galaxy evolution. Even though our results are supported by many previous studies, we acknowledge that any differences between our analyses and others is likely attributed to the phenomenon of cosmic variance, differences between galaxy surveys and environment detection and isolation techniques.
6. Conclusions
We have studied the effects of environment on galaxy evolution across
![]() $2.0\leq z<4.2$
using mass-limited
$2.0\leq z<4.2$
using mass-limited
![]() ${\rm log(M_{*}/M_\odot)}\geq9.5$
COSMOS sources from the ZFOURGE survey. We divided our sample into eight redshift slices and searched for low-, intermediate-, and high-density environments using the 7NN algorithm. We discovered new overdense candidates across four redshift slices,
${\rm log(M_{*}/M_\odot)}\geq9.5$
COSMOS sources from the ZFOURGE survey. We divided our sample into eight redshift slices and searched for low-, intermediate-, and high-density environments using the 7NN algorithm. We discovered new overdense candidates across four redshift slices,
![]() $2.0\leq z<2.2$
(
$2.0\leq z<2.2$
(
![]() $z_{1}$
),
$z_{1}$
),
![]() $2.2\leq z<2.4$
(
$2.2\leq z<2.4$
(
![]() $z_{2}$
),
$z_{2}$
),
![]() $3.1\leq z<3.4$
(
$3.1\leq z<3.4$
(
![]() $z_{6}$
) and
$z_{6}$
) and
![]() $3.8\leq z<4.2$
(
$3.8\leq z<4.2$
(
![]() $z_{8}$
). Our main findings are as follows:
$z_{8}$
). Our main findings are as follows:
-
1. The
 $z_{1}$
and
$z_{1}$
and
 $z_{2}$
high-density environments exhibit elevated quiescent fractions, contain
$z_{2}$
high-density environments exhibit elevated quiescent fractions, contain
 ${\rm log(M_{*}/M_\odot)}\geq10.2$
massive sources and suppressed star formation activity. Average stellar masses of
${\rm log(M_{*}/M_\odot)}\geq10.2$
massive sources and suppressed star formation activity. Average stellar masses of
 $z_{1}$
and
$z_{1}$
and
 $z_{2}$
were reported as
$z_{2}$
were reported as
 ${\rm log(M_{*}/M_\odot)}\sim10.220\pm0.096$
and
${\rm log(M_{*}/M_\odot)}\sim10.220\pm0.096$
and
 $\sim10.571^{+0.139}_{-0.136}$
, respectively. sSFRs decreased from low to high density by
$\sim10.571^{+0.139}_{-0.136}$
, respectively. sSFRs decreased from low to high density by
 $\sim$
34% and
$\sim$
34% and
 $\sim$
60% for
$\sim$
60% for
 $z_{1}$
and
$z_{1}$
and
 $z_{2}$
, respectively.
$z_{2}$
, respectively. -
2. The results for
 $z_{1}$
and
$z_{1}$
and
 $z_{2}$
suggest that
$z_{2}$
suggest that
 $z<2.4$
high-density environments already consist of evolved, passive galaxies. The significant build-up of stellar mass may also be indicative of merger processes.
$z<2.4$
high-density environments already consist of evolved, passive galaxies. The significant build-up of stellar mass may also be indicative of merger processes. -
3. With elevated stellar masses, we may have evidence to suggest that the
 $z_{6}$
and
$z_{6}$
and
 $z_{8}$
high-density environments have begun to influence galaxy evolution, but require more complete samples to confirm this finding.
$z_{8}$
high-density environments have begun to influence galaxy evolution, but require more complete samples to confirm this finding.
While the primary quenching mechanism is difficult to disentangle, our findings suggest that there is a correlation between high redshift galaxy evolution and environment. With our results also implying that the Butcher–Oemler effect and SFR-density relation may not reverse at higher redshifts, it seems that the role of environment in galaxy evolution continues to be a challenge requiring further investigation.
Acknowledgement
We thank the anonymous referee for constructive comments that improved aspects of the paper. This research includes data collected by the 6.5-m Magellan Telescopes at the Las Campanas Observatory, Chile. Data analysis was carried out using the Python 3 coding language. Packages of Python that were employed in this paper include matplotlib, a library for creating high quality graphs, Astropy, a community-developed package that contains functions for astronomical research, and NumPy, a library for scientific computing. This research received no specific grant from any funding agency, commercial, or not-for-profit sectors.
Data Availability
Not applicable.