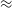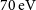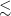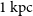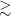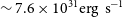1. Introduction
Although radio emission was detected earlier (Burke-Spolaor et al. Reference Burke-Spolaor2011), discovery of the spin period of PSR J0837
![]() $-$
2454 and measurements of the pulsar’s timing parameters were only made recently (Pol et al. Reference Pol2021). These measurements yielded a pulsar period
$-$
2454 and measurements of the pulsar’s timing parameters were only made recently (Pol et al. Reference Pol2021). These measurements yielded a pulsar period
![]() $P=629\ \mbox{ms}$
and spin period time derivative
$P=629\ \mbox{ms}$
and spin period time derivative
![]() $\dot{P}=3.49\times10^{-13}\mbox{s s}^{-1}$
, which imply a characteristic spin-down age
$\dot{P}=3.49\times10^{-13}\mbox{s s}^{-1}$
, which imply a characteristic spin-down age
![]() $\tau_\textrm{c}=28\,600\ \mbox{yr}$
, magnetic field
$\tau_\textrm{c}=28\,600\ \mbox{yr}$
, magnetic field
![]() $B=1.5\times10^{13}\mbox{ G}$
, and spin-down luminosity
$B=1.5\times10^{13}\mbox{ G}$
, and spin-down luminosity
![]() $\dot{E}=5.5\times10^{34}\mbox{ erg s}^{-1}$
. These parameters suggest PSR J0837
$\dot{E}=5.5\times10^{34}\mbox{ erg s}^{-1}$
. These parameters suggest PSR J0837
![]() $-$
2454 is a young, strongly magnetic, mildly energetic pulsar but not particularly unique among the general pulsar population, although it is apparently also a rotating radio transient (RRAT; see RRATalogFootnote a and Abhishek et al. Reference Abhishek, Tanushree, Hegde and Konar2022). What makes PSR J0837
$-$
2454 is a young, strongly magnetic, mildly energetic pulsar but not particularly unique among the general pulsar population, although it is apparently also a rotating radio transient (RRAT; see RRATalogFootnote a and Abhishek et al. Reference Abhishek, Tanushree, Hegde and Konar2022). What makes PSR J0837
![]() $-$
2454 special is its three-dimensional spatial position and the implications of this position.
$-$
2454 special is its three-dimensional spatial position and the implications of this position.
PSR J0837
![]() $-$
2454 is located at R.A.
$-$
2454 is located at R.A.
![]() $=08^\textrm{h}37^\textrm{m}57.73^\textrm{s}\pm0.06^\textrm{s}$
, decl.
$=08^\textrm{h}37^\textrm{m}57.73^\textrm{s}\pm0.06^\textrm{s}$
, decl.
![]() $=-24^\circ54'30''\pm1''$
(J2000), which leads to a Galactic longitude and latitude of
$=-24^\circ54'30''\pm1''$
(J2000), which leads to a Galactic longitude and latitude of
![]() $247.58^\circ$
and
$247.58^\circ$
and
![]() $9.77^\circ$
, respectively (Pol et al. Reference Pol2021). The high latitude is particularly noteworthy since this means that PSR J0837
$9.77^\circ$
, respectively (Pol et al. Reference Pol2021). The high latitude is particularly noteworthy since this means that PSR J0837
![]() $-$
2454 is possibly located far above the Galactic plane. The radio observations of Pol et al. (Reference Pol2021) gave a dispersion measure (DM) of
$-$
2454 is possibly located far above the Galactic plane. The radio observations of Pol et al. (Reference Pol2021) gave a dispersion measure (DM) of
![]() $143.1\pm0.1\mbox{ pc cm}^{-3}$
from scattering by interstellar electrons, which implies a pulsar distance of 6.3 kpc using the NE2001 model of the Galactic electron density (Cordes & Lazio Reference Cordes and Lazio2002) or
$143.1\pm0.1\mbox{ pc cm}^{-3}$
from scattering by interstellar electrons, which implies a pulsar distance of 6.3 kpc using the NE2001 model of the Galactic electron density (Cordes & Lazio Reference Cordes and Lazio2002) or
![]() $>$
$>$
![]() $25\mbox{ kpc}$
using the YMW16 model (Yao, Manchester, & Wang Reference Yao, Manchester and Wang2017). At the former distance, the pulsar’s height above the plane is 1.1 kpc, while the latter distance gives a height
$25\mbox{ kpc}$
using the YMW16 model (Yao, Manchester, & Wang Reference Yao, Manchester and Wang2017). At the former distance, the pulsar’s height above the plane is 1.1 kpc, while the latter distance gives a height
![]() $\gg1\mbox{ kpc}$
. Thus if the large distance inferred from the radio measurements is correct, then PSR J0837
$\gg1\mbox{ kpc}$
. Thus if the large distance inferred from the radio measurements is correct, then PSR J0837
![]() $-$
2454 is far out of the Galactic plane and is very likely to be one of the only known pulsars to be born from a runaway O/B star (see Pol et al. Reference Pol2021, for more details), and its characteristics would provide insights into the pulsar’s origin and connection to other neutron stars.
$-$
2454 is far out of the Galactic plane and is very likely to be one of the only known pulsars to be born from a runaway O/B star (see Pol et al. Reference Pol2021, for more details), and its characteristics would provide insights into the pulsar’s origin and connection to other neutron stars.
On the other hand, pulsar distances inferred using radio DMs can occasionally be discrepant from distances measured via other techniques (see, e.g. Deller et al. Reference Deller2019). In the case of PSR J0837
![]() $-$
2454, radio imaging shows diffuse emission around PSR J0837
$-$
2454, radio imaging shows diffuse emission around PSR J0837
![]() $-$
2454, which could imply a much lower distance if associated with the pulsar. In particular, GLEAM radio data show a
$-$
2454, which could imply a much lower distance if associated with the pulsar. In particular, GLEAM radio data show a
![]() $\sim$
$\sim$
![]() $1.5^\circ$
diameter circular structure surrounding PSR J0837
$1.5^\circ$
diameter circular structure surrounding PSR J0837
![]() $-$
2454 that could be a supernova remnant (Hurley-Walker et al. Reference Hurley-Walker2017). If this structure is indeed a supernova remnant and is the remnant left over from the birth of PSR J0837
$-$
2454 that could be a supernova remnant (Hurley-Walker et al. Reference Hurley-Walker2017). If this structure is indeed a supernova remnant and is the remnant left over from the birth of PSR J0837
![]() $-$
2454, then the distance is estimated to be 0.9 kpc (Pol et al. Reference Pol2021). Alternatively, H
$-$
2454, then the distance is estimated to be 0.9 kpc (Pol et al. Reference Pol2021). Alternatively, H
![]() $\alpha$
observations from SHASSA (Gaustad et al. Reference Gaustad, McCullough, Rosing and Van Buren2001) show enhanced diffuse emission around PSR J0837
$\alpha$
observations from SHASSA (Gaustad et al. Reference Gaustad, McCullough, Rosing and Van Buren2001) show enhanced diffuse emission around PSR J0837
![]() $-$
2454 (but not coincident with the potential supernova remnant), which could contribute to the aforementioned DM and could imply an even lower distance of 0.2 kpc (Pol et al. Reference Pol2021). At these two short distance possibilities, the pulsar’s height above the Galactic plane is either 151 or 34 pc and thus not particularly unusual. However, what would be extraordinary in this case is the pulsar’s low X-ray luminosity, which would make PSR J0837
$-$
2454 (but not coincident with the potential supernova remnant), which could contribute to the aforementioned DM and could imply an even lower distance of 0.2 kpc (Pol et al. Reference Pol2021). At these two short distance possibilities, the pulsar’s height above the Galactic plane is either 151 or 34 pc and thus not particularly unusual. However, what would be extraordinary in this case is the pulsar’s low X-ray luminosity, which would make PSR J0837
![]() $-$
2454 one of the coolest young neutron stars known, and its characteristics would provide crucial constraints on neutron star cooling theory and nuclear physics properties.
$-$
2454 one of the coolest young neutron stars known, and its characteristics would provide crucial constraints on neutron star cooling theory and nuclear physics properties.
A short 1.5 ks Swift XRT observation was taken on 2021 April 28 (ObsID 00014291001) and detected PSR J0837
![]() $-$
2454 at a 0.2–10 keV count rate of 0.0013 counts s
$-$
2454 at a 0.2–10 keV count rate of 0.0013 counts s
![]() $^{-1}$
and an estimated 0.3–10 keV flux of
$^{-1}$
and an estimated 0.3–10 keV flux of
![]() $\sim7\times10^{-14}\mbox{erg s}^{-1}$
cm
$\sim7\times10^{-14}\mbox{erg s}^{-1}$
cm
![]() $^{-2}$
. PSR J0837
$^{-2}$
. PSR J0837
![]() $-$
2454 was also detected by eROSITA in eRASS:4 but only at 0.2–0.7 keV, indicating it is a very soft X-ray source (Mayer & Becker Reference Mayer and Becker2024). The Swift flux means that the X-ray luminosity of PSR J0837
$-$
2454 was also detected by eROSITA in eRASS:4 but only at 0.2–0.7 keV, indicating it is a very soft X-ray source (Mayer & Becker Reference Mayer and Becker2024). The Swift flux means that the X-ray luminosity of PSR J0837
![]() $-$
2454 is
$-$
2454 is
![]() $L_\textrm{X}\sim 7\times10^{30}\mbox{erg s}^{-1}$
at a distance of 0.9 kpc (note this luminosity estimate does not account for X-ray absorption or spectral characteristics). Young neutron stars of age
$L_\textrm{X}\sim 7\times10^{30}\mbox{erg s}^{-1}$
at a distance of 0.9 kpc (note this luminosity estimate does not account for X-ray absorption or spectral characteristics). Young neutron stars of age
![]() $\sim$
$\sim$
![]() $3\times 10^4\mbox{ yr}$
have thermal X-ray luminosities
$3\times 10^4\mbox{ yr}$
have thermal X-ray luminosities
![]() $\sim$
$\sim$
![]() $10^{32}$
–
$10^{32}$
–
![]() $10^{33}\mbox{ erg s}^{-1}$
(see, e.g. Potekhin et al. Reference Potekhin, Zyuzin, Yakovlev, Beznogov and Shibanov2020), and young pulsars often have a non-thermal magnetosphere or pulsar wind component to their X-ray luminosities (see, e.g. Becker Reference Becker and Becker2009). Cool neutron stars like PSR J0837
$10^{33}\mbox{ erg s}^{-1}$
(see, e.g. Potekhin et al. Reference Potekhin, Zyuzin, Yakovlev, Beznogov and Shibanov2020), and young pulsars often have a non-thermal magnetosphere or pulsar wind component to their X-ray luminosities (see, e.g. Becker Reference Becker and Becker2009). Cool neutron stars like PSR J0837
![]() $-$
2454 (and PSR J0007+7303, PSR B1727
$-$
2454 (and PSR J0007+7303, PSR B1727
![]() $-$
47, and PSR B2334+61) are crucial sources because their low luminosities point to cooling that invoke fast direct Urca neutrino emission processes, which is only allowed for high core proton fractions and only predicted by some nuclear equations of state (Lattimer et al. Reference Lattimer, Pethick, Prakash and Haensel1991; Page & Applegate Reference Page and Applegate1992; see, e.g. Potekhin, Pons, & Page Reference Potekhin, Pons and Page2015, for review). Thus the few sources like PSR J0837
$-$
47, and PSR B2334+61) are crucial sources because their low luminosities point to cooling that invoke fast direct Urca neutrino emission processes, which is only allowed for high core proton fractions and only predicted by some nuclear equations of state (Lattimer et al. Reference Lattimer, Pethick, Prakash and Haensel1991; Page & Applegate Reference Page and Applegate1992; see, e.g. Potekhin, Pons, & Page Reference Potekhin, Pons and Page2015, for review). Thus the few sources like PSR J0837
![]() $-$
2454 are critical astronomical objects for probing fundamental physics at supranuclear densities.
$-$
2454 are critical astronomical objects for probing fundamental physics at supranuclear densities.
Here we report the analyses of new radio observations using the Parkes Murriyang telescope and Very Long Baseline Array (VLBA) and the first long X-ray observations of PSR J0837
![]() $-$
2454. In Section 2, we discuss the observational data and our analysis procedure, while in Section 3, we describe results from these observing campaigns. In Section 4, we discuss the implications of our results for the distance to PSR J0837
$-$
2454. In Section 2, we discuss the observational data and our analysis procedure, while in Section 3, we describe results from these observing campaigns. In Section 4, we discuss the implications of our results for the distance to PSR J0837
![]() $-$
2454 and the low measured luminosity and surface temperature in the context of how neutron stars cool over time. In Section 5, we summarize our findings.
$-$
2454 and the low measured luminosity and surface temperature in the context of how neutron stars cool over time. In Section 5, we summarize our findings.
2. Observations and data analysis
2.1 Radio
The biggest uncertainty around PSR J0837
![]() $-$
2454 is that the DM derived distance (
$-$
2454 is that the DM derived distance (
![]() $d>6$
kpc) places this pulsar at the edge of the Galaxy and at an anomalous z-height (
$d>6$
kpc) places this pulsar at the edge of the Galaxy and at an anomalous z-height (
![]() $>$
1 kpc), while a distance estimated from diffuse emission in optical and radio give a much lower value (
$>$
1 kpc), while a distance estimated from diffuse emission in optical and radio give a much lower value (
![]() $d<1$
kpc) (Pol et al. Reference Pol2021). To conclusively determine the distance, we conducted observations of PSR J0837
$d<1$
kpc) (Pol et al. Reference Pol2021). To conclusively determine the distance, we conducted observations of PSR J0837
![]() $-$
2454 using the VLBA to measure an astrometric parallax. We coupled these VLBA observations with observations using the ultra-wide Low (UWL) receiver (Hobbs et al. Reference Hobbs2020) on the Parkes Murriyang radio telescope, in order to produce a timing solution for gating the VLBA data and to study the spectro-temporal properties of the pulsar with the wide bandwidth and sensitivity of the UWL. Here we describe our observations using both instruments.
$-$
2454 using the VLBA to measure an astrometric parallax. We coupled these VLBA observations with observations using the ultra-wide Low (UWL) receiver (Hobbs et al. Reference Hobbs2020) on the Parkes Murriyang radio telescope, in order to produce a timing solution for gating the VLBA data and to study the spectro-temporal properties of the pulsar with the wide bandwidth and sensitivity of the UWL. Here we describe our observations using both instruments.
2.1.1 Parkes Murriyang observations
We obtained UWL observations of PSR J0837
![]() $-$
2454 from 2021 October to 2022 March and 2022 October to 2023 March for a total of 18 observing epochs. These observation windows were chosen to overlap with our VLBA observations so that we could mitigate the large red noise of this pulsar (Pol et al. Reference Pol2021) and produce an accurate timing solution for VLBA gating observations. The first six epochs in the first observing window had a total integration time of 1 h, while the other epochs in both windows had a total integration time of 30 min. The observations used the medusa backend, with observations performed in the ‘fold’ mode, 30 s sub-integration time, 1 MHz resolution across the full 704–4 032 MHz band, 1 024 phase bins across one rotation, and full Stokes polarisation information. In addition to the pulsar, each observation also monitored the local noise diode for flux and polarisation calibration.
$-$
2454 from 2021 October to 2022 March and 2022 October to 2023 March for a total of 18 observing epochs. These observation windows were chosen to overlap with our VLBA observations so that we could mitigate the large red noise of this pulsar (Pol et al. Reference Pol2021) and produce an accurate timing solution for VLBA gating observations. The first six epochs in the first observing window had a total integration time of 1 h, while the other epochs in both windows had a total integration time of 30 min. The observations used the medusa backend, with observations performed in the ‘fold’ mode, 30 s sub-integration time, 1 MHz resolution across the full 704–4 032 MHz band, 1 024 phase bins across one rotation, and full Stokes polarisation information. In addition to the pulsar, each observation also monitored the local noise diode for flux and polarisation calibration.
We processed the data using psrchive and pypulse. We identified and zapped radio frequency interference (RFI) using clfd (Morello et al. Reference Morello2019), which is a smart RFI removal algorithm. Any sources of RFI missed by this algorithm were manually zapped using pazi. We used separate, archival observations of PKS B0407
![]() $-$
658 for flux calibration, and long-track observations of PSR J0437
$-$
658 for flux calibration, and long-track observations of PSR J0437
![]() $-$
4715 were used as the input to the polarisation calibration pcm routine in psrchive for polarisation calibration. These files were used with pac -cT to calibrate the flux and polarisation for each epoch.
$-$
4715 were used as the input to the polarisation calibration pcm routine in psrchive for polarisation calibration. These files were used with pac -cT to calibrate the flux and polarisation for each epoch.
Following calibration, we measured the rotation measure (RM) at each epoch using the brute force approach in rmfit, where we searched for RMs between
![]() $-$
3 000 to 3 000 rad m
$-$
3 000 to 3 000 rad m
![]() $^{-2}$
with a step size of 6 rad m
$^{-2}$
with a step size of 6 rad m
![]() $^{-2}$
. We use ionFR (Sotomayor-Beltran et al. Reference Sotomayor-Beltran2013) to calculate the ionospheric Faraday rotation contribution to the measured total RM. We use the International GNSS Service global ionospheric total electron content maps (Hernández-Pajares et al. Reference Hernández-Pajares2009; Noll Reference Noll2010) and the International Geomagnetic Reference Field (Thébault et al. Reference Thébault2015) as inputs to ionFR. We obtain ionospheric RMs in the range of
$^{-2}$
. We use ionFR (Sotomayor-Beltran et al. Reference Sotomayor-Beltran2013) to calculate the ionospheric Faraday rotation contribution to the measured total RM. We use the International GNSS Service global ionospheric total electron content maps (Hernández-Pajares et al. Reference Hernández-Pajares2009; Noll Reference Noll2010) and the International Geomagnetic Reference Field (Thébault et al. Reference Thébault2015) as inputs to ionFR. We obtain ionospheric RMs in the range of
![]() $-$
3.15 to
$-$
3.15 to
![]() $-$
0.65 rad m
$-$
0.65 rad m
![]() $^{-2}$
(negative values in the Southern hemisphere due to the orientation of Earth’s geomagnetic field), which are used to obtain the non-terrestrial RM from
$^{-2}$
(negative values in the Southern hemisphere due to the orientation of Earth’s geomagnetic field), which are used to obtain the non-terrestrial RM from
![]() $\textrm{RM}_\textrm{ISM} = RM_\textrm{tot} - RM_\textrm{ion}$
. The best-fit RM value was used to correct the observation for Faraday rotation with pam -R.
$\textrm{RM}_\textrm{ISM} = RM_\textrm{tot} - RM_\textrm{ion}$
. The best-fit RM value was used to correct the observation for Faraday rotation with pam -R.
2.1.2 Very Long Baseline Array observations
We observed PSR J0837
![]() $-$
2454 using VLBA a total of twelve times between 2022 October and 2024 May (project code BD256). Observations were made using
$-$
2454 using VLBA a total of twelve times between 2022 October and 2024 May (project code BD256). Observations were made using
![]() $8\times32$
MHz sub-bands placed in the range 1 392–1 744 MHz and avoiding known regions of radio frequency interference. Each observation was 1.5 h in duration, spending around 60% of the time on the target field and interleaving with 50 s scans on a phase reference source (ICRF J084656.6
$8\times32$
MHz sub-bands placed in the range 1 392–1 744 MHz and avoiding known regions of radio frequency interference. Each observation was 1.5 h in duration, spending around 60% of the time on the target field and interleaving with 50 s scans on a phase reference source (ICRF J084656.6
![]() $-$
260750) every
$-$
260750) every
![]() $\sim$
3 min. The bright source IERS B0742+103 was observed at the end of each observation to calibrate the instrumental bandpass.
$\sim$
3 min. The bright source IERS B0742+103 was observed at the end of each observation to calibrate the instrumental bandpass.
Data were correlated using the DiFX software correlator and employing an ephemeris derived from Parkes monitoring to provide pulse-phase-resolved gating to improve the image signal-to-noise ratio on the pulsar field (Deller et al. Reference Deller2011). For most observations, two such correlation passes were run – one producing a single ‘matched filter’ output in which the pulse was weighted by the expected profile and summed in phase, and another in which 20 equally spaced pulsar ‘bins’ were produced, each spanning 5% of the pulse phase. In addition to these pulsar datasets, we produced a number of other visibility datasets from scans on the pulsar. First, a dataset centred at the pulsar position without any pulse-phase-resolved gating was used (the ‘ungated’ pulsar dataset). Additionally, three other correlator passes were undertaken at the position of other compact radio sources visible within the VLBA primary beam, in order to provide information that could be used for calibration refinement. In a preliminary observation of the PSR J0837
![]() $-$
2454 field taken prior to the first astrometric observation, we imaged every known radio source within
$-$
2454 field taken prior to the first astrometric observation, we imaged every known radio source within
![]() $\sim$
25 arcmin of PSR J0837
$\sim$
25 arcmin of PSR J0837
![]() $-$
2454 and identified three sources with flux densities ranging from 7–20 mJy that contained compact source components detectable by VLBA. Correlations centred at each of these positions provided three ‘in-beam calibrator’ datasets.
$-$
2454 and identified three sources with flux densities ranging from 7–20 mJy that contained compact source components detectable by VLBA. Correlations centred at each of these positions provided three ‘in-beam calibrator’ datasets.
Data reduction made use of the psrvlbreduce pipeline from Ding et al. (Reference Ding2023) and employed standard phase and amplitude calibration techniques as described therein. After calibration, a
![]() $2''\times2''$
area centred on the nominal pulsar position was imaged, using both the gated and the ungated datasets (to guard against the eventuality that the pulsar ephemeris was insufficiently well modelled at the time of any given observation). Naturally weighted images, with a typical angular resolution of
$2''\times2''$
area centred on the nominal pulsar position was imaged, using both the gated and the ungated datasets (to guard against the eventuality that the pulsar ephemeris was insufficiently well modelled at the time of any given observation). Naturally weighted images, with a typical angular resolution of
![]() $5\times25$
milliarcsec, were made at all epochs, with a typical image rms of
$5\times25$
milliarcsec, were made at all epochs, with a typical image rms of
![]() $\sim$
60
$\sim$
60
![]() $\mu$
Jy/beam in the ungated image. PSR J0837
$\mu$
Jy/beam in the ungated image. PSR J0837
![]() $-$
2454 was detected in 5 of 12 observations with a significance ranging from 7.5
$-$
2454 was detected in 5 of 12 observations with a significance ranging from 7.5
![]() $\sigma$
to 13
$\sigma$
to 13
![]() $\sigma$
in one bin of the binned datasets. The pulsar was not detected in the first three observations – as can be seen in Fig. 2, this corresponds to a time at which the flux density is at a minimum value. In the 4th and 5th observation, no ‘binned’ datasets were produced, and the pulsar was not detected in the matched-filter or ungated datasets. At the time of submission, the final two observations had not yet been correlated and released. Where detected, the cleaned VLBA images of PSR J0837
$\sigma$
in one bin of the binned datasets. The pulsar was not detected in the first three observations – as can be seen in Fig. 2, this corresponds to a time at which the flux density is at a minimum value. In the 4th and 5th observation, no ‘binned’ datasets were produced, and the pulsar was not detected in the matched-filter or ungated datasets. At the time of submission, the final two observations had not yet been correlated and released. Where detected, the cleaned VLBA images of PSR J0837
![]() $-$
2454 show a source size which is inconsistent with a point-source, demonstrating that the pulsar is significantly affected by angular broadening due to multi-path propagation in the turbulent ionised interstellar medium. Because the point spread function of the interferometer is elongated at these low declinations (a typical beam size was
$-$
2454 show a source size which is inconsistent with a point-source, demonstrating that the pulsar is significantly affected by angular broadening due to multi-path propagation in the turbulent ionised interstellar medium. Because the point spread function of the interferometer is elongated at these low declinations (a typical beam size was
![]() $5\times20$
milliarcsec), useful constraints on the intrinsic source size are best obtained under the assumption of a circularly symmetric scatter–broadened source, although it is also possible that the scatter–broadening is mildly asymmetric. These returned a source size in the range 8–10 millisarcsec. The extragalactic calibrator sources that were observed in–beam contemporaneously with the pulsar showed a slightly larger degree of angular broadening, with sizes ranging from 12–20 milliarcsec, although this may also partly reflect intrinsic source structure.
$5\times20$
milliarcsec), useful constraints on the intrinsic source size are best obtained under the assumption of a circularly symmetric scatter–broadened source, although it is also possible that the scatter–broadening is mildly asymmetric. These returned a source size in the range 8–10 millisarcsec. The extragalactic calibrator sources that were observed in–beam contemporaneously with the pulsar showed a slightly larger degree of angular broadening, with sizes ranging from 12–20 milliarcsec, although this may also partly reflect intrinsic source structure.
2.2 X-ray
XMM-Newton observed PSR J0837
![]() $-$
2454 on 2023 April 24–26 (ObsID 0900150101) for about 90 ks with EPIC in large window mode and using the thin optical filter. Large window mode was chosen due to its higher time resolution, 47.7 ms for pn, which allows for measurement of the 629 ms spin period of the pulsar. We process EPIC MOS and pn observation data files (ODFs) using the Science Analysis Software (SAS) 20.0.0 tasks emproc and epproc, respectively. To remove periods of background flaring, we extract single event (
$-$
2454 on 2023 April 24–26 (ObsID 0900150101) for about 90 ks with EPIC in large window mode and using the thin optical filter. Large window mode was chosen due to its higher time resolution, 47.7 ms for pn, which allows for measurement of the 629 ms spin period of the pulsar. We process EPIC MOS and pn observation data files (ODFs) using the Science Analysis Software (SAS) 20.0.0 tasks emproc and epproc, respectively. To remove periods of background flaring, we extract single event (
![]() $\mbox{PATTERN}=0$
), high energy (
$\mbox{PATTERN}=0$
), high energy (
![]() $>$
10 keV for MOS and 10–12 keV for pn) light curves from which we determine low and steady count rate thresholds of
$>$
10 keV for MOS and 10–12 keV for pn) light curves from which we determine low and steady count rate thresholds of
![]() $0.2\mbox{ counts s}^{-1}$
for MOS and
$0.2\mbox{ counts s}^{-1}$
for MOS and
![]() $0.4\mbox{ counts s}^{-1}$
for pn. We use these thresholds to generate good time intervals (GTIs) with tabgtigen, which we then use to produce flare-cleaned events with evtselect and barycenter these events with barycen. The resulting data have effective exposure times of 85 ks for MOS and 77 ks for pn. We use both edetect and wavdetect to check the source position and find consistent values within the uncertainty of the MOS (and pn) on-axis point spread function of 4
$0.4\mbox{ counts s}^{-1}$
for pn. We use these thresholds to generate good time intervals (GTIs) with tabgtigen, which we then use to produce flare-cleaned events with evtselect and barycenter these events with barycen. The resulting data have effective exposure times of 85 ks for MOS and 77 ks for pn. We use both edetect and wavdetect to check the source position and find consistent values within the uncertainty of the MOS (and pn) on-axis point spread function of 4
![]() $^{\prime\prime}$
, with R.A.
$^{\prime\prime}$
, with R.A.
![]() $=08^\textrm{h}37^\textrm{m}57.7^\textrm{s}$
, decl.
$=08^\textrm{h}37^\textrm{m}57.7^\textrm{s}$
, decl.
![]() $=-24^\circ 54'30''$
(J2000). This position is fully consistent with the radio position, and thus we can positively associate our X-ray point source with that of PSR J0837
$=-24^\circ 54'30''$
(J2000). This position is fully consistent with the radio position, and thus we can positively associate our X-ray point source with that of PSR J0837
![]() $-$
2454. Fig. 1 shows the MOS1, MOS2, and pn images, and PSR J0837
$-$
2454. Fig. 1 shows the MOS1, MOS2, and pn images, and PSR J0837
![]() $-$
2454 is clearly evident in each dataset.
$-$
2454 is clearly evident in each dataset.

Figure 1. X-ray field of PSR J0837
![]() $-$
2454 from XMM-Newton MOS1 (left), MOS2 (middle), and pn (right) in large window mode. Source counts are extracted from a 20
$-$
2454 from XMM-Newton MOS1 (left), MOS2 (middle), and pn (right) in large window mode. Source counts are extracted from a 20
![]() $^{\prime\prime}$
radius circle, while background counts are extracted from an annulus with inner and outer radii of 22
$^{\prime\prime}$
radius circle, while background counts are extracted from an annulus with inner and outer radii of 22
![]() $^{\prime\prime}$
and 32
$^{\prime\prime}$
and 32
![]() $^{\prime\prime}$
, respectively.
$^{\prime\prime}$
, respectively.
We consider the regions denoted in Fig. 1 for extracting MOS and pn source counts. These are determined by first using eregionanalyse, which indicates an optimum circular extraction radius of about 20
![]() $^{\prime\prime}$
. Using epatplot, we do not find the source counts to be significantly affected by pile-up. We extract source and background counts for timing and spectral analysis using
$^{\prime\prime}$
. Using epatplot, we do not find the source counts to be significantly affected by pile-up. We extract source and background counts for timing and spectral analysis using
![]() $\mbox{PATTERN}\le12$
and
$\mbox{PATTERN}\le12$
and
![]() $\le4$
for MOS and pn, respectively, and
$\le4$
for MOS and pn, respectively, and
![]() $\mbox{FLAG}=0$
for spectra. We apply light curve corrections using epiclccorr. We calculate source and background areas and account for bad pixels and chip gaps using backscale. We then compute rmf and arf files. We measure background-subtracted counts of 740, 720, and 4 100 and count-rates of 0.0087, 0.0084, and 0.053 counts s
$\mbox{FLAG}=0$
for spectra. We apply light curve corrections using epiclccorr. We calculate source and background areas and account for bad pixels and chip gaps using backscale. We then compute rmf and arf files. We measure background-subtracted counts of 740, 720, and 4 100 and count-rates of 0.0087, 0.0084, and 0.053 counts s
![]() $^{-1}$
for MOS1, MOS2, and pn, respectively. In order to improve statistics, we combine the MOS1 and MOS2 spectra using epicspeccombine. We bin spectra using specgroup to a minimum of 25 photons per bin for the combined MOS spectrum and for the pn spectrum.
$^{-1}$
for MOS1, MOS2, and pn, respectively. In order to improve statistics, we combine the MOS1 and MOS2 spectra using epicspeccombine. We bin spectra using specgroup to a minimum of 25 photons per bin for the combined MOS spectrum and for the pn spectrum.
3. Results
3.1 Radio spectral properties
Fig. 2 shows the mean integrated flux density of PSR J0837
![]() $-$
2454 over the Parkes observing campaign. This pulsar shows a significant amount of variation in the flux density over both short and long timescales, which is likely indicative of both refractive and diffractive scintillation from the intervening interstellar medium (ISM). On the other hand, neither the DM nor RM show any evidence for significant variations over the same timespan. Using a median
$-$
2454 over the Parkes observing campaign. This pulsar shows a significant amount of variation in the flux density over both short and long timescales, which is likely indicative of both refractive and diffractive scintillation from the intervening interstellar medium (ISM). On the other hand, neither the DM nor RM show any evidence for significant variations over the same timespan. Using a median
![]() $\textrm{RM} = 360.72$
rad m
$\textrm{RM} = 360.72$
rad m
![]() $^{-2}$
and a DM of 143.1 pc cm
$^{-2}$
and a DM of 143.1 pc cm
![]() $^{-3}$
, we can derive an average magnetic field strength along the line of sight,
$^{-3}$
, we can derive an average magnetic field strength along the line of sight,
To measure the spectrum of PSR J0837
![]() $-$
2454, we do not require the full native resolution of 1 MHz offered by the UWL receiver. Thus we downsampled our data to 8 frequency bins and calculated the mean integrated flux density in each bin. The spectrum calculated with this method for every epoch is shown in Fig. 3 using transparent square markers. Given the large flux density variation as a function of time, we also averaged the per-epoch spectrum to get the mean spectrum, which is shown using solid purple markers in Fig. 3, where the uncertainty is given by the standard deviation of the measured flux density in each bin. A power-law fit (
$-$
2454, we do not require the full native resolution of 1 MHz offered by the UWL receiver. Thus we downsampled our data to 8 frequency bins and calculated the mean integrated flux density in each bin. The spectrum calculated with this method for every epoch is shown in Fig. 3 using transparent square markers. Given the large flux density variation as a function of time, we also averaged the per-epoch spectrum to get the mean spectrum, which is shown using solid purple markers in Fig. 3, where the uncertainty is given by the standard deviation of the measured flux density in each bin. A power-law fit (
![]() $S_{\nu} \propto \nu^{\alpha}$
) to this mean spectrum yields a spectral index of
$S_{\nu} \propto \nu^{\alpha}$
) to this mean spectrum yields a spectral index of
![]() $\alpha = 0.13 \pm 0.6$
, though we note that this flat spectrum is likely due to effects of refractive scintillation, similar to that seen in, e.g. PSR J1740+1000 (McLaughlin et al. Reference McLaughlin, Arzoumanian, Cordes, Backer, Lommen, Lorimer and Zepka2002).
$\alpha = 0.13 \pm 0.6$
, though we note that this flat spectrum is likely due to effects of refractive scintillation, similar to that seen in, e.g. PSR J1740+1000 (McLaughlin et al. Reference McLaughlin, Arzoumanian, Cordes, Backer, Lommen, Lorimer and Zepka2002).

Figure 2. Mean integrated flux density over time from Parkes Murriyang UWL observations of PSR J0837
![]() $-$
2454 starting on 2021 October 3 (MJD 59490). Errors shown are 1
$-$
2454 starting on 2021 October 3 (MJD 59490). Errors shown are 1
![]() $\sigma$
.
$\sigma$
.

Figure 3. Radio spectrum from Parkes Murriyang UWL observations of PSR J0837
![]() $-$
2454. Light colored points indicate mean integrated flux densities for each epoch of observation, while dark purple points indicate the average at each frequency. Errors shown are 1
$-$
2454. Light colored points indicate mean integrated flux densities for each epoch of observation, while dark purple points indicate the average at each frequency. Errors shown are 1
![]() $\sigma$
.
$\sigma$
.
3.2 Updated radio timing model
Using our radio data, we also generated a new timing solution for PSR J0837
![]() $-$
2454. Since there was no significant variation in the DM relative to the fiducial DM used in the fold-mode observations, we held the DM fixed to this value. Given that there are no significant DM variations, we time and frequency scrunched each observation and, along with the standard profile from Pol et al. (Reference Pol2021), derived a corresponding time-of-arrival (TOA) for each epoch using pat.
$-$
2454. Since there was no significant variation in the DM relative to the fiducial DM used in the fold-mode observations, we held the DM fixed to this value. Given that there are no significant DM variations, we time and frequency scrunched each observation and, along with the standard profile from Pol et al. (Reference Pol2021), derived a corresponding time-of-arrival (TOA) for each epoch using pat.
The timing model and the corresponding residuals are shown in Table 1 and Fig. 4, respectively. We used PINT (Luo et al. Reference Luo2019, Reference Luo2021) to time the pulsar, including modeling the white (EFAC only) and red noise (Susobhanan et al. Reference Susobhanan2024). We used the timing model from Pol et al. (Reference Pol2021) to initialize our timing model after which the parameters were allowed to vary. We tried including more frequency derivatives, parallax, and proper motion to the timing model, but none of these parameters were found significant via an f-test.
Similar to Pol et al. (Reference Pol2021), we notice significant red noise in the residuals for this pulsar. Without an explicit red noise process in the timing model, the red noise was absorbed in the fits to the sky-position of the pulsar, resulting in underestimating the uncertainty on the measured right ascension and declination for the pulsar by
![]() $\sim$
4 and
$\sim$
4 and
![]() $\sim$
6, respectively. To accurately reflect the uncertainties on these parameters, we include a red noise model with only a single harmonic, as determined using the WaveX model in PINT (Susobhanan et al. Reference Susobhanan2024). We also attempted to phase connect the TOAs from these observations with those collected in Pol et al. (Reference Pol2021), but we were unsuccessful due to the large red noise present in this pulsar.
$\sim$
6, respectively. To accurately reflect the uncertainties on these parameters, we include a red noise model with only a single harmonic, as determined using the WaveX model in PINT (Susobhanan et al. Reference Susobhanan2024). We also attempted to phase connect the TOAs from these observations with those collected in Pol et al. (Reference Pol2021), but we were unsuccessful due to the large red noise present in this pulsar.
3.3 VLBA astrometric results
The 7–13
![]() $\sigma$
detections described in Section 2.1.2 enable us to measure the position of PSR J0837
$\sigma$
detections described in Section 2.1.2 enable us to measure the position of PSR J0837
![]() $-$
2454 with a nominal accuracy of 0.5–1 milliarcsec in right ascension and 1–2 milliarcsec in declination at each epoch. However, these statistical uncertainties do not encompass any residual calibration errors, which can be substantial, particularly at low observing elevations as is necessary for the VLBA at these declinations (e.g. Deller et al. Reference Deller2019). In this instance, the significant angular broadening of the calibrator sources also means that longer integration times are required to achieve sufficient signal-to-noise ratio on the calibrators, which further degrades the astrometric quality as the interpolation time increases.
$-$
2454 with a nominal accuracy of 0.5–1 milliarcsec in right ascension and 1–2 milliarcsec in declination at each epoch. However, these statistical uncertainties do not encompass any residual calibration errors, which can be substantial, particularly at low observing elevations as is necessary for the VLBA at these declinations (e.g. Deller et al. Reference Deller2019). In this instance, the significant angular broadening of the calibrator sources also means that longer integration times are required to achieve sufficient signal-to-noise ratio on the calibrators, which further degrades the astrometric quality as the interpolation time increases.
Table 1. Parameters for PSR J0837
![]() $-$
2454.
$-$
2454.


Figure 4. Post-fit residuals, along with 1
![]() $\sigma$
uncertainties, from the Parkes timing campaign starting on 2021 October 3 (MJD 59490). Red noise is clearly visible, with the overall RMS of 100
$\sigma$
uncertainties, from the Parkes timing campaign starting on 2021 October 3 (MJD 59490). Red noise is clearly visible, with the overall RMS of 100
![]() $\mu$
s in the residuals being comparable to the timing solution obtained in Pol et al. (Reference Pol2021). We are unable to phase connect the TOAs from this observing campaign to those from Pol et al. (Reference Pol2021).
$\mu$
s in the residuals being comparable to the timing solution obtained in Pol et al. (Reference Pol2021). We are unable to phase connect the TOAs from this observing campaign to those from Pol et al. (Reference Pol2021).
In Table 2, we show the results of a straightforward least squares fit to the reference position, proper motion, and parallax for PSR J0837
![]() $-$
2454 based on the VLBA results, and we plot the model against the observed positions as a function of time in Fig. 5. However, significant unmodelled systematic errors are present in the data, as can be seen from the
$-$
2454 based on the VLBA results, and we plot the model against the observed positions as a function of time in Fig. 5. However, significant unmodelled systematic errors are present in the data, as can be seen from the
![]() $\chi^2$
of the fit. We discuss the degree to which these results (and a future extension to the VLBA astrometry) can constrain the distance to the pulsar in Section 4.1. Finally, we note that the uncertainty in the reference position of the pulsar, which is not quoted in Table 2, is dominated by the uncertainty in the in-beam calibrator positions, which themselves were referenced to the primary phase calibrator located at a larger angular separation – this uncertainty is likely to be on the order of 5 milliarcsec in the current dataset.
$\chi^2$
of the fit. We discuss the degree to which these results (and a future extension to the VLBA astrometry) can constrain the distance to the pulsar in Section 4.1. Finally, we note that the uncertainty in the reference position of the pulsar, which is not quoted in Table 2, is dominated by the uncertainty in the in-beam calibrator positions, which themselves were referenced to the primary phase calibrator located at a larger angular separation – this uncertainty is likely to be on the order of 5 milliarcsec in the current dataset.
Table 2. VLBA astrometric results for PSR J0837
![]() $-$
2454.
$-$
2454.


Figure 5. The offset of PSR J0837
![]() $-$
2454 from the fitted reference position in right ascension (top) and declination (bottom) as a function of time. As discussed in the text, the error bars are from the image plane fit to the pulsar position only and are underestimated (particularly in declination).
$-$
2454 from the fitted reference position in right ascension (top) and declination (bottom) as a function of time. As discussed in the text, the error bars are from the image plane fit to the pulsar position only and are underestimated (particularly in declination).
3.4 X-ray pulsation search and pulse profile
Fig. 6 shows power spectra of the pn data generated using powspec in FTOOLS (Blackburn Reference Blackburn, Shaw, Payne and Hayes1995). A peak at 1.58845 Hz (629.545 ms) is evident and corresponds to the spin frequency of PSR J0837
![]() $-$
2454. Note that Pol et al. (Reference Pol2021) measured a spin frequency of 1.58878890 Hz (
$-$
2454. Note that Pol et al. (Reference Pol2021) measured a spin frequency of 1.58878890 Hz (
![]() $P=629.41024\mbox{ ms}$
) and spin frequency time derivative of
$P=629.41024\mbox{ ms}$
) and spin frequency time derivative of
![]() $({-}8.808\pm0.004)\times10^{-13}\mbox{ Hz s}^{-1}$
[
$({-}8.808\pm0.004)\times10^{-13}\mbox{ Hz s}^{-1}$
[
![]() $\dot{P}=(3.490\pm0.002)\times10^{-13}\mbox{ s s}^{-1}$
] at MJD 55588.628331, such that the expected spin frequency at the time of the XMM-Newton observation is
$\dot{P}=(3.490\pm0.002)\times10^{-13}\mbox{ s s}^{-1}$
] at MJD 55588.628331, such that the expected spin frequency at the time of the XMM-Newton observation is
![]() $1.5884\pm0.0007$
Hz (
$1.5884\pm0.0007$
Hz (
![]() $629.5\pm0.4$
ms), which matches that from the power spectrum here.
$629.5\pm0.4$
ms), which matches that from the power spectrum here.

Figure 6. Power spectra from pn data for 0.5–1 keV (top) and 0.2–10 keV (bottom). The peak at 1.58845 Hz is the spin frequency of PSR J0837
![]() $-$
2454.
$-$
2454.
Next, we perform acceleration searches using PRESTO (Ransom, Eikenberry, & Middleditch Reference Ransom, Eikenberry and Middleditch2002). Data are folded at the candidate pulse frequency using prepfold, and a refined frequency is determined. We find the strongest pulsations at a frequency of 1.58845213(9) Hz or period of 629.54368(4) ms (at MJD 60059.0334841) in the energy range 0.5–1 keV. We then use photonphase in PINT (Luo et al. Reference Luo2021) to calculate the rotation phase for each photon. The resulting pulse profiles in various energy bands are shown in Fig. 7. Pulsations are only clearly evident at
![]() $E<1\mbox{ keV}$
. For the sinusoidal pulse profiles at 0.2–10 keV and 0.5–1 keV, the pulsed fractions [
$E<1\mbox{ keV}$
. For the sinusoidal pulse profiles at 0.2–10 keV and 0.5–1 keV, the pulsed fractions [
![]() $=\mbox{(max-min)/(max+min)}$
] are 17% and 39%, respectively.
$=\mbox{(max-min)/(max+min)}$
] are 17% and 39%, respectively.

Figure 7. Pulse profile of PSR J0837
![]() $-$
2454, obtained by folding the pn data in the energy ranges 0.2–0.5, 0.5–1, 1–2, 2–10, and 0.2–10 keV at the 629.544 ms spin period. Errors shown are 1
$-$
2454, obtained by folding the pn data in the energy ranges 0.2–0.5, 0.5–1, 1–2, 2–10, and 0.2–10 keV at the 629.544 ms spin period. Errors shown are 1
![]() $\sigma$
.
$\sigma$
.
3.5 X-ray spectral analysis
Fig. 8 shows the combined MOS (MOS1+MOS2) and pn spectra. We perform model fits to these spectra using Xspec 12.14.0 (Arnaud Reference Arnaud, Jacoby and Barnes1996). For the spectral model, we include several components. First, we use constant to account for a possible instrumental difference between MOS and pn spectral normalisations, and we fix its value to 1 for the pn spectrum and allow it to vary for the combined MOS spectrum. Next, we include a component to account for photoelectric absorption by the interstellar medium, i.e. tbabs with abundances from Wilms, Allen, & McCray (Reference Wilms, Allen and McCray2000) and cross-sections from Verner et al. (Reference Verner, Ferland, Korista and Yakovlev1996). To model the intrinsic spectrum of PSR J0837
![]() $-$
2454, we first consider a single component comprising a power law (PL; powerlaw), blackbody (BB; bbodyrad), or neutron star atmosphere. For the last, we use a magnetic partially ionized hydrogen atmosphere model (nsmaxg; Ho, Potekhin, & Chabrier Reference Ho, Potekhin and Chabrier2008; Ho Reference Ho, Petit, Jardine and Spruit2014) and fix the model parameters of neutron star mass and radius to
$-$
2454, we first consider a single component comprising a power law (PL; powerlaw), blackbody (BB; bbodyrad), or neutron star atmosphere. For the last, we use a magnetic partially ionized hydrogen atmosphere model (nsmaxg; Ho, Potekhin, & Chabrier Reference Ho, Potekhin and Chabrier2008; Ho Reference Ho, Petit, Jardine and Spruit2014) and fix the model parameters of neutron star mass and radius to
![]() $M=1.4\,{\rm M}_\odot$
and
$M=1.4\,{\rm M}_\odot$
and
![]() $R=10\mbox{ km}$
, respectively. We also tried a non-magnetic fully ionized hydrogen atmosphere model (nsatmos; Heinke et al. Reference Heinke, Rybicki, Narayan and Grindlay2006), a non-magnetic partially ionized hydrogen, helium, or carbon atmosphere model (nsx; Ho & Heinke Reference Ho and Heinke2009), and a magnetic partially ionized carbon, oxygen, or neon atmosphere model (Mori & Ho Reference Mori and Ho2007), but none of these provide good fits and thus will not be discussed further.
$R=10\mbox{ km}$
, respectively. We also tried a non-magnetic fully ionized hydrogen atmosphere model (nsatmos; Heinke et al. Reference Heinke, Rybicki, Narayan and Grindlay2006), a non-magnetic partially ionized hydrogen, helium, or carbon atmosphere model (nsx; Ho & Heinke Reference Ho and Heinke2009), and a magnetic partially ionized carbon, oxygen, or neon atmosphere model (Mori & Ho Reference Mori and Ho2007), but none of these provide good fits and thus will not be discussed further.

Figure 8. Spectra of PSR J0837
![]() $-$
2454 from MOS1+MOS2 and pn data. Top panel shows data with 1
$-$
2454 from MOS1+MOS2 and pn data. Top panel shows data with 1
![]() $\sigma$
errors (crosses) and spectral model (dashed lines for each component). Bottom panel shows
$\sigma$
errors (crosses) and spectral model (dashed lines for each component). Bottom panel shows
![]() $\chi^2=\mbox{(data-model)/error}$
. The spectral model shown here is a
$\chi^2=\mbox{(data-model)/error}$
. The spectral model shown here is a
![]() $B=10^{13}\mbox{ G}$
thin partially-ionized hydrogen atmosphere with two temperature components; a two temperature blackbody model yields similar results (see text and Table 3 for details).
$B=10^{13}\mbox{ G}$
thin partially-ionized hydrogen atmosphere with two temperature components; a two temperature blackbody model yields similar results (see text and Table 3 for details).
The results of fits with a single component model for the intrinsic spectrum of PSR J0837
![]() $-$
2454, i.e. either power law, blackbody, or atmosphere model, are given in Table 3. We see that the power law model not only has the worst fit of the three, but the best-fit power law index
$-$
2454, i.e. either power law, blackbody, or atmosphere model, are given in Table 3. We see that the power law model not only has the worst fit of the three, but the best-fit power law index
![]() $\Gamma\approx 8$
is unrealistic. Meanwhile, thermal models provide better fits if the distance to the pulsar is taken to be less than a few kpc. For example, in order for the best-fit blackbody emission radius
$\Gamma\approx 8$
is unrealistic. Meanwhile, thermal models provide better fits if the distance to the pulsar is taken to be less than a few kpc. For example, in order for the best-fit blackbody emission radius
![]() $R^\infty$
[
$R^\infty$
[
![]() $=R(1-2GM/c^2R)^{-1/2}$
] to be less than
$=R(1-2GM/c^2R)^{-1/2}$
] to be less than
![]() $\sim$
$\sim$
![]() $19\mbox{ km}$
(corresponding to a maximum neutron star radius
$19\mbox{ km}$
(corresponding to a maximum neutron star radius
![]() $R\approx 13-15\mbox{ km}$
), then the distance must be
$R\approx 13-15\mbox{ km}$
), then the distance must be
![]() $d<4\mbox{ kpc}$
(after accounting for gravitational redshift). Similarly assuming that the entire stellar surface emits at a single uniform temperature, the best-fit atmosphere model gives a distance of only 90 pc. We note that nsmaxg models with
$d<4\mbox{ kpc}$
(after accounting for gravitational redshift). Similarly assuming that the entire stellar surface emits at a single uniform temperature, the best-fit atmosphere model gives a distance of only 90 pc. We note that nsmaxg models with
![]() $B=2$
, 4, or
$B=2$
, 4, or
![]() $7\times10^{12}\mbox{ G}$
yield fits that are about as good as that of
$7\times10^{12}\mbox{ G}$
yield fits that are about as good as that of
![]() $10^{13}\mbox{ G}$
and have best-fit parameters
$10^{13}\mbox{ G}$
and have best-fit parameters
![]() $N_\textrm{H}$
increasing,
$N_\textrm{H}$
increasing,
![]() $T_\textrm{eff}^\infty$
decreasing, and d decreasing with lower values of B, while fits are poor for models with lower and higher magnetic fields, i.e.
$T_\textrm{eff}^\infty$
decreasing, and d decreasing with lower values of B, while fits are poor for models with lower and higher magnetic fields, i.e.
![]() $10^{10}$
–
$10^{10}$
–
![]() $10^{12}\mbox{ G}$
and
$10^{12}\mbox{ G}$
and
![]() $(2-3)\times10^{13}\mbox{ G}$
. The absorbed 0.3–10 keV flux is
$(2-3)\times10^{13}\mbox{ G}$
. The absorbed 0.3–10 keV flux is
![]() $7.2\times10^{-14}\mbox{ erg s}^{-1}$
cm
$7.2\times10^{-14}\mbox{ erg s}^{-1}$
cm
![]() $^{-2}$
, so that the unabsorbed 0.3–10 keV X-ray luminosity
$^{-2}$
, so that the unabsorbed 0.3–10 keV X-ray luminosity
![]() $L^\infty_\textrm{X}\sim3.3\times10^{31}\mbox{ erg s}^{-1}(d/0.9\mbox{ kpc})^2$
and bolometric luminosity
$L^\infty_\textrm{X}\sim3.3\times10^{31}\mbox{ erg s}^{-1}(d/0.9\mbox{ kpc})^2$
and bolometric luminosity
![]() $L^\infty\sim7.6\times10^{31}\mbox{ erg s}^{-1}(d/0.9\mbox{kpc})^2$
.
$L^\infty\sim7.6\times10^{31}\mbox{ erg s}^{-1}(d/0.9\mbox{kpc})^2$
.
Table 3. Results of spectral modeling.

Errors are
![]() $1\sigma$
.
$1\sigma$
.
aXspec models: PL=powerlaw, BB=bbodyrad.
bNeutron star mass
![]() $M=1.4\,{\rm M}_\odot$
and radius
$M=1.4\,{\rm M}_\odot$
and radius
![]() $R=10\mbox{ km}$
are fixed, such that a redshift of 1.3 is used to convert between unredshifted and redshifted values. Distance is allowed to vary with fit, while fraction of surface emitting is fixed to 1. Magnetic field
$R=10\mbox{ km}$
are fixed, such that a redshift of 1.3 is used to convert between unredshifted and redshifted values. Distance is allowed to vary with fit, while fraction of surface emitting is fixed to 1. Magnetic field
![]() $B=10^{13}\mbox{ G}$
is assumed (see text for other values).
$B=10^{13}\mbox{ G}$
is assumed (see text for other values).
Next, we consider two component models for fitting the measured spectra, on top of constant and tbabs, in particular, two power laws (PL+PL), a blackbody and a power law (BB+PL), or two blackbodies (BB+BB). For two power laws, the best-fit does not yield an improvement in
![]() $\chi^2$
, and the second power law only has an upper limit on its normalisation. Meanwhile, the best-fit results for BB+PL and BB+BB are given in Table 3. While we see an improvement in
$\chi^2$
, and the second power law only has an upper limit on its normalisation. Meanwhile, the best-fit results for BB+PL and BB+BB are given in Table 3. While we see an improvement in
![]() $\chi^2$
for BB+PL compared to only a power law or only a blackbody, with the power law providing the primary flux at
$\chi^2$
for BB+PL compared to only a power law or only a blackbody, with the power law providing the primary flux at
![]() $>$
$>$
![]() $1\mbox{ keV}$
, the power law index is still a high
$1\mbox{ keV}$
, the power law index is still a high
![]() $\Gamma>5$
. Meanwhile, two blackbodies yield a much improved fit (
$\Gamma>5$
. Meanwhile, two blackbodies yield a much improved fit (
![]() $\Delta\chi^2=25.4$
for two extra degrees of freedom, so that a f-test gives a probability of
$\Delta\chi^2=25.4$
for two extra degrees of freedom, so that a f-test gives a probability of
![]() $3\times10^{-6}$
). The second blackbody with a higher temperature and small emitting region could be interpreted as emission from a hot spot on the neutron star surface that rotates to generate the pulsations detected and described in Section 3.4. The size of the colder blackbody limits the distance to PSR J0837
$3\times10^{-6}$
). The second blackbody with a higher temperature and small emitting region could be interpreted as emission from a hot spot on the neutron star surface that rotates to generate the pulsations detected and described in Section 3.4. The size of the colder blackbody limits the distance to PSR J0837
![]() $-$
2454 to be
$-$
2454 to be
![]() $d<1.7\mbox{ kpc}$
. We note for completeness that we also fit the spectra with nsmaxg+PL, with best-fit results shown in Table 3. The small improvement of the best-fit over only nsmaxg shows that the addition of the power law (to better fit the spectra at high energies) is not really needed. This difference with the BB+PL results is because neutron star atmosphere model spectra are harder at high energies than blackbody spectra at the same temperature due to the atmospheric opacity decreasing with energy, such that higher energy photons come from deeper, hotter layers of the atmosphere (see, e.g. Pavlov et al. Reference Pavlov, Shibanov, Zavlin, Meyer, Alpar, Kiziloglu and van Paradijs1995). This also implies that fitting spectra with a single blackbody gives a higher temperature and smaller emitting region compared to fitting with an atmosphere model, as evident from the results given in Table 3.
$d<1.7\mbox{ kpc}$
. We note for completeness that we also fit the spectra with nsmaxg+PL, with best-fit results shown in Table 3. The small improvement of the best-fit over only nsmaxg shows that the addition of the power law (to better fit the spectra at high energies) is not really needed. This difference with the BB+PL results is because neutron star atmosphere model spectra are harder at high energies than blackbody spectra at the same temperature due to the atmospheric opacity decreasing with energy, such that higher energy photons come from deeper, hotter layers of the atmosphere (see, e.g. Pavlov et al. Reference Pavlov, Shibanov, Zavlin, Meyer, Alpar, Kiziloglu and van Paradijs1995). This also implies that fitting spectra with a single blackbody gives a higher temperature and smaller emitting region compared to fitting with an atmosphere model, as evident from the results given in Table 3.
Finally, we fit the X-ray spectra using a two component neutron star atmosphere model, like the two component blackbody model described above. Such a model with emission from a small hot magnetic polar cap and emission from the remaining cooler surface can produce rotation modulated pulsations. A more robust distance estimate can also be determined. Since a single atmosphere model provides a good fit to the observed spectra without a need for a second component and guided by the good fit of the two blackbody model, the model we use here is a thin atmosphere model. A thin atmosphere is one whose physical thickness is such that the atmosphere is optically thick (
![]() $\tau>1$
) at low energies and optically thin (
$\tau>1$
) at low energies and optically thin (
![]() $\tau<1$
) at high energies. Thus the observed high energy photons arise from a condensed surface beneath the gaseous atmosphere, and this condensed surface emits blackbody-like emission (away from features such as electron and ion cyclotron resonances; see, e.g. van Adelsberg et al. Reference van Adelsberg, Lai, Potekhin and Arras2005; Potekhin et al. Reference Potekhin, Suleimanov, van Adelsberg and Werner2012; Potekhin Reference Potekhin2014). Such thin atmospheres were first used to model the spectrum of the strongly magnetic (
$\tau<1$
) at high energies. Thus the observed high energy photons arise from a condensed surface beneath the gaseous atmosphere, and this condensed surface emits blackbody-like emission (away from features such as electron and ion cyclotron resonances; see, e.g. van Adelsberg et al. Reference van Adelsberg, Lai, Potekhin and Arras2005; Potekhin et al. Reference Potekhin, Suleimanov, van Adelsberg and Werner2012; Potekhin Reference Potekhin2014). Such thin atmospheres were first used to model the spectrum of the strongly magnetic (
![]() $10^{12}$
–
$10^{12}$
–
![]() $10^{13}\mbox{ G}$
) neutron stars RX J0720.4
$10^{13}\mbox{ G}$
) neutron stars RX J0720.4
![]() $-$
3125 (Motch, Zavlin, & Haberl Reference Motch, Zavlin and Haberl2003) and RX J1856.5
$-$
3125 (Motch, Zavlin, & Haberl Reference Motch, Zavlin and Haberl2003) and RX J1856.5
![]() $-$
3754 (Ho Reference Ho2007; Ho et al. Reference Ho, Kaplan, Chang, van Adelsberg and Potekhin2007). Here we use nsmaxg models with condensed surface spectra from van Adelsberg et al. (Reference van Adelsberg, Lai, Potekhin and Arras2005). The best-fit results are shown in Table 3 and Fig. 8 (for a Thomson depth of 0.7, corresponding to an atmosphere thickness of 3.8 cm). We see that the best-fit is as good as the two blackbody fit and a better fit than that of a single atmosphere. Taking the cool component as being due to the entire neutron star surface, we estimate the distance to PSR J0837
$-$
3754 (Ho Reference Ho2007; Ho et al. Reference Ho, Kaplan, Chang, van Adelsberg and Potekhin2007). Here we use nsmaxg models with condensed surface spectra from van Adelsberg et al. (Reference van Adelsberg, Lai, Potekhin and Arras2005). The best-fit results are shown in Table 3 and Fig. 8 (for a Thomson depth of 0.7, corresponding to an atmosphere thickness of 3.8 cm). We see that the best-fit is as good as the two blackbody fit and a better fit than that of a single atmosphere. Taking the cool component as being due to the entire neutron star surface, we estimate the distance to PSR J0837
![]() $-$
2454 to be
$-$
2454 to be
![]() $d\sim1\mbox{ kpc}$
. Results for somewhat larger depths than 0.7 are roughly within the uncertainties given in Table 3 and tend toward lower temperatures and a smaller distance, while smaller depths produce essentially blackbodies in X-rays.
$d\sim1\mbox{ kpc}$
. Results for somewhat larger depths than 0.7 are roughly within the uncertainties given in Table 3 and tend toward lower temperatures and a smaller distance, while smaller depths produce essentially blackbodies in X-rays.
We note here that the best-fit interstellar absorption
![]() $N_\textrm{H}$
is in the range
$N_\textrm{H}$
is in the range
![]() $\sim$
$\sim$
![]() $(1.8-2)\times10^{21}\mbox{ cm}^{-2}$
. These are a factor of 2–3 larger than the Galactic column density of
$(1.8-2)\times10^{21}\mbox{ cm}^{-2}$
. These are a factor of 2–3 larger than the Galactic column density of
![]() $N_\textrm{H}=7.3\times10^{20}\mbox{ cm}^{-2}$
in the direction of PSR J0837
$N_\textrm{H}=7.3\times10^{20}\mbox{ cm}^{-2}$
in the direction of PSR J0837
![]() $-$
2454 (HI4PI Collaboration et al. 2016). On the other hand, the empirical relation between
$-$
2454 (HI4PI Collaboration et al. 2016). On the other hand, the empirical relation between
![]() $N_\textrm{H}$
and dispersion measure from He, Ng, & Kaspi (Reference He, Ng and Kaspi2013) yields
$N_\textrm{H}$
and dispersion measure from He, Ng, & Kaspi (Reference He, Ng and Kaspi2013) yields
![]() $N_\textrm{H}=4\times10^{21}\mbox{ cm}^{-2}$
for the pulsar’s DM of
$N_\textrm{H}=4\times10^{21}\mbox{ cm}^{-2}$
for the pulsar’s DM of
![]() $143.1\mbox{pc cm}^{-3}$
. The relatively large
$143.1\mbox{pc cm}^{-3}$
. The relatively large
![]() $N_\textrm{H}$
from our spectral fits, as well as the high DM, could be indicating significant material in our line-of-sight from, for example, a supernova remnant. This material may also contribute to the strong scattering seen in radio observations.
$N_\textrm{H}$
from our spectral fits, as well as the high DM, could be indicating significant material in our line-of-sight from, for example, a supernova remnant. This material may also contribute to the strong scattering seen in radio observations.
4. Discussion
4.1 Implications on distance to and kinematics
As shown in Section 3.2, while we are able to produce an updated timing solution, we are unable to phase connect the new observations with those taken in Pol et al. (Reference Pol2021). Consequently, we are unable to measure a timing parallax and infer the distance to the pulsar. While we detect the pulsar in a number of the VLBA observations, the signal-to-noise ratio and hence astrometric precision is lower than expected. As shown in Table 2, the five available position measurements imply a best-fit parallax of 0.6 milliarcsec and hence best-fit distance of 1.7 kpc. The
![]() $\chi^2$
value of 42 for 5 degrees of freedom shows that the parallax uncertainty of 0.24 milliarcsec is likely to be significantly underestimated, perhaps by a factor of three or more. Accordingly, we cannot measure the distance using the current dataset but can only say that very nearby distances are increasingly disfavoured. For instance, even assuming that the uncertainty is underestimated by a factor of 5, a distance below 330 pc would be excluded at 95% confidence. An extended VLBA astrometric campaign would rapidly improve the distance constraints in three ways: (1) the additional data points would improve the statistical precision of the astrometric fit, (2) the larger ensemble of data points would allow the true distribution of the systematic error terms to be better estimated, and (3) the improved time baseline would greatly reduce the covariance between proper motion (in right ascension) and parallax, reducing the parallax uncertainty.
$\chi^2$
value of 42 for 5 degrees of freedom shows that the parallax uncertainty of 0.24 milliarcsec is likely to be significantly underestimated, perhaps by a factor of three or more. Accordingly, we cannot measure the distance using the current dataset but can only say that very nearby distances are increasingly disfavoured. For instance, even assuming that the uncertainty is underestimated by a factor of 5, a distance below 330 pc would be excluded at 95% confidence. An extended VLBA astrometric campaign would rapidly improve the distance constraints in three ways: (1) the additional data points would improve the statistical precision of the astrometric fit, (2) the larger ensemble of data points would allow the true distribution of the systematic error terms to be better estimated, and (3) the improved time baseline would greatly reduce the covariance between proper motion (in right ascension) and parallax, reducing the parallax uncertainty.
The current, uncertain lower limit to the distance based on the VLBA astrometry can still be compared to constraints on the pulsar distance based on fits to its X-ray spectrum. As described in Section 3.5, all the spectral models that provide a good fit to the data imply a distance less than that predicted from the NE2001 and YMW16 DM models. The X-ray spectra give a distance to PSR J0837
![]() $-$
2454 of
$-$
2454 of
![]() $d \lesssim 1$
kpc, similar to the indirectly estimated distances found in Pol et al. (Reference Pol2021). This is not in tension with the VLBA results, although these favor a distance towards the upper end of this range.
$d \lesssim 1$
kpc, similar to the indirectly estimated distances found in Pol et al. (Reference Pol2021). This is not in tension with the VLBA results, although these favor a distance towards the upper end of this range.
Finally, we note that the VLBA proper motion implies a relatively low transverse velocity for the system. While the exact value depends on the assumed distance, a reasonable maximum can be estimated by taking a distance at the upper end of the range allowed by the X-ray spectral modelling and assuming the same factor-of-five increase in the nominal VLBA uncertainties. In this case, the proper motion upper limit is
![]() $\lesssim$
10 mas yr
$\lesssim$
10 mas yr
![]() $^{-1}$
, corresponding to a transverse velocity of
$^{-1}$
, corresponding to a transverse velocity of
![]() $\lesssim$
50 km s
$\lesssim$
50 km s
![]() $^{-1}$
, considerably slower than most pulsars (e.g. Igoshev Reference Igoshev2020).
$^{-1}$
, considerably slower than most pulsars (e.g. Igoshev Reference Igoshev2020).
4.2 Neutron star cooling implications
For the purposes of the discussion in this section, we assume a distance to PSR J0837
![]() $-$
2454 of 0.9 kpc, derived from associating diffuse emission detected by GLEAM to be the supernova remnant left over from the formation of the pulsar. At this distance, the measured X-ray flux results in a thermal luminosity of
$-$
2454 of 0.9 kpc, derived from associating diffuse emission detected by GLEAM to be the supernova remnant left over from the formation of the pulsar. At this distance, the measured X-ray flux results in a thermal luminosity of
![]() $L^\infty\sim7.6\times10^{31}\mbox{ erg s}^{-1} (d/0.9\mbox{ kpc})^2$
. The best-fit spectral model of a neutron star
$L^\infty\sim7.6\times10^{31}\mbox{ erg s}^{-1} (d/0.9\mbox{ kpc})^2$
. The best-fit spectral model of a neutron star
![]() $B=10^{13}\mbox{ G}$
atmosphere yields a surface temperature of
$B=10^{13}\mbox{ G}$
atmosphere yields a surface temperature of
![]() $T_\textrm{eff}^\infty=5.8\times10^5\mbox{ K}$
. Both the luminosity and temperature are low compared to most neutron stars of age
$T_\textrm{eff}^\infty=5.8\times10^5\mbox{ K}$
. Both the luminosity and temperature are low compared to most neutron stars of age
![]() $<$
$<$
![]() $10^5\mbox{ yr}$
, which have
$10^5\mbox{ yr}$
, which have
![]() $L^\infty>10^{32}\mbox{ erg s}^{-1}$
and
$L^\infty>10^{32}\mbox{ erg s}^{-1}$
and
![]() $T_\textrm{eff}^\infty>6\times10^5\mbox{ K}$
, as shown in Fig. 9. On the other hand, the
$T_\textrm{eff}^\infty>6\times10^5\mbox{ K}$
, as shown in Fig. 9. On the other hand, the
![]() $L^\infty$
and
$L^\infty$
and
![]() $T_\textrm{eff}^\infty$
of PSR J0837
$T_\textrm{eff}^\infty$
of PSR J0837
![]() $-$
2454 are comparable to those of three pulsars of approximately similar age, i.e. PSR J0007+7303 (
$-$
2454 are comparable to those of three pulsars of approximately similar age, i.e. PSR J0007+7303 (
![]() $L^\infty<3\times10^{31}\mbox{erg s}^{-1}$
,
$L^\infty<3\times10^{31}\mbox{erg s}^{-1}$
,
![]() $\log T_\textrm{eff}^\infty<6.4$
, and age
$\log T_\textrm{eff}^\infty<6.4$
, and age
![]() $\sim9\mbox{ kyr}$
; Caraveo et al. Reference Caraveo, De Luca, Marelli, Bignami, Ray, Saz Parkinson and Kanbach2010; Martín, Torres, & Pedaletti 2016; Potekhin et al. Reference Potekhin, Zyuzin, Yakovlev, Beznogov and Shibanov2020), PSR B1727
$\sim9\mbox{ kyr}$
; Caraveo et al. Reference Caraveo, De Luca, Marelli, Bignami, Ray, Saz Parkinson and Kanbach2010; Martín, Torres, & Pedaletti 2016; Potekhin et al. Reference Potekhin, Zyuzin, Yakovlev, Beznogov and Shibanov2020), PSR B1727
![]() $-$
47 (
$-$
47 (
![]() $L^\infty<3\times10^{31}\mbox{erg s}^{-1}$
,
$L^\infty<3\times10^{31}\mbox{erg s}^{-1}$
,
![]() $\log T_\textrm{eff}^\infty<5.6$
, and age
$\log T_\textrm{eff}^\infty<5.6$
, and age
![]() $\sim50\mbox{ kyr}$
; Shternin et al. Reference Shternin, Kirichenko, Zyuzin, Yu, Danilenko, Voronkov and Shibanov2019; Potekhin et al. Reference Potekhin, Zyuzin, Yakovlev, Beznogov and Shibanov2020), and PSR B2334+61 (
$\sim50\mbox{ kyr}$
; Shternin et al. Reference Shternin, Kirichenko, Zyuzin, Yu, Danilenko, Voronkov and Shibanov2019; Potekhin et al. Reference Potekhin, Zyuzin, Yakovlev, Beznogov and Shibanov2020), and PSR B2334+61 (
![]() $L^\infty\sim5\times10^{31}\mbox{ erg s}^{-1}$
,
$L^\infty\sim5\times10^{31}\mbox{ erg s}^{-1}$
,
![]() $\log T_\textrm{eff}^\infty\approx5.6$
, and age
$\log T_\textrm{eff}^\infty\approx5.6$
, and age
![]() $\sim7.7\mbox{ kyr}$
; Yar-Uyaniker, Uyaniker, & Kothes Reference Yar-Uyaniker, Uyaniker and Kothes2004; McGowan et al. Reference McGowan, Zane, Cropper, Vestrand and Ho2006; Potekhin et al. Reference Potekhin, Zyuzin, Yakovlev, Beznogov and Shibanov2020). It is worth noting that the ages of these three pulsars are estimated from their associated supernova remnant and each age is lower than the characteristic spin-down age of the pulsar (i.e.
$\sim7.7\mbox{ kyr}$
; Yar-Uyaniker, Uyaniker, & Kothes Reference Yar-Uyaniker, Uyaniker and Kothes2004; McGowan et al. Reference McGowan, Zane, Cropper, Vestrand and Ho2006; Potekhin et al. Reference Potekhin, Zyuzin, Yakovlev, Beznogov and Shibanov2020). It is worth noting that the ages of these three pulsars are estimated from their associated supernova remnant and each age is lower than the characteristic spin-down age of the pulsar (i.e.
![]() $\tau_\textrm{c}=14$
kyr for PSR J0007+7303, 80 kyr for PSR B1727
$\tau_\textrm{c}=14$
kyr for PSR J0007+7303, 80 kyr for PSR B1727
![]() $-$
47, and 41 kyr for PSR B2334+61). This may indicate that the age of PSR J0837
$-$
47, and 41 kyr for PSR B2334+61). This may indicate that the age of PSR J0837
![]() $-$
2454 is lower than its characteristic age of 28.6 kyr.
$-$
2454 is lower than its characteristic age of 28.6 kyr.

Figure 9. Observed luminosity
![]() $L^\infty$
(left) and temperature
$L^\infty$
(left) and temperature
![]() $T^\infty$
(right) as functions of neutron star age. Data points are from Potekhin et al. (Reference Potekhin, Zyuzin, Yakovlev, Beznogov and Shibanov2020) (see also https://www.ioffe.ru/astro/NSG/thermal/), except the stars which denote PSR J0837
$T^\infty$
(right) as functions of neutron star age. Data points are from Potekhin et al. (Reference Potekhin, Zyuzin, Yakovlev, Beznogov and Shibanov2020) (see also https://www.ioffe.ru/astro/NSG/thermal/), except the stars which denote PSR J0837
![]() $-$
2454. Solid lines show cooling curves from neutron star cooling simulations for neutron star masses
$-$
2454. Solid lines show cooling curves from neutron star cooling simulations for neutron star masses
![]() $M=1.3$
, 1.4, 1.5, 1.6, 1.7, and
$M=1.3$
, 1.4, 1.5, 1.6, 1.7, and
![]() $1.8\,{\rm M}_\odot$
(from top to bottom) using the BSk24 nuclear equation of state and an iron envelope and including neutron superfluidity in the crust and core and proton superconductivity in the core, while dashed lines are for a hydrogen envelope; note that direct Urca cooling becomes active for BSk24 at
$1.8\,{\rm M}_\odot$
(from top to bottom) using the BSk24 nuclear equation of state and an iron envelope and including neutron superfluidity in the crust and core and proton superconductivity in the core, while dashed lines are for a hydrogen envelope; note that direct Urca cooling becomes active for BSk24 at
![]() $M>1.59\,{\rm M}_\odot$
(see text for details).
$M>1.59\,{\rm M}_\odot$
(see text for details).
The luminosity and temperature of most neutron stars can be explained by ‘slow’ neutrino cooling predominately from the modified Urca processes and enhanced by Cooper pairing processes, with variations due to each neutron star’s envelope composition and age (Gusakov et al. Reference Gusakov, Kaminker, Yakovlev and Gnedin2004; Page et al. Reference Page, Lattimer, Prakash and Steiner2004; see, e.g. Potekhin, Pons, & Page Reference Potekhin, Pons and Page2015, for review). An envelope composed of light elements is more effective at conducting interior heat and makes the surface temperature closer to that of the interior temperature and thus higher than the surface temperature for an envelope composed of heavy elements. The age determines how much of the crust and core neutrons and core protons are in a superfluid and superconducting state, respectively, in particular the ratio between the interior temperature T relative to the (theoretically-uncertain) critical temperatures
![]() $T_\textrm{c}$
for neutron superfluidity and proton superconductivity. When
$T_\textrm{c}$
for neutron superfluidity and proton superconductivity. When
![]() $T/T_\textrm{c}<1$
, cooling processes that depend on matter being in a non-superfluid state are suppressed, while cooling by Cooper pair breaking and formation of superfluid matter becomes effective.
$T/T_\textrm{c}<1$
, cooling processes that depend on matter being in a non-superfluid state are suppressed, while cooling by Cooper pair breaking and formation of superfluid matter becomes effective.
The low luminosity and temperature of neutron stars like PSR J0837
![]() $-$
2454 point to neutrino cooling processes in these stars that operate much faster than modified Urca and Cooper pairing. Neutrino emission by direct Urca reactions is such a fast cooling process, but it requires a high proton fraction (
$-$
2454 point to neutrino cooling processes in these stars that operate much faster than modified Urca and Cooper pairing. Neutrino emission by direct Urca reactions is such a fast cooling process, but it requires a high proton fraction (
![]() $\gtrsim$
$\gtrsim$
![]() $0.11$
) in the neutron star core (Lattimer et al. Reference Lattimer, Pethick, Prakash and Haensel1991; Page & Applegate Reference Page and Applegate1992). Such high proton fractions are only reached in neutron stars of high mass, and some theoretical nuclear equations of state (EOSs) do not even yield the necessary proton fractions at their predicted maximum mass. For example, direct Urca cooling can occur in neutron stars with mass
$0.11$
) in the neutron star core (Lattimer et al. Reference Lattimer, Pethick, Prakash and Haensel1991; Page & Applegate Reference Page and Applegate1992). Such high proton fractions are only reached in neutron stars of high mass, and some theoretical nuclear equations of state (EOSs) do not even yield the necessary proton fractions at their predicted maximum mass. For example, direct Urca cooling can occur in neutron stars with mass
![]() $M>1.96\,{\rm M}_\odot$
for the APR EOS (Akmal, Pandharipande, & Ravenhall Reference Akmal, Pandharipande and Ravenhall1998) and
$M>1.96\,{\rm M}_\odot$
for the APR EOS (Akmal, Pandharipande, & Ravenhall Reference Akmal, Pandharipande and Ravenhall1998) and
![]() $M>1.59\,{\rm M}_\odot$
for the BSk24 EOS but does not occur for the BSk26 EOS (Pearson et al. Reference Pearson, Chamel, Potekhin, Fantina, Ducoin, Dutta and Goriely2018) and the SLy4 EOS (Douchin & Haensel Reference Douchin and Haensel2001).
$M>1.59\,{\rm M}_\odot$
for the BSk24 EOS but does not occur for the BSk26 EOS (Pearson et al. Reference Pearson, Chamel, Potekhin, Fantina, Ducoin, Dutta and Goriely2018) and the SLy4 EOS (Douchin & Haensel Reference Douchin and Haensel2001).
To illustrate the above, we perform neutron star cooling simulations using the neutron star cooling code from Ho, Glampedakis, & Andersson (Reference Ho, Glampedakis and Andersson2012b,a), with revised neutrino emissivities for modified Urca (Shternin, Baldo, & Haensel Reference Shternin, Baldo and Haensel2018), plasmon decay (Kantor & Gusakov Reference Kantor and Gusakov2007), and neutron triplet pairing (Leinson Reference Leinson2010) and superfluid suppression factors (Gusakov Reference Gusakov2002) (see Potekhin & Chabrier Reference Potekhin and Chabrier2018, for discussion of some of the above). We use the BSk24 EOS (Pearson et al. Reference Pearson, Chamel, Potekhin, Fantina, Ducoin, Dutta and Goriely2018) and parameterisation of superfluid and superconductor energy gaps from Ho et al. (Reference Ho, Elshamouty, Heinke and Potekhin2015) for the SFB neutron singlet model (Schwenk, Friman, & Brown Reference Schwenk, Friman and Brown2003), TToa neutron triplet model (Takatsuka & Tamagaki Reference Takatsuka and Tamagaki2004), and CCDK proton singlet model (Chen et al. Reference Chen, Clark, Davé and Khodel1993). It is important to note that the resulting cooling evolutions vary greatly on the assumed EOS and superfluid and superconductor energy gaps; nevertheless our conclusions on direct Urca cooling and neutron star mass are still valid across most of these theoretical model variations.
The luminosity and temperature evolutions from our cooling simulations are shown in Fig. 9 for an iron envelope and neutron star masses
![]() $M=1.3,1.4,\ldots,1.8\,{\rm M}_\odot$
, as well as for a hydrogen envelope and
$M=1.3,1.4,\ldots,1.8\,{\rm M}_\odot$
, as well as for a hydrogen envelope and
![]() $M=1.3$
and
$M=1.3$
and
![]() $1.6\,{\rm M}_\odot$
. We see that cooling curves for masses below the direct Urca threshold of
$1.6\,{\rm M}_\odot$
. We see that cooling curves for masses below the direct Urca threshold of
![]() $1.59\,{\rm M}_\odot$
(and for same envelope composition) do not differ much from each other except at early times. These slow cooling curves can explain the luminosity and temperatures (or their limits) of most observed neutron stars given their ages (or limits on their ages) when we allow some to have a light element envelope. Meanwhile, some of the more luminous and hotter sources are magnetars, which are heated internally by magnetic field decay that is not included in our present calculations but are included in works such as Kaminker et al. (Reference Kaminker, Yakovlev, Potekhin, Shibazaki, Shternin and Gnedin2006), Ho, Glampedakis, & Andersson (Reference Ho, Glampedakis and Andersson2012b), Viganò et al. (Reference Viganò, Rea, Pons, Perna, Aguilera and Miralles2013), Skiathas & Gourgouliatos (Reference Skiathas and Gourgouliatos2024). On the other hand, we see that cooling curves for masses above the direct Urca threshold decrease to much lower luminosities and temperatures earlier and that fast cooling curves such as these can match the measurements of neutron stars such as PSR J0837
$1.59\,{\rm M}_\odot$
(and for same envelope composition) do not differ much from each other except at early times. These slow cooling curves can explain the luminosity and temperatures (or their limits) of most observed neutron stars given their ages (or limits on their ages) when we allow some to have a light element envelope. Meanwhile, some of the more luminous and hotter sources are magnetars, which are heated internally by magnetic field decay that is not included in our present calculations but are included in works such as Kaminker et al. (Reference Kaminker, Yakovlev, Potekhin, Shibazaki, Shternin and Gnedin2006), Ho, Glampedakis, & Andersson (Reference Ho, Glampedakis and Andersson2012b), Viganò et al. (Reference Viganò, Rea, Pons, Perna, Aguilera and Miralles2013), Skiathas & Gourgouliatos (Reference Skiathas and Gourgouliatos2024). On the other hand, we see that cooling curves for masses above the direct Urca threshold decrease to much lower luminosities and temperatures earlier and that fast cooling curves such as these can match the measurements of neutron stars such as PSR J0837
![]() $-$
2454. Therefore this indicates that, not only does PSR J0837
$-$
2454. Therefore this indicates that, not only does PSR J0837
![]() $-$
2454 have a high mass, but also the true nuclear equation of state should be one that can produce stable neutron stars with a high enough proton fraction in the core to allow direct Urca neutrino emission processes.
$-$
2454 have a high mass, but also the true nuclear equation of state should be one that can produce stable neutron stars with a high enough proton fraction in the core to allow direct Urca neutrino emission processes.
5. Summary
PSR J0837
![]() $-$
2454 is a young radio pulsar at a high Galactic latitude with an inferred magnetic field of
$-$
2454 is a young radio pulsar at a high Galactic latitude with an inferred magnetic field of
![]() $\sim$
$\sim$
![]() $10^{13}\mbox{ G}$
but uncertain distance. Using XMM-Newton, we detected its spin pulsations and thus identify it as a X-ray pulsar for the first time. The X-ray pulse profile of PSR J0837
$10^{13}\mbox{ G}$
but uncertain distance. Using XMM-Newton, we detected its spin pulsations and thus identify it as a X-ray pulsar for the first time. The X-ray pulse profile of PSR J0837
![]() $-$
2454 is broad, sinusoidal, strongest at low energies, and probably produced by emission from a rotating hot spot on a cooler surface based on properties of the spectrum. The X-ray spectrum can be described as a soft thermal spectrum that can be well-fit by a predominately cool component with a blackbody temperature of 70 eV or atmosphere temperature of 50 eV, as well as a 160–180 eV hot spot component. Results of the spectral analysis also indicate PSR J0837
$-$
2454 is broad, sinusoidal, strongest at low energies, and probably produced by emission from a rotating hot spot on a cooler surface based on properties of the spectrum. The X-ray spectrum can be described as a soft thermal spectrum that can be well-fit by a predominately cool component with a blackbody temperature of 70 eV or atmosphere temperature of 50 eV, as well as a 160–180 eV hot spot component. Results of the spectral analysis also indicate PSR J0837
![]() $-$
2454 is at a distance of
$-$
2454 is at a distance of
![]() $\lesssim$
$\lesssim$
![]() $1\mbox{ kpc}$
, which is much less than that inferred from the DM of the radio data but in agreement with other information from radio and optical. VLBA astrometry presently only provide a lower limit to the distance, favouring a distance
$1\mbox{ kpc}$
, which is much less than that inferred from the DM of the radio data but in agreement with other information from radio and optical. VLBA astrometry presently only provide a lower limit to the distance, favouring a distance
![]() $\gtrsim$
330 pc.
$\gtrsim$
330 pc.
Assuming a distance of 0.9 kpc, the measured luminosity of
![]() $7.6 \times 10^{31}\mbox{ erg s}^{-1}(d/\mbox{0.9 kpc})^2$
implies PSR J0837
$7.6 \times 10^{31}\mbox{ erg s}^{-1}(d/\mbox{0.9 kpc})^2$
implies PSR J0837
![]() $-$
2454 is one of the coldest young neutron stars known. Neutron star cooling theory indicates that such a low luminosity and temperature are only achievable if PSR J0837
$-$
2454 is one of the coldest young neutron stars known. Neutron star cooling theory indicates that such a low luminosity and temperature are only achievable if PSR J0837
![]() $-$
2454 has a mass high enough to activate fast direct Urca neutrino emission processes. Such a condition requires a nuclear EOS that can reach a high proton fraction in the stellar core of stable high mass neutron stars.
$-$
2454 has a mass high enough to activate fast direct Urca neutrino emission processes. Such a condition requires a nuclear EOS that can reach a high proton fraction in the stellar core of stable high mass neutron stars.
The distance to PSR J0837
![]() $-$
2454 remains the primary uncertainty regarding this source. We are unable to measure a timing parallax through our Parkes data due to the high red noise present in this pulsar’s emission, while the angular broadening of the pulsar in VLBA imaging led to lower astrometric precision than originally anticipated. An extension of the VLBA observations presented here could improve the precision of the VLBA parallax by a factor of several and provide a distance measurement, as opposed to the current lower limit. Confirmation of a supernova remnant association would also help with the distance and provide an estimate of the pulsar’s true age.
$-$
2454 remains the primary uncertainty regarding this source. We are unable to measure a timing parallax through our Parkes data due to the high red noise present in this pulsar’s emission, while the angular broadening of the pulsar in VLBA imaging led to lower astrometric precision than originally anticipated. An extension of the VLBA observations presented here could improve the precision of the VLBA parallax by a factor of several and provide a distance measurement, as opposed to the current lower limit. Confirmation of a supernova remnant association would also help with the distance and provide an estimate of the pulsar’s true age.
Acknowledgement
The authors are grateful to Harsha Blumer, Natasha Hurley-Walker, and Simon Johnston for discussions and support. N.P. thanks Rahul Sengar, David Kaplan, and Michael Lam for useful suggestions and discussion regarding processing the radio timing data. The authors thank the anonymous referee for comments that led to improvements in the paper. W.C.G.H. appreciates the use of computer facilities at the Kavli Institute for Particle Astrophysics and Cosmology.
Funding statement
W.C.G.H. acknowledges support through grant 80NSSC24K0329 from NASA. N.P was supported through NSF Physics Frontiers Center award PFC-2020265.
Competing interests
None.
Data availability statement
The data underlying this article will be shared on reasonable request to the corresponding author.