Gamma-Ray Burst Jets and their Radio Observations

Abstract

Radio observations play a key role in studying the jets that power GRBs, the most luminous cosmic explosions. They are crucial for determining the GRB jet energy, the external density, and the microphysical parameters of relativistic collisionless shocks, from afterglow broadband modeling. Radio image size measurements are rare, but provide extremely useful information. The “radio flare” peaking after ~1 day helps constrain the magnetisation and magnetic-field structure of GRB outflows. This review discusses the current observational and modeling status, focusing on the afterglow and outlining prompt radio emission searches, along with recent theoretical progress in GRB jet dynamics, focusing on magnetic acceleration, jet propagation inside a massive star progenitor (for long GRBs), the reverse shock, and the late afterglow. Great progress has been made in our understanding of magnetic acceleration, collimation and later sideways expansion of GRB jets, with interesting implications for the prompt, reverse shock, and afterglow emission. We outline how theory and observations were combined to study GRB jet physics and their immediate environment. Finally, potential paths are suggested for combining theory and observations to achieve greater progress, and some prospects for the future are discussed in light of the expected improvements in observational capabilities and theoretical advances.

1 INTRODUCTION

Jets are a common phenomenon in astrophysical sources. They span a wide range of size length scales, starting with stellar-sized jets emanating from newly forming stars or X-ray binary systems, up to jets that are larger than our galaxy by a few orders of magnitude and originate in active galactic nuclei (AGN). They are usually attributed to accretion of matter with high specific angular momentum onto a compact central source. The jet outflow velocities also span a large range, from a few ×10² km s⁻¹ in newly forming stars to almost the speed of light c in X-ray binaries or AGN. This is consistent with the expectation that the outflow velocities near the base of the jet should be comparable to the escape velocity from the central object.

The jets in gamma-ray bursts (GRBs) are the most extreme jets in terms of outflow velocities (with Lorentz factors typically in the range Γ ~ 10² − 10³) and jet power (with isotropic-equivalent luminosities typically in the range L ~ 10⁵⁰ – 10⁵³ erg s⁻¹). They differ from most other astrophysical jet sources by being very short-lived, where the duration of their prompt γ-ray emission is expected to reasonably reflect the activity time of their central source. Another important difference, which is observational rather than intrinsic, is that GRB jets are usually unresolved and seen as point sources in our instruments. This is due to their intrinsically small size, especially at early times, and their cosmological distances, which result in very small angular sizes (e.g. typically of the order of a micro-arcsecond for the GRB afterglow image after 1 d). The size has been inferred weeks to years after the GRB in only a few radio afterglow images. For this reason, we can learn about their jet structure only indirectly.

In fact, the evidence for jets in GRBs is also indirect and not as strong as in other source classes where the jets are resolved. The main lines of evidence for jets in GRBs are (for more details see section 3 of Granot & Ramirez-Ruiz 2013): (i) the analogy to other astrophysical jet sources; (ii) collimation into a narrow jet reduces the energy requirements for the γ-ray emission, which in some cases exceeds a solar rest energy if isotropic (the record being 4.9M _⊙ c ² for GRB 080916C; Abdo et al. 2009) and is very difficult to account for with a stellar mass progenitor; (iii) long duration GRBs are associated with the death of massive stars, and a spherical explosion cannot put the required energy (of ≳10⁵¹ erg) into ejecta with Lorentz factors ≳10² that are needed in order to avoid excessive pair production in the emitting region (e.g. Tan, Matzner, & McKee 2001); and (iv) pan-chromatic steepening of the afterglow light curve decay, known as jet breaks, which are related to the time at which the observer sees the total angular extent of the jet, and were predicted before they were observed (Rhoads 1997, 1999; Sari, Piran, & Halpern 1999).

GRBs divide into two classes according to their γ-ray duration and spectral hardness (Kouveliotou et al. 1993). Long-soft GRBs (with a duration of ≳2 s, typically a few tens of seconds and up to hundreds or even thousands of seconds in rare cases) are associated with the death of massive stars, and in particular several of them at relatively low redshifts are securely (spectroscopically) associated with core-collapse supernovae (SNe) of Type Ic (Stanek et al. 2003; Hjorth et al. 2003; Woosley & Bloom 2006). The origin of short-hard GRBs (with a duration of ≲2 s, typically a few tenths of seconds and down to a few milliseconds in some cases) is less clear, but they appear in both low and high star formation environments, and their most popular progenitor model is a binary merger of two neutron stars or a neutron star and a black hole (Eichler et al. 1989; Narayan, Paczyński, & Piran 1992; Nakar 2007; Lee & Ramirez-Ruiz 2007). These two classes of GRBs correspond to different progenitors and represent different types of explosive events that likely significantly vary in the environment in which the GRB jet propagates, as well as the total energy output, duration, or initial degree of jet collimation. However, both theory and observations suggest that the macrophysics or global dynamics of the relativistic outflow and the microphysics of the particles and small-scale magnetic fields that produce their observed emission are remarkably similar.

Observations across the electromagnetic spectrum, from high-energy γ-rays to long-wavelength radio waves, and from the short-lived prompt emission to the long-lived afterglow emission, have taught us a lot about GRB jets. In particular, we have learned about the jet structure and dynamics, as well as the relevant emission processes, the properties of the circumburst medium, and the microphysical properties of collisionless relativistic shocks. The dominant emission mechanism of the so-called afterglow is thought to be synchrotron radiation, which gives rise to a broad spectrum covering many orders of magnitude in observing frequency (e.g. Sari, Piran, & Narayan 1998; Granot & Sari 2002), in good agreement with afterglow observations (e.g. Galama et al. 1998a; Piran 2004). Further support for a synchrotron origin of the afterglow emission is provided by linear polarisation measurements, typically at the level of ~1% − 3%, in the optical or near-infrared afterglows of several GRBs (e.g. Covino et al. 1999; Wijers et al. 1999; Rol et al. 2000; Greiner et al. 2003; Covino et al. 2004). The evolution of the synchrotron spectrum is determined by the jet dynamics, as well as by the microphysics of collisionless relativistic shocks.

Radio observations have always played a crucial role in GRB studies, first of all by establishing that the outflow velocity is indeed initially relativistic by means of indirect and direct source size measurements, as well as by complementing the broadband spectrum, and by revealing phenomena unique to the radio band. The number of well-sampled radio light curves across a broad frequency range is limited thus far, especially in comparison with the higher observing frequency bands, but the few well-studied GRBs provide a wealth of information on GRB jet physics. Furthermore, we are standing at the beginning of a new era in radio astronomy, with most of the major radio observatories being upgraded and several new facilities being built, increasing sensitivities and bandwidth, and improving spectral, temporal, and spatial resolution, all very promising for GRB studies.

In this review we will first (in Section 2) describe the characteristics of radio afterglows, their role in the broadband studies of GRBs, radio source size measurements, and searches for prompt radio emission. This will be followed (in Sections 3 and 4) by a brief overview of select theoretical topics in GRB jets, which are either of particular relevance to radio observations, or in which there has been recent progress. In particular, we will discuss the jet angular structure and afterglow light curves for different observers (Section 3) as well as the jet dynamics (acceleration, propagation inside the progenitor star, the reverse shock, and dynamics during the afterglow; Section 4), both from an analytical and a numerical point of view. Next, we will combine the jet theory and radio observations by discussing a few well-studied GRBs (Section 5). Finally, we will discuss prospects for the future (improved observational capabilities at radio frequencies and theoretical outlook; Section 6), summarise, and draw some conclusions (Section 7).

2 GRB RADIO OBSERVATIONS

Since the initial discovery in 1997 that the prompt γ-ray emission of GRBs is followed by longer lasting emission at X-ray (Costa et al. 1997), optical (van Paradijs et al. 1997), and radio (Frail et al. 1997) frequencies, this long-lived afterglow has been detected and monitored in hundreds of GRBs. Radio afterglow emission from a GRB was first discovered in GRB 970508, the second GRB for which emission at wavelengths other than γ-rays was found, and the one that conclusively ended the distance debate by measuring the cosmological redshift in its optical afterglow spectrum (being z = 0.835 for this particular GRB). Since its launch on 20 November 2004, the Swift satellite (Gehrels et al. 2004) has revolutionised the follow-up of GRBs: nowadays 93% of the GRBs that are detected in soft γ-rays (by its Burst Alert Telescope—BAT) are also detected at X-ray energies (by its X-Ray Telescope—XRT), while 75% are detected at optical wavelengths—significantly higher fractions than before the launch of Swift. The fraction of radio detections, however, has been fairly constant at one-third before and after the launch of Swift (Chandra & Frail 2012). In the last 2 yr, with the upgrade of the very large array (VLA), resulting in significantly better sensitivity, the rate of GRBs detected by Swift/BAT and also detected in the radio has increased to ~60% (Hancock, Gaensler, & Murphy 2013).

Although GRBs are intrinsically highly luminous, they appear faint because of their cosmological distances, with radio flux densities typically at the sub-mJy level. Such flux levels are only accessible to the largest radio telescopes in the world, which indeed have been and are being used in this field of research. Most notable are the VLA, Westerbork Synthesis Radio Telescope (WSRT), Australia Telescope Compact Array (ATCA), Giant Metrewave Radio Telescope (GMRT), and the Arcminute Microkelvin Imager (AMI, the former Ryle Telescope). In this section, we will discuss the main observational results that have come from the observing campaigns on these facilities and the insights we have gained from them.

2.1 Radio light curves and sample

The light curves of GRB afterglows display a very different behaviour at radio wavelengths than they do at optical or X-ray wavelengths. At X-ray and optical wavelengths the overall light curve trend is a decaying one, especially after the first hours from the prompt γ-ray emission. The flux usually decays as a power law with time, where its decay rate can vary significantly, both between GRBs and within one GRB light curve. In addition, flares in X-rays and sometimes also in the optical have been found in the first minutes to hours, superimposed on the underlying smooth power-law flux decay.

In the radio bands, however, the light curves are mostly rising during those first hours or days, and peak on a timescale of days to weeks, or even months to years at the lowest radio frequencies. The total duration of the afterglow is also quite different in the radio than at shorter wavelengths. While in X-rays or optical the flux decays typically within several days to weeks below the sensitivity limits of the largest telescopes or satellites, or in the optical it disappears into the host galaxy, some radio afterglows have been detected for months to years. The most famous examples are GRB 970508 (Frail et al. 1997; Galama et al. 1998b; Frail, Waxman, & Kulkarni 2000), GRB 980703 (Berger, Kulkarni, & Frail 2001; Frail et al. 2003), and the longest lasting one by far—GRB 030329 (Berger et al. 2003a; Frail et al. 2005; Resmi et al. 2005; van der Horst et al. 2005; Pihlström et al. 2007; van der Horst et al. 2008; Mesler et al. 2012; Mesler & Pihlström 2013), which is in fact still detectable now, just over a decade after the initial GRB trigger. See the top panels of Figure 1 for the light curves of these three GRBs.

Figure 1. Radio light curves at 4.9 and 8.5 GHz (top panels) and spectral indices (bottom panels) for GRBs 970508 (Frail et al. 1997; Galama et al. 1998b; Frail et al. 2000), 980703 (Berger et al. 2001; Frail et al. 2003), and 030329 (Berger et al. 2003a; Frail et al. 2005; Resmi et al. 2005; van der Horst et al. 2005; Pihlström et al. 2007; van der Horst et al. 2008; Mesler et al. 2012; Mesler & Pihlström 2013). In contrast with the fast decaying light curves at X-ray and optical frequencies, the radio light curves rise and peak on a time-scale of weeks, and can last for months to years. The spectral index α (where F _ν∝ν^α) between 4.9 and 8.5 GHz varies significantly due to the spectral evolution and scintillation effects. The dashed lines in the bottom panels indicate spectral indices of 2, 1/3, and −0.6 (see Section 2.2 for further details).

The current sample of GRB afterglows with well-monitored radio light curves is small compared to the samples of optical and X-ray light curves. The typical radio fluxes turn out to be relatively close to the detection threshold of the largest radio telescopes, which makes the radio sample sensitivity limited (Chandra & Frail 2012). However, it has recently been suggested, based on stacking of the radio visibility data of many GRBs, that the low detection rate is due to the presence of two distinct populations of radio-bright and radio-faint GRBs (Hancock et al. 2013). However, this analysis cannot determine what the flux distributions of these two tentative populations are. The VLA, with the significantly better sensitivity after its upgrade, and in the future the Square Kilometer Array (SKA), will be able to test whether there is one flux distribution of which we have only seen the tip of the iceberg, or whether there are indeed two distinct populations. If the latter is confirmed, then correlated studies with the properties of afterglows at higher frequencies and the prompt γ-ray emission will provide clues about the nature of this dichotomy: whether they differ in their progenitors or that there is some other fundamental intrinsic difference; or if they differ only in their environments; or that there are some other physical processes affecting the radio detectability.

Even though sensitivity plays an important role in detecting radio afterglows, those that have been detected are not necessarily the nearest ones. The lowest redshift GRBs have been detected at radio frequencies, like GRB 980425 at z = 0.0085 (Kulkarni et al. 1998) and GRB 060218 at z = 0.034 (Soderberg et al. 2006a; Kaneko et al. 2007); and also the highest redshift ones, GRB 050904 at z = 6.30 (Frail et al. 2006) and GRB 090423 at z = 8.26 (Chandra et al. 2010). It has been shown that past z ~ 1 the detection rate is practically insensitive to redshift (Frail et al. 2006). Further evidence for this comes from the fact that the samples of radio-detected and non-detected GRBs are from the same redshift populations, and that the average redshift of radio-detected GRBs is z ≃ 1.8, close to the average of the overall sample of GRBs (Chandra & Frail 2012). This can be explained by the effects of cosmological redshift and time dilation counteracting the dimming due to the source distance (Ciardi & Loeb 2000).

After these general properties of the light curves and sample of GRB radio afterglows, we will now discuss the observational characteristics that provide insight into the physics and dynamics of GRB jets, and put them in context of the existing models.

2.2 Broadband modelling

GRBs are usually modelled and interpreted within the context of the fireball model (Cavallo & Rees 1978; Rees & Meszaros 1992). However, the jet acceleration mechanism is not very important for its late-time dynamics during the afterglow stage. Compactness arguments imply that the prompt γ-ray emission region must be moving towards us with an ultra-relativistic Lorentz factor, Γ ≳ 10² − 10^2.5 in order to avoid excessive pair production in the source (e.g. Ruderman 1975; Krolik & Pier 1991; Lithwick & Sari 2001; Granot, Cohen-Tanugi, & do Couto e Silva 2008). The early onset time of the afterglow emission also suggests that the outflow produced by the central engine is accelerated to ultra-relativistic speeds with bulk Lorentz factors up to several hundreds or more. As the outflow ploughs through the external medium, it sweeps it up by driving a strong relativistic forward external shock into it, while the outflow itself is decelerated by a reverse shock (or by its work on the shocked external medium if the outflow is highly magnetised and thus suppresses the reverse shock). After sweeping up a sufficient amount of external medium the outflow decelerates significantly and transfers most of its energy to the shocked external medium. The forward shock going into the external medium, often referred to as the afterglow shock or blast wave, accelerates swept-up electrons to relativistic random velocities and amplifies the magnetic field behind the shock. As a result, the relativistic electrons emit synchrotron radiation in the magnetic fields behind the shock, thus producing the bulk of the afterglow emission. The synchrotron spectrum is broadband, ranging from radio to X-ray frequencies. Other emission processes like inverse Compton or synchrotron self-Compton radiation may also play a role, but only at X-ray or higher energies and not in the radio regime.

The broadband synchrotron spectrum can be derived by integrating the single-electron spectrum over a power-law distribution of electron energies with slope p (Pacholczyk 1970; Rybicki & Lightman 1979), dN_e /dγ _e ∝ γ^−p _e for γ _e > γ _m . The resulting spectrum can be characterised by the peak flux and usually three characteristic frequencies: the peak frequency ν _m , which corresponds to the minimum energy of the electron energy distribution (γ _e = γ _m ); the cooling frequency ν _c , corresponding to the energetic electrons that cool on the dynamical timescale; and the synchrotron self-absorption frequency ν_sa. These characteristic frequencies are not static but evolve over time, as does the peak flux, resulting in a variety of light curves at different observing frequencies. Figure 2 shows the different possible afterglow synchrotron spectra. Although in principle any ordering of the spectral break frequencies corresponding to any of the five spectra shown in Figure 2 is possible, the most relevant for broadband modelling including radio observations are typically ν_sa < ν _m < ν _c (spectrum 1) for the first days to weeks and ν _m < ν_sa < ν _c (spectrum 2) for later times (Sari et al. 1998; Granot & Sari 2002). Note that besides ν_c, ν_m and ν_sa there is a fourth break frequency, ν_ac, which corresponds to the self-absorption frequency of the non-cooled electrons but appears only for fast cooling (ν_c < ν_m, in spectra 4 and 5), which is usually over by the times at which radio afterglows are detected.

Figure 2. The afterglow synchrotron spectrum, calculated for the Blandford & McKee (1976) self-similar solution of an ultra-relativistic spherical blast wave, under standard assumptions, using the accurate form of the synchrotron spectral emissivity and integration over the emission from the whole volume of shocked material behind the forward external (afterglow) shock (for details, see Granot & Sari 2002). The different panels show the five possible broadband spectra of the afterglow synchrotron emission, each corresponding to a different ordering of the spectral break frequencies. Each spectrum consists of several power-law segments (PLSs; each shown with a different colour and labelled by a different letter A–H), which smoothly join at the break frequencies (numbered 1–11). The broken power-law spectrum, which consists of the asymptotic PLSs that abruptly join at the break frequencies (and is widely used in the literature), is shown for comparison. Most PLSs appear in more than one of the five different broadband spectra. Indicated next to the arrows are the temporal scaling of the break frequencies and the flux density at the different PLSs, for a uniform (ISM; k = 0) and stellar wind (WIND; k = 2) external density profile, where ρ_ext = AR ^−k .

The characteristic frequencies and the peak flux can be written in terms of the following macro- and microphysical parameters: the kinetic energy E of the blast wave, the number density n of the surrounding medium (or the mass density ρ_ext = AR ^−k for a power-law external density profile, which is parameterised by A and k), and the ratios ε _B and ε _e , respectively, of the energy density in the magnetic field and in the power-law electron energy distribution, and the total internal energy density (Sari et al. 1998; Wijers & Galama 1999; Granot, Ramirez-Ruiz, & Loeb 2005). The details of the evolution of the spectrum, and the exact relations between the observable spectral parameters and the derived physical parameters, are determined by the jet dynamics. As an example, Figure 2 shows the temporal scalings of the different break frequencies and fluxes in the different power-law segments of the spectrum, for the Blandford & McKee (1976) self-similar solution of a spherical ultra-relativistic blast wave in a uniform or wind-like external medium.

In order to constrain the full set of physical parameters and the jet dynamics, it is essential to obtain well-sampled light curves in the various frequency regimes. While the cooling frequency is typically situated between the optical and X-ray regime or even above the X-ray energy range, ν _m is already below the infrared even at very early times and moves down towards the radio regime, while ν_sa is found at radio frequencies from the first observations onwards. The fact that the peak of the spectrum is below optical and X-ray frequencies causes their light curves to decay from the start, and the radio light curves to rise until the spectral peak passes through the observing bands.

The spectral peak can be ν _m or ν_sa, depending on their ordering at that particular moment (for slow cooling that is most relevant in the radio; see Figure 2), and thus the peak in the radio light curves can correspond to ν _m or ν_sa passing through. This can even vary between light curves at different frequencies for one given GRB, as best illustrated by the light curves of GRB 030329 spanning more than an order of magnitude in observed radio frequencies (Figure 3; van der Horst et al. 2008). In the bottom right panel of Figure 1 the spectral index between 4.9 and 8.5 GHz evolves from ~2 to ~−0.6 when ν_sa moves through the observing bands, corresponding to spectrum 2 in Figure 2. The spectral index of ~−0.6 is the optically thin one of −(p−1)/2 for p ~ 2.2. The early-time scatter is caused by interstellar scintillation (ISS; Section 2.5.2) while the late-time scatter is due to the low flux levels at late times. The bottom left panel of Figure 1 shows an example of the spectrum 1 in Figure 2. Despite large scatter due to the effects of ISS, it can be seen that for GRB 970508 the spectral index is consistent with 1/3 between ~30 and ~90 d after the burst, after which it evolves to an optically thin spectral index when ν _m evolves to lower frequencies.

Figure 3. Radio light curves of GRB 030329 (van der Horst et al. 2008), obtained with WSRT and GMRT (solid symbols), and VLA, ATCA, and Ryle Telescope (open diamonds); open triangles are 3σ upper limits. The dotted line shows a fit to the first 100 d, while the solid line represents a model in which the afterglow shock becomes non-relativistic after 80 d. Both fits are for a homogeneous ambient medium (k = 0). The dash-dotted line represents an alternative model involving a very wide extra jet component suggested by van der Horst et al. (2005), which has been disproved by the late-time data at the lowest observing frequencies.

Besides constraining the full broadband spectrum, there is another unique feature of radio light curves in broadband modelling. Since some afterglows are detectable for long times at radio frequencies, the blast wave evolution can be studied once it becomes trans-relativistic and eventually non-relativistic. The non-relativistic phase is of particular interest because it is expected that during the trans-relativistic phase the outflow starts to spread sideways, and eventually approaches spherical symmetry once the blast wave is sufficiently non-relativistic. The latter phase can be used to determine the total energetics without any large uncertainties regarding the jet collimation and relativistic beaming effects, which can influence energy estimates based on broadband modelling at early times. Such radio calorimetry has indeed been done for a few GRBs, most notably GRB 970508 (Frail et al. 2000; Berger, Kulkarni, & Frail 2004), GRB 980703 (Berger et al. 2004), and GRB 030329 (Frail et al. 2005; van der Horst et al. 2008). For all three GRBs the energy derived by means of this radio calorimetry is a few times 10⁵¹ erg. This is in fact a lower limit to the true energy, both since it is derived through minimum energy considerations, and because of a degeneracy in parameters (Eichler & Waxman 2005) where if only a fraction of m_e /m_p < ξ _e ≤ 1 of the electrons takes part in the power-law energy distribution, the observed emission remains unchanged for E→E/ξ _e , ρ→ρ/ξ _e , ε _e →ξ _e ε _e , ε _B →ξ _e ε _B . This arises since the observed emission is determined by the number and energy of the radiating electrons in the power-law energy distribution, the magnetic field strength, and the global dynamics, i.e. the bulk velocity or Lorentz factor and location of the emitting electrons as a function of time, all of which remain unchanged under this transformation of parameter values. Specifically, since E/ρ remains unchanged, then so do all lengths, times, and hydrodynamic dimensionless quantities such as the bulk or random Lorentz factor (see Granot 2012). However, the total densities scale as 1/ξ _e , and for each radiating electron in the power-law energy distribution, there are 1/ξ _e protons as well as (1 − ξ _e )/ξ _e non-power-law electrons, which do not contribute to the observed radiation but nonetheless dominate the total energy and cause it to also scales as 1/ξ _e .

2.2.1 Dark bursts

A particular subset of GRBs for which broadband modelling can be performed and in which radio observations play an important role is the class of dark bursts, GRBs without an optical afterglow or one that is dimmer than expected from the observed X-ray emission. There are several plausible reasons that might cause the optical darkness: (1) an emission process that is producing extra X-ray emission but no optical emission on top of the synchrotron spectrum; (2) a high redshift, which pushes the Lyman-alpha forest caused by neutral hydrogen absorption in the intergalactic gas into the optical observing bands and makes them optically dimmer or even completely undetectable; or (3) optical extinction in the GRB host galaxy. Since we know that other emission processes besides synchrotron emission may play a role at X-ray energies, for instance inverse Compton emission, the first reason is something to take into account but cannot explain the extreme optical darkness displayed by some GRBs. The high redshift can be verified fairly easily by comparing the optical observations with simultaneous (near-)infrared observations to see if the flux depletion over multiple wavelengths can indeed be explained by the Lyman-alpha forest. The third reason for optical darkness is the most common one and can also be explored by combining radio observations with an X-ray light curve and performing broadband modelling. If the light curves are well-sampled, preferably in several radio bands, the spectrum and its evolution can be well constrained, and subsequently the optical extinction can be estimated.

Dark bursts are usually classified in two ways: either based on the ratio of the optical and X-ray flux at a given time, assuming that the spectral index has to be softer than −0.5, which is based on the physical assumption that p must be larger than 2 (Jakobsson et al. 2004); or by comparing the optical-to-X-ray spectral index with the X-ray spectral index, making less physical assumptions (van der Horst et al. 2009). There are a few GRBs that are classified as very optically dark whichever of the two methods are used and that have bright radio afterglows.

GRB 051022 is one of the darkest GRBs ever detected in terms of the optical-to-X-ray spectral index and was associated with a bright host galaxy, enabling the determination of the redshift (z = 0.809) without the detection of the optical afterglow (Castro-Tirado et al. 2007). Although there were no radio detections simultaneously with the deep optical upper limits, which is usually the case in the first hours to half a day after a GRB trigger, the radio afterglow was detected and monitored at later times. Broadband modelling of the radio and X-ray light curves, combined with the deep optical limits, revealed a large optical extinction of >5 mag in the line of sight to the GRB, much larger than the average extinction in the host galaxy (Rol et al. 2007). The host galaxies of GRB 110709B and GRB 111215A have also been identified, but their redshift is less certain. However, with the redshift constraints available and by performing broadband modelling including the well-sampled radio light curves, the lower limits on the optical extinction are even larger than for GRB 051022 (Zauderer et al. 2013), and all three GRBs are likely situated in very dusty environments within their host galaxies.

2.3 Radio flares and polarisation

Not all GRBs detected in the radio show the characteristic long-term behaviour of radio afterglows. In some GRBs the peak occurs within the first day or couple of days, and the rise and decay can be steeper than the usual decay observed in radio afterglows. This is indicative of a different origin for this early emission, and these radio flares have been attributed to the reverse shock that propagates back into the outflow and decelerates it. This reverse shock emission was first discovered with the bright optical flash (Akerlof et al. 1999) and following radio flare (Kulkarni et al. 1999) in GRB 990123. A second reverse shock candidate came in the same year with GRB 991216 (Frail et al. 2000), although the radio light curve decay was in this case less rapid than for GRB 990123. After these two GRBs there have been others with early peaks, but mostly at optical wavelengths and even while prompt γ-rays are still being detected (e.g. Yost et al. 2007; Rykoff et al. 2009), where the most striking example is the naked-eye burst GRB 080319B (Racusin et al. 2008b). These early optical detections, however, are not necessarily of emission coming from the reverse shock, and the majority do not show a radio flare. The few cases that have been suggested to be reverse shock emission are based on only a few observations, which hampers any firm conclusions about the origin of the radio emission.

This situation changed recently with GRB 130427A, a relatively nearby GRB (at z = 0.34), which is very bright across the spectrum, even up to high-energy γ-rays (Perley et al. 2013; Ackermann et al. 2013; Kouveliotou et al. 2013; Preece et al. 2013; Maselli et al. 2013). An early optical flash has been reported for this GRB (Vestrand et al. 2013), and also a very bright radio counterpart has been found within the first day (Laskar et al. 2013; van der Horst et al., in preparation; Anderson et al., in preparation). Broadband modelling from radio to X-ray frequencies at early times requires more than one emission component, and the available data can be well described by a combination of a forward and a reverse shock component (Laskar et al. 2013; Perley et al. 2013). The reverse-shock modelling indicates that the jet is moving through a low density medium, a feature that has also been found for GRB 990123. It has been suggested that in these cases the shock cools slowly, which enables the reverse shock to radiate longer than in most other GRBs (Laskar et al. 2013; Perley et al. 2013).

An important ingredient for studying GRB jet physics is polarisation, and in particular measuring the polarisation of the reverse shock emission, as it probes the magnetic field structure in the original outflow. Linear polarisation at the few percent level has been found at optical and near-infrared wavelengths when the emission was thought to originate from the forward shock (Covino et al. 1999; Wijers et al. 1999; Wiersema et al. 2012; see, however, Steele et al. 2009). At radio wavelengths no polarisation has been detected, and the most constraining upper limits for the forward shock polarisation have been determined for GRB 030329 at a level of <1.0% (Taylor et al. 2005) at ν = 8.4 GHz and t = 7.7 d. A contemporaneous optical linear polarisation of 2.2 ± 0.3% was measured (Greiner et al. 2003), but radio polarisation lower than the optical one is likely since ν = 8.4 GHz was below the self-absorption frequency at that time, which suppresses the polarisation. These measurements provide important information regarding the jet, its structure, and the structure of its magnetic field. The magnetic field structure in the original outflow is best constrained by the linear polarisation of the reverse shock emission, and the deepest radio upper limits on it have been obtained for GRB 991216 at less than 7% (Granot & Taylor 2005). These upper limits seem to indicate that the magnetic field cannot be fully structured on large scales. Although there could be depolarisation due to matter along the line of sight to the GRB, the required large depolarisation is not very likely (Granot & Taylor 2005).

2.4 Radio prompt emission searches

Radio flares associated with reverse shocks are expected to occur on a timescale of several hours to a few days after a gamma-ray trigger. However, some models predict radio emission at even shorter timescales, in particular models in which the jet is magnetically dominated and coherent radio emission is produced (e.g. Usov & Katz 2000; Sagiv & Waxman 2002; Moortgat & Kuijpers 2006). There have been several efforts, before and shortly after the discovery of GRB afterglows, focusing on the detection of such early-time radio emission, especially at low radio frequencies (Baird et al. 1975; Inzani et al. 1982; Dessenne et al. 1996; Benz & Paesold 1998; Balsano 1999). These studies did not result in detections, and the upper limits were not very constraining on any of the models. The GRB locations were at that time also not always as accurately known as they are nowadays, which makes any possible detections of radio bursts and associations with GRBs quite uncertain.

After the discovery of afterglows the focus of radio observations shifted to the longer timescales, but over the last couple of years the prompt radio emission has gained interest at observatories covering both low and high radio frequencies, and using imaging or searches in time series. These observation campaigns have been prompted not only by theoretical considerations, but also by the discovery of fast radio bursts of likely cosmological but unknown origin (Lorimer et al. 2007; Thornton et al. 2013), for which GRBs are possible candidates (Totani 2013; Zhang 2013).

The first telescope probing the first minutes to a few hours after GRB triggers in the image plane is AMI, which triggers as soon as possible on any GRB detected by Swift in the Northern Hemisphere (Staley et al. 2013). The field of view of AMI is large enough to cover the the Swift/BAT prompt localisation, which makes this kind of immediate follow-up possible. The response times depend on the source position on the sky, but have several times been as fast as 5 min after the GRB trigger. Although for most GRBs this is after the gamma-ray emission has stopped, any prompt radio emission could be delayed, both intrinsically and due to propagation effects in the interstellar and intergalactic medium. The 1 - h observations at 15 GHz result in sensitivities at sub-mJy levels. The earliest detection so far of a GRB radio counterpart was at 8 h after GRB 130427A (Anderson et al., in preparation), which was extremely bright at all energies. At that time the radio emission was produced by the reverse shock (Vestrand et al. 2013; Laskar et al. 2013; Perley et al. 2013) and not by coherent radio emission.

In the time domain a search for short radio flashes was performed with a radio telescope at the Parkes radio observatory, which was triggered on nine GRBs and in which a candidate single pulse at 1.4 GHz was found for two GRBs (Bannister et al. 2012). These pulses were 6 and 25 ms long, at 10³ and 5·10² s after the trigger, respectively. Although these two tentative detections are not statistically significant, they are a strong motivation to search for more of these bursts. Several new observatories at low radio frequencies are searching for early-time emission in the image and time domain. The initial results of those studies are starting to surface. For instance, the observations with the first station of the Long Wavelength Array (LWA1), which observes in the tens of MHz range. Odenberger et al. (2013) searched through ~18 months of data in the LWA1 archive at the trigger times, and following few hours (to account for the propagation delays in the interstellar and intergalactic medium), of GRBs detected by Swift/BAT, the Monitor of All-sky X-ray Image (MAXI) aboard the International Space Station, and the Fermi Gamma-ray Burst Monitor (GBM). Although the positional accuracy of the latter is typically several degrees, the field-of-view of LWA1 at its low observing frequencies is large enough to cover a significantly large fraction of the sky than the Fermi/GBM location uncertainty region. No prompt GRB emission has been found in images with 5 s integration times, at sensitivities better than previous studies, but these sensitivities are still far from what will be reached by several new low-frequency radio telescopes in the near future (see Section 6.1).

2.5 Size measurements

For several types of sources, it is possible to make images of the jet. Using ‘regular’ imaging is possible for the large-scale AGN jets, but very long baseline interferometry (VLBI) is required for the smallest scales in AGN jets or for the jets in X-ray binaries. Directly imaging the jet, or measuring the size of the jet and its evolution, are important for constructing and testing the theoretical models. Since GRBs are found at cosmological distances but their jets are smaller than a parsec in size, obtaining resolved images is extremely hard even with VLBI. Nonetheless, the image size evolution has been measured in one relatively nearby case, GRB 030329. The source size evolution can also be determined indirectly by utilising the effects of ISS, as has been done for a few GRBs. In this section, we discuss the results of these direct and indirect size measurements, and their implications for broadband modelling.

2.5.1 Very Long Baseline Interferometry

GRB 030329 was bright at all observable frequencies, mainly due to its low redshift of z = 0.1685. Its proximity and radio brightness made a direct size measurement using VLBI possible for the first and only time thus far. Global VLBI was necessary to reach sub-milliarcsecond (mas) resolution: at 25 d the source was 0.07 mas in size ¹ and it was 0.17 mas at 83 d (Taylor et al. 2004). Given the redshift, this implies source sizes of 0.2 and 0.5 parsec, respectively, and an average apparent expansion speed between the two epochs of 3 − 5 times the speed of light (and a slightly higher value between the time of the GRB and the first epoch; see Figure 4).

Figure 4. Evolution of the source size of GRB 030329. All the solid symbols are size measurements or upper limits obtained with VLBI (Taylor et al. 2004; 2005; Pihlström et al. 2007; Mesler et al. 2012), while the open symbol indicates an estimate based on scintillation effects (Berger et al. 2003a). Top panel: evolution of the angular diameter (in milli-arcseconds; left y-axis) and the corresponding physical size D (in cm; right y-axis). Bottom panel: evolution of the average apparent expansion velocity ⟨β_app⟩ = (1 + z)D/2ct. Note that 1 mas corresponds to 2.85 pc at the redshift z = 0.1685 of GRB 030329.

This was a direct proof of the relativistic expansion of GRB jets and provided support for the fireball model (Oren, Nakar, & Piran 2004; Granot et al. 2005a), since the measured image size agreed with the expectations from afterglow models, which only weakly depends on the model parameters (although it does not tell us anything about the outflow composition or jet acceleration mechanism). After the first VLBI observations there have been two more source size measurements, at 217 d (Taylor et al. 2005) and 806 d (Pihlström et al. 2007), and a constraining upper limit at 2032 d, i.e. ~5.5 yr after the GRB trigger (Mesler et al. 2012). The source size measurements have been combined with broadband modelling of the available radio light curves to better constrain the physical parameters and possibly the lateral spreading of the jet (Granot et al. 2005a; Pihlström et al. 2007; Mesler et al. 2012; Mesler & Pihlström 2013). Although the latter could not be significantly constrained, modelling of the light curves and source size evolution gave consistent results, for instance in the derived physical parameters like the blast wave energy and the transition from the trans-relativistic to non-relativistic expansion phase.

Besides the size measurements, constraints on the proper motion have also been placed by the VLBI observations: <0.07 mas/yr using the latest VLBI observation, implying an upper limit <0.73 c (Mesler et al. 2012). This upper limit is consistent with the picture that in order to see the prompt γ-ray emission our line of sight should be within the initial jet aperture, in which case the cumulative proper motion of the flux centroid is indeed expected to be less than the current radius (i.e. half the diameter) of the image (Granot & Loeb 2003; Pihlström et al. 2007; Mesler et al. 2012), or equivalently, the mean proper motion speed is less than the average apparent expansion velocity of the image (shown in the lower panel of Figure 4). This is in contrast with viewing the jet significantly off of its symmetry axis, in which case the cumulative proper motion could exceed the image size (Granot & Loeb 2003). One more implication is that the cannonball model, in which plasmoids with extremely high Lorentz factors are ejected instead of a jet (Dado, Dar, & De Rujula 2004), is inconsistent with the proper motion upper limits (Mesler et al. 2012).

2.5.2 Interstellar scintillation

Variations in the observed radio flux due to ISS have been observed in many sources, mainly pulsars and AGN. There are different types of scintillation, depending on the observing frequency and the angular size of the object. In general, propagation effects in the interstellar medium cause the flux of a compact source to vary, while a source larger than a certain angular size will not display this behaviour (Rickett 1990). GRBs have shown strong modulations of their radio light curves (Goodman 1997), with the first example being GRB 970508 (Frail et al. 1997; 2000), and many more GRBs since then having displayed a similar behaviour. These variations do not only occur between observations on different days, but also intra-day variability has been observed, for instance in GRB 070125 (Chandra et al. 2008). In all GRBs the variations become weaker over time, because of the jet's evolution: its angular size starts out smaller than the characteristic angular scale for ISS, but it grows with time until it eventually exceeds this scale and the variations become smaller. Measuring the strength of this scintillation behaviour and the time at which it quenches provide an indirect estimate of the source size.

There are in general two types of ISS: weak and strong scattering. In weak scattering there are only small phase changes over the first Fresnel zone of the radio waves due to fluctuations in the density of free electrons in the medium in between us and the source, usually in the interstellar medium of our galaxy. When the wavefront is highly distorted on scales smaller than the first Fresnel zone, this is called strong scattering and produces much larger flux modulations than weak scattering. Strong scattering can be divided up into: (i) refractive scintillation, caused by focusing and defocusing of the wave front by large-scale inhomogeneities, which is a broadband phenomenon; and (ii) diffractive scintillation, caused by interference between rays diffracted by small-scale irregularities in the interstellar medium, which is modulating the flux over a narrow frequency band.

For any particular GRB the angular scales for the three types of ISS, as well as the scintillation strength and timescale, can be estimated (Walker 1998) using the NE2001 model of the distribution of free electrons in our galaxy (Cordes & Lazio 2002). The scintillation strength is first of all determined by the observing frequency. Observations above a transition frequency ν₀ are typically in the weak scattering regime, while observations at lower frequencies are affected by strong scattering. The angular scales and modulation indices, i.e. the fractional flux variations (or the ratio of the standard deviation and mean value of the flux density), can be expressed in terms of the angular size of the first Fresnel zone θ_F0 at an observing frequency ν equal to the transition frequency ν₀, with θ_F0 = 2.1 × 10⁴ SM ^0.6ν ^{− 2.2} ₀μas. The scattering measure SM and ν₀ depend on the location of the source in the sky and can be determined from the NE2001 model (Cordes & Lazio 2002), with typical values of SM ~ 10^−3.5 kpc/m^20/3 and ν₀ ~ 10 GHz, resulting in values for θ_F0 of a few μas. The equations for the angular scale, time scale and modulation index, for weak, refractive and diffractive scintillation are given in Table 1. It is clear from this table that the modulation indices for weak and refractive scattering are highest when the observing frequency is close to ν₀, but they are always smaller than the modulation index of diffractive scattering, which is 1 for the source angular size θ_s < θ_d. The angular size for diffractive scintillation is smaller than for refractive or weak scattering though, so for GRB radio afterglows it can only play a significant role at early times when the jet is still compact enough. Furthermore, diffractive scintillation is a narrow-band phenomenon, and is only a significant effect when one observes with a frequency resolution Δν_obs < Δν_dc = ν(ν/ν₀)^17/5, while for Δν_obs>Δν_dc the modulation index will be suppressed by a factor of ~N ^−1/2 = (Δν_obs/ν)^−1/2(ν/ν₀)^17/10 due to effective averaging over N = Δν_obs/Δν_dc mutually incoherent frequency ranges, each with the decorrelation bandwidth Δν_dc.

Table 1. Angular scales, time scales, and modulation indices for weak, refractive, and diffractive ISS, with ν₀ the transition frequency between weak and strong scattering, θ_F0 the angular size of the first Fresnel zone at this frequency, ν the observing frequency, and θ_s the source angular size. For GRBs, ν₀ is typically ~10 GHz and θ_F0 is a few μas.

Figure 1 shows the effects of scintillation on three well-studied GRBs. GRB 030329 was relatively nearby, and as a result ISS affected the light curves only in the first couple of weeks, since the source size became larger than the ISS angular sizes quickly. The angular size at which this happened could be estimated, as shown in Figure 4. GRBs 970508 and 980703 were situated at a higher redshift, and thus the ISS effects lasted longer. Quenching of the scintillation could also be used in those two GRBs to estimate the source size evolution, which was consistent with the results from broadband modelling (Frail et al. 2000). We note that the NE2001 model provides rather good estimates for lines-of-sight in our galaxy, but is quite uncertain for sources off the galactic plane. Therefore the size estimates for GRBs based on this method should be treated with caution. Some broadband modelling efforts include scintillation estimates by adding them to the radio flux uncertainties, to account for the large values of their fitting statistic (usually χ²), but this should be done cautiously.

2.6 Searching for off-axis GRB jets

So far we have discussed the observations of GRB afterglows for which we have detected the prompt γ-ray emission. Given the collimation of GRB outflows, combined with relativistic beaming effects, there is also a large fraction of the total population of GRBs for which we do not see any emission coming from the jet at early times, and in particular we do not detect their prompt γ-ray emission. However, the deceleration of the jet during the afterglow and its eventual sideways expansion cause the beaming of its radiation to decrease with time. Eventually, at sufficiently late times, the expanding beaming cone of the afterglow radiation reaches our line of sight and the jet's afterglow emission becomes visible. The importance of such events for constraining the degree of collimation of GRB jets was realised early on (Rhoads 1997), and they have been called ‘orphan afterglows’. No orphan afterglow has been clearly detected yet, but their detection prospects and implications of existing limits on the detection rate have been studied at X-ray (Woods & Loeb 1999; Nakar & Piran 2003), optical (Dalal, Griest, & Pruet 2002; Totani & Panaitescu 2002; Nakar, Piran, & Granot 2002; Rhoads 2003; Rau, Greiner & Schwartz 2006) and radio (Perna & Loeb 1998; Levinson et al. 2002; Gal-Yam et al. 2006; Soderberg et al. 2006b; Bietenholz et al. 2013) frequencies.

Eventually, the emission from the jet becomes roughly isotropic, varying only by a factor of order unity between different observers, when the jet becomes sub-relativistic, as well as more spherical, on a time scale of months to years after the GRB. At such late times the afterglow is detectable only at radio frequencies. Since GRBs of the long-soft class—a large fraction of all GRBs—are associated with Type Ic SNe, it has been suggested to search for such orphan radio afterglows at late times at the positions of relatively nearby SNe of this type (Paczynski 2001; Granot & Loeb 2003), and there have been searches dedicated to this purpose (e.g. Berger et al. 2003b; Soderberg et al. 2006b; Bietenholz et al. 2013). These searches have not resulted in any clear detections of off-axis GRB jets so far.

There have been Type Ic SNe detected at radio wavelengths that were considered as off-axis jet candidates, such as SN 2001em (Granot & Ramirez-Ruiz 2004). Given its proximity, with a distance of ~80 Mpc, an initially relativistic jet would have been resolved with VLBI, but the observations showed an unresolved source (Bietenholz & Bartel 2005; Paragi et al. 2005; Bietenholz & Bartel 2007; Schinzel et al. 2009). This has lead to the suggestion that the radio emission was produced by an interaction of the SN ejecta with a dense circumstellar shell (Chugai & Chevalier 2006). We note that there have been other SNe that were detected at radio frequencies within a few days after the optical discoveries and were candidates for jet-like emission. SN 2008D was discovered because of an X-ray flash, but modelling of the radio light curves and VLBI observations led to the conclusion that the emitting outflow was non-relativistic (Soderberg et al. 2008; Bietenholz, Soderberg, & Bartel 2009; van der Horst et al. 2011). SN 2009bb was extremely radio bright, and based on the light curves, Soderberg et al. (2010) concluded that the ejecta were mildly relativistic (~0.85c), which could not be further constrained with VLBI observations (Bietenholz et al. 2010). While the latter velocity determination was model dependent, for SN 2007gr (Paragi et al. 2010) the size expansion was constrained directly with VLBI to be mildly relativistic (at least ~0.6c). However, in the latter case Soderberg et al. (2010) concluded from modelling of the radio and X-ray light curves that the expansion is non-relativistic (~0.2c). For a more detailed review of the VLBI results on Type Ic SNe including the off-axis jet candidates, see Bietenholz (2013).

Despite a number of interesting candidates for mildly relativistic and/or collimated outflows from radio SNe, there have been no clear detections of off-axis relativistic GRB-like jets to this date. In principle this could put constraints on the number of Type Ic SNe harbouring jets, or on the average jet opening angle. However, it should be noted that the SNe associated with GRBs have broad lines in their optical spectra, which significantly reduces the sample of candidates for off-axis GRB jet emission. Nevertheless, current limits imply that only a fraction of such broad-lined SNe Ib/c could harbour energetic, relativistic jets that produce bright radio emission, with luminosities comparable to observed radio afterglows of GRBs at cosmological distances (Bietenholz et al. 2013). Moreover, radio surveys of nearby SNe Ib/c are also useful for constraining the presence of other types of relativistic jets that do not reach high enough Lorentz factors to produce a GRB and/or are somewhat less energetic (Granot & Ramirez-Ruiz 2004). This arises since as long as the jet initially reaches a Lorentz factor Γ₀≳ a few, its late-time radio emission (after its deceleration radius) is largely independent of Γ₀. The latter also holds at earlier times, around or after the peak time, for off-axis viewing angles that are outside of the jet's initial beaming cone, i.e. as long as Γ₀ > 1/(θ_obs − θ₀). This can be very interesting for constraining the fraction of engine-driven SNe Ib/c, which may also be related to the large typical inferred asphericity of these explosions.

3 JET STRUCTURES AND LIGHT CURVES

It is hard to infer the GRB jet angular structure because of the lack of resolved GRB images. Moreover, due to relativistic beaming we can observe only emission coming from angles ≲1/Γ relative to our line of sight (where Γ is the bulk Lorentz factor of the emitting material). This corresponds to very small angles, ≲Γ⁻¹ ₀ ≲ 10⁻² rad, during the prompt emission where the initial Lorentz factor Γ₀ is very high, Γ₀ ≳ 100. Hence, the prompt γ-ray emission probes only a very small region near the line of sight (of solid angle ~πΓ⁻² ₀, or a fraction ~Γ⁻² ₀/4 ~ 10⁻⁷ − 10^−4.5 of the total solid angle), and does not provide information about the structure of the outflow that propagates in other directions. Fortunately, the Lorentz factor of the emitting material decreases with time during the afterglow, since the afterglow shock decelerates as it sweeps up the external medium. The decrease in Γ reduces the degree of relativistic beaming, thus allowing us to observe afterglow emission from a wider range of angles (of ≲Γ⁻¹ from our line of sight). This increase in the size of the visible region enables us to probe the jet structure over increasingly larger angular scales. In this section we discuss the various jet structures presented in the literature and the resulting light curves at different observing angles.

3.1 The jet angular structure

Most works consider a jet with axial symmetry, both for simplicity, and since this is expected to zeroth order in most theoretical models. Moreover, the jet is usually assumed to be double-sided, with reflection symmetry about the plane normal to its symmetry axis that intersects the central source. The angular structure of such a jet can be described by the dependence on polar angle θ (in the range 0 ≤ θ ≤ π/2) of the initial distribution of its total energy (excluding rest energy) content per solid angle, $\mathcal {E}$ , and its initial Lorentz factor Γ₀. The initial Lorentz factor distribution, Γ₀(θ), affects mainly the prompt γ-ray emission and early afterglow, as it is largely forgotten after the local deceleration time or radius t _dec(θ) ~ R _dec(θ)/2cΓ² ₀(θ), while $\mathcal {E}(\theta )$ affects also the late-time afterglow emission. The structure of GRB jets is important for deducing their event rate and total energy, as well as for requirements on the jet production mechanisms. Several different jet structures have been suggested in the literature. They are shown in Figure 5 and briefly discussed below.

Figure 5. An illustration of various jet structures that have been discussed in the literature, in terms of the initial distribution of their energy per solid angle (excluding rest energy), $\mathcal {E} = dE/d\Omega$ , with the angle θ from the jet symmetry axis, in a log-log scale. Both the normalisation of $\mathcal {E}$ and the typical angular scale may vary in most models, and their values in this figure were chosen to be more or less typical (from Granot 2005).

The uniform jet (UJ, or ‘top hat’) model is the most popular model for the angular structure of GRB jets (Rhoads 1997; 1999; Panaitescu & Mészáros 1999; Sari et al. 1999; Kumar & Panaitescu 2000a; Moderski, Sikora, & Bulik 2000; Granot et al. 2001; 2002; Ramirez-Ruiz & Madau 2004; Ramirez-Ruiz et al. 2005), where $\mathcal {E}$ and Γ₀ are uniform within some finite half-opening angle, θ_j, and sharply drop outside of θ_j (thick solid blue line in Figure 5). Another rather popular jet structure is the universal structured jet (USJ) model (Mészáros, Rees, & Wijers 1998; Lipunov, Postnov, & Prokhorov 2001; Rossi, Lazzati, & Rees 2002; Zhang & Mészáros 2002), where $\mathcal {E}$ and Γ₀ vary smoothly with θ, as a power law outside of some narrow core angle, usually with equal energy per decade in θ, $\mathcal {E}\propto \theta ^{-2}$ (thick dashed red line in Figure 5). The power-law wings can either extend all the way to the equator (θ = π/2), or terminate at a somewhat smaller angle, but still of order unity, as the universality requires it to accommodate the largest inferred angles of tens of degrees. In the UJ model the different values of the jet break time, t _j, in the afterglow light curve arise mainly due to different initial values θ₀ for θ_j (and to a lesser degree due to different ambient densities). In the USJ model, all GRB jets are assumed to be identical, and the different values of t _j arise mainly due to different viewing angles, θ_obs, from the jet axis. Moreover, the expression for t _j is similar to that for a uniform jet with $\mathcal {E}\rightarrow \mathcal {E}(\theta =\theta _{\rm obs})$ and θ₀→θ_obs.

An alternative jet structure with a Gaussian angular profile (thin dashed-dotted green line in Figure 5) has also been proposed in the literature (Zhang & Mészáros 2002; Kumar & Granot 2003). The main reasoning behind it is that it can serve as a more realistic version of a uniform jet, where the edges are smooth rather than sharp. A Gaussian jet, $\mathcal {E}(\theta )\propto \exp (-\theta ^2/2\theta _0^2)$ , can be thought of as being intermediate between the UJ and USJ models. It is, however, closer to the UJ model than to the canonical version of USJ model, which has equal energy per decade in the wings ( $\mathcal {E}\propto \theta ^{-2}$ , where the wings dominate the total jet energy by about an order of magnitude) in the sense that the energy in the wings of a Gaussian jet is much smaller than in its core.

An additional jet structure that is gradually being considered more seriously is a two-component jet (Pedersen et al. 1998; Frail et al. 2000; Berger et al. 2003a; Huang et al. 2004; Peng, Königl, & Granot 2005; Racusin et al. 2008a), with a narrow uniform jet of initial Lorentz factor Γ₀ ≳ 100 surrounded by a wider uniform jet with Γ₀ ~ 10 − 30 (thin dashed black line in Figure 5). A jet structure with such properties was predicted both in the context of the cocoon in the collapsar model (Ramirez-Ruiz, Celotti, & Rees 2002) and in the context of a hydromagnetically driven neutron-rich jet (Vlahakis, Peng, & Königl 2003). Phenomenologically, this model was invoked to explain rebrightening episodes in the afterglow light curves of GRBs 030329 (Berger et al. 2003a) and 030723 (Huang et al. 2004). Detailed calculations, however, show that it cannot produce very sharp features in the light curve (Granot 2005), and in particular cannot account for these sharp observed rebrightening episodes. Another motivation for such a jet structure arises from the energetics of GRBs, as it might help reduce the high efficiency requirements from the prompt γ-ray emission (Peng, Königl, & Granot 2005). Later Swift observations (e.g. Nousek et al. 2006) have taught us, however, that the two-component jet model does not significantly help reduce the required γ-ray efficiency (Granot, Königl, & Piran 2006) despite being able to reproduce the early X-ray afterglow light curves.

Another jet structure that has been suggested (Levinson & Eichler 1993; 2000; Eichler & Levinson 2003; 2004; Lazzati & Begelman 2005; Tchekhovskoy, McKinney, & Narayan 2008) has a cross-section in the shape of a ring at angle θ _c , and is sometimes referred to as a ‘hollow cone’ (thin solid magenta line in Figure 5), which is uniform within θ _c < θ < θ _c +Δθ where Δθ ≪ θ _c . An extreme variant of this structure is a ‘fan’ shaped jet where Δθ ≪ θ _c +Δθ = π/2 (thick dashed-dotted cyan line in Figure 5). However, it produces only a modest steepening across the jet break (Granot 2005) and is not very well motivated on theoretical grounds.

Finally, there are non-axi-symmetric jet structures that have been suggested in the literature, such as the ‘patchy shell’ model (Kumar & Piran 2000; Nakar & Oren 2004) or its extreme version—the ‘mini-jets’ model (Yamazaki, Ioka, & Nakamura 2004). For a more detailed discussion of the different models for the jet angular structure and how they might be constrained using GRB observations we refer readers to Granot (2007) or Granot & Ramirez-Ruiz (2013). For the purposes of this review it is most important to mention that the jet angular structure might be probed using afterglow observations, and in particular the shape of the afterglow light curves and the evolution of its linear polarisation.

From all the topics on jet dynamics that are discussed in the next section, the one that is most strongly affected by the jet's initial angular structure is its late-time dynamics well after the energy in the outflow is transferred to the shocked external medium. There we will consider primarily a UJ model, since it has been most extensively studied.

3.2 Light curves for different observers

Examples of afterglow light curves for different jet models and viewing angles are shown in Figure 6 for the optical and in Figure 7 in the radio. For an initially perfectly uniform jet with sharp edges, numerical simulations show that slower material is generated at the sides of the jet, whose velocity points sideways relative to the spherical radial direction. Both effects cause less beaming of the radiation within the jet aperture leading to more flux seen by observers at large off-axis viewing angles (θ_obs>θ₀), and a more gradual rise to the peak, with a peak flux that is larger compared to that for an on-axis observer at the same observed time. This can be seen when comparing the top and second panel of Figures 6 and 7. For large off-axis viewing angles the peak occurs when the beaming cone of the jet's radiation reaches our line of sight, and then the light curve approaches that for an on-axis observer. In the top panel of Figure 7 the hydrodynamic simulation has been supplemented before its onset with a conical wedge with half-opening angle θ₀ = 0.2 taken out of the Blandford & McKee (1976) self-similar solution that was also used for its initial conditions. The transition between the two can be seen as a sharp increase in flux that quickly saturates to a shallower rise of the flux. Before this transition the flux rises rapidly, similar to the semi-analytic models, while after the transition it rises more moderately because of the hydrodynamics effects mentioned above. It is important to keep such effects in mind when using a simple (semi-)analytic jet model.

Figure 6. Afterglow optical (ν = 5 × 10¹⁴ Hz) light curves for different jet angular structures, dynamics, and viewing angles (from Eichler & Granot 2006). The viewing angles are θ_obs/θ₀ = 0, 0.5, 1, 1.5, 2, 3, 4, 5, where θ₀ is the (initial) half-opening angle for the uniform jet (two top panels) and the core angle (θ₀ = 0.1) for the Gaussian jet (two bottom panels). Top panel: an initially uniform jet with sharp edges and half-opening angle θ₀ = 0.2 whose dynamics are calculated using a hydrodynamic simulation (Granot et al. 2002). The other panels show results for a semi-analytic dynamical model (without lateral spreading). Second panel: a uniform jet with sharp edges (θ₀ = 0.1). Two bottom panels: a Gaussian jet, in energy per solid angle $\mathcal {E}$ , and either a Gaussian or uniform initial Lorentz factor Γ₀. All cases do not include a counter-jet, and thus the light curves are not shown up to very late times.

Figure 7. Similar to Figure 6 but in the radio (ν = 1 GHz). The hydrodynamic simulations (top panel) are from J. Granot, F. De Colle, & E. Ramirez-Ruiz, in preperation, as in Figure 8, and include a counter-jet that produces a late-time bump in the light curves. For the semi-analytic models, shown in the bottom three panels, there is no lateral spreading and no counter-jet (which makes them not very realistic at late times). In all cases E _k,iso = 10⁵³ erg, n = 1 cm⁻³, p = 2.5, ε _e = ε _B = 0.1. The sharp break in the on-axis (θ_obs = 0) light curve corresponds to the passage of ν _m (from ν < ν _m < ν _c before the break to ν _m < ν < ν _c after the break; self-absorption is not included here). The jet break is earlier and is much less pronounced in the radio, and thus much harder to observe.

For a jet with a Gaussian distribution of $\mathcal {E}(\theta )$ , if Γ₀(θ) also has a Gaussian profile (which corresponds to a constant rest mass per solid angle in the outflow), then the afterglow light curves are rather similar to those for a uniform jet (third panel of Figures 6 and 7; Kumar & Granot 2003). On the other hand, for a Gaussian $\mathcal {E}(\theta )$ but a constant Γ₀(θ) the light curves for off-axis viewing angles (i.e. outside the jet's core) have a much higher flux at early times, compared to a Gaussian Γ₀(θ) or a uniform jet because of a dominant contribution from the jet material that emits along the line of sight, which in this case has an early deceleration time (bottom panel of Figures 6 and 7; Eichler & Granot 2006; Granot, Ramirez-Ruiz, & Perna 2005). After this material along the line of sight is decelerated by the external medium, the light curves join those for an initially Gaussian Γ₀(θ) (compare the third and bottom panels of Figures 6 and 7).

Figure 8 shows light curves based on hydrodynamic simulations (De Colle et al. 2012a; 2012b), for different viewing angles and a power-law external density profile (ρ_ext = AR ^−k ) ranging from a uniform medium as expected for the ISM (k = 0) to a wind-like profile (k = 2 for a constant mass-loss stellar wind). It also includes two intermediate cases (k = 1, 1.5), which might correspond to the wind of a massive star progenitor whose properties vary near the end of its life. The late-time bump in the light curve corresponding to the counter-jet coming into view is clearly present for a k = 0 but becomes less pronounced as k increases and almost disappears for k = 2 (De Colle et al. 2012b). The rise to the peak for large off-axis viewing angles is also much less sharp for larger k (more stratified external media compared to a uniform medium with k = 0) as the jet decelerates more slowly causing its beaming cone to approach the line of sight more gradually.

Figure 8. Afterglow radio (ν = 1 GHz) light curves for hydrodynamic simulations of an initially uniform jet for different viewing angles, θ_obs = 0, 0.4, 0.8, π/2, and different values of the external density power-law index, k = 0, 1, 1.5, 2, where ρ_ext = AR ^−k (from J. Granot et al., in preparation). Initial conditions are a conical wedge of half-opening angle θ₀ = 0.2 rad taken out of the Blandford & McKee (1976) self-similar spherical solution with an energy of E _k,iso = 10⁵³ erg (and a true energy E≈2 × 10⁵¹ erg for a double-sided jet) when the Lorentz factor of matter just behind the shock is 20. The external density is chosen to be n ₀ = 1 cm⁻³ for k = 0 and to have the same jet-break radius (and approximately the same density at that radius) for k>0 (corresponding to A _* = 1.65 for k = 2). The light curves are supplemented by the emission from before the simulation onset time using a conical wedge like that used in the initial conditions.

4 JET DYNAMICS

GRB jet dynamics can be divided into several different stages. First, the jet must be launched near the central source. The launching is likely magnetic, possibly through the Blandford-Znajek mechanism that operates in a rapidly accreting newly formed stellar mass black hole. Alternatively, the jet may originate from a magneto-hydrodynamic (MHD) pulsar-type wind for a millisecond magnetar central engine of long GRBs. Neutrino - anti-neutrino annihilation may also play an important role. This stage is still not well understood.

Next, the jet must be accelerated. The two main candidates for the dominant acceleration mechanism are magnetic acceleration (discussed in detail in Section 4.1) and thermal acceleration (by the radiation pressure in an optically thick electron-positron, photon and baryon plasma—the fireball model). For GRBs of the long-soft class, which are associated with the death of a massive star, the jet must bore its way out of the progenitor star. The jet propagation inside the progenitor star is discussed in Section 4.2.

The collimation of the jet is expected to be linked to its acceleration, and can be assisted by the interaction with the external medium (e.g. with the progenitor star in the case of long GRBs), by the accretion disk wind, and by magnetic hoop stress. Its resulting angular structure far from the source is important for its late-time dynamics, which governs the afterglow emission. A coasting phase is expected for thermal acceleration and may also occur in magnetic acceleration models. The coasting phase ends at the deceleration radius R _dec, where most of the energy is transferred to the shocked external medium. Unless the ejecta shell is highly magnetised at R _dec, it will be significantly decelerated by the time it reaches R _dec by a reverse shock, whose characteristics are discussed in Section 4.3.

At R > R _dec most of the energy is already in the shocked external medium, and therefore the outflow composition and radial profile are essentially forgotten, but the jet angular profile persists. Locally, the flow approaches the Blandford & McKee (1976) spherical self-similar solution (with the local value of the isotropic equivalent energy in the jet). Once Γ drops below 1/θ₀, at radii R > R _j, significant jet lateral expansion is possible, but until very recently it was unclear to what extent it occurs in practice. Recent progress on this topic is discussed in Section 4.4. The flow eventually becomes Newtonian and spherical, approaching the Sedov-Taylor self-similar solution.

4.1 Magnetic acceleration

Magnetic acceleration likely plays a key role not only in GRBs, but also in other relativistic jet sources, such as AGN or micro-quasars. It has been realised early on that the (quasi-steady) thermal acceleration (the main competing acceleration mechanism) and collimation of initially very hot and high-pressure material near the source to highly super-sonic speeds (e.g. the ‘twin exhaust’ model for AGN jets; Blandford & Rees 1974) faces serious difficulties under realistic astrophysical conditions (i.e. it is subject to various instabilities; Smith et al. 1981). Therefore, in light of the difficulties faced by thermal acceleration, magnetic fields play an important role in many models for the launching, collimation and acceleration of relativistic jets. In particular, in AGN jets the Thompson optical depth even near the source is not high enough for thermal acceleration by the radiation pressure to work well.

Most magnetic acceleration models assume a steady flow, as this may adequately describe outflows that vary slowly enough with time, and since it significantly simplifies the relevant dynamical equations, allowing analytic self-similar solutions (e.g. Begelman & Li 1992; Vlahakis & Königl 2003) with the additional standard assumptions of axial symmetry and ideal MHD (i.e. no dissipation of magnetic energy). An advantage of magnetic acceleration is that strong large-scale magnetic fields near the source may help avoid excessive mass loading and thus enable the jets to reach relativistic speeds.

It has been known for a long time (Goldreich & Julian 1970) that a (quasi-)spherical highly magnetised steady flow can effectively accelerate only up to an asymptotic Lorentz factor Γ_∞ ~ σ^1/3 ₀ and magnetisation σ_∞ ~ σ^2/3 ₀ where σ₀ ≫ 1 is the initial value of the magnetisation parameter σ (the ratio of electromagnetic to matter energy flux or enthalpy density). That is to say, most of the energy remains in electromagnetic form, i.e. a Poynting flux dominated flow. Collimation of the flow by an external pressure that leads to an asymptotic jet half-opening angle θ_j can increase Γ_∞ and decrease σ_∞ by up to a factor of ~θ^−2/3 _j. This occurs since lateral causal contact in the jet (that is required for efficient acceleration) is maintained if θ_j does not exceed the Mach angle, θ_j ≲ θ_M ~ σ^1/2/Γ, where energy conservation implies σΓ ~ σ₀ as long as the flow remains highly magnetised, σ ≫ 1. However, even under the most favourable conditions the asymptotic magnetisation remains σ_∞ ≥ 1, which does not allow efficient energy dissipation in internal shocks within the outflow (Lyubarsky 2009; 2010a; Komissarov et al. 2009). It has been pointed out (Tchekhovskoy, Narayan, & McKinney 2010; Komissarov, Vlahakis, & Königl 2010) that a sudden drop in the external pressure, as may occur for instance when a GRB jet exits its progenitor star, can result in a sudden additional acceleration that can lead to Γ_∞θ_j ≫ 1 as inferred in GRBs, but still with σ_∞ ≥ 1.

These difficulties faced by the ‘standard’ steady, axi-symmetric and non-dissipative (or ideal MHD) magnetic acceleration, or its limitations, have led on the one hand to the suggestion that the jets might remain Poynting flux dominated at large distances from the source and the observed emission is the result of magnetic reconnection events rather than internal shocks (Blandford 2002; Lyutikov 2006). As less extreme alternatives, other models suggested increasing the acceleration efficiency by relaxing one of the standard assumptions, such as axi-symmetry—leading to non-axi-symmetric instabilities that randomise the magnetic field orientation (Heinz & Begelman 2000). Since a highly tangled magnetic field effectively behaves like a relativistic fluid (with an adiabatic index of 4/3), this leads to efficient acceleration, similar to thermal acceleration of relativistic outflows. This is also related to relaxing the assumption of ideal MHD (or a non-dissipative flow), since both the kink instability mentioned above (Drenkhahn & Spruit 2002), as well as other instabilities (such as the Kruskal-Schwarzschild instability in a striped wind; Lyubarsky 2010b) can lead to magnetic reconnection, i.e. gradual magnetic dissipation, which in turn enhances the acceleration due to the conversion of magnetic to thermal energy, where the thermal pressure efficiently accelerates the outflow.

Finally, a natural alternative is replacing the usual assumption of steady state by strong time dependence. For a long time, the latter impulsive regime was sparsely studied, and mainly in the non-relativistic case (Contopoulos 1995). However, recently a new impulsive magnetic acceleration mechanism was found that operates in the relativistic case (Granot, Komissarov, & Spitkovsky 2011), which can be much more efficient than magnetic acceleration in steady flows, and can lead to low magnetisations, σ ≪ 1, thus enabling efficient dissipation in internal shocks. The more efficient acceleration that reflects a qualitatively different behaviour of impulsive outflows can be very relevant for GRBs, as well as for other relativistic jet sources such as tidal disruptions and flares in AGN or micro-quasars, or even giant flares in soft gamma repeaters (SGRs, thought to be magnetars—highly magnetised neutron stars). This new impulsive acceleration mechanism also triggered renewed interest in this topic (e.g. Levinson 2010; Lyutikov 2011; Granot 2012a; 2012b; Komissarov 2012).

Figure 9 shows the results for an impulsive magnetic acceleration test case (from Granot et al. 2011), featuring a finite cold shell of plasma initially uniform (with width l ₀, rest mass density ρ₀ and magnetic field B ₀), highly magnetised (σ₀ = B ² ₀/4πρ₀ c ² ≫ 1) and at rest, whose back leans against a conducting ‘wall’ while its front faces vacuum. At t = 0 a strong, self-similar rarefaction wave forms at the vacuum interface in the front of the shell and propagates towards its back, reaching the wall at t = t ₀ ≈ l ₀/c. By that time the shell's energy-weighted mean Lorentz factor and magnetisation are 〈Γ〉 ~ σ^1/3 ₀ and 〈σ〉 ~ σ^2/3 ₀, respectively. At t > t ₀ the shell detaches from the wall, keeps an almost constant width (l≈2l ₀) and accelerates as 〈Γ〉 ~ σ₀/〈σ〉 ~ (σ₀ t/t ₀)^1/3 up to the coasting time t_c = σ² ₀ t ₀. At t > t_c the shell starts coasting at 〈Γ〉 ~ σ₀ while its width grows (l/2l ₀ ~ t/t_c ) and its magnetisation rapidly decreases (〈σ〉 ~ t ₀/t), leading to complete conversion of magnetic to kinetic energy and allowing strong shocks to develop in the flow, which can result in a large radiative efficiency.

Figure 9. A simple test case for impulsive magnetic acceleration: the energy-weighted mean Lorentz factor 〈Γ〉 of a finite cold shell of plasma initially uniform (with l ₀, rest mass density ρ₀, and magnetic field B ₀), highly magnetised (σ₀ = B ² ₀/4πρ₀ c ² ≫ 1; σ₀ = 30 was used here), and at rest, whose back leans against a conducting ‘wall’ while its front faces vacuum (from Granot et al. 2011), versus the time t in units of the shell's initial fast magnetosonic crossing time t ₀ ≈ l ₀/c. The analytic expectations (dotted and dashed-dotted lines) and the results of numerical simulations (diamond symbols joined by a solid line) are in very good agreement.

Depicted in Figure 10 is the evolution of a similar shell in spherical geometry that propagates into an external medium with a power-law density profile, ρ_ext = AR ^−k (from Granot 2012a). The initial shell magnetisation σ₀ and density ρ₀∝1/σ₀ are allowed to vary while keeping fixed the values of the initial time t ₀ or length scale R ₀ (with t ₀ ≈ R ₀/c), energy E or power L (with E ~ Lt ₀ ≈ LR ₀/c), and external density ρ_ext(R ₀) = AR ^−k ₀ (k < 2 in this figure), which imply a fixed value of the critical Lorentz factor Γ_cr ~ (f ₀σ₀)^{1/(8 − 2k)} where f ₀ = ρ₀/ρ_ext(R ₀) is the initial density ratio of the shell and the external medium, and R _cr ~ R ₀Γ² _cr is the critical radius. Figure 10 shows the two dynamical regimes most relevant for GRBs. The purple line shows Regime I (1 < σ₀ < Γ_cr or a sufficiently low external density) where the shell initially expands as if into vacuum and only after becoming kinetically dominated (at R_c where R_c < R _cr < R _Γ) and expanding radially (at R_c < R < R _Γ) is it significantly decelerated by the external medium through a strong relativistic reverse shock, that can produce a bright emission that peaks on a timescale larger than the duration of the prompt GRB emission (the familiar low-σ ‘thin shell’; Sari & Piran 1995). Eventually, at R = R _Γ, most of the energy is transferred to the shocked external medium and the flow approaches the Blandford & McKee (1976) self-similar solution.

Figure 10. Evolution of the typical (or energy-weighted average) Lorentz factor Γ with the distance R ≈ ct from the central source, for a spherical finite cold shell propagating into an external medium with a power-law density profile, ρ_ext = AR ^−k (from Granot 2012a).

The green line in Figure 10 shows Regime II (1 < Γ_cr < σ₀ < Γ^{3(4 − k)/2} _cr) where the shell is significantly affected by the external medium while it is still Poynting flux dominated (at R > R_u ~ R ₀(f ₀σ^−1/3 ₀)^{3/(10 − 3k)}), thus suppressing the reverse shock (which is either non-existent or very weak). The shell remains highly magnetised and gradually transfers its energy to the shocked external medium through pdV work across the contact discontinuity up to R _cr, after which the flow approaches the Blandford-McKee solution. In this regime no significant reverse shock emission is expected, and the onset of the afterglow (i.e. the peak of the emission from the shocked external medium) is expected to be on a timescale comparable to the prompt GRB duration (i.e. a high-σ ‘thick shell’).

In addition, there are other regimes not shown in Figure 10. In Regime III (1 < Γ^3(4−k)/2 _cr < σ₀) the external density is high enough that there is no impulsive acceleration stage where 〈Γ〉∝R ^1/3, and instead 〈Γ〉 ~ σ₀/〈σ〉∝R ^(k−2)/4 at R ₀ < R < R _cr ~ R _dec, and then approaches the Blandford-McKee solution (its observational signatures are expected to be similar to Regime II). In Regime IV (Γ_cr < 1) the external density is so high that the flow remains Newtonian all along (as might happen while the GRB jet is propagating inside a massive star progenitor). There is also an exotic Regime II* that exists only in a highly stratified external medium (10/3 < k < 4), where the external shock accelerates down the steep external density gradient and decouples from the original shell, carrying a small fraction of the total energy, while the original shell travels in its wake essentially as if into vacuum, similar to Regime I.

The simple test case described so far for impulsive magnetic acceleration may perhaps be directly applicable to giant flares from SGRs, but not to most astrophysically relevant relativistic jet sources. In practice, the variability times in GRBs (as well as in AGN and micro-quasars) are typically large enough that the flow should first undergo quasi-steady collimation-induced acceleration that saturates, and only later the impulsive acceleration kicks in and operates until the flow becomes kinetically dominated (for details see Section 5 of Granot et al. 2011).

The effects of multiple sub-shells in the outflow can be important, and the collisions between them may provide efficient energy dissipation that can power the GRB emission (Granot 2012b; Komissarov 2012). They may also allow a low-σ ‘thick shell’, i.e. a strong relativistic reverse shock peaking on a timescale comparable to the prompt GRB emission, which is not possible for a single shell. For a long-lived source (e.g. AGN) with initial sub-shell widths l ₀ and separations l _gap each sub-shell can expand by a factor of 1+l _gap/l ₀, and its magnetic energy decreases by the same factor (where σ_∞ ~ l ₀/l _gap), and may be converted to kinetic or internal energy, or radiation. For a finite source activity, the merged shell can still expand further and convert more magnetic energy into other forms (even without interaction with an external medium).

Important related points that warrant further study are the transition from impulsive to quasi-steady collimation induced acceleration, both in a single shell and in multiple sub-shells, as well as the dissipation in the interaction between sub-shells and its effect on the outflow acceleration and the resulting emission, such as a possible photospheric spectral component.

4.2 Jet propagation inside the progenitor star (for long GRBs)

There is significant evidence connecting GRBs of the long-soft class to the death of massive stars (e.g. Woosley & Bloom 2006, and reference therein). In particular, some long GRBs have a secure spectroscopic association with core-collapse SNe of Type Ic, which imply a massive star progenitor stripped of both hydrogen and helium from its envelope. There is also some spectroscopic evidence for a fast stellar wind from a Wolf-Rayet progenitor star in the afterglow optical spectrum. This has led to the realisation that the jet must first bore its way through the envelope of the massive star progenitor before it can produce the prompt γ-ray emission well outside of the star (as implied by intrinsic pair opacity or compactness arguments), and later produce the afterglow emission at even larger radii, several orders of magnitude larger than the radius of the progenitor star (which is ≲10¹¹ cm).

The propagation of a GRB jet inside its progenitor star was studied numerically using special relativistic hydrodynamic simulations, both in 2D and in 3D (Aloy et al. 2000; Zhang, Woosley, & MacFadyen 2003; Zhang, Woosley, & Heger 2004; Morsony, Lazzati, & Begelman 2007; Mizuta & Aloy 2009). The jet is typically injected at some inner radius (which is larger than physically expected, due to numerical resolution considerations and the large dynamical range between the injection and stellar radii), with a Lorentz factor Γ _j,0 of a few to several in the radial direction, uniformly within a cone (of half-opening angle θ₀ of several to a few tens of degrees) centred around the star's rotational axis. The jet is typically collimated by the star (through a strong collimation shock near its base, and weaker ones later on) and manages to exit the star and eventually reach a Lorentz factor close to its maximal possible value (which is set at the injected energy per unit rest energy), and narrow jets of a few to several degrees are obtained in most simulations. After being collimated by a strong collimation shock near its base, the jet propagates in an approximately cylindrical manner until the jet material near its head is strongly decelerated by a termination (or reverse) shock, and diverted sideways to feed a high-pressure inner cocoon of shocked jet material, which is surrounded by an outer cocoon of shocked stellar material. It has been suggested that shear instabilities in the jet-cocoon boundary may cause variability in the jet that eventually leads to internal shocks in the outflow that may be responsible for the prompt GRB emission (Zhang et al. 2003; Morsony, Lazzati, & Begelman 2010).

The ram pressure balance of the shocked jet and stellar materials at the head ² determines the head's velocity, which in turn depends on its cross-section that is self-consistently determined through the collimation of the jet by the cocoon. The ‘feedback’ between the cocoon and jet structures complicates this problem and has caused difficulties in its analytic modelling, making a satisfactory fully self-consistent analytic model rather illusive. Nonetheless, this problem was addressed analytically by many authors and progress has been made despite the difficulties (Begelman & Cioffi 1989; Mészáros & Waxman 2001; Matzner 2003; Lazzati & Begelman 2005; Morsony et al. 2007).

Most notably, a recent study by Bromberg et al. (2011) has managed to construct a self-consistent analytic model that agrees with the results of numerical simulations. It provides a better understanding of the numerical results, and of the behaviour of this system under general conditions. They find that the jet dynamics are governed by the dimensionless ratio $\tilde{L}$ of the energy density in the jet (assumed here to be one-sided for simplicity) just upstream of its head and the rest mass energy density of the external material in front of the jet's head, ρ _a c ². The jet is collimated for $\tilde{L}<\theta _0^{-4/3}$ , where it is initially conical with θ _j = θ₀ until the collimation shock, then cylindrical until exiting the star with $\theta _j=\theta _0^2\max (\tilde{L}^{1/4},\tilde{L}^{3/4})$ , and then it expands sideways to become (quasi-)conical again, asymptotically reaching θ _j ≈θ₀. In this regime $\tilde{L}\sim [L_j/(\rho _a t^2\theta _0^4 c^5)]^{2/5}$ where L_j is the jet luminosity. The head of the jet is Newtonian for $\tilde{L}<1$ (where its speed in units of c is $\beta _h \approx \tilde{L}^{1/2}$ ) and relativistic for $\tilde{L}>1$ (where $\Gamma _h\approx 2^{-1/2}\tilde{h}^{1/4}$ and $\tilde{h}$ the dimensionless specific enthalpy). For $\tilde{L}>\theta _0^{-4/3}$ the jet is un-collimated and keeps its injection half-opening angle all along, θ _j = θ₀, while in this regime $\tilde{L} \sim L_j/(\rho _a t^2\theta _0^2 c^5)$ . The head is typically at most mildly relativistic when it breaks out of the star, and the resulting analytic expression for the breakout time was used in order to compare the predictions of the collapsar model for the duration distribution of long GRBs with observations (Bromberg et al. 2012), where a nice agreement was found, which supports this picture.

As discussed in Section 4.1, there are compelling physical arguments why it is likely that the jet is initially cold and highly magnetised, rather than hot and hydrodynamic. It is therefore important to study the dynamics of such a highly magnetised, Poynting flux dominated jet inside the progenitor star. This may provide observational predictions that can eventually help distinguish between magnetic and thermal launching of the jet. Here we outline some key results and expectations from Bromberg et al. (in preparation). The flow must decelerate in order to match the head's velocity, but the jet's high magnetisation suppresses strong shocks and thus prevents shocks from facilitating this deceleration, which is instead achieved by a convergence of the jet towards its head. The resulting narrower jet head compared to a hydrodynamic jet results in a faster head propagation speed, and the head becomes relativistic well inside the star, crossing it at almost its light crossing time, resulting in a shorter break-out time. This may affect the resulting long GRB duration distribution. Moreover, the relativistic head implies that only a small fraction (~Γ⁻² _h ) of the jet power is injected into the cocoon while the jet bores its way out of the star, so that the cocoon is expected to be significantly less energetic compared to a hydrodynamic jet. This may be manifested by less energy injection towards the SN explosion, and smaller SN kinetic energies.

For a highly magnetised jet the dynamics and its head velocity are determined primarily by the dimensionless ratio of the energy density in the jet near the light-cylinder r_L and the rest mass density of the external medium just in front of the head, a ~ L_j /(πρ _a c ³ r ² _L ) (where a one-sided jet is assumed here for simplicity). The head's proper velocity is given by u_h ≡Γ _h β _h ~ r_h /r_L ~ min (a ^1/6, a ^1/5), where r_h is the head's lateral size. The result that the head's proper velocity u_h and its lateral size r_h are essentially independent of the details of the jet structure significantly simplifies this problem and allows for (semi-)analytic solutions.

Recently, Levinson & Begelman (2013) have analysed this problem analytically and argued that current-driven instabilities likely disrupt the jet well inside the star and dissipate most of its magnetic energy into heat, thus reducing it into an essentially hydrodynamic jet. However, Bromberg et al. (in preparation) argue that for typical parameters of GRB jets and their progenitor stars such instabilities are unlikely to completely disrupt the jet, which will instead remain largely intact and highly magnetised throughout its propagation inside the star. This results in important differences in the jet dynamics, and warrants further study, i.e. by 3D relativistic MHD simulations that could test the jet's stability to non-axi-symmetric instabilities.

4.3 Reverse shock and its emission

4.3.1 The basic dynamics

If the GRB outflow is not highly magnetised, it is eventually decelerated through a reverse shock, as it sweeps up the external medium. We first consider a uniform shell of ejecta, in a spherical geometry. This can serve as a good local approximation for a non-spherical flow that does not vary significantly in the lateral direction on angular scales ≲1/Γ that are causally connected. Consider a shell of initial width Δ₀ and Lorentz factor Γ₀ in the lab frame, propagating into an external density ρ₁(R). A forward shock is driven into the ambient medium, while the ejecta are decelerated by a reverse shock. Thus four regions exist: (1) unshocked external medium, (2) shocked external medium, (3) shocked ejecta, and (4) unshocked (freely expanding) ejecta. The velocities are measured relative to region 1, while the pressure p and rest mass density ρ (or number density n) are measured in the fluid rest frame. Let subscript i between 1 and 4 refer to region i, and a subscript ij refer to the relative velocity of regions i and j, such that Γ _i1 = Γ_1i = Γ _i . Given Γ₄ = Γ₀, Γ₁ = 1, ρ₄, ρ₁, and assuming the shell of ejecta and external medium are both cold (p_i ≪ ρ _i c ² for i = 1, 4), there are 8 unknown hydrodynamic quantities (ρ₂, p ₂, Γ₂, ρ₃, p ₃, Γ₃, and the Lorentz factors of the forward and reverse shock fronts) that can be found from the conditions across the contact discontinuity separating regions 2 and 3 (p ₂ = p ₃ and Γ₂ = Γ₃≡Γ) as well as the shock jump conditions (continuity of the energy, momentum, and particle fluxes) across the forward and reverse shocks (between regions 1 and 2, and 4 and 3, respectively). For simplicity this is treated in planar symmetry, and the spherical nature of the flow enters only when the evolution of the flow with radius is considered.

One may obtain an approximate estimate of the dynamics at this stage by equating the ram pressure of the incoming fluid from regions 4 and 1, as seen from the contact discontinuity (the rest frame of regions 2 and 3): ρ₁ u ² ₂₁ ~ ρ₄ u ² ₃₄, where u = Γβ is the proper velocity. For equal density of the unperturbed shell and external medium, ρ₄ = ρ₁, we must have exactly the same strength for the reverse and forward shock, and thus the same upstream to downstream proper velocity, u ₂₁ = u ₃₄, because of the symmetry of the problem in this case. For our assumed relativistic outflow (Γ₄ = Γ₀ ≫ 1) this implies that both the forward and reverse shocks are relativistic, with u ₂₁ = u ₄₃ = [(Γ₄ − 1)/2]^1/2≈(Γ₄/2)^1/2 ≫ 1. As long as the forward shock is relativistic then 1 ≪ Γ₃ = Γ₂ ≈ u ₂₁ ~ u ₃₄(ρ₄/ρ₁)^1/2, and if the reverse shock is also relativistic then we also have 1 ≪ u ₄₃≈Γ₄₃≈Γ₄/2Γ₃, which together imply a relatively simple solution: Γ₂≈(Γ₀/2)^1/2(ρ₄/ρ₁)^1/4 and Γ₃₄≈(Γ₀/2)^1/2(ρ₁/ρ₄)^1/4 (Sari & Piran 1995). This shows that the condition for the forward shock to be relativistic is Γ² ₀ ≫ ρ₁/ρ₄, which is typically always satisfied, so that u ₂₁≈Γ₂ and u ₄₃ ~ Γ₂(ρ₁/ρ₄)^1/2. The condition for the reverse shock to be relativistic is Γ² ₀ ≫ ρ₄/ρ₁, which can be expressed as Ψ ≫ 1 in terms of the parameter Ψ≡Γ² ₀ρ₁/ρ₄ that measures the strength of the reverse shock. The reverse shock is Newtonian in the opposite limit, Ψ ≪ 1, and in this case it only slightly decelerates the ejected shell material, Γ₂≈Γ₀, which implies that u ₄₃ ~ Γ₀(ρ₁/ρ₄)^1/2 = Ψ^1/2 ≪ 1.

The relative upstream to downstream proper velocity across the reverse shock can be conveniently expressed in terms of Ψ, u ₄₃ ~ min (Ψ^1/4, Ψ^1/2), where Ψ≡Γ² ₀ρ₁/ρ₄ ~ Ac ²Γ⁴ ₀ R ^2−k Δ/E ~ Γ⁴ ₀ R ^2−k Δ/l ^3−k for a power-law external density, ρ₁ = AR ^−k (Granot 2012a), and l ~ (E/Ac ²)^{1/(3 − k)} is the Sedov length. For a narrow distribution of Lorentz factors the shell's width remains approximately constant and close to it initial value, Δ≈Δ₀, and therefore Ψ ∝ R ^2−k . This implies that for k < 2 the reverse shock is initially Newtonian and strengthens with radius. If, on the other hand, there is a reasonable spread in the Lorentz factor of the outflow, δΓ₀ ~ Γ₀, then the shell starts to spread radially at the spreading radius R _s ~ Γ² ₀Δ₀, and its width evolves as Δ/Δ₀ ~ max (1, R/R _s). At R > R _s it spreads linearly with radius, Δ∝R, which implies that Ψ∝R ^3−k , and therefore then the reverse shock strengthens for k < 3.

If the reverse shock is relativistic by the time it finishes crossing the shell, then most of the energy is transferred to the shocked external medium within a single shell crossing time. If there is only a very small spread in Γ₀ (δΓ₀ ≪ Γ₀) then the reverse shock can still be Newtonian when it finishes crossing the shell. In this case a large number of Newtonian shocks and rarefaction waves may need to cross the shell before most of the energy is transferred to the shocked external medium (Sari & Piran 1995). However, if there is a reasonable spread in the Lorentz factor of the outflow, δΓ₀ ~ Γ₀, then the shell starts to spread before the reverse shock finishes crossing it, in such a way that by the time it crosses the shell the reverse shock already becomes mildly relativistic, so that most of the energy is transferred to the shocked external medium in a single shell crossing time (Sari & Piran 1995). The dividing line between these two cases corresponds to 1 = Ψ(R _s) ~ Γ^2(4−k) ₀(Δ₀/l)^3−k , where Ψ(R _s)>1 implies a relativistic reverse shock or a ‘thick’ shell and Ψ(R _s) < 1 implies a Newtonian reverse shock (without spreading) or a ‘thin’ shell.

Please note that most of the energy is transferred to the shocked external medium at a radius R _dec ~ lΓ^{−2/(3 − k)} _dec where Γ_dec = Γ(R _dec) ~ min [Γ₀, Γ_cr] and

(1) \begin{eqnarray} \Gamma _{\rm cr} &=&\left(\frac{l}{\Delta _0}\right)^{(3-k)/2(4-k)} \nonumber\\ &=&\left\lbrace {\begin{array}{cc}280\,\zeta ^{3/8}E_{53}^{1/8}n_0^{-1/8}T_{50}^{-3/8} & (k=0)\,\\[9pt] 70\zeta ^{1/4}E_{53}^{1/4}A_*^{-1/4}T_{50}^{-1/4} & (k=2)\ , \end{array}}\right. \end{eqnarray}

where ζ = (1+z)/2, T _GRB = (1+z)Δ₀/c = 50T ₅₀ s is the observed duration of the GRB, E = 10⁵³ E ₅₃ erg is the (isotropic equivalent) energy of the flow, and n = n ₀ cm⁻³ = A/m_p for k = 0, while A _* = A/(5 × 10¹¹ g cm⁻¹) for k = 2. For Γ₀>Γ_cr we have a thick shell or relativistic reverse shock, and the observed deceleration time is similar to the duration of the GRB, t _dec ~ R _dec/2cΓ² _dec ~ (1+z)Δ₀/c ~ T _GRB. For Γ₀ < Γ_cr we have a Newtonian (or at most mildly relativistic) reverse shock or a thin shell, and in this case t _dec ~ (l/c)Γ^{−2(4 − k)/(3 − k)} ₀ > T _GRB (where l/c ~ t _NR is the non-relativistic transition time) and is given by

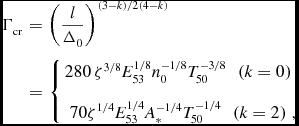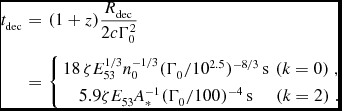(2) \begin{eqnarray} t_{\rm dec} &=& (1+z)\frac{R_{\rm dec}}{2c\Gamma _0^2} \\ \nonumber &=& \left\lbrace {\begin{array}{cc}18\,\zeta E_{53}^{1/3}n_0^{-1/3}(\Gamma _0/10^{2.5})^{-8/3}\,{\rm s} & (k=0)\ ,\\[3pt] 5.9\zeta E_{53} A_*^{-1}(\Gamma _0/100)^{-4}\,{\rm s} & (k=2)\ . \end{array}}\right. \end{eqnarray}

The possibility of a long-lived reverse shock due to a smooth distribution of energy as a function of Lorentz factor in the ejecta was pointed out by Sari & Mészáros (2000), who also studied the observational implications. Internal shocks would eventually lead to a radial profile in the outflow where slower material resides behind faster material, and gradually catches up with the forward shock after the latter decelerates to a somewhat smaller Lorentz factor. A self-similar solution has been found for a power-law external density profile and a power law in the ejecta energy as a function of Lorentz factor (Nakamura & Shigeyama 2006). This solution indicates that the reverse shock is much weaker (e.g. the upstream to downstream relative proper velocity across the shock is much smaller) than naively expected. This may result in a significantly weaker emission from the reverse shock compared to the naive assumption that the reverse shock is mildly relativistic (as was made in Sari & Mészáros 2000). Such ‘energy injection’ into the forward shock was invoked to explain the shallow decay phase observed in the early X-ray afterglows by Swift, in addition to a different type of energy injection due to a long-lived activity of the central source (e.g. Nousek et al. 2006; Granot & Kumar 2006). However, here we shall focus on the radio emission from after the passage of the reverse shock through a uniform ejecta shell, where the shock crossing occurs on a timescale comparable to the duration of the prompt γ-ray emission, without any additional energy injection.

4.3.2 The radio flare and its polarisation

In terms of the observable emission signatures, there is the prompt optical flash that is observed in some GRBs, and lasts while the reverse shock is crossing the ejecta shell. After the reverse shock finishes crossing the shell, the electrons in the shell cool adiabatically while its magnetic field and Lorentz factor gradually decrease as its width (in the radial direction) increases and it settles in the back of the flow (locally described by the Blandford & McKee 1976 solution) behind an increasing amount of newly shocked external medium behind the forward shock. This results in a sharp decay of the optical flux, roughly as t ⁻² (Sari & Piran 1999; Kobayashi & Sari 2000; Nakar & Piran 2004).

More generally, this causes the peak synchrotron frequency from the reverse shock to decrease with time, until after about a day since the prompt GRB the reverse shock emission peaks in the radio. This peak in the radio emission has been dubbed the radio flare. One of the best cases for a reverse shock emission was the optical flash from GRB 990123 (Akerlof et al. 1999). While the optical flash alone already provided compelling evidence for a reverse shock origin (Sari & Piran 1999), together with the radio flare observed for this GRB (Kulkarni et al. 1999) the evidence for a reverse shock origin becomes significantly stronger (Nakar & Piran 2005). Moreover, this provides valuable information about the composition of the outflow (its magnetisation near the deceleration radius could not have been very high in order to allow the formation of a strong reverse shock) and about the external medium (with a low density near the deceleration radius, as expected for the ISM but not for a stellar wind). A high external density at R _dec would cause the cooling frequency ν _c to be below the optical, so by the shell crossing time the optical flux from the line of sight is exponentially suppressed, resulting in a steeper decay due to high latitude emission—emission from large off-axis angles (θ>1/Γ) that arrives at later times (~R _decθ²/2c) due to the curvature of the shock front (Kumar & Panaitescu 2000b). This also suppresses the radio flare (even if ν _c is above the radio at the shell crossing time) as it would peak earlier, still suffer from self-absorption, and the electrons may suffer significant energy losses of both radiative and adiabatic origin.

Since the radio flare emission arises from the original ejecta, its polarisation properties can probe the magnetic field structure in the outflow (Granot & Königl 2003; Granot & Taylor 2005). Moreover, since the ejecta Lorentz factor decreases between the prompt optical flash that typically lasts for tens of seconds and the radio flare that typically peaks after a day or so, they probe different angular scales in the ejecta, as the visible region is within an angle of ~1/Γ around our line of sight. At the time of the radio flare (a day or so after the GRB) typically Γ~10 (and the Lorentz factor of the original ejecta shell is somewhat lower than that of the newly shocked external medium) so that an angle of ~1/Γ~0.1 rad around the line of sight may be probed. Moreover, the radio flare often peaks on a timescale comparable to the jet break time, t_j , and thus much of the jet is visible at that time (for a uniform jet).

For example, one might consider a magnetic field in the ejecta that consists of many coherent patches, in which the magnetic field is approximately uniform, which are randomly oriented with respect to each other, and have a typical angular size θ _B ≳ 1/Γ₀ (which can be thought of as the magnetic field correlation length). In this case, a large degree of polarisation might be expected in the optical flash, close to the maximal value for synchrotron emission from a uniform magnetic field: P ~ P _max = (1 − α)/(5/3 − α) for an optically thin spectral slope F _ν∝ν^α (Granot 2003). However, if Γθ _B < 1 during the radio flare, the polarisation is then expected to be reduced by a factor of ~1/Γθ _B to P ~ Γθ _B P _max and the position angle should generally be different, due to averaging over N ~ (Γθ _B )⁻² incoherent patches (Granot & Königl 2003; Granot & Taylor 2005).

For a globally ordered toroidal magnetic field in the jet, the position angle of the linear polarisation is not expected to change between the optical flash and radio flare. The degree of polarisation, however, is expected to vary with time, and depends on the ratio of the observed time t (i.e. the peak of the radio flare) and the jet break time t_j . The measured upper limits for three different radio flares (from Granot & Taylor 2005) are shown in Figure 11 superimposed on the theoretical expectations for a uniform jet (in the top two panels, for different viewing angles) and for a structured jet with a narrow core and wings with equal energy per decade in θ (bottom panel). The expectations are shown for the two plausible spectral power-law segments: α = 1/3 or α = −(p − 1)/2 (i.e. −0.75 for p = 2.5). Since P _max = (1 − α)/(5/3 − α), a higher value of α produces a higher degree of polarisation. Nevertheless, even the lowest values for optically thin synchrotron emission, α = 1/3 and P _max = 1/2, still produce a fairly high degree of polarisation.

Figure 11. Upper limits (3 σ) for the linear polarization of the radio flare emission overlaid on the theoretical polarisation light curves for a toroidal magnetic field in the GRB ejecta (from Granot & Taylor 2005). The error bars represent the uncertainty in the determination of the jet break time t_j from the optical afterglow light curve. The top two panels are for a uniform jet (Granot & Taylor 2005) of half-opening angle θ₀. The different lines, from top to bottom, are for the viewing angles θ_obs/θ₀ = 0.9, 0.8, . . ., 0.1. The main part of these two panels is for α = d log F _ν/d log ν = 1/3 and P _max = (1−α)/(5/3 − α) = 1/2, while the inset is for α = −0.75 and P _max≈0.72 (with a = −α). In the top panel the Lorentz factor of the ejecta is assumed to remain equal to that of the freshly shocked fluid just behind the forward shock (FS), while the middle panel is assumed to follow the Blandford & McKee (1976) self-similar solution (BM). The bottom panel is for a structured jet where the energy per solid angle drops as θ⁻² outside of some small core angle (taken from Lazzati et al. 2004). In this case P(t/t_j ) is practically independent of θ_obs.

For a uniform jet, the degree of polarisation near the jet break time, P(t ~ t_j ), significantly increases with the normalised viewing angle θ_obs/θ₀, and goes to zero at θ_obs = 0 (i.e. for an observer exactly along the jet symmetry axis). Therefore, the upper limits on the polarisation (Granot & Taylor 2005) put upper limits on θ_obs/θ₀, which also depend on the dynamical model for the GRB ejecta. For GRB 991216 these limits are θ_obs/θ₀≲0.4 and 0.55 for the dynamical models used in the top and middle panels of Figure 11, respectively.

The model that is most severely constrained by these upper limits on the polarisation is a toroidal magnetic field together with a structured jet (see lower panel of Figure 11). In this case all of the upper limits are significantly below the predictions of this model (by a factor of ≳6 for GRB 991216). This makes a predominantly toroidal magnetic field in the GRB ejecta together with a structured jet hard to reconcile with the data.

4.4 Jet dynamics during the afterglow

4.4.1 Reconciling between analytic models and numerical simulations

Similar to most studies of GRB jet dynamics during the afterglow phase, we focus here on an initially uniform jet with well defined, sharp edges. The jet dynamics have been studied mainly analytically (e.g. Rhoads 1999; Sari et al. 1999; Panaitescu & Kumar 2001a) and numerically using two dimensional special relativistic hydrodynamic simulations (e.g. Granot et al. 2001; Zhang & MacFadyen 2009; van Eerten, Zhang, & MacFadyen 2010), as well as with an intermediate ‘thin shell’ approach (Kumar & Granot 2003) where the dynamical equations are integrated over the radial profile of the shocked fluid, thus reducing them to a set of 1D partial differential equations. The analytic models have predicted a rapid sideways expansion, with an exponential growth of the jet half-opening angle θ_j with radius R at R > R _j where Γ drops below 1/θ₀. Numerical simulations, however, have shown a much more modest lateral expansion, with a quasi-logarithmic growth of θ_j(R > R _j), where most of the energy remains within the initial jet half-opening angle θ₀ until the flow becomes mildly relativistic, and only then the flow starts to gradually approach spherical symmetry. Such a behaviour is obtained in analytic models under the crude approximation that the jet does not expand sideways significantly until it becomes non-relativistic (Granot et al. 2005a).

So far most simulations were for an initial jet half-opening angle θ₀ = 0.2, or even larger θ₀. Recently, however, Wygoda, Waxman, & Frail (2011) and van Eerten & MacFadyen (2012) have performed simulations also for narrower initial jets, down to θ₀ = 0.05. Wygoda et al. (2011) have found that significant lateral spreading starts when Γ drops below θ⁻¹ ₀, as predicted by analytic models, and tried to reconcile the apparent discrepancy with analytic models by attributing it to their small range of validity after significant lateral spreading starts (1 ≪ Γ < θ⁻¹ ₀) for the typical modest values of θ₀ used in the simulations. In contrast, van Eerten & MacFadyen (2012) concluded that there is no exponential lateral expansion, and even in the narrow-jet case it is better described by logarithmic spreading.

This debate was reconciled by Granot & Piran (2012), who constructed generalised analytic models that remain valid when the jet becomes wide or sub-relativistic. In particular, they considered two different recipes for the lateral expansion:

(3) \begin{equation} \frac{d\theta _j}{d\ln R} = \frac{\beta _\theta }{\beta _r} \approx \frac{1}{\Gamma ^{1+a}\theta _j^a}\ ,\quad \quad a = \left\lbrace {\begin{array}{l}1\quad \quad (\hat{\beta }=\hat{n})\ ,\\ 0\quad (u^{\prime }_\theta \sim 1)\ .\end{array}}\right. \end{equation}

The first, old recipe (a = 0) was used in most previous analytic works and corresponds to a mildly relativistic lateral expansion speed in the jet's comoving rest frame (u′_θ ~ 1). The second, new recipe (a = 1) is based on the jump conditions for oblique shocks of arbitrary proper velocity u = Γβ, which imply that the velocity of fluid just behind the shock front (in the downstream region) is in the direction of the local shock normal (i.e. perpendicular to the shock front at that location, $\hat{\beta } = \hat{n}$ ; Kumar & Granot 2003) in the upstream rest frame. Granot & Piran (2012) also considered two different recipes for sweeping up the external medium, and named them after the shape of the swept-up region. In the ‘trumpet’ model external medium is swept up only at the front of the jet (part of a sphere within a double-sided cone), while in the ‘conical’ model it is also swept up along its sides, so that once the jet becomes spherical the swept-up mass equals that originally within a sphere of the same radius (while it is smaller in the trumpet model). These two recipes are the basis of two new analytic models, which remain valid for slow, wide jets. For comparison, results have also been obtained for the old ‘relativistic’ model, which breaks down when the jet becomes mildly relativistic or wide (and sweeps up mass similarly to the trumpet model).

Their new analytic models fit the results of numerical simulations much better (see left panel of Figure 12), mainly because they remain valid also in the mildly relativistic, quasi-spherical regime. They show that for modest initial jet half-opening angles, θ₀, the outflow is not sufficiently ultra-relativistic when its Lorentz factor reaches Γ = 1/θ₀ and therefore the sideways expansion is rather slow, showing no rapid, exponential phase. On the other hand, jets with an extremely narrow initial half-opening angle (θ₀ ≪ 10^−1.5 for k = 0 or θ₀ ≪ 10⁻² for k = 2; see left panel of Figure 12), which are still sufficiently ultra-relativistic at Γ = 1/θ₀, do show a phase of rapid, exponential lateral expansion. However, even such jets that expand sideways exponentially are still not spherical when they become sub-relativistic. Afterglow observations suggest that most GRB jets likely fall into the former category, i.e. are not initially sufficiently narrow and therefore do not go through a stage of exponential lateral expansion, consistent with the simulations of van Eerten & MacFadyen (2012), as well as earlier simulations starting from Granot et al. (2001).

Figure 12. Left: Comparison, for θ₀ = 0.2 rad and k = 0 (for an external density profile ρ_ext∝R ^−k ), between the analytic models of Granot & Piran (2012) (thin lines) and the results of 2D special relativistic hydrodynamic simulations (from De Colle et al. 2012a, 2012b) of a jet with initial conditions of a conical wedge of half-opening angle θ₀ taken out of the Blandford & McKee (1976) self-similar solution (thick dot-dashed black line), in terms of the jet proper velocity (u = Γβ), half-opening angle (θ _j ), as well as normalised parallel (r _∥) and perpendicular (r _⊥) sizes. The green, red, and blue lines are for the relativistic, trumpet, and conical models, respectively. Thin solid lines are for the new recipe for lateral expansion (a = 1) while thin dashed lines are for the old recipe (a = 0). Right: Comparison between the relativistic (solid lines), trumpet (dot-dashed lines), and conical (dashed lines) models of Granot & Piran (2012) in terms of the evolution of θ _j with the normalised radius r, for k = 0, 1, 2 (top to bottom panels), where all models use the new recipe for the jet's lateral spreading (a = 1). Results are shown for log ₁₀(θ₀) = −3, −2.5, . . . , −0.5 (using different colours). The values of θ₀ = 1, π/2 and the critical radius r_c = [(3 − k)/2]^{(3−a)/[(1+a)(3−k)]} where lateral spreading is expected to become significant are shown for reference.

4.4.2 An afterglow jet propagating into a stratified medium

At least some GRBs of the long-soft class are clearly (spectroscopically) associated with Type Ic SNe, and thus with the death of a massive star. This implies that the afterglow shock propagates into the pre-explosion stellar wind, and suggests a stratified external medium with a density profile ρ_ext = AR ^−k . For a constant wind velocity v_w to mass-loss rate $\dot{M}_w$ ratio, k = 2 and $A =\dot{M}_w/(4\pi v_w)$ . However, as $\dot{M}_w/v_w$ might vary before the explosion and is rather uncertain, it is worth to also consider other values of k. This has been investigated analytically by various groups, mostly in a practical sense by fitting GRB afterglow data with models in which k is a free parameter (e.g. Yost et al. 2003; Starling et al. 2008; van der Horst 2007; Leventis et al. 2012; 2013).

Recently, 2D special relativistic hydrodynamic simulations have been performed for k = 0, 1, 2 by De Colle et al. (2012b), using the Mezcal code (De Colle et al. 2012a). The initial conditions were taken to be a conical wedge of half-opening angle θ₀ = 0.2 rad taken from the spherical, self-similar Blandford-McKee solution. They find that the jet dynamics in stratified external media (k = 1, 2) are broadly similar to those in a uniform external medium (k = 0). In particular, the jet half-opening angle starts increasing logarithmically with time (or radius) once the Lorentz factor Γ drops below θ⁻¹ ₀ (as θ₀ is modest; see Section 4.4.1). For larger k values, however, the lateral expansion speed is initially faster while Γ>θ⁻¹ ₀ but slower at late times, since it increases as Γ decreases (see, e.g. Eq. 3), which in turn occurs more slowly for larger k (e.g. in the spherical case Γ∝M ^−1/2∝R ^{(k − 3)/2}), while Γ(t _j)≈θ⁻¹ ₀ for all k (such a behaviour is also seen in analytic models, e.g. Granot 2007; Granot & Piran 2012). Therefore, for larger k values the jet is initially wider at the same value of Γ ≥ θ⁻¹ ₀ while later on at Γ < θ⁻¹ ₀ it becomes Newtonian and approaches spherical symmetry more slowly. This occurs since the jet's lateral size R _⊥ keeps growing, while its parallel size (along it symmetry axis) R _∥ essentially stalls for k = 0 as the jet becomes sub-relativistic, until the flow approaches spherical symmetry (see Figure 13). Such a behaviour also occurs in analytic or semi-analytic models (Granot et al. 2005a; Granot & Piran 2012, see lower left panel of Figure 12).

Figure 13. The transverse (R _⊥) and parallel (R _∥) size of the jet, averaged over the total energy excluding rest mass, as a function of the lab frame time in units of the jet break time for k = 0, 1, 2 (from De Colle et al. 2012b).

The shape of the jet break for k = 0, 1, 2 is shown in the top panel of Figure 14. De Colle et al. (2012b) find that contrary to analytic expectations (Kumar & Panaitescu 2000a), there is a reasonably sharp jet break in the light curve for k = 2. What is more, the shape of the jet break is affected more by the viewing angle θ_obs (within the initial jet aperture, θ_obs ≤ θ₀) than by the external density profile slope k (for 0 ≤ k ≤ 2). Steeper density profiles (i.e. larger k values) are found to produce more gradual jet breaks while larger θ_obs cause smoother and later appearing jet breaks. For θ_obs = 0 most of the steepening occurs within a factor of ~2 − 4 in time for 0 ≤ k ≤ 2 while for θ_obs ~ (0.5 − 1)θ₀ it takes ~1 − 2 decades for 0 ≤ k ≤ 2.

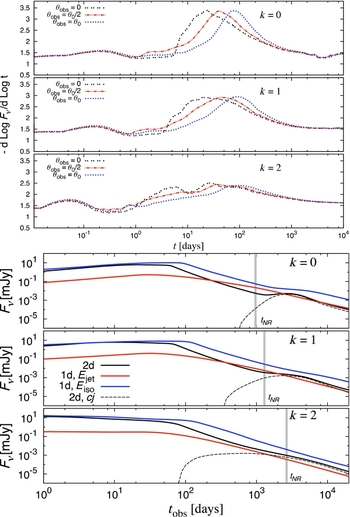
Figure 14. Top: Jet break shape—the temporal decay index −dlog F _ν/dlog t _obs as a function of the observed time t _obs (including electron cooling, at ν = 10¹⁷ Hz >max (ν _m , ν _c ). Bottom: Radio (ν = 1 GHz) light curves for k = 0, 1, 2 simulations in 2D, 1D with E = E _jet, and for a cone with half-opening angle θ₀ computed from spherical 1D simulations with E = E _iso (for θ_obs = 0). The contribution due to the counter-jet is included in the light curves, and explicitly shown (dashed curves) for the 2D simulations (from De Colle et al. 2012b). The sharp break in the light curve corresponds to the passage of ν _m (from ν < ν _m < ν _c before the break to ν _m < ν < ν _c after the break; self-absorption is not included here). The jet break, at t_j ~ a few weeks, is much less pronounced in the radio, and thus much harder to observe.

The radio light curves for the 2D simulations are shown by the black lines in the bottom panel of Figure 14. The counter-jet becomes visible as it turns sub-relativistic. For k = 0 this results in a clear bump-like feature in the light curve (as also shown by van Eerten & MacFadyen 2011). For larger k values, however, the jet decelerates and comes into view more gradually, causing only a mild flattening in the radio light curve that might be hard to discern when k = 2. Also shown in the bottom panel of Figure 14 are light curves for a spherical 1D simulation with the same true energy (orange lines), and for a double-sided cone of half-opening angle θ₀ taken from a spherical 1D simulation (from De Colle et al. 2012a) with the same isotropic equivalent energy (blue lines). Late-time radio calorimetry usually assumes a spherical flow near the non-relativistic transition time t _NR (thick vertical grey lines), and is thus likely to consistently over-estimate the true energy by up to a factor of a few for k = 2, but either over-predict or under-predict it by a smaller factor for k = 0, 1 (as can be seen by comparing the orange and black lines in the figure).

5 RELATING THEORY & OBSERVATIONS

Our current understanding of GRBs and their jets is based on observations of the prompt γ-ray emission from thousands of GRBs and the afterglow emission from several hundreds of GRBs, across the electromagnetic spectrum, as well as on the theoretical advances, in particular in GRB jet dynamics and the relevant physical processes and emission mechanisms, both through analytic and numerical work. In the previous sections we have highlighted the roles that radio observations play in unveiling the physics of GRB jets, in both the spectral and temporal domain, most importantly by complementing the broadband spectrum. In this section we further discuss and quantify some of these aspects.

5.1 Broadband modelling

Several groups have performed broadband modelling studies on samples of GRB afterglows including radio observations (e.g. Wijers & Galama 1999; Panaitescu & Kumar 2001b; 2002; Yost et al. 2003; Cenko et al. 2010; 2011). It is clear from these studies that the various modelling methods lead to different results for the same GRBs. Nonetheless, these efforts seem to indicate that there is a large spread in the physical parameters of the jet, the external medium, and collisionless relativistic shocks (see Figure 15). The top panel of Figure 15 shows the collimation corrected energies E _jet ~ 10⁵⁰ − 10⁵² erg versus the external medium number densities n ~ 10⁻³ − 10² cm⁻³ (for a uniform medium; k = 0) or A _* ~ 10⁻² − 10^−0.5 g cm⁻¹ (for a wind-like medium; k = 2). The jet initial half-opening angles θ₀ ranges from less than one degree up to tens of degrees.

Figure 15. Top: The collimation corrected energy versus density for GRBs that have been modelled using their broadband radio, optical, and X-ray data (black symbols from Panaitescu & Kumar 2002; grey symbols from Cenko et al. 2010, 2011). The densities are n in case of a homogeneous medium (solid symbols) and A _* in case of a stellar wind (open symbols). Middle: ε _e and ε _B for the same GRBs as in the top panel, plus those from Panaitescu (2005) (black squares). Indicated are lines for ε _e = ε _B (equipartition) and ε _e = (ε _B )^1/2 (Medvedev 2006). Bottom: The electron energy distribution power-law index p versus the density structure power-law index k, based on optical and X-ray spectra and light curves, for a sample of GRBs with good spectral and temporal coverage (Starling et al. 2008; Curran et al. 2009).

The shock microphysical parameters are typically in the range ε _e ~ 10⁻² − 10⁻¹, ε _B ~ 10⁻⁵ − 10⁻¹, and p ~ 2 − 3. The middle panel of Figure 15 shows ε _e versus ε _B . Medvedev (2006) predicted a relation between these two parameters, ε _e ≈(ε _B )^1/2, based on physical arguments for a Weibel instability mediated relativistic collision shock in an electron-proton plasma. He had further argued that such a strong correlation is supported by the data, in particular the values of ε _e and ε _B inferred by Panaitescu (2005). However, we do not find such a correlation, where the best fit data from Panaitescu (2005) (or all the data shown in the middle panel of Figure 15) give a Spearman rank correlation coefficient of 0.12 (0.16) with a chance probability of 0.73 (0.42). We also show this predicted relation, as well as a linear one, for easier visual comparison with the inferred values.

Based on these results there does not seem to be universality in any of the parameters, also in the shock microphysics ones. Studies based on optical and X-ray light curves, and optical-to-X-ray spectra, can determine p and k, when making standard model assumptions. These studies confirm the non-universality of p, and also show that k varies between different GRBs, sometimes consistent with 0 (homogeneous medium) and not with 2 (wind-like medium), and vice versa (see bottom panel of Figure 15; Starling et al. 2008; Curran et al. 2009). We note that these studies assume that we are viewing exactly along the jet symmetry axis (θ_obs = 0), which may have an effect mostly on the inferred values of k, because a non-negligible θ_obs can change the light curve slopes and k is determined by both the spectral and temporal slopes, while p is determined by the spectral slope alone.

While the instantaneous density in front of the shock as well as its energy and shock microphysics parameters can be determined from the instantaneous spectrum, the external density profile and in particular its power-law index k require such a modelling over a long time. However, in principal, the shock microphysics parameters might vary with time, which could have similar observational signatures and thus be degenerate with a different value of k, which is different than its true value. An important way to break such a degeneracy is through measuring the afterglow image size measurements. Such measurements could also help test the jet dynamics, and in particular its degree of lateral spreading (see Figure 16), although this is a bit challenging. Another way to probe the value of k is through its implications for the contribution of the counter-jet to the light curve, where k = 0 is expected to produce a pronounced late-time bump while k = 2 will only produce a very mild flattening, which might be hard to clearly observe (see upper panel of Figure 8). The time of a counter-jet bump would probe E/A (for an external density ρ_ext = AR ^−k ) since it scales as (E/A)^{1/(3 − k)} (with some dependence of the numerical coefficient on k and θ_obs, as can be seen in Figure 8).

Figure 16. Fits of the evolution of the GRB 030329 VLBI image size up to 83 d (Granot et al. 2005a) with the later time size measurements over-plotted (Mesler et al. 2012). In Model 1 there is significant lateral spreading during the trans-relativistic phase in the blast wave evolution, while in Model 2 there is no spreading until the non-relativistic phase.

We note, however, that there is not only a large spread in parameters obtained for different GRBs, but also a significant spread in parameters for individual GRBs obtained by different groups. Therefore, the shock microphysical parameters, or at least some of them, might potentially still be universal, at least at early enough times while the shock is still highly relativistic (Γ ≫ 1). Once the shock is no longer highly relativistic one might envision a dependence of the shock microphysics parameters on the shock Lorentz factor or its proper velocity. Furthermore, different assumptions or constraints on some of the parameters (e.g. the observing angle θ_obs or the microphysical parameters) can lead to significantly different values for the parameters, even if one uses the same method (van Eerten, van der Horst, & MacFadyen 2012; Leventis et al. 2013). Studies involving decent sized samples (e.g. Panaitescu & Kumar 2001b) indicate that there is indeed a spread in the parameters. Future modelling efforts of larger samples using one method and the same assumptions for all GRBs, and using more accurate modelling codes (van Eerten et al. 2012; Granot & Piran 2012) should clarify how large this spread truly is.

5.2 A case study: GRB 030329

The GRB radio afterglow with the best spectral and temporal coverage by far is GRB 030329, with well-sampled radio light curves over two orders of magnitude in observing frequency (0.64 − 95 GHz), starting half a day after the initial trigger and still detectable a decade later (over almost four orders of magnitude in time). With these observations it has been possible to follow the evolution of the afterglow shock from the ultra-relativistic to the non-relativistic phase and perform detailed broadband modelling (see Figure 3; Berger et al. 2003a; Frail et al. 2005; Resmi et al. 2005; van der Horst et al. 2005; 2008). From all the modelling efforts, including those at optical and X-ray frequencies, two main interpretations have emerged.

One interpretation was that the GRB 030329 had a two-component jet (Berger et al. 2003a) consisting of an initially very fast and fairly narrow jet (with θ₀ ~ 5°) contributing mostly to prompt γ-ray emission as well as the optical and X-ray light curves, and an initially slower and wider jet (with θ₀ ~ 17°) powering the radio light curves (a broadly similar model was also considered by Resmi et al. 2005; van der Horst et al. 2008). In particular, Berger et al. (2003a) have attributed the sharp bump in the optical light curve that peaked at t ~ 1.5 d (Lipkin et al. 2004) to the deceleration time of the wide jet component. However, it was later shown that the deceleration of a wider jet component cannot produce such a sharp feature in the light curve, and instead produces a much wider and smoother peak (Granot 2005).

An alternative interpretation of the sharp bump in the optical light curve at t ~ 1.5 d, as well as a few additional bumps that are seen in the most detailed optical light curve up to several days (Lipkin et al. 2004) are naturally explained as a series of refreshed shocks—slow shells that were ejected from the source early on (near the end of its prompt activity) that catch up with the afterglow shock at relatively late times, and inject energy into it (Granot, Nakar, & Piran 2003). This nicely explains the optical light curve and the relatively sub-energetic early γ-ray and X-ray emission. Moreover, the radio light curves appear to be very similar to the expectations from hydrodynamic simulations of a single initially uniform jet (see, e.g. the top panel of Figure 8), where the sharp break in their light curve can be attributed to the passage of ν _m , without requiring a second (wide) jet component.

Broadband modelling from radio to X-ray frequencies is challenging due to the many bumps in the optical light curves, but modelling of the radio light curves by themselves already provides good constraints on the physical parameters since the evolution of ν_sa, ν _m and the peak flux can be determined accurately. The physical parameters obtained by modelling only the early times, only the late times, and both at the same time, are consistent within a factor of a few even though the methods and assumptions are different for the various groups (see van der Horst et al. 2008, for a discussion). The parameter with the largest spread, about one order of magnitude, is the external density, which is caused by the fact that it depends strongly on the precise values for ν_a and ν_m.

An important extra ingredient in the modelling of GRB 030329 are the VLBI size measurements, as discussed in Section 2.5.1. Granot et al. (2005a) and Mesler & Pihlström (2013) have performed combined modelling of the image size evolution and the light curves, and they find good agreement and again comparable physical parameters. As can be seen in Figure 16, the source size measurements favour a uniform ambient medium (k = 0) over a wind-like external density profile (k = 2) (Granot et al. 2005a), which has also been found by broadband modelling (van der Horst et al. 2008; Mesler et al. 2012). This result appears to be in contrast with the predictions for the emission coming from the counter-jet. The upper panel of Figure 8 or the bottom panel of Figure 14 show that in the case of a homogeneous medium (k = 0) there should be a bump or at least a clear flattening in the light curve at late times caused by emission coming from the counter-jet, while in the stellar wind case (k = 2) this is merely a mild flattening. This kind of bump has not been observed in the GRB 030329 light curves (Mesler & Pihlström 2013, see also the top right panel of Figure 1).

One possible way out of this apparent discrepancy is by relaxing the usual assumption that the counter-jet is intrinsically identical to the jet pointing towards us, and encounters a similar density and radial profile of the external medium. Although many astrophysical jet sources do show two jets, they are not necessarily identical or symmetrical. However, this is in most cases due to a double-sided AGN jet that is ejected quite symmetrically but interacts with different external density profiles on either side, at large distances from the source. On the other hand, the immediate environment of a GRB jet is very different, and it is less clear how reasonable is the required difference in external density, where the counter-jet should interact with an external density lower by a factor of several or more over at least a factor of a few in radius (assuming the two jets are intrinsically similar). More generally, the lack of a late-time rebrightening or flattening can provide constraints on the presence and properties of the counter-jet.

5.3 Newtonian transition: Shock microphysical parameters

The usual assumption that is made when modelling the synchrotron afterglow emission is that all electrons take part in a power-law energy distribution behind the shock. However, in general, the fraction ξ _e of electrons that take part in such a power-law distribution is expected to be less than unity, where the bulk of the electrons form a relativistic Maxwellian, as their energy distribution is thermalised behind the shock (e.g. Eichler & Waxman 2005; Giannios & Spitkovsky 2009). In particular, particle in cell simulations suggest that ξ _e can be as low as a few percent (Spitkovsky 2008a; Martins et al. 2009). The minimal electron Lorentz factor of the power-law energy distribution, γ _m , and its average Lorentz factor 〈γ _e 〉, are given (for p > 2) by

(4) \begin{equation} \gamma _m = \frac{p-2}{p-1}\langle {\gamma _e}\rangle = 1 + \frac{p-2}{p-1}\frac{\epsilon _e}{\xi _e}\frac{m_p}{m_e}(\Gamma _{12}-1)\ , \end{equation}

where Γ₁₂ is the relative upstream to downstream Lorentz factor across the afterglow shock. However, since this power-law energy distribution is assumed to consist of only relativistic electrons (which can emit the observed synchrotron radiation), the usual assumptions break down once γ _m drops below 2, or γ _m − 1 < 1 (Granot et al. 2006). When the shock becomes Newtonian then $\Gamma _{12}-1\approx \frac{1}{2}\beta _{12}^2$ and

(5) \begin{equation} \gamma _m-1 \approx \frac{p-2}{p-1}\frac{\epsilon _e}{\xi _e}\frac{m_p}{m_e}\left(\frac{\beta _{12}^2}{2}\right) = \frac{g\epsilon _{e,-1}}{\xi _e}\left(\frac{\beta _{12}}{0.18}\right)^2\ , \end{equation}

where ε _e,−1 = ε _e /0.1 and g = 3(p − 2)/(p − 1) (=1 for p = 2.5) so that γ _m − 1 < 1 corresponds to

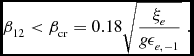(6) \begin{equation} \beta _{12} < \beta _{\rm cr} = 0.18\sqrt{\frac{\xi _e}{g\epsilon _{e,-1}}}\ . \end{equation}

Once β₁₂ drops below the critical value of β_cr, the usual assumptions of a constant ξ _e and ε _e must break down. Granot et al. (2006) have considered, in the context of the radio afterglow from the giant flare of SGR 1806 − 20 (e.g. Gaensler et al. 2005), the plausible scenario in which ε _e remains constant while ξ _e starts decreasing from its previous value (which is assumed to be constant) in such a way that γ _m ≈2 is maintained, i.e. ξ _e = gε _e,−1(β₁₂/0.18)²∝β² ₁₂. For an external density that scales as R ^−k and a spherical Newtonian flow, ξ _e ∝β² ₁₂∝R ^k−3∝t ^{−2(3−k)/(5−k)}.

For a uniform external density, the resulting flux decay rate in the most relevant power-law segment of the spectrum for late-time radio observations (PLS G in Figure 2) is F _ν∝ν^(1−p)/2 t ^−3(p+1)/10 (Granot et al. 2006), while more generally F _ν∝ν^(1−p)/2 t ^{−3(p+1)/[2(5 − k)]}. This decay rate is significantly shallower for a uniform external medium (but somewhat steeper for a wind-like external medium with k = 2 for p < 3) compared to that for the usual assumptions made in GRB afterglow modelling at the Newtonian regime, which gives F _ν∝ν^{(1 − p)/2} t ^{−[3(5p−7)−2k(2p−3)]/[2(5−k)]}. For the radio afterglow of the giant flare from SGR 1806 − 20, for which p≈2.5 was inferred from the observations and a uniform external medium (k = 0) is expected, this predicts F _ν∝t ^−1.05 (Granot et al. 2006), which is in very good agreement with the observed t ⁻¹ − t ^−1.1 at late times (Gelfand et al. 2005). This effect was recently also pointed out in the context of late-time GRB radio afterglows (Sironi & Giannios 2013). In general, such late-time radio observations from GRBs, SGR giant flares, or other synchrotron emitting shocks that gradually decelerate from mildly relativistic to Newtonian speeds can help investigate the shock microphysics in this intriguing transition regime.

6 PROSPECTS FOR THE FUTURE

6.1 New instrumentation

Although we have learned a lot about GRB jets from radio observations, there are still several open questions for which a new generation of radio observatories could provide answers. There is a large international effort to build the Square Kilometer Array this decade, which will revolutionise radio astronomy. Many precursor telescopes are being built, commissioned, or are already operational: the Australian Square Kilometer Array Pathfinder (ASKAP; 0.7 − 1.8 GHz; Johnston et al. 2008); MeerKAT in South-Africa (0.58 − 14.5 GHz, but not continuous frequency coverage; Booth & Jonas 2012); the Low Frequency Array (LOFAR; 10 − 240 MHz; van Haarlem et al. 2013), with the core in The Netherlands but stations in several European countries; the Murchison Widefield Array (MWA; 80 − 300 MHz; Tingay et al. 2013) in Australia; and the Long Wavelength Array (LWA; 10 − 88 MHz; Ellingson et al. 2013) in the USA. Transient sources, including GRBs, are among the key science objectives for all these observatories. Besides these new facilities, several others that have been pivotal in GRB research up to now have been upgraded, or are in that process: the VLA upgrade, the focal-plane array system Apertif on WSRT, AMI as the Ryle Telescope upgrade, the new back-ends of the ATCA and the Very Long Baseline Array (VLBA), and also the increasing use of e-VLBI providing real-time data transfer and processing. All these new and upgraded facilities will not only explore a larger spectral range, going down to the lowest frequency radio wave passing through the Earth's atmosphere, but also will provide improved sensitivities, bandwidth, and spatial, spectral and temporal resolution. These improvements will be important for advancing our understanding of GRB jet physics in several ways.

First of all the improved sensitivity, in particular for the VLA, will have a big impact on the number of detected GRBs and significantly increase the sample size. A few years of observations with the upgraded VLA should be able to make it clear whether the current sample is indeed sensitivity limited (Chandra & Frail 2012) or if there are two distinct populations of GRB radio afterglows (Hancock et al. 2013). The number of GRBs with well-sampled radio light curves for broadband modelling to determine the physical parameters is expected to increase significantly, not only by observing deeper in terms of sensitivity but also over a larger frequency range. Especially late-time, low-frequency observations will be important for performing true radio calorimetry, years or even decades after the GRB trigger (van der Horst et al. 2008).

Another significant improvement in observational capabilities over the last few years is that the radio regime has entered time-domain astronomy. Several phenomena are delayed at radio frequencies compared to optical or X-rays, but there is also part of the observational parameter space that has not been explored until recently, in particular the first minutes to hours after a GRB trigger. AMI 15 GHz follow-up of Swift triggers, with sub-mJy sensitivity levels, did result in the earliest detection of a long GRB at radio frequencies, GRB 130427A, within 8 h after the burst of γ-rays (Anderson et al., in preparation). A couple of months later the earliest radio detection of a short GRB was found at the same timescale with the VLA, namely GRB 130603B (Fong et al. 2013). Besides searches at the traditional radio frequencies, there are also efforts ongoing at low radio frequencies, for instance with LOFAR, MWA and LWA, to search for early-time, possible prompt coherent emission. Detections of, or limits on, such emission could provide an important clue for the jet production and collimation mechanisms.

6.2 VLBI prospects

Crucial for theoretical and modelling efforts are matching observational efforts. Of particular value are direct source size measurements with VLBI, putting independent constraints on the physical parameters and possibly probing the jet structure directly. The process of e-VLBI (Conway 2009), which allows near-realtime VLBI observations, has enabled significantly faster follow-up of transients than traditional VLBI. Although it is logistically difficult to organise global e-VLBI observations, this is technically feasible and should be possible in the near future. Although the combined radio brightness and proximity of GRB 030329 has been unique so far, the observational advances that have been made over the last years put us in a great position to study a similar event in even better detail when it occurs. Such a study could be improved by VLBI at higher radio frequencies, thus achieving even better resolution, or with Space VLBI, as demonstrated by the observations performed with the VLBI Space Observatory Programme (VSOP; Hirabayashi et al. 2000) and RadioAstron ³ . Although in Space VLBI the sensitivities and data rates are currently limited, this is certainly an interesting prospect for future high-resolution observations.

In the context of time-domain astronomy, it is now also feasible to trigger e-VLBI observations at similar timescales as with the ‘regular’ radio telescopes. Although measuring the GRB source size is not expected at that time yet, such observations with for instance the European VLBI Network (EVN) or VLBA are still very useful. In particular, they will not only provide deep observations with good sensitivity, but could also distinguish early on between GRB emission from a faint AGN or radio emission from star formation in the host galaxy (which will be resolved out with VLBI). Moreover, they can produce an early accurate location of the flux centroid, that could be used to constrain the proper motion at later epochs. VLBI can also play an important role in time-domain searches, due to better sensitivity than single dish telescopes, and also because the various telescopes in the VLBI arrays have different radio frequency interference (RFI) environments and different back-end systems, making it easier to identify events that are not astrophysical in nature.

6.3 Modelling and numerical simulations

All the aforementioned observational improvements tie in perfectly with the improved broadband modelling efforts. Recently is has become possible to directly fit hydrodynamic simulations including detailed emission calculations to broadband light curves (van Eerten et al. 2012), which enables taking into account effects that are not accounted for (properly) in most analytical models, for instance the jet orientation with respect to the observer (Granot et al. 2001; 2002; van Eerten & MacFadyen 2012; De Colle et al. 2012b) and the delayed jet break at radio frequencies due to synchrotron self-absorption (van Eerten et al. 2011). At the same time, new physically derived analytical models, both analytic jet models (Granot & Piran 2012) or analytic spherical models calibrated to hydrodynamic simulations (Leventis et al. 2013) are available for broadband modelling now. With the increased sample of broadband data sets and more accurate modelling efforts, it will be possible to better determine the physical parameters and constrain the jet lateral spreading.

More generally, there is a steady improvement in the capabilities of numerical simulations also to study earlier phases in the jet dynamics. This includes the launching of the jet using general relativistic MHD simulations from an accretion disc around a rotating black hole (e.g. Koide et al. 2000; Nishikawa et al. 2005; McKinney 2006; Krolik & Hawley 2010; Tchekhovskoy & McKinney 2012; McKinney, Tchekhovskoy, & Blandford 2012) or from the merger of two neutron stars (e.g. Liu et al. 2008; Rezzolla et al. 2011; Shibata et al. 2011; Palenzuela et al. 2013) or a neutron star and a black hole (Chawla et al. 2010; Etienne et al. 2012; Etienne, Paschalidis, & Shapiro 2012), as well as jet formation and propagation inside the progenitor star of a long-soft GRB, also in special relativity and both for a collapsar (e.g. Nagataki 2009; Harikae, Takiwaki, & Kotake 2009) and for a millisecond magnetar (e.g. Komissarov & Barkov 2007; Bucciantini et al. 2008; 2012). These simulations have put those models for the central engine on much firmer ground, and may help test their predictions against observations.

What is more, these earlier stages of the jet dynamics are what set the stage, or determine the initial conditions for its late-time evolution during the afterglow, which directly affects the afterglow broadband modelling. There has been significant progress also in the numerical studies of the jet's late time evolution (see Section 4.4). Such numerical simulations could improve the accuracy of late-time radio calorimetry. The great improvements in the simulations of the different stages in the jet dynamics may soon make it feasible to simulate the jet dynamics within a single simulation from close to the source, well within its progenitor star (for long GRBs) as it breaks out of the star, is eventually decelerated by the external medium and finally becomes sub-relativistic and approaches the Sedov-Taylor solution. Since at present it is possible to simulate the jet dynamics only one stage at a time, such a unification of the different stages could lead to great progress, and more firmly relate the properties of the central source and the jet launching, collimation, acceleration and composition, to the observational signatures as manifested in the GRB prompt emission and afterglow.

Moreover, there has been considerable progress in our understanding of collisionless shock physics, largely thanks to particle in cell simulations, both in the relativistic regime (Spitkovsky 2008a; 2008b; Chang, Spitkovsky, & Arons 2008; Martins et al. 2009; Keshet et al. 2009; Sironi & Spitkovsky 2009a; 2009b; Nishikawa et al. 2009; Frederiksen et al. 2010; Sironi & Spitkovsky 2011; Sironi, Spitkovsky, & Arons 2013), as well as in the mildly relativistic (e.g. Murphy et al. 2010) or Newtonian (e.g. Amano & Hoshino 2007; Kato & Takabe 2008; Amano & Hoshino 2009; 2010; Riquelme & Spitkovsky 2011; Gargaté & Spitkovsky 2012) regimes. This has already contributed greatly to the field, and is likely to continue to do so for time to come. All these numerical efforts naturally go hand in hand with the analytic work on these topics, and a symbiotic relation has already greatly contributed to the progress in the field, and is expected to do so in the future as well. Keep in mind that the state of the art knowledge on shock microphysics when modelling the afterglow observations is important in order to get the most out of the data, and try to test the theoretical predictions.

6.4 Testing the theory with observations

6.4.1 Probing turbulence behind the shock

Another motivation for early and sensitive radio observations is in order to try and test the prediction (Granot, Piran, & Sari 2000) of the existence of a power-law segment in the self-absorbed portion of the fast-cooling synchrotron spectrum where F _ν∝ν^11/8 (PLS C that appears in spectra 4 and 5 in Figure 2). It originates from the fact that electrons further away from the shock front are colder as they had more time to cool (since they were accelerate very close to the shock front). Therefore, at lower frequencies the location l ₁ where the optical depth to synchrotron self-absorption equals unity, and most of the photons that escape and reach us are emitted, is closer to the shock front where the electrons are hotter and their higher effective temperature scales as T _eff∝ν^−5/8 causing the flux density scale as F _ν∝T _eff(ν)ν²∝ν^11/8. Once l ₁ becomes smaller than the width of the thin cooling layer behind the shock in which most electrons have not yet had enough time to cool, T _eff becomes constant and F _ν∝ν² (i.e. there is a transition to PLS B in Figure 2). However, this strongly relies on an orderly and laminar bulk motion of the fluid behind the shock, in which the time since the shock passage of each fluid element is proportional to its distance from the shock front. If, on the other hand, there is strong turbulence behind the shock, this might cause significant mixing and disrupt this picture, resulting in a much more uniform effective temperature distribution that dues not strongly depend on the distance from the shock front, and thus eliminate PLS C. Therefore, its detection or lack thereof can help to observationally constrain the degree of turbulence behind relativistic collisionless shocks. This may prove observationally challenging, since it not only requires a short response time and good sensitivity, but one also has to observe at high radio frequencies to make sure there are no strong ISS effects. However, a direct measurement of this spectral feature could be very rewarding.

6.4.2 Jet breaks and jet angular structure

Another example of how observations can be used in order to constrain the underlying physics is to use the sharpness of the jet break in the afterglow light curve in order to constrain the jet angular structure. As discussed in Section 4.4.2 (see top panel of Figure 14), the jet break is sharpest when viewed on-axis (θ_obs = 0) and for a uniform external medium (k = 0; assuming that the density doesn't increase with radius, k ≥ 0). However, some of the observed jet breaks are very sharp and rather close to this maximal expected sharpness for an initially uniform jet with sharp edges. If the jet has smoother edges or significant energy in its wings, then this is expected to smoothen the jet break, which might contradict the sharpest observed jet break, and thus rule out such a jet angular structure (at least for those GRBs with such sharp jet breaks). To better quantify the constraints this implies for the jet initial angular structure would require a set of hydrodynamic models for different jet structures, calculating their afterglow light curves, and comparing to observations. A sharp jet break is expected and observed mainly in the optical or X-ray, while its signatures in the radio are much less pronounced. Nevertheless, multiple light curves at very different frequency ranges are crucial in order to establish a jet break origin for a steepening in the light curve, since there are several other potential causes for such a steepening, which might serve as jet break impostors. This leaves an important role for radio observations in such an endeavour.

6.4.3 Orphan afterglows

Orphan afterglow surveys in the radio could provide very valuable information about the angular structure of GRB jets, and are expected to have improved capabilities and prospects of detection in upcoming years. However, one of the biggest challenges that they are expected to face is how to distinguish between genuine orphan GRB jets, typically viewed far off-axis, and other types of radio transients, which could act as impostors (such as AGN, etc.). From the theoretical perspective, it would be very helpful to reliably and robustly study the expected observational signatures of such relativistic jets viewed off-axis. In particular, their expected spectrum, light curve, polarisation, image size and proper motion. While this was to some extent done analytically (e.g. Granot et al. 2001; Granot & Loeb 2003), when faced with real observations it is important to make predictions that are as realistic as possible. Therefore, the best strategy would probably be to use 2D special relativistic hydrodynamic simulations, for different initial jet angular structures and different external density profiles. While this is a considerable undertaking, it should prove important in the foreseeable future.

6.4.4 Outflow magnetisation and magnetic field structure

The degree of magnetisation of the GRB jet, and in particular whether it is launched magnetically and is initially Poynting flux dominated, is one of the most important open questions in the field. It is an active topic of research and is likely to be all the more so in the future. There are various observations that might help to test this. One way (see Section 4.2) is through the signature that a magnetic versus an hydrodynamic jet propagating inside the progenitor star of a long-soft GRB would have on the long GRB duration distribution and on the energy injection into the cocoon and through it into the accompanying SN explosion (where a highly magnetised jet is expected to inject less energy). Another relevant observation is the ‘radio flare’ that usually peaks after a day or so, which together with the prompt optical flash can help establish a reverse-shock origin of this emission (see Section 4.3). This can have important implications for the external density near the deceleration radius R _dec (where a high density causes a sharp decay of the optical emission and suppresses the radio flare), as well as for the magnetisation of the outflow near R _dec, σ(R _dec). In particular, for the ‘thin shell’ case where the peak of the optical or X-ray afterglow emission and the end of the optical flash, both identified with the deceleration time t _dec, is significantly later than the duration of the GRB prompt γ-ray emission, t _dec ≫ T _GRB, one expects a low magnetisation σ(R _dec) ~ T _GRB/t _dec ≪ 1 (Granot 2012a, see Section 4.1), which can be tested from the modelling of the reverse shock emission.

Once a reverse-shock origin of the radio flare can be reasonably established, the polarisation of both the optical flash and the radio flare can be used to probe the magnetic field structure in the outflow, which is of great interest as it has some implications for the jet composition, acceleration and launching mechanisms. While currently the best upper limit on radio polarisation during a radio flare is < 7% (Granot & Taylor 2005), the increased sensitivity of the VLA and other telescopes should be able to constrain the polarisation to the 1% level when ~10 μJy sensitivities are reached. This requires dedicated observations with integration times of a few hours, but the scientific gain is high. Another way of probing the magnetic field structure, which is much more challenging from the observational point of view, is through the measurement of the polarisation of the prompt GRB emission at hard X-ray to soft γ-ray energies, where some missions are scheduled to be launch in the upcoming years (e.g. Costa 2013, and references therein).

6.4.5 Newtonian transition: Dynamics and shock microphysics

Radio observations can follow GRB afterglow emission out to late times, when their shock becomes mildly relativistic, then sub-relativistic, and eventually Newtonian. This is also valid for other impulsive relativistic or at least initially mildly relativistic sources, such as tidal disruptions of a star by a super-massive black hole or an outflow from an SGR giant flare. As pointed out in Section 5.3, such radio observations can be used in order to study the evolution of the shock microphysics parameters as the shock transitions between the relativistic and Newtonian regimes. The focus in Section 5.3 was on the parameter ξ _e —the fraction of electrons behind the shock that take part in a power-law relativistic energy distribution. However, such late radio observations can also be used to study other shock microphysics parameters (namely, ε _e , ε _B , p). It is important to keep in mind, though, that the relativistic to Newtonian transition usually involves a rather complicated dynamics, as the spherical Sedov-Taylor solution can be approached rather slowly. Moreover, the dynamics combines with the expected evolution of the shock microphysics parameters to determine the observed light curve and spectrum, which can result in significant degeneracy between the two. Therefore, it is important to both model the dynamics as realistically and accurately as possible, using hydrodynamic simulations, and acquire additional observations that could help break this degeneracy, such as measurements of the image size and shape, its flux centroid motion, and polarisation.

7 SUMMARY AND CONCLUSIONS

This review has focused on recent progress in our understanding of GRB jet physics and the important role played by radio afterglow observations in achieving such progress. It aims to encourage a close connection and good interaction between theory and observation, which can be very fruitful and help improve our understanding of the relevant underlying physics. To this end, some existing examples and a number of promising paths for the future have been outlined. The radio observations were described in Section 2, while some of the most relevant aspects of GRB jet physics and some recent theoretical progress was outlined in Sections 3 and 4. A few examples of how theory and observations can be combined in order to maximise their scientific impact were spelled out in Section 5. Finally, prospects for the future were discussed in Section 6, in terms of instrumentation, observations, modelling, theory, and some specific examples of how they might be combined together.

GRB radio afterglow observations have been described in Section 2. The current observational sample and the main radio afterglow properties were discussed (Section 2.1), along with how these observations are modelled in order to infer the underlying physical parameters of the afterglow jet (Section 2.2), also stressing the role of radio observations in studying optically dark bursts (Section 2.2.1). Observations of the radio flare emission, which typically peaks after a day or so, and its polarisation properties were summarised (Section 2.3) as well as what physics could be learned from them. The searches for emission at minutes to hours after the initial gamma-ray trigger, and possible prompt radio emission, were also discussed (Section 2.4), in particular in the light of several new radio facilities recently coming online. Size measurements of the radio afterglow image were outlined (Section 2.5), covering both direct measurements through VLBI (Section 2.5.1) and indirect measurements through interstellar scintillation (ISS; Section 2.5.2). The search for orphan afterglows in the radio—namely GRB-like jets pointing away from us that become visible only at late times—was described (Section 2.6) both in the context of sky surveys, but mainly in targeted searches of nearby Type Ib/c supernovae.

The GRB jet angular structure and its effects on the afterglow light curve were described in Section 3. Models for the GRB jet angular structure that have been studied in the literature were briefly outlined in Section 3.1. Some examples of light curves for different viewing angles and different (power-law) external density profiles have been shown in Section 3.2, and discussed in a more general physical context.

The GRB jet dynamics have been discussed in Section 4. Following a brief general description of the different stages in the jet dynamics, specific topics have been chosen to receive special attention and be outlined in much more detail, owing to recent progress and/or their potential relevance to radio observations. Magnetic acceleration, which has been gaining popularity recently, was discussed in Section 4.1, focusing on recent progress in the effects of strong time dependence of the outflow emanating from the central source. The newly discovered impulsive acceleration mechanism was described, along with some of its potentially observable implications. Section 4.2 focused on the propagation of the GRB jet inside a massive star progenitor (relevant for long GRBs), and contrasted the different expectations for a hydrodynamic jet versus a highly magnetised (Poynting flux dominated) jet. For the latter, the head of the jet becomes relativistic early on, leading to a faster breakout time (with potential effects on the long GRB duration distribution) and significantly less energy injection into the cocoon and thus into the kinetic energy of the accompanying supernova explosion (which can be estimated from observations). The reverse shock was discussed in Section 4.3, both in terms of its basic dynamics (Section 4.3.1) and in terms of it observational signature (Section 4.3.2), with special attention on its radio flare emission and its polarisation properties (which can probe the magnetic field structure in the ejecta).

The jet dynamics during the afterglow stage, and its implications, were discussed in Section 4.4. A long apparent discrepancy between analytic and numerical results for the jet dynamics, and in particular its degree of lateral spreading, was recently reconciled (Section 4.4.1) by constructing new analytic models that are valid also when the jet is no longer very narrow or highly relativistic. The exponential sideways expansion generically predicted by previous analytic models occurs only for jets that are initially extremely narrow (θ₀ ≪ 10^−1.5 for k = 0 or θ₀ ≪ 10⁻² for k = 2) and even then it is suppressed once the jet becomes sufficiently wide. Afterglow observations suggest that most GRB jets are not initially sufficiently narrow and therefore do not go through a stage of exponential lateral expansion, consistent with the result of hydrodynamic simulations. Section 4.4.2 described recent results of hydrodynamic simulations of the afterglow jet propagating into different external density power-law profiles (ρ_ext = AR ^−k ). A more sharply dropping external density (larger k) leads to a more gradual deceleration, and a wider jet at the same Lorentz factor before the jet break time, but it then takes longer for it to become sub-relativistic and approach spherical symmetry. The slower jet deceleration for larger k leads to a smoother jet break, but still much sharper than previous analytic predictions, and the effect of the viewing angle within the initial jet aperture (0 ≤ θ_obs ≤ θ₀) on the sharpness of the jet break is even somewhat larger than that of the external density profile (for 0 ≤ k ≤ 2). Finally, a larger k suppresses the late-time bump in the radio light curve due to the counter-jet coming into view.

Examples of how observations and theory might be combined in order to achieve greater progress than either of the two would on their own, have been discussed in Section 5. Those included afterglow broadband modelling in general (Section 5.1), the most elaborately studied radio afterglow of GRB 030329 as a case study (Section 5.2), and the study of the evolution of the shock microphysical parameters (and in particular the fraction ξ _e of electrons taking part in a power-law relativistic energy distribution) as the shock becomes sub-relativistic and Newtonian using late-time radio observations (Section 5.3).

Finally, prospects for the future have been discussed in Section 6. The host of new instruments expected to come online and the planned improvements in the capabilities of existing instruments were outlined in Sections 6.1 and 6.2. Their potential relation to recent and expected progress in the modelling and in numerical simulations was mentioned in Section 6.3. The remaining sub-sections were devoted to particular examples of how specific observations, especially in the radio, could be used in order to test specific model predictions and their underlying physics. The early radio spectrum could probe turbulence behind the shock (Section 6.4.1). The sharpness of the jet break could constrain its angular structure (Section 6.4.2). Numerical simulations and modelling could help distinguish between true orphan radio afterglows and impostors (Section 6.4.3). Radio flare observations, together with the optical flare and afterglow onset can help probe the outflow magnetisation magnetic field structure (Section 6.4.4). Finally, late-time radio observations can help study the evolution of the different shock microphysics parameters as it transitions from the relativistic to the the Newtonian regime (Section 6.4.5). The latter applies not only to GRB afterglows, but also to other sources with a relativistic shock that decelerates and becomes Newtonian (e.g. a tidal disruption or SGR giant flare).