Updated studies on exomoons in the HD 23079 system

Abstract

We re-evaluate the outer edge of orbital stability for possible exomoons orbiting the radial velocity planet discovered in the HD 23079 system. In this system, a solar-type star hosts a Jupiter-mass planet in a nearly circular orbit in the outer stellar habitable zone. The outer stability limit of exomoons is deduced using N-body and tidal migration simulations considering a large range of initial conditions, encompassing both prograde and retrograde orbits. In particular, we extend previous works by evaluating many values in the satellite mean anomaly to identify and exclude regions of quasi-stability. Future observations of this system can make use of our results through a scale factor relative to the currently measured minimum mass. Using a constant time lag tidal model (Hut 1981), we find that plausible tidal interactions within the system are insufficient to induce significant outward migration toward the theoretical stability limit. While current technologies are incapable of detecting exomoons in this system, we comment on the detectability of putative moons through Doppler monitoring within direct imaging observations in view of future research capacities.

1. Introduction

The detection of HD 23079b, reported by Tinney et al. (2002), was a successful outcome of the Anglo-Australian Planet Search. HD 23079b, a Jupiter-type planet, is hosted by a solar-type star with a temperature of about 6 000 K (Bonfanti et al. 2015); see Table 1 for details. This system is located in the Southern sky in the constellation Reticulum. HD 23079b is in a nearly circular orbit situated at the outskirts of the stellar habitable zone (HZ) that extends between 0.87 and 2.03 au (optimistic limits; see Kopparapu et al. 2013, 2014).

Table 1. Stellar and planetary parameters.

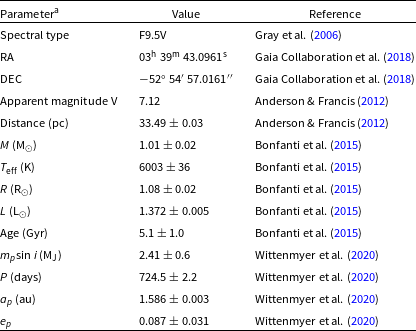
^a All parameters and symbols have their customary meaning.

The relatively low level of stellar activity of HD 23079, consistent with its age of $\sim$ 5 Gyr (see Section 2.1), tends to favour the existence of a habitable circumstellar environment; see, e.g., Ribas et al. (2005), Lammer et al. (2009), Ramirez (2018) for more general discussions. However, massive planets such as HD 23079b with orbits located within stellar HZ tend to thwart the existence of habitable terrestrial planets owing to the onset of orbital instabilities (e.g., Jones, Sleep, & Chambers 2001; Noble, Musielak, & Cuntz 2002; (e.g., Jones, Sleep, & Chambers 2001; Noble, Musielak, & Cuntz 2002; Agnew et al. 2017, 2018). Nevertheless, there is a significant possibility for the existence of habitable Trojan planets and/or habitable exomoons (in orbit about HD 23079b), as demonstrated via detailed simulations; see Eberle et al. (2011) and Cuntz et al. (2013), respectively.

The search for exomoons has been an active endeavour after the launch of the Kepler Space Telescope, while many works (Sartoretti & Schneider 1999; Cabrera & Schneider 2007; Kipping 2009a, b) preceding the Kepler era laid the theoretical groundwork for their detection through transit timing and duration variations. However, such methods have limitations (Kipping & Teachey 2020; Kipping 2021) and photometric observations can still lead to false positives, including one candidate for Kepler-90g (Kipping et al. 2015a).

Fortunately, there are other methods proposed for exomoon detection including using a planet profile determined by the average light curve (Simon et al. 2012), optimising with respect to the orbital sampling effect (Heller 2014; Heller, Hippke, & Jackson 2016; Hippke 2015), Doppler monitoring of directly imaged exoplanets (Agol et al. 2015; Vanderburg, Rappaport, & Mayo 2018) or examining the radio emissions from giant exoplanets (Noyola, Satyal, & Musielak 2014, 2016). Another motivation for our study stems from the recent discovery of a circumplanetary disk (system PDS 70), indicating the ongoing formation of one or more exomoons in alignment with the Hill radius criterion (Benisty et al. 2021).

Theoretical constraints aid in the interpretation of observations and can be useful to quickly validate whether a exomoon candidate is plausible or not (Quarles, Li, & Rosario-Franco 2020b). One of these constraints is the combined tidal interaction between the host star, planet and moon (Barnes & O’Brien 2002; Sasaki, Barnes, & O’Brien 2012; Sasaki & Barnes 2014; Lainey et al. 2020) that generally depends on a wide range of parameters (e.g., tidal Love number and tidal quality factor). Spalding, Batygin, & Adams (2016) explored how the so-called ‘evection resonance’ can cause significant growth in a moon’s eccentricity, which can lead to the moon’s tidal breakup or escape from the planet’s gravitational influence.

Nearby (Payne et al. 2013) and distant planetary companions (Grishin et al. 2017) can also drive an exomoon along a similar path to destruction. Even without these confounding interactions, Domingos, Winter, & Yokoyama (2006) produced estimates for exomoon stability using three-body interactions, but these results represent the upper boundary of a transition region for stability (Dvorak 1986). Recently, Rosario-Franco et al. (2020) determined a revised fitting formula for the (more conservative) lower stability boundary for prograde satellites, whereas Quarles et al. (2021) derived a similar fitting formula for retrograde satellites.

In this study, we revisit the existence of possible exomoons in the HD 23079 system based on more generalised assumptions and an improved methodology. Our paper is structured as follows. In Section 2, we summarize our theoretical approach. Our results and discussion are conveyed in Section 3 including comparisons to previous works. Here we also comment on the observability of possible HD 23079 exomoons. In Section 4, we report our summary and conclusions.

2. Theoretical approach

2.1. Stellar and planetary parameters

HD 23079 is a solar-type star of spectral type F9.5V (Gray et al. 2006) with an effective temperature of about 6 003 K (Bonfanti et al. 2015); see Table 1. Its mass and radius are given as $1.01 \pm 0.02$ M $_\odot$ and $1.08 \pm 0.02$ R $_\odot$ , respectively. HD 23079 has an age of approximately 5 Gyr (Saffe, Gómez, & Chavero 2005; Bonfanti et al. 2015), which implies a relatively low level of chromospheric activity—a notable feature in support of circumstellar habitability (e.g., Kasting & Catling 2003; Lammer et al. 2009; Kaltenegger 2017). The minimum mass $m_{p}{\sin}i$ of the planet HD 23079b, discovered by Tinney et al. (2002), has been identified as $2.41 \pm 0.6$ M $_{\rm J}$ ; however, the exact value of $m_{p}$ is unknown owing to the inherent limitations of the radial velocity (RV) method.

The stellar luminosity is about 35% larger than that of the Sun; hence, the HZ of HD 23079 is notably wider and further extended than the Solar HZ. In fact, the outer limits of the conservative and optimistic HZ are identified as 1.93 and 2.03 au, respectively. The orbital parameters of the planet, i.e., the semimajor axis $a_{p}$ and the eccentricity $e_{p}$ , are given as 1.586 $\pm$ 0.003 au and 0.087 $\pm$ 0.031, respectively, indicating that HD 23079b is situated in a nearly circular orbit within the stellar HZ at an orbital distance akin to that of Mars relative to the Sun. The planetary Hill radius is given as:

(1) \begin{equation} R_{\rm H} = a_{p}\left(\frac{m_{p}+m_{\rm sat}}{3M_\star}\right)^{1/3},\end{equation}

which includes the planet, satellite and stellar mass ( $m_{p}$ , $m_{\rm sat}$ , and $M_\star$ , respectively) in addition to the planetary semimajor axis $a_{p}$ . In physical units, the Hill radius is approximately 0.144 au using the appropriate values from Table 1. This formulation of the Hill radius is appropriate because the planetary eccentricity is low and no significant third body exists that can substantially force the planetary eccentricity (Quarles et al. 2021).

2.2. N-body simulations

To investigate the potential for exomoons in HD 23079, we perform a series of numerical simulations that identify the orbital stability of an Earth-mass satellite orbiting HD 23079b, a Jupiter-like planet. The numerical simulations are carried out using the general N-body software REBOUND (Rein & Liu 2012) with its IAS15 adaptive step integration scheme (Rein & Spiegel 2015). The IAS15 integrator is necessary because our study explores both prograde ( $i_{\rm sat} = 0^\circ$ ) and retrograde ( $i_{\rm sat} = 180^\circ$ ) satellite orbits, where the latter can be highly eccentric. Adaptive step integrators, although more accurate, can also be more computationally expensive.

We set the initial timestep equal to 5% of the shortest satellite orbital period ( $\sim$ 0.007 yr for prograde or $\sim$ 0.017 yr for retrograde) and define 0.0001 yr as the minimum allowed timestep with the default accuracy parameter $10^{-9}$ used for the IAS15 integrator. Cuntz et al. (2013) showed that the outcomes of simulations are identical for timesteps smaller than the prescribed minimum using other adaptive timestep methods. The simulation timescale of our N-body integrations is $10^5$ years, which is typical for determining the stability limits for hierarchical systems within large parameter spaces (Rosario-Franco et al. 2020; Quarles et al. 2020a; Quarles et al. 2021).

Each simulation begins centered around the host star, HD 23079, with the host planet and satellite added hierarchically using a Jacobi coordinate system (see Figure 1). The planet begins at its periastron position $\omega_{p}$ and the line of apsides $\Omega_{p}$ is used as the reference direction ( $\omega_{p} = \Omega_{p} = 0^\circ$ ). An initial condition is classified as potentially stable if the satellite does not encounter either of our stopping criteria to detect instabilities. We stop our simulations and classify an initial condition as unstable if the putative satellite: (a) crosses the planet’s Hill radius thereby leaving the region over which the planet’s gravitational influence dominates over that of the star or (b) collides with the host planet over a given timescale. In addition, we require that a stable initial condition does not depend on the initial mean anomaly $\theta$ of the satellite (Figure 1), which largely excludes islands of quasi-stability due to MMRs (Mudryk & Wu 2006).

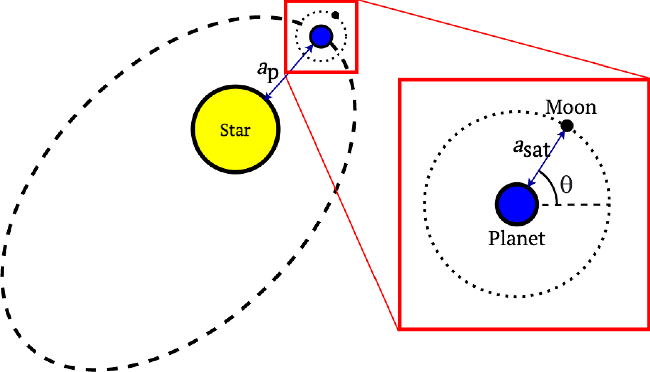
Figure 1. Representation of the initial conditions of the HD 23079 system in our calculations: (a) Planet HD 23079b (blue dot) orbits star HD 23079 (yellow dot). (b) An exomoon (black dot) orbits HD 23079b. Initially, the planet HD 23079b starts at perihelion and the exomoon starts at a random angle ( $\theta$ ) with respect to the planet for each simulation.

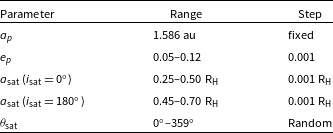
Cuntz et al. (2013) explored a parameter space that varied the initial planetary semimajor axis, eccentricity and the satellite’s semimajor axis $a_{\rm sat}$ . Recent observations (Wittenmyer et al. 2020) greatly narrowed the uncertainty of the planetary semimajor axis; therefore, we keep the planetary semimajor axis fixed ( $a_{p} = 1.586$ au) throughout this work. However, we evaluate simulations varying the planetary eccentricity $e_{\rm sat}$ from 0.05 to 0.12 in 0.001 steps motivated by the observational uncertainties. The prograde simulations are evaluated using a satellite semimajor axis from 0.25 to 0.5 R $_{\rm H}$ in steps of 0.001 R $_{\rm H}$ , where R $_{\rm H}$ is the planet’s Hill radius and the range in R $_{\rm H}$ is motivated by previous observational and dynamical studies of satellites (Cruikshank et al. 1982; Saha & Tremaine 1993; Domingos et al. 2006; Jewitt & Haghighipour 2007; Donnison 2010; Rosario-Franco et al. 2020; Quarles et al. 2021). Many studies (Henon 1970; Hamilton & Burns 1991; Morais & Giuppone 2012; Grishin et al. 2017; Quarles et al. 2021) have demonstrated that retrograde orbital stability extends to larger values of the satellite semimajor axis compared to the prograde case. Thus, we increased the $a_{\rm sat}$ range to 0.45–0.70 R $_{\rm H}$ with a 0.001 R $_{\rm H}$ step size. In physical units, a 0.001 R $_{\rm H}$ step corresponds to approximately 0.0001 au, noting that we scale the steps with respect to the Hill radius as this approach will allow our results to scale with improved characterisations of the planetary and stellar parameters, if available. The parameter ranges for our N-body simulations are summarized in Table 2.

Table 2. N-body simulation parameters.

In each simulation, the moon begins on a circular orbit that is apsidally aligned ( $\omega_{\rm sat}=\Omega_{\rm sat}=0^\circ$ ) with the planetary orbit. For each combination of planetary eccentricity and the satellite’s semimajor axis, 20 simulations are evolved using a random mean anomaly $\theta$ for the satellite chosen from 0 $^\circ$ – $359^\circ$ . We use a parameter $f_{\rm stab}$ to summarize these trials, which represents the fraction of stable simulations for a given ( $e_{p}, a_{\rm sat}$ ) combination.

2.3. Satellite orbital migration due to tides

A satellite’s long-term evolution is affected by tides raised on its host planet, where the induced tidal bulge slows the planet’s rotation over billion-year timescales. Through the conservation of angular momentum, the satellite can fall toward the planet or migrate outward toward the Hill radius. The satellite’s migration depends on whether its orbital period $T_{\rm sat}$ is greater than (outward migration) or less than (inward migration) the host planet’s rotation period $P_{\rm rot}$ . We begin the satellite on a circular, coplanar orbit relative to the Roche radius ( $a_{\rm sat}=3R_{\rm roche}$ ) with the satellite treated as a fluid satellite, and Roche radius calculated via:

(2) \begin{equation} R_{\rm roche} \approx 2.44 R_{p}(\rho_{p}/\rho_{\rm sat})^{1/3},\end{equation}

where the planet radius $R_{p}$ is assumed to equal the radius of Jupiter given the well-established trends in the mass radius relation for giant planets (Fortney et al. 2007; Chen & Kipping 2017), the planet density $\rho_{p}$ is 1.33 g cm^–3 (Jupiter-like), and the satellite density is 5.515 g cm^–3 (Earth-like). A satellite at 3 $\times$ the Roche radius begins an orbital period of $\sim$ 18 h. From theoretical calculations and numerical simulations of giant planet formation (Takata & Stevenson 1996; Batygin 2018), giant planets are expected to be rapid rotators ( $\sim$ 3 h) due to gas accretion or rotate more slowly ( $\sim$ 10–12 h) like the Solar System giant planets if magnetic braking is efficient. Since the satellite’s orbital period ( $\sim$ 18 h at $3 R_{\rm roche}$ ) is greater than the expected spin period of giant planets, the satellite will undergo outward migration.

Equilibrium tidal models are commonly prescribed within two types: constant phase lag (CPL; Goldreich & Soter 1966) or constant time lag (CTL; Hut 1981). Both models require an assumption for the Love number $k_2$ (Love 1911) and a moment of inertia factor $\alpha$ , for which we use Jupiter-like values (0.565 and 0.2756, respectively) determined from the Juno probe (Ni 2018; Idini & Stevenson 2021). The tidal models differ in their approach to approximating the tidal dissipation $\epsilon$ , where the CPL model implements a constant Q and the CTL model uses a constant timelag $\tau$ .

Both models yield similar results for small satellite-planet mass ratios, but the CTL model more accurately represents the tidal forcing frequencies (Ogilvie 2014); thus, we use a CTL model. The constant timelag $\tau$ is unknown for HD 23079b; hence, we assume a Jupiter-like value ( $\tau_{\rm J}\sim 0.035$ s) while evaluating models over several orders of magnitude ( $10^{-2}-10^2\;\tau_{\rm J}$ ). The planetary mass given in Table 1 is determined through the RV method, which allows an observer to determine the minimum mass $m_{p}$ . Therefore, we evolve the tidal model considering three host planet masses (1, 1.5 and 2 $m_{p}$ ) with a Jupiter-like $\tau$ . Herein we use the CTL model derived by Hut (1981) assuming zero planetary obliquity, which is equivalent to the formalism described in more recent approaches (Leconte et al. 2010; Heller, Leconte, & Barnes 2011; Barnes 2017).

The tidal evolution with respect to time t is described by the following equations:

(3) \begin{align}\frac{da_i}{dt} &= \frac{2a_i^2 Z_{{p},j}}{G m_{p} m_j} \left(\frac{f_2(e_i)}{\beta^{12}(e_i)} \frac{\Omega_{p}}{n_j} - \frac{f_1(e_i)}{\beta^{15}(e_i)} \right),\qquad \end{align}

(4) \begin{align}\frac{de_i}{dt} &= \frac{11a_ie_i Z_{{p},j}}{2G m_{p} m_j} \left(\frac{f_4(e_i)}{\beta^{12}(e_i)} \frac{\Omega_{p}}{n_j} - \frac{18}{11}\frac{f_3(e_i)}{\beta^{13}(e_i)} \right), \end{align}

and

(5) \begin{align} \frac{d\Omega_{p}}{dt} = \sum_j \frac{Z_{{p},j}}{2 \alpha_{p} m_{p} R^2_{p} n_j} \left(\frac{2 f_2(e_j)}{\beta^{12}(e_j)} - \frac{f_5(e_j)}{\beta^9(e_j)} \frac{\Omega_{p}}{n_j}\right),\end{align}

where

(6) \begin{equation}Z_{{p},j} \equiv 3G^2k_{2,p}\tau_{p} m^2_j ( m_{p} + m_j ) \frac{R_{p}^5}{a_i^9}\end{equation}

and

(7) \begin{equation} \begin{aligned} \beta(e) &= \sqrt{1 - e^2}, \\[3pt] f_1(e) &= 1 + \frac{31}{2}e^2 + \frac{255}{8}e^4 + \frac{185}{16}e^6 + \frac{25}{64}e^8, \\[3pt] f_2(e) &= 1 + \frac{15}{2}e^2 + \frac{45}{8}e^4 + \frac{5}{16}e^6 \\[3pt] f_3(e) &= 1 + \frac{15}{4}e^2 + \frac{15}{8}e^4 + \frac{5}{64}e^6, \\[3pt] f_4(e) &= 1 + \frac{3}{2}e^2 + \frac{1}{8}e^4,\\[3pt] f_5(e) &= 1 + 3e^2 + \frac{3}{8}e^4.\end{aligned}\end{equation}

Equations (3) and (4) describe the semimajor axis and eccentricity evolution of either the planet or satellite through the subscript i. The subscript j represents either the host star or the satellite that is raising the tide on the planet, where $n_j$ is the respective orbital mean motion. Equation (5) describes the spin evolution of the planet, where the moon is assumed to be synchronously rotating and the changes to the host star’s spin are negligible. The subscript j in Equation (5) represents either the host star or the satellite that is contributing to spin-down the planet. A Jupiter-like value is used for the moment of inertia factor ( $\alpha_{p}=0.565$ ) and G represents the Newtonian constant of gravitation.

3. Results and Discussion

3.1. Model simulations

Recent observations by Benisty et al. (2021) revealed the existence of a circumplanetary disk around PDS 70c, a planet observed to be in the process of accreting gas. After this stage, more massive satellites could be acquired through processes of tidal capture and pull down (Hamers & Portegies Zwart 2018) as has been suggested for the candidate exomoon Kepler 1625b-I (Teachey & Kipping 2018). Assuming that exomoons form soon after the epoch of planet formation, such moons must survive against perturbations from the host star to be observed in the present day ( $\sim$ 5 Gyr; Bonfanti et al. 2015). Our goal is to determine the stability boundary of putative satellites around the host planet, HD 23079b. Previously, Eberle et al. (2011) and Cuntz et al. (2013) discussed the orbital stability limit of an Earth-mass object in this system as a Trojan planet or a natural satellite within the planet’s Hill radius.

We examine the orbital stability limit for prograde and retrograde orbits using N-body simulations with REBOUND (see Section 2.2). These simulations consider a range of initial planetary eccentricity consistent with current observational constraints (Wittenmyer et al. 2020). Rosario-Franco et al. (2020) and Quarles et al. (2021) provided rough estimates for the stability limit in terms of the planet’s Hill radius, whereas here we explore this system in much finer detail. Similar to Rosario-Franco et al. (2020) and Quarles et al. (2021), we use the lower critical orbit (Rabl & Dvorak 1988) to define the stability limit, which is a more conservative approach that excludes regions of quasi-stability.

Figure 2 demonstrates the results of our simulations in terms of initial semimajor axis of the satellite $a_{\rm sat}$ (in R $_{\rm H}$ ) and the planetary eccentricity $e_{p}$ . Figure 2a and b are colour-coded using the parameter $f_{\rm stab}$ , which is defined as the fraction of 20 simulations with random mean anomalies for the satellite that survive for $10^5$ yr. The values of $f_{\rm stab}$ range from 0.0 to 1.0, where the cells with $f_{\rm stab}<0.05$ (wholly unstable) are colored white. The fully stable ( $f_{\rm stab}=1$ ; black) cells are used in our calculation of the stability boundary, while the values between the extremes illustrate regions of quasi-stability. The dashed (cyan) curves mark the stability limit previously determined for prograde (Rosario-Franco et al. 2020) and retrograde (Quarles et al. 2021) satellites, respectively.

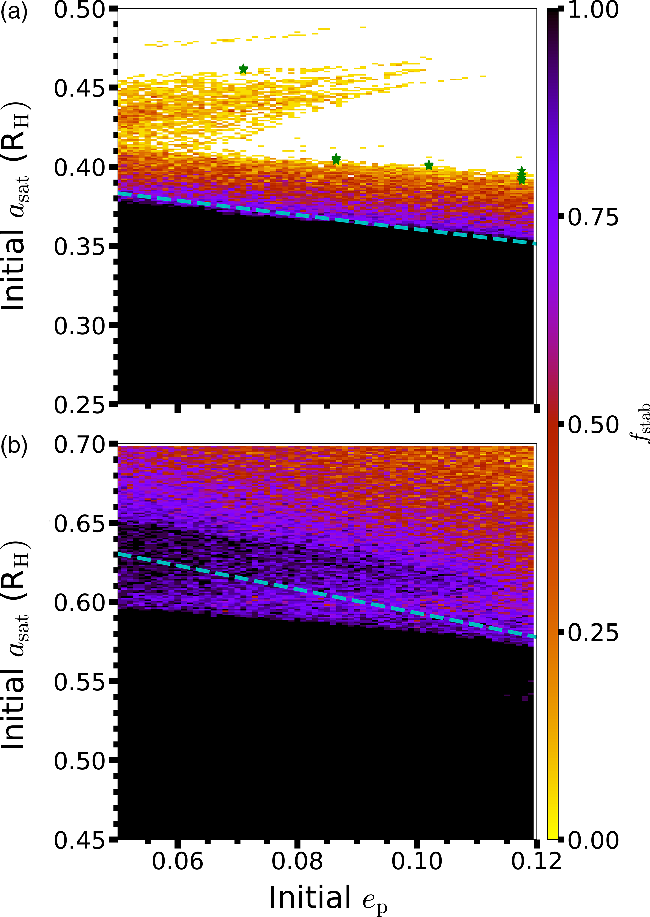
Figure 2. Numerical estimates for the stability of (a) prograde and (b) retrograde exomoons orbiting HD 23079b as a function of the satellite’s initial semimajor axis $a_{\rm sat}$ in units of the planetary Hill radius R $_{\rm H}$ and the planetary eccentricity $e_{p}$ . The colour code represents the fraction $f_{\rm stab}$ (out of 20) of stable simulations for a $10^5$ yr timescale; it shows which initial parameters depend on the initial placement of the satellite through its mean anomaly $\theta_{\rm sat}$ . The white cells denote cases where zero trial simulations survive for $10^5$ yr and, conversely, the black cells denote cases where all the trial simulations survive. The cyan (dashed) lines mark the expected stability limits for (a) prograde (Rosario-Franco et al. 2020) and (b) retrograde (Quarles et al. 2021) orbiting exommons. The green stars in (a) mark the previous estimates from Cuntz et al. (2013), which are found to lie at the border of the quasi-stable regime.

For prograde orbits (Figure 2a), the stability limit extends to 0.37 R $_{\rm H}$ for the lowest consider planet eccentricity and decreases to 0.35 R $_{\rm H}$ for larger planetary eccentricity. Our stability limit closely agrees with the stability fitting formula by Rosario-Franco et al. (2020). Beyond this boundary, there is a gradient of quasi-stability over a small range in satellite semimajor axis. At $\sim$ 0.43 R $_{\rm H}$ , there is a 6:1 (first-order) mean motion resonance (MMR) between the planet and satellite orbits (Quarles et al. 2021). The MMR excites the satellite’s eccentricity over time, which allows for the satellite to escape as its apocenter extends beyond the upper critical orbit ( $\approx$ 0.5 R $_{\rm H}$ ; Domingos et al. 2006). The MMR’s resonant angle depends on the relative orientation (i.e., mean anomaly) of the planetary and satellite orbits and particular starting angles can survive for longer periods, if the satellite returns to approximately the same phase after six orbits. Cuntz et al. (2013) used a single initial mean anomaly for the satellite, which largely corresponds to the upper critical orbit (green stars in Figure 2a).

For retrograde orbits (Figure 2b), the continuously stable region extends to $\sim$ 0.59 R $_{\rm H}$ for $e_{p}$ = 0.05 and recedes to $\sim$ 0.57 R $_{\rm H}$ for $e_{p}$ = 0.12 in a similar manner as the stability limit for Figure 2a. For the initial planetary eccentricity from 0.05 to 0.10, there is a stable peninsula corresponding to a 7:2 (second-order) MMR. As MMRs increase in order, the magnitude of the eccentricity excitation decreases (Murray & Dermott 1999). Moreover, the weakened Coriolis force and shorter interaction times for retrograde orbits (Henon 1970) also reduce the magnitude of secular eccentricity excitation. Quarles et al. (2021) considered a coarser grid of simulations, which did not resolve the gap created by the 4:1 (first-order) MMR. Hence, the stability limit was slightly over-estimated (dashed curve) in their work. However, it is a better approximation of the stability limit compared to previous works that focused on the upper critical orbit (Domingos et al. 2006; Cuntz et al. 2013). The limits for retrograde orbits from Cuntz et al. (2013) are larger than 0.7 R $_{\rm H}$ as are those by Domingos et al. (2006). Hence, the previous results from Cuntz et al. (2013) are not shown in Figure 2b.

Available mass measurements of HD 23079b are based on the RV method; thus, only the minimum mass is known implying the true mass of HD 23079b could be higher. Generally, we expect the true mass to differ by a factor of 1/ $\sin(\pi/4)$ (or $\sim$ 1.4) assuming an isotropic distribution restricted to prograde orbits for the planetary inclination on the sky plane. In Figure 2, we use the minimum mass $m_{p}$ in all our calculations. Estimates of the exoplanet mass distribution (Jorissen, Mayor, & Udry 2001; Ananyeva et al. 2020) indicate that planets with a substantially increased mass are rare and thus we expect the true mass of HD 23079b to differ from the minimum mass by only a small factor. Hence, we perform another set of stability simulations for prograde moons with the host planet’s mass is increased to 1.5 $m_{p}$ (i.e., 3.62 M $_{\rm J}$ ).

Figure 3 shows the stability limit (in au) for the minimum mass $m_{p}$ (black) and the increased mass $m_{p}^\prime$ (red) as a function of the planetary eccentricity $e_{p}$ . The stability limit (in au) clearly increases for a larger planet mass because the respective Hill radius is larger (see Equation (1)). Thus, we expect the red curve to scale by a factor $\mu = m_{p}^\prime/m_{p}$ . Comparing the two curves (black and red) indicates that the stability limit increases by a factor of $\sim$ 1.14 (i.e., ${1.5^{1/3}}$ ). If future observations reveal a planetary mass beyond the minimum value, the stability limits as obtained can be readily adjusted through a simple scale factor (Wittenmyer et al. 2020).

Figure 3. Stability limits for prograde exomoons assuming the minimum planet mass of $m_{p} = 2.41 {\rm M}_{\rm J}$ (black) and an increased mass of $m_{p}^{\prime} = 3.62~{\rm M}_{\rm J}$ (red). The best-fit curves scale as a power law with the mass ratio $\mu = m_{p}^{\prime}/m_{p}$ . Note that the y-axis values are in physical units (au) instead of R $_{\rm H}$ .

3.2. Tidal migration

The orbits of natural satellites (including our Moon) have migrated since the time of their formation due to de-spinning of their host planet from tides raised from the Sun and the satellites (Goldreich & Soter 1966; Goldreich 1966; Touma & Wisdom, 1998; Ćuk & Stewart 2012). We evaluate the possible extent of migration for a putative Earth-mass moon orbiting HD 23079b using Equations (3)–(5), which describe the tidal migration based on the CTL model (Hut 1981; Barnes 2017). The satellite begins on a circular orbit at $3 R_{\rm roche}$ (or $\approx$ 0.015 R $_{\rm H}$ ), where the initial planetary rotation period is varied from 3 to 12 h in 0.25 h steps. Piro (2018) showed that the satellite’s semimajor axis after 10 Gyr can differ depending on the assumed planetary rotation rate. To test this dependence on the assumed $e_{p}$ , we consider a range of values from 0.05 to 0.13 in steps of 0.01.

From our calculations, we find that there were no notable changes in the final semimajor axis for all $e_{p}$ values considered in this study. This is because the host planet is not close to the star and thus the stellar tides are largely negligible. However, the host star also has a larger influence on the satellite’s orbit and impacts the satellite’s eccentricity. This kind of forcing depends on the semimajor axis ratio ( $a_{\rm sat}$ / $a_{p}$ ) and the planetary eccentricity ( $e_{p}$ /(1- $e_{p}^2)$ ) (e.g., Heppenheimer 1978; Andrade-Ines & Eggl 2017); both of which are very small. Since the moon’s forced eccentricity is small, the eccentricity contribution to the star-planet and planet-moon tides is also small. Therefore, we present results that only use $e_{p}$ = 0.09 in our simulations.

Figure 4 demonstrates the final semimajor axis of the satellite as a function of the assumed planetary rotation period due to the tidal evolution over 10 Gyr. We use the observationally determined minimum mass of the planet ( $m_{p}$ = 2.41 M $_{\rm J}$ ) and a Jupiter-like constant time lag ( $\tau_{p}$ = $\tau_{\rm J}$ ) for HD 23079b. The magenta line (with dots) represents this nominal case in Figure 4a and b. The final semimajor axis of the satellite under our nominal conditions is $\sim$ 0.0545 R $_{\rm H}$ for the fastest rotation period (3 h) and $\sim$ 0.043 R $_{\rm H}$ for the slowest rotation period (12 h). Observations from the RV method restrict the planetary mass measurement to the minimum mass, a limitation that could be overcome in the future. We analyze several other cases that vary the assumed planetary mass by a factor of 1.5 and 2 (see Figure 4a). The satellite’s final semimajor axis $a_{\rm fin}$ decreases for a larger planetary mass (relative to minimum mass $m_{p}$ ) by the mass ratio $\mu$ $=m_{p}^\prime/m_{p}$ , which scales by a power law; i.e., $a_{\rm fin}^\prime \propto \mu^{-1/12}a_{\rm fin}(P_{\rm rot})$ .

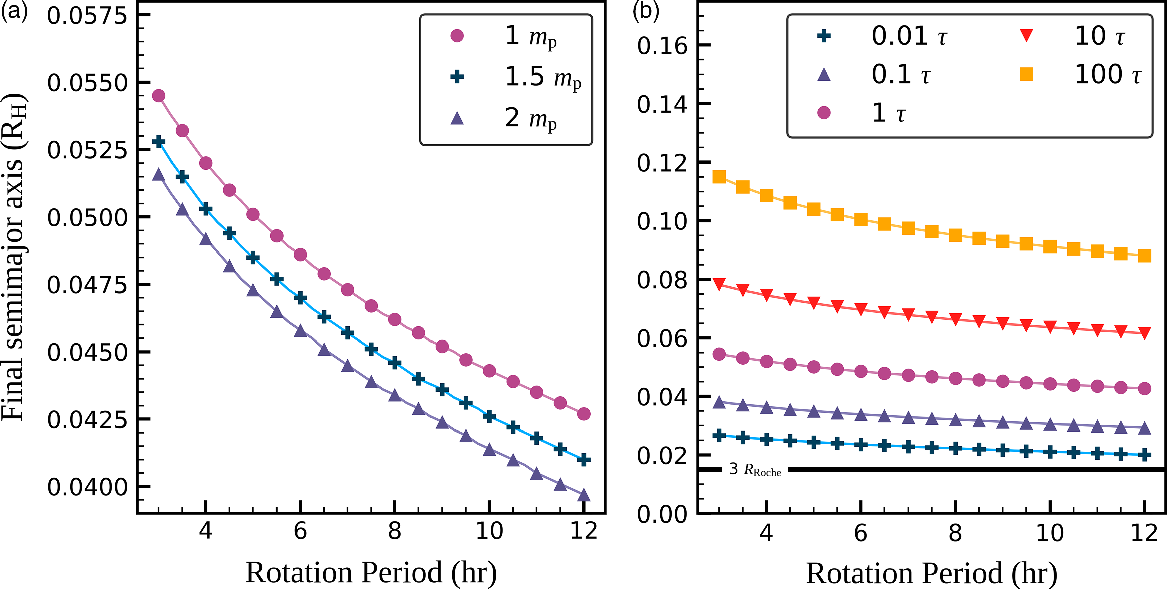
Figure 4. Relationship between the satellite’s final semimajor axis and the planetary rotation period based on tidal model simulations for different values of $m_{p}$ and $\tau$ . (a) Results varying the assumed planetary mass (1.0 $m_{p}$ , 1.5 $m_{p}$ , and 2.0 $m_{p}$ ) while using a Jupiter-like tidal time lag $\tau$ . (b) Results varying the tidal time lag from 0.01 $\tau$ to 100 $\tau$ . The horizontal line in (b) at 0.015 R $_{\rm H}$ represents $3 R_{\mathrm{Roche}}$ . Note the difference in the y-axis ranges between panel (a) and (b). Additionally, the 1 $m_{p}$ curve in (a) and the 1 $\tau$ cure in (b) are identical. In panel (b), only every other calculation has been depicted by a marker for increased clarity of the figure.

In Figure 4b, we vary the dissipation strength through the constant time lag over four orders of magnitude ( $C_\tau = 10^{-2}-10^{2} \tau$ ). Interestingly, a 100-fold increase in $\tau$ (orange squares in Figure 4b) results in a doubling of the final satellite semimajor axis when the planetary rotation period $P_{\rm rot}$ is 3 h; i.e., $a_{\rm fin}^\prime \propto C_\tau^{1/6}a_{\rm fin}(P_{\rm rot})$ . The satellite’s semimajor axis evolution (see Equation (3)) depends linearly on the assumed value for $\tau_{ p}$ , but it also depends non-linearly on $\tau_{p}$ through the changes in the planetary rotation rate $\Omega_{p}$ (see Equation (5)). The combination of those dependencies are the likely underlying cause of the empirically derived scaling relation.

Irregardless of the assumed parameters for the tidal evolution, the final $a_{\rm sat}$ is far from the stability limit, where the largest final $a_{\rm sat}$ is only $\sim$ 1/3 of the prograde stability limit. The tidal force is known to decrease rapidly with distance. Thus, starting the satellite at most separations would not affect the satellite’s potential stability (Quarles et al. 2020b). However, the CTL model considers tidal migration secularly without any interruptions due to MMRs or changes in the internal evolution of the host planet (Touma & Wisdom 1998). Realistically, such interactions could include slowing down the migration process temporarily. In fact, this kind of behavior may have occurred for our Moon (Sasaki et al. 2012). Tidal evolution with multiple moons could also induce some volcanic activity as is the case for Io (Peale, Cassen, & Reynolds 1979.) and potentially affect an exomoon’s habitability (Heller & Barnes 2013), but such considerations are beyond the scope of this work.

3.3. Observability of possible exomoons in the HD 23079 system

The detection of exomoons is currently extremely challenging but their detection is technically feasible, where Sartoretti & Schneider (1999) showed the transit method as a promising avenue for their eventual discovery. A dedicated search for exomoons within the Kepler data (Kipping et al. 2012, 2013a,b, 2014, 2015b) has yet to confirm an exomoon, while noting that Kepler 1625b-I represents an interesting candidate (Teachey & Kipping 2018). To observe an exomoon in the HD 23079 system, a different approach is required since the host planet was discovered through the RV method (Tinney et al. 2002; Wittenmyer et al. 2020) and is not known to transit its host star relative to our line-of-sight. The expected semi-amplitude $K_{\rm o}$ from the stellar motion about the center-of-mass is $\sim$ 54 m s^–1, where the addition of an Earth-mass satellite orbiting HD 23079b would introduce a small additional variation ( $<$ 1 m s^–1). Consequently, the most promising technique is Doppler monitoring within direct imaging observations (Vanderburg et al. 2018), where an RV signal is extracted from the host planet’s reflex motion after accounting for variations in the host planet’s reflected light.

The host planet’s semi-amplitude $K_{p}$ induced by an exomoon (Vanderburg et al. 2018; Perryman 2018) is given by the following:

(8) \begin{equation} K_{p} = \left(\frac{m_{\rm sat}\sin{i_{\rm sat}}}{m_{p} + m_{\rm sat}}\right) \sqrt{\frac{Gm_{\rm sat}}{a_{\rm sat}\left(1-e_{\rm sat}^2\right)}},\end{equation}

where the satellite orbital inclination $i_{\rm sat}$ is relative to the observer’s line-of-sight and should be similar in magnitude to the observed planetary inclination due to tidal evolution of the planet-satellite pair (Porter & Grundy 2011). Although the system is not known to transit, we assume that $i_{\rm sat}=90^\circ$ to estimate the maximum $K_{p}$ . Figure 5 demonstrates the maximum satellite induced $K_{p}$ as a function of the satellite semimajor axis $a_{\rm sat}$ in units of R $_{\rm H}$ , where the reflex velocity on the planet’s orbit about the barycenter decreases as the satellite semimajor axis increases ( $K_{p} \propto a_{\rm sat}^{-1/2}$ ). The black, red, and blue solid curves mark when an Earth-mass, a standard super-Earth (8 M $_\oplus$ ), or a Neptune (17 M $_\oplus$ ), respectively, is assumed for the satellite and the RV minimum mass ( $m_{p}=2.41 {\rm M}_{\rm J}$ ) is used. The dashed curves are provided to show how much the satellite-induced RV signal decreases, if the assumed planetary mass is doubled (2 $m_{p}$ ).

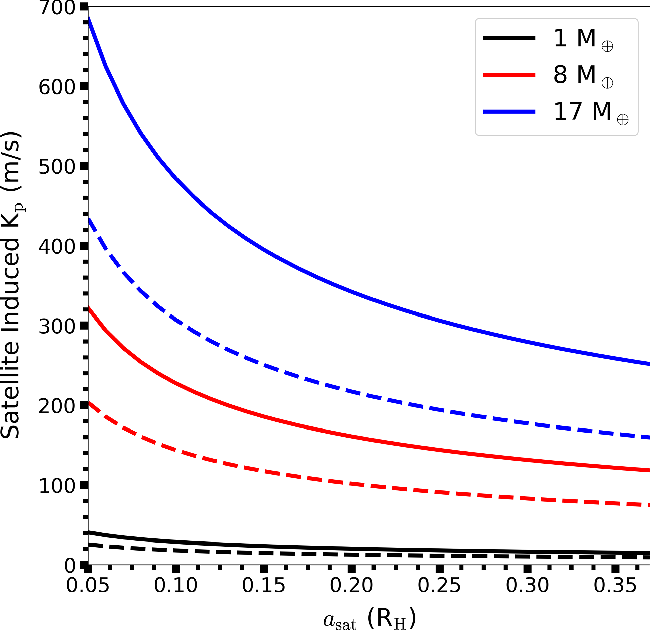
Figure 5. The RV semi-amplitude $K_{p}$ induced by a satellite with respect to the the planet-satellite semimajor axis $a_{\rm sat}$ in units of the host planet’s Hill radius R $_{\rm H}$ . The solid curves represent values assuming the minimum mass ( $m_{p} = 2.41 {\rm M}_{\rm J}$ ) is the true planetary mass. The dashed curves illustrate the reduction in $K_{p}$ for double the minimum mass (2 $m_{p}$ ). The curves are colour-coded (black, red and blue) to mark the differences in the assumed satellite mass (1, 8 and 17 M $_\oplus$ , respectively).

Figure 5 shows that massive ( $\gtrsim$ 8 M $_\oplus$ ), prograde-orbiting satellites could produce a Keplerian signal with an RV semi-amplitude greater than $\sim$ 100 m s^–1, even with a satellite semimajor axis near the stability limit. Keplerian signals from prograde, Earth-mass satellites are limited to $\sim$ 20–40 m s^–1. Retrograde-orbiting satellites stably orbit at larger separations with $a_{\rm sat} \leq 0.59\:{\rm R}_{\rm H}$ , but the resulting Keplerian signal would be less optimal for the observability.

The current best RV precision is $\sim$ 1 m s^–1, where this precision level is only attainable for bright ( $V<10$ ) stars. The host star in HD 23079 is relatively bright ( $V=7.12$ ; Anderson & Francis 2012), but the direct imaging method proposed by Vanderburg et al. (2018) would allow the analysis of the much fainter reflected light from the planet, which would be much more limited in precision ( $\sim$ 1 500 m s^–1). However, large (30 m class) telescopes (e.g., Giant Magellan Telescope; Jaffe et al. 2016) are on the horizon and should be available in the foreseeable future. They would make Doppler surveys of directly imaged planets attainable due to the much larger S/N compared to current technology affecting the RV precision (Quanz et al. 2015). In particular, the detection of Keplerian signals from massive exomoons with an RV semi-amplitude greater than $\sim$ 100 m s^–1 would be feasible.

4. Summary and conclusions

The aim of our study is to further explore the possibility of exomoons in the HD 23079 system. In this system, a solar-type star of spectral class F9.5V hosts a Jupiter-mass planet in a nearly circular orbit situated in the outer segment of the stellar HZ. Previous studies have examined the orbital stability limit of an Earth-mass object in this system as a Trojan planet (Eberle et al. 2011) or a natural satellite (Cuntz et al. 2013). We focus on the latter to more accurately identify the stability limits for prograde and retrograde exomoons within observational constraints, including the recent work by Wittenmyer et al. (2020).

In the past year, Rosario-Franco et al. (2020) updated the fitting formulas for the stability limit for prograde-orbiting satellites in terms of the planet’s Hill radius, whereas Quarles et al. (2021) improved the fitting formulas for retrograde systems. We follow the prior approaches, in much finer detail, for the HD 23079 system, where the stability limits determined herein specifically exclude regions of quasi-stability and resonances. Additionally, we evaluate multiple satellite mean anomalies, which allows us to overcome some limitations from previous works (e.g., Domingos et al. 2006).

Our study shows that the system of HD 23079 is a highly promising candidate for hosting potentially habitable exomoons despite the fact that the outer stability limit is modestly reduced. Noting that HD 23079b’s mass is not exactly known—as due to the RV detection technique only a minimum value could hitherto been identified—our results are still applicable, if a more precise mass value becomes available as the outer orbital stability limit follows a well-defined scaling law, i.e., $(m_{p}^\prime/m_{p})^{1/3}$ ; see text for details. The outward migration due to tides does not greatly affect the potential stability of exomoons in a CTL tidal model (Hut 1981; Barnes 2017), where we find that a putative satellite’s migration distance the stellar lifetime scales inversely to the 1/12th power in mass ratio $\mu$ when comparing different assumptions on planetary mass from the sky plane inclination. Moreover, we find that migration distance scales inversely to the 1/6th power in the assumed tidal time lag parameter $\tau$ relative to a Jupiter-like value. Scaling relations, in either the mass or tidal time lag, would assist in the general search for exomoons as well as future observations of the HD 23079 system.

We also explore the observability of putative HD 23079 exomoons. Current technologies are incapable of identifying moons in that system; however, future developments hold promise. As the transit method is unavailable for finding exomoons in HD 23079, Doppler monitoring within direct imaging observations might offer positive outcomes. Note that large (30 m class) telescopes (e.g., Giant Magellan Telescope; Jaffe et al. 2016) should be available in the foreseeable future. The much larger S/N from telescopes with a large mirror would make Doppler surveys of directly imaged planets attainable, where the Keplerian signals from Earth-mass exomoons with an RV semi-amplitude greater than $\sim$ 100 m s^–1 would be possible (Vanderburg et al. 2018).