Single-molecule orientation-localization microscopy: Applications and approaches

Abstract

Single-molecule orientation-localization microscopy (SMOLM) builds upon super-resolved localization microscopy by imaging orientations and rotational dynamics of individual molecules in addition to their positions. This added dimensionality provides unparalleled insights into nanoscale biophysical and biochemical processes, including the organization of actin networks, movement of molecular motors, conformations of DNA strands, growth and remodeling of amyloid aggregates, and composition changes within lipid membranes. In this review, we discuss recent innovations in SMOLM and cover three key aspects: (1) biophysical insights enabled by labeling strategies that endow fluorescent probes to bind totargets with orientation specificity; (2) advanced imaging techniques that leverage the physics of light-matter interactions and estimation theory to encode orientation information with high fidelity into microscope images; and (3) computational methods that ensure accurate and precise data analysis and interpretation, even in the presence of severe shot noise. Additionally, we compare labeling approaches, imaging hardware, and publicly available analysis software to aid the community in choosing the best SMOLM implementation for their specific biophysical application. Finally, we highlight future directions for SMOLM, such as the development of probes with improved photostability and specificity, the design of “smart” adaptive hardware, and the use of advanced computational approaches to handle large, complex datasets. This review underscores the significant current and potential impact of SMOLM in deepening our understanding of molecular dynamics, paving the way for future breakthroughs in the fields of biophysics, biochemistry, and materials science.

Introduction

Single molecules (SMs) have emerged as powerful, noninvasive probes for studies spanning biology, biochemistry, biophysics, and material science (Metskas and Rhoades, 2020; Möckl and Moerner, 2020; Lelek et al., 2021; Bustamante et al., 2021) since they were first observed using optical methods over three decades ago (Moerner and Kador, 1989; Betzig and Chichester, 1993; Xie, 1996). Their capability to discern and quantify intricate nanoscale processes at the molecular level continues to drive innovation in the field of microscopy. Over the last few decades, single-molecule localization microscopy (SMLM) (Betzig et al., 2006; Hess et al., 2006; Rust et al., 2006; Sharonov and Hochstrasser, 2006) has revolutionized our ability to visualize cellular structures with unprecedented resolution surpassing the Abbé diffraction limit of ~250 nm. These techniques leverage the active control of fluorescence “on–off” states to reduce the concentration of emitting molecules, precisely localize the SMs, and reconstruct an image of the underlying structure with a typical resolution on the order of 10 nanometers (Moerner, 2015). During the past two decades, the field continues to innovate with sequential (Reinhardt et al., 2023), energy-transfer (Ghosh et al., 2019; Hauke et al., 2023; Chen et al., 2024a), interferometric (Shtengel et al., 2009; Aquino et al., 2011; Huang et al., 2016), and adaptive (Balzarotti et al., 2017; Cnossen et al., 2020; Gwosch et al., 2020; Weber et al., 2023; Sahl et al., 2024) imaging techniques, pushing practical localization precision to the molecular scale (<1 nm).

In the decade since the Nobel Prize in Chemistry 2014, developments have shifted toward functional imaging, i.e., sophisticated methods capable of imaging physicochemical properties beyond where molecules are located (Steves et al., 2024). Examples include measuring the emission spectrum (Zhang et al., 2015; Bongiovanni et al., 2016; Brenner et al., 2023), fluorescence lifetime (Thiele et al., 2020; Oleksiievets et al., 2022), and orientation and rotational diffusion, i.e., “wobble,” (Backlund et al., 2014; Valades Cruz et al., 2016; Shaban et al., 2017) of individual molecules. Methods that simultaneously image molecular positions and orientations, termed single-molecule orientation-localization microscopy (SMOLM), have been shown to improve localization accuracy in SMLM since changes in orientation can be mistakenly perceived as changes in molecular position (Engelhardt et al., 2011; Backlund et al., 2012, 2014; Lew and Moerner, 2014; Backlund et al., 2016). Moreover, SMOLM offers profound insights into molecular structures and dynamics at the nanoscale that cannot be resolved in SMLM, such as the organization of amyloid aggregates (Shaban et al., 2017; Ding et al., 2020; Ding and Lew, 2021; Zhou et al., 2024a; Sun et al., 2024), conformations of DNA strands (Ha et al., 1996, 1998; Backer et al., 2016, 2019; Mazidi et al., 2019; Hulleman et al., 2021), structure of actin networks (Valades Cruz et al., 2016; Curcio et al., 2020; Rimoli et al., 2022), and the dynamic movements of molecular motors (Sosa et al., 2001; Peterman et al., 2001; Forkey et al., 2003; Beausang et al., 2013; Lippert et al., 2017).

In a typical SMOLM experiment, the target is labeled with fluorescent probes whose orientations convey useful information. Importantly, the fluorescent probe and labeling method must be chosen carefully. For example, a rigid bifunctional attachment strategy useful for probing the rotational motions of molecular motors is unlikely to be adaptable for characterizing the conformations of disordered proteins. In addition, fluorogenic “turn-on” probes, in contrast to conventional fluorophores, offer a degree of environmental sensitivity that can synergistically complement the orientational data measured by SMOLM.

The emitted fluorescence is then collected and modulated by an imaging system, and images are captured using photon-counting cameras. Since a standard fluorescence microscope has poor sensitivity for measuring molecular orientation, it must be modified to measure fluorescence emission under varying pumping polarization, manipulate the polarization and/or phase of the fluorescence emission, or both. These advancements, combined with algorithms capable of detecting dim fluorescent emitters and robustly estimating 2D/3D position and 2D/3D orientation simultaneously, are essential to quantify the rotational dynamics of SMs precisely and accurately.

In this review, we discuss new developments in these aspects of SMOLM and organize our coverage as follows. (Techniques that used polarized light to measure micro- and mesoscale biological structures are covered excellently elsewhere (Alonso, 2023; Brasselet and Alonso, 2023).) In the first section, we introduce various biophysical applications of SMOLM and labeling strategies that enable fluorophore orientations to sensitively probe the target of interest. We then discuss how light interacts with fluorescent molecules and vice versa, which establishes how microscope images can be used to sensitively measure molecular orientation. We next describe various methods for measuring SM orientations, followed by coverage of image analysis methods, including iterative methods for solving inverse problems and deep learning-based algorithms. The review concludes with an outlook suggesting future directions for SMOLM.

Sensing biomolecular architectures at the nanoscale: labeling strategies and applications

SMOLM can be applied to study a wide variety of targets, e.g., protein assemblies, nucleic acids, and lipids, and a broad variety of labeling and photochemistry have been harnessed to enable fluorophore orientations to faithfully probe the organization of biomolecules within the sample. We summarize recently reported labeling strategies in SMOLM in Figure 1 and their applications in Figures 2–4 and Table 1.

Figure 1. Representative labeling techniques in SMOLM. (a) Alexa Fluor 488-phalloidin conjugate labeling an actin filament (F-actin) (adapted from Rimoli et al., 2022). (b) Position and orientation of bis-((N-iodoacetyl)piperazinyl) sulfonerhodamine (BSR) on the kinesin protein structure (adapted from Sosa et al., 2001). (c) B-form double-stranded DNA internally labeled with covalently attached Cy3 and Cy5 dyes (adapted from Mortensen et al., 2015). (d) Concept of molecular tension DNA probes (adapted from Brockman et al., 2018). (e) Molecular rotors transiently bind to amyloid fibrils (adapted from Sarkar et al., 2023). (f) SYTOX orange dye intercalating within λ-DNA (adapted from Backer et al., 2016). (g) 1,1′-Dioctadecyl-3,3,3′,3′-Tetramethylindocarbocyanine Perchlorate (DiI) and merocyanine 540 (MC540) bound to gel- and fluid-like supported lipid bilayers, respectively (adapted from Lu et al., 2020).

Table 1. Labeling strategies for SMOLM and their applications

Emitters other than single molecules, with various labeling strategies and applications: Fluorescence from quantum rods (Lippert et al., 2017; Ohmachi et al., 2012), scattered light from gold nanorods (Beckwith and Yang, 2021), and optically detected magnetic resonance imaging using nitrogen-vacancy centers in diamond (Backlund et al., 2017).

Covalent labeling of target structures

Many SMLM techniques, e.g., stochastic optical reconstruction microscopy (STORM) (Rust et al., 2006) and (fluorescence) photoactivation localization microscopy [(f)PALM] (Betzig et al., 2006; Hess et al., 2006) achieve SM blinking via specific photochemical conditions, e.g., by using specific illumination intensities and/or chemical imaging buffers. The target is labeled by covalently attaching an organic fluorophore or via fusing it to a fluorescent protein (Li and Vaughan, 2018). Due to the high rotational mobility of many chemical linkers (Sahoo et al., 2007; Doose et al., 2007; Sindbert et al., 2011; Chen et al., 2013; Beane et al., 2014; Gräwe and Stein, 2021), fluorescent probes usually rotate independently of the target molecule. Therefore, the probe and its attachment to the target must be carefully designed for SMOLM measurements. Here, we introduce labeling strategies that constrain the orientation of the fluorophores in a controlled relationship to the target structure.

Organization of actin filaments via covalent conjugation to phalloidin

The structural organization of actin filaments is crucial for various cellular processes, including motility, division, and force generation, all of which are fundamental to understanding cell mechanics. Accurately interpreting the orientational dynamics of fluorescent probes when studying actin filaments depends significantly on the rigidity of the linker connecting the fluorophore to the target molecule. Importantly, the orientational dynamics of fluorescent probes are influenced by both environmental forces (e.g., solvent collisions) and forces induced by the target of interest. It has been shown that even though phalloidin binds sufficiently rigidly to actin filaments, different linkers between the fluorophore and phalloidin exhibit different rigidities (Figure 1a).

Measuring the orientations of phalloidin-conjugated fluorescent molecules under identical labeling conditions, Valades Cruz et al. show that Atto 633-phalloidin exhibits a perpendicular orientation to actin stress fibers with a small wobble angle, whereas Alexa 488-phalloidin exhibits parallel orientations to actin stress fibers with slightly greater wobble angle (Figure 2a) (Valades Cruz et al., 2016). Alexa 647-phalloidin freely rotates due to its larger structure, which makes it inappropriate for studying actin fiber architectures using SMOLM. Comparing the wobbling behavior of differently charged dye molecules, including negatively charged Alexa 488, positively charged Atto 633, and neutral Atto 565, the authors surmise that the differences in wobbling of phalloidin conjugates are mostly attributed to the linker length; the linker length of Atto 565 is similar to that of Alexa 488, and they exhibit similar wobbling behavior. Similar relative degrees of rotational flexibility were also observed by (Figure 2b) Bruggeman et al. (2024).

Figure 2. Imaging protein assemblies using SMOLM. (a) Polar-dSTORM imaging of actin stress fibers labeled with Alexa Fluor 488, Atto 633, and Alexa Fluor 647. Colors indicate the polarization factor P, equivalent here to linear dichroism LD, superimposed on grayscale dSTORM images (adapted from Valades Cruz et al., 2016). (b) Representative raw and hue-saturation-value (HSV) images of phalloidin-AF488 and phalloidin-AF647 bound to actin in fixed HeLa cells and distributions of the average degree of linear polarization (DoLP) for both fluorophores. Hue: angle of linear polarization (AoLP); saturation: DoLP; value: brightness (adapted from Bruggeman et al., 2024). (c) 4polar-STORM imaging of actin filament organization in fixed U2OS cells with color-coded wobbling angles $ \delta $ (Alexa Fluor 488-phalloidin-labeled F-actin; adapted from Rimoli et al., 2022). The zoomed-in regions (1–4) show the (top) STORM and (bottom) 4polar-STORM images; lines indicate orientation, and colors represent wobble angles. (d) TAB SMOLM images of amyloid fibrils transiently labeled with LDS722, color-coded by (left) polar angle $ \theta $ (rad) and (middle) wobble angle $ \varOmega $ (sr). The polar angle histogram reveals two distinct binding modes (adapted from Sarkar et al., 2023). (e) Visualization of growing and decaying amyloid-beta fibrils using (top) SMLM and (bottom) SMOLM with lines color-coded according to Nile blue orientation (adapted from Sun et al., 2024). (f) SMOLM images and orientation distributions for representative KFE8^L, KFE8^D, and Aβ42 fibrils (adapted from Zhou et al., 2024a). In each figure, Nile red orientations are plotted and color-coded relative to the long axis ( $ {u}_x $ ) of each fiber.

Using the phalloidin-conjugated fluorophores, Rimoli et al. recently showed that SMOLM can resolve different nanoscale organizations of actin filament-based structures in mammalian cells (Figure 2c) (Rimoli et al., 2022); thin ventral and transverse arc stress fibers consist of highly aligned actin filaments, whereas thick peripheral and off-plane oriented dorsal stress fibers and focal adhesions consist of filaments with mixed orientations. The observations, especially within the dense assemblies, are uniquely enabled by orientation measurements using SMOLM.

Motor protein dynamics via bifunctional conjugation

Understanding the motions of motor proteins is crucial for understanding their mechanical and functional roles in cellular processes. One effective labeling strategy to study these dynamics is to attach fluorophores using more than one chemical linker to the target molecule, e.g., a bifunctional fluorophore that attaches to two separate residues of the target protein. In this way, the fluorophore’s orientation is rigidly tied to the orientation of the target. For example, bifunctional rhodamine (Corrie et al., 1998) bound to two cysteines has been used to resolve the tilt, twist, and movement of myosin motors (Corrie et al., 1999; Forkey et al., 2003; Yildiz et al., 2003).

Beausang et al. show the stepping events of myosin V at sub-millisecond temporal resolution by labeling calmodulins along the lever arm with rhodamine (Beausang et al., 2013). They observed short-lived substeps (~10 to 15 ms), marked by highly disordered lever-arm orientations, which were interpreted as random fluctuations occurring when the detached head searched for the next binding site. The increased wobble during every other step aligns with the hand-over-hand mechanism and thermal search. These findings extend our understanding of the mechanical and thermal dynamics involved in the biophysical function of myosin V.

Another fluorophore, bis-((N-iodoacetyl)piperazinyl) sulfonerhodamine (BSR) has been used to track the translation and rotation of kinesin along microtubules (Figure 1b) (Peterman et al., 2001; Sosa et al., 2001; Asenjo et al., 2003). Attaching BSR to specific cysteine residues on kinesin enables precise monitoring of its orientation relative to the microtubule. SMOLM measurements revealed that, in the presence of AMP-PNP (a nonhydrolyzable analog of ATP), the kinesin motor domain maintains a rigid orientation with respect to the microtubule. Interestingly, in the presence of ADP, the motor domain transitions to a highly mobile state, which may be crucial for the 8-nm stepping motion of kinesin during processive movement (Sosa et al., 2001). A later study showed that these measured orientations align well with a hand-over-hand movement mechanism (Asenjo et al., 2003).

Other multifunctional linkers, e.g., fluorescein arsenical hairpin (FlAsH) (Griffin et al., 1998) and ReAsH (Adams et al., 2002), its resorufin-based cousin, that bind to four cysteines of a target protein, may also be used in SMOLM. Both FlAsH and ReAsH only become fluorescent upon proper binding and orientation of the tetracysteine motif (Walker et al., 2016). The drawback of these multifunctional strategies is that the labeling yield is generally low, and improperly labeled species, e.g., with only a single functional attachment, must be carefully removed to avoid artifacts (Peterman et al., 2001).

DNA structure, dynamics, and tension sensing via covalent conjugation

Recent advancements have also showcased SMOLM’s utility for elucidating the structure and dynamics of engineered DNA structures (Cho et al., 2023; Zhan et al., 2023). A study using short double-stranded DNA molecules internally labeled with two distinct fluorophores (Cy3 and Cy5, Figure 1c) by Mortensen et al. demonstrated the ability to resolve fluorophore separations as small as 10 base pairs, while accurately determining the 3D orientation of DNA molecules. Their findings establish the use of short, double-labeled DNA molecules as probes for mapping the 3D orientation of any structure to which they can be firmly attached (Mortensen et al., 2015, 2016).

Similarly, Hübner et al. utilized 2D rectangular DNA origami to study the binding orientations of ATTO 647N, ATTO 643, and Cy5 in different nanoenvironments (Figure 3a) (Hübner et al., 2021). They found that the nanoenvironment is crucial in determining the orientation of fluorophores. For instance, creating additional space by omitting nucleotides adjacent to a double-stranded region leads to stronger binding and a narrower, more defined distribution of dye orientations. Additionally, the dynamics of dye molecules around a DNA helix is affected by electrostatic and hydrophobic interactions, which complicates the accurate prediction of their final orientation within a DNA origami structure.

Figure 3. Imaging nucleic-acid structures and flexibility using SMOLM. (a) DNA helical winding of a scaffold strand (gray) and ssDNA staple (red line) labeled with a fluorophore (red dot), and orientation distributions of ATTO 647N and ATTO 643 within DNA origami structures 1 and 2 (adapted from Hübner et al., 2021). (b) (top) AFM and (bottom) three SMOLM views of Cy5 orientations within 4-arm Holliday Junction complexes (HJs) with interduplex angles of 60°, 90°, and 120° (adapted from Cervantes-Salguero et al., 2024). Mean orientations of populations and subpopulations are denoted by red and blue arrows, respectively. (c) Controlled orientations of doubly linked Cy3 and Cy5 molecules within DNA origami structures featuring different numbers of missing base pairs (adapted from Adamczyk et al., 2022). (d) (top left) Diagram and (bottom) SMOLM image of a plectoneme formed by a single supercoiled DNA molecule and distribution of SYTOX orange orientations along a typical individual strand aligned along the x-axis (adapted from Hulleman et al., 2021). Colors represent azimuthal orientations (top right) Typical orientation distribution of a supercoiled strand before it twists around itself. (e) Histograms of fluorescence polarization of DNA intercalators under stretching forces of 3, 7, and 35 pN (left to right) above the onset of the overstretching transition, along with illustrations of tilted intercalators (adapted from Backer et al., 2019).

Cervantes-Salguero et al. explored the use of DNA origami to manipulate directly the orientations of cyanine dyes (Cervantes-Salguero et al., 2022) and to control the interduplex angles of dye-labeled Holliday Junction complexes (Figure 3b) (Cervantes-Salguero et al., 2024). They discovered that sequence-dependent partial intercalation of the dye could control its polar angle throughout a full revolution of a DNA double helix with a dispersion as small as ±4.5° within a 1.7 nm range. Additionally, they characterized experimentally the orientational constraints that Holliday Junctions impose on dye orientations; tuning the template conformation enabled the dye-template heterogeneity to be minimized.

In related work, Adamczyk et al. have demonstrated direct DNA engineering to control Cy5 and Cy3 orientations by doubly linking them to hybridized strands while leaving unpaired bases in the origami scaffold (Figure 3c) (Adamczyk et al., 2022). By varying the number of unpaired bases (from 0 to 8), the orientations of Cy5 and Cy3 were adjusted from perpendicular to parallel relative to the DNA double helix. With no unpaired bases, the dyes remained constrained and aligned perpendicularly. As the number of unpaired bases increased to 2, 4, or 6, the increased flexibility of the linker and additional spatial accommodation allowed the dyes greater rotational mobility when interacting with the DNA. At eight unpaired bases, the linkers fully extended, causing the fluorophores to align parallel to the DNA and become rotationally constrained.

Another promising application of SMOLM uses labeled DNA nanostructures to sense mechanical forces. Studies have shown that when Cy3B is covalently attached to the terminus of a DNA duplex, it aligns perpendicularly to the duplex’s long axis (Iqbal et al., 2008). Consequently, when attached to DNA hairpin-based tension probes, the 3D orientation of piconewton cellular receptor forces can be determined using ensemble fluorescence polarization (Figure 1d) (Brockman et al., 2018; Blanchard et al., 2021). SMOLM has the potential to improve the sensitivity of these sensors to the single-molecule level.

Transient labeling of target structures

Binding-activated fluorescence is another mechanism to achieve SM blinking. In point accumulation for imaging in nanoscale topography (PAINT) (Sharonov and Hochstrasser, 2006; Kuo and Hochstrasser, 2011; Tholen et al., 2023), the fluorescence quantum yield of Nile red (NR), merocyanine 540, and other lipophilic probes increases within a non-polar chemical environment, e.g., when bound to a lipid bilayer. Since this initial demonstration, many variants of binding-activated SM blinking have been developed, including amyloid binding using amyloidophilic dyes (TAB, Spehar et al., 2018), DNA labeling using intercalating dyes (binding-activated localization microscopy, BALM (Schoen et al., 2011), and labeling a variety of biomolecules using dye-labeled oligonucleotides (DNA-PAINT, Jungmann et al., 2010, 2014; Steen et al., 2024). Unlike STORM and (f)PALM, which are limited by photobleaching of the fluorescent probes, the PAINT family of methods can collect an infinite number of localizations, due to the nearly limitless supply of fresh labels, in principle. The precise nature of dye-target interaction determines how the orientation of a fluorophore is related to the dynamics or organization of the target sample. Here, we discuss some PAINT-based methods that have been used in SMOLM.

Amyloid aggregate structure and dynamics via transient binding of amyloidophilic dyes

A fundamental question in the study of amyloid-related neurodegenerative diseases, such as Alzheimer’s, is how the structural organization of amyloid aggregates influences their pathological behavior. SMOLM is a powerful tool to reveal these nanoscale structural characteristics, providing insights that go beyond conventional methods like atomic force microscopy (AFM) and cryo-electron microscopy (cryo-EM). For example, the amyloidophilic dyes thioflavin T (ThT) (Spehar et al., 2018) and thioflavin X (ThX) (Needham et al., 2020), in addition to the lipophilic dyes Nile red (Ding et al., 2020) and Nile blue (Sun et al., 2024), have been used to transiently label amyloid aggregates for SMLM and SMOLM. These dyes only emit fluorescence when they are in the vicinity of the hydrophobic fibril surface; otherwise, their fluorescence quantum yield is low. SMOLM has shown that these dyes bind in a preferential direction to the grooves formed by cross-β sheets within fibrils, i.e., parallel to the fibril backbone (Krebs et al., 2005; Ding et al., 2020). Moreover, TAB dyes appear to exhibit a variety of orientations when bound to smaller oligomers (Ding et al., 2020; Ding and Lew, 2021), suggesting that these dyes may be useful for quantifying the organization of amyloid aggregates and studying how they disrupt cell membranes (Danzer et al., 2007; Outeiro et al., 2008). One significant development in TAB imaging is the use of dyes with improved signal-to-background ratios (SBR); Ding et al. reported that the background when using NR is reduced by 10-fold compared to ThT (Ding et al., 2020; Ding and Lew, 2021). Further, ThX exhibits a 5-fold improvement in brightness and a 7-fold increase in binding affinity compared to ThT (Needham et al., 2020) with the potential to produce dramatically more detailed SMOLM measurements.

Amyloid fibrils, such as those formed by amyloid-beta and alpha-synuclein, and other β-sheet peptide self-assemblies have since emerged as exciting applications for SMOLM studies using these dyes. For instance, Sarkar et al. discovered that SYPRO orange and LDS722, two molecular rotor dyes, exhibit distinct orientation characteristics when bound to amyloid fibrils compared to NR (Figures 1e and 2d) (Sarkar et al., 2023). Besides a population oriented parallel to the fibril, they observed an additional population with an inclined orientation, indicating diverse binding modes at different sites such as the fibril core, interfibril grooves, surface edges, ditches, and confined spaces in the fibril network. This structural diversity is crucial for understanding the biophysical properties of these environments, such as variations in local polarity, viscosity, and specific interactions like hydrogen bonding or π–π stacking.

Another critical biophysical question is understanding how the underlying molecular organization influences the growth and decay of fibrillar structures. Sun et al. used Nile blue to investigate the architecture and dynamics of Aβ42 fibrils (Figure 2e) (Sun et al., 2024). SMOLM revealed that assemblies with ordered and uniformly oriented structures are indicative of stable Aβ42 fibrils. Further, fibrils that show increasing uniformity are typically in a state of growth, whereas those that become more disordered correspond to decaying structures. SMOLM also revealed that locally disordered regions can facilitate large-scale fibrillar remodeling.

In another study, Zhou et al. used NR to reveal the helical (bilayer) ribbon architecture of fibrils of the engineered peptide KFE8 and recombinant Aβ42. Precise SMOLM measurements quantified the tilt of both the inner and outer layers of the fibrils relative to the long axis (Figure 2f) (Zhou et al., 2024a). Moreover, SM orientations revealed that the architectures of both KFE8 and Aβ42 are consistent with a helical bilayer ribbon, rather than a helical monolayer. However, KFE8 exhibits larger tilt angles, resulting in a higher diameter-to-pitch ratio, which indicates a more pronounced helicity; Aβ42 resembles an approximately straight line with only a modest backbone tilt. Without orientation data, these differences are difficult to discern in SMLM. SMOLM further enabled the differentiation of polymorphic branched and curved morphologies in KFE8, revealing significantly greater backbone heterogeneity compared to the more uniform straight Aβ42 fibrils.

DNA structure and dynamics via transient binding of DNA intercalators

The fluorescence of many DNA intercalating dyes (Flors et al., 2009) is enhanced upon binding to double-stranded DNA; imaging these dyes at the SM level enables binding-activated localization microscopy (BALM) (Schoen et al., 2011). It has been shown that SYTOX orange binds perpendicularly to the axis of λ-DNA (Figure 1f) (Backer et al., 2016), and YOYO-1 dyes exhibit a primary binding mode perpendicular to the DNA axis and a secondary binding mode parallel to the DNA axis (Larsson et al., 1994; Valades Cruz et al., 2016; Mazidi et al., 2019). Therefore, they have been used to resolve tangling, bending, and supercoiling of DNA (Figure 3d) (Hulleman et al., 2021). In contrast to SYTOX orange and YOYO-1, SiR-Hoechst exhibits nonspecific binding orientations due to its flexible four-carbon linker even though Hoechst is directly attached to the DNA strand. Therefore, it is not suitable for SMOLM (Backer et al., 2016).

Studies have shown that the orientation of intercalators can reveal structural differences between B-DNA and mechanically extended S-DNA. Backer et al. demonstrated that when DNA is stretched beyond the overstretching transition, intercalators like YOYO-1 exhibit a significant tilt, with an angle of approximately 54° relative to the S-DNA axis, in contrast to their typical perpendicular orientation (~90°) in B-DNA (Figure 3e) (Backer et al., 2019). This tilting provides the first experimental evidence of inclined base pairs in mechanically stretched DNA, offering a clearer understanding of the S-DNA conformation. However, the authors caution that the precise inclination of S-DNA base pairs might be perturbed by the presence of intercalators.

Lipid membrane structure and composition via transient binding of lipophilic dyes

The manner by which lipophilic probes transiently bind to model and cellular membranes is governed by the chemical environment and the molecular interactions within these complex assemblies. For example, the transition dipole moment of DiI (1,1′-Dioctadecyl-3,3,3′,3′-tetramethylindocarbocyanine perchlorate, DiIC₁₈(3)) bound to DPPC (1,2-Dipalmitoyl-sn-glycero-3-phosphocholine) supported lipid bilayers (SLBs) is oriented parallel to the membrane, as its hydrocarbon chains are incorporated in the nonpolar core while the chromophore headgroup resides in the polar region of the lipid bilayer. In contrast, the orientations of merocyanine 540 (MC540) are mostly perpendicular to a more fluid membrane composed of DOPC (1,2-Dioleoyl-sn-glycero-3-phosphocholine); MC540 also exhibits larger wobble angles in these membranes (Figure 1g) (Lu et al., 2020). Thus, the orientations of transiently bound probes measured via SMOLM reveal the chemical composition and fluidity of nanodomains within both model and cellular membranes.

The orientation spectra of NR molecules are extremely sensitive to the cholesterol concentration within the SLBs; they are confined and perpendicular to the membrane at high cholesterol concentrations and are relatively free to wobble at low cholesterol concentrations along the polar direction (parallel to the lipid acyl chains) (Figure 4a) (Ding and Lew, 2021). This behavior aligns with the “umbrella model” of lipid bilayers, where cholesterol condenses the lipid environment and creates ordered domains that restrict molecular movement. NR-membrane interactions have also facilitated the use of spherical supported lipid bilayers as 3D calibration targets for SMOLM (Wu et al., 2022a; Zhang et al., 2023; Bruggeman et al., 2024). However, its structural analog Nile blue is insensitive to cholesterol concentration within the membrane, emphasizing the importance of properly choosing probes for sensing specific membrane characteristics.

Figure 4. Imaging lipid membranes using SMOLM. (a) Distribution of polar angle ( $ \theta $ ) and wobble angles ( $ \alpha $ along the polar direction and $ \beta $ perpendicular to the polar direction) of Nile red (NR) within DPPC bilayers with and without cholesterol (adapted from Ding and Lew, 2021). (b) SMOLM images of NR before and after successive sphingomyelinase (SMase) treatments reveal compositional changes within the liquid-ordered (Lo) domain and minor changes in domain size and shape during the treatment (adapted from Lu et al., 2020). (c) Nanodomains within SLBs sensed by transiently binding NR molecules using the raPol microscope (adapted from Zhang et al., 2022). (Left) localization density per 100 × 100 nm² in the azimuthally polarized channel; (middle) polar angle $ \theta $ (deg); (right) wobble angle $ \Omega $ (sr). (d) Orientations of Nile red (NR) transiently bound to spherical supported lipid bilayers (SLBs) after a 7-day incubation (left) without and (right) with Aβ42 monomers (adapted from Zhang et al., 2023). Localizations are color-coded by (top) polar angle $ \theta $ (deg) and (bottom) wobble angle $ \Omega $ (sr). All images are lateral (xy) views unless otherwise marked. (e) SMOLM images of an HEK-293T cell. Localizations are (left) color-coded by and (right) oriented along azimuthal angle $ \phi $ (deg). (Right) Zoomed image of the boxed region at left, color-coded by wobble angle $ \Omega $ (sr). The inset histogram shows the distribution of the measured wobble angle within the regions marked by yellow and white boxes (adapted from Zhang et al., 2023).

SMOLM has been used to study enzyme-induced reorganization of lipid domains. For instance, Lu et al. visualized the restructuring of lipid domains by sphingomyelinase (SMase), an enzyme that catalyzes the hydrolysis of sphingomyelin into ceramide by measuring the orientation spectra of NR and MC540 (Figure 4b) (Lu et al., 2020). Upon the addition of SMase, membrane composition shifted as ceramide formed and reorganized the structure. A dose-dependent disappearance of cholesterol-rich liquid-ordered domains was observed, and these regions were replaced by ceramide-rich domains.

Zhang et al. recently reported simultaneous ordering and damage of a lipid bilayer caused by cholesterol-loaded methyl-β-cyclodextrin via tracking the orientations and positions of single NR molecules transiently bound to DPPC SLBs (Figure 4c) (Zhang et al., 2022). The study revealed that while cholesterol deposition reduces NR’s rotational diffusion, MβCD-chol somewhat counter-intuitively increases translational motions within the membrane as it nonuniformly dissolves the SLB. Therefore, SMOLM’s ability to measure rotations and positions simultaneously yields insights into complex changes in membrane structure that cannot be quantified via traditional single-particle tracking or polarization anisotropy alone.

SMOLM with NR has also been applied to study complex membrane-amyloid interactions with single-molecule sensitivity. Zhang et al. demonstrated that when amyloid aggregates infiltrate lipid membranes, they significantly change the rotational dynamics of NR molecules. Specifically, NR exhibited increased wobble angles in regions infiltrated by amyloid aggregates compared to those in pure DPPC SLBs. Further, the study found that Aβ42 aggregates interacting with lipid membranes tend to form smaller assemblies, such as oligomers and protofibrils, rather than fully developed fibrils (Figure 4d).

Such dye-membrane interactions are not limited to model systems. For example, SMOLM has revealed diverse binding modes of MC540 on cell membranes, influenced by several factors including membrane tension, fluidity, and potential (Zhang et al., 2023). Imaging the wobble angle of MC540 reveals that the rigidity of the coverslip reduces membrane fluidity near the cell-coverslip interface, while lipids at the tip of a membrane protrusion are more fluid than those in surrounding regions (Figure 4e).

Other labeling strategies and applications

SMs embedded within polymer films can also be used to detect architectural changes and mechanical fractures since rotational motions are sometimes more sensitive to these changes compared to translational motions. Early SM orientation measurements used defocused imaging to map the orientations of dye molecules at various positions within dendrimers and below and above the glass transition temperature of the host material (Melnikov et al., 2007; Dedecker et al., 2009; Zheng et al., 2010; Ham et al., 2014; Paeng and Kaufman, 2016). More recently, researchers have used SMOLM to detect the nanoscale softening (Zhang et al., 2018) and deformation (Krause et al., 2016; Wang et al., 2019) of polymer matrices as fluorophore orientations change.

Besides SMs, the orientations of luminescent and scattering nanoparticles can also be resolved by imaging systems. For example, quantum nanorods are much brighter probes compared to typical fluorescent molecules and have been used for studying the force-generating mechanism of dynein molecules (Lippert et al., 2017). Tracking the orientation and position of gold nanorods using scattering light has been shown to achieve sub-millisecond temporal resolution (Beckwith and Yang, 2021) as the number of signal photons is no longer limited by photobleaching. However, since the size of typical quantum rods is 10 or 100 times compared to that of organic fluorophores, SMOLM is generally a less perturbative choice for studying biochemical processes. A similar concept to SMOLM has also been implemented in optically detected magnetic resonance imaging using nitrogen-vacancy centers in diamonds (Backlund et al., 2017).

Choosing the appropriate labeling strategy for SMOLM

The advantages and limitations of various labeling strategies, along with their applications, are summarized in Table 1. It is important to note that any exogenous probe can introduce perturbations to the biophysical structure or process under study. For instance, SYTOX orange DNA intercalators (Figure 1f), which increase quantum yield upon binding to DNA, may trap non-canonical conformations such as unstacked flanking bases upon interacting with the biomolecular surface (Biebricher et al., 2015; Kolbeck et al., 2024). Such alterations in local DNA structure can affect the conformational dynamics of the system and potentially influence the orientation data obtained through SMOLM. These perturbative effects, which may also occur with other intercalating dyes, must be carefully considered when interpreting results. Similarly, internal labeling strategies using Cy3 and Cy5 dyes (Figure 1c) can disturb local DNA conformation by replacing nucleotides within the backbone, leading to structural disorder and rapid orientational dynamics of the probe. A recent study using polarization-sensitive fluorescence microscopy has shown that Cy3 labeled single-stranded-double-stranded DNA junctions undergo significant conformational changes depending on the position and temperature (Heussman et al., 2022), and Maurer et al. further demonstrated that DNA “breathing” at these junctions can shift between multiple conformational macrostates (Maurer et al., 2023). Fluorescent dyes can also perturb peptide aggregates; Sun et al. used the photo-oxidation of thioflavin T, a common amyloidophilic dye, to induce growth, depolymerization, and remodeling within Aβ42 fibrils (Figure 2e) (Sun et al., 2024). Therefore, control experiments are essential to quantify the extent of dye-induced perturbations and to ensure reliable interpretation of SMOLM data.

When selecting probe-labeling strategies for SMOLM, it is important to balance the need for site-specific information with the risk of structural disruption. Covalent labeling offers precise control over fluorophore orientation relative to the attachment site (Budiarta et al., 2024) and can provide valuable insights into the conformational dynamics of protein domains. However, rigidly attaching a fluorophore to a target protein domain with a high yield may interfere with function or may not be feasible, depending on the domain’s inherent flexibility. On the other hand, transient binding approaches mitigate these issues by avoiding high concentrations of covalently bound fluorophores; this method allows for temporary, low-concentration interactions of the dye with the target system, thereby reducing the number of labeled molecules compared to conventional labeling strategies. However, precise targeting of transiently binding probes to specific protein domains remains a challenge (Steen et al., 2024). As is the case with SMLM, proper choice of the labeling strategy is essential for ensuring useful and robust orientation measurements with minimal perturbation in SMOLM.

Interaction between light and fluorescent molecules

In this section, we introduce how light interacts with fluorescent molecules (Valeur, 2002; Novotny and Hecht, 2012). A photon from an optical field may be absorbed by a molecule, resulting in an electronic state transition from the singlet ground state $ {S}_0 $ , i.e., the highest occupied molecular orbital, to various vibrational levels of the singlet excited state $ {S}_1 $ , i.e., the lowest unoccupied molecular orbital. After a fast vibrational relaxation (typically on the order of a few picoseconds), the molecule decays to the lowest energy level of $ {S}_1 $ . After a few nanoseconds, i.e., the fluorescence or excited-state lifetime, the molecule returns to a vibrationally excited state of $ {S}_0 $ by emitting a red-shifted fluorescence photon with lower energy. The molecule may also lose its energy via nonradiative relaxation such as vibration and collision and return to the ground state, which reduces the number of photons emitted. Therefore, the quality of a molecule as a fluorophore is measured by its quantum yield (Valeur, 2002)

(1) $$ {\eta}_{\mathrm{q}}=\frac{\gamma_{\mathrm{r}}}{\gamma_{\mathrm{r}}+{\gamma}_{\mathrm{nr}}}, $$

where $ {\gamma}_{\mathrm{r}} $ is the fluorescence rate and $ {\gamma}_{\mathrm{nr}} $ is the nonradiative relaxation rate; molecules with a quantum yield above 10% are usually considered quite fluorescent. Some widely-used fluorophores in single-molecule imaging, e.g., NR (Kucherak et al., 2010) and Rhodamine 6G (Fischer and Georges, 1996), may exhibit a quantum yield of >90% depending on the local environment (Li and Vaughan, 2018; Jradi and Lavis, 2019).

When a molecule is in the excited state $ {S}_1 $ , it may also undergo intersystem crossing due to spin-orbital coupling and enter a long-lived (microseconds to seconds) and reactive triplet state $ {T}_1 $ . Upon entering this state, the molecule cannot undergo repeated absorption and emission cycles; it appears to go dark. From the triplet state $ {T}_1 $ , the molecule may return to $ {S}_0 $ via phosphorescence or nonradiative relaxation. It may also undergo chemical reactions with singlet oxygen and other reactive oxygen species and permanently lose its ability to fluoresce. This process is termed photobleaching, which fundamentally limits the number of photons emitted by a fluorescent molecule and is determined by the intrinsic photophysics and photochemistry of the fluorophore (Cordes et al., 2011; Ha and Tinnefeld, 2012; Gust et al., 2014). The total number of photons emitted by an SM may be increased by decreasing the photobleaching rate via quenching the triplet state, e.g., using photostabilizers, reducing or oxidizing agents, and oxygen-scavenging systems (Rasnik et al., 2006; Aitken et al., 2008; Vogelsang et al., 2008; Dave et al., 2009; Hoffman et al., 2011; Lee et al., 2013; Nahidiazar et al., 2016; Glembockyte et al., 2016; Sauer and Heilemann, 2017), or enhancing the emission rate using plasmonic nanoantennas (Kinkhabwala et al., 2009; Wientjes et al., 2016; Kaminska et al., 2018; Grabenhorst et al., 2020). However, one must note that these methods could potentially perturb the imaging targets themselves (Tosheva et al., 2020). In addition, nearby plasmonic nanoparticles will also distort the image of each fluorophore (Lim et al., 2016; Raab et al., 2017; Goldwyn et al., 2018; Zuo et al., 2019; Bloksma and Zijlstra 2021; Zuo et al., 2021; Moon et al., 2023; Huijben et al., 2024), compared to typical dipolar emission.

The orientation of fluorescent molecules relative to the applied optical field affects how they interact. Briefly, we may describe the interaction between a charge-neutral nanoparticle with an optical field by writing the multipolar interaction Hamiltonian (Novotny and Hecht, 2012)

(2) $$ {\displaystyle \begin{array}{c}H={\boldsymbol{p}}_e\cdotp \boldsymbol{E}-{\boldsymbol{p}}_m\cdotp \boldsymbol{B}-\left[\boldsymbol{Q}\nabla \right]\cdotp \boldsymbol{E}-\dots, \end{array}} $$

where vectors $ {\boldsymbol{p}}_e $ and $ {\boldsymbol{p}}_m $ represent the total electric and magnetic dipole moments, respectively, the matrix $ \boldsymbol{Q} $ represents the electric quadrupole moment, $ \boldsymbol{E} $ and $ \boldsymbol{B} $ represent the electric and magnetic fields, respectively, and $ {\boldsymbol{p}}_e\cdotp \boldsymbol{E}={\boldsymbol{p}}_e^{\top}\boldsymbol{E} $ represents the dot or inner product between vectors $ {\boldsymbol{p}}_e $ and $ \boldsymbol{E} $ . For typical SM imaging experiments where both illumination and emission are manipulated in the far-field, the magnetic dipole and electric quadrupole interactions are orders of magnitude weaker compared to the electric dipole interaction. Therefore, we describe the photon absorption and emission processes using only the electric dipole moments.

The transition dipole moment is the electric dipole moment associated with the transition between two quantum states. The absorption dipole moment describes the transition between initial state $ {S}_0 $ and final state $ {S}_1 $ ; the emission dipole moment describes the transition between initial state $ {S}_1 $ and final state $ {S}_0 $ . Here, we omit the amplitude and only describe the orientation of a transition dipole using a unit vector (Figure 5a)

(3) $$ {\displaystyle \begin{array}{c}\boldsymbol{\mu} ={\left[\begin{array}{ccc}{\mu}_x& {\mu}_y& {\mu}_z\end{array}\right]}^{\top }={[\begin{array}{ccc}\sin \theta \cos \phi & \sin \theta \sin \phi & \cos \theta \end{array}]}^{\top },\end{array}} $$

where $ z $ represents the direction of the optical axis. Note that due to the two-fold degeneracy of a dipole moment, this unit vector is defined over a unit hemisphere. We only consider linear dipoles here; chirality may be modeled as a coherent superposition of multiple linear dipoles with spatial phase differences (Cyphersmith et al., 2011). Fundamentally, the orientation of the transition dipole moment $ \boldsymbol{\mu} $ determines how the molecule interacts with the polarization of the optical field.

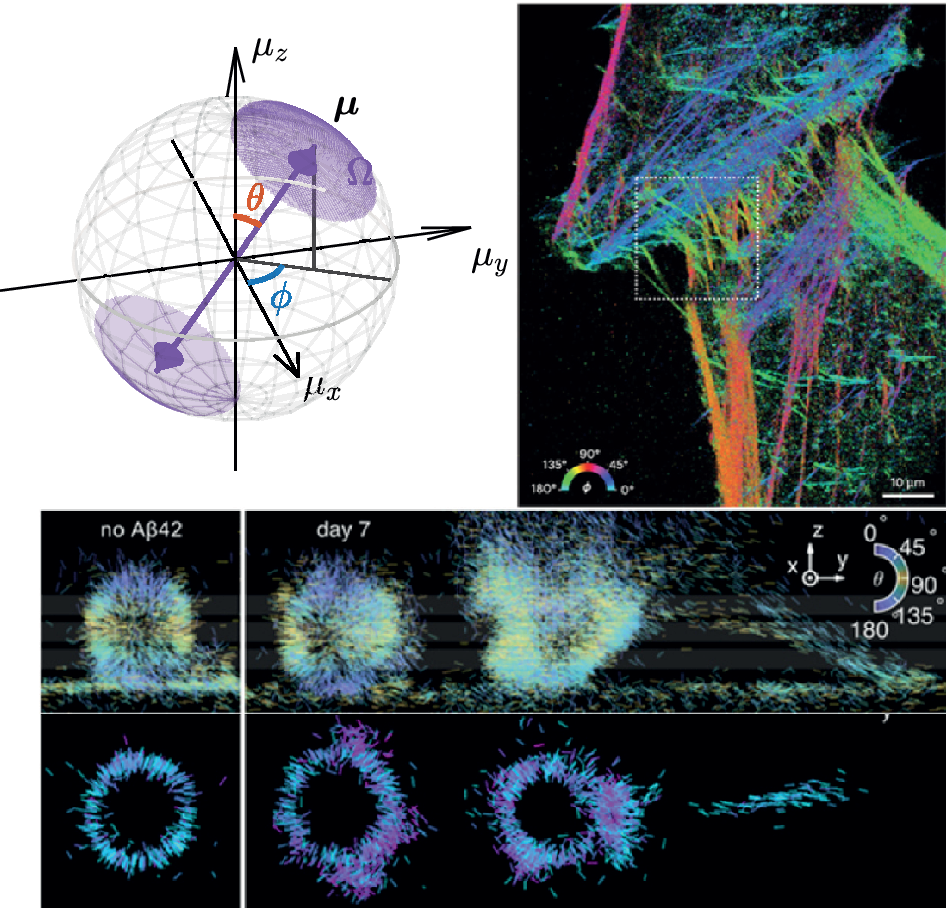
Figure 5. (a) Molecular orientation represented by a unit vector $ \boldsymbol{\mu} ={\left[{\mu}_x,{\mu}_y,{\mu}_z\right]}^{\top }={\left[\sin \theta \cos \phi, \sin \theta \sin \phi, \cos \theta \right]}^{\top } $ . The wobble is modeled as a hard-edged cone with cone solid angle $ \Omega $ . (b) Excitation light in typical SMOLM. A Kohler lens (KL) is used to produce a collimated illumination beam above the objective lens (OL). The absorption probability is a function of the angle between the absorption dipole moment $ {\boldsymbol{\mu}}_{\mathrm{abs}} $ and the excitation optical field $ {\boldsymbol{E}}_{\mathrm{ex}} $ (green arrows). The absorption probability is maximized if $ {\boldsymbol{\mu}}_{\mathrm{abs}} $ is parallel to $ {\boldsymbol{E}}_{\mathrm{ex}} $ . Colorbar: normalized absorption probability. (c) Depolarization, i.e., a non-zero angle between $ {\boldsymbol{\mu}}_{\mathrm{abs}} $ and $ {\boldsymbol{\mu}}_{\mathrm{em}} $ caused by rotation during the fluorescence lifetime between the absorption and emission events. (d) Depolarization caused by energy transfer between chromophores of a YOYO-1. (e,f) Anisotropic rotational diffusion models for SMs. (e) Cone half angles $ \alpha $ and $ \beta $ represent the area within which the molecule can wobble, and (f) $ \psi $ describes the preferred direction of the wobble.

Absorption dipole moments

We now briefly introduce a model for light absorption by an SM. The transition dipole moment can be described as a quantum mechanical state transition, given by

(4) $$ {\displaystyle \begin{array}{c}{\boldsymbol{\mu}}_{\mathrm{abs}}=\left\langle {\psi}_1\right|q\boldsymbol{r}\left|{\psi}_0\right\rangle =q\iiint {\psi}_1{\left(\boldsymbol{r}\right)}^{\ast}\;\boldsymbol{r}\;{\psi}_0\left(\boldsymbol{r}\right)\;{d}^3\boldsymbol{r},\end{array}} $$

where $ q $ represents the charge and $ \boldsymbol{r} $ represents its position. Kets $ \left|{\psi}_0\right\rangle $ and $ \left|{\psi}_1\right\rangle $ represent the states associated with ground state $ {S}_0 $ and excited state $ {S}_1 $ , respectively. According to Fermi’s golden rule (Shankar, 2012), the SM’s rate of transition from $ {S}_0 $ to $ {S}_1 $ in the presence of excitation field $ {\boldsymbol{E}}_{\mathrm{ex}}={\left[{E}_x,{E}_y,{E}_z\right]}^{\top } $ is given by (Figure 5b)

(5) $$ {\displaystyle \begin{array}{c}{P}_{\mathrm{abs}}\propto {\left|\left\langle {\psi}_1\right|{\boldsymbol{E}}_{\mathrm{ex}}\cdotp \boldsymbol{r}\left|{\psi}_0\right\rangle \right|}^2\propto {\left|{\boldsymbol{E}}_{\mathrm{ex}}\cdotp {\boldsymbol{\mu}}_{\mathrm{abs}}\right|}^2.\end{array}} $$

A molecule at its ground state $ {S}_0 $ is more likely to absorb an incident photon if the polarization of the photon is parallel to the absorption dipole moment $ {\boldsymbol{\mu}}_{\mathrm{abs}} $ . In contrast, the absorption probability is zero if the absorption dipole moment is perpendicular to the polarization of the local electric field $ {\boldsymbol{E}}_{\mathrm{ex}} $ .

Emission dipole moments

Suppose a molecule with an emission dipole moment of $ {\boldsymbol{\mu}}_{\mathrm{em}} $ located at $ \boldsymbol{r}={\left[0,0,0\right]}^{\top } $ relaxes from excited state $ {S}_1 $ to ground state $ {S}_0 $ and emits a photon. The classical far-field emission at position $ {\boldsymbol{r}}_{\mathrm{ff}} $ can be found by solving the electromagnetic wave equation for an oscillating dipole source (Novotny and Hecht, 2012), yielding (Figure 6a)

(6) $$ {\displaystyle \begin{array}{c}{\boldsymbol{E}}_{\mathrm{ff}}={c}_{\mathrm{ff}}{\hat{\boldsymbol{r}}}_{\mathrm{ff}}\times \left({\boldsymbol{\mu}}_{\mathrm{em}}\times {\hat{\boldsymbol{r}}}_{\mathrm{ff}}\right)={c}_{\mathrm{ff}}\left(\unicode{x1D540}-{\hat{\boldsymbol{r}}}_{\mathrm{ff}}{\hat{\boldsymbol{r}}}_{\mathrm{ff}}^{\top}\right){\boldsymbol{\mu}}_{\mathrm{em}},\end{array}} $$

where the unit vector

(7) $$ {\displaystyle \begin{array}{c}{\hat{\boldsymbol{r}}}_{\mathrm{ff}}=\frac{{\boldsymbol{r}}_{\mathrm{ff}}}{\left|{\boldsymbol{r}}_{\mathrm{ff}}\right|}={[\begin{array}{ccc}\sin {\theta}_{\mathrm{ff}}\cos {\phi}_{\mathrm{ff}}& \sin {\theta}_{\mathrm{ff}}\sin {\phi}_{\mathrm{ff}}& \cos {\theta}_{\mathrm{ff}}\end{array}]}^{\top}\end{array}} $$

represents the viewing direction, $ {c}_{\mathrm{ff}} $ is a normalization factor, $ \unicode{x1D540} $ represents the identity matrix, and $ {\hat{\boldsymbol{r}}}_{\mathrm{ff}}{\hat{\boldsymbol{r}}}_{\mathrm{ff}}^{\top } $ represents the outer product of $ {\hat{\boldsymbol{r}}}_{\mathrm{ff}} $ with itself. Therefore,

(8) $$ {\displaystyle \begin{array}{c}{I}_{\mathrm{ff}}={\left|{\boldsymbol{E}}_{\mathrm{ff}}\right|}^2\propto \left({\boldsymbol{\mu}}_{\mathrm{em}}-{\hat{\boldsymbol{r}}}_{\mathrm{ff}}{\hat{\boldsymbol{r}}}_{\mathrm{ff}}^{\top }{\boldsymbol{\mu}}_{\mathrm{em}}\right)\cdotp \left({\boldsymbol{\mu}}_{\mathrm{em}}-{\hat{\boldsymbol{r}}}_{\mathrm{ff}}{\hat{\boldsymbol{r}}}_{\mathrm{ff}}^{\top }{\boldsymbol{\mu}}_{\mathrm{em}}\right)=1-{\left({\hat{\boldsymbol{r}}}_{\mathrm{ff}}\cdotp {\boldsymbol{\mu}}_{\mathrm{em}}\right)}^2,\end{array}} $$

Figure 6. Schematic diagram of dipole emitters (a) within a medium of matched RI and (b) near the RI interface between the sample ( $ {n}_2 $ ) and lens immersion medium ( $ {n}_1 $ ). The objective lens captures a pseudo-spherical wave ( $ {\boldsymbol{E}}_{\mathrm{ff}} $ and $ {\boldsymbol{E}}_{\mathrm{ff},3} $ ) and converts it to a pseudo-plane wave ( $ {\boldsymbol{E}}_{\mathrm{BFP}} $ ). Useful unit vectors, angles, and lengths for the derivation in this section are labeled in the figure. (c) Positions of a dipole emitter relative to the RI interface ( $ {z}_{\mathrm{SM}} $ ) and the nominal focal plane ( $ {z}_f $ ). (d-f) Representative intensity distributions at the BFP for SMs with orientations of (i) $ \theta ={0}^{\circ } $ , (ii) $ \left[\theta, \phi \right]=\left[{45}^{\circ },{90}^{\circ}\right] $ , and (iii) $ \left[\theta, \phi \right]=\left[{90}^{\circ },{90}^{\circ}\right] $ when (d) the sample RI matches that of the lens immersion medium (1.515) and when the sample RI is (e) $ {n}_2=1.33 $ and (f) $ {n}_2=1 $ . The numerical aperture is $ \mathrm{NA}=1.4 $ . Colorbar: normalized intensity.

i.e., the fluorescence intensity has a sine-square dependence on the angle between the molecular orientation $ {\boldsymbol{\mu}}_{\mathrm{em}} $ and viewing direction $ {\hat{\boldsymbol{r}}}_{\mathrm{ff}} $ . In addition, optical field is always perpendicular to the propagation direction, i.e.,

(9) $$ {\displaystyle \begin{array}{c}{\hat{\boldsymbol{r}}}_{\mathrm{ff}}\cdotp {\boldsymbol{E}}_{\mathrm{ff}}\propto {\hat{\boldsymbol{r}}}_{\mathrm{ff}}\cdotp {\boldsymbol{\mu}}_{\mathrm{em}}-{\hat{\boldsymbol{r}}}_{\mathrm{ff}}^{\top }{\hat{\boldsymbol{r}}}_{\mathrm{ff}}\;{\hat{\boldsymbol{r}}}_{\mathrm{ff}}^{\top }{\boldsymbol{\mu}}_{\mathrm{em}}=0.\end{array}} $$

Note that even though both the absorption and emission dipole moments can be used for measuring the orientation of fluorescent molecules, they are not necessarily parallel to each other. Depolarization between the absorption and emission dipoles can be quantified by measuring fluorescence anisotropy (see next section for detailed discussion). The relationship between the fluorescence lifetime and rotational correlation time determines how far the molecule may rotate between an absorption and an emission event. A molecule’s emission dipole moment $ {\boldsymbol{\mu}}_{\mathrm{em}} $ is decoupled from its absorption dipole moment $ {\boldsymbol{\mu}}_{\mathrm{abs}} $ when the molecule’s rotation is much faster compared to its fluorescence lifetime (Lew et al., 2013; Backlund et al., 2014; Stallinga, 2015), which is typical for SMs in liquids. The correlation between $ {\boldsymbol{\mu}}_{\mathrm{em}} $ and $ {\boldsymbol{\mu}}_{\mathrm{abs}} $ becomes prominent when the rotational correlation time is comparable to the lifetime, e.g, when molecules are embedded within dense lipid membranes (Halder et al., 2018). Even for molecules that are immobilized within rigid substrates like polymer matrices, it is reported that these two vectors may exhibit an inclination angle of more than 20° from each other (Karedla et al., 2015) due to the interactions between molecular orbitals and the chemical environment, and the possibility of relaxation into energy states other than $ {S}_0 $ .

Methods for measuring the orientation of fluorescent molecules

Many methods have been developed to measure the orientation of fluorescent molecules (Rosenberg et al., 2005; Backlund et al., 2014). For example, one can simply add a polarizing beamsplitter (PBS) to a widefield microscope and measure linear dichroism (LD), given by

(10) $$ {\displaystyle \begin{array}{c} LD=\frac{\sum {I}_x-\sum {I}_y}{\sum {I}_x+\sum {I}_y},\end{array}} $$

where $ \sum {I}_x $ and $ \sum {I}_y $ represent the total numbers of $ x $ - and $ y $ -polarized emission photons detected. The LD value is an implicit measure of emitter orientation. Further, it has been shown that the rotational mobility of an SM can be determined using the temporal autocorrelation of the LD value (fluorescence anisotropy correlation) (Zondervan et al., 2007). Testa et al. combined SMLM with polarization-sensitive fluorescence detection, showing that 2D histograms of x- and y-polarized fluorescence can reveal the rotational mobility of molecules, as demonstrated in living mammalian cells (Testa et al., 2008). However, despite its simplicity, LD suffers from orientational degeneracy, i.e., multiple molecular orientations produce the same LD value, e.g., zero in the cases of $ \boldsymbol{\mu} ={\left[\pm 1/\sqrt{2},\pm 1/\sqrt{2},0\right]}^{\top } $ and $ \boldsymbol{\mu} ={\left[0,0,1\right]}^{\top } $ . Increasing inclinations out of the xy-plane and increasing wobble also produce LD values closer to zero. To overcome these limitations, one can either manipulate the polarization and/or phase of the collected fluorescence photons (Fourkas, 2001; Rimoli et al., 2022) or measure the response of an emitter to various excitation polarizations over time (Forkey et al., 2003; Beausang et al., 2013; Backer et al., 2019), similar to measuring the polarization of scattered light under various illumination polarizations (Beckwith and Yang, 2021).

Another parameter associated with molecular orientation is fluorescence anisotropy, typically denoted by $ r $ (not to be confused with position $ \boldsymbol{r} $ ) (Harms et al., 1999; Gradinaru et al., 2010). When a molecule is excited by linearly polarized light, fluorescence intensities collected along polarization directions parallel and orthogonal to the illumination are denoted $ {I}_{\parallel } $ and $ {I}_{\perp } $ , respectively. The fluorescence anisotropy, given by $ r=\left({I}_{\parallel }-{I}_{\perp}\right)/\left({I}_{\parallel }+2{I}_{\perp}\right) $ , quantifies the degree of rotation a molecule undergoes between absorption and emission. Although the orientation of a molecule cannot be directly measured, anisotropy is extremely sensitive to the rotation of the molecule. An anisotropy value of 0 indicates random emission polarization and free rotational motion, whereas an anisotropy value of 1 represents completely polarized emission from a rotationally fixed emitter. Gould et al. demonstrated (P)-FPALM, a method for simultaneously imaging the positions and anisotropies of single molecules under linearly polarized excitation light, enabling the study of molecular orientations within biological structures, such as mouse fibroblasts expressing Dendra2-actin or Dendra2-hemagglutinin (Gould et al., 2008).

A more sophisticated method for measuring molecular orientation involves measuring Stokes parameters (Alonso, 2023), e.g., by using a camera with an integrated polarizer above each pixel (Bruggeman et al., 2024) or by using a specific configuration of waveplates and polarizing beamsplitters (Mehta et al., 2016; Rimoli et al., 2022). Conventionally, the Stokes parameter $ {s}_0 $ characterizes light intensity, while $ {s}_1 $ through $ {s}_3 $ ( $ {s}_8 $ for 3D Stokes parameters) describes light polarization. The degree of linear polarization (DoLP) and angle of linear polarization (AoLP) can be computed using (Bruggeman et al., 2024)

$$ \mathrm{DoLP}=\sqrt{\frac{s_1^2+{s}_2^2}{s_0^2}}\hskip0.6em \mathrm{and} $$

(11) $$ {\displaystyle \begin{array}{c}\mathrm{AoLP}=\frac{1}{2}{\tan}^{-1}\left(\frac{s_2}{s_1}\right),\end{array}} $$

where DoLP is determined by the polar angle $ \theta $ , and AoLP is equal to the azimuthal angle $ \phi $ . Further, there is an analogy between describing light polarization, which spans from linearly polarized to unpolarized, and the rotational dynamics of a molecule, which can be either fixed in a specific orientation or freely rotating. See “Modeling the rotational diffusion of fluorescent molecules” for more details.

In this section, we introduce two major categories of orientation-measurement methods: modulating the polarization of excitation light and detecting the polarization of the emitted fluorescence to measure the absorption dipole moment and modulating fluorescence emission to measure the emission dipole moment. As noted previously, although we classify these methods into absorption and emission-based, these two dipole moments are often coupled in practical experiments. In particular, the alignment of polarized excitation light with the absorption dipole moments can introduce a selection bias, thereby altering the observed distribution of emission dipole moments (Zhang et al., 2022; Munger et al., 2023), especially for slowly rotating molecules.

Excitation polarization modulation and polarization-sensitive detection were combined

The principle of measuring the orientation of the absorption dipole moment $ {\boldsymbol{\mu}}_{\mathrm{abs}} $ using excitation modulation is as described by Eq. (5); an $ x $ -oriented molecule is most likely to absorb an $ x $ -polarized photon, and it is impossible for it to absorb a $ y $ - or $ z $ -polarized photon. The analogous statements are true for other polarization-orientation combinations.

Here, we denote $ {\boldsymbol{\mu}}_{\mathrm{abs}} $ by $ \boldsymbol{\mu} $ for simplicity. An SM is excited sequentially using illumination light of $ N $ unique polarizations $ {\boldsymbol{E}}_1,\dots, {\boldsymbol{E}}_N $ . The expected total number of photons $ {I}_i $ , with $ i\in \left\{1,2,\dots, N\right\} $ , detected from an SM excited by electric field polarization $ {\boldsymbol{E}}_i $ is given by

(12) $$ {\displaystyle \begin{array}{c}{I}_i\propto {\left|\left[\begin{array}{ccc}{E}_{x,i}& {E}_{y,i}& {E}_{z,i}\end{array}\right]{\left[\begin{array}{ccc}{\mu}_x& {\mu}_y& {\mu}_z\end{array}\right]}^{\top}\right|}^2\\ {}=\left[\begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}{\left|{E}_{x,i}\right|}^2& {\left|{E}_{y,i}\right|}^2\end{array}& {\left|{E}_{z,i}\right|}^2& 2\operatorname{Re}\left\{{E}_{x,i}^{\ast }{E}_{y,i}\right\}\end{array}& 2\operatorname{Re}\left\{{E}_{x,i}^{\ast }{E}_{z,i}\right\}& 2\operatorname{Re}\left\{{E}_{y,i}^{\ast }{E}_{z,i}\right\}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{\mu}_x^2\\ {}{\mu}_y^2\\ {}{\mu}_z^2\end{array}\\ {}\begin{array}{c}{\mu}_x{\mu}_y\\ {}{\mu}_x{\mu}_z\\ {}{\mu}_y{\mu}_z\end{array}\end{array}\right].\end{array}} $$

Since each absorption and emission event arises from a specific molecular orientation $ \boldsymbol{\mu} $ at time $ t $ , any intensity measured using a photon-counting detector can be written as a temporal average over the acquisition interval $ T $ . Therefore, we define the second-order moments $ \boldsymbol{m}={\left[{m}_{xx},{m}_{yy},{m}_{zz},{m}_{xy},{m}_{xz},{m}_{yz}\right]}^{\top } $ of the transition dipole as

(13) $$ {\displaystyle \begin{array}{c}{m}_{ij}=\frac{1}{T}{\int}_0^T{\mu}_i{\mu}_j\mathrm{d}t,\hskip0.84em i,j\in \left\{x,y,z\right\}.\end{array}} $$

Further, assuming ergodicity, $ {m}_{ij} $ can also represent a corresponding average in orientation space. The forward imaging model is, therefore, given by

(14) $$ {\displaystyle \begin{array}{c}\boldsymbol{I}=s\left[\begin{array}{c}\begin{array}{c}{I}_1\\ {}{I}_2\end{array}\\ {}\begin{array}{c}\vdots \\ {}{I}_N\end{array}\end{array}\right]\\ {}=s\left[\begin{array}{cc}\begin{array}{ccc}{\left|{E}_{x,1}\right|}^2& {\left|{E}_{y,1}\right|}^2& {\left|{E}_{z,1}\right|}^2\\ {}{\left|{E}_{x,2}\right|}^2& {\left|{E}_{y,2}\right|}^2& {\left|{E}_{z,2}\right|}^2\end{array}& \begin{array}{ccc}2\operatorname{Re}\left\{{E}_{x,1}^{\ast }{E}_{y,1}\right\}& 2\operatorname{Re}\left\{{E}_{x,1}^{\ast }{E}_{z,1}\right\}& 2\operatorname{Re}\left\{{E}_{y,1}^{\ast }{E}_{z,1}\right\}\\ {}2\operatorname{Re}\left\{{E}_{x,2}^{\ast }{E}_{y,2}\right\}& 2\operatorname{Re}\left\{{E}_{x,2}^{\ast }{E}_{z,2}\right\}& 2\operatorname{Re}\left\{{E}_{y,3}^{\ast }{E}_{z,3}\right\}\end{array}\\ {}\begin{array}{ccc}\vdots & \vdots & \vdots \\ {}{\left|{E}_{x,N}\right|}^2& {\left|{E}_{y,N}\right|}^2& {\left|{E}_{z,N}\right|}^2\end{array}& \begin{array}{ccc}\vdots & \vdots & \vdots \\ {}2\operatorname{Re}\left\{{E}_{x,N}^{\ast }{E}_{y,N}\right\}& 2\operatorname{Re}\left\{{E}_{x,N}^{\ast }{E}_{z,N}\right\}& 2\operatorname{Re}\left\{{E}_{y,N}^{\ast }{E}_{z,N}\right\}\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{m}_{xx}\\ {}{m}_{yy}\\ {}{m}_{zz}\end{array}\\ {}\begin{array}{c}{m}_{xy}\\ {}{m}_{xz}\\ {}{m}_{yz}\end{array}\end{array}\right],\end{array}} $$

where $ s $ is the brightness scaling factor.

In the special case where the SMs are only excited by collimated epifluorescence illumination along the $ z $ direction (optical axis) (Backer et al., 2016), the $ z $ -polarized component $ {E}_{z,i}=0,\forall i $ . This excitation method is only sensitive to the normalized projection of the orientational second moments into the $ xy $ plane, as given by

(15) $$ {\displaystyle \begin{array}{c}{\zeta}_{ij}=\frac{1}{T}{\int}_0^T{\zeta}_i{\zeta}_j dt\hskip0.48em i,j\in \left\{x,y\right\},\end{array}} $$

where

(16) $$ {\displaystyle \begin{array}{c}{\zeta}_i=\frac{\mu_i}{\sqrt{\mu_x^2+{\mu}_y^2}}\hskip0.48em i\in \left\{x,y\right\}.\end{array}} $$

The forward imaging model is simplified as

(17) $$ {\displaystyle \begin{array}{c}I=s\left[\begin{array}{c}\begin{array}{ccc}{\left|{E}_{x,1}\right|}^2& {\left|{E}_{y,1}\right|}^2& 2\operatorname{Re}\left\{{E}_{x,1}^{\ast }{E}_{y,1}\right\}\\ {}{\left|{E}_{x,2}\right|}^2& {\left|{E}_{y,2}\right|}^2& 2\operatorname{Re}\left\{{E}_{x,2}^{\ast }{E}_{y,2}\right\}\end{array}\\ {}\begin{array}{ccc}\vdots & \vdots & \vdots \\ {}{\left|{E}_{x,N}\right|}^2& {\left|{E}_{y,N}\right|}^2& 2\operatorname{Re}\left\{{E}_{x,N}^{\ast }{E}_{y,N}\right\}\end{array}\end{array}\right]\left[\begin{array}{c}{\zeta}_{xx}\\ {}{\zeta}_{yy}\\ {}{\zeta}_{xy}\end{array}\right].\end{array}} $$

Using a series of fluorescence images obtained from varying angles of in-plane polarized excitation, achieved by continuously rotating a half-wave plate, Zhanghao et al. demonstrated super-resolution dipole orientation mapping in both fixed and live cells (Zhanghao et al., 2016). With three in-plane excitation polarizations that are 60° apart, Backer et al. achieved precisions of 2.5° for the azimuthal angle $ \phi $ and 22 nm for lateral localization with 8424 signal photons and 158 background photons detected per pixel (Backer et al., 2016).

Note that even though solving the inverse problem associated with Eqs. (14) and (17) is computationally cheap, the main challenge using excitation modulation is that each SM needs to remain in the emissive state with a stable orientation for at least $ N $ sequential frames. One must also ensure that $ {\boldsymbol{E}}_i $ is well known via careful calibration to obtain accurate measurements (Thorsen et al., 2022).

Another challenge of measuring the 3D orientation without measurement degeneracy using the method in Eq. (14) is the complex optical setup required for 3D polarization modulation (Thorsen et al., 2022). One method to overcome this challenge is to combine in-plane excitation polarization modulation [Eq. (17)] with polarized detection. Compared to only using LD [Eq. (10)], the addition of using x- and y-polarized excitation eliminates some measurement degeneracies. For example, the LD values for a rotationally fixed molecule with an orientation of $ \boldsymbol{\mu} ={\left[1/\sqrt{2},1/\sqrt{2},0\right]}^{\top } $ and a freely wobbling molecule are both zero for unpolarized/circularly polarized excitation. In contrast, the LD value for an isotropic emitter is positive under x-polarized excitation and negative under y-polarized excitation, while the LD values are both zero for the fixed molecule under x- and y-polarized excitation. This method was recently used for measuring the structure of S-DNA (Backer et al., 2019). One can further increase the number of excitation and/or detection polarizations used to eliminate all orientation degeneracies. For example, 8 excitation polarizations and 2 detection polarizations were used to image the walking mechanics of Myosin V (Beausang et al., 2013). Note that since the detected intensities using this method are functions of both the absorption and emission dipole moments, any depolarization, e.g., intramolecular or intermolecular energy transfer (Figure 5c) (Carlsson et al., 1994), bending of the fluorescent molecule’s backbone due to environmental interactions (Karedla et al., 2015), or rotation during the fluorescence lifetime (Figure 5d), may affect or bias the orientation and wobble measurements (Backer et al., 2019).

Another advantage of excitation polarization modulation is its compatibility with imaging modalities beyond SMOLM. A recently introduced approach known as MINFLUX-L (minimal photon fluxes – line-shaped dark spots) integrates excitation polarization modulation with MINFLUX (Zhan et al., 2022). This method uses linearly polarized line-shaped dark spots to probe molecules, thereby estimating 2D positions ( $ {\sigma}_{xy}=12.3 $ nm) and azimuthal angles ( $ {\sigma}_{\phi }={26.6}^{\circ } $ ) using only 15 detected photons. Excitation modulation is also compatible with super-resolution techniques that image multiple fluorophores at once. For example, in optical lock-in detection super-resolution dipole orientation mapping (OLID-SDOM) (Guan et al., 2022), a continuously rotating excitation polarization is used to achieve background suppression and enable orientation measurements.

An attempt to achieve super-resolution using polarized excitation was proposed by Hafi et al. (2014). This method leverages the different responses of dipole emitters to varying excitation polarizations to distinguish between closely positioned molecules with different orientations and thereby improve resolution beyond the diffraction limit. However, its feasibility was questioned, especially when the orientation of emitters within a diffraction-limited area is homogeneous (Frahm and Keller, 2016). In response to these concerns, Hafi et al. acknowledged that the conditions necessary for resolution improvement via excitation polarization modulation require further investigation (Hafi et al., 2016).

Back focal plane imaging

To measure the emission dipole moment of fluorescent molecules, a forward imaging model that maps $ {\boldsymbol{\mu}}_{\mathrm{em}} $ to the measurement space is required. The theory of image formation of dipole emitters has been discussed in many works (Böhmer and Enderlein, 2003; Lieb et al., 2004; Axelrod, 2012; Novotny and Hecht, 2012; Backer and Moerner, 2014, 2015; Chandler et al., 2019a). Here, we briefly derive the forward imaging model for two important cases that arise from Eq. (6): a matched case, where the SM is embedded within a homogeneous environment whose refractive index (RI) matches that of the objective lens immersion medium (Figure 6a), and a mismatched case, where the SM is embedded in a sample environment with an RI ( $ {n}_2 $ ) different from that of the immersion medium ( $ {n}_1 $ , Figure 6b). For simplicity, we denote $ {\boldsymbol{\mu}}_{\mathrm{em}} $ by $ \boldsymbol{\mu} $ in this section.

We first evaluate the case where the sample RI ( $ {n}_1 $ ) matches that of the immersion medium ( $ {n}_2 $ ). We denote the direction of the s- and p-polarized light using unit vectors (Figure 6a)

(18a) $$ {\displaystyle \begin{array}{c}{\boldsymbol{\nu}}_s={\left[\begin{array}{ccc}-\sin {\phi}_{\mathrm{ff}}& \cos {\phi}_{\mathrm{ff}}& 0\end{array}\right]}^{\top}\end{array}} $$

(18b) $$ {\displaystyle \begin{array}{c}{\boldsymbol{\nu}}_p={[\begin{array}{ccc}\cos {\theta}_{\mathrm{ff}}\cos {\phi}_{\mathrm{ff}}& \cos {\theta}_{\mathrm{ff}}\sin {\phi}_{\mathrm{ff}}& -\sin {\theta}_{\mathrm{ff}}\end{array}]}^{\top },\end{array}} $$

where $ {\theta}_{\mathrm{ff}} $ and $ {\phi}_{\mathrm{ff}} $ are the polar and azimuthal angles associated with the propagation direction $ {\hat{\boldsymbol{r}}}_{\mathrm{ff}} $ [Eq. (7)]. The far-field emission can be written as

(19) $$ {\displaystyle \begin{array}{c}{\boldsymbol{E}}_{\mathrm{ff}}={A}_s{\boldsymbol{\nu}}_s+{A}_p{\boldsymbol{\nu}}_p,\end{array}} $$

where scalars

(20a) $$ {\displaystyle \begin{array}{c}{A}_s={\boldsymbol{\nu}}_s\cdotp {\boldsymbol{E}}_{\mathrm{ff}}\hskip0.36em \mathrm{and}\end{array}} $$

(20b) $$ {\displaystyle \begin{array}{c}{A}_p={\boldsymbol{\nu}}_p\cdotp {\boldsymbol{E}}_{\mathrm{ff}}\end{array}} $$

represent the amplitudes of the s- and p-polarized light observed from direction $ {\hat{\boldsymbol{r}}}_{\mathrm{ff}} $ , respectively. The objective lens collects this fluorescence and collimates it such that it propagates parallel to the optical axis. That is, p-polarized light within the sample is rotated to a polarization along the direction

(21) $$ {\displaystyle \begin{array}{c}{\boldsymbol{\nu}}_r={\left[\cos {\phi}_{\mathrm{ff}},,,\hskip2pt ,\sin {\phi}_{\mathrm{ff}},,,\hskip2pt ,0\right]}^{\top}\end{array}} $$

with polar coordinates within the back focal plane (BFP) expressed as $ {\rho}_{\mathrm{BFP}}={f}_{\mathrm{OL}}\sin {\theta}_{\mathrm{ff}} $ and $ {\phi}_{\mathrm{BFP}}={\phi}_{\mathrm{ff}} $ and $ {f}_{\mathrm{OL}} $ denoting the focal length of the objective lens. Therefore, the optical field at the BFP is given by

(22) $$ {\displaystyle \begin{array}{c}\hskip-11.5pc {\boldsymbol{E}}_{\mathrm{BFP}}\left({\rho}_{\mathrm{BFP}},{\phi}_{\mathrm{BFP}}\right)={A}_s{\boldsymbol{\nu}}_s+{A}_p{\boldsymbol{\nu}}_r\\ {}={c}_{\mathrm{BFP}}\mathrm{Circ}\left(\frac{\rho_{\mathrm{BFP}}{n}_1}{\hskip0.35em {f}_{\mathrm{OL}}\mathrm{NA}}\right){\left(\cos {\theta}_{\mathrm{ff}}\right)}^{-1/2}\left({\boldsymbol{\nu}}_s{\boldsymbol{\nu}}_s^{\top }+{\boldsymbol{\nu}}_r{\boldsymbol{\nu}}_p^{\top}\right)\left(\unicode{x1D540}-{\hat{\boldsymbol{r}}}_{\mathrm{ff}}{\hat{\boldsymbol{r}}}_{\mathrm{ff}}^{\top}\right)\boldsymbol{\mu} \\ {}\hskip-17pc ={\boldsymbol{G}}_{BFP}\boldsymbol{\mu}, \end{array}} $$

where the scalar $ {c}_{\mathrm{BFP}} $ is a normalization factor (set to 1 here—the field may be normalized further) and NA is the numerical aperture of the objective. The circular indicator function $ \mathrm{Circ}\left(\rho \right) $ represents a finite aperture and is equal to 1 for $ \rho <1 $ and 0 otherwise. The apodization factor $ {\left(\cos {\theta}_{\mathrm{ff}}\right)}^{-1/2} $ maps the equal-angular distribution of energy in object space to a planar projection on the BFP while guaranteeing that the total energy entering the objective lens is identical to that within the BFP. That is,

(23) $$ {\displaystyle \begin{array}{c}\hskip-3em {\int}_{\phi_{\mathrm{ff}}=0}^{2\pi }{\int}_{\theta_{\mathrm{ff}}=0}^{\theta_0}{\left|{\boldsymbol{E}}_{\mathrm{ff}}\right|}^2\sin {\theta}_{\mathrm{ff}}\mathrm{d}{\theta}_{\mathrm{ff}}\;\mathrm{d}{\phi}_{\mathrm{ff}}\\ {}={\int}_{\phi_{\mathrm{BFP}}=0}^{2\pi }{\int}_{\rho_{\mathrm{BFP}}=0}^{f_{\mathrm{OL}}{\theta}_0}{\left|{\boldsymbol{E}}_{\mathrm{BFP}}\right|}^2{\rho}_{\mathrm{BFP}}\;\mathrm{d}{\rho}_{\mathrm{BFP}}\;\mathrm{d}{\phi}_{\mathrm{BFP}},\end{array}} $$

where

(24) $$ {\displaystyle \begin{array}{c}{c}_{\mathrm{ff}}\sin {\theta}_{\mathrm{ff}}\mathrm{d}{\theta}_{\mathrm{ff}}={\left|{\left(\cos {\theta}_{\mathrm{ff}}\right)}^{-\frac{1}{2}}\right|}^2{c}_{\mathrm{BFP}}{\rho}_{\mathrm{BFP}}\;\mathrm{d}{\rho}_{\mathrm{BFP}}.\end{array}} $$

Representative images of the intensity distribution given by Eq. (22) at the BFP for several molecular orientations are shown in Figure 6d.

Next, we evaluate the case when the sample RI differs from that of the immersion medium, which usually happens during typical biological imaging; the sample’s RI is often close to that of water ( $ {n}_2=1.33 $ ), whereas the immersion medium often has a larger RI (e.g., $ {n}_1=1.515 $ ) in order to achieve a higher collection NA. We define the following unit vectors (Figure 6b)

(25a) $$ {\displaystyle \begin{array}{c}{\boldsymbol{\nu}}_{p,1}={[\begin{array}{ccc}\cos {\theta}_{\mathrm{ff},1}\cos {\phi}_{\mathrm{ff}}& \cos {\theta}_{\mathrm{ff},1}\sin {\phi}_{\mathrm{ff}}& -\sin {\theta}_{\mathrm{ff},1}\end{array}]}^{\top}\hskip0.36em \mathrm{and}\end{array}} $$

(25b) $$ {\displaystyle \begin{array}{c}{\boldsymbol{\nu}}_{p,2}={[\begin{array}{ccc}\cos {\theta}_{\mathrm{ff},2}\cos {\phi}_{\mathrm{ff}}& \cos {\theta}_{\mathrm{ff},2}\sin {\phi}_{\mathrm{ff}}& -\sin {\theta}_{\mathrm{ff},2}\end{array}]}^{\top}\end{array}} $$

to represent the directions of p-polarized light within the lens immersion medium ( $ {n}_1 $ ) and sample ( $ {n}_2 $ ). Propagation directions $ {\theta}_{\mathrm{ff},1} $ and $ {\theta}_{\mathrm{ff},2} $ are related by

(26) $$ {\displaystyle \begin{array}{c}{n}_1\sin {\theta}_{\mathrm{ff},1}={n}_2\sin {\theta}_{\mathrm{ff},2}\end{array}} $$

according to Snell’s law. The polarization direction of the s-polarized light remains unchanged. The fields immediately before ( $ {\boldsymbol{E}}_{\mathrm{ff},2} $ ) and after ( $ {\boldsymbol{E}}_{\mathrm{ff},1} $ ) propagating through the RI interface are written as (Figure 6b)

(27a) $$ {\displaystyle \begin{array}{c}\hskip0.48em {\boldsymbol{E}}_{\mathrm{ff},2}=\frac{c_{\mathrm{ff},2}}{\cos {\theta}_{\mathrm{ff},2}}\left({\boldsymbol{\nu}}_s^{\top }{\boldsymbol{E}}_{\mathrm{ff},0}{\boldsymbol{\nu}}_s+{\boldsymbol{\nu}}_{p,2}^{\top }{\boldsymbol{E}}_{\mathrm{ff},0}{\boldsymbol{\nu}}_{p,2}\right)\hskip0.36em \mathrm{and}\end{array}} $$

(27b) $$ {\displaystyle \begin{array}{c}{\boldsymbol{E}}_{\mathrm{ff},1}=\frac{c_{\mathrm{ff},2}}{\cos {\theta}_{\mathrm{ff},2}}\left({t}_s{\boldsymbol{\nu}}_s^{\top }{\boldsymbol{E}}_{\mathrm{ff},0}{\boldsymbol{\nu}}_s+{t}_p{\boldsymbol{\nu}}_{p,2}^{\top }{\boldsymbol{E}}_{\mathrm{ff},0}{\boldsymbol{\nu}}_{p,1}\right),\end{array}} $$

where from Eq. (6), we have

(28a) $$ {\displaystyle \begin{array}{c}{\boldsymbol{E}}_{\mathrm{ff},0}={c}_{\mathrm{ff}}\left(\unicode{x1D540}-{\hat{\boldsymbol{r}}}_{\mathrm{ff},2}{\hat{\boldsymbol{r}}}_{\mathrm{ff},2}^{\top}\right)\boldsymbol{\mu}, \end{array}} $$

(28b) $$ {\displaystyle \begin{array}{c}{\hat{\boldsymbol{r}}}_{\mathrm{ff},2}={\left[\sin {\theta}_{\mathrm{ff},2}\cos {\phi}_{\mathrm{ff}},,,\hskip2pt ,\sin {\theta}_{\mathrm{ff},2}\sin {\phi}_{\mathrm{ff}},,,\hskip2pt ,\cos {\theta}_{\mathrm{ff},2}\right]}^{\top },\end{array}} $$

$ {c}_{\mathrm{ff},2} $ is a normalization factor, and

(29a) $$ {\displaystyle \begin{array}{c}{t}_s=\frac{2{n}_2\cos {\theta}_{\mathrm{ff},2}}{n_1\cos {\theta}_{\mathrm{ff},1}+{n}_2\cos {\theta}_{\mathrm{ff},2}}\hskip0.36em \mathrm{and}\end{array}} $$

(29b) $$ {\displaystyle \begin{array}{c}{t}_p=\frac{2{n}_2\cos {\theta}_{\mathrm{ff},2}}{n_1\cos {\theta}_{\mathrm{ff},2}+{n}_2\cos {\theta}_{\mathrm{ff},1}}\end{array}} $$

are the Fresnel transmission coefficients for s- and p-polarized light. The field right before entering the objective lens is, therefore, given by

(30) $$ {\displaystyle \begin{array}{c}{\boldsymbol{E}}_{\mathrm{ff},3}=\frac{c_{\mathrm{ff},1}\cos {\theta}_{\mathrm{ff},1}}{\cos {\theta}_{\mathrm{ff},2}}\left({t}_s{\boldsymbol{\nu}}_s^{\top }{\boldsymbol{E}}_{\mathrm{ff},0}{\boldsymbol{\nu}}_s+{t}_p{\boldsymbol{\nu}}_{p,2}^{\top }{\boldsymbol{E}}_{\mathrm{ff},0}{\boldsymbol{\nu}}_{p,1}\right),\end{array}} $$

where $ \cos {\theta}_{\mathrm{ff},1} $ and $ \cos {\theta}_{\mathrm{ff},2} $ represent the amplitude normalization factors corresponding to the spherical waves and $ {c}_{\mathrm{ff},1} $ (assumed to be 1 here) is a normalization factor. Similar to Eq. (22), accounting for the apodization factor, the optical field observed at the BFP is given by

(31) $$ {\displaystyle \begin{array}{c}{\boldsymbol{E}}_{\mathrm{BFP}}\left(u,v\right)\\ {}={c}_{\mathrm{BFP}}\mathrm{Circ}\left(\frac{\rho_{\mathrm{BFP}}{n}_1}{\hskip0.35em {f}_{\mathrm{OL}}\mathrm{NA}}\right)\frac{{\left(\cos {\theta}_{\mathrm{ff},1}\right)}^{\frac{1}{2}}}{\cos {\theta}_{\mathrm{ff},2}}\left({t}_s{\boldsymbol{\nu}}_s{\boldsymbol{\nu}}_s^{\top }+{t}_p{\boldsymbol{\nu}}_r{\boldsymbol{\nu}}_{p,2}^{\top}\right)\left(\unicode{x1D540}-{\hat{\boldsymbol{r}}}_{\mathrm{ff},2}{\hat{\boldsymbol{r}}}_{\mathrm{ff},2}^{\top}\right)\\ {}\boldsymbol{\mu} ={\boldsymbol{G}}_{\mathrm{BFP}}\boldsymbol{\mu} \\ {}=\left[\begin{array}{ccc}{g}_x^{(x)}\left(u,v\right)& {g}_y^{(x)}\left(u,v\right)& {g}_z^{(x)}\left(u,v\right)\\ {}{g}_x^{(y)}\left(u,v\right)& {g}_y^{(y)}\left(u,v\right)& {g}_z^{(y)}\left(u,v\right)\\ {}0& 0& 0\end{array}\right]\boldsymbol{\mu}, \end{array}} $$

where

(32a) $$ {\displaystyle \begin{array}{c}{\rho}_{\mathrm{BFP}}={f}_{\mathrm{OL}}\sin {\theta}_{\mathrm{ff},1},\end{array}} $$

(32b) $$ {\displaystyle \begin{array}{c}u=\sin {\theta}_{\mathrm{ff},1}\cos {\phi}_{\mathrm{ff}},\hskip0.36em \mathrm{and}\end{array}} $$

(32c) $$ {\displaystyle \begin{array}{c}v=\sin {\theta}_{\mathrm{ff},1}\sin {\phi}_{\mathrm{ff}}.\end{array}} $$

Entries $ {g}_i^{(j)} $ , with $ i,j\in \left\{x,y,z\right\} $ , are termed the ( $ j $ -polarized) basis fields at the BFP. They represent the fields produced by $ x $ -, $ y $ -, and $ z $ -oriented dipoles, and any intermediate orientation $ \boldsymbol{\mu} $ produces a linear combination of these basis fields $ {g}_i $ .

Finally, for a molecule located at $ \boldsymbol{r}={\left[x,y,{z}_{\mathrm{SM}}\right]}^{\top } $ , where $ {z}_{\mathrm{SM}} $ (Figure 6c) is the distance of the SM to the RI interface from above, the electric field at the BFP is given by

(33) $$ {\displaystyle \begin{array}{c}{\boldsymbol{E}}_{\mathrm{BFP}}\left(u,v;\boldsymbol{r},\boldsymbol{\mu} \right)=\\ {}\exp \left[\frac{j2\pi }{\lambda}\left({n}_1 xu+{n}_1 yv-{n}_1{z}_f\cos {\theta}_{ff,1}+{n}_2{z}_{\mathrm{SM}}\cos {\theta}_{ff,2}\right)\right]{\boldsymbol{G}}_{\mathrm{BFP}}\boldsymbol{\mu} \\ {}=\exp \left\{\frac{j2\pi {n}_1}{\lambda}\left[ xu+ yv-{z}_f\sqrt{1-{u}^2-{v}^2}+{z}_{\mathrm{SM}}\sqrt{{\left(\frac{n_2}{n_1}\right)}^2-{u}^2-{v}^2}\right]\right\}{\boldsymbol{G}}_{\mathrm{BFP}}\boldsymbol{\mu}, \end{array}} $$

where $ {z}_f $ represents the position of the nominal focal plane above the RI interface. We note that Eq. (33) assumes an ideal objective lens, and any (possibly field-dependent) optical aberrations (Fu et al., 2023; Liu et al., 2024; Xiao et al., 2024; Xu et al., 2020) can change the amplitude or phase or both of $ {\boldsymbol{E}}_{\mathrm{BFP}}\left(u,v;\boldsymbol{r},\boldsymbol{\mu} \right) $ .

The intensity of x- and y-polarized fluorescence at the BFP is given by

(34) $$ {\displaystyle \begin{array}{c}\left[\begin{array}{c}{I}_x\\ {}{I}_y\end{array}\right]=\\ {}s\left[\begin{array}{cc}\begin{array}{ccc}{\left|{g}_x^{(x)}\right|}^2& {\left|{g}_y^{(x)}\right|}^2& {\left|{g}_z^{(x)}\right|}^2\\ {}{\left|{g}_x^{(y)}\right|}^2& {\left|{g}_y^{(y)}\right|}^2& {\left|{g}_z^{(y)}\right|}^2\end{array}& \begin{array}{ccc}2\operatorname{Re}\left\{{g}_x^{(x)\ast }{g}_y^{(x)}\right\}& 2\operatorname{Re}\left\{{g}_x^{(x)\ast }{g}_z^{(x)}\right\}& 2\operatorname{Re}\left\{{g}_y^{(x)\ast }{g}_z^{(x)}\right\}\\ {}2\operatorname{Re}\left\{{g}_x^{(y)\ast }{g}_y^{(y)}\right\}& 2\operatorname{Re}\left\{{g}_x^{(y)\ast }{g}_z^{(y)}\right\}& 2\operatorname{Re}\left\{{g}_y^{(y)\ast }{g}_z^{(y)}\right\}\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{m}_{xx}\\ {}{m}_{yy}\\ {}{m}_{zz}\end{array}\\ {}\begin{array}{c}{m}_{xy}\\ {}{m}_{xz}\\ {}{m}_{yz}\end{array}\end{array}\right].\\ {}\end{array}} $$

Representative images of the intensity distribution given by Eqs. (31) and (32) at the BFP are shown in Figure 6e,f. The molecule is located at $ \boldsymbol{r}={\left[0,0,0\right]}^{\top } $ and the nominal focal plane position $ {z}_f=0 $ . The bright ring in these images represents the supercritical light coming from the evanescent fields near the SM that are transformed into propagating waves in the immersion medium (Axelrod, 2012). These intensity patterns can directly be used to measure the orientation of fluorophores (Lieb et al., 2004).

Modeling the rotational diffusion of fluorescent molecules

According to Eqs. (14) and (34), optical imaging is sensitive to the second-order orientational moments $ \boldsymbol{m} $ of SMs instead of their first-order transition dipole moments $ \boldsymbol{\mu} $ . To interpret these values of $ \boldsymbol{m} $ , several models have been proposed to describe dipole orientation and wobble. One approach is to first rearrange the second moments into a 3 × 3 positive semidefinite (Zhou et al., 2024b) Hermitian matrix $ \boldsymbol{M} $ , which can be decomposed as

(35) $$ {\displaystyle \begin{array}{c}\boldsymbol{M}=\left[\begin{array}{ccc}{m}_{xx}& {m}_{xy}& {m}_{xz}\\ {}{m}_{xy}& {m}_{yy}& {m}_{yz}\\ {}{m}_{xz}& {m}_{yz}& {m}_{zz}\end{array}\right]={\sum}_{i=1}^3{\lambda}_i{\boldsymbol{\nu}}_i{\boldsymbol{\nu}}_i^{\top}\\ {}=\frac{3{\lambda}_1-1}{2}{\boldsymbol{\nu}}_1{\boldsymbol{\nu}}_1^{\top }+\frac{3-3{\lambda}_1}{2}\frac{\unicode{x1D540}}{3}+\frac{\lambda_2-{\lambda}_3}{2}\left({\boldsymbol{\nu}}_2{\boldsymbol{\nu}}_2^{\top }-{\boldsymbol{\nu}}_3{\boldsymbol{\nu}}_3^{\top}\right),\end{array}} $$

where $ \unicode{x1D540} $ represents the identity matrix and the scalars $ {\lambda}_i $ and vectors $ {\boldsymbol{\nu}}_i $ correspond to the ith eigenvalue and eigenvector of $ \boldsymbol{M} $ , in the order of descending $ {\lambda}_i $ . Therefore, the second moments $ \boldsymbol{M} $ perceived by the imaging system may be interpreted as a weighted mixture of several components: a fixed dipole of orientation $ \boldsymbol{\mu} ={\boldsymbol{\nu}}_1 $ , an isotropic emitter ( $ \unicode{x1D540}/3 $ ), and an orthogonal nuisance term that arises from asymmetric rotation.

If the molecule diffuses in all directions equally (Zhang and Lew, 2019), thereby exhibiting isotropic rotational diffusion, then the smaller eigenvalues $ {\lambda}_2 $ and $ {\lambda}_3 $ are identical. We may define rotational constraint $ \gamma =\left(3{\lambda}_1-1\right)/2 $ such that

(36) $$ {\displaystyle \begin{array}{c}\boldsymbol{M}=\gamma {\boldsymbol{\nu}}_1{\boldsymbol{\nu}}_1^{\top }+\frac{1-\gamma }{3}\unicode{x1D540},\end{array}} $$

where the individual second moments are given by

$$ {m}_{ii}=\gamma {\mu}_i^2+\frac{1-\gamma }{3}\hskip0.48em \mathrm{and} $$

(37) $$ {\displaystyle \begin{array}{c}{m}_{ij}=\gamma {\mu}_i{\mu}_j,\hskip1.44em i,j\in \left\{x,y,z\right\},i\ne j.\end{array}} $$

The rotational constraint $ \gamma \in \left[0,1\right] $ represents the degree to which the molecule’s emission is consistent with a fixed dipole (Backer and Moerner, 2014, 2015; Backer et al., 2016); $ \gamma =0 $ represents an isotropic emitter. We may parameterize this isotropic rotational diffusion as uniform wobble within a hard-edged cone of half angle $ {\alpha}_s $ , and thus, $ \gamma $ can be written as

(38) $$ {\displaystyle \begin{array}{c}\gamma =1-3{m}_{xx{\left(\right|}_{{\boldsymbol{\unicode{x03BD}}}_1={\left[0,0,1\right]}^{\top }}}\\ {}=1-\frac{3\int_0^{\alpha_s}{\int}_0^{2\unicode{x03C0}}{\left(\sin {\theta}^{\prime}\cos {\phi}^{\prime}\right)}^2\sin {\theta}^{\prime }d{\phi}^{\prime }d{\theta}^{\prime }}{\int_0^{\alpha_s}{\int}_0^{2\unicode{x03C0}}\sin {\theta}^{\prime }d{\phi}^{\prime }d{\theta}^{\prime }}=\frac{\cos^2{\alpha}_s+\cos {\alpha}_s}{2}.\end{array}} $$

Alternatively, Eq. (38) is equivalent to

(39) $$ {\displaystyle \begin{array}{c}\gamma =1-\frac{3\varOmega }{4\pi }+\frac{\varOmega^2}{8{\pi}^2},\end{array}} $$

where $ \varOmega \in \left[0,2\unicode{x03C0} \right] $ represents the solid angle subtended by the cone on the orientation hemisphere (Figure 5a). A rotationally fixed molecule has a cone solid angle of 0, while a freely rotating molecule has $ \varOmega =2\unicode{x03C0} $ .

Ding et al. and Zhou et al. further investigated molecules exhibiting anisotropic wobble, specifically focusing on scenarios where the eigenvalues $ {\lambda}_2 $ and $ {\lambda}_3 $ are not identical (Ding and Lew, 2021; Zhou et al., 2024b). In these cases, one may consider a molecule wobbling uniformly within an elliptical cone of distinct angles of $ \alpha $ and $ \beta $ along the long and short axes, respectively. The eigenvalues (Eq. (35)) can be expressed as

$$ {\lambda}_1=\frac{1}{3\Omega}{\int}_{\phi^{\prime }=0}^{2\pi }1-{t}^3\left({\phi}^{\prime}\right)\mathrm{d}{\phi}^{\prime }, $$

$$ {\lambda}_2=\frac{1}{3\Omega}{\int}_{\phi^{\prime }=0}^{2\pi}\left({t}^3\left({\phi}^{\prime}\right)-3t\left({\phi}^{\prime}\right)+2\right){\sin}^2\left({\phi}^{\prime}\right)\mathrm{d}{\phi}^{\prime }, $$

$$ {\lambda}_3=\frac{1}{3\Omega}{\int}_{\phi^{\prime }=0}^{2\pi}\left({t}^3\left({\phi}^{\prime}\right)-3t\left({\phi}^{\prime}\right)+2\right){\cos}^2\left({\phi}^{\prime}\right)\mathrm{d}{\phi}^{\prime }, $$

$$ \Omega =2\pi -{\int}_{\phi^{\prime }=0}^{2\pi }t\left({\phi}^{\prime}\right)\mathrm{d}{\phi}^{\prime },\hskip0.84em \mathrm{and} $$

(40) $$ {\displaystyle \begin{array}{c}t\left(\phi^{\prime}\right)=\cos \left(\max \theta \left(\phi \right)\right)=\sqrt{1-\frac{\sin^2\left(\alpha \right)+{\sin}^2\left(\beta \right)}{\sin^2\left(\beta \right){\cos}^2\left(\phi \right)+{\sin}^2\left(\alpha \right){\sin}^2\left(\phi \right)}},\end{array}} $$

where $ \max \theta \left(\phi \right) $ represents the boundary of the anisotropic wobble cone, rotated so that its center points along the $ {\mu}_z $ axis, parameterized by the maximum value of $ \theta $ as a function of $ \phi $ . The corresponding eigenvectors are given by

$$ {\boldsymbol{\nu}}_2=\left[\begin{array}{c}-\cos \theta \cos \phi \sin \psi -\sin \phi \cos \psi \\ {}-\cos \theta \sin \phi \sin \psi +\cos \phi \cos \psi \\ {}\sin \theta \sin \psi \end{array}\right]\hskip0.48em \mathrm{and} $$

(41) $$ {\boldsymbol{\nu}}_3=\left[\begin{array}{c}\cos \theta \cos \phi \cos \psi -\sin \phi \sin \psi \\ {}\cos \theta \sin \phi \cos \psi -\cos \phi \sin \psi \\ {}-\sin \theta \cos \psi \end{array}\right]. $$

One may model the anisotropy as having long and short axes oriented parallel and perpendicular to the optical axis (Figure 5e) or rotated by an arbitrary angle $ \psi $ (Figure 5f). Importantly, one may interpret the eigen decomposition of $ \boldsymbol{M} $ as expressing $ \boldsymbol{m} $ in a rotated coordinate system with $ {\mu}_z^{\prime } $ aligned with the dipole’s mean orientation and an equivalent second moment vector $ {\boldsymbol{m}}^{\prime }={\left[{\lambda}_3,{\lambda}_2,{\lambda}_1,0,0,0\right]}^{\top } $ . Therefore, the eigenvalues are simply equal to the first three squared second moments, each of which must be non-negative (Zhou et al., 2024b).

Alternatively, rotational dynamics can be expressed using generalized 3D Stokes parameters $ {s}_i $ , analogous to those used in standard polarimetry (Curcio et al., 2020). The relationship between the second moments and the Stokes parameters is given by

$$ {s}_1=2{s}_0\left({m}_{xx}-{m}_{yy}\right), $$

$$ \left[\begin{array}{ccc}{s}_2& {s}_4& {s}_6\end{array}\right]=2{s}_0\left[\begin{array}{ccc}{m}_{xy}& {m}_{xz}& {m}_{yz}\end{array}\right], $$

$$ {s}_3={s}_5={s}_7=0, $$

(42) $$ {\displaystyle \begin{array}{c}{s}_8=\sqrt{3}{s}_0\left({m}_{xx}+{m}_{yy}-{m}_{zz}\right)/2.\end{array}} $$

Note that $ {s}_3 $ , $ {s}_5 $ , and $ {s}_7 $ are zero since we assume that the SMs have no chirality. We also note that spherical harmonics $ {Y}_l^m\left(\theta, \phi \right) $ may also be used as a basis to describe molecular rotational dynamics (Chandler et al., 2019b). These harmonics are convenient as a complete orthogonal basis for functions on a sphere, and they form the foundation of a unified framework for analyzing the image formation of individual dipoles and ensembles thereof (Chandler et al., 2019a, 2019b, 2020). Compared to fluorescence anisotropy, which projects orientation space into a single parameter, each of the aforementioned models provides a more detailed, high-dimensional description of SM rotational motions, and we recommend their use whenever possible.

This analysis has key implications for the temporal resolution of SMOLM techniques. Since any fluorescence measurement involves collecting some number of photons over time, SMOLM wobble measurements, quantified via rotational constraint $ \gamma $ or angles $ {\alpha}_s $ , $ \alpha $ , and $ \beta $ , therefore represent the degree of rotational diffusion that a molecule exhibits during the integration time. The choice of integration time typically balances several factors, including the duration of each fluorescence burst or fluorophore binding event, hardware limitations of the detector, and the desired angular precision of the measurement. Typical exposure times are 10 to 100 milliseconds for widefield imaging cameras (Table 1), which are useful for probing binding, phase separation, and aggregation dynamics (Nettels et al., 2024). Newly developed arrays of avalanche diodes have <200 ps precision (Bucci et al., 2024; Radmacher et al., 2024) for timing photon arrivals and can be adapted for SMOLM. Further, one may use SMOLM to track a molecule’s mean orientation $ \boldsymbol{\mu} $ and wobble $ \gamma $ , as well as its translational movements, over time, thereby enabling high-dimensional tracking of biomolecular dynamics.

Dipole-spread function engineering via modulating phase and polarization

The optical field at the image plane can be found by calculating the Fourier transform of the (modulated) field at the BFP (Figure 6d–f). Here, we denote any possible linear operation on the field at the BFP using a spatially varying Jones matrix

(43) $$ {\displaystyle \begin{array}{c}\boldsymbol{J}\left(u,v\right)=\left[\begin{array}{cc}{J}_{11}\left(u,v\right)& {J}_{12}\left(u,v\right)\\ {}{J}_{21}\left(u,v\right)& {J}_{22}\left(u,v\right)\end{array}\right].\end{array}} $$

The image plane electric field for an in-focus emitter located at the origin ( $ x=y={z}_{\mathrm{SM}}={z}_f=0 $ ) is therefore given by

(44) $$ {\displaystyle \begin{array}{c}{\boldsymbol{E}}_{\mathrm{img}}\left(\xi, \eta \right)=\mathcal{F}\left\{\boldsymbol{J}{\boldsymbol{G}}_{\mathrm{BFP}}\boldsymbol{\mu} \right\}=\mathcal{F}\left\{\boldsymbol{J}{\boldsymbol{G}}_{\mathrm{BFP}}\right\}\boldsymbol{\mu} ={\boldsymbol{G}}_{\mathrm{img}}\boldsymbol{\mu} \\ {}=\left[\begin{array}{ccc}{G}_x^{(x)}\left(\xi, \eta \right)& {G}_y^{(x)}\left(\xi, \eta \right)& {G}_z^{(x)}\left(\xi, \eta \right)\\ {}{G}_x^{(y)}\left(\xi, \eta \right)& {G}_y^{(y)}\left(\xi, \eta \right)& {G}_z^{(y)}\left(\xi, \eta \right)\\ {}0& 0& 0\end{array}\right]\boldsymbol{\mu}, \end{array}} $$

where $ \left(\xi, \eta \right) $ represents coordinates within the image plane and $ \mathcal{F}\left\{\cdotp \right\} $ represents a 2D Fourier transform performed by the tube lens [TL1 and TL2, Figure 7a]. Entries $ {G}_i^{(j)} $ , with $ i,j\in \left\{x,y,z\right\} $ , are termed the basis fields at the image plane. Note that due to the Fourier transform, $ {\boldsymbol{E}}_{\mathrm{img}} $ is shift-invariant with respect to the lateral position $ \left(x,y\right) $ of the molecule. However, the basis fields exhibit changes in their shapes when the molecule is defocused.

Figure 7. Representative images of recently developed and widely used dipole spread functions (DSFs). (a) Principle of a fluorescence microscope with polarized detection using a polarizing beamsplitter (PBS). An objective lens (OL) is placed at one focal length away from the dipole emitter. The tube lenses (TL1, TL2) perform optical Fourier transforms on the field at the back focal plane (BFP) modulated by an optical component represented by a $ 2\times 2 $ complex tensor $ \boldsymbol{J}\left(u,v\right) $ and create the DSF at the detector plane. Images for molecules with various orientations and wobble using the (b) standard DSF (i) unpolarized and focused (Mortensen et al., 2010), (ii) polarized and focused (Ding et al., 2020), (iii) unpolarized and defocused (Böhmer and Enderlein, 2003), (c) double-helix DSF, (d) multi-spot DSFs (i–iv) quadrated (Backer et al., 2013), bisected (Backer et al., 2014), tri-spot (Zhang et al., 2018), duo-spot (Lu et al., 2020 DSFs), (e) vortex DSF (Ding and Lew, 2021; Hulleman et al., 2021), (f) radially and azimuthally polarized (raPol) standard DSF (Zhang et al., 2022), (g) pixOL (Wu et al., 2022a), and (h) CHIDO (Curcio et al., 2020). (j) Images from eight channels of the multi-view-reflector (MVR) microscope (Zhang et al., 2023). Molecule with (1) $ \left[\theta, \phi \right]=\left[{90}^{\circ },{0}^{\circ}\right] $ , (2) $ \left[\theta, \phi \right]=\left[{90}^{\circ },{90}^{\circ}\right] $ , (3) $ \theta ={0}^{\circ } $ , and (4) $ \left[\theta, \phi \right]=\left[{45}^{\circ },{0}^{\circ}\right] $ . (5) Isotropic emitter. Purple: in-focus molecules; green: molecules defocused by (b) 500 nm and (c–h) 200 nm. Color bar: normalized intensity; scale bar: 500 nm.

Similar to Eqs. (14) and (34), the forward imaging model using emission modulation can be written as

(45) $$ {\displaystyle \begin{array}{c}\boldsymbol{I}=\left[\begin{array}{c}{I}^{(x)}\\ {}{I}^{(y)}\end{array}\right]=s\left[\begin{array}{cc}\begin{array}{ccc}{B}_{xx}^{(x)}& {B}_{yy}^{(x)}& {B}_{zz}^{(x)}\\ {}{B}_{xx}^{(y)}& {B}_{yy}^{(y)}& {B}_{zz}^{(y)}\end{array}& \begin{array}{ccc}{B}_{xy}^{(x)}& {B}_{xz}^{(x)}& {B}_{yz}^{(x)}\\ {}{B}_{xy}^{(y)}& {B}_{xz}^{(y)}& {B}_{yz}^{(y)}\end{array}\end{array}\right]\boldsymbol{m}=s\boldsymbol{Bm}\\ {}=s\left[\begin{array}{cc}\begin{array}{ccc}{\left|{G}_x^{(x)}\right|}^2& {\left|{G}_y^{(x)}\right|}^2& {\left|{G}_z^{(x)}\right|}^2\\ {}{\left|{G}_x^{(y)}\right|}^2& {\left|{G}_y^{(y)}\right|}^2& {\left|{G}_z^{(y)}\right|}^2\end{array}& \begin{array}{ccc}2\operatorname{Re}\left\{{G}_x^{(x)\ast }{G}_y^{(x)}\right\}& 2\operatorname{Re}\left\{{G}_x^{(x)\ast }{G}_z^{(x)}\right\}& 2\operatorname{Re}\left\{{G}_y^{(x)\ast }{G}_z^{(x)}\right\}\\ {}2\operatorname{Re}\left\{{G}_x^{(y)\ast }{G}_y^{(y)}\right\}& 2\operatorname{Re}\left\{{G}_x^{(y)\ast }{G}_z^{(y)}\right\}& 2\operatorname{Re}\left\{{G}_y^{(y)\ast }{G}_z^{(y)}\right\}\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{m}_{xx}\\ {}{m}_{yy}\\ {}{m}_{zz}\end{array}\\ {}\begin{array}{c}{m}_{xy}\\ {}{m}_{xz}\\ {}{m}_{yz}\end{array}\end{array}\right],\end{array}} $$

where $ {B}_{ij}^{(k)} $ , with $ i,j\in \left\{x,y,z\right\} $ and $ k\in \left\{x,y\right\} $ , are termed the $ k $ -polarized basis images describing the response (dipole spread function, DSF) of the imaging system to a dipole emitter. For unpolarized detection, the detected image is given by $ {I}^{(x)}+{I}^{(y)} $ , a mixture of both polarized images. We can also resolve $ {I}^{(x)} $ and $ {I}^{(y)} $ separately by placing a PBS in the emission path (Figure 7a).

For an unpolarized conventional microscope without additional modulation at the BFP, i.e., $ {J}_{11}\left(u,v\right)={J}_{22}\left(u,v\right)=1 $ and $ {J}_{12}\left(u,v\right)={J}_{21}\left(u,v\right)=0 $ , SM orientation can be measured by fitting the shape of the measured images to the theoretical model [Figure 7b(i)] (Mortensen et al., 2010); the image corresponding to an in-( $ xy $ ) plane molecule exhibits an elliptical shape with an elongation direction parallel to the molecular orientation [Figure 7b(i)(1,2)] while the image corresponding to a $ z $ -oriented molecule exhibits a donut shape [Figure 7b(i)(3)]. One can also separate the $ x $ - and $ y $ -polarized emission light to obtain more distinct basis images for x- and y-oriented molecules [Figure 7b(ii)(1,2)]. This polarization-resolved DSF was used to resolve the structural heterogeneity within amyloid aggregates (Ding et al., 2020). Both the unpolarized and polarized standard DSFs are typically implemented to image molecules located close to the air-glass or water–glass interface because the additional phase caused by refractive index mismatch further improves orientational sensitivity by breaking the symmetry in the basis fields (Ding et al., 2020; Zhang and Lew, 2021b). The standard DSF can also be implemented with a defocus of ~500 nm to 1 μm (Böhmer and Enderlein, 2003). While localization precision is reduced as the photons are spread across a larger area, the more distinct images [Figure 7b(iii)] significantly improve orientational sensitivity. Defocused imaging has been used for imaging rotations of SMs embedded within polymers (Dickson et al., 1998; Patra et al., 2004; Uji-i et al., 2006) and resolving the stepping of Myosin V motors (Toprak et al., 2006).

Engineering phase masks

Since the early 1980s (Cathey et al., 1984; Dowski and Cathey, 1995; Ojeda-Castañeda et al., 1986), point-spread function (PSF) engineering has been explored to extend the capabilities of conventional microscopes. In the case of SMOLM, by manipulating the optical field at the BFP using a spatially varying Jones matrix $ \boldsymbol{J}\left(u,v\right) $ , one can improve the orientational sensitivity of the microscope and make more accurate and precise measurements. Experimentally, engineered DSFs are often implemented by adding a 4f system to the detection path of a fluorescence microscope that facilitates easy access to the BFP. Many DSFs, e.g., the double-helix (DH) DSF (Pavani and Piestun, 2008; Pavani et al., 2009; Backlund et al., 2012), multi-spot DSFs (Backer et al., 2013, 2014; Zhang et al., 2018; Lu et al., 2020), vortex DSFs (Ding and Lew, 2021; Hulleman et al., 2021), and pixel-wise optimized DSF (Wu et al., 2022a) engineered for measuring 3D orientation and localization (pixOL), are designed using phase-only modulation, i.e.,

$$ {J}_{11}\left(u,v\right)=\exp \left[\hskip0.3em , jk{\psi}_x\left(u,v\right)\right], $$

$$ {J}_{22}\left(u,v\right)=\exp \left[ jk{\psi}_y\left(u,v\right)\right],\hskip0.36em \mathrm{and} $$

(46) $$ {\displaystyle \begin{array}{c}{J}_{12}\left(u,v\right)={J}_{21}\left(u,v\right)=0,\end{array}} $$

where $ {\psi}_x\left(u,v\right) $ and $ {\psi}_y\left(u,v\right) $ are the additional phase masks added to the $ x $ and $ y $ -polarized BFP, respectively. These DSFs can be implemented using a single spatial light modulator in a 4f system (Figure 8a,b), as shown in (Backlund et al., 2012; Backer et al., 2014; Zhang et al., 2018). In this configuration, the phase masks $ {\psi}_x\left(u,v\right) $ and $ {\psi}_y\left(u,v\right) $ may simply be rotated versions of each other.

Figure 8. (a, b) Schematic of a polarization-sensitive 4f imaging system appended to the detection path of a fluorescence microscope for modulating the phase at the back focal plane (BFP) using a spatial light modulator (SLM). (a) After separating the $ x $ (red) and $ y $ (blue) polarized fluorescence using a polarizing beamsplitter (PBS), light is guided towards a pyramid mirror and (b) reflected upwards towards the SLM. Both $ x $ and $ y $ -polarized BFP are positioned at the same area on the SLM. Arrows on the phase mask represent the light polarization on the SLM. Both imaging channels are collected using camera C1. (c) Schematic of the raMVR microscope. After turning radially and azimuthally polarized fluorescence to $ x $ - and $ y $ -polarized light using a variable wave plate (VaWP) and a vortex wave plate (VWP), a PBS and two sets of pyramid mirrors separate lights into eight detection channels, captured by cameras C1 and C2.

The double-helix (DH) DSF was originally designed for measuring the axial position $ {z}_{\mathrm{SM}} $ of SMs (Pavani and Piestun, 2008; Pavani et al., 2009); the image of a single emitter exhibits two lobes revolving around each other as a function of $ {z}_{\mathrm{SM}} $ . It may be implemented using an SLM or by placing a commercially available transmissive phase plate (Gahlmann et al., 2013) in the BFP of an imaging system. The orientation information is encoded in the relative brightness of the lobes (Backlund et al., 2012). For example, in the $ x $ -polarized imaging channel, one lobe is significantly brighter compared to the other if the molecule is tilted within the $ xz $ -plane by ~ $ {45}^{\circ } $ [Figure 7c(4)]. In their work, the authors note that by simultaneously estimating the position and orientation of SMs using the DH DSF, orientation-induced systematic localization errors (Engelhardt et al., 2011) may be greatly improved; the experimental standard deviation averaged over a 2 μm depth range is reduced from 116 nm to 34 nm with 5925 signal photons and 9 background photons per pixel detected. One limitation of the DH DSF is that the image of z-oriented molecules is difficult to distinguish from those of isotropic emitters [Figure 7c(3,5)]. Consequently, the authors note that their localization correction works best for intermediately inclined molecules, i.e., $ \theta \in \left[{35}^{\circ },{75}^{\circ}\right] $ .

The design of another family of DSFs, the multi-spot DSFs, leverages the fact that the intensity distribution at the BFP changes as a function of molecular orientation (Figure 7d). These techniques segment the BFP into multiple sections, and various linear phase ramps are placed in these sections. Since the Fourier transform of a linear phase gradient is a lateral shift of the kernel, the additional phase creates a multi-spot DSF at the image plane, where each spot exhibits a lateral shift depending on the phase ramp in the corresponding area at the BFP. Intuitively, orientation information is encoded in the relative brightness between the spots, similar to the DH DSF.

Two early methods, the quadrated [Figure 7d(i)] (Backer et al., 2013) and bisected [Figure 7d(ii)] (Backer et al., 2014) DSFs, both use a symmetric partitioning strategy. The quadrated DSF imaged dicyanomethylenedihydrofuran-N-6 (DCDHF-N-6) molecules embedded within polymethyl methacrylate (PMMA) with orientation precisions of $ {\sigma}_{\theta }={1.8}^{\circ } $ and $ {\sigma}_{\phi }={1.7}^{\circ } $ and 2370 photons detected. The bisected DSF is resolved by the 3D position and orientation of SMs attached to microtubules in a BSC-1 cell within an axial range of 500 nm. Similar to the DH DSF, the bisected DSF can also remove orientation-induced localization errors and resolve the axial position $ z $ of an SM using the relative positions of its spots. However, both the quadrated and bisected DSFs exhibit an orientational degeneracy when distinguishing between z-oriented molecules versus isotropic emitters. The tri-spot DSF [Figure 7d(iii)] (Zhang et al., 2018) was later developed to eliminate the degeneracy by creating six linearly independent basis images; i.e., six spots within the image plane are used to estimate all six second-order orientational moments $ \boldsymbol{m} $ . Therefore, it can measure not only the orientation but also the rotational “wobble” of a molecule within a cone of solid angle $ \Omega $ during a camera frame (see Modeling the rotational diffusion of fluorescent molecules for details). It was used to resolve anisotropic emission from fluorescent beads and SMs embedded within polymers, as well as SM orientation and wobble dynamics within supported lipid membranes (Lu et al., 2020). Precisions of $ {\sigma}_{\theta }={6.0}^{\circ } $ and $ {\sigma}_{\phi }={10.6}^{\circ } $ for measuring orientation and $ {\sigma}_{\Omega}=0.11\pi $ sr for measuring the wobble cone angle were reported for 1300 signal photons and 5 background photons per pixel detected. The duo-spot DSF [Figure 7d(iv)] (Lu et al., 2020) was also designed based on the intensity distribution at the BFP specifically for distinguishing in-plane molecules from $ z $ -oriented molecules. For in-plane molecules, two spots with similar brightness were observed in each polarization channel [Figure 7d(iv)(1,2)]; for z-oriented molecules, only one spot in each channel will be detected [Figure 7d(iv)(3)]. It was also used in lipid membrane imaging, yielding precisions of $ {\sigma}_{\theta }={8.4}^{\circ } $ , $ {\sigma}_{\phi }={21.8}^{\circ } $ , and $ {\sigma}_{\Omega}=0.16\pi $ sr with 950 signal photons and 5 background photons per pixel detected.

The vortex DSF is implemented by adding a vortex phase plate, which is usually used in STED microscopy to create a donut-shaped depletion laser pattern, to the emission path. The features of this DSF are opposite of those of the standard DSF (Figure 7b); images corresponding to in-plane molecules exhibit a donut shape [Figure 7e(1)], whereas images corresponding to $ z $ -oriented molecules are single-focused spots [Figure 7e(3)]. The orientational measurement precisions of both the unpolarized [Figure 7e(i)] (Hulleman et al., 2021) and ( $ x $ and $ y $ ) polarized [Figure 7e(ii)] (Ding and Lew 2021) vortex DSFs are superior to those of the analogous standard DSFs. The unpolarized vortex DSF was used to resolve different periodicities of plectoneme structures where two helices intertwine with each other within supercoiled DNA. Imaging λ-DNA on a tilted coverslip, it achieved an orientation precision of $ {\sigma}_{\theta }={3.1}^{\circ } $ , $ {\sigma}_{\phi }={5.5}^{\circ } $ , and a wobble precision of $ {\sigma}_{\Omega}=0.37 $ sr (converted from the published measurements), as well as localization precisions of $ {\sigma}_{xy}=5.6 $ nm along the lateral direction and $ {\sigma}_z=27 $ nm along the axial direction with 4000 signal photons and 10 background photons/pixel detected (Hulleman et al., 2021). The polarized vortex DSF achieves orientation precisions of $ {\sigma}_{\theta }={4.5}^{\circ } $ and $ {\sigma}_{\phi }={7.7}^{\circ } $ and a lateral localization precision of $ {\sigma}_{xy}=12.5 $ nm with 510 signal photons and 2.3 background photons/pixel detected. Further, the authors show that this DSF is capable of resolving anisotropic wobbling, i.e., a molecule that diffuses rotationally within an elliptical cone (Zhou et al., 2024b), within a single camera frame (see Modeling the rotational diffusion of fluorescent molecules for details). They find that NR molecules bound within DPPC SLBs tend to wobble along the direction parallel to acyl chains; whereas those bound to Aβ42 oligomers exhibit a wide distribution for wobble anisotropy.

Another phase mask was designed by numerical optimization, i.e., maximizing the Fisher information (Moon and Stirling, 2000) of measuring the orientational second moments, similar to that used to create the tetrapod DSF (Shechtman et al., 2015) for 3D SMLM. This method, termed pixel-wise DSF engineering for measuring the 3D orientation and localization (pixOL) (Wu et al., 2022a), produced a phase mask with a smaller phase gradient compared to other engineered phase masks. The basis images exhibit similar features to those of the $ x $ and $ y $ -polarized ( $ xy $ Pol) standard DSF when in focus (Figure 7g, purple). However, it breaks the defocus symmetry of the standard DSF and is more suitable for 3D imaging (Figure 7g, green). Over a 700 nm depth range, the pixOL DSF achieves an orientation precision of $ {\sigma}_{\boldsymbol{\mu}}={4.1}^{\circ } $ (an arc length on the orientation unit sphere, i.e., a geometric average between $ {\sigma}_{\theta } $ and $ {\sigma}_{\phi } $ that accounts for their correlation), a wobble precision of $ {\sigma}_{\Omega}=0.44 $ sr, and localization precisions of $ {\sigma}_{xy}=23.2 $ nm along the lateral direction and $ {\sigma}_z=19.5 $ nm with 2500 signal photons and 3 background photons/pixel detected. As a proof of principle, the authors demonstrate this DSF by imaging NR molecules bound within a spherical SLB consisting of DPPC and 40% cholesterol. The pixOL measurements showed that NR molecules are highly constrained to an orientation perpendicular to the membrane—an ideal calibration target for 3D SMOLM.

Beyond classical optimization, machine learning can also be used for phase mask design in a manner similar to technologies developed for 3D SMLM (Nehme et al., 2020). Here, the goal is to use deep learning to explore the high dimensional design space robustly and construct a phase mask that is optimal for a specific measurement task; i.e., the optimized design achieves a minimized error rate. Jointly minimizing the error of measuring 3D position and 3D orientation, Jouchet et al. used this technique to produce the Arrowhead phase mask (Jouchet et al., 2023). Imaging single DCDHF-N-6 molecules within PMMA, the arrowhead mask achieves experimental precisions of $ {\sigma}_{\boldsymbol{\mu}}={4.3}^{\circ } $ for orientation, $ {\sigma}_{xy}=11 $ nm for lateral position, and $ {\sigma}_z=33.6 $ nm for axial position with a median of 3900 signal photons and 80 background photons/pixel detected (see Image analysis methods for details on Arrowhead DSF analysis and estimation).

Polarization modulation

Besides modulating the phase at the BFP, one can also manipulate fluorescence polarization, i.e., apply spatially varying polarization rotation in the BFP before polarization splitting, to measure SM orientation. In this case, the cross elements $ {J}_{12}\left(u,v\right) $ and $ {J}_{21}\left(u,v\right) $ are no longer zero. For polarization-only modulation, the optical component can be described by a spatially varying real tensor, e.g., separating the radially and azimuthally polarized fluorescence by placing a vortex (half) wave plate (Zhang et al., 2022), or equivalently, a y-phi mask (Backlund et al., 2016) or two SLMs (Hashimoto et al., 2015), at the BFP. The design rationale is based on the toroidal emission pattern of dipole emitters; a molecule oriented along the optical axis $ z $ emits radially polarized light. Separating the radially polarized light from the azimuthal polarization improves one’s sensitivity to detect changes in polar angle; the relevant real tensor is given by

(47) $$ {\displaystyle \begin{array}{c}\boldsymbol{J}=\left[\begin{array}{cc}\cos {\phi}_{\mathrm{ff}}& \sin {\phi}_{\mathrm{ff}}\\ {}-\sin {\phi}_{\mathrm{ff}}& \cos {\phi}_{\mathrm{ff}}\end{array}\right].\end{array}} $$

This method, termed the radially and azimuthally polarized (raPol) standard DSF (Zhang et al., 2022), exhibits excellent orientation measurement performance; with 5000 signal photons and 30 background photons/pixel detected, it achieves precisions of $ {\sigma}_{\theta }={1.7}^{\circ } $ , $ {\sigma}_{\phi }={1.4}^{\circ } $ , and $ {\sigma}_{\Omega}=0.16 $ sr. Further, due to its more compact size compared to other engineered DSFs (Figure 7f), it exhibits a localization precision of $ {\sigma}_{xy}=2.2 $ nm under the aforementioned SBR, comparable to that using the $ x $ and $ y $ polarized standard DSF. Its detectability under low SBR is also comparable to $ xy $ Pol and is superior to those of other engineered DSFs. It has been shown that measuring molecule locations in the azimuthally polarized channel removes orientation-induced localization bias (Backlund et al., 2016). Given its superior sensitivity to detecting $ z $ -oriented molecules [Figure 7f(3)] and excellent localization and orientation precision (Zhang and Lew, 2021b), it was used to image NR molecules within planar SLBs and resolved coupling between absorption and emission dipole orientations. It also detected changes in translational and rotational diffusions of NR molecules induced by cholesterol (Zhang et al., 2022).

The recently introduced Multi-View Reflector (MVR) microscope (Figure 7j) further extends SMOLM’s capabilities (Zhang et al., 2023). In addition to separating radially and azimuthally polarized fluorescence, it incorporates two sets of pyramid mirrors to split light at the BFP and creates eight detection channels. The system’s DSF exhibits similar characteristics to multi-spot DSFs; the relative intensity and position of spots within each channel indicate the orientation and axial position of the emitter, respectively. Despite the complexity of this system (Figure 8c), it showcases remarkable robustness to background fluorescence; since background photons are spread across the eight detection channels along with the signal photons, its effective SBR is better than those of multi-spot DSFs. While imaging SLBs on silica spheres, the MVR microscope experimentally achieves an isotropic 3D localization precision of 10.9 nm and orientation precision of $ {2.0}^{\circ } $ across a 1.5-micron axial range. It also showed great robustness against aberrations induced by refractive-index mismatches and was used for studying Aβ42-membrane interactions and heterogeneities in fixed HEK-293T cell membranes.

Unlike phase-only and polarization-only modulations of the fluorescence at the BFP, Coordinate and Height super-resolution Imaging with Dithering and Orientation (CHIDO) (Ramkhalawon et al., 2013; Vella and Alonso, 2019; Curcio et al., 2020) uses a single stressed-engineered optic (SEO) to modulate both phase and polarization simultaneously. Its complex tensor is given by

(48) $$ {\displaystyle \begin{array}{c}\boldsymbol{J}=\cos \left(\frac{c_{\mathrm{st}}{\rho}_{\mathrm{BFP}}}{2}\right)\left[\begin{array}{cc}1& 0\\ {}0& 1\end{array}\right]+j\sin \left(\frac{c_{\mathrm{st}}{\rho}_{\mathrm{BFP}}}{2}\right)\left[\begin{array}{cc}\cos {\phi}_{\mathrm{ff}}& -\sin {\phi}_{\mathrm{ff}}\\ {}-\sin {\phi}_{\mathrm{ff}}& -\cos {\phi}_{\mathrm{ff}}\end{array}\right].\end{array}} $$

It creates a set of linearly independent basis images that rotate when a molecule is defocused (Figure 7h). The precise features and the performance of this DSF depend on the stress coefficient $ {c}_{\mathrm{st}} $ ( $ 1.2\pi $ in Figure 7h). With 40,000 signal photons detected, CHIDO experimentally achieves a lateral localization precision of $ {\sigma}_{xy}=13 $ nm, an axial localization precision of $ {\sigma}_z=50 $ nm, and a precision for measuring the wobble angle $ {\sigma}_{\Omega}=0.9 $ for molecules attached to F-actin filaments whose tilt angles from the fiber are within $ {20}^{\circ } $ .

Choosing the appropriate technique for SMOLM

With a myriad of techniques developed in recent years, choosing an SMOLM design can be daunting. Recent studies adapt classical and quantum estimation theory to find optimal imaging systems for both SMLM (Tsang, 2015; Tsang et al., 2016; Lupo and Pirandola, 2016; Rehacek et al., 2017; Ang et al., 2017; Backlund et al., 2018; Tsang, 2019; Prasad and Yu, 2019) and SMOLM (Zhang and Lew, 2019, 2020, 2021a; Beckwith and Yang, 2021). For example, in the absence of background photons, one must minimize the phase variation in the detected optical field in order to measure the molecular orientation of rotationally fixed molecules as precisely as possible (Zhang and Lew, 2020). With these performance limits, one can compare existing methods and evaluate how efficient a technique is at extracting maximum information from a fixed number of signal photons.

Here, we recommend choosing specific criteria based upon the target sample and measurement task. Various advantages and limitations of each approach are summarized in Table 2. In absorption-based techniques, the choice of excitation and detection strategies depends on the expected orientation and rotational dynamics of the target molecules. When most molecules align perpendicularly to the optical axis, using a standard epifluorescence excitation beam traveling along the optical axis of the objective lens with multiple in-plane polarizations is adequate for studying orientational characteristics; see, for example, (Backer et al., 2016). In contrast, when the molecular orientation exhibits a prominent axial component, it becomes necessary to either integrate emission polarization separation or implement 3D polarization modulation through tilted illumination (Thorsen et al., 2022).

Table 2. Applications, benefits, and limitations of techniques for SMOLM

For emission-based methods, we follow a recent work (Zhang and Lew, 2021b) to compare some of the aforementioned DSFs using Fisher information. From estimation theory, the best-possible standard deviation of any unbiased estimator is given by the square root of the Cramér-Rao lower bound (CRB), which is the inverse of the Fisher information matrix (Chao et al., 2016). Critically, DSFs whose spatial intensity distribution $ \boldsymbol{I} $ changes more strongly with orientation exhibit superior sensitivity for measuring SM orientation. DSFs with more compact footprints, e.g., $ xy $ Pol, raPol, vortex DSFs, pixOL, and CHIDO, generally exhibit superior measurement precision compared to DSFs that are spread over a larger area, e.g., the DH DSF and multi-spot DSFs. Intuitively, they also are easier to detect above noise and therefore are more suitable in SM experiments whose photon budgets are limited. As shown in Figure 9a-d, raPol exhibits the highest overall position-orientation precision in thin samples for SMs at the coverslip-sample interface when the sample is defocused by approximately 200 nm. Other compact DSFs also perform well, similarly outperforming larger DSFs including the MVR microscope. However, a key disadvantage is that the subtle features of the DSFs must be measured with high sensitivity to obtain precise and accurate estimates of SM orientations and positions. Therefore, performance may degrade due to optical aberrations or miscalibration of the system. For example, CHIDO performs 5–6 times worse in experiments compared to the CRB (Curcio et al., 2020; Hulleman et al., 2021). Moreover, performance degradation may be worse when imaging deeply within biological tissues. In contrast, larger DSFs that encode SM orientations in the relative brightness of their spots and SM (axial) position in the positions of the spots are more robust to optical aberrations; precise shape-fitting is not as critical. For example, the MVR microscope exhibits both excellent measurement precision and robustness against aberrations. Further, it exhibits better precision compared to compact DSFs in thick samples over a depth range of 1.5 microns (Figure 9e–h). However, it requires careful alignment of a complex optical system.

Figure 9. Best-possible precisions, given by the square root of the Cramér-Rao lower bound, of measuring SM position and orientation in (a–d) thin and (e–h) thick samples using various SMOLM techniques. For thin samples, we report precisions of (a) the average orientation $ \boldsymbol{\mu} $ , (b) wobble angle $ \Omega $ , (c) 2D position $ x $ , and (d) combined precision for orientational second moments $ \boldsymbol{m} $ and 2D position $ x $ as a function of nominal focal plane position $ {z}_f $ . All SMs are positioned at $ z=0 $ nm (at the glass-media interface). For thick samples, we report precisions of (e) average orientation $ \boldsymbol{\mu} $ , (f) wobble angle $ \Omega $ , (g) 3D position $ \boldsymbol{r} $ , and (h) combined precision for orientational second moments $ \boldsymbol{m} $ and 3D position $ \boldsymbol{r} $ as a function of molecular position $ z $ . The nominal focal plane is set at $ {z}_f=1200 $ nm. For all simulations, we assume that the sample has a refractive index $ {n}_2=1.33 $ (equal to that of water) and that 5000 signal photons and 40 background photons per pixel total across all channels are collected. See (Zhang and Lew, 2021b) for details on how each quantity is defined and calculated.

Image analysis methods

Accurately and precisely estimating the position and orientation of molecules is crucial for SMOLM; a selection of publicly available software is summarized in Table 3. Many SMOLM algorithms separate the detection and estimation tasks; they first detect and localize SMs and then subsequently estimate their orientations (Figure 10a). For example, to detect smaller DSFs such as pixOL (Wu et al., 2022a), one might use the images of an in-focus emitter or Gaussian DSF for detection and localization. Orientation estimation and (3D) position refinement can be achieved using pattern matching (Patra et al., 2004; Aguet et al., 2009) or maximum likelihood estimation (MLE) (Hulleman et al., 2021). In contrast, 2D and/or 3D localization of the double-helix DSF and multi-spot DSFs involve localizing the spots, either by fitting Gaussian spots (Backlund et al., 2012; Backer et al., 2014) or employing other algorithms like ThunderSTORM (Ovesný et al., 2014; Zhang et al., 2018). The orientation can be calculated by using the spot brightness ratio or directly estimated using an MLE.

Table 3. Publicly available image analysis software for SMOLM

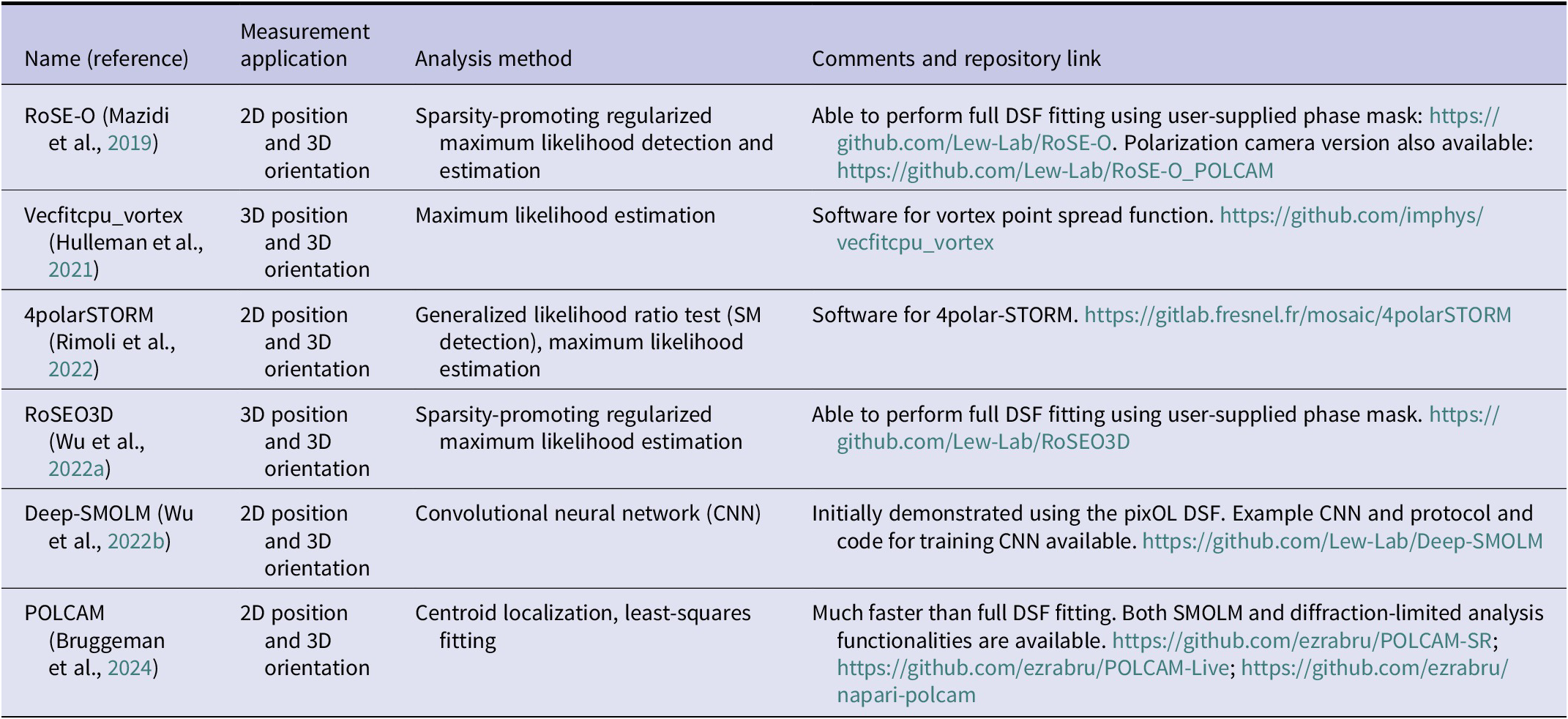
Figure 10. Workflow of detection and estimation algorithms in SMOLM. (a) A raw fluorescence image can be processed using (i) an SM detection algorithm. (ii) The detected SM images can be fitted to the forward imaging model using an MLE; a reconstruction of the raw image using the fit parameters is shown in (iii). (b) The image can also be fitted to the forward imaging model using a sparsity-promoting MLE (reconstruction shown in (b)), or (c) through a (i) convolutional neural network that generates an (ii) upsampled stack representing the position and orientation of SMs. The final output of these algorithms is a list of SM positions and orientations.

Here, we show MLE for estimating the second-order orientational moments $ \boldsymbol{m} $ . Other orientational parameters, such as the Stokes parameters, can be estimated similarly as long as a forward model is written that explicitly models both signal and noise within the detected images. We assume that the number of detected photons at pixel $ i $ follows a Poisson distribution, i.e., $ {\hat{I}}_i\sim \mathrm{Poisson}\left({I}_i+{b}_i\right) $ , where $ {I}_i $ is given by Eq. (45) and $ {b}_i $ represents the expected background. Therefore, the estimated brightness and the second-order moment vector are estimated by minimizing the Poisson negative log-likelihood (NLL), i.e.,

(49) $$ {\displaystyle \begin{array}{c}\left(\hat{s},\hat{\boldsymbol{m}}\right)=\underset{s,\boldsymbol{m}}{\mathrm{argmin}}\left[{\sum}_i{\hat{I}}_i\log \frac{I_i\left(s,\boldsymbol{B},\boldsymbol{m}\right)+{b}_i}{b_i}-{I}_i\right].\end{array}} $$

This equation can be further refined using a first-order approximation by including the gradient of $ \boldsymbol{B} $ with respect to the molecule’s 3D position for robust, computationally efficient subpixel-scale localization (Mazidi et al., 2019). The second moments $ \hat{\boldsymbol{m}} $ can be mapped to the first-order transition dipole moments $ \hat{\boldsymbol{\mu}} $ and wobble $ \hat{\Omega} $ using a Fisher information (FI)-weighted, mean square-error cost function, i.e.,

(50) $$ {\displaystyle \begin{array}{c}\left(\hat{\boldsymbol{\mu}},\hat{\Omega}\right)=\underset{\boldsymbol{\mu}, \Omega}{\mathrm{argmin}}\left\{{\left[{\boldsymbol{m}}^{\prime}\left(\boldsymbol{\mu}, \Omega \right)-\hat{\boldsymbol{m}}\right]}^{\top}\;\mathbf{FI}\;\left[{\boldsymbol{m}}^{\prime}\left(\boldsymbol{\mu}, \Omega \right)-\hat{\boldsymbol{m}}\right]\right\},\end{array}} $$

where $ {\boldsymbol{m}}^{\prime } $ is given by Eq. (37).

A significant drawback of separating the detection and estimation algorithms is the difficulty in handling high molecular density, thus restricting acquisition speed. An alternative strategy is to leverage the inherent sparsity of SM blinking in SMOLM experiments through a regularized MLE (Figure 10b) and solve the molecular detection and position and orientation estimation tasks simultaneously. Instead of minimizing the Poisson NLL, a sparsity-promoting regularizer, e.g., the $ \ell $ 2 norm of intensity-weighted second moments $ \hat{\boldsymbol{m}} $ associated with each spatial grid point, is added to the cost function. Mazidi et al. demonstrated that such an algorithm performs closely to the theoretical bound given by the CRB even in highly overlapping areas (Mazidi et al., 2019). However, one limitation, especially for 3D SMOLM, is that iterative optimization algorithms tend to be computationally expensive and slow (Bruggeman et al., 2024).

Recently, deep learning, particularly convolutional neural networks (CNNs), has emerged as a powerful tool for SM image analysis due to its superior pattern recognition capabilities. Inspired by recent advancements in CNN-based 3D localization algorithms (Möckl et al., 2020; Nehme et al., 2020; Speiser et al., 2021), Wu et al. introduced an approach named Deep-SMOLM to detect SMs and simultaneously estimate their 2D positions and 3D orientations (Wu et al., 2022b) (Figure 10c). Two polarized images are input to the NN, and six upsampled images are produced, each representing the 2D spatial distribution of one of the six second-order orientational moments. A post-processing step converts these images into a list of 2D positions and 3D orientations. Using both simulated and experimentally acquired images with highly overlapping pixOL DSFs, the NN demonstrates measurement precision close to the theoretical limit (3.8° orientation, 0.32 sr wobble angle, and 8.5 nm lateral position using 1000 detected photons) and a tenfold improvement in speed over iterative approaches. The aforementioned Arrowhead DSF also makes use of an NN for position and orientation estimation (Jouchet et al., 2023). First, SMs within the field of view are coarsely located using the standard DSF (e.g., by turning off the SLM), and then centered and cropped ROIs containing the Arrowhead DSF are fed to the analysis NN to produce 3D position and 3D orientation estimates. The NN was able to analyze ~150,000 DSF images at a rate of 4 ms per molecule. Clearly, the use of NNs for SMOLM image analysis holds tremendous promise for accelerating precise 6D measurements of SMs.

Conclusion and outlook

In this review, we have explored the latest advancements in SMOLM, highlighting its expanding role across various research areas. Our discussion spans a range of innovative labeling techniques and advanced imaging methods that offer unparalleled insights into molecular orientations and dynamics. Recent work highlights the crucial roles of fluorescent probes for visualizing the complex organization and dynamics of actin filaments, DNA structures, amyloid aggregates, and cellular membranes, among others. Additionally, we have reviewed various imaging techniques that underscore both the potential and the challenges of SMOLM. These methods aim to optimize the measurement of molecular orientations from multiple perspectives, including the fundamental physics of light-matter interactions as well as principles of estimation theory. Further, the incorporation of advanced computational tools improves the accuracy and precision of these measurements. Overall, the insights presented in this review underscore how SMOLM advances our understanding of biological and biochemical processes at the nanoscale.

As we envision the future of SMOLM, several developments are key to further expanding its capabilities and adoption in biophysical studies. The development of new fluorescent probes is crucial for advancing SMOLM (Grimm et al., 2023). Future probes should aim for enhanced photostability, higher quantum yield, and improved binding specificity to target structures, while also minimizing perturbative effects. These improvements would significantly enhance the SBR in SMOLM measurements by boosting signal levels and reducing the off-structure background. Improved brightness (photons/s) is particularly critical when studying the orientational dynamics of SMs in the complex environments of biological systems. Engineering new probes that specifically bind to certain biomarkers or protein domains, react to cellular environmental changes, and change their optical properties in response to specific chemical interactions and environments will also be particularly beneficial (Kikuchi et al., 2023; Wu et al., 2023; Bhuskute et al., 2024; Erkamp et al., 2024; Zhu et al., 2024).

Continuous innovation in imaging systems is essential for overcoming the limitations of existing methods and achieving accurate, precise, and robust measurements. Measurement precision could be further enhanced by using adaptive hardware, where the imaging system is iteratively updated to progressively measure the orientation of a single molecule more precisely, as is done for molecular positions in MINFLUX (Balzarotti et al., 2017; Cnossen et al., 2020; Gwosch et al., 2020; Weber et al., 2023; Sahl et al., 2024). Recent developments in single-photon avalanche diode (SPAD) array detectors (Bucci et al., 2024) have the potential to provide precise photon arrival timing as well as location information for SMOLM, thereby enabling SMOLM to probe faster biochemical processes including protein folding and conformational dynamics. Existing emission-based methods (engineered DSFs) could be combined with selective illumination techniques like light-sheet illumination (Gustavsson et al., 2018; Nelson et al., 2024) to improve the SBR. Further, measuring higher-order orientational moments, i.e., measuring absorption and emission dipole moments simultaneously using both excitation and emission modulation, could enable more detailed studies of rotational dynamics with improved angular resolution (Chen et al., 2024b). In these ways, each precious fluorescence photon can be utilized more efficiently for higher precision measurements.

Advanced computational imaging techniques will also play a significant role in the future of SMOLM. The integration of modern computer vision methodologies, such as neural fields (Park et al., 2019; Mildenhall et al., 2022; Zhou et al., 2023; Zhang et al., 2024) or diffusion models (Waibel et al., 2023; Hui et al., 2024), could potentially improve estimation performance, allowing for the extraction of more detailed information from larger and more complex datasets. Especially when engineered DSFs and estimation algorithms are optimized jointly, these computational advances could potentially handle images with higher molecular density, thereby improving imaging speed and overall data throughput.

With numerous opportunities for technological innovation, we expect SMOLM to have significant contributions to elucidating the nanoscale organization and dynamics of biological and chemical systems in the near future. Higher precision measurements of both 3D position and 3D orientation have a unique power to reveal new insights, and we eagerly anticipate SMOLM to have far-ranging applications from understanding fundamental biological processes to developing new materials and nanotechnologies.