Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-11T08:40:59.826Z Has data issue: false hasContentIssue false
  • English
  • Français

Recherche à voisinage variable de graphes extrémaux 13. à propos dela maille*

Published online by Cambridge University Press:  08 April 2006

Mustapha Aouchiche  and
Pierre Hansen
Mustapha Aouchiche
Affiliation:
Département de mathématiques et génie industriel, École Polytechnique de Montréal, Qc, Canada; Mustapha.Aouchiche@gerad.ca
Pierre Hansen
Affiliation:
GERAD et Service de l'enseignement des méthodes quantitatives de gestion HEC Montréal, Qc, Canada; Pierre.Hansen@gerad.ca
Get access

Abstract

Le système AutoGraphiX (AGX1 et AGX2) permet,parmi d'autres fonctions, la génération automatique de conjectures enthéorie des graphes et, dans une version plus récente, la preuve automatique de conjectures simples. Afind'illustrer ces fonctions et le type de résultats obtenus, nous étudions systématiquement ici des conjecturesobtenues par ce système et de la forme $\underline{b}_{n} \, \le \, g\,\oplus \,i \, \le \, \overline{b}_{n}$ 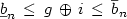où g désigne la maille (ou longueur du plus petit cycle) du graphe G=(V, E), i un autre invariant choisi parmi le nombre de stabilité, le rayon, le diamètre, le degré minimum, moyen ou maximum, $\underline{b}_{n} $ 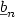et $ \overline{b}_{n} $ 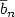des fonctions de l'ordre n = |V| de G les meilleures possibles, enfin $ \oplus $ 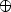correspond à une des opérations +,-,×,/. 48 telles conjectures sont obtenues: les plus simples sont démontréesautomatiquement et les autres à la main. De plus 12 autres conjecturesouvertes et non encore étudiées sont soumises aux lecteurs.

Keywords

GrapheinvariantconjectureAGXmaille.
Type
Research Article
Information
RAIRO - Operations Research , Volume 39 , Issue 4 , October 2005 , pp. 275 - 293
Copyright
© EDP Sciences, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

M. Aouchiche, J.-M. Bonnefoy, A. Fidahoussen, G. Caporossi, P. Hansen, L. Hiesse, J. Lacheré and A. Monhait, Variable Neighborhood Search for Extremal Graphs. 14. The AutoGraphiX 2 System. Global Optimization: From Theory to Implementation, edited by L. Liberti and N. Maculan, Springer (2005).
M. Aouchiche, G. Caporossi and P. Hansen, Automated Comparison of Graph Invariants. Les Cahiers du GERAD, G–2005–40, rapport technique, HEC Montréal (2005) 21 pages.
S. Belhaiza, N.M.M. de Abreu, P. Hansen and C.S. Oliveira, Variable Neighborhood Search for Extremal Graphs 11. Bounds on Algebraic Connectivity, edited by D. Avis, A. Hertz and O. Marcotte, Graph Theory and Combinatorial Optimization, Dordrecht, Kluwer (2005) 1–16.
Brigham, R. C. and Dutton, R. D., Compilation, A of Relations between Graph Invariants. Networks 21 (1991) 421–455. CrossRef
Caporossi, G., Cvetkovic, D., Gutman, I. and Hansen, P., Variable Neighborhood Search for Extremal Graphs. 2. Finding Graphs with Extremal Energy. J. Chem. Inform. Comput. Sci. 39 (1999) 984–996. CrossRef
Caporossi, G., Gutman, I. and Hansen, P., Variable Neighborhood Search for Extremal Graphs. 4. Chemical Trees with Extremal Connectivity Index. Comput. Chem. 23 (1999) 469–477. CrossRef
Caporossi, G. and Hansen, P., Variable Neighborhood Search for Extremal Graphs. I. The AutoGraphiX System. Discrete Math. 212 (2000) 29–44. CrossRef
Caporossi, G. and Hansen, P., Variable Neighborhood Search for Extremal Graphs. V. Three Ways to Automate Finding Conjectures. Discrete Math. 276 (2004) 81–94. CrossRef
Chung, F.R.K., The Average Distance and the Independence Number. J. Graph Theory 12 (1988) 229–235. CrossRef
Cvetković, D., Simić, S., Caporossi, G. and Hansen, P., Variable Neighborhood Search for Extremal Graphs. III. On the Largest Eigenvalue of Color-Constrained Trees. Linear Multilinear Algebra 49 (2001) 143–160. CrossRef
D. Cvetković and S. Simić, Graph Theoretical Results Obtained by the Support of the Expert System “GRAPH” - an Extended Survey. In [13].
Fajtlowicz, S., Conjectures, On of Graffiti. Discrete Math. 72 (1988) 113–118. CrossRef
Graphs and Discovery. DIMACS Series in Discrete Math. and Theoretical Computer Science, edited by S. Fajtlowicz, P. Fowler, P. Hansen, M. Janowitz and F. Roberts, Providence, AMS (2005).
I. Gutman, P. Hansen and H. Mélot, Variable Neighborhood Search for Extremal Graphs. 10. Comparison of Irregularity Indices for Chemical Trees. J. Chem. Inform. Comput. Sci. (2005, to appear).
Hansen, P., Computers in Graph Theory. Graph Theory Notes of New York 43 (2002) 20–34.
P. Hansen, How Far Is, Should and Could Be Conjecture-Making in Graph Theory an Automated Process ? In [13].
Hansen, P. and Mélot, H., Variable Neighborhood Search for Extremal Graphs. 6. Analyzing Bounds for the Connectivity Index. J. Chem. Inform. Comput. Sci. 43 (2003) 1–14. CrossRef
P. Hansen and H. Mélot, Variable Neighborhood Search for Extremal Graphs. 9. Bounding the Irregularity of a Graph. In [13].
Hansen, P. and Mladenović, N., Variable Neighborhood Search: Principles and Applications. Eur. J. Oper. Res. 130 (2001) 449–467. CrossRef
Mladenović, N. and Hansen, P., Variable Neighborhood Search. Comput. Oper. Res. 24 (1997) 1097–1100. CrossRef
Nordhaus, E.A. and Gaddum, J.W., Complementary Graphs, On. Amer. Math. Monthly 63 (1956) 175–177. CrossRef
B.A. Smith, Private communication (2004).
P. Turán, Eine Extremalaufgabe aus der Graphentheorie. (Hungarian) Mat. Fiz. Lapok 48 (1941) 436–452.
Written on the wall. Electronic file available from http://math.uh.edu/~clarson/ (1999).
* Cet article est le treizième de la série “Variable Neighborhood Search for Extremal Graphs” publiée à partir de 1998 (voir bibliographie). La recherche présentée a bénéficié du support de la Chaire HEC en Exploitation de Données et de la subvention CRSNG No. 105574-1998.