Published online by Cambridge University Press: 18 July 2007
In this paper we will deal with the balance properties of the infinite binary words associated to β-integers when β is a quadratic simple Pisot number. Those words are the fixed points of the morphisms of the type $\varphi(A)=A^pB$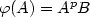 , $\varphi(B)=A^q$
, $\varphi(B)=A^q$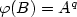 for $p\in\mathbb N$
for $p\in\mathbb N$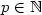 , $q\in\mathbb N$
, $q\in\mathbb N$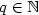 , $p\geq q$
, $p\geq q$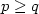 , where $\beta=\frac{p+\sqrt{p^2+4q}}{2}$
, where $\beta=\frac{p+\sqrt{p^2+4q}}{2}$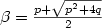 . We will prove that such word is t-balanced with $t=1+\left[(p-1)/(p+1-q)\right]$
. We will prove that such word is t-balanced with $t=1+\left[(p-1)/(p+1-q)\right]$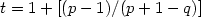 . Finally, in the case that p < q it is known [B. Adamczewski, Theoret. Comput. Sci.273 (2002) 197–224] that the fixed point of the substitution $\varphi(A)=A^pB$
. Finally, in the case that p < q it is known [B. Adamczewski, Theoret. Comput. Sci.273 (2002) 197–224] that the fixed point of the substitution $\varphi(A)=A^pB$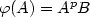 , $\varphi(B)=A^q$
, $\varphi(B)=A^q$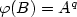 is not m-balanced for any m. We exhibit an infinite sequence of pairs of words with the unbalance property.
is not m-balanced for any m. We exhibit an infinite sequence of pairs of words with the unbalance property.