Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T17:42:02.609Z Has data issue: false hasContentIssue false
  • English
  • Français

Workspace optimization of a class of zero-torsion parallel wrists

Published online by Cambridge University Press:  23 May 2018

Yuanqing Wu Open the ORCID record for Yuanqing Wu [Opens in a new window]  and
Marco Carricato
Yuanqing Wu*
Affiliation:
Department of Industrial Engineering, University of Bologna, Viale Risorgimento 2, 40136 Bologna, BO, Italy. E-mail: marco.carricato@unibo.it
Marco Carricato
Affiliation:
Department of Industrial Engineering, University of Bologna, Viale Risorgimento 2, 40136 Bologna, BO, Italy. E-mail: marco.carricato@unibo.it
*
*Corresponding author. E-mail: yuanqing.wu@unibo.it
Get access Rights & Permissions [Opens in a new window]

Summary

We present singularity-free workspace optimization of a class of two-degree-of-freedom (2-DoF) parallel wrists with large rotation range capability. The wrists in consideration are kinematically equivalent to two families of 2-DoF homokinetic couplings. The first family comprises fully parallel wrists with N (N ≥ 3) double-universal (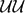$\mathcal{UU}$) legs. The second family comprises spherical N-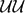$\mathcal{UU}$ parallel wrists with interconnecting revolute (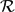$\mathcal{R}$) joints. Both families belong to the more general class of zero-torsion parallel manipulators, and are, therefore, collectively referred to as zero-torsion wrists (ZTWs). We carry out a unified singularity-free workspace optimization by utilizing geometric properties of zero-torsion motion manifolds. Our work may serve as a conceptual guide to the design of ZTWs for large tilt-angle applications.

Keywords

Symmetric subspaceParallel mechanismSingularity analysisWorkspace optimization
Type
Articles
Information
Robotica , Volume 37 , Special Issue 7: Computational Kinematics Conference, CK 2017 , July 2019 , pp. 1174 - 1189
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Merlet, J.-P., Parallel Robots, volume 128 (Springer Science & Business Media, Dordrecht, The Netherlands, 2006).Google Scholar
Gosselin, C. and Angeles, J., “Singularity analysis of closed-loop kinematic chains,” IEEE Trans. Robot. Autom. 6 (3), 281–290 (1990).CrossRefGoogle Scholar
Conconi, M. and Carricato, M., “A new assessment of singularities of parallel kinematic chains,” IEEE Trans. Robot. 25 (4), 757–770 (2009).CrossRefGoogle Scholar
Chablat, D. and Wenger, P., “Architecture optimization of a 3-DOF translational parallel mechanism for machining applications, the orthoglide,” IEEE Trans. Robot. Autom. 19 (3), 403–410 (2003).CrossRefGoogle Scholar
Pierrot, F., Reynaud, C. and Fournier, A., “Delta: A simple and efficient parallel robot,” Robotica 8 (2), 105–109 (1990).CrossRefGoogle Scholar
Kong, X. and Gosselin, C. M., “Type synthesis of 3-DOF translational parallel manipulators based on screw theory,” J. Mech. Des. 126 (1), 83–92 (2004).CrossRefGoogle Scholar
Pierrot, F., Nabat, V., Company, O., Krut, S. and Poignet, P., “Optimal design of a 4-DOF parallel manipulator: From academia to industry,” IEEE Trans. Robot. 25 (2), 213–224 (2009).CrossRefGoogle Scholar
Gosselin, C. M. and Hamel, J.-F., “The Agile Eye: A High-Performance Three-Degree-of-Freedom Camera-Orienting Device,” Proceedings of the IEEE International Conference on Robotics and Automation, IEEE, San Diego, CA, USA (1994) pp. 781–786.Google Scholar
Vischer, P. and Clavel, R., “Argos: A novel 3-DoF parallel wrist mechanism,” Int. J. Robot. Res. 19 (1), 5–11 (2000).CrossRefGoogle Scholar
Rosheim, M. E. and Sauter, G. F., “New High-Angulation Omni-Directional Sensor Mount,” Proceedings of the International Symposium on Optical Science and Technology, International Society for Optics and Photonics, Seattle, WA, United States (2002) pp. 163–174.Google Scholar
Carricato, M. and Parenti-Castelli, V., “A novel fully decoupled two-degrees-of-freedom parallel wrist,” Int. J. Robot. Res. 23 (6), 661–667 (2004).CrossRefGoogle Scholar
Kong, X. and Gosselin, C. M., “Type synthesis of 3-dof spherical parallel manipulators based on screw theory,” J. Mech. Des. 126 (1), 101–108 (Mar. 2004).CrossRefGoogle Scholar
Hervé, J. M., “Uncoupled actuation of pan-tilt wrists,” IEEE Trans. Robot. 22 (1), 56–64 (2006).CrossRefGoogle Scholar
Wu, Y. and Carricato, M., “Design of a Novel 3-DoF Serial-Parallel Robotic Wrist: A Symmetric Space Approach,” Proceedings of the International Symposium on Robotics Research (ISRR 2015), Sestri Levante, Italy (2015) pp. 389–404.Google Scholar
Bonev, I. A. and Ryu, J., “A new approach to orientation workspace analysis of 6-DOF parallel manipulators,” Mech. Mach. Theory 36 (1), 15–28 (2001).CrossRefGoogle Scholar
Carricato, M., “Decoupled and homokinetic transmission of rotational motion via constant-velocity joints in closed-chain orientational manipulators,” J. Mech. Robot. 1 (4), 041008 (2009).CrossRefGoogle Scholar
Hunt, K. H., “Constant-velocity shaft couplings: A general theory,” J. Eng. Ind. 95 (2), 455–464 (1973).CrossRefGoogle Scholar
Culver, I. H., “Constant velocity universal joint,” US Patent 3,477,249, Nov. 11, 1969.Google Scholar
Sone, K., Isobe, H. and Yamada, K., “High angle active link,” In: Special Issue Special Supplement to Industrial Machines, NTN Corporation, Osaka, Japan (2004).Google Scholar
Kong, X., Yu, J. and Li, D., “Reconfiguration analysis of a two degrees-of-freedom 3-4R parallel manipulator with planar base and platform,” J. Mech. Robot. 8 (1), 011019 (2016).CrossRefGoogle Scholar
Wu, Y., Li, Z. and Shi, J., “Geometric Properties of Zero-Torsion Parallel Kinematics Machines,” Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), IEEE, Taipei, Taiwan (2010) pp. 2307–2312.Google Scholar
Bonev, I. A., Zlatanov, D. and Gosselin, C. M., “Advantages of the Modified Euler Angles in the Design and Control of PKMs,” Proceedings of the Parallel Kinematic Machines International Conference, Citeseer, Chemnitz, Germany (2002) pp. 171–188.Google Scholar
Wu, Y., Löwe, H., Carricato, M. and Li, Z., “Inversion symmetry of the Euclidean group: Theory and application to robot kinematics,” IEEE Trans. Robot. 32 (2), 312–326 (2016).CrossRefGoogle Scholar
Wu, Y. and Carricato, M., “Synthesis and singularity analysis of N-$\mathcal{UU}$ parallel wrists: A symmetric subspace approach,” J. Mech. Robot. 9 (5), 051013-1–051013–11, (Aug. 2017).CrossRefGoogle Scholar
Yu, J., Dong, X., Pei, X. and Kong, X., “Mobility and singularity analysis of a class of two degrees of freedom rotational parallel mechanisms using a visual graphic approach,” J. Mech. Robot. 4 (4), 041006 (2012).CrossRefGoogle Scholar
Murray, R. M., Li, Z., Sastry, S. S. and Sastry, S. S.,” A Mathematical Introduction to Robotic Manipulation (CRC Press, Boca Raton, FL, 1994).Google Scholar
Ben-Horin, P. and Shoham, M., “Application of Grassmann–Cayley algebra to geometrical interpretation of parallel robot singularities,” Int. J. Robot. Res. 28 (1), 127–141 (2009).CrossRefGoogle Scholar
Kanaan, D., Wenger, P., Caro, S. and Chablat, D., “Singularity analysis of lower mobility parallel manipulators using Grassmann–Cayley algebra,” IEEE Trans. Robot. 25 (5), 995–1004 (2009).CrossRefGoogle Scholar
Zoppi, M., Zlatanov, D. and Molfino, R., “On the velocity analysis of interconnected chains mechanisms,” Mech. Mach. Theory 41 (11), 1346–1358 (2006).CrossRefGoogle Scholar
Venanzi, S. and Parenti-Castelli, V., “A new technique for clearance influence analysis in spatial mechanisms,” J. Mech. Des. 127 (3), 446–455 (2005).CrossRefGoogle Scholar
Meng, J., Zhang, D. and Li, Z., “Accuracy analysis of parallel manipulators with joint clearance,” J. Mech. Des. 131 (1), 011013 (2009).CrossRefGoogle Scholar
Meng, J., Zhang, D. and Li, Z., “Assembly Problem of Overconstrained and Clearance-Free Parallel Manipulators,” Proceedings of the IEEE International Conference on Robotics and Automation, IEEE, Roma, Italy (2007) pp. 1183–1188.Google Scholar
Pottmann, H., Peternell, M. and Ravani, B., “An introduction to line geometry with applications,” Comput.-Aided Des. 31 (1), 3–16 (1999).CrossRefGoogle Scholar
Voglewede, P. A. and Ebert-Uphoff, I., “Overarching framework for measuring closeness to singularities of parallel manipulators,” IEEE Trans. Robot. 21 (6), 1037–1045 (2005).CrossRefGoogle Scholar
Bohigas, O., Numerical Computation and Avoidance of Manipulator Singularities Ph.D. Thesis (Universidad Politécnica de Cataluña, 2013).Google Scholar
Chablat, D. and Wenger, P., “A Six Degree-of-Freedom Haptic Device Based on the Orthoglide and A Hybrid Agile Eye,” Proceedings of the ASME 2006 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, American Society of Mechanical Engineers, Philadelphia, Pennsylvania, USA (Sept. 10–13, 2006) pp. 795–802.Google Scholar
Wu, Y., Wang, H. and Li, Z., “Quotient kinematics machines: Concept, analysis, and synthesis,” J. Mech. Robot. 3 (4), 041004 (2011).CrossRefGoogle Scholar
Merlet, J.-P., “Jacobian, manipulability, condition number, and accuracy of parallel robots,” J. Mech. Des. 128 (1), 199–206 (2006).CrossRefGoogle Scholar
Gosselin, C. and Angeles, J., “A global performance index for the kinematic optimization of robotic manipulators,” J. Mech. Des. 113 (3), 220–226 (1991).CrossRefGoogle Scholar
O'Brien, J. F. and Wen, J. T., “Redundant Actuation for Improving Kinematic Manipulability,” Proceedings of the IEEE International Conference on Robotics and Automation, IEEE, Detroit, MI, USA, USA (1999) pp. 1520–1525.Google Scholar
Müller, A., “Redundant Actuation of Parallel Manipulators,” In: Parallel Manipulators, Towards New Applications (InTech, Vienna, Austria, 2008).Google Scholar
Chakarov, D., “Study of the antagonistic stiffness of parallel manipulators with actuation redundancy,” Mech. Mach. Theory 39 (6), 583–601 (2004).CrossRefGoogle Scholar
Li, C., Wu, Y., Wu, J., Shi, W., Dai, D., Shi, J. and Li, Z., “Cartesian Stiffness Evaluation of a Novel 2-DoF Parallel Wrist Under Redundant and Antagonistic Actuation,” Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, IEEE, Tokyo, Japan (2013) pp. 959–964.Google Scholar
Müller, A., “Internal preload control of redundantly actuated parallel manipulators–its application to backlash avoiding control,” IEEE Trans. Robot. 21 (4), 668–677 (2005).CrossRefGoogle Scholar