Published online by Cambridge University Press: 03 March 2010
Detecting the presence of genetically modified plants (adventitious presence of unwanted transgenic plants, AP) from outcrossing species such as maize requires a method that lowers laboratory costs without losing precision. Group testing is a procedure in which groups that contain several units (plants) are analysed without having to inspect individual plants, with the purpose of estimating the prevalence of AP in a population at a low cost without losing precision. When pool (group) testing is used to estimate the prevalence of AP (p), there are sampling procedures for calculating a confidence interval (CI); however, they usually do not ensure precision in the estimation of p. This research proposes a method to determine the number of pools (g), given a pool size (k), that ensures precision in the estimated proportion of AP (that is, it ensures a narrow CI). In addition, the study computes the maximum likelihood estimator of p under pool testing and its exact CI, considering the detection limit of the laboratory, d, and the concentration of AP per unit (c). The proposed sample procedure involves two steps: (1) obtain a sample size that guarantees that the mean width of the CI (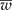 ) is narrower than the desired width (ω); and (2) iteratively increase the sample size until
) is narrower than the desired width (ω); and (2) iteratively increase the sample size until 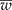 is smaller than the desired width (ω) with a specified degree of certainty (γ). Simulated data were created and tables are presented showing the different possible scenarios that a researcher may encounter. An R program is given and explained that will reproduce the results and make it easy for the researcher to create other scenarios.
is smaller than the desired width (ω) with a specified degree of certainty (γ). Simulated data were created and tables are presented showing the different possible scenarios that a researcher may encounter. An R program is given and explained that will reproduce the results and make it easy for the researcher to create other scenarios.