Electrical excitation of the local earth for resonant, wireless energy transfer

Abstract

Here we demonstrate wireless energy transfer that exploits the conductivity and permittivity of soil to create a potential gradient on the surface around an earthed electrode, distributing electrical energy over the area. This generated surface potential can be amplified using a special standing-wave receiver for harnessing the distributed energy. We have experimentally mapped the surface potential around the electrode and plotted the received energy covering an area of 1200 m². Key operating parameters are determined with a discussion on optimizing the system efficiency. This technique could address the challenge of distributing electrical energy to many low power devices over large outdoor areas without the use of wires.

I. INTRODUCTION

Outdoor environmental monitoring and data collection using low power consuming sensors are critical in many application areas including border security, pollution management, weather forecasting, and agriculture to name a few. Much of this monitoring is carried out in locations where electrical energy is either difficult to deliver, expensive to install, or completely absent. When a large monitoring network is required, with a multitude of sensing devices, it is challenging to supply energy to each device. Recent research has focused on energy harvesting to address the issue of multi-sensor networks where each sensor is equipped with its own energy scavenger [1–4]. Many of these harvesting methods are presently limited to power levels in the microwatt scale [5, 6] due to the surrounding electromagnetic (EM) energy being relatively low. When monitoring devices are equipped with telemetry, the power requirements can drastically increase to the milliwatt range. To address this challenge we propose an approach where energy from a fixed location (battery, generator, solar panel, grid, etc.) is distributed over a desired outdoor area without wires allowing the local EM energy level to be greatly increased. Present wireless techniques using transmitter/receiver electric or magnetic field coupling may not be good candidates as the distances are limited by the magnitude of the fields emitted [7, 8]. Instead, it may be possible to exploit the properties of the natural surroundings to create efficient wireless energy transfer.

In many locations the soil may be good enough to act as an electrical energy conduit. It is well known that soil possesses the ability to support electric currents over a certain frequency band [9–11]. Single-Wire Earth Return systems have exploited this fact for many decades in rural areas where the cost to install two-terminal (forward and return) wiring is not economical [12]. Other examples that use the earth as an electrical conduit include EM geophysics for underground mapping [13, 14] and surface to mine communications [15, 16]. Older literature from the pre-World War I era can be found describing similar techniques [17–20]; the most notable of this literature being the works of Nikola Tesla [19, 20]. Unfortunately, very little scientific documentation exists that supports Tesla's claim of power transfer through the earth. Replications of his patents are observed to only operate in a close range where capacitive coupling between the transmitter and receiver are strong [21]. Tesla's long distance claims have yet to be reproduced and intense controversy remains on this subject. While Tesla's exact methods may never be known, his dream of wireless power is definitely a motivation for researchers. Here we present our own method of wireless energy distribution, which utilizes the earth's surface as the transfer medium to allocate energy over an area. The premise of this work lies with creating an oscillating vertical dipole within the earth.

II. EXPERIMENTAL METHODS AND THEORY

Figure 1 depicts a diagram of the experimental setup used in this study. The system takes the form of a vertical electrode geometry [17], where 1.5 m electrodes are used to connect an alternating voltage source (20 V_RMS) to the earth. The difficulty of drilling a hole for the bottom electrode was overcome by finding a sufficient location where erosion created a steep ravine. A surface electrode was placed on the top of the ravine, level with the surrounding land. A second electrode was placed at the bottom of the ravine (approximately 40 m below the top).

Fig. 1. Diagram of experimental setup depicting an oscillating dipole in the earth. (Upper left) Photograph of the 260 kHz receiver with an LED attached as the load at a distance of approximately 2.5 m from the surface electrode. The photograph was taken in full daylight.

Two helical, quarter standing-wave resonators were constructed and used as the receivers in this study. The first receiver consisted of 2300 turns of 26 gauge enameled wire wound on a plastic frame 1 m long and 0.58 m in diameter. This receiver exhibited an electrical standing wave resonant frequency of 25 kHz. A second receiver was constructed in a similar manner but smaller, having 915 turns of 22 gauge wire wound around a frame 0.6 m long and 0.165 m in diameter. This second receiver generated a standing-wave resonance of 260 kHz (an order of magnitude higher in frequency). A cork-screw stainless steel stake 0.2 m in length was used to connect the bottom terminal of the receiver with the soil. When the receivers were used to deliver energy to a load, the load was positioned between the bottom terminal of the receiver and the stainless steel stake, as depicted in Fig. 1. Each receiver was then sequentially positioned at a distance ( $\vec r$ ) and measurements were taken.

The geometry of Fig. 1 forms an oscillating vertical dipole within the soil. The field distributions of an electric dipole have been rigorously investigated over the last two centuries [22–26]. The electric field (E-field) of an oscillating dipole can be separated into three main regions: the static region proportional to 1/r ³, the intermediate region proportional to 1/r ², and the far region (or radiation region) proportional to 1/r, where r is the distance from the dipole origin [24]. The complete nature of the dipole E-field can be represented as [24]

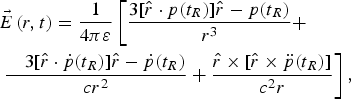(1) $$\eqalign{& \vec E\left( {r,t} \right) = \displaystyle{1 \over {4\pi \varepsilon}} \left[ {\displaystyle{{3[\hat r \cdot p(t_R)]\hat r - p(t_R)} \over {r^3}} +} \right. \cr & \left. {\displaystyle{{\quad 3[\hat r \cdot \dot p(t_R)]\hat r - \dot p(t_R)} \over {cr^2}} + \displaystyle{{\hat r \times [\hat r \times \ddot p(t_R)]} \over {c^2r}}} \right],} $$

where p(t _R ) is the dipole moment derived for a retarded time (t _R ), $\dot p(t_R)$ , and $\ddot p(t_R)$ are the 1st and 2nd order time derivatives, respectively, and ε is permittivity of the medium. The E-field distribution creates a time varying potential gradient within the soil and along the surface in the direction of $\vec r$ (Fig. 1), with $\vec r$ signifying a trigonometric function with respect to the center of the dipole. Mathematically deriving this potential involves integrating equation (1) with respect to the distance (r). This may take the form of a fitting function for the potential $\Phi (\vec r)$ as

(2) $$\Phi \left( {\vec r} \right) = \displaystyle{A \over {r^2}} + \displaystyle{B \over r} + C\ln \left( r \right) + D,$$

where, A is proportional to the charge distribution q in the media, B is proportional to the conduction or displacement current dq/dt within the media, C is proportional to the acceleration of charge d ² q/dt ² (which relates to the EM radiation input to the media), and D is a constant, which comes from the E-field integration. $\Phi (\vec r)$ is therefore the redistribution of potential from the voltage source into various components where A, B, C, and D are parameters related to both the electrode and soil properties (resistivity, permittivity, and permeability). The exact relation between the soil properties and the fitting parameters is still under investigation. Here we obtain the values from the experimentally recorded potential distribution along the ground and fit this measured data to equation (2).

To measure $\Phi (\vec r)$ as a function of distance, helical quarter-wave receivers were excited in a manner similar to our previous work [27], with the earth surface replacing the aluminum sheets. Such receivers use stray capacitance to complete the electrical circuit and therefore do not require a second electrode for a return. Any alternating voltage source applied to the base of the receiver is passively amplified when the frequency of the source matches the standing-wave resonance of the receiver. When investigating a surface potential along the earth, the passive amplification allows a unique single-contact mapping of $\Phi (\vec r)$ around the surface electrode, which hitherto has never been documented to our knowledge.

Each receiver was calibrated such that their output standing-wave E-field would correspond to a known bottom terminal input voltage. The calibration was made by attaching a wire field-probe via a non-conducting rod 50 cm from the top terminal of each receiver. The field-probe was connected to a battery operated digital oscilloscope (Tektronix TDS2024C). When a voltage source was applied to the bottom terminal of either receiver, with the frequency set to the standing-wave resonant mode, the receiver's output E-field would induce a voltage on the probe. The voltage source was then swept through a range of magnitudes and a calibration curve was made (Fig. 2). The input voltage versus induced field-probe signal was approximately linear and is plotted on a log–log scale to more clearly display the smaller calibrated magnitudes, with the measured slope indicating the calibration factor (CF) for each receiver. Once calibrated, any unknown potential applied to the bottom terminal of the receiver could be found by multiplying the measured oscilloscope voltage reading from the field-probe with the CF. In this way, the potential along the earth around the surface electrode was measured.

Fig. 2. Calibration curves for both receivers. The CF are the slopes of the lines, given in the inset next to the legend. Multiplication of the CF with the measured voltage from the field-probe yields the voltage applied to the bottom terminal of the receiver.

III. EARTH DIPOLE IMPEDANCE MEASUREMENTS

The degree to which the medium stores or dissipates energy can be found by measuring the complex impedance of the soil between the electrodes. To do this, we recorded the voltage, current, and corresponding phase angle input to the dipole at varying frequencies without the presence of any receiver. A plot of the resistance and reactance versus source frequency is shown in Fig. 3(a) (with the modulus plotted in Fig. 3(b) as the red square trace labeled Vertical One Surface Electrode). The applied voltage from the source was 20 V_RMS. The average soil resistance for the setup was found to be 45 Ω for frequencies below 30 kHz, which gradually increased to 70 Ω at 300 kHz (red diamond trace of Fig. 3(a)). Beyond 300 kHz, the resistance rose drastically while the reactance went to zero, indicating a resonance mode where nearly all energy from the source is dissipated into the soil as radiated heat and/or EM waves. Adding a second surface electrode (Fig. 3(c) middle), separated 9 m from the first and electrically connected, reduced the impedance by 10 Ω, bringing the average impedance to 35 Ω for frequencies below 30 kHz (blue triangle trace of Fig. 3(b)). It should be noted that while only the modulus is plotted, the impedance reduction happened in the resistive portion of the complex impedance. This 10 Ω change had a very minimal effect on the reactance, justifying the plot of the modulus only.

Fig. 3. (a) Complex impedance for a vertical electrode configuration with only one electrode on the surface. (b) Impedance spectra for different electrode geometries, all with 40 m electrode spacing. The red (square) trace is the spectrum for a vertical geometry with one surface electrode and one bottom electrode. The blue (triangle) trace is the response with two surface electrodes and one bottom electrode, yielding a reduction in impedance. The green (diamond) trace shows the impedance spectrum for a horizontal electrode geometry with the same 40 m electrode spacing. (c) Illustration of the three different electrode configurations tested where, (top) is a vertical geometry with one surface electrode, (middle) is a vertical geometry with two surface electrodes, and (bottom) is a horizontal geometry where both electrodes are at the surface.

Analyzing the ratio of real to imaginary components provides the effective dissipation factor (d-factor) given by ρε, which is a measure of the energy loss between the electrodes at different frequencies (Fig. 4). Two extreme conditions thus arise. In the reactive limit, the medium appears purely dielectric. Electrical energy placed in the medium would be stored and discharged as the source voltage rose and fell (similar to a capacitor). At the other extreme, the medium acts purely resistive, dissipating all applied energy in the form of heat and/or EM radiation. The experimental data showed a combination of both properties that varied linearly until a radiation mode was achieved at 585 kHz as shown in the dashed red line of Fig. 4.

Fig. 4. Plot of the dissipation factor of the soil between the dipole electrodes at different frequencies. The inset shows the resistivity per unit area measured as a function of frequency emphasizing that while the resistivity does not change significantly within the linear regime (below 300 kHz), the reactive contribution causes the dissipation to reduce to a minimum before the non-linear inflection point.

IV. DIPOLE ORIENTATIONS

We observed that the flow of charge within the soil produced a potential gradient along the surface. For grounding rods (connected in either horizontal or vertical dipole configurations) the current flow in circular paths through the soil with an applied voltage between the rods [11, 15]. These current paths are illustrated in Fig. 3(c) for both vertical and horizontal geometries. The conduction of this current through the soil exists within a finite volume. The total electrical resistance (R) between the electrodes is given by Pouillet's law

(3) $$R = \displaystyle{{\rho d} \over {{\mathchar'26\mkern-10mu \lambda}}},$$

where ρ is the resistivity (Ω-m) of the soil, d is the separation distance (m) between the electrodes, and $\mathchar'26\mkern-10mu\lambda $ is the cross-sectional area (m²) traversed by the current. The formulation of resistance for spherical current flow is quite involved [28, 29], yet the basic proportionality of distance versus area remains the same. It can be seen through equation (3) that a greater area ( $\mathchar'26\mkern-10mu\lambda $ ) for the same electrode separation (d) and resistivity (ρ) would yield a lower total resistance (R) as the cross-sectional area increases with the square of the radius in contrast to the electrode separation, which is linear. This also explains the experimental reduction of resistance from 45 to 35 Ω (Fig. 3(b)) when a second surface electrode was added, as it increased the effective area of charge flow.

Most literature employs a horizontal electrode configuration (Fig. 3(c) bottom) for earth-based studies (as two surface electrodes are easier to install). This led us to investigate whether there would be any differences between the vertical and horizontal geometries. We hypothesized that a vertical electrode configuration would exhibit a lower resistance as multiple parallel current paths would occur within the ground due to the current being forced to traverse each soil strata; effectively increasing the area $(\mathchar'26\mkern-10mu\lambda )$ of conduction. This would be different in a horizontal configuration where both electrodes are at the surface, as current does not flow normal to all intervening strata layers. Therefore, strata with lower resistivity would become a preferential current channel and reduce the parallel pathways – lowering the effective area and increasing the total resistive losses.

We tested our hypothesis by creating an alternate horizontal configuration using the initial surface electrode and installing a second (1.5 m long) grounding rod at a 40 m separation distance on the surface (Fig. 3(c) bottom). The overall impedance was observed to be much higher (80–107 Ω in resistance) than the vertical configurations for frequencies below 100 kHz with the sharper impedance rise occurring beyond 100 kHz (green diamond trace of Fig. 3(b)). The reactive component was also found to be lower than that of the vertical electrode geometry. The results of Fig. 3(b) appear to support our hypothesis though more studies are needed to identify the exact distribution of these currents underground (a very challenging task). We would also like to note that the single contact measurements with the quarter-wave receivers for the horizontal configuration were difficult to conduct as the horizontal geometry creates a current loop with the surface wire and returning earth. This produced a magnetic field that would couple to the receivers, making it difficult to separate the time varying surface potential with induction from the magnetic field. For the vertical dipole geometry, the magnetic field was at right angles to the receivers and therefore had no major influence on their operation – the excitation being from the displacement of charges on the surface only.

V. SURFACE POTENTIAL MEASUREMENTS

The surface potential measurements were made from 1 to 21 m, in 3 m increments, moving away in a straight line from the surface electrode. Figure 5(a) is a plot of the measured potential for both the 25 kHz (black square points) and 260 kHz (red circle points) receivers, respectively. These data points were fit using equation (2) for both frequencies allowing us to experimentally determine the parameters A, B, C, and D. These parameter values are given in the inset table of Fig. 5(a) with the fitting curve traces shown as solid lines (black for 25 kHz and red for 260 kHz). Each fitting trace follows a 99.982% accuracy with the experimental data, verifying the use of equation (2) to describe the phenomena. Next we measured the radial distribution of $\Phi (\vec r)$ around the surface electrode. We were restricted from a complete 360° surface mapping at 20 m radius, as a dense tree line was to the right with the ravine directly behind (the ravine being too steep to record measurements on). The maximum, unhindered radius was 7.5 m for this experiment. Figure 5(b) shows a 3D plot of the voltage distribution over the 7.5 m radius. It can be seen from the figure that the distribution was symmetric and follows the curve of Fig. 5(a).

Fig. 5. (a) Surface potential measured with two different receivers as a function of distance away from the surface electrode. Equation (2) was used as the fitting function and the traces are shown by the solid lines (red for 260 kHz and black for 25 kHz). The parameters A, B, C, and D were determined by fitting the traces to the experimental data. These fitting parameters are shown in the inset with A and B being near-field contributions to the surface potential and C representing the far field contribution. D is a constant from integration and its physical meaning is still being investigated. (b) 3D plot of measured potential over a 7.5 m radius around the surface electrode.

The surface potential attenuation at 25 kHz (having a lower resistivity) is only slightly less than that of 260 kHz. With 260 kHz being an order of magnitude higher in frequency than 25 kHz, it is interesting that both frequencies produced nearly identical charge distributions on the surface for the same applied source voltage. From the fitted parameters (Fig. 5(a)), components A and B represent the most significant contributions to the surface potential, with component C being an order of magnitude lower. These results are indicative of the dipole operating in a non-radiating, near-field regime. It can be concluded that for the linear d-factor dependence region (frequencies below 300 kHz in Fig. 4), the electrical function of the system is most similar to a lossy capacitor with the distributed charges over the area acting as an extension of the surface electrode creating a virtual “plate.” It is likely that a matching virtual plate of opposite polarity also exists around the bottom electrode underground. The capacitive impedance behavior was found to be stronger at the higher frequencies right before the inflection point. This notion is also supported by the values of the fitting parameters as A (proportional to the charge distribution) is greater at 260 kHz, whereas conduction/displacement current B plays a higher roll at 25 kHz.

In our previous work [27], the surfaces of conducting objects (such as metal foils, desks, and cabinets) also functioned as one plate of a virtual capacitor. By driving these virtual capacitors at the standing-wave resonant frequency of a helical receiver, we were able to wirelessly deliver power to a load anywhere on the surface. In this study, we produced the same effect using both 25 and 260 kHz receivers. A 30 Ω load was connected in series with the receiver and its ground connection (see Fig. 1). We then recorded the voltage drop across the load at varying distances away from the surface electrode and calculated the received power to the load (Fig. 6). At a distance of 1.5 m, approximately 300 mW was delivered with either frequency. At the maximum measured distance (20 m), we received 80 µW at 25 kHz and 7 µW at 260 kHz. The difference in received power possibly stemming from the slightly higher resistance of 70 Ω at 260 kHz compared with 45 Ω at 25 kHz (Fig. 3(b)). These resistances are a product of both conduction and dielectric losses in the soil. As frequencies are increased, dielectric losses would be expected to escalate. This would restrict the distribution of alternating charges at the surface and generate a slight attenuation of the received power at the higher frequency (similar to adding an additional resistor between the receiver and surface electrode). Regardless, these received energy levels are more than adequate for low power sensing applications [5] making this method a good candidate for large monitoring networks. For a more visual indication of power transfer, we replaced the 30 Ω resistor with two LEDs and photographed their operation approximately 2.5 m from the surface electrode using the 260 kHz receiver. This is shown at the left-hand side in Fig. 1. The smaller inset picture at the lower left of the photograph is a close-up of the stainless steel stake used to connect the bottom terminal of the receiver to the earth.

Fig. 6. Received power at receding distance away from the surface electrode. The efficiency is plotted in the inset. It can be seen that while the 25 kHz yielded a slightly higher received power, the transfer efficiency is dependent on the reactance of the system as higher reactance corresponds to less power dissipated in the soil. For this reason, the 260 kHz drive frequency yielded a better transfer efficiency with distance.

The efficiency of the system (with the 30 Ω load) is plotted in the inset of Fig. 6. The efficiency was calculated based on the power consumed by the load divided by the power loss at the input of the dipole (corresponding to the total active power placed in the system)

(4) $$\eta = \displaystyle{{P_L} \over {V_SI_S\cos (\varphi )}},$$

where P _L is the power dissipated in the load (30 Ω), V _S is the measured voltage of the source, I _S is the measured current from the source going into the dipole, and ϕ is the phase angle between V _S and I _S . At a distance of 1.5 m, the energy transfer efficiency was 80% for the 260 kHz frequency while at 25 kHz the efficiency was only 4%. It took a distance of 3 m for the 260 kHz frequency to reach an efficiency of 6%. The efficiency is clearly the highest when the dissipation in the soil is the lowest, yet the resistivity at 260 kHz (Fig. 3(a)) was slightly higher than at 25 kHz. The major effect in efficiency is due to the difference in reactance between the two frequencies.

The power efficiency results along with the d-factor curves give insight on how to improve the energy transfer in the system. The key goal should be to lower the resistance as much as possible and at the same time maximize the reactance. While the resistivity of the soil does not change, system resistance can be lowered by adding a greater number of surface electrodes. As the total resistance is reduced, the phase angle should be made to approach a limit of −90°, where the dipole will become, to a high degree, a capacitor. Since the maximum reactive energy input to the system occurs at the inflection point of the radiation mode, the electrode separation depth will dictate the operating frequency of choice (with lower frequencies generally exhibiting less dissipative losses in the soil – which may result in a lower number of surface electrodes needed when lowering the resistance). This frequency can be calculated as

(5) $$f = \displaystyle{c \over {2\sqrt {\varepsilon _r} d}},$$

where c is the speed of light, ε _r is the relative permittivity of the medium (approximately 41 for these experiments), and d is the electrode separation (equivalent to half the wavelength for a dipole). Once dissipation in the unloaded system is minimized, it may be possible to extend the distance by increasing the applied voltage of the dipole. We limited the input voltage to 20 V_RMS for both safety and regulation reasons. Operating at higher voltages (taking care that the step potential is kept low and that any minute radiation does not exceed regulatory limits at the operating frequency) may theoretically extend the distance as more charge will be available to distribute over the area. However, further work is needed to quantify the voltage versus distance dependence of such buried dipoles and the relative changes to parameters A, B, C, and D that ensue. In addition, the change of parameters A, B, C, and D at different frequencies is also needed in order to better model system operation.

VI. THEORETICAL ESTIMATIONS

It may be possible to theoretically estimate the system's operation for increasing voltages by making a few initial assumptions. The first assumption is that the values of the near-field parameters A and B will change approximately linearly with the applied source voltage while the values of the far field parameters C and D will remain nearly unchanged. This assumption is based on the fact that as voltage is increased, both the quantity and rate of change of charge will proportionally increase regardless of the system's geometry and operating frequency while the acceleration of charge is dependent on both frequency and geometry, which is greatly restricted in this situation (as the system is operated at the inflection point of the radiation mode). The second assumption is that the soil properties remain constant (i.e. moisture changes from joule/dielectric heating are neglected) during operation. Last, we assume the same dipole length between the electrodes (40 m) as presented earlier. This allows us to use the experimentally determined fitting parameters found in the table inset of Fig. 3. Equation (2) may then take the form

(6) $$\Phi \left( {\vec r} \right) = \alpha \left( {\displaystyle{A \over {r^2}} + \displaystyle{B \over r}} \right) + C\ln \left( r \right) + D,$$

where α is an amplification factor corresponding to 1 at an input voltage of 20 V_RMS (the operating voltage of the measured data). Figure 7(a) is a plot of the estimated field distribution for the 260 kHz receiver along the ground with different input voltages to the buried dipole. The plots show an upward shift in the voltage level at the 20 m distance, with a predicted surface potential of 91 V for a 10 kV input. A surface potential of this magnitude would be capable of delivering nearly 100 W to a load at 20 m; though it should be noted that the voltage source would need to be capable of supplying a very large reactive power (nearly 300 kVAR).

Fig. 7. (a) Estimated potential distribution with increasing voltage to the buried vertical dipole. (b) Plot of the input dipole voltage with the corresponding distance at which the surface potential becomes 2.5 V. (Inset) Minimum distance at which the step potential along the ground is less than or equal to 25 V/m for different input voltage magnitudes with a small diagram of a person illustrating the definition of step potential, which is the voltage difference between the feet of a person making a step.

Another interesting calculation is the system response beyond 20 m. With a surface potential of 2.5 V we experimentally found it possible to deliver nearly 100 mW to a 30 Ω load. Figure 7(b) shows the estimated distance at which the system would obtain a surface potential of 2.5 V for varying input dipole voltages. For a 10 kV input at 260 kHz, the 2.5 V surface potential would occur at 1 km. For 25 kHz a lower input voltage would be needed to achieve the same 2.5 V surface potential at a 1 km distance. However, it should be noted that the active power dissipation at 25 kHz was much larger due to the increased conduction current. It is possible that with a larger electrode separation (dipole length), 25 kHz could be tuned, using equation (5), near the inflection point of the radiation mode and produce a much more efficient operation (less resistive losses with an input phase angle closer to 90°). This would have an advantage as the input voltages to the dipole could be lower. The insert of Fig. 7(b) is a plot of the minimum distance at which the step potential around the electrode is considered safe, being equal to or below 25 V/m [30]. Closer to the surface electrodes, the step potential would exceed the 25 V/m limit and certain safety precautions would need to be set in place, such as a fence restricting access or an insulated/elevated platform over the ground. It should be noted that the “unsafe” region only accounts for less than 1% of the total distribution for both frequencies.

While the figures shown in this section are only estimates based upon ongoing experiments, these theoretical scaling approximations are very promising. Such a system could be readily interfaced with current EM energy scavengers to enhance the local EM energy level without increasing the EM radiation in the environment. One advantage of this method is that a constant power source can be distributed over the area, eliminating the direct dependence on natural conditions such as sunlight, vibrations, and wind. A very promising application for this technology is the operation of agricultural sensors and low power robotics. Through a technique known as phased arraying, it should be possible to both restrict the energy to specific locations while intensifying its magnitude. Fields and pastures could not only operate soil and animal monitoring sensors, but small robots could be powered continuously to maintain plant development or eliminate pests. Beyond agriculture, the residential applications may include “energized” backyards where the same phased arraying techniques are applied to small buried dipoles within the designated area. This would constrain the electrical energy within the yard allowing wireless outdoor lighting and lawn equipment. Further system scaling would open more applications as greater power delivery is achieved.

VII. CONCLUSIONS

We have shown that this method requires maximum reactive energy placed in the transmission medium in order to produce efficient energy transfer (somewhat of an oxymoron in contemporary philosophy). The classical interpretation has always been based on the minimization or cancelation of reactive components in order to efficiently transfer power. Here we show the reverse of this paradigm. Our method is most simply understood as limiting energy dissipation in one physical element so that this energy may be resonantly collected and dissipated in another. The receiver could thus be viewed as the transmission line (where at resonance the reactive components of the receiver do cancel) while the dipole and surrounding soil are simply an extension of the voltage source.

In conclusion, we demonstrated a practical way of utilizing surface potentials near an earthed electrode to deliver power to a load over a large outdoor area. Optimization focused on maximizing the reactive components in the system can improve the efficiency by orders of magnitude when operated at the near-field regime of the buried oscillating dipole. The transfer distances and efficiencies reported here were for an un-optimized, proof of concept, system. The 80% efficiency at 1.5 m is comparable with many near-field WPT techniques. However, the theoretical transfer distance that can be achieved with this method is not limited or based on field coupling physics, and instead relies on the redistribution of time varying charges along the surface to excite the receiver. Theoretical scaling shows promising results as the estimated transfer distance may be extendable to much greater distances than what is possible using other methodologies. This technique may have immediate applications in powering distributed monitoring devices such as military and agricultural sensors. While the power levels measured here are at a capacity to operate low energy devices, continuing research on this method to expand the distance, improve efficiency, reduce receiver size, and increase power could one day offer revolutionary and possibly disruptive technological impacts for society.