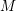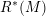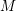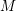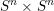Tautological rings for high-dimensional manifolds

Abstract

We study tautological rings for high-dimensional manifolds, that is, for each smooth manifold $M$ the ring $R^{\ast }(M)$ of those characteristic classes of smooth fibre bundles with fibre $M$ which is generated by generalised Miller–Morita–Mumford classes. We completely describe these rings modulo nilpotent elements, when $M$ is a connected sum of copies of $S^{n}\times S^{n}$ for $n$ odd.

1 Introduction

Let $E^{k+d}$ and $B^{k}$ be connected compact smooth oriented manifolds, and let $\unicode[STIX]{x1D70B}:E\rightarrow B$ be a smooth fibre bundle (i.e. a proper submersion) with fibre $M^{d}$ . Then there is a $d$ -dimensional oriented vector bundle $T_{\unicode[STIX]{x1D70B}}=\text{Ker}(D\unicode[STIX]{x1D70B})$ over $E$ . If $c\in H^{\ast }(B\text{SO}(d);\mathbb{Q})$ is a rational characteristic class of such vector bundles, we define the associated generalised Miller–Morita–Mumford class to be the fibre integral

$$\begin{eqnarray}\unicode[STIX]{x1D705}_{c}(\unicode[STIX]{x1D70B})=\int _{\unicode[STIX]{x1D70B}}c(T_{\unicode[STIX]{x1D70B}})\in H^{\ast -d}(B;\mathbb{Q}).\end{eqnarray}$$

For a basis ${\mathcal{B}}\subset H^{\ast }(B\text{SO}(d);\mathbb{Q})$ this defines a ring homomorphism

$$\begin{eqnarray}\displaystyle \mathbb{Q}[\unicode[STIX]{x1D705}_{c}\mid c\in {\mathcal{B}}] & \longrightarrow & \displaystyle H^{\ast }(B;\mathbb{Q})\nonumber\\ \displaystyle \unicode[STIX]{x1D705}_{c} & \longmapsto & \displaystyle \unicode[STIX]{x1D705}_{c}(\unicode[STIX]{x1D70B}).\nonumber\end{eqnarray}$$

We let $I_{M}\subset \mathbb{Q}[\unicode[STIX]{x1D705}_{c}\mid c\in {\mathcal{B}}]$ be the ideal consisting of those polynomials in the classes $\unicode[STIX]{x1D705}_{c}$ which vanish on every such smooth fibre bundle with fibre $M$ , and define the tautological ring of $M$ to be the associated quotient ring

$$\begin{eqnarray}R^{\ast }(M)=\mathbb{Q}[\unicode[STIX]{x1D705}_{c}\mid c\in {\mathcal{B}}]/I_{M}.\end{eqnarray}$$

The name ‘tautological ring’ is borrowed from the $d=2$ case, where it usually refers to the subring of the cohomology ring (or Chow ring) of moduli spaces of Riemann surfaces which is generated by certain tautological classes $\unicode[STIX]{x1D705}_{i}$ (which in our notation correspond to $\unicode[STIX]{x1D705}_{e^{i+1}}$ ). Our definition coincides with the usual one in this case. There is a large literature on these rings; see [Mum83, Loo95, Fab99, Mor03].

We shall be interested in manifolds of even dimension $d=2n$ , in which case $H^{\ast }(B\text{SO}(2n);\mathbb{Q})=\mathbb{Q}[p_{1},p_{2},\ldots ,p_{n-1},e]$ and we take ${\mathcal{B}}$ to be the basis of monomials in these classes. Writing $W_{g}$ for the connected sum of $g$ copies of $S^{n}\times S^{n}$ , our goal in this paper is to study the structure of $R^{\ast }(W_{g})$ modulo the nilradical $\sqrt{0}$ , i.e. the ideal of nilpotent elements, and our main result can be stated as follows.

Theorem 1.1. Let $n$ be odd. Then:

1. (i) $R^{\ast }(W_{0})/\sqrt{0}=\mathbb{Q}[\unicode[STIX]{x1D705}_{ep_{1}},\unicode[STIX]{x1D705}_{ep_{2}},\ldots ,\unicode[STIX]{x1D705}_{ep_{n}}]$ ;

2. (ii) $R^{\ast }(W_{1})/\sqrt{0}=\mathbb{Q}$ ;

3. (iii) $R^{\ast }(W_{g})/\sqrt{0}=\mathbb{Q}[\unicode[STIX]{x1D705}_{ep_{1}},\unicode[STIX]{x1D705}_{ep_{2}},\ldots ,\unicode[STIX]{x1D705}_{ep_{n-1}}]$ for $g>1$ .

In fact, (i) already holds before taking the quotient by the nilradical, and it holds for $n$ both even and odd (see § 5.3).

As the Krull dimension of a ring is unchanged upon taking the quotient by the nilradical, we may also conclude that $R^{\ast }(W_{0})$ has Krull dimension $n$ , $R^{\ast }(W_{1})$ has Krull dimension 0, and $R^{\ast }(W_{g})$ has Krull dimension $n-1$ as long as $g>1$ .

We shall also study two closely related tautological rings. Firstly, we may consider fibre bundles $\unicode[STIX]{x1D70B}:E^{k+2n}\rightarrow B^{k}$ with fibre $M^{2n}$ equipped with a section $s:B\rightarrow E$ . To such a fibre bundle and a $c\in {\mathcal{B}}$ we may also associate the characteristic class $c(\unicode[STIX]{x1D70B},s)=s^{\ast }(c(T_{\unicode[STIX]{x1D70B}}))$ , so in this case a ring homomorphism is defined,

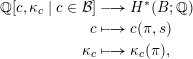$$\begin{eqnarray}\displaystyle \mathbb{Q}[c,\unicode[STIX]{x1D705}_{c}\mid c\in {\mathcal{B}}] & \longrightarrow & \displaystyle H^{\ast }(B;\mathbb{Q})\nonumber\\ \displaystyle c & \longmapsto & \displaystyle c(\unicode[STIX]{x1D70B},s)\nonumber\\ \displaystyle \unicode[STIX]{x1D705}_{c} & \longmapsto & \displaystyle \unicode[STIX]{x1D705}_{c}(\unicode[STIX]{x1D70B}),\nonumber\end{eqnarray}$$

and we let $I_{(M,\star )}\subset \mathbb{Q}[c,\unicode[STIX]{x1D705}_{c}\mid c\in {\mathcal{B}}]$ denote the ideal of those polynomials in the $c$ and $\unicode[STIX]{x1D705}_{c}$ which vanish on all such bundles; we write $R^{\ast }(M,\star )$ for the associated quotient ring.

Theorem 1.2. Let $n$ be odd.

1. (i) For each $c\in {\mathcal{B}}$ , $(2-2g)\cdot c=\unicode[STIX]{x1D705}_{ec}\in R^{\ast }(W_{g},\star )/\sqrt{0}$ .

2. (ii) For $g\neq 1$ , the map

   $$\begin{eqnarray}R^{\ast }(W_{g})/\sqrt{0}\longrightarrow R^{\ast }(W_{g},\star )/\sqrt{0}\end{eqnarray}$$
   is an isomorphism.

3. (iii) The class $e\in R^{\ast }(W_{1},\star )$ is nilpotent, and the map

   $$\begin{eqnarray}\mathbb{Q}[p_{1},p_{2},\ldots ,p_{n-1}]\longrightarrow R^{\ast }(W_{1},\star )/\sqrt{0}\end{eqnarray}$$
   is an isomorphism.

Secondly, we may consider fibre bundles $\unicode[STIX]{x1D70B}:E^{k+2n}\rightarrow B^{k}$ with fibre $M^{2n}$ equipped with an embedding $S:D^{2n}\times B\rightarrow E$ over $B$ (or, equivalently, with a normally framed section). The restriction $s=S|_{\{0\}\times B}$ defines a section, but the fact that it is framed means that $c(\unicode[STIX]{x1D70B},s)=0$ . Hence in this case we denote by $I_{(M,D^{2n})}\subset \mathbb{Q}[\unicode[STIX]{x1D705}_{c}\mid c\in {\mathcal{B}}]$ the ideal of polynomials in the $\unicode[STIX]{x1D705}_{c}$ which vanish on all such bundles, and write $R^{\ast }(M,D^{2n})$ for the associated quotient ring. The following is immediate from Theorems 1.1 and 1.2(i).

Corollary 1.3. If $n$ is odd, then $R^{\ast }(W_{g},D^{2n})/\sqrt{0}=\mathbb{Q}$ for all $g$ .

The second author has shown (see [Gri13, Theorem 1.1]) that for $n$ odd the ring $R^{\ast }(W_{g})$ is finitely generated as a $\mathbb{Q}$ -algebra, and hence $R^{\ast }(W_{g},D^{2n})$ is too. (In fact, [Gri13, Theorem 1.1] only shows this for $g>1$ , but in Proposition 5.7 we will show that $R^{\ast }(W_{g},\star )$ , and hence $R^{\ast }(W_{g},D^{2n})$ , is finitely generated for all $g$ .) Corollary 1.3 therefore implies the following result.

Corollary 1.4. If $n$ is odd, then $R^{\ast }(W_{g},D^{2n})$ is a finite-dimensional rational vector space for all  $g$ .

It would be interesting to have a computation of the ring $R^{\ast }(W_{g},D^{2n})$ for some $g>1$ . In proving these theorems, we obtain results about the vanishing of certain elements in $R^{\ast }(M)/\sqrt{0}$ for any manifold $M$ (in Theorem 2.1) and about the algebraic independence of certain elements in $R^{\ast }(W_{g})/\sqrt{0}$ for $n$ even (in Theorem 4.1). We cannot obtain results as conclusive as Theorem 1.1 for $n$ even, as our argument relies on [Gri13], which does not apply in this case.

2 Nilpotence of the Hirzebruch ${\mathcal{L}}$ -classes

In this section, we prove that certain generalised Miller–Morita–Mumford classes are nilpotent in $R^{\ast }(M)$ for any smooth even-dimensional manifold $M^{2n}$ . We will later apply this together with results from [Gri13] to the manifolds $W_{g}$ in order to obtain an upper bound on $R^{\ast }(W_{g})/\sqrt{0}$ .

2.1 (Modified) Hirzebruch ${\mathcal{L}}$ -classes

We first define certain cohomology classes $\tilde{{\mathcal{L}}}_{i}\in H^{4i}(B\text{SO}(2n);\mathbb{Q})$ . Consider the graded ring $\mathbb{Q}[x_{1},\ldots ,x_{n}]$ in which each variable $x_{1},\ldots ,x_{n}$ has degree 2. We define homogenous symmetric polynomials $\tilde{{\mathcal{L}}}_{i}$ by the expression

$$\begin{eqnarray}\tilde{{\mathcal{L}}}=2^{n}+\tilde{{\mathcal{L}}}_{1}+\tilde{{\mathcal{L}}}_{2}+\cdots =\mathop{\prod }_{i=1}^{n}\frac{x_{i}}{\operatorname{tanh}x_{i}/2}.\end{eqnarray}$$

(The function $x/(\operatorname{tanh}x/2)$ is even, so the above expresses $\tilde{{\mathcal{L}}}_{i}$ as a symmetric polynomial in $x_{1}^{2},x_{2}^{2},\ldots ,x_{n}^{2}$ .) The subring of symmetric polynomials is generated by the elementary symmetric polynomials $\unicode[STIX]{x1D70E}_{i,n}(x_{1}^{2},\ldots ,x_{n}^{2})$ , so we may express $\tilde{{\mathcal{L}}}_{i}$ as a polynomial $\tilde{{\mathcal{L}}}_{i}(\unicode[STIX]{x1D70E}_{1,n},\ldots ,\unicode[STIX]{x1D70E}_{n,n})$ , and we write

$$\begin{eqnarray}\tilde{{\mathcal{L}}}_{i}=\tilde{{\mathcal{L}}}_{i}(p_{1},p_{2},\ldots ,p_{n})\in H^{4i}(B\text{SO}(2n);\mathbb{Q})\end{eqnarray}$$

for this polynomial evaluated at the Pontrjagin classes. Note that these differ from the usual Hirzebruch $L$ -classes, ${\mathcal{L}}_{i}$ , by a factor: $\tilde{{\mathcal{L}}}_{i}=2^{n-2i}{\mathcal{L}}_{i}$ . These classes may be written as

$$\begin{eqnarray}\tilde{{\mathcal{L}}}_{i}=2^{n}(2^{2i-1}-1)\frac{B_{i}}{(2i)!}\cdot p_{i}+(\text{polynomial in lower Pontrjagin classes})\end{eqnarray}$$

where $B_{i}$ is the $i$ th Bernoulli number; cf. [MS74, Problem 19-C] (this uses the convention of [MS74, Appendix B], in which $B_{i}=(-1)^{i}\cdot 2i\cdot \unicode[STIX]{x1D701}(1-2i)$ ). In particular, these leading coefficients are never zero, so $\tilde{{\mathcal{L}}}_{1},\tilde{{\mathcal{L}}}_{2},\ldots ,\tilde{{\mathcal{L}}}_{n}$ generate the same subring of $H^{\ast }(B\text{SO}(2n);\mathbb{Q})$ as $p_{1},p_{2},\ldots ,p_{n}$ .

2.2 Nilpotence due to the Hirzebruch signature theorem

For any manifold $M^{2n}$ , the characteristic classes $\tilde{{\mathcal{L}}}_{i}\in H^{4i}(B\text{SO}(2n);\mathbb{Q})$ give rise to the corresponding generalised Miller–Morita–Mumford classes $\unicode[STIX]{x1D705}_{\tilde{{\mathcal{L}}}_{i}}\in R^{\ast }(M)$ . Our present goal is to prove the following.

Theorem 2.1. The classes $\unicode[STIX]{x1D705}_{\tilde{{\mathcal{L}}}_{i}}\in R^{\ast }(M)$ are nilpotent for all natural numbers $i\geqslant 1$ such that $4i-2n\neq 0$ (all natural numbers if $n$ is odd).

The main ingredient in the proof is a parametrised version of the Hirzebruch signature theorem, due to Atiyah [Ati69], which relates the classes $\unicode[STIX]{x1D705}_{\tilde{{\mathcal{L}}}_{i}}$ to classes arising from the cohomology of an arithmetic group.

Let $M^{2n}$ be an oriented manifold, and let $H=H^{n}(M;\mathbb{Z})/\text{torsion}$ . It is a consequence of Poincaré duality that the $(-1)^{n}$ -symmetric pairing

$$\begin{eqnarray}\unicode[STIX]{x1D706}:H\otimes _{\mathbb{Z}}H\stackrel{\cup }{\longrightarrow }H^{2n}(M;\mathbb{Z})/\text{torsion}=H^{2n}(M;\mathbb{Z})\stackrel{{\sim}}{\longrightarrow }\mathbb{Z}\end{eqnarray}$$

is non-degenerate. Any homotopy equivalence of $M$ preserving its orientation therefore induces an isometry of the $(-1)^{n}$ -symmetric form $(H,\unicode[STIX]{x1D706})$ . In particular, if $\unicode[STIX]{x1D70B}:E\rightarrow B$ is a smooth oriented fibre bundle with fibre $M$ , there is a homomorphism

$$\begin{eqnarray}\unicode[STIX]{x1D719}:\unicode[STIX]{x1D70B}_{1}(B)\longrightarrow \text{Aut}(H,\unicode[STIX]{x1D706})\end{eqnarray}$$

from the fundamental group of $B$ to the group of isometries of $(H,\unicode[STIX]{x1D706})$ , inducing a map $\unicode[STIX]{x1D719}:B\rightarrow B\text{Aut}(H,\unicode[STIX]{x1D706})$ .

We may further consider the induced $(-1)^{n}$ -symmetric form $\unicode[STIX]{x1D706}_{\mathbb{R}}$ on $H_{\mathbb{R}}=H\otimes _{\mathbb{Z}}\mathbb{R}$ . There are now two cases, depending on the parity of $n$ . If $n$ is odd, then $(H_{\mathbb{R}},\unicode[STIX]{x1D706}_{\mathbb{R}})$ is a non-degenerate skew-symmetric form over $\mathbb{R}$ , and so is determined by its rank. This identifies $\text{Aut}(H_{\mathbb{R}},\unicode[STIX]{x1D706}_{\mathbb{R}})$ with $\text{Sp}_{2g}(\mathbb{R})$ , where $H_{\mathbb{R}}$ has dimension $2g$ . If $n$ is even, then $(H_{\mathbb{R}},\unicode[STIX]{x1D706}_{\mathbb{R}})$ is a non-degenerate symmetric form over $\mathbb{R}$ , and so is determined by its rank and signature. This identifies $\text{Aut}(H_{\mathbb{R}},\unicode[STIX]{x1D706}_{\mathbb{R}})$ with $\text{O}_{p,q}(\mathbb{R})$ , where $H_{\mathbb{R}}$ has dimension $p+q$ and signature $p-q$ . We thus obtain a composition

$$\begin{eqnarray}B\overset{\unicode[STIX]{x1D719}}{\longrightarrow }B\text{Aut}(H,\unicode[STIX]{x1D706})\longrightarrow B\text{Aut}(H_{\mathbb{R}},\unicode[STIX]{x1D706}_{\mathbb{R}})=\left\{\begin{array}{@{}l@{}}B\text{Sp}_{2g}(\mathbb{R}),\quad \\ B\text{O}_{p,q}(\mathbb{R}).\quad \end{array}\right.\end{eqnarray}$$

Now Atiyah’s work [Ati69, §4] implies that the classes $\unicode[STIX]{x1D705}_{\tilde{{\mathcal{L}}}_{i}}$ are pulled back via this composition, so in particular they are in the image of $\unicode[STIX]{x1D719}^{\ast }:H^{\ast }(B\text{Aut}(H,\unicode[STIX]{x1D706});\mathbb{Q})\rightarrow H^{\ast }(B;\mathbb{Q})$ . Theorem 2.1 is then an immediate consequence of the fact that all positive-degree elements of $H^{\ast }(B\text{Aut}(H,\unicode[STIX]{x1D706});\mathbb{Q})$ are nilpotent; this is because $\text{Aut}(H,\unicode[STIX]{x1D706})$ is an arithmetic group, and so has finite virtual cohomological dimension and hence in particular finite $\mathbb{Q}$ -cohomological dimension.

3 Relations modulo nilpotence

The main result (Theorem 2.7) of [Gri13] implies that when $n$ is odd, for any oriented manifold bundle $E\rightarrow B$ with fibre $W_{g}$ and even-dimensional classes $a,b\in H^{\ast }(E;\mathbb{Q})$ such that $\unicode[STIX]{x1D70B}_{!}(a)=0$ and $\unicode[STIX]{x1D70B}_{!}(b)=0$ , the class $\unicode[STIX]{x1D70B}_{!}(ab)$ is nilpotent. We shall use the following stronger statement, which will be deduced quite formally from [Gri13, Theorem 2.7].

Theorem 3.1. Let $\unicode[STIX]{x1D70B}:E\rightarrow B$ be a fibration with homotopy fibre homotopy-equivalent to $W_{g}=g(S^{n}\times S^{n})$ for $n$ odd, such that the action of $\unicode[STIX]{x1D70B}_{1}(B,b)$ on $H^{2n}(\unicode[STIX]{x1D70B}^{-1}(b);\mathbb{Q})$ is trivial. For classes $a,b\in H^{\ast }(E;\mathbb{Q})$ such that $A=|\unicode[STIX]{x1D70B}_{!}(a)|$ and $B=|\unicode[STIX]{x1D70B}_{!}(b)|$ are even, if $\unicode[STIX]{x1D70B}_{!}(a)^{k}=0$ and $\unicode[STIX]{x1D70B}_{!}(b)^{l}=0$ , then $\unicode[STIX]{x1D70B}_{!}(ab)^{(2g+1)(Ak+Bl)}=0$ .

If $g\neq 1$ , this is a consequence of [Gri13, Lemma 5.7]. The proof we present here is independent of genus.

Proof. First, suppose that both $A$ and $B$ are at least $2$ . Let $F$ be defined by the homotopy fibre sequence

$$\begin{eqnarray}F\longrightarrow K(\mathbb{Q},A)\times K(\mathbb{Q},B)\overset{\unicode[STIX]{x1D704}_{A}^{k}\times \unicode[STIX]{x1D704}_{B}^{l}}{\longrightarrow }K(\mathbb{Q},kA)\times K(\mathbb{Q},lB),\end{eqnarray}$$

where the map between the Eilenberg–MacLane spaces is given by the product of the appropriate powers of the fundamental cohomology classes. If $A$ and $B$ are even, it is an elementary calculation to see that

$$\begin{eqnarray}H^{\ast }(F;\mathbb{Q})=\mathbb{Q}[\unicode[STIX]{x1D704}_{A},\unicode[STIX]{x1D704}_{B}]/(\unicode[STIX]{x1D704}_{A}^{k},\unicode[STIX]{x1D704}_{B}^{l})\end{eqnarray}$$

and that $F$ is also simply connected. Thus $F$ has $\mathbb{Q}$ -cohomological dimension $Ak+Bl-1$ .

As $\unicode[STIX]{x1D70B}_{!}(a)^{k}=0$ and $\unicode[STIX]{x1D70B}_{!}(b)^{l}=0$ , the map

$$\begin{eqnarray}(\unicode[STIX]{x1D70B}_{!}(a),\unicode[STIX]{x1D70B}_{!}(b)):B\longrightarrow K(\mathbb{Q},A)\times K(\mathbb{Q},B)\end{eqnarray}$$

representing $(\unicode[STIX]{x1D70B}_{!}(a),\unicode[STIX]{x1D70B}_{!}(b))$ lifts to a map $f:B\rightarrow F$ , and we let $B^{\prime }$ denote the homotopy fibre of $f$ and $i:B^{\prime }\rightarrow B$ the evaluation map. The class $i^{\ast }(\unicode[STIX]{x1D70B}_{!}(ab))$ is the same as $\unicode[STIX]{x1D70B}_{!}^{\prime }(a^{\prime }b^{\prime })$ , where $\unicode[STIX]{x1D70B}^{\prime }:E^{\prime }\rightarrow B^{\prime }$ is the pullback of $\unicode[STIX]{x1D70B}$ along $i$ , and $a^{\prime }$ and $b^{\prime }$ are the pullbacks of $a$ and $b$ along the map $E^{\prime }\rightarrow E$ covering $i$ . The classes $\unicode[STIX]{x1D70B}_{!}^{\prime }(a^{\prime })$ and $\unicode[STIX]{x1D70B}_{!}^{\prime }(b^{\prime })$ are trivial, so by [Gri13, Theorem 2.7] we have $\unicode[STIX]{x1D70B}_{!}^{\prime }(a^{\prime }b^{\prime })^{2g+1}=0$ . Thus $\unicode[STIX]{x1D70B}_{!}(ab)^{2g+1}$ lies in the kernel of $i^{\ast }$ and so has positive Serre filtration with respect to the map $f$ . Hence $\unicode[STIX]{x1D70B}_{!}(ab)^{(2g+1)(Ak+Bl)}$ has Serre filtration at least $Ak+Bl$ , which is beyond the $\mathbb{Q}$ -cohomological dimension of $F$ , so it is zero as required.

Finally, if $A=0$ and $B=0$ , then the situation becomes that of [Gri13, Theorem 2.7]; this leaves the case of $A=0$ and $B\geqslant 2$ . In this case we must have $\unicode[STIX]{x1D70B}_{!}(a)=0$ , and the above argument can be followed using the homotopy fibre of $\unicode[STIX]{x1D704}_{B}^{l}:K(\mathbb{Q},B)\rightarrow K(\mathbb{Q},Bl)$ in place of  $F$ .◻

Let us also recall some further results from [Gri13], as well as a convenient relation between $R^{\ast }(W_{g})$ and $R^{\ast }(W_{g},\star )$ . We shall often write $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}(W_{g})=2-2g$ for the Euler characteristic of  $W_{g}$ .

Lemma 3.2. Let $n$ be odd.

1. (i) For any $c\in {\mathcal{B}}$ , we have

   (1) $$\begin{eqnarray}\unicode[STIX]{x1D712}^{2}c-\unicode[STIX]{x1D712}\unicode[STIX]{x1D705}_{ec}-\unicode[STIX]{x1D712}e\unicode[STIX]{x1D705}_{c}+\unicode[STIX]{x1D705}_{e^{2}}\unicode[STIX]{x1D705}_{c}=0\in R^{\ast }(M_{g},\star )/\sqrt{0}.\end{eqnarray}$$

2. (ii) We have

   (2) $$\begin{eqnarray}(\unicode[STIX]{x1D712}-2)\unicode[STIX]{x1D712}e+\unicode[STIX]{x1D705}_{e^{2}}=0\in R^{\ast }(M_{g},\star )/\sqrt{0}.\end{eqnarray}$$

3. (iii) If $g\neq 1$ then the map

   $$\begin{eqnarray}R^{\ast }(W_{g})\longrightarrow R^{\ast }(W_{g},\star )\end{eqnarray}$$
   is injective.

Proof. Statement (i) is [Gri13, Example 5.19] but taking $a=\unicode[STIX]{x1D712}\unicode[STIX]{x1D708}_{(1\ast )}-e_{(\ast )}$ and $b=\unicode[STIX]{x1D712}p_{(\ast )}-e_{(\ast )}\unicode[STIX]{x1D705}_{p}$ to avoid dividing by $\unicode[STIX]{x1D712}$ . Assertion (ii) is [Gri13, Example 5.17].

For (iii), suppose that $x\in R^{\ast }(W_{g})$ is a tautological class which vanishes in $R^{\ast }(W_{g},\star )$ , and let $\unicode[STIX]{x1D70B}:E\rightarrow B$ be a fibre bundle with fibre $W_{g}$ . Then the pullback fibre bundle $\unicode[STIX]{x1D70B}^{\prime }:\unicode[STIX]{x1D70B}^{\ast }E\rightarrow E$ is a fibre bundle with fibre $W_{g}$ and canonical section, so $\unicode[STIX]{x1D70B}^{\ast }(x(\unicode[STIX]{x1D70B}))=0$ . But then

$$\begin{eqnarray}(2-2g)\cdot x(\unicode[STIX]{x1D70B})=\unicode[STIX]{x1D70B}_{!}(e(T_{\unicode[STIX]{x1D70B}})\cdot \unicode[STIX]{x1D70B}^{\ast }(x(\unicode[STIX]{x1D70B})))=0\end{eqnarray}$$

and $2-2g\neq 0$ , so $x(\unicode[STIX]{x1D70B})=0$ . This holds for any fibre bundle $\unicode[STIX]{x1D70B}$ , so $x=0\in R^{\ast }(W_{g})$ .◻

Proposition 3.3. Let $n$ be odd, let $I=(i_{1},i_{2},\ldots ,i_{n})$ be a sequence and $p_{I}=p_{1}^{i_{1}}p_{2}^{i_{2}}\cdots p_{n}^{i_{n}}$ the associated monomial in the Pontrjagin classes, and write $|I|=\sum _{j=1}^{n}i_{j}$ .

1. (i) The class $\unicode[STIX]{x1D705}_{p_{I}}$ is nilpotent in $R^{\ast }(W_{g})$ .

2. (ii) We have

   $$\begin{eqnarray}\unicode[STIX]{x1D712}^{|I|}\cdot \unicode[STIX]{x1D705}_{ep_{I}}=\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D705}_{ep_{j}}^{i_{j}}\in R^{\ast }(W_{g})/\sqrt{0}.\end{eqnarray}$$

3. (iii) If $g>1$ then the class $e$ is nilpotent in $R^{\ast }(W_{g},\star )$ .

4. (iv) If $g\geqslant 1$ then for all $k>1$ the class $\unicode[STIX]{x1D705}_{e^{k}}$ is nilpotent in $R^{\ast }(W_{g})$ .

In Proposition 5.5 we will show that $e\in R^{\ast }(W_{1},\star )$ is also nilpotent, though the proof is very different from that of this proposition.

Proof. (i) By Theorem 2.1, the class $\unicode[STIX]{x1D705}_{\tilde{{\mathcal{L}}}_{i}}$ is nilpotent for all $i$ . Therefore, for any monomial $\tilde{{\mathcal{L}}}_{J}=\tilde{{\mathcal{L}}}_{1}^{j_{1}}\tilde{{\mathcal{L}}}_{2}^{j_{2}}\cdots \tilde{{\mathcal{L}}}_{n}^{j_{n}}$ , the class $\unicode[STIX]{x1D705}_{\tilde{{\mathcal{L}}}_{J}}$ is nilpotent by Theorem 3.1. As the $\tilde{{\mathcal{L}}}_{i}$ and the $p_{i}$ generate the same subring of $H^{\ast }(B\text{SO}(2n);\mathbb{Q})$ , it follows that any monomial $p_{I}$ may be written as a polynomial in the $\tilde{{\mathcal{L}}}_{i}$ , and hence each class $\unicode[STIX]{x1D705}_{p_{I}}$ is nilpotent.

(ii) Let $\unicode[STIX]{x1D70B}:E\rightarrow B$ be a fibre bundle with fibre $W_{g}$ , and for a monomial $p_{J}$ in the Pontrjagin classes let us write

$$\begin{eqnarray}(p_{J})^{\prime }=\unicode[STIX]{x1D712}ep_{J}-e\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D705}_{ep_{J}}).\end{eqnarray}$$

We compute that

$$\begin{eqnarray}\unicode[STIX]{x1D705}_{(p_{J})^{\prime }p_{i}}=\unicode[STIX]{x1D70B}_{!}(\unicode[STIX]{x1D712}ep_{i}p_{J}-ep_{i}\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D705}_{ep_{J}}))=\unicode[STIX]{x1D712}\unicode[STIX]{x1D705}_{ep_{i}p_{J}}-\unicode[STIX]{x1D705}_{ep_{i}}\unicode[STIX]{x1D705}_{ep_{J}}\end{eqnarray}$$

and that $\unicode[STIX]{x1D705}_{(p_{J})^{\prime }}=0$ because $\unicode[STIX]{x1D70B}_{!}(e)=\unicode[STIX]{x1D712}$ . By (i) the class $\unicode[STIX]{x1D705}_{p_{i}}$ is nilpotent, so by applying Theorem 3.1 it follows that $\unicode[STIX]{x1D705}_{(p_{J})^{\prime }p_{i}}$ is nilpotent. Therefore $\unicode[STIX]{x1D712}\unicode[STIX]{x1D705}_{ep_{i}p_{J}}=\unicode[STIX]{x1D705}_{ep_{i}}\unicode[STIX]{x1D705}_{ep_{J}}$ modulo nilpotents. These identities hold for any such fibre bundle, so they hold in $R^{\ast }(W_{g})$ , which by induction proves (ii).

(iii) By (i), the class $\unicode[STIX]{x1D705}_{e^{2}}=\unicode[STIX]{x1D705}_{p_{n}}$ is nilpotent, so by (2) it follows that $e\in R^{\ast }(W_{g},\star )$ is also nilpotent as long as $g>1$ .

(iv) Suppose first that $g=1$ , so that $\unicode[STIX]{x1D705}_{e}=0$ . Then, as

$$\begin{eqnarray}\unicode[STIX]{x1D705}_{e^{2l}}=\unicode[STIX]{x1D705}_{p_{n}^{l}}\quad \text{ and }\quad \unicode[STIX]{x1D705}_{e^{2l+1}}=\unicode[STIX]{x1D705}_{ep_{n}^{l}},\end{eqnarray}$$

it follows from (i) that the former are nilpotent, and then from Theorem 3.1 that the latter are too.

For $g>1$ the class $\unicode[STIX]{x1D705}_{e}$ is not itself nilpotent. However, writing

$$\begin{eqnarray}\unicode[STIX]{x1D705}_{e^{2l}}=\unicode[STIX]{x1D705}_{p_{n}^{l}}\quad \text{ and }\quad \unicode[STIX]{x1D705}_{e^{2l+1}}=\unicode[STIX]{x1D705}_{e^{3}p_{n}^{l-1}},\end{eqnarray}$$

we see that the same argument will go through as soon as we show that $\unicode[STIX]{x1D705}_{e^{3}}$ is nilpotent.

Applying (1) with $c=p_{n}=e^{2}$ gives

$$\begin{eqnarray}\unicode[STIX]{x1D712}^{2}p_{n}-\unicode[STIX]{x1D712}\unicode[STIX]{x1D705}_{ep_{n}}-\unicode[STIX]{x1D712}e\unicode[STIX]{x1D705}_{p_{n}}+\unicode[STIX]{x1D705}_{e^{2}}\unicode[STIX]{x1D705}_{p_{n}}=0\in R^{\ast }(M_{g},\star )/\sqrt{0}.\end{eqnarray}$$

The class $\unicode[STIX]{x1D705}_{p_{n}}$ is nilpotent by (i), so we find that $\unicode[STIX]{x1D705}_{ep_{n}}=\unicode[STIX]{x1D712}p_{n}\in R^{\ast }(W_{g},\star )/\sqrt{0}$ . By (iii) the class $p_{n}=e^{2}$ is nilpotent, and therefore so is $\unicode[STIX]{x1D705}_{ep_{n}}=\unicode[STIX]{x1D705}_{e^{3}}$ in the ring $R^{\ast }(W_{g},\star )$ . By Lemma 3.2(iii), the natural ring map $R^{\ast }(W_{g})\rightarrow R^{\ast }(W_{g},\star )$ is injective, so $\unicode[STIX]{x1D705}_{e^{3}}$ is nilpotent in $R^{\ast }(W_{g})$ too, as required.◻

Corollary 3.4. Let $n$ be odd. Then:

1. (i) $R^{\ast }(W_{0})/\sqrt{0}$ is generated by $\unicode[STIX]{x1D705}_{ep_{1}},\unicode[STIX]{x1D705}_{ep_{2}},\ldots ,\unicode[STIX]{x1D705}_{ep_{n}}$ ;

2. (ii) $R^{\ast }(W_{1})/\sqrt{0}=\mathbb{Q}$ ;

3. (iii) $R^{\ast }(W_{g})/\sqrt{0}$ is generated by $\unicode[STIX]{x1D705}_{ep_{1}},\unicode[STIX]{x1D705}_{ep_{2}},\ldots ,\unicode[STIX]{x1D705}_{ep_{n-1}}$ for $g>1$ .

Proof. It follows from Proposition 3.3(i) and (ii) that for any $g$ the ring $R^{\ast }(W_{g})/\sqrt{0}$ is generated by the elements $\unicode[STIX]{x1D705}_{ep_{1}},\unicode[STIX]{x1D705}_{ep_{2}},\ldots ,\unicode[STIX]{x1D705}_{ep_{n}}$ .

For $g=1$ we have $\unicode[STIX]{x1D705}_{e}=0$ . It follows from Theorem 3.1 and Proposition 3.3(i) that the $\unicode[STIX]{x1D705}_{ep_{i}}$ are nilpotent, and so $R^{\ast }(W_{1})/\sqrt{0}=\mathbb{Q}$ .

For $g>1$ it follows from Proposition 3.3(iv) that $\unicode[STIX]{x1D705}_{ep_{n}}=\unicode[STIX]{x1D705}_{e^{3}}$ is nilpotent. So $R^{\ast }(W_{g})/\sqrt{0}$ is generated by the elements $\unicode[STIX]{x1D705}_{ep_{1}},\unicode[STIX]{x1D705}_{ep_{2}},\ldots ,\unicode[STIX]{x1D705}_{ep_{n-1}}$ .◻

Corollary 3.5. Let $n$ be odd and $c\in {\mathcal{B}}$ ; then $\unicode[STIX]{x1D712}c=\unicode[STIX]{x1D705}_{ec}\in R^{\ast }(W_{g},\star )/\sqrt{0}$ .

Proof. If $g=1$ then $\unicode[STIX]{x1D712}c=0$ , but also $\unicode[STIX]{x1D705}_{ec}$ is nilpotent by Corollary 3.4(ii). If $g\neq 1$ then $\unicode[STIX]{x1D712}\neq 0$ , and by (1) we have

$$\begin{eqnarray}\unicode[STIX]{x1D712}^{2}c-\unicode[STIX]{x1D712}\unicode[STIX]{x1D705}_{ec}-\unicode[STIX]{x1D712}e\unicode[STIX]{x1D705}_{c}+\unicode[STIX]{x1D705}_{e^{2}}\unicode[STIX]{x1D705}_{c}=0\in R^{\ast }(W_{g},\star )/\sqrt{0}.\end{eqnarray}$$

The class $\unicode[STIX]{x1D705}_{e^{2}}=\unicode[STIX]{x1D705}_{p_{n}}$ is nilpotent by Proposition 3.3(i), and the class $e$ is nilpotent by Proposition 3.3(iii); this gives the required equation.◻

Proof of Theorem 1.2(i) and (ii).

Statement (i) is Corollary 3.5. For (ii), note that if $g\neq 1$ , it follows that the map

$$\begin{eqnarray}R^{\ast }(W_{g})/\sqrt{0}\longrightarrow R^{\ast }(W_{g},\star )/\sqrt{0}\end{eqnarray}$$

is surjective, and under the same condition this map is injective by Lemma 3.2(iii).◻

In order to prove Theorem 1.1, we must show that the generators of the rings $R^{\ast }(W_{g})/\sqrt{0}$ given in Corollary 3.4 are algebraically independent. That is the subject of the next section.

4 Algebraic independence

In this section, we finish the proof of Theorem 1.1 by showing the following.

Theorem 4.1. Let $n$ be either odd or even, and set $\unicode[STIX]{x1D716}=1$ if $n$ is odd and $\unicode[STIX]{x1D716}=0$ if $n$ is even. Then:

1. (i) the map $\mathbb{Q}[\unicode[STIX]{x1D705}_{ep_{1}},\unicode[STIX]{x1D705}_{ep_{2}},\ldots ,\unicode[STIX]{x1D705}_{ep_{n}}]\rightarrow R^{\ast }(W_{0})/\sqrt{0}$ is injective;

2. (ii) the map $\mathbb{Q}[\unicode[STIX]{x1D705}_{ep_{1}},\unicode[STIX]{x1D705}_{ep_{2}},\ldots ,\unicode[STIX]{x1D705}_{ep_{n-\unicode[STIX]{x1D716}}}]\rightarrow R^{\ast }(W_{g})/\sqrt{0}$ is injective for $g>1$ .

When $n$ is odd, we have shown in Corollary 3.4 that these maps are both surjective, so Theorem 1.1 follows immediately. We first explain the proof of this theorem in case (i), as it is a simpler instance of the strategy we shall use to prove (ii). Consider the fibre bundle

$$\begin{eqnarray}S^{2n}\longrightarrow B\text{SO}(2n)\overset{\unicode[STIX]{x1D70B}}{\longrightarrow }B\text{SO}(2n+1),\end{eqnarray}$$

which defines a ring homomorphism $R^{\ast }(W_{0})\rightarrow H^{\ast }(B\text{SO}(2n+1);\mathbb{Q})$ . The target is the ring $\mathbb{Q}[p_{1},p_{2},\ldots ,p_{n}]$ , which contains no nilpotent elements, so the nilradical is in the kernel of this homomorphism. We may therefore consider the composition

$$\begin{eqnarray}\mathbb{Q}[\unicode[STIX]{x1D705}_{ep_{1}},\unicode[STIX]{x1D705}_{ep_{2}},\ldots ,\unicode[STIX]{x1D705}_{ep_{n}}]\longrightarrow R^{\ast }(W_{0})/\sqrt{0}\overset{\unicode[STIX]{x1D719}}{\longrightarrow }H^{\ast }(B\text{SO}(2n+1);\mathbb{Q}).\end{eqnarray}$$

The fibre bundle $\unicode[STIX]{x1D70B}$ arises as the unit sphere bundle of the tautological bundle $\unicode[STIX]{x1D6FE}_{2n+1}\rightarrow B\text{SO}(2n+1)$ , so there is a bundle isomorphism $\unicode[STIX]{x1D716}^{1}\,\oplus \,T_{\unicode[STIX]{x1D70B}}\cong \unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6FE}_{2n+1}$ , and hence $p_{i}(T_{\unicode[STIX]{x1D70B}})=\unicode[STIX]{x1D70B}^{\ast }(p_{i})$ . Thus we compute

$$\begin{eqnarray}\unicode[STIX]{x1D719}(\unicode[STIX]{x1D705}_{ep_{i}})=\unicode[STIX]{x1D70B}_{!}(e(T_{\unicode[STIX]{x1D70B}})\cdot \unicode[STIX]{x1D70B}^{\ast }(p_{i}))=\unicode[STIX]{x1D70B}_{!}(e(T_{\unicode[STIX]{x1D70B}}))\cdot p_{i}=2\cdot p_{i}\end{eqnarray}$$

(as $\unicode[STIX]{x1D712}(S^{2n})=2$ ), so the composition is injective, which proves (i).

Remark 4.2. This fibre bundle also shows that Proposition 3.3(iii) and (iv) cannot be improved in the case of $g=0$ . Indeed, the vertical tangent bundle for the fibre bundle above is easily seen to be the tautological $2n$ -dimensional bundle over $B\text{SO}(2n)$ , so that $e(T_{\unicode[STIX]{x1D70B}})=e\in H^{2n}(B\text{SO}(2n);\mathbb{Q})$ , which is not nilpotent. Furthermore, $\unicode[STIX]{x1D705}_{e^{2k+1}}=\unicode[STIX]{x1D705}_{ep_{n}^{k}}=2\cdot p_{n}^{k}\in H^{\ast }(B\text{SO}(2n+1);\mathbb{Q})$ is not nilpotent either.

Our strategy for proving (ii) will be similar, and we begin by constructing a fibre bundle with fibre $W_{g}$ and whose base is the classifying space of a Lie group.

4.1 Constructing the Lie group action

Let $G$ be the Lie group $\text{SO}(n)\times \text{SO}(n)$ . An action of $G$ on the manifold $W_{g}$ gives rise to a smooth fibre bundle $E\rightarrow BG$ with fibre $W_{g}$ . We will construct an example of such an action for which the characteristic classes $\unicode[STIX]{x1D705}_{ep_{i}}$ with $1\leqslant i\leqslant d-\unicode[STIX]{x1D716}$ are algebraically independent in $H^{\ast }(BG;\mathbb{Q})$ . In our construction, $W_{g}$ will appear as a boundary of another $G$ -invariant manifold.

The standard $n$ -dimensional representation of $\text{SO}(n)$ gives rise to two $n$ -dimensional representations of $G=\text{SO}(n)\times \text{SO}(n)$ . For $i=1,2$ , we let $V_{i}$ be the representation of $G$ where the $i$ th copy of $\text{SO}(n)$ acts in the standard way and the other copy acts trivially. Let $\mathbb{R}$ denote the trivial one-dimensional representation.

Proposition 4.3. The $G$ -representation $W=V_{1}\,\oplus \,V_{2}\,\oplus \,\mathbb{R}$ contains an embedded compact smooth manifold with boundary $H_{g}\subset W$ that has the following properties:

1. (i) $\dim H_{g}=\dim W=2n+1$ ;

2. (ii) $H_{g}$ is $G$ -invariant, so $\unicode[STIX]{x2202}H_{g}$ is also $G$ -invariant;

3. (iii) $\unicode[STIX]{x2202}H_{g}$ is a smooth manifold diffeomorphic to $W_{g}$ .

Proof. We first illustrate the idea behind the construction of $H_{g}$ by presenting a construction that compromises on the smoothness conditions but is correct up to homeomorphism.

Let $B(V_{1},1)$ and $B(V_{2}\,\oplus \,\mathbb{R},1)$ denote the unit balls in the respective representations. For any $g\in \mathbb{N}$ and a sufficiently small $\unicode[STIX]{x1D700}>0$ , it is possible to embed $g$ balls of radius $\unicode[STIX]{x1D700}$ inside $B(V_{2}\,\oplus \,\mathbb{R},1)$ as disjoint and $\text{SO}(n)$ -invariant subspaces. We can thus define the following subspaces, both invariant under the $G$ -action ( $X_{g}$ is depicted in Figure 1):

$$\begin{eqnarray}\displaystyle X_{g} & = & \displaystyle B(V_{2}\,\oplus \,\mathbb{R},1)\Big\backslash\biggl(\bigsqcup _{g}B(V_{2}\,\oplus \,\mathbb{R},\unicode[STIX]{x1D700})\biggr)\subset V_{2}\,\oplus \,\mathbb{R},\nonumber\\ \displaystyle H_{g}^{\prime } & = & \displaystyle B(V_{1},1)\times X_{g}\subset V_{1}\,\oplus \,V_{2}\,\oplus \,\mathbb{R}.\nonumber\end{eqnarray}$$

The manifold $H_{g}^{\prime }\subset W$ has codimension 0 and is $G$ -invariant. Moreover, $\unicode[STIX]{x2202}H_{g}^{\prime }$ is by definition the boundary of a $(2n+1)$ -manifold obtained by attaching $g$ trivial unlinked $n$ -handles to $D^{2n+1}$ , so it is homeomorphic to  $W_{g}$ .

Figure 1. A cross-section of $X_{g}\subset \mathbb{R}^{3}$ for $(n,g)=(2,3)$ ; $\text{SO}(2)$ acts by rotating about the axis.

Figure 2. The corner $C$ and the rounded corner $S$ .

The construction so far does not prove the proposition, as $\unicode[STIX]{x2202}H_{g}^{\prime }$ is not a smooth submanifold of $W$ . We would like to smooth out the corners of the manifold $H_{g}^{\prime }$ to obtain a manifold $H_{g}$ that is again $G$ -invariant but has smooth boundary. The boundary of $H_{g}^{\prime }$ is not smooth at the set $\unicode[STIX]{x2202}B(V_{1},1)\times \unicode[STIX]{x2202}X_{g}\subset \unicode[STIX]{x2202}H_{g}$ .

The Riemannian metrics on $B(V_{1},1)$ and $X_{g}$ induced by those of $V_{1}$ and $V_{2}\,\oplus \,\mathbb{R}$ are $\text{SO}(n)$ -invariant. Choosing inward-pointing, nowhere-vanishing, $\text{SO}(n)$ -invariant vector fields on $\unicode[STIX]{x2202}B(V_{1},1)$ and $\unicode[STIX]{x2202}X_{g}$ (which may be achieved by choosing an inward-pointing, nowhere-vanishing vector field and then averaging over $\text{SO}(n)$ ) and integrating them, we can find a $G$ -invariant neighbourhood

$$\begin{eqnarray}U^{\prime }=\unicode[STIX]{x2202}B(V_{1},1)\times \unicode[STIX]{x2202}X_{g}\times C{\hookrightarrow}V_{1}\,\oplus \,V_{2}\,\oplus \,\mathbb{R}\end{eqnarray}$$

where $C=\{(x,y)\in \mathbb{R}^{2}\mid x,y\geqslant 0\}$ and has the trivial $G$ -action.

Let $S\subset C$ be a strictly convex subset of $C$ that agrees with $C$ in a complement of a compact set around the origin, but has a smooth boundary diffeomorphic to $\mathbb{R}$ (see Figure 2). We replace $U^{\prime }$ with its ( $G$ -invariant) subset $U=\unicode[STIX]{x2202}B(V_{1},1)\times \unicode[STIX]{x2202}X_{g}\times S$ to obtain $H_{g}$ . This $H_{g}$ clearly satisfies conditions (i) and (ii) of Proposition 4.3. Finally, $\unicode[STIX]{x2202}H_{g}$ is by definition the boundary of a smooth $(2n+1)$ -manifold obtained by attaching $g$ trivial unlinked $n$ -handles to $D^{2n+1}$ and smoothing corners, so it is diffeomorphic to  $W_{g}$ .◻

4.2 Proof of Theorem 4.1(ii)

Let us write

$$\begin{eqnarray}W_{g}\longrightarrow E\overset{\unicode[STIX]{x1D70B}}{\longrightarrow }B\text{SO}(n)\times B\text{SO}(n)\end{eqnarray}$$

for the fibre bundle of Proposition 4.3, which, as $H^{\ast }(B\text{SO}(n)\times B\text{SO}(n);\mathbb{Q})$ has no nilpotent elements, gives a ring homomorphism

$$\begin{eqnarray}\unicode[STIX]{x1D719}:R^{\ast }(W_{g})/\sqrt{0}\longrightarrow H^{\ast }(B\text{SO}(n)\times B\text{SO}(n);\mathbb{Q}).\end{eqnarray}$$

Theorem 4.1(ii) will follow if we show that $\unicode[STIX]{x1D719}(\unicode[STIX]{x1D705}_{ep_{1}}),\unicode[STIX]{x1D719}(\unicode[STIX]{x1D705}_{ep_{2}}),\ldots ,\unicode[STIX]{x1D719}(\unicode[STIX]{x1D705}_{ep_{n-\unicode[STIX]{x1D716}}})$ are algebraically independent.

By Proposition 4.3, the fibre bundle $\unicode[STIX]{x1D70B}$ arises as a codimension-one subbundle of the vector bundle $V_{1}\,\oplus \,V_{2}\,\oplus \,\mathbb{R}$ . We thus obtain a bundle isomorphism $\mathbb{R}\,\oplus \,T_{\unicode[STIX]{x1D70B}}\cong \unicode[STIX]{x1D70B}^{\ast }(V_{1}\,\oplus \,V_{2}\,\oplus \,\mathbb{R})$ , and hence $p_{i}(T_{\unicode[STIX]{x1D70B}})=\unicode[STIX]{x1D70B}^{\ast }(p_{i}(V_{1}\,\oplus \,V_{2}))$ . Therefore

$$\begin{eqnarray}\unicode[STIX]{x1D719}(\unicode[STIX]{x1D705}_{ep_{i}})=\unicode[STIX]{x1D70B}_{!}(e(T_{\unicode[STIX]{x1D70B}}))\cdot p_{i}(V_{1}\,\oplus \,V_{2})=\unicode[STIX]{x1D712}\cdot p_{i}(V_{1}\,\oplus \,V_{2}).\end{eqnarray}$$

As $\unicode[STIX]{x1D712}\neq 0$ , because we have assumed $g>1$ , the following lemma finishes the proof.

Lemma 4.4. The classes $p_{i}(V_{1}\,\oplus \,V_{2})$ for $1\leqslant i\leqslant n-\unicode[STIX]{x1D716}$ are algebraically independent in $H^{\ast }(B\text{SO}(n)\times B\text{SO}(n);\mathbb{Q})$ .

Proof. Recall from [MS74, Theorem 15.21] that in terms of the Pontrjagin and Euler classes of the tautological bundle over $B\text{SO}(d)$ , we have

$$\begin{eqnarray}H^{\ast }(B\text{SO}(d);\mathbb{Q})=\left\{\begin{array}{@{}ll@{}}\mathbb{Q}[p_{1},\ldots ,p_{(d-1)/2}]\quad & \text{ for }d\text{ odd},\\ \mathbb{Q}[p_{1},\ldots ,p_{d/2-1},e]\quad & \text{ for }d\text{ even}.\end{array}\right.\end{eqnarray}$$

Moreover, if $d$ is even then $p_{d/2}=e^{2}$ . In all cases, if $i>(d-\unicode[STIX]{x1D716})/2$ then $p_{i}=0$ .

The block sum map $s:\text{SO}(n)\times \text{SO}(n)\rightarrow \text{SO}(2n)$ gives a map

$$\begin{eqnarray}Bs^{\ast }:R=H^{\ast }(B\text{SO}(2n);\mathbb{Q})\longrightarrow S=H^{\ast }(B\text{SO}(n)\times B\text{SO}(n);\mathbb{Q})\end{eqnarray}$$

on cohomology, and the claim is that it is injective when restricted to the subalgebra $\mathbb{Q}[p_{1},p_{2},\ldots ,p_{n-\unicode[STIX]{x1D716}}]$ . As the block sum map is faithful, it follows from a theorem of Venkov [Ven59] that $S$ is finitely generated as a module over $R$ . By the above, $S$ is a polynomial ring on $n-1$ generators if $n$ is odd, or on $n$ generators if $n$ is even; $R$ is a polynomial algebra on $n$ generators.

We shall use the following result from commutative algebra: if $f:U\rightarrow V$ is a finite morphism between polynomial rings on the same (finite) number of generators, then it is injective. If it were not, then $\text{Ker}(f)$ would be a proper prime ideal (because $V$ , and hence $\text{Im}(f)$ , is an integral domain), so $U/\text{Ker}(f)$ would have strictly smaller Krull dimension than $U$ . But as $V$ is also finite over $U/\text{Ker}(f)$ , it too would have strictly smaller Krull dimension than $U$ , which is a contradiction.

If $n$ is even, then $Bs^{\ast }:R\rightarrow S$ is a finite morphism between polynomial rings on the same number of generators, so it is injective. If $n$ is odd, note that $e\in H^{2n}(B\text{SO}(2n);\mathbb{Q})=R$ lies in the kernel of $Bs^{\ast }$ (as $V_{1}\,\oplus \,V_{2}$ has trivial Euler class), so instead $R/(e)\rightarrow S$ is a finite morphism between polynomial rings on the same number of generators, and hence is injective. In either case, the subalgebra $\mathbb{Q}[p_{1},p_{2},\ldots ,p_{n-\unicode[STIX]{x1D716}}]$ of $H^{\ast }(B\text{SO}(2n);\mathbb{Q})$ injects under the block sum map.◻

5 Addenda

5.1 Classifying spaces

We have defined the tautological ring $R^{\ast }(M)$ as a quotient of the abstract polynomial ring $\mathbb{Q}[\unicode[STIX]{x1D705}_{c}\mid c\in {\mathcal{B}}]$ , but it may also be described as a subring of the cohomology of the classifying space $B\text{Diff}^{+}(M)$ of the group of orientation-preserving diffeomorphisms of $M$ .

Precisely, if $\unicode[STIX]{x1D70B}:E\rightarrow B$ is equipped with the structure of a smooth oriented numerable fibre bundle with fibre $M^{d}$ , albeit without assuming that $E$ and $B$ are themselves oriented compact smooth manifolds, then we still have a vertical tangent bundle $T_{\unicode[STIX]{x1D70B}}$ and a cohomological pushforward $\unicode[STIX]{x1D70B}_{!}$ , so we may still define

$$\begin{eqnarray}\unicode[STIX]{x1D705}_{c}(\unicode[STIX]{x1D70B})=\unicode[STIX]{x1D70B}_{!}(c(T_{\unicode[STIX]{x1D70B}}))\in H^{\ast }(B;\mathbb{Q}).\end{eqnarray}$$

The projection map

$$\begin{eqnarray}E\text{Diff}^{+}(M)\times _{\text{Diff}^{+}(M)}M\longrightarrow B\text{Diff}^{+}(M)\end{eqnarray}$$

is the universal example of such a fibre bundle, so there are universal classes $\unicode[STIX]{x1D705}_{c}\in H^{\ast }(B\text{Diff}^{+}(M);\mathbb{Q})$ .

Lemma 5.1. The ring homomorphism $\mathbb{Q}[\unicode[STIX]{x1D705}_{c}\mid c\in {\mathcal{B}}]\rightarrow H^{\ast }(B\text{Diff}^{+}(M);\mathbb{Q})$ has kernel $I_{M}$ , and hence its image is isomorphic to $R^{\ast }(M)$ .

Proof. The only point which needs discussion is that we defined $I_{M}$ in terms of the collection of all smooth fibre bundles over compact smooth oriented manifolds (in other words, proper submersions $\unicode[STIX]{x1D70B}:E^{k+d}\rightarrow B^{k}$ ), and $B\text{Diff}^{+}(M)$ is not one.

Let us write $I_{M}^{\prime }$ for the kernel of this ring homomorphism. As $B\text{Diff}^{+}(M)$ carries the universal smooth oriented fibre bundle with fibre $M$ , any class in $I_{M}^{\prime }$ must be trivial when evaluated on any proper submersion $\unicode[STIX]{x1D70B}:E^{k+d}\rightarrow B^{k}$ , so $I_{M}^{\prime }\subset I_{M}$ . The reverse inclusion holds because a rational cohomology class is zero if and only if it evaluates to zero on every rational homology class, and every rational homology class is represented by a map from a smooth (stably framed) manifold.◻

The analogous argument identifies $R^{\ast }(M,\star )$ with a subring of the cohomology of $B\text{Diff}^{+}(M,\star )$ , the classifying space of the group of orientation-preserving diffeomorphisms of $M$ which fix a point $\star \in M$ , and identifies $R^{\ast }(M,D^{d})$ with a subring of the cohomology of $B\text{Diff}^{+}(M,D^{d})$ , the classifying space of the group of orientation-preserving diffeomorphisms of $M$ which fix a disc $D^{d}\subset M$ .

5.2 Other classes of fibre bundles

We have defined the tautological ring $R^{\ast }(M)=\mathbb{Q}[\unicode[STIX]{x1D705}_{c}\mid c\in {\mathcal{B}}]/I_{M}$ in terms of the ideal $I_{M}$ of polynomials in the $\unicode[STIX]{x1D705}_{c}$ which vanish when evaluated on every smooth oriented fibre bundle with fibre $M$ . By varying this condition, we may form the following related tautological rings:

1. (i) $R_{\text{torelli}}^{\ast }(M)$ , defined in terms of the ideal of polynomials in the $\unicode[STIX]{x1D705}_{c}$ which vanish on every smooth oriented fibre bundle with fibre $M$ and homologically trivial action of the fundamental group of the base;

2. (ii) $R_{0}^{\ast }(M)$ , defined in terms of the ideal of polynomials in the $\unicode[STIX]{x1D705}_{c}$ which vanish on every smooth oriented fibre bundle with fibre $M$ and isotopically trivial action of the fundamental group of the base.

These are related by surjective ring homomorphisms

$$\begin{eqnarray}R^{\ast }(M)\longrightarrow R_{\text{torelli}}^{\ast }(M)\longrightarrow R_{0}^{\ast }(M).\end{eqnarray}$$

It follows from our results that for $M=W_{g}$ and $n$ odd, these maps all become isomorphisms after dividing out each ring by its nilradical: §§ 2 and 3 give relations in $R^{\ast }(W_{g})/\sqrt{0}$ , whereas § 4 shows algebraic independence of classes in $R_{0}^{\ast }(W_{g})/\sqrt{0}$ . In fact, this is true quite generally.

Proposition 5.2. Let $M$ be a simply connected manifold of dimension $d>5$ . Then

$$\begin{eqnarray}R^{\ast }(M)/\sqrt{0}\longrightarrow R_{\text{torelli}}^{\ast }(M)/\sqrt{0}\longrightarrow R_{0}^{\ast }(M)/\sqrt{0}\end{eqnarray}$$

are isomorphisms. The same holds for $(M,\star )$ and $(M,D^{d})$ .

Proof. Both maps are epimorphisms by definition, so it is enough to show that the composition is an isomorphism. Sullivan has shown [Sul77, Theorem 13.3] that under the stated conditions the mapping class group $\unicode[STIX]{x1D6E4}_{M}=\unicode[STIX]{x1D70B}_{0}(\text{Diff}^{+}(M))$ is commensurable to an arithmetic group. In particular, it has finite virtual cohomological dimension and hence finite $\mathbb{Q}$ -cohomological dimension.

Letting $\text{Diff}_{0}^{+}(M)$ denote the path component of the identity, there is a fibration sequence

$$\begin{eqnarray}B\text{Diff}_{0}^{+}(M)\overset{i}{\longrightarrow }B\text{Diff}^{+}(M)\overset{p}{\longrightarrow }B\unicode[STIX]{x1D6E4}_{M}\end{eqnarray}$$

and an associated Serre spectral sequence. We then proceed much as in the proof of Theorem 3.1: any class in

$$\begin{eqnarray}\text{Ker}(i^{\ast }:H^{\ast }(B\text{Diff}^{+}(M);\mathbb{Q})\rightarrow H^{\ast }(B\text{Diff}_{0}^{+}(M);\mathbb{Q}))\end{eqnarray}$$

has positive Serre filtration, so some power of it has Serre filtration beyond the $\mathbb{Q}$ -cohomological dimension of $B\unicode[STIX]{x1D6E4}_{M}$ . Such a power is therefore zero, showing that $\text{Ker}(i^{\ast })$ consists of nilpotent elements and hence that the map

$$\begin{eqnarray}i^{\ast }:H^{\ast }(B\text{Diff}^{+}(M);\mathbb{Q})/\sqrt{0}\longrightarrow H^{\ast }(B\text{Diff}_{0}^{+}(M);\mathbb{Q})/\sqrt{0}\end{eqnarray}$$

is injective. The result now follows from the discussion of classifying spaces in the previous section.

For $(M,\star )$ and $(M,D^{d})$ the argument is identical, except that one uses the relative mapping class groups of these pairs. For $M$ simply connected, the natural map $\unicode[STIX]{x1D6E4}_{(M,\star )}\rightarrow \unicode[STIX]{x1D6E4}_{M}$ is an isomorphism, as can be seen from the fibration sequence $M\rightarrow B\text{Diff}^{+}(M,\star )\rightarrow B\text{Diff}^{+}(M)$ . The fibration $\text{SO}(d)\rightarrow B\text{Diff}^{+}(M,D^{d})\rightarrow B\text{Diff}^{+}(M,\star )$ shows that $\unicode[STIX]{x1D6E4}_{(M,D^{d})}\rightarrow \unicode[STIX]{x1D6E4}_{(M,\star )}$ is onto with kernel of order at most 2. Thus $\unicode[STIX]{x1D6E4}_{(M,D^{d})}$ still has finite $\mathbb{Q}$ -cohomological dimension.◻

5.3 Genus zero

For the manifold $W_{0}=S^{2n}$ , we can improve Theorem 1.1 to say that

$$\begin{eqnarray}R^{\ast }(W_{0})=\mathbb{Q}[\unicode[STIX]{x1D705}_{ep_{1}},\unicode[STIX]{x1D705}_{ep_{2}},\ldots ,\unicode[STIX]{x1D705}_{ep_{n}}];\end{eqnarray}$$

that is, we do not need to divide by the nilradical, nor do we need a condition on the parity of $n$ . Let $\unicode[STIX]{x1D70B}:E\rightarrow B$ be a fibre bundle with fibre $S^{2n}$ . We use the following two stronger versions of our results.

Lemma 5.3. We have $\unicode[STIX]{x1D705}_{\tilde{{\mathcal{L}}}_{i}}(\unicode[STIX]{x1D70B})=0\in H^{\ast }(B;\mathbb{Q})$ .

Proof. Observe that in the proof of Theorem 2.1, the group $\text{Aut}(H,\unicode[STIX]{x1D706})$ is trivial when $g=0$ . Therefore, the classes $\unicode[STIX]{x1D705}_{\tilde{{\mathcal{L}}}_{i}}(\unicode[STIX]{x1D70B})$ must be pulled back through the cohomology of the contractible space $B\text{Aut}(H,\unicode[STIX]{x1D706})$ .◻

Lemma 5.4. If $p,q\in H^{\ast }(E;\mathbb{Q})$ satisfy $\unicode[STIX]{x1D70B}_{!}(p)=0$ and $\unicode[STIX]{x1D70B}_{!}(q)=0$ , then $\unicode[STIX]{x1D70B}_{!}(pq)=0$ .

Proof. It follows from the Gysin sequence for $\unicode[STIX]{x1D70B}$ that there is a $p^{\prime }\in H^{\ast }(B;\mathbb{Q})$ such that $p=\unicode[STIX]{x1D70B}^{\ast }(p^{\prime })$ ; but then $\unicode[STIX]{x1D70B}_{!}(pq)=\unicode[STIX]{x1D70B}_{!}(\unicode[STIX]{x1D70B}^{\ast }(p^{\prime })q)=p^{\prime }\cdot \unicode[STIX]{x1D70B}_{!}(q)=0$ .◻

It follows from Lemma 5.3 that $\unicode[STIX]{x1D705}_{\tilde{{\mathcal{L}}}_{i}}=0\in R^{\ast }(W_{0})$ , and so, by Lemma 5.4, $\unicode[STIX]{x1D705}_{\tilde{{\mathcal{L}}}_{J}}=0\in R^{\ast }(W_{0})$ for any monomial $\tilde{{\mathcal{L}}}_{J}$ . As these give a basis for the subring of $H^{\ast }(B\text{SO}(2n);\mathbb{Q})$ generated by Pontrjagin classes, we have that $\unicode[STIX]{x1D705}_{p_{I}}=0$ too. For a fibre bundle $\unicode[STIX]{x1D70B}:E\rightarrow B$ with fibre $S^{2n}$ , by the Gysin sequence we therefore have $p_{I}=\unicode[STIX]{x1D70B}^{\ast }((p_{I})^{\prime })$ for some $(p_{I})^{\prime }\in H^{\ast }(B;\mathbb{Q})$ , and so

$$\begin{eqnarray}\unicode[STIX]{x1D705}_{ep_{I}}(\unicode[STIX]{x1D70B})=\unicode[STIX]{x1D70B}_{!}(e(T_{\unicode[STIX]{x1D70B}})\unicode[STIX]{x1D70B}^{\ast }((p_{I})^{\prime }))=\unicode[STIX]{x1D70B}_{!}(e(T_{\unicode[STIX]{x1D70B}}))\cdot (p_{I})^{\prime }=2(p_{I})^{\prime }.\end{eqnarray}$$

In particular, we may express $\unicode[STIX]{x1D705}_{ep_{I}}(\unicode[STIX]{x1D70B})$ by a universal formula in the $p_{i}^{\prime }={\textstyle \frac{1}{2}}\unicode[STIX]{x1D705}_{ep_{i}}(\unicode[STIX]{x1D70B})$ ; so $\unicode[STIX]{x1D705}_{ep_{1}},\unicode[STIX]{x1D705}_{ep_{2}},\ldots ,\unicode[STIX]{x1D705}_{ep_{n}}$ generate $R^{\ast }(W_{0})$ . They are algebraically independent in this ring as we have already shown that they are algebraically independent in $R^{\ast }(W_{0})/\sqrt{0}$ .

5.4 Genus one

We have two outstanding claims to prove in the $g=1$ case. The first is Theorem 1.2(iii), and the second is that $R^{\ast }(W_{1},\star )$ is finitely generated, so that $R^{\ast }(W_{1},D^{2n})$ is too and we can deduce Corollary 1.4 from Corollary 1.3.

5.4.1 The Euler class

We first prove the analogue of Proposition 3.3(iii) for $g=1$ .

Proposition 5.5. The class $e\in R^{\ast }(W_{1},\star )$ is nilpotent.

Our proof of this proposition will use the following result, which would seem to be quite generally useful in the study of tautological rings.

Theorem 5.6. Let $B$ be a finite CW-complex, let $\unicode[STIX]{x1D70B}:E\rightarrow B$ and $\unicode[STIX]{x1D70B}^{\prime }:E^{\prime }\rightarrow B$ be smooth fibre bundles with closed $d$ -manifold fibres, and let $f:E\rightarrow E^{\prime }$ be a map over $B$ which is a fibre homotopy equivalence. Then $f^{\ast }(e(T_{\unicode[STIX]{x1D70B}^{\prime }}))=e(T_{\unicode[STIX]{x1D70B}})\in H^{d}(E;\mathbb{Z})$ .

Proof. We refer to [BG76] for background on the following, and to [MS06, ch. 15] for technical details of fibrewise Spanier–Whitehead duality. For a space $X$ over $B$ , let $X_{+}=X\sqcup B$ be the associated ex-space, and let $\unicode[STIX]{x1D6F4}_{B}^{\infty }X_{+}$ denote the fibrewise suspension spectrum. By [BG76, Theorem 4.7] or [MS06, Theorem 15.1.1], the parametrised spectrum $\unicode[STIX]{x1D6F4}_{B}^{\infty }E_{+}$ is dualisable, and in fact its dual can be made rather explicit. Choose a smooth embedding $E\subset B\times \mathbb{R}^{N}$ with tubular neighbourhood $U$ and projection $p:U\rightarrow E$ , and let $U_{B}^{+}$ denote the one-point compactification of $U$ formed fibrewise over $B$ , so there is a canonical section $s_{\infty }:B\rightarrow U_{B}^{+}$ given by the points at $\infty$ . There is then a map

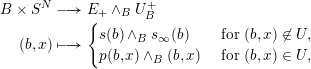$$\begin{eqnarray}\displaystyle B\times S^{N} & \longrightarrow & \displaystyle E_{+}\wedge _{B}U_{B}^{+}\nonumber\\ \displaystyle (b,x) & \longmapsto & \displaystyle \left\{\begin{array}{@{}ll@{}}s(b)\wedge _{B}s_{\infty }(b)\quad & \text{ for }(b,x)\not \in U,\\ p(b,x)\wedge _{B}(b,x)\quad & \text{ for }(b,x)\in U,\end{array}\right.\nonumber\end{eqnarray}$$

giving a map

$$\begin{eqnarray}\unicode[STIX]{x1D707}_{E}:\unicode[STIX]{x1D6F4}_{B}^{\infty }B_{+}\longrightarrow \unicode[STIX]{x1D6F4}_{B}^{\infty }E_{+}\wedge _{B}\unicode[STIX]{x1D6F4}_{B}^{\infty -N}U_{B}^{+}\end{eqnarray}$$

of parametrised spectra which exhibits $\unicode[STIX]{x1D6F4}_{B}^{\infty }E_{+}$ and $\unicode[STIX]{x1D6F4}_{B}^{\infty -N}U_{B}^{+}$ as Spanier–Whitehead duals. There is therefore a complementary duality map

$$\begin{eqnarray}\hat{\unicode[STIX]{x1D707}}_{E}:\unicode[STIX]{x1D6F4}_{B}^{\infty -N}U_{B}^{+}\wedge _{B}\unicode[STIX]{x1D6F4}_{B}^{\infty }E_{+}\longrightarrow \unicode[STIX]{x1D6F4}_{B}^{\infty }B_{+},\end{eqnarray}$$

and the composition

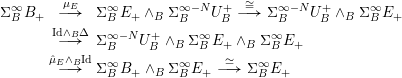$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}_{B}^{\infty }B_{+} & \overset{\unicode[STIX]{x1D707}_{E}}{\longrightarrow } & \displaystyle \unicode[STIX]{x1D6F4}_{B}^{\infty }E_{+}\wedge _{B}\unicode[STIX]{x1D6F4}_{B}^{\infty -N}U_{B}^{+}\overset{\cong }{\longrightarrow }\unicode[STIX]{x1D6F4}_{B}^{\infty -N}U_{B}^{+}\wedge _{B}\unicode[STIX]{x1D6F4}_{B}^{\infty }E_{+}\nonumber\\ \displaystyle & \overset{\text{Id}\wedge _{B}\unicode[STIX]{x1D6E5}}{\longrightarrow } & \displaystyle \unicode[STIX]{x1D6F4}_{B}^{\infty -N}U_{B}^{+}\wedge _{B}\unicode[STIX]{x1D6F4}_{B}^{\infty }E_{+}\wedge _{B}\unicode[STIX]{x1D6F4}_{B}^{\infty }E_{+}\nonumber\\ \displaystyle & \overset{\hat{\unicode[STIX]{x1D707}}_{E}\wedge _{B}\text{Id}}{\longrightarrow } & \displaystyle \unicode[STIX]{x1D6F4}_{B}^{\infty }B_{+}\wedge _{B}\unicode[STIX]{x1D6F4}_{B}^{\infty }E_{+}\overset{\simeq }{\longrightarrow }\unicode[STIX]{x1D6F4}_{B}^{\infty }E_{+}\nonumber\end{eqnarray}$$

is a lift of the Becker–Gottlieb transfer of $\unicode[STIX]{x1D70B}$ to parametrised spectra. Dualising this map gives a map of parametrised spectra

$$\begin{eqnarray}\unicode[STIX]{x1D716}_{E}:\unicode[STIX]{x1D6F4}_{B}^{\infty -N}U_{B}^{+}\longrightarrow \unicode[STIX]{x1D6F4}_{B}^{\infty }B_{+}\end{eqnarray}$$

and so, upon base changing along $B\rightarrow \{\ast \}$ and then collapsing $B$ to a point, we obtain a map of spectra

$$\begin{eqnarray}c:\unicode[STIX]{x1D6F4}^{\infty -N}U^{+}\longrightarrow \unicode[STIX]{x1D6F4}^{\infty }B_{+}\longrightarrow \unicode[STIX]{x1D6F4}^{\infty }S^{0}.\end{eqnarray}$$

On the other hand, $U$ is homeomorphic to the normal bundle $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}$ of $E$ in $B\times \mathbb{R}^{N}$ , so $U^{+}$ is homeomorphic to the Thom space $\text{Th}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}})$ . The pullback along $c$ of the canonical cohomology class in $H^{0}(\unicode[STIX]{x1D6F4}^{\infty }S^{0};\mathbb{Z})$ , followed by the Thom isomorphism (as $T_{\unicode[STIX]{x1D70B}}$ , and hence $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70B}}$ , is oriented), therefore gives a class in $H^{d}(E;\mathbb{Z})$ . It follows from the Poincaré–Hopf theorem that this is $e(T_{\unicode[STIX]{x1D70B}})$ .

The analogous construction, using a tubular neighbourhood $E^{\prime }\subset V\subset B\times \mathbb{R}^{N}$ , describes $e(T_{\unicode[STIX]{x1D70B}^{\prime }})$ . The point is that the above construction uses only fibrewise Spanier–Whitehead duality, and so if $D(f_{+}):\unicode[STIX]{x1D6F4}_{B}^{\infty -N}V_{B}^{+}\rightarrow \unicode[STIX]{x1D6F4}_{B}^{\infty -N}U_{B}^{+}$ is the dual of $f_{+}$ , then we have

$$\begin{eqnarray}\unicode[STIX]{x1D716}_{E}\circ D(f_{+})\simeq \unicode[STIX]{x1D716}_{E^{\prime }}:\unicode[STIX]{x1D6F4}_{B}^{\infty -N}V_{B}^{+}\longrightarrow \unicode[STIX]{x1D6F4}_{B}^{\infty }B_{+}.\end{eqnarray}$$

Therefore, as under the Thom isomorphism $D(f_{+})^{\ast }$ induces the map $(f^{\ast })^{-1}:H^{\ast }(E;\mathbb{Z})\rightarrow H^{\ast }(E^{\prime };\mathbb{Z})$ , we have $f^{\ast }(e(T_{\unicode[STIX]{x1D70B}^{\prime }}))=e(T_{\unicode[STIX]{x1D70B}})$ .◻

The arguments in this proof can be refined to define an Euler class of the vertical tangent bundle, $e(T_{\unicode[STIX]{x1D70B}})\in H^{d}(E;\mathbb{Z})$ , when $\unicode[STIX]{x1D70B}:E\rightarrow B$ is a fibration whose fibre is a Poincaré duality space of dimension $d$ . In particular, for such a Poincaré duality space $M^{d}$ , one can define the universal such class $e\in H^{d}(B\text{hAut}^{+}(M,\star );\mathbb{Z})$ .

Proof of Proposition 5.5.

Let $\unicode[STIX]{x1D70B}:E^{k+2n}\rightarrow B^{k}$ be a homologically trivial smooth oriented fibre bundle with fibre $W_{1}$ , and let $s:B\rightarrow E$ be a section. We will show that $s^{\ast }(e(T_{\unicode[STIX]{x1D70B}}))=0\in H^{2n}(B;\mathbb{Q})$ , so that $e=0\in R_{\text{torelli}}^{\ast }(W_{1},\star )$ . Hence, by Proposition 5.2, $e$ is nilpotent in $R^{\ast }(W_{1},\star )$ .

Under the stated assumptions, the Serre spectral sequence for $\unicode[STIX]{x1D70B}$ has a product structure and collapses, giving classes $a,b\in H^{n}(E;\mathbb{Z})$ which restrict to a basis of $H^{n}(W_{1};\mathbb{Z})$ . The obstructions to finding a lift

lie in $H^{i+1}(E;\unicode[STIX]{x1D70B}_{i}(S^{n}\times S^{n}))$ for $n<i<k+2n$ , which are all torsion groups.

Let $\cdots \rightarrow B_{2}\overset{f_{1}}{\rightarrow }B_{1}\overset{f_{0}}{\rightarrow }B_{0}=B$ be a tower of finite $k$ -dimensional CW-complexes in which each $f_{i}^{\ast }:H^{\ast }(B_{i};\mathbb{Z})\rightarrow H^{\ast }(B_{i+1};\mathbb{Z})$ annihilates all torsion but is rationally injective. (Such a tower may be formed as follows: an $n$ -torsion class $x\in H^{j}(B_{i};\mathbb{Z})$ arises via Bockstein from a class $x^{\prime }\in H^{j-1}(B_{i};\mathbb{Z}/n)$ represented by a map $g_{x}:B_{i}\rightarrow K(\mathbb{Z}/n,j-1)$ , and $B_{i+1}$ may be taken to be a $k$ -skeleton of the homotopy fibre of the product of the maps $g_{x}$ over all torsion classes $x\in H^{\ast }(B_{i};\mathbb{Z})$ .) We may pull back $\unicode[STIX]{x1D70B}$ and $s$ to obtain homologically trivial bundles $\unicode[STIX]{x1D70B}_{i}:E_{i}\rightarrow B_{i}$ with sections $s_{i}$ . All of these also have Serre spectral sequences which have a product structure and collapse, and they are connected by maps $\hat{f}_{i}:E_{i+1}\rightarrow E_{i}$ covering the  $f_{i}$ .

It follows that $\hat{f}_{i}^{\ast }$ always sends a torsion class to one of higher Serre filtration, so in particular (as the Serre spectral sequence for each $\unicode[STIX]{x1D70B}_{i}$ has three rows) the composition of three such maps annihilates any torsion class. Therefore a finite composition of such maps annihilates all obstructions to finding the dashed lift above, so for some $i$ we have a map $t:E_{i}\rightarrow S^{n}\times S^{n}$ splitting the inclusion of the fibre. It follows that $\unicode[STIX]{x1D70B}_{i}$ is fibre homotopy-equivalent to the trivial $W_{1}$ -bundle, and hence by Theorem 5.6 we have

$$\begin{eqnarray}e(T_{\unicode[STIX]{x1D70B}_{i}})=0\in H^{n}(E_{i};\mathbb{Z})\end{eqnarray}$$

and so $s_{i}^{\ast }e(T_{\unicode[STIX]{x1D70B}_{i}})=0\in H^{n}(B_{i};\mathbb{Z})$ . The maps $f_{i}^{\ast }$ were rationally injective, and so $s^{\ast }e(T_{\unicode[STIX]{x1D70B}})=0\in H^{2n}(B;\mathbb{Q})$ , as required.◻

Finally, we can prove the third part of Theorem 1.2.

Proof of Theorem 1.2(iii).

We have shown that $e$ is nilpotent in $R^{\ast }(W_{1},\star )$ . Consider the fibre bundle

$$\begin{eqnarray}S^{n}\times S^{n}\longrightarrow B\text{SO}(n)\times B\text{SO}(n)\overset{\unicode[STIX]{x1D70B}}{\longrightarrow }B\text{SO}(n+1)\times B\text{SO}(n+1)\end{eqnarray}$$

and let $\unicode[STIX]{x1D70B}^{\prime }:E\rightarrow B\text{SO}(n)\times B\text{SO}(n)$ be the fibre bundle obtained by pulling $\unicode[STIX]{x1D70B}$ back along itself. Then $\unicode[STIX]{x1D70B}^{\prime }$ has a section $s^{\prime }$ , and the ring $H^{\ast }(B\text{SO}(n)\times B\text{SO}(n);\mathbb{Q})$ has no nilpotent elements, so there is a ring homomorphism

$$\begin{eqnarray}\unicode[STIX]{x1D719}:R^{\ast }(W_{1},\star )/\sqrt{0}\longrightarrow H^{\ast }(B\text{SO}(n)\times B\text{SO}(n);\mathbb{Q}).\end{eqnarray}$$

There is a bundle isomorphism $(s^{\prime })^{\ast }(T_{\unicode[STIX]{x1D70B}^{\prime }})\cong V_{1}\,\oplus \,V_{2}$ , so $\unicode[STIX]{x1D719}(p_{i})=p_{i}(V_{1}\,\oplus \,V_{2})$ . It follows from Lemma 4.4 that $p_{1},p_{2},\ldots ,p_{n-1}\subset R^{\ast }(W_{1},\star )/\sqrt{0}$ are algebraically independent.◻

5.4.2 Finite generation

The proof in [Gri13] showing that $R^{\ast }(W_{g})$ is finitely generated does not apply to the $g\leqslant 1$ case. We have computed $R^{\ast }(W_{0})$ completely, and can observe that it is finitely generated, which leaves only the case $g=1$ to consider. In fact, we do not know whether this ring is finitely generated. However, we have the following result.

Proposition 5.7. For all $g\geqslant 0$ , the ring $R^{\ast }(W_{g},\star )$ is finitely generated.

Proof. Our argument follows [Gri13, Example 5.19 and Lemma 5.20], and we shall freely use the language and notation of that paper. We work in the space ${\mathcal{M}}_{g}(\{1,2,\star \})$ with three marked points $1,2$ and $\star$ . Let $p\in H^{\ast }(B\text{SO}(2n);\mathbb{Q})$ be even-dimensional, and define

$$\begin{eqnarray}\displaystyle a & = & \displaystyle p_{(\star )}-\unicode[STIX]{x1D708}_{(1\star )}\unicode[STIX]{x1D705}_{p}\in H^{\ast }({\mathcal{M}}_{g}(\{1,2,\star \});\mathbb{Q}),\nonumber\\ \displaystyle b & = & \displaystyle \unicode[STIX]{x1D708}_{(1\star )}-\unicode[STIX]{x1D708}_{(2\star )}\in H^{\ast }({\mathcal{M}}_{g}(\{1,2,\star \});\mathbb{Q}).\nonumber\end{eqnarray}$$

Both of these classes push forward to zero in $H^{\ast }({\mathcal{M}}_{g}(\{1,2\});\mathbb{Q})$ . According to [Gri13, Theorem 2.7], we therefore have

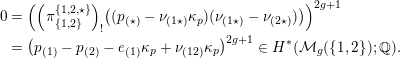$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \Bigl(\vphantom{\mathop{\sum }^{1}}\Bigl(\unicode[STIX]{x1D70B}_{\{1,2\}}^{\{1,2,\star \}}\Bigr)_{!}((p_{(\star )}-\unicode[STIX]{x1D708}_{(1\star )}\unicode[STIX]{x1D705}_{p})(\unicode[STIX]{x1D708}_{(1\star )}-\unicode[STIX]{x1D708}_{(2\star )}))\Bigr)^{2g+1}\nonumber\\ \displaystyle & = & \displaystyle (p_{(1)}-p_{(2)}-e_{(1)}\unicode[STIX]{x1D705}_{p}+\unicode[STIX]{x1D708}_{(12)}\unicode[STIX]{x1D705}_{p})^{2g+1}\in H^{\ast }({\mathcal{M}}_{g}(\{1,2\});\mathbb{Q}).\nonumber\end{eqnarray}$$

For any $q\in H^{\ast }(B\text{SO}(2n);\mathbb{Q})$ , the above relation can be multiplied by $q_{(2)}$ and pushed forward to $H^{\ast }({\mathcal{M}}_{g}(1);\mathbb{Q})$ to obtain a relation that expresses $\unicode[STIX]{x1D705}_{p^{2g+1}q}$ in terms of decomposable elements in the tautological subring $R^{\ast }(W_{g},\star )\subset H^{\ast }({\mathcal{M}}_{g}(1);\mathbb{Q})$ . (Recall that this ring is generated by the $\unicode[STIX]{x1D705}_{c}$ as well as $c$ for $c\in H^{\ast }(B\text{SO}(2n);\mathbb{Q})$ .) As explained in [Gri13, proof of Theorem 1.1], this is sufficient to show that the ring is finitely generated.◻

It follows that the ring $R^{\ast }(W_{g},D^{2n})$ is also finitely generated.