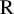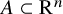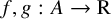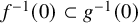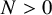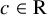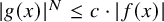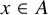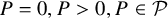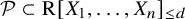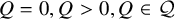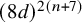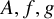Improved effective Łojasiewicz inequality and applications

Abstract

Let $\mathrm {R}$ be a real closed field. Given a closed and bounded semialgebraic set $A \subset \mathrm {R}^n$ and semialgebraic continuous functions $f,g:A \rightarrow \mathrm {R}$ such that $f^{-1}(0) \subset g^{-1}(0)$, there exist an integer $N> 0$ and $c \in \mathrm {R}$ such that the inequality (Łojasiewicz inequality) $|g(x)|^N \le c \cdot |f(x)|$ holds for all $x \in A$. In this paper, we consider the case when A is defined by a quantifier-free formula with atoms of the form $P = 0, P>0, P \in \mathcal {P}$ for some finite subset of polynomials $\mathcal {P} \subset \mathrm {R}[X_1,\ldots ,X_n]_{\leq d}$, and the graphs of $f,g$ are also defined by quantifier-free formulas with atoms of the form $Q = 0, Q>0, Q \in \mathcal {Q}$, for some finite set $\mathcal {Q} \subset \mathrm {R}[X_1,\ldots ,X_n,Y]_{\leq d}$. We prove that the Łojasiewicz exponent in this case is bounded by $(8 d)^{2(n+7)}$. Our bound depends on d and n but is independent of the combinatorial parameters, namely the cardinalities of $\mathcal {P}$ and $\mathcal {Q}$. The previous best-known upper bound in this generality appeared in P. Solernó, Effective Łojasiewicz Inequalities in Semi-Algebraic Geometry, Applicable Algebra in Engineering, Communication and Computing (1991) and depended on the sum of degrees of the polynomials defining $A,f,g$ and thus implicitly on the cardinalities of $\mathcal {P}$ and $\mathcal {Q}$. As a consequence, we improve the current best error bounds for polynomial systems under some conditions. Finally, we prove a version of Łojasiewicz inequality in polynomially bounded o-minimal structures. We prove the existence of a common upper bound on the Łojasiewicz exponent for certain combinatorially defined infinite (but not necessarily definable) families of pairs of functions. This improves a prior result of Chris Miller (C. Miller, Expansions of the real field with power functions, Ann. Pure Appl. Logic (1994)).

1 Introduction

L. Schwartz conjectured that if f is a real analytic function and T a distribution in some open subset $\Omega \subset \mathrm {R}^n$ , then there exists a distribution S satisfying $f S = T$ . As a main tool in proving this conjecture, Łojasiewicz [33] proved that if V is the set of real zeros of f, and x in a sufficiently small neighborhood of a point $x_0$ in V, there exists a constant d such that

$$\begin{align*}|f(x)| \geq d \cdot \mathrm{dist}(x,V)^d, \end{align*}$$

where $\mathrm {dist}(x,V)$ denotes the distance of x from V. In case f is a polynomial, the result was obtained by Hörmander [20].

Several variants of Łojasiewicz inequality have appeared in the literature both in the semialgebraic and analytic categories. In the semialgebraic category, the following slightly more general version of the above inequality appears in [11, Corollary 2.6.7].

Unless otherwise specified, $\mathrm {R}$ is a fixed real closed field for the rest of the paper.

Theorem 1.1. Let $A \subset \mathrm {R}^n$ be a closed and bounded semialgebraic set, and let $f,g: A \to \mathrm {R}$ be continuous semialgebraic functions. Furthermore, suppose that $f^{-1}(0) \subset g^{-1}(0)$ . Then there exist $c \in \mathrm {R}$ and an integer $\rho> 0$ depending on A, f and g such that

(1.1) $$ \begin{align} |g(x)|^{\rho} \le c\cdot |f(x)|, \quad \forall x \in A. \end{align} $$

We denote the infimum of $\rho $ by $\mathcal {L}(f,g \mid A)$ which is called the Łojasiewicz exponent.

The inequality (1.1) is usually called the Łojasiewicz inequality and has found many applications (independent of the division problem of L. Schwartz) – for example, in singularity theory, partial differential equations and optimization. We survey some of these applications later in the paper and improve some of these results using the version of Łojasiewicz inequality proved in the current paper.

Driven by the applications mentioned above there has been a lot of interest in obtaining effective bounds on $\mathcal {L}(f,g \mid A)$ .

2 Main results

In this paper, we prove new quantitative versions of the inequality (1.1) in the semialgebraic (and more generally in the o-minimal context). Before stating our results, we introduce a few necessary definitions.

Definition 2.1 ( $\mathcal {P}$ -formulas and semialgebraic sets).

Let $\mathcal {P} \subset \mathrm {R}[X_1,\ldots ,X_n]$ , $\mathcal {Q} \subset \mathrm {R}[X_1,\ldots ,X_n,Y]$ be finite sets of polynomials. We will call a quantifier-free first-order formula (in the theory of the reals) with atoms $P=0, P>0, P< 0, P \in \mathcal {P}$ to be a $\mathcal {P}$ -formula. Given any first-order formula $\Phi (X_1,\ldots ,X_n)$ in the theory of the reals (possibly with quantifiers), we will denote by ${\mathcal R}(\Phi ,\mathrm {R}^n)$ the set of points of $\mathrm {R}^n$ satisfying $\Phi $ , and call ${\mathcal R}(\Phi ,\mathrm {R}^n)$ the realization of $\Phi $ . We will call the realization of a $\mathcal {P}$ -formula a $\mathcal {P}$ -semialgebraic set. A $\mathcal {Q}$ -semialgebraic function is a function whose graph is a $\mathcal {Q}$ -semialgebraic set.

We denote by $\mathrm {R}[X_1,\ldots ,X_n]_{\leq d}$ the subset of polynomials in $\mathrm {R}[X_1,\ldots ,X_n]$ with degrees $\leq d$ .

2.1 Semialgebraic case

We prove the following theorem in the semialgebraic setting which improves the currently best-known upper bound [46] in a significant way (see Section 4 below).

Theorem 2.2. Let $d \geq 2$ , $\mathcal {P} \subset \mathrm {R}[X_1,\ldots ,X_n]_{\leq d}, \mathcal {Q} \subset \mathrm {R}[X_1,\ldots ,X_n,Y]_{\leq d}$ , $A \subset \mathrm {R}^n$ a closed and bounded $\mathcal {P}$ -semialgebraic set and $f,g: A \rightarrow \mathrm {R}$ continuous $\mathcal {Q}$ -semialgebraic functions, satisfying $f^{-1}(0) \subset g^{-1}(0)$ .

Then there exist $c = c(A,f,g) \in \mathrm {R}$ and $N \leq (8 d)^{2(n+7)}$ such that for all $x \in A$ ,

(2.1) $$ \begin{align} |g(x)|^{N} \leq c \cdot |f(x)|. \end{align} $$

In other words,

(2.2) $$ \begin{align} \mathcal{L}(f,g \mid A) \leq (8 d)^{2(n+7)} = d^{O(n)}. \end{align} $$

In the special case where $\mathrm {R} = \mathbb {R}$ and

$$\begin{align*}\mathcal{P} \subset \mathbb{Z}[X_1,\ldots,X_n]_{\leq d}, \ \mathcal{Q} \subset \mathbb{Z}[X_1,\ldots,X_n,Y]_{\leq d} \end{align*}$$

and the bit-sizes of the coefficients of the polynomials in $\mathcal {P},\mathcal {Q}$ are bounded by $\tau $ , there exists

(2.3) $$ \begin{align} c \leq \min\{2^{\tau d^{O(n^2)}},2^{\tau d^{O(n\log d)}}\} \end{align} $$

such that the inequality (2.1) holds with $N =(8 d)^{2(n+7)}$ .

Remark 2.3 (Sharpness.)

The inequality (2.2) is nearly tight. The following slight modification of examples given in [46, Page 2] or [21, Example 15] shows that right-hand side of inequality (2.2) cannot be made smaller than $d^n$ . The constants ( $8$ in the base and $14$ in the exponent) in our bound can possibly be improved (for example, by using a better estimation in the inequality (5.1) in Proposition 5.5 and using a slightly more accurate degree bound). However, this would lead to a much more unwieldy statement which we prefer to avoid. The coefficient $2$ of n in the exponent, however, seems inherent to our method.

Example 2.4. Let $A:=\{x \in \mathbb {R}^n \mid x_1^2+\cdots +x_n^2 \le 1\}$ be the compact semialgebraic set, and consider the semialgebraic functions $f,g:A \to \mathbb {R}$ defined by

$$ \begin{align*} f&:=|X_2-X_1^{d_1}|+ \cdots + |X_n - X_{n-1}^{d_{n-1}}| + |X_n^{d_n}|,\\ g&:=\sqrt{X_1^2+\cdots+X_n^2}, \end{align*} $$

where $d_1,\ldots ,d_n \in \mathbb {Z}_{> 0}$ . It is easy to see that $f^{-1}(0)=g^{-1}(0) = \{0\}$ . Then for sufficiently small $|t|$ the vector $x(t):=(t,t^{d_1},\ldots ,t^{d_1\cdots d_{n-1}})$ belongs to A, and we have

$$ \begin{align*} f(x(t))=|t|^{d_1\cdots d_n}, \qquad g(x(t))=\sqrt{t^2+\cdots+t^{2d_1\cdots d_{n-1}}}, \end{align*} $$

which implies $|g(x(t))|^{d_1\cdots d_n} \le c \cdot |f(x(t))|$ for some positive constant c. Letting $d_1=\cdots =d_n=d$ , then it follows that $\mathcal {L}(f,g \mid A) \ge d^n$ .

Remark 2.5 (Independence from the combinatorial parameter).

An important feature of the bound in Theorem 2.2 is that the right-hand side of inequality (2.2) depends only on the maximum degree of the polynomials in $\mathcal {P} \cup \mathcal {Q}$ and is independent of the cardinalities of the sets $\mathcal {P},\mathcal {Q}$ . This is not the case for the previous best-known general bound due to Solernó [46] which depended on the sum of the degrees of the polynomials appearing in the descriptions of A, f and g and thus implicitly on the number of polynomials involved in these descriptions. This fact, that our bound is independent of the number of polynomials, plays an important role in the applications that we discuss later in the paper. For example, it is exploited crucially in the proof of Theorem 2.11 (see below). Also, note that the feature of being independent of combinatorial parameters is also present in some prior work that we discuss in detail in Section 3.1. But these results (notably that of Kollár [22] and also [43]) come with certain important restrictions and/or with a worse bound. In contrast, our result is completely general and nearly optimal.

Remark 2.6 (Separation of combinatorial and algebraic parts).

Separating the roles of combinatorial and algebraic parameters has a long history in quantitative real algebraic geometry. We include (see Section 4 below) a discussion and several prior examples of such results. The Łojasiewicz inequality is clearly a foundational result in real algebraic geometry. Hence, asking for a similar distinction in quantitative bounds on the Łojasiewicz exponent is a very natural question. Finally, the underlying idea behind making this distinction allows us to formulate and prove a version of the Łojasiewicz inequality valid over polynomially bounded o-minimal structures (see Theorem 2.20) which is stronger than the one known before.

Remark 2.7. It is not possible to obtain a uniform bound (i.e., a bound only in terms of d, n and possibly the combinatorial parameters) on the constant c in Theorem 2.2.

As mentioned earlier, Theorem 2.2 leads to improvements in several applications where Łojasiewicz inequality plays an important role. We discuss some of these applications in depth in Section 6 but mention an important one right away.

2.2 Application to error bounds

Study of error bounds (defined next) is a very important topic in optimization theory and computational optimization (see, for example, [44] and the references cited therein).

Definition 2.8 (Error bounds and residual function).

Let $M,E \subset \mathrm {R}^n$ . An error bound on E with respect to M is an inequality

(2.4) $$ \begin{align} \mathrm{dist}(x,M)^{\rho} \le \kappa \cdot \psi(x), \qquad \forall x \in E, \end{align} $$

where $ \rho , \kappa> 0$ , $\psi :M \cup E \to \mathrm {R}_{\geq 0}$ is some function (called a residual function) such that $\psi (x)=0$ iff $x \in M$ , and

(2.5) $$ \begin{align} \mathrm{dist}(x,M):=\inf_{y}\{\|x-y\| \mid y \in M\}. \end{align} $$

The study of error bounds was motivated by the implementation of iterative numerical optimization algorithms and the proximity of solutions to the feasible or optimal set. Thus, from the optimization point of view, the set M in (2.4) can be the feasible set (polyhedron, a slice of the positive semidefinite cone, a basic semialgebraic set, etc.) or the optimal set of an optimization problem (see (6.4)), E is a set of interest (e.g., iterates of an iterative algorithm or central solutions [6]), and a residual function $\psi $ measures the amount of violation of the equations and inequalities defining M at a given solution of E. See [44] for other applications of error bounds in optimization.

Theorem 2.9. If M is nonempty and semialgebraic, $\psi $ is semialgebraic and E is a closed and bounded semialgebraic set, then the error bound (2.4) exists with an integer $\rho \ge 1$ and for some $\kappa> 0$ .

Proof. Notice that (2.4) with a nonempty semialgebraic set M (see [11, Proposition 2.2.8] or the proof of Lemma 5.9), a semialgebraic function $\psi $ , and a closed and bounded semialgebraic set E is a special case of (1.1). Thus, the existence of an integer $\rho \ge 1$ follows from Theorem 1.1.

Remark 2.10. Notice that if $M \supset y \to \infty $ , then $\|x-y\| \to \infty $ as well. Thus, if M is closed and semialgebraic, then $\inf _{y}$ in (2.5) can be replaced by $\min _{y}$ [11, Theorem 2.5.8].

Now, we prove the following quantitative version of Theorem 2.9.

Theorem 2.11. Let M be a basic closed semialgebraic set defined by

(2.6) $$ \begin{align} M:=\{x \in \mathrm{R}^n \mid g_i(x) \le 0, \ h_j(x) = 0, \ i=1,\ldots,r, \ j=1,\ldots,s\}, \end{align} $$

where $g_i,h_j \in \mathrm {R}[X_1,\ldots , X_n]_{\le d}$ , and let E be a closed and bounded $\mathcal {P}$ -semialgebraic subset of $\mathrm {R}^n$ with $\mathcal {P} \subset \mathrm {R}[X_1,\ldots ,X_n]_{\leq d}$ . Let $\psi : M \cup E \rightarrow \mathrm {R}_{\ge 0}$ be the semialgebraic function defined by

(2.7) $$ \begin{align} \psi(x)=\sum_{j=1}^s |h_j(x)| + \sum_{i=1}^r \max\{g_i(x),0\}. \end{align} $$

If M is nonempty, then there exist a positive constant $\kappa $ and an integer $\rho \ge 1$ such that (2.4) holds, with $\rho =d^{O(n^2)}$ .

Moreover, if $ \dim M = 0$ (i.e., M is a finite subset of $\mathrm {R}^n$ ), then (2.4) holds with $\rho \le (8d)^{2(n+7)} = d^{O(n)} $ .

Remark 2.12. Example 2.4 indicates that the upper bound on $\rho $ cannot be better than $d^n$ .

Remark 2.13. The error bounds of Theorem 2.11 have been stated, for the purpose of applications to optimization, only in reference to the basic semialgebraic set (2.6) and the residual function (2.7). However, the results of Theorem 2.11 are still valid if we replace (2.6) by any nonempty $\mathcal {Q}$ -semialgebraic set M and (2.7) by any $\mathcal {Q}'$ -semialgebraic residual function, where

$$ \begin{align*} \mathcal{Q} \subset \mathrm{R}[X_1,\ldots,X_n]_{\leq d} \ \ \text{and} \ \ \mathcal{Q}' \subset \mathrm{R}[X_1,\ldots,X_n,Y]_{ \leq d^{O(n)}}; \end{align*} $$

see Corollary 2.14.

Theorem 2.11 significantly improves the bound $D^{n^{c_1}}$ in [46, Theorem 7] derived for a slight variation of (2.4), in which the residual function is replaced by a function measuring the violations only with respect to the inequalities $g_i(x) \le 0$ in the description (2.6) of M. In this upper bound, D is the sum of degrees of polynomials and $c_1$ is universal positive integer. Furthermore, the upper bound on $\rho $ in Theorem 2.11 is independent of r and s (the number of polynomial equations and inequalities in (2.6)), which is particularly important for optimization purposes. Thus, if $r,s = \omega (n^2)$ , the first part of Theorem 2.11 improves the best current error bound result [30, Corollary 3.8] with explicit exponent

(2.8) $$ \begin{align} \rho = \min\big\{(d+1)(3d)^{n+r+s-1},d(6d-3)^{n+r-1}\big\}. \end{align} $$

Furthermore, when M is a finite subset of $\mathrm {R}^n$ and $r =\omega (n)$ , the second part of Theorem 2.11 improves the result in [30, Theorem 4.1] with explicit exponent

(2.9) $$ \begin{align} \rho = \frac{(2d-1)^{n+r}+1}{2}. \end{align} $$

The improvements mentioned above are particularly relevant to nonlinear semidefinite systems, nonlinear semidefinite optimization and semidefinite complementarity problems; see, for example, [29, 18], where r might depend exponentially on n. In that case, the application of (2.8) and (2.9) would result in a doubly exponential bound. The problem of estimation of the exponent $\rho $ in the error bounds of positive semidefinite systems failing the Slater condition [16, Page 23] is posed in [29, Page 106] where it is stated ‘Presently, we have no idea of what this exponent ought to be except in trivial cases’. Corollary 2.14 quantifies the error bound exponent in [29, Proposition 6] and gives an answer to this question in the special case of polynomial mappings.

Corollary 2.14. Let $\mathbb {S}_+^p$ be the cone of symmetric $p \times p$ positive semidefinite matrices (with entries in $\mathrm {R}$ ), let M be defined as

$$ \begin{align*} M:=\{X \in \mathbb{S}^p \mid \ g_i(X) \le 0, \ i=1,\ldots,r\}, \end{align*} $$

where $g_i:\mathbb {S}^p \to \mathrm {R}$ is a polynomial function of degree d, and let E be a closed and bounded $\mathcal {P}$ -semialgebraic subset of $\mathrm {R}^{p^2}$ with $\mathcal {P} \subset \mathrm {R}[X_1,\ldots ,X_{p^2}]_{\leq d}$ . If $M \cap \mathbb {S}_+^p \neq \emptyset $ , then there exist $\kappa \in \mathrm {R} $ and $\rho =\max \{d,p\}^{O(p^4)}$ such that

$$ \begin{align*} \mathrm{dist}(x,M \cap \mathbb{S}_+^p)^{\rho} \le \kappa \cdot \max\Big\{\mathrm{dist}(x,M), \max\{-\lambda_{\min}(x),0\}\Big\}, \quad \mbox{ for all } x \in E. \end{align*} $$

2.3 O-minimal case

Many finiteness results of semialgebraic geometry generalize to arbitrary o-minimal expansions of $\mathbb {R}$ (we refer the reader to [48] and [14] for the definition of o-minimal structures and the corresponding finiteness results).

However, Miller proved the following theorem for polynomially bounded o-minimal expansion of $\mathbb {R}$ . An o-minimal expansion of $\mathbb {R}$ is polynomially bounded if for every definable function $f:\mathbb {R} \rightarrow \mathbb {R}$ , there exist $N \in \mathbb {N}, c \in \mathbb {R}$ such that $|f(x)| < x^N$ for all $x> c$ . Examples of polynomially bounded o-minimal expansions of $\mathbb {R}$ include the structure of semialgebraic sets, and also that of globally sub-analytic sets.

Theorem 2.15 [40, Theorem 5.4, Page 94].

Let $A \subset \mathbb {R}^n$ be a compact set definable in a polynomially bounded o-minimal expansion of $\mathbb {R}$ , and let $f,g:A \rightarrow \mathbb {R}$ be definable continuous functions such that $f^{-1}(0) \subset g^{-1}(0)$ . Then there exist $N \in \mathbb {N}$ and $c> 0, c \in \mathbb {R}$ such that $|g(a)|^N \leq c\cdot f(a)$ for all $a \in A$ .

Remark 2.16. Theorem 2.15 clearly does not extend to arbitrary o-minimal expansions of $\mathbb {R}$ (for example, o-minimal expansions in which the exponential function is definable). However, there exists a more nuanced version that is true for arbitrary o-minimal expansions of $\mathbb {R}$ [32, Theorem 1].

It does not seem possible to give a meaningful quantitative version of Theorem 2.15 in such a general context. However, we formulate below a more uniform version of Theorem 2.15 (see Theorem 2.20).

2.3.1 Extension of the notion of combinatorial complexity to arbitrary o-minimal structures

Although the notion of algebraic complexity in the context of general o-minimal structure does not make sense in general, one can still talk of combinatorial complexity [4]. The following result is illustrative (see also Proposition 5.12 for another example) and can be obtained by combining [4, Theorem 2.3] and the approximation theorem proved in [17].

Fix an o-minimal expansion of $\mathbb {R}$ , and suppose that $\mathcal {A}$ is a definable family of closed subsets of $\mathbb {R}^n$ . Then there exists a constant $C = C(\mathcal {A})> 0$ having the following property. Suppose that $\mathcal {S} \subset \mathcal {A}$ is a finite subset and S a subset of $\mathbb {R}^n$ belonging to the Boolean algebra of subsets of $\mathbb {R}^n$ generated by $\mathcal {S}$ such that

(2.10) $$ \begin{align} \sum_i b_i(S) \leq C \cdot s^n, \end{align} $$

where $s = \mathrm {card}(\mathcal {S})$ and $b_i(\cdot )$ denotes the i-th Betti number [3]. Notice that this bound does depend on the combinatorial parameter s. Note also that it follows from Hardt’s triviality theorem for o-minimal structures [14] that the Betti numbers of the sets appearing in any definable family are bounded by a constant (depending on the family). However, the family of sets S to which the inequality (2.10) applies is not necessarily a definable family.

In view of the inequality (2.10), it is an interesting question whether one can prove a quantitative version of Miller’s result with a uniform bound on the Łojasiewicz exponent in the same setting as above – so that the bound applies to a family (not necessarily definable) of definable sets S and functions $f,g$ simultaneously – as in inequality (2.10).

2.3.2 Łojasiewicz inequality in polynomially bounded o-minimal structures

For the rest of this section, we fix a polynomially bounded o-minimal expansion of $\mathbb {R}$ . Before stating our theorem, we need to use a notation and a definition.

Notation 2.17. A definable family of subsets of $\mathbb {R}^n$ parametrized by a definable set A is a definable subset $\mathcal {A} \subset A \times \mathbb {R}^n$ . For $a \in A$ , we will denote by $\mathcal {A}_a = \pi _2(\pi _1^{-1}(a) \cap \mathcal {A})$ , where $\pi _1: A \times \mathbb {R}^n \rightarrow A$ , $\pi _2:A \times \mathbb {R}^n \rightarrow \mathbb {R}^n$ are the two projection maps. We will often abuse notation and refer to the definable family by $\mathcal {A}$ .

Definition 2.18. Given a definable family $\mathcal {A}$ of subsets of $\mathbb {R}^n$ parametrized by a definable set A and a finite subset $A' \subset A$ , we call a subset $S \subset \mathbb {R}^n$ to be a $(\mathcal {A},A')$ -set if it belongs to the Boolean algebra of subsets of $\mathbb {R}^n$ generated by the tuple $(\mathcal {A}_a)_{a \in A'}$ . We will call a subset $S \subset \mathbb {R}^n$ , a $\mathcal {A}$ -set if S is a $(\mathcal {A},A')$ -set for some finite set $A' \subset A$ . If the graph of a definable function f is a $\mathcal {A}$ -set, we will call f a $\mathcal {A}$ -function. (Note that the family of $\mathcal {A}$ -sets is in general not a definable family of subsets of $\mathbb {R}^n$ .)

Example 2.19. If we take the o-minimal structure $\mathbb {R}_{\mathrm {sa}}$ of semialgebraic sets, then for each fixed d, the family of semialgebraic sets which are $\mathcal {P}$ -semialgebraic sets where $\mathcal {P}$ varies over all finite subsets of $\mathbb {R}[X_1,\ldots ,X_n]_{\leq d}$ is an example of a family of $\mathcal {A}$ -sets for an appropriately chosen $\mathcal {A}$ . Note that this family is not a semialgebraic family.

Example 2.19 suggests a way to obtain a quantitative Łojasiewicz inequality valid over any polynomially bounded o-minimal structure.

Theorem 2.20 (Łojasiewicz inequality for $\mathcal {A}$ -sets and $\mathcal {B}$ -functions for any pair of definable families $\mathcal {A}$ and $\mathcal {B}$ ).

Let $\mathcal {A}$ be a definable family of subsets of $\mathbb {R}^n$ parametrized by the definable set A, and let $\mathcal {B}$ be a definable family of subsets of $\mathbb {R}^{n+1}$ parametrized by the definable set B.

Then there exists $N = N(\mathcal {A},\mathcal {B})> 0$ having the following property. For any triple of finite sets $(A',B',B")$ with $A' \subset A, B',B" \subset B$ , there exists $c = c(A',B',B") \in \mathbb {R}$ such that for each closed and bounded $(\mathcal {A},A')$ -set S, a $(\mathcal {B},B')$ -set F and a $(\mathcal {B},B")$ -set G such that $F,G$ are graphs of definable functions $f,g:\mathbb {R}^n \rightarrow \mathbb {R}$ continuous on S with $f|_S^{-1}(0) \subset g|_S^{-1}(0)$ , and for all $x \in S$ ,

$$\begin{align*}|g(x)|^N \leq c \cdot |f(x)|. \end{align*}$$

Remark 2.21 (Theorem 2.20 generalizes Theorem 2.15).

Notice that as in Theorem 2.2, the combinatorial parameter (namely, $\mathrm {card}(A' \cup B' \cup B")$ ) plays no role. It is also more general than the Łojasiewicz inequality in Theorem 2.15 as the inequality holds with the same value of N for a large, potentially infinite family (not necessarily definable) of triples $(S,f,g)$ and not just for one triple as in Theorem 2.15.

2.4 Outline of the proofs of the main theorems

We now outline the key ideas behind the proofs of the theorems stated in the previous section.

Our proof of Theorem 2.2 follows closely the proof of the similar qualitative statement in [11] with certain important modifications. One main tool that we use to obtain our quantitative bound is a careful analysis of the degrees of certain polynomials appearing in the output of an algorithm (Algorithm 14.6 (block elimination)) described in the book [3]. ¹ This algorithm is an intermediate algorithm for the effective quantifier elimination algorithm described in [3] and takes as input a finite set of polynomials $\mathcal {P} \subset \mathrm {R}[Y,X]$ and produces as output a finite set $\mathrm {BElim}_X(\mathcal {P}) \subset \mathrm {R}[Y]$ having the property that for each connected component C of the realization of each realizable sign condition (see Notation 5.2) the set of sign conditions realized by $\mathcal {P}(y,X)$ is constant as y varies over C. The precise mathematical statement describing the above property of the output of the block elimination algorithm (including a bound on the degrees of the polynomials output) is summarized in Proposition 5.5. The proof of the bound on degrees borrows heavily from the complexity analysis of the algorithm that already appears in [3] but with an added part corresponding to the last step of the algorithm. This last step uses another algorithm (namely, Algorithm 11.54 (restricted elimination) in [3]), and we use the complexity analysis of this algorithm as well.

We also need a quantitative statement on the growth of a semialgebraic function of one variable at infinity whose graph is defined by polynomials of a given degree. It is important for us that the growth is bounded only by the upper bound on the degree and not on the size of the formula describing the graph. This is proved in Lemma 5.3.

Note that the technique of utilizing complexity estimates of algorithms to prove quantitative bounds in real algebraic geometry is not altogether new. For example, similar ideas have been used to prove a quantitative curve selection lemma [9] and bounds on the radius of a ball guaranteed to intersect every connected component of a given semialgebraic set [8], amongst other such results.

Theorem 2.11 is an application of Theorem 2.2 with one key extra ingredient. We prove (see Lemma 5.9) that if M is a $\mathcal {P}$ -semialgebraic set with $\mathcal {P} \subset \mathrm {R}[X_1,\ldots ,X_n]_{\leq d}$ , then the graph of the distance function, $\mathrm {dist}(\cdot ,M)$ , can be described by a quantifier-free formula involving polynomials having degrees at most $d^{O(n)}$ . A more naive approach (for example that in [46]) involving quantifier elimination would involve elimination of two blocks of quantified variables with a quantifier alternation and would lead to a degree bound of $d^{O(n^2)}$ . The formula describing the graph of $\mathrm {dist}(\cdot ,M)$ that we obtain is very large from the point of view of combinatorial complexity (compared to the more naive approach) but with a better degree bound. We leverage now the fact that our bound on the Łojasiewicz exponent is independent of the combinatorial parameter and apply Theorem 2.2 to obtain the stated result.

The proof of Theorem 2.20 is similar to that of proof Theorem 2.2 with the following important difference. Proposition 5.5 which plays a key role in the proof of Theorem 2.2 is replaced by a quantitative version of the existence theorem for cylindrical definable decomposition adapted to finite subfamilies of a family $\mathcal {F}$ of definable subsets of $\mathrm {R}^n$ in any o-minimal structure. The important quantitative property that we need is not the size of the decomposition but the fact that each cell of the decomposition is determined in a certain fixed definable way from a certain finite number, $N(n)$ , of the sets of the given finite subfamily of $\mathcal {F}$ (the key point being that the number $N(n)$ is independent of the cardinality of the finite subfamily). The existence of such decompositions in o-minimal structures was first observed in [4, Theorem 2.5] (see Proposition 5.13 below), and it is closely related (in fact equivalent) to the fact that o-minimal structures are distal in the sense of model theory (see [47]).

The rest of the paper is organized as follows. In Section 3, we survey prior work on proving bounds on the Łojasiewicz exponent at various levels of generality and also survey prior work on proving error bounds. In Section 4, in order to put the current paper in context, we include a discussion of the role that the separation of combinatorial and algebraic complexity has played in quantitative real algebraic geometry. In Section 5, we prove the main theorems after introducing the necessary definitions and preliminary results. In Section 6, we discuss some further applications of our main theorem. Finally, in Section 7 we end with some open problems.

3 Prior and related work

3.1 Prior results on Łojasiewicz inequality

Solernó [46, Theorem 3 (ii)] proved that (1.1) holds with $\rho = D^{c_1 n}$ , in which $c_1$ is a universal constant and D is an upper bound on the sum of the degrees of polynomials in $\mathcal {P}$ and $\mathcal {Q}$ . Since D is an upper bound on the sum of the degrees of polynomials in $\mathcal {P}$ and $\mathcal {Q}$ , the bound in [46, Theorem 3] depends implicitly on the cardinalities of $\mathcal {P}$ and $\mathcal {Q}$ (unlike Theorem 2.2). In the case of polynomials with integer coefficients, Solernó [46, Theorem 3 (ii)] also proves an upper bound of $2^{\tau {D^{c_2 \cdot n^2}}}$ on the constant c (following the same notation as in (1.1)) where D is an upper bound on the sum of the degrees of polynomials in $\mathcal {P}$ and $\mathcal {Q}$ and $c_2$ is a universal constant. This bound should be compared with inequality (2.3) in Theorem 2.2.

In a series of papers [23, 25, 26], Kurdyka, Spodzieja and Szlachcińska proved several quantitative results on Łojasiewicz inequality. We summarize them as follows. Let $S \subset \mathbb {R}^n$ be a closed semialgebraic set, and let

$$ \begin{align*} S = S_1 \cup \cdots \cup S_k \end{align*} $$

be a decomposition [11] of S into k closed basic $\mathcal {P}_i$ -semialgebraic subsets $S_i$ with $\mathcal {P}_i \subset \mathbb {R}[X_1,\ldots ,X_n]_{\le d_i}$ , each involving $r_i$ polynomial inequalities. Let $r(S)$ be the minimum of $\max \{r_1,\ldots ,r_k\}$ over all possible decompositions of S, and let $\deg (S)$ denote the minimum of $\max \{d_1,\ldots ,d_k\}$ over all decompositions for which $r_i \le r(S)$ . Further, let $F: S \to \mathbb {R}^s$ be a continuous semialgebraic mapping, and suppose that $\mathbf {0} \in S$ and $F(\mathbf {0})= \mathbf {0}$ . Then there exists [25, Corollary 2.2] (see also [26]) an upper bound

(3.1) $$ \begin{align} \bar{d}(6\bar{d}-3)^{n+s+\bar{r}-1} \end{align} $$

on the Łojasiewicz exponent of

(3.2) $$ \begin{align} \|F(x)\| \ge c \cdot \mathrm{dist}\big(x,F^{-1}(\mathbf{0}) \cap S\big)^{\rho}, \quad \forall x \in S, \ \|x\| < \varepsilon, \end{align} $$

where

$$ \begin{align*} \bar{d}&=\max\big\{\deg(S),\deg(\mathrm{graph}(F))\big\},\\ \bar{r} &= r(S) + r(\mathrm{graph}(F)). \end{align*} $$

If $x=\mathbf {0}$ is an isolated zero of F, then the upper bound is $((2\bar {d}-1)^{n+s+\bar {r}}+1)/2$ .

Note that the above bounds do depend on the number of polynomials. Also, notice that $\bar {d}$ and $\bar {r}$ in the upper bound (3.1) are both different from d and the number of inequalities in the semialgebraic description of f, g and A in Theorem 2.2. In fact, $\bar {r}$ and $\bar {d}$ are the number of inequalities and the maximum degree of polynomials in the minimal semialgebraic description of $\mathrm {graph}(F)$ and S. It was proved in [13] that $\bar {r}$ is bounded by $n(n+1)/2$ , but it is not clear how d blows up for a minimal decomposition. Because of this, we cannot directly compare the bound in (3.1) to that of Theorem 2.2 proved in the current paper.

Let $f:S \to \mathbb {R}$ be a Nash function [11, Definition 2.9.3], where S is a compact semialgebraic subset of $\mathbb {R}^n$ . Osińska-Ulrych et al. [42] showed that

$$ \begin{align*} |f(x)| \ge c \cdot \mathrm{dist}\big(x,f^{-1}(0)\big)^{2(2\bar{d}-1)^{3n+1}}, \quad \forall x \in S, \end{align*} $$

in which $\bar {d}=\deg _S(f):=\max \{\deg _a(f) \mid a \in S\}$ , and $\deg _a(f)$ is the degree of the unique irreducible $P \in \mathbb {R}[X_1,\ldots ,X_n,Y]$ such that $P(x,f(x))=0$ for all x in a connected neighborhood of a.

Kollár [22] considered the problem of improving Solernó’s results [46]. He obtained significant improvements but under certain restrictions. More precisely, given a semialgebraic set M as in (2.6), with $\max _i\{f_i(x)\}> 0$ for all $x \in M$ for $0 < \|x\| \ll 1$ , and $\max _i\{f_i(\mathbf {0})\} = 0$ , he proved that ([22, Theorem 4]) there exist constants $c,\varepsilon> 0$ such that

(3.3) $$ \begin{align} \max_i\{f_i(x)\} \ge c \cdot \|x\|^{B(n-1)d^n} \ \ \text{for all} \ x \in M \ \text{with} \ \|x\| < \varepsilon, \end{align} $$

where $B(n):=\binom {n}{\lfloor (n/2) \rfloor }$ . Notice that the exponent $B(n-1)d^n \leq (2 d)^n$ in (3.3) is a little better than the bound in Theorem 2.2. It is also the case that similar to our result, Kollár’s bound is independent of the combinatorial parameters (i.e., number of polynomials occurring in the definition of M and the number of $f_i$ ’s). However, unlike Theorem 2.2, the pair of functions $\max _i\{f_i(x)\}, ||\cdot ||$ in Kollár’s theorem is quite restrictive, and so inequality (3.3) is difficult to apply directly – for instance, in applications to error bounds considered in this paper (Theorem 2.11). Moreover, the restriction that $\mathbf {0}$ has to be an isolated zero of $\max _i\{f_i(x)\}$ may not be satisfied in many applications, restricting the utility of (3.3).

More recently, Osińska-Ulrych et al. [43] proved that $\mathcal {L}(f,g \mid \mathbb {B}^n) \le \bar {d}^{4n+1}$ in which $\bar {d}$ is the degree of polynomials describing f and g, $\mathbb {B}^n$ is the unit ball in $\mathbb {R}^n$ , and $\bar {d}$ is a bound on the degrees of polynomials defining the graphs of $f,g$ as well as on certain polynomials giving a suitable semialgebraic decomposition of $\mathbb {B}^n$ adapted to $f,g$ . Note that $\bar {d}$ could be larger than the degrees of the polynomials defining $f,g$ . This bound is also independent of the combinatorial parameters but asymptotically weaker than the one in Theorem 2.2, and the setting is more restrictive (since the bound is not directly in terms of the degrees of the polynomials appearing in the definition of $f,g$ ).

3.2 Other forms of Łojasiewicz inequality

Several other forms of Łojasiewicz inequality have appeared in the literature. Let $f:U \to \mathbb {R}$ be a real analytic function, where $U \subset \mathbb {R}^n$ is neighborhood of $\mathbf {0} \in \mathbb {R}^n$ . If $f(\mathbf {0}) = 0$ and $\nabla f(\mathbf {0}) = \mathbf {0}$ , then there exist a neighborhood $U'$ of $0$ and $\varrho < 1$ , $c>0$ such that

(3.4) $$ \begin{align} |\nabla f(x)| \ge c \cdot|f(x)|^{\varrho}, \quad \forall x \in U', \end{align} $$

which is known as Łojasiewicz gradient inequality. The infimum of $\varrho $ satisfying (3.4) is called the Łojasiewicz exponent of f, and it is denoted by $\varrho (f)$ . If $f\in \mathbb {R}[X_1,\ldots ,X_n]_{\le d}$ and has an isolated singularity at zero, then there exists an upper bound [19]

$$ \begin{align*} \varrho(f) \le 1-\frac{1}{(d-1)^n+1}. \end{align*} $$

Under a weaker condition of having nonisolated singularity at the origin, D’Acunto and Kurdyka showed [15] that

(3.5) $$ \begin{align} \varrho(f) \le 1-\frac{1}{\max\{d(3d-4)^{n-1},2d(3d-3)^{n-2}\}}. \end{align} $$

A more general result is given by [42] for a Nash function $f:U \to \mathbb {R}$ , where U is a connected neighborhood of $\mathbf {0} \in \mathbb {R}^n$ . If $f(\mathbf {0}) = 0$ and $\nabla f(\mathbf {0}) = \mathbf {0}$ , then (3.4) holds with

$$ \begin{align*} \varrho(f) \le 1-\frac{1}{2(2\bar{d}-1)^{3n+1}}, \end{align*} $$

where $\bar {d}$ is the degree of the unique irreducible $P \in \mathbb {R}[X_1,\ldots ,X_n,Y]$ such that $P(x,f(x))=0$ for all $x \in U$ . If, in addition to the latter condition, $\frac {\partial P}{\partial y} (x, f (x)) \neq 0$ for all $x \in U$ , then there exists a stronger upper bound

$$ \begin{align*} \varrho(f) \le 1-\frac{1}{\max\{2\bar{d}(2\bar{d}-1),\bar{d}(3\bar{d}-2)^n\} +1}. \end{align*} $$

3.3 Prior work on error bounds

Error bounds were generalized to analytic systems and basic semialgebraic sets in [39, Theorem 2.2] and [37, Theorem 2.2] based on the analytic form of Łojasiewicz inequality and Hörmander’s results [20] but without explicit information about the exponent. Recently, an explicit error bound with respect to M, defined in (2.6), was given in [30], where the exponent depends exponentially on the dimension and the number of polynomial equations and inequalities; see (2.8). The exponent (2.8) follows from (3.5) and the generalized differentiation in variational analysis.

In case that M is defined by a single convex polynomial inequality, that is, $r=1$ , $s=0$ , then (2.4) holds with $\rho = (d-1)^n +1$ [31, Theorem 4.2]. Additionally, if there exists an $x \in M$ such that $g(x) < 0$ , then $\rho = 1$ with $E=\mathbb {R}^n$ [31, Theorem 4.1]. More generally, there exists [12, Corollary 3.4]

(3.6) $$ \begin{align} \rho = \min\Bigg\{\frac{(2d-1)^n+1}{2}, \binom{n-1}{\lfloor(n-1)/2\rfloor} d^n\Bigg\} \end{align} $$

such that the error bound (2.4) holds, where

$$ \begin{align*} \psi(x)= \max_{i \in \{1,\ldots,r\}} (\max\{g_i(x),0\}). \end{align*} $$

A complete survey of error bounds in optimization and their applications to algorithms and sensitivity analysis can be found in [29, 44].

4 Combinatorial and algebraic complexity

A key feature of the bound in Theorem 2.2 is that it is independent of the cardinality of $\mathcal {P}$ and $\mathcal {Q}$ and depends only on the bound on the maximum degree of the polynomials in $\mathcal {P} \cup \mathcal {Q}$ and n. In fact, in many quantitative results (upper bounds on various quantities) in real algebraic geometry involving a $\mathcal {P}$ -semialgebraic set, a fruitful distinction can be made between the dependence of the bound on the cardinality of the set $\mathcal {P}$ and on the maximum degrees (or some other measure of the complexity) of the polynomials in $\mathcal {P}$ . The former is referred to as the combinatorial part and the latter as the algebraic part of the bound (see [5]). This distinction is important in many applications (such as in discrete and computational geometry), where the algebraic part of the bounds are treated as bounded by a fixed constant and only the combinatorial part is considered interesting.

The following examples illustrate the different nature of the dependencies on the combinatorial and the algebraic parameters in quantitative bounds appearing in real algebraic geometry and put in context the key property of Theorem 2.2 stated in the beginning of this subsection.

1. 1. (Bound on Betti numbers.) Suppose that $S \subset \mathrm {R}^n$ is a $\mathcal {P}$ - semialgebraic set and $V = \mathrm {Z}(Q,\mathrm {R}^n)$ a real algebraic set. Suppose that $\dim _{\mathrm {R}} V = p$ , and the degrees of Q and the polynomials in $\mathcal {P}$ are bounded by d. Then,

   (4.1) $$ \begin{align} \sum_i b_i(S \cap V) \leq s^p (O(d))^n, \end{align} $$
   where $s = \mathrm {card}(\mathcal {P})$ and $b_i(\cdot )$ denotes the i-th Betti number [3]. Notice the different dependence of the bound on s and d.

2. 2. (Quantitative curve selection lemma.) The curve selection lemma [35, 36] (see also [41]) is a fundamental result in semialgebraic geometry. The following quantitative version of this lemma was proved in [9].

   Theorem (Quantitative curve selection lemma).

   Let $\mathcal {P} \subset \mathrm {R}[X_1,\ldots ,X_n]_{\leq d}$ be a finite set, S a $\mathcal {P}$ -semialgebraic set and $x \in \overline {S}$ . Then there exist $t_0\in \mathrm {R}, t_0> 0$ , and a semialgebraic path $\varphi : [0,t_0) \rightarrow \mathrm {R}^n$ with

   $$\begin{align*}\varphi(0) = x, \ \varphi ((0,t_0)) \subset S \end{align*}$$

   such that the degree of the Zariski closure of the image of $\varphi $ is bounded by

   $$\begin{align*}(O(d))^{4n+3}. \end{align*}$$

   Notice that the bound on the degree of the image of the curve $\varphi $ in the above theorem has no combinatorial part, that is, there is no dependence on the cardinality of $\mathcal {P}$ (unlike the bound in (4.1)).

3. 3. (Effective quantifier elimination) Quantifier elimination is a key property of the theory of the reals and has been studied widely from the complexity viewpoint. The following quantitative version appears in [7].

   Theorem 4.1 (Quantifier elimination).

   Let $\mathcal {P} \subset \mathrm {R}[X_{[1]},\ldots , X_{[\omega ]}, Y]_{\leq d}$ be a finite set of s polynomials, where $X_{[i]}$ is a block of $k_i$ variables, and Y a block of $\ell $ variables. Let

   $$\begin{align*}\Phi (Y) = (Q_1 X_{[1]})\cdots (Q_\omega X_{[\omega]}) \Psi(X_{[1]},\ldots, X_{[\omega]}, Y) \end{align*}$$

   be a quantified-formula, with $Q_i \in \{\exists ,\forall \}$ and $\Psi $ a $\mathcal {P}$ -formula. Then there exists a quantifier-free formula

   $$\begin{align*}\Psi (Y) = \bigvee_{i=1}^{I} \bigwedge_{j=1}^{J_{i}} \Big( \bigvee_{n=1}^{N_{ij}} \mathbf{sign} (P_{ijn} (Y))= \sigma_{ijn} \Big) , \end{align*}$$

   where $P_{ijn} (Y)$ are polynomials in the variables Y, $\sigma _{ijn} \in \{0,1, - 1\}$ ,

   $$ \begin{align*} I \leq &\ s^{(k_{\omega} +1) \cdots (k_{1} +1) ( \ell +1)} d^{O (k_{\omega} ) \cdots O (k_{1} ) O ( \ell )} ,\\ J_{i} \leq &\ s^{(k_{\omega} +1) \cdots (k_{1} +1)} d^{O (k_{\omega} ) \cdots O (k_{1} )} ,\\ N_{ij} \leq &\ d^{O (k_{\omega} ) \cdots O (k_{1} )} , \end{align*} $$

   equivalent to $\Phi $ , and the degrees of the polynomials $P_{ijk}$ are bounded by $d^{O (k_{\omega } ) \cdots O (k_{1} )}$ .

   Moreover, if the polynomials in $\mathcal {P}$ have coefficients in $\mathbb {Z}$ with bit-sizes bounded by $\tau $ , the polynomials $P_{ijk}$ also have integer coefficients with bit-sizes bounded by $\tau d^{O (k_{\omega } ) \cdots O (k_{1} )O(\ell )}$ .

   Notice that the bound on the degrees of the polynomials appearing in the quantifier-free formula is independent of the combinatorial parameter $s =\mathrm {card}(\mathcal {P})$ . This fact will play a key role in the proof of the main theorem (Theorem 2.2) below.

5 Proofs of the main results

5.1 Proof of Theorem 2.2

Before proving Theorem 2.2, we need some preliminary results.

5.1.1 Cylindrical definable decomposition

The notion of cylindrical definable decomposition (introduced by Łojasiewicz [34, 35]) plays a very important role in semialgebraic and more generally o-minimal geometry [14]. We include its definition below for the sake of completeness and also for fixing notation that will be needed later.

Definition 5.1 (Cylindrical definable decomposition).

Fixing the standard basis of $\mathrm {R}^n$ , we identify for each $i,1 \leq i \leq n$ , $\mathrm {R}^i$ with the span of the first i basis vectors. Fixing an o-minimal expansion of $\mathrm {R}$ , a cylindrical definable decomposition of $\mathrm {R}$ is an $1$ -tuple $(\mathcal {D}_1)$ , where $\mathcal {D}_1$ is a finite set of subsets of $\mathrm {R}$ , each element being a point or an open interval, which together gives a partition of $\mathrm {R}$ . A cylindrical definable decomposition of $\mathrm {R}^n$ is an n-tuple $(\mathcal {D}_1,\ldots ,\mathcal {D}_n)$ , where each $\mathcal {D}_i$ is a decomposition of $\mathrm {R}^i$ , $(\mathcal {D}_1,\ldots , \mathcal {D}_{n-1})$ is a cylindrical decomposition of $\mathrm {R}^{n-1}$ and $\mathcal {D}_n$ is a finite set of definable subsets of $\mathrm {R}^n$ (called the cells of $\mathcal {D}_n$ ) giving a partition of $\mathrm {R}^n$ consisting of the following: For each $C \in \mathcal {D}_{n-1}$ , there is a finite set of definable continuous functions $f_{C,1}, \ldots , f_{C,N_C}: C \rightarrow \mathrm {R}$ such that $f_{C_1} < \cdots < f_{C,N_C}$ , and each element of $\mathcal {D}_n$ is either the graph of a function $f_{C,i}$ or of the form

1. (a) $\{ (x,t) \;\mid \; x\in C, \ t < f_{C,1}(x) \}$ ,

2. (b) $\{ (x,t) \;\mid \; x\in C, \ f_{C,i}(x) < t < f_{C,i+1}(x) \}$ ,

3. (c) $\{ (x,t) \;\mid \; x\in C, \ f_{C,N_C}(x) < t \}$ ,

4. (d) $\{ (x,t) \;\mid \; x\in C \}$

(the last case arising is if the set of functions $\{f_{C,i} | 1 \leq i \leq N_C \}$ is empty).

We will say that the cylindrical definable decomposition $(\mathcal {D}_1,\ldots ,\mathcal {D}_n)$ is adapted to a definable subset S of $\mathrm {R}^n$ , if for each $C \in \mathcal {D}_n$ , $C \cap S$ is either equal to C or empty.

In the semialgebraic case, we will refer to a cylindrical definable decomposition by cylindrical algebraic decomposition.

In the semialgebraic case, we will use the following extra notion.

5.1.2 Sign conditions

Notation 5.2 (Sign conditions and their realizations).

Let $\mathcal {P}$ be a finite subset of $\mathrm {R}[X_1,\ldots ,X_n]$ . For $\sigma \in \{0,1,-1\}^{\mathcal {P}}$ , we call the formula $\bigwedge _{P \in \mathcal {P}} (\mathbf {sign}(P) = \sigma (P))$ to be a sign condition on $\mathcal {P}$ and call its realization the realization of the sign condition $\sigma $ . We say that a sign condition is realizable if its realization is not empty.

We denote by $\mathrm {Cc}(\mathcal {P})$ the set of semialgebraically connected components of the realizations of each realizable sign condition on $\mathcal {P}$ .

We say that a cylindrical algebraic decomposition $\mathcal {D} = (\mathcal {D}_1,\ldots , \mathcal {D}_n)$ of $\mathrm {R}^n$ is adapted to $\mathcal {P}$ if for each cell C of $\mathcal {D}_n$ , and each $P \in \mathcal {P}$ , $\mathbf {sign}(P(x))$ is constant for $x \in C$ . (This implies in particular that each element of $\mathrm {Cc}(\mathcal {P})$ is a union of cells of $\mathcal {D}_n$ .)

Lemma 5.3. Let $\mathcal {F} \subset \mathrm {R}[X_1,X_2]_{\leq p}$ be a finite set of nonzero polynomials. Let $f:\mathrm {R} \rightarrow \mathrm {R}$ be a semialgebraic map such that

$$\begin{align*}\mathrm{graph}(f) = \{(x,f(x)) \mid x \in \mathrm{R}\} = \bigcup_{C \in \mathcal{C}} C \end{align*}$$

for some subset $\mathcal {C} \subset \mathrm {Cc}(\mathcal {F})$ .

Then, there exist $a, c \in \mathrm {R}$ such that for all $x \geq a$ ,

$$\begin{align*}|f(x)| \leq c \cdot x^p. \end{align*}$$

Proof. Consider a cylindrical algebraic decomposition $\mathcal {D} = (\mathcal {D}_1,\mathcal {D}_2)$ of $\mathrm {R}^2$ (with coordinates $X_1,X_2$ ) adapted to the set $\mathcal {F}$ .

This implies that each $C \in \mathrm {Cc}(\mathcal {F})$ is a union of cells of $\mathcal {D}_2$ . Let $a_0 < a_1 <\cdots < a_n=a$ be the end points of the intervals giving the partition of $\mathrm {R}$ (corresponding to the $X_1$ coordinate) in the decomposition $\mathcal {D}_1$ .

Since the cylindrical decomposition $\mathcal {D}$ is adapted to $\mathcal {F}$ , and $\mathrm {graph}(f) =\bigcup _{C \in \mathcal {C}} C $ for some subset $\mathcal {C} \subset \mathrm {Cc}(\mathcal {F})$ , $\dim (C) \leq 1$ for each $C \in \mathcal {C}$ since

$$\begin{align*}\dim(C) \leq \dim (\mathrm{graph}(f)) = 1. \end{align*}$$

Hence, there exists for each $C \in \mathcal {C}$ a polynomial $F \in \mathcal {F}$ such that $F(x) = 0$ for all $x \in C$ .

Also, since $\mathrm {graph}(f) =\bigcup _{C \in \mathcal {C}} C $ and each $C \in \mathcal {C}$ is a union of cells of $\mathcal {D}$ , there exists a continuous semialgebraic function $\gamma : (a,\infty ) \rightarrow \mathrm {R}$ such that $\mathrm {graph}(\gamma ) \subset \mathrm {graph}(f)$ , and $\mathrm {graph}(\gamma )$ is a cell of $\mathcal {D}_2$ .

Let $C \in \mathrm {Cc}(\mathcal {C})$ be the unique element of $\mathcal {C}$ which contains $\mathrm {graph}(\gamma )$ , and $F \in \mathcal {F}$ such that $F(x) = 0$ for all $x \in C$ .

The lemma now follows from [11, Proposition 2.6.1] noting that

$$\begin{align*}\deg(F) \leq p.\\[-39pt] \end{align*}$$

Notation 5.4 (Realizable sign conditions).

For any finite set of polynomials $\mathcal {P} \subset \mathrm {R}[X_1,\ldots ,X_k]$ we denote by

$$\begin{align*}\mathrm{SIGN} (\mathcal{P}) \subset \{0, 1, - 1\}^{\mathcal{P} } \end{align*}$$

the set of all realizable sign conditions for $\mathcal {P}$ over $\mathrm {R}^k$ , that is,

$$\begin{align*}\mathrm{SIGN} (\mathcal{P}) = \{ \sigma \in \{0, 1, -1\}^{\mathcal{P}} \;\mid\; {\mathcal R}(\sigma,\mathrm{R}^n) \neq \emptyset\}. \end{align*}$$

Proposition 5.5. Let $\mathcal {P} \subset \mathrm {R} [ Y,X]$ , with $Y = (Y_{1} , \ldots ,Y_{\ell }), X = (X_{1} ,\ldots ,X_{k})$ be a finite set of polynomials. Then there exists a finite subset $\mathrm {BElim}_{X} ( \mathcal {P} ) \subset \mathrm {R} [Y]$ such that for each $C \in \mathrm {Cc}(\mathrm {BElim}_{X} ( \mathcal {P} ))$ , $\mathrm {SIGN} (\mathcal {P} (y, X))$ is fixed as y varies over C.

If the degrees of the polynomials in $\mathcal {P}$ are bounded by $d \geq 2$ , then the degrees of the polynomials in $\mathrm {BElim}_{X} ( \mathcal {P} )$ is bounded by

(5.1) $$ \begin{align} 8 d^2 (2k(2d + 2) + 2)(2d + 3)(2d + 6)^2(2d + 5)^{2k-2} < (8 d)^{2k+4}. \end{align} $$

Proof. Let $\mathrm {BElim}_X(\mathcal {P})$ be the set of polynomials denoted by the same formula in the output of Algorithm 14.6 (block elimination) in [3]. The fact that for each $C \in \mathrm {Cc}(\mathrm {BElim}_{X} ( \mathcal {P} ))$ , $\mathrm {SIGN} (\mathcal {P} (y, X))$ is fixed as y varies over C is a consequence of Proposition 14.10 in [3].

To obtain the upper bound on the degrees of the polynomials in $\mathrm {BElim}_{X} ( \mathcal {P})$ , we follow the complexity analysis of Algorithm 14.6 (block elimination) in [3] using the same notation as in the algorithm. The algorithm first computes a set $\mathrm {UR}_X(\mathcal {P})$ whose elements are tuples $v = (f,g_0,\ldots ,g_k)$ of polynomials in $T,Y,{\varepsilon },\delta $ (here, ${\varepsilon }$ and $\delta $ are infinitesimals and T is one variable). It is proved in the complexity analysis of the algorithm that the degrees of the polynomials in T appearing in the various tuples $v \in \mathrm {UR}_X(\mathcal {P})$ are bounded by

$$\begin{align*}D = (2d + 6)(2d + 5)^{k-2}, \end{align*}$$

and their degrees in Y (as well as in ${\varepsilon },\delta $ ) are bounded by

$$\begin{align*}D' = (2k(2d + 2) + 2)(2d + 3)(2d + 6)(2d + 5)^{k-2}. \end{align*}$$

It follows that for each $P \in \mathcal {P}$ , and $v = (f,g_0,\ldots ,g_k) \in \mathrm {UR}_X(\mathcal {P})$ , the degree in T of the polynomial

$$\begin{align*}P_v = g_0^e P\Big(\frac{g_1}{g_0},\ldots,\frac{g_k}{g_0}\Big), \end{align*}$$

where e is the least even integer greater than $\deg (P) \leq d$ , is bounded by $(d+1) D \leq 2 d D$ , and similarly the degree in Y of $P_v$ is bounded by $2 d D'$ . The same bounds apply to all polynomials in the set $\mathcal {F}_v$ introduced in the algorithm, where $\mathcal {F}_v$ consists of f, the derivatives of f with respect to T, and $P_v$ (defined above) for each $P \in \mathcal {P}$ .

It now follows from the complexity analysis of Algorithm 11.54 (restricted elimination) in [3] that the degrees in Y of the polynomials in $ \mathrm {RElim}_T(f,\mathcal {F}_v)$ are bounded by

$$ \begin{align*} 2 (2 d D) (2 d D') &= 8 d^2 D D'\\&= 8 d^2 (2k(2d + 2) + 2)(2d + 3)(2d + 6)^2(2d + 5)^{2k-2} \\&\leq (8 d^2) \cdot ( 6 k d) \cdot (4 d) \cdot (5 d)^2 \cdot (4 d)^{2k-2}\\&= 8\cdot 6 \cdot 4 \cdot 5^2 \cdot k \cdot d^6 \cdot (4 d)^{2k-2}\\&= \frac{ 3 \cdot 5^2}{4^3} \cdot k \cdot (4 d)^{2k+4}\\&< (8 d)^{2k+4}. \end{align*} $$

Denoting $\mathcal {B}_v \subset \mathrm {R}[Y]$ the set of coefficients of the various polynomials in $\mathrm {RElim}_T(f,\mathcal {F}_v)$ written as polynomials in ${\varepsilon },\delta $ , we immediately obtain that the degrees in Y of polynomials in $\mathcal {B}_v$ are bounded by

$$\begin{align*}8 d^2 (2k(2d + 2) + 2)(2d + 3)(2d + 6)^2(2d + 5)^{2k-2} < (8 d)^{2k+4}. \end{align*}$$

The proposition follows since according to the algorithm

$$\begin{align*}\mathrm{BElim}_X(\mathcal{P}) = \bigcup_{v \in \mathrm{UR}_X(\mathcal{P})} \mathcal{B}_v.\\[-47pt] \end{align*}$$

Lemma 5.6. Suppose that $\mathcal {P} \subset \mathrm {R} [Y, X]$ with $Y = (Y_{1} , \ldots ,Y_{\ell }), X = (X_{1} ,\ldots ,X_{k})$ and $\Phi $ is $\mathcal {P}$ -formula. Then there exist subsets $\mathcal {C}_\exists , \mathcal {C}_\forall \subset \mathrm {Cc}(\mathrm {BElim}_{X} ( \mathcal {P} ))$ such that

$$ \begin{align*} {\mathcal R}((\exists X) \Phi,\mathrm{R}^\ell) =& \bigcup_{C \in \mathcal{C}_\exists} C, \\ {\mathcal R}((\forall X) \Phi,\mathrm{R}^\ell) =& \bigcup_{C \in \mathcal{C}_\forall} C. \end{align*} $$

Proof. The lemma follows from the fact that for each $C \in \mathrm {Cc}(\mathrm {BElim}_{X} ( \mathcal {P} ))$ , the set $\mathrm {SIGN} (\mathcal {P} (y, X))$ is fixed as y varies over C (Proposition 5.5) and the observation that for each $y \in \mathrm {R}^\ell $ , the truth or falsity of each of the formulas

$$ \begin{align*} (\exists X) \Phi(y,X), \ (\forall X) \Phi(y,X) \end{align*} $$

is determined by the set $\mathrm {SIGN}(\mathcal {P}(y,X))$ .

The following proposition is the key ingredient in the proof of Theorem 2.2. It can be viewed as a quantitative version of Proposition 2.6.4 in [11] (which is not quantitative). Our proof is similar in spirit to the proof of Proposition 2.6.4 in [11] but differs at certain important points making it possible to achieve the quantitative bound claimed in the proposition.

Proposition 5.7. Let $d \geq 2$ , $\mathcal {P} \subset \mathrm {R}[X_1,\ldots ,X_n]_{\leq d}$ and

$$\begin{align*}\mathcal{P}_f, \mathcal{P}_g \subset \mathrm{R}[X_1,\ldots,X_n,Y]_{\leq d} \end{align*}$$

be finite sets of polynomials. Let $A \subset \mathrm {R}^n$ be a closed $\mathcal {P}$ -semialgebraic set, $f: A \rightarrow \mathrm {R}$ a continuous semialgebraic function whose graph is a $\mathcal {P}_f$ -semialgebraic set, and $g: \{x \in A \;\mid \; f(x) \neq 0\} \rightarrow \mathrm {R}$ a continuous semialgebraic function whose graph is a $\mathcal {P}_g$ -semialgebraic set. Then there exists $N \leq (8 d)^{2n + 10}$ such that the function $f^N g$ extended by $0$ on $\{ x \in A \; \mid \; f(x)=0\}$ is semialgebraic and continuous on A.

Proof. Suppose that $A = {\mathcal R}(\Phi ,\mathrm {R}^n)$ , $\mathrm {graph}(f) = {\mathcal R}(\Phi _f, \mathrm {R}^{n+1})$ and $\mathrm {graph}(g) = {\mathcal R}(\Phi _g, \mathrm {R}^{n+1})$ , where $\Phi $ is a $\mathcal {P}$ -formula, $\Phi _f$ is a $\mathcal {P}_f$ -formula and $\Phi _g$ is a $\mathcal {P}_g$ -formula.

For each $x \in A, u \in \mathrm {R}$ , we define

$$\begin{align*}A_{x,u} = \{y \in A \;\mid\; ||y - x|| \leq 1, \ u |f(y)| = 1 \}. \end{align*}$$

We define $\Theta (X,U,Y,V)$ to be the quantifier-free formula

$$ \begin{align*} \Phi(Y) \; \wedge \; (||Y & - X||^2 - 1 \leq 0) \\ & \;\wedge\; \\ \big(((V> 0) \; \wedge \; (U V - 1 = 0)) & \;\vee \; ((V < 0) \; \wedge \; (U V +1 =0))\big)\\ & \;\wedge \; \\ & \Phi_f(Y,V). \end{align*} $$

Observe that for each $x\in A$ and $u \in \mathrm {R}$ ,

$$\begin{align*}{\mathcal R}(\Theta(x,u,\cdot,\cdot),\mathrm{R}^{n+1}) = \mathrm{graph}(f|_{A_{x,u}}). \end{align*}$$

The semialgebraic set $A_{x,u}$ is closed and bounded, and we define the semialgebraic function

$$\begin{align*}v(x,u) = \begin{cases} 0 &\mbox{ if } A_{x,u} = \emptyset, \\ \sup\{|g(y)| \;\mid\; y \in A_{x,u}\} &\mbox{ otherwise}. \end{cases} \end{align*}$$

Let $\Lambda _0(X,U,W)$ denote the following first-order (quantified) formula:

$$ \begin{align*} (\forall(Y,V,Z)) \ (W \geq 0) & \; \wedge \; \big((\Theta(X,U,Y,V) \;\wedge\; \Phi_g(Y,Z)) \; \Longrightarrow\\ & ((Z \geq 0) \; \wedge \; (W \geq Z)) \; \vee \; ((Z \leq 0) \; \wedge \; (W \geq -Z))\big). \end{align*} $$

Finally, let $\Lambda (X,U,W)$ denote the formula

$$\begin{align*}(\forall W') \; \Lambda_0(X,U,W') \; \Longrightarrow \; (0 \leq W \leq W'). \end{align*}$$

Notice that $\Lambda (x,u,w)$ is true if and only if $w = v(x,u)$ . Also, notice that for each $x\in A$ , $\Lambda (x,U,W)$ is equivalent to a formula

$$\begin{align*}(\forall (Y,V,W',Z)) \; \Psi_x(Y,V,Z,U,W,W'), \end{align*}$$

where $\Psi _x$ is an $(n+5)$ -ary $\mathcal {P}_x$ -formula with some finite set $\mathcal {P}_x \subset \mathrm {R}[Y,V,Z,U,W,W']_{\leq d}$ (since we assume $d \geq 2$ ).

Let

$$\begin{align*}\mathcal{Q}_x = \mathrm{BElim}_{Y,V,W',Z}(\mathcal{P}_x) \subset \mathrm{R}[U,W] \end{align*}$$

(see Proposition 5.5).

Then, using the degree bound in Proposition 5.5 we have that for each $Q \in \mathcal {Q}_x$ , $\deg (Q) < (8 d)^{2(n+3) + 4} = (8 d)^{2n +10}$ .

It now follows from Lemma 5.3 that there exists $c = c(x)$ such that for all $u \geq c(x)$ ,

$$\begin{align*}|v(x,u)| \leq c \cdot u^p, \end{align*}$$

with $p < (8 d)^{2n +10}$ .

This means that

$$\begin{align*}|f(y)|^p |g(y)| \leq c(x) \end{align*}$$

on $\{y \in A \; \mid \; f(y) \neq 0 \ \mbox { and } \ ||y - x|| \leq 1 \}$ for $|f(y)|$ sufficiently small. The function $f^{N}g$ extended by $0$ is then semialgebraic and continuous at x, where $N = p+1 \leq (8 d)^{2n+10}$ . This completes the proof.

Theorem 5.8. Let $d \geq 2$ , and

$$\begin{align*}\mathcal{P} \subset \mathrm{R}[X_1,\ldots,X_n]_{\leq d}, \ \mathcal{P}_f, \mathcal{P}_g \subset \mathrm{R}[X_1,\ldots,X_n,Y]_{\leq d}. \end{align*}$$

Let $A \subset \mathrm {R}^n$ be a closed $\mathcal {P}$ -semialgebraic set, $f,g: A \rightarrow \mathrm {R}$ be continuous semialgebraic functions whose graphs are $\mathcal {P}_f$ -semialgebraic, respectively, $\mathcal {P}_g$ -semialgebraic set, and such that $f^{-1}(0) \subset g^{-1}(0)$ . Then there exist $N \le (8 d)^{2(n+7)}$ and a continuous semialgebraic function $h:A \rightarrow \mathrm {R}$ such that $g^N = h f$ on A.

Proof. Suppose that $A = {\mathcal R}(\Phi ,\mathrm {R}^n)$ , $\mathrm {graph}(f) = {\mathcal R}(\Phi _f, \mathrm {R}^{n+1})$ and $\mathrm {graph}(g) = {\mathcal R}(\Phi _g, \mathrm {R}^{n+1})$ , where $\Phi $ is a $\mathcal {P}$ -formula, $\Phi _f$ is a $\mathcal {P}_f$ -formula and $\Phi _g$ is a $\mathcal {P}_g$ -formula.

Let $\widetilde {A} = \{(x,f(x),g(x)) | \ x \in A\} \subset \mathrm {R}^{n+2}$ . The function $1/f$ is continuous semialgebraic on $\{(x,u,v) \in \widetilde {A} \; \mid \; g(x) \neq 0\}$ , and its graph is defined by the formula

$$\begin{align*}\Phi_g(X,V) \wedge (V \neq 0) \wedge \Phi_f(X,U) \wedge (UW - 1=0). \end{align*}$$

Moreover, using Proposition 5.7 there exists $N \leq (8 d)^{2(n+2) + 10} = (8d)^{2(n + 7)}$ such that the function $\widetilde {h}:\widetilde {A} \rightarrow \mathrm {R}$ defined by

$$\begin{align*}\widetilde{h}(x,u,v) = \begin{cases} 0 &\mbox{ if } f(x) = 0, \\ g^N(x)/f(x) &\mbox{ if } f(x) \neq 0 \end{cases} \end{align*}$$

is continuous. Since $\widetilde {h}$ does not depend on $u,v$ , we get a continuous and semialgebraic function $h(x) = \widetilde {h}(x,f(x),g(x))$ on A, and $g^N = h f$ .

Proof of Theorem 2.2.

In order to prove inequality (2.2), use Theorem 5.8 with $c = \sup _{x \in A} |h(x)|$ , noticing that c exists since A is assumed to be closed and bounded.

We now prove inequality (2.3). The set of $c \subset \mathbb {R}, c> 0$ for which inequality (2.1) holds for all $x \in A$ is defined by

$$\begin{align*}\Theta(C) := (C> 0) \wedge \left((\forall (X,U,V)) \left(\Phi(X) \wedge \Phi_f(X,U) \wedge \Phi_g(X,V) \right) \Longrightarrow ( V^{2 N} \leq C^2 \cdot U^2)\right), \end{align*}$$

where $\Phi $ is a $\mathcal {P}$ -formula describing A, and $\Phi _f,\Phi _g$ are $\mathcal {Q}$ -formulas describing the graphs of f and g, and $N \le (8 d)^{2(n+7)}$ .

Using Theorem 4.1, we obtain that $\Theta (C)$ is equivalent to a quantifier-free formula $\widetilde {\Theta }(C)$ such that the bit-sizes of the coefficients of the polynomials appearing in $\widetilde {\Theta }(C)$ is bounded by $\tau d^{O(n^2)}$ , and their degrees are bounded by $d^{O(n^2)}$ . Now, using Cauchy’s bound ([3, Lemma 10.2]), the largest real root amongst the real roots of the polynomials appearing in $\widetilde {\Theta }(C)$ is bounded by $2^{\tau d^{O(n^2)}}$ . It follows that there exists $c = 2^{\tau d^{O(n^2)}}$ for which the inequality (2.1) holds.

Using the repeated squaring technique (see below) at the cost of introducing $O(n \log d)$ new variables, it is possible to write another universally quantified formula, namely

$$ \begin{align*} \Theta'(C) := (C> 0) \wedge &\big((\forall (T_1,\ldots,T_M,X,U,V)) (\Phi(X) \wedge \Phi_f(X,U) \wedge \Phi_g(X,V) \wedge \\ & (T_1= V) \wedge (T_2 = T_1^2) \wedge \cdots \wedge (T_{M} = T_{M-1}^2)) \Longrightarrow ( T_M^2 \leq C^2 \cdot U^2)\big), \end{align*} $$

equivalent to $\Theta (C)$ in which all the polynomials appearing have degrees bounded by d (instead of $d^{O(n)}$ as in the formula $\Theta $ ). The number of quantified variables in the formula $\Theta '$ equals $M+n+2$ , where $M = O(\log N) = O(n \log d)$ .

Now, using Theorem 4.1 and Cauchy’s bound as before we obtain a bound of $2^{\tau d^{O(n\log d)}}$ on c.

5.2 Proof of Theorem 2.11

First, we need the following lemma.

Lemma 5.9. Let $\mathcal {P} \subset \mathrm {R}[X_1,\ldots ,X_n]_{\le d}$ and $S \subset \mathrm {R}^n$ a nonempty $\mathcal {P}$ -semialgebraic set. Then there exists $\mathcal {Q} \subset \mathrm {R}[X_1,\ldots ,X_n,U]$ such that the graph of the function $\mathrm{dist} (\cdot ,S):\mathrm {R}^n \rightarrow \mathrm {R}$ is a $\mathcal {Q}$ -semialgebraic set and $\max _{Q \in \mathcal {Q}} \deg (Q) = d^{O(n)}$ .

Before proving Lemma 5.9, we need a new notion (that of Thom encoding of real roots of a polynomial) that will be needed in the proof. The following proposition appears in [3, Proposition 2.36].

Proposition 5.10 (Thom’s lemma).

[3, Proposition 2.36] Let $P \subset \mathrm {R}[X]$ be a univariate polynomial, $\mathrm {Der}(P)$ the set of derivatives of P and $\sigma \in \{-1,0,1\}^{\mathrm {Der}(P)}$ . Then ${\mathcal R} ( \sigma ,\mathrm {R})$ is either empty, a point or an open interval.

Note that it follows immediately from Proposition 5.10, that for any $P \in \mathrm {R}[X]$ and $x \in \mathrm {R}$ such that $P(x) = 0$ , the sign condition $\sigma $ realized by $\mathrm {Der}(P)$ at x characterizes the root x. We call $\sigma $ the Thom encoding of the root x of P.

Proof of Lemma 5.9.

Let $\Phi $ be a $\mathcal {P}$ -formula such that ${\mathcal R}(\Phi ,\mathrm {R}^n) = S$ . Let

$$\begin{align*}W = \{(x,t) \;\mid\; \exists y \in S \mbox{ with } t = ||x-y||\}. \end{align*}$$

Then for each $x \in \mathrm {R}^n$ ,

$$\begin{align*}\mathrm{dist}(x,S) = \inf W_x, \end{align*}$$

where $W_x$ denotes the one-dimensional fiber of W over x with respect to the projection along the t coordinate.

It is also clear from the definition that W is the image under projection along the y coordinates of the semialgebraic set $V \subset \mathrm {R}^n \times \mathrm {R}^n \times \mathrm {R}$ defined by

$$\begin{align*}V = \{(x,y,t) \;\mid\; y \in S \mbox{ and } t = ||x-y||\}. \end{align*}$$

Let $\Theta (X,Y,T)$ be the formula

$$\begin{align*}\Phi(Y) \wedge (T^2 = ||X-Y||^2) \wedge (T \geq 0). \end{align*}$$

Then, it is clear that $\Theta $ is a $\mathcal {P}'$ -formula for some finite subset $\mathcal {P}' \subset \mathrm {R}[X,Y,T]_{\leq d}$ (assuming $d \geq 2$ ), and moreover ${\mathcal R}(\Theta , \mathrm {R}^{2n+1}) = V$ .

Now, apply Theorem 4.1 to the quantified formula $(\exists Y) \Theta (X,Y,T)$ and obtain a quantifier-free $\mathcal {F}$ -formula, $\widetilde {\Theta }$ equivalent to $\Theta $ , where $\mathcal {F}$ is some finite subset of $\mathrm {R}[X,T]$ and

$$\begin{align*}D = \max_{F \in \mathcal{F}} \deg(F) = d^{O(n)}. \end{align*}$$

Notice that ${\mathcal R}(\widetilde {\Theta },\mathrm {R}^{n+1}) = W$ , and for each $x \in \mathrm {R}^n$ ,

$$\begin{align*}\inf W_x = \mathrm{dist}(x,S) \end{align*}$$

is a real root of some polynomial in $\mathcal {F}$ .

Let $\mathcal {F} = \{F_1,\ldots ,F_N\}$ . We denote

$$\begin{align*}\mathrm{Der}_T(F_i) = \{F_i, F_i',\ldots,F_i^{(D)} \} \end{align*}$$

the set of derivatives of $F_i$ with respect to T.

For $1 \leq i \leq N$ , and $\sigma \in \{-1,0,1\}^{\mathrm {Der}_T(F_i)}$ , denote by $\Psi _{i,\sigma }$ the quantifier-free formula,

$$\begin{align*}(\forall T) \left(\bigwedge_{0 \leq j \leq D} (\mathbf{sign}(F_i^{(j)}) = \sigma(F_i^{(j)}))\right) \Longrightarrow \left((\forall T') \widetilde{\Theta}(X,T') \Longrightarrow (T \leq T')\right). \end{align*}$$

Using Theorem 4.1 one more time, let $\widetilde {\Psi }_{i,\sigma }$ be a quantifier-free formula equivalent to $\Psi _{i,\sigma }$ and let the set of polynomials appearing in $\widetilde {\Psi }_{i,\sigma }$ be denoted by $\mathcal {Q}_{i,\sigma }$ .

The semialgebraic set ${\mathcal R}(\widetilde {\Psi }_{i,\sigma },\mathrm {R}^n)$ is the set consisting of points $x \in \mathrm {R}^n$ such that $\mathrm{dist} (x,S)$ equals the (at most one) real root of the polynomial $F_i(x,T)$ with Thom encoding $\sigma $ . Notice that the maximum degree of polynomials in $\mathcal {Q}_{i,\sigma }$ is bounded by $D^{O(1)} = d^{O(n)}$ .

Finally, let

$$\begin{align*}\Psi = \bigwedge_{i,\sigma} \left(\widetilde{\Psi}_{i,\sigma} \Longrightarrow \left(\bigwedge_{0 \leq j \leq D} (\mathbf{sign}(F_i^{(j)}) = \sigma(F_i^{(j)}))\right)\right), \end{align*}$$

and

$$\begin{align*}\mathcal{Q} = \bigcup_{1 \leq i \leq N} \left(\mathrm{Der}_T(F_i) \cup \bigcup_{\sigma \in \{-1,0,1\}^{\mathrm{Der}_T(F_i)}} \mathcal{Q}_{i,\sigma}\right). \end{align*}$$

It is clear from the above construction that, $\Psi $ is a $\mathcal {Q}$ -formula, and ${\mathcal R}(\Psi ,\mathrm {R}^{n+1})$ is the graph of the function $\mathrm{dist} (\cdot ,S)$ , and the degrees of the polynomials in $\mathcal {Q}$ are bounded by $d^{O(n)}$ . This proves the lemma.

Remark 5.11. In [46, Theorem 7], the graph of the semialgebraic function $\mathrm{dist} (x,S)$ (with S being closed) is described by the following quantified formula with two blocks of quantifiers

(5.2) $$ \begin{align} (\exists Y) \ (\forall Y') \ \ \neg \Phi(Y') \vee \big(\Phi(Y) \wedge (||X-Y||^2 = T^2) \wedge (T \ge 0) \wedge (||X-Y'||^2\ge T^2)\big), \end{align} $$

where ${\mathcal R}(\Phi ,\mathrm {R}^n) = S$ and $(\exists Y)$ and $(\forall Y')$ are two blocks of variables each of size n with different quantifiers; see also [11, Proposition 2.2.8]. The effective quantifier elimination (Theorem 4.1) applied to (5.2) yields a quantifier-free formula with polynomials having degrees bounded by $d^{O(n^2)}$ , where d is an upper bound on the degrees of the polynomials in $\Phi $ . The formula given in Lemma 5.9 describing the graph of the same function involves polynomials of degrees at most $d^{O(n)}$ (though it may involve many more polynomials than the one in (5.2)) which is an improvement over the bound of $d^{O(n^2)}$ obtained by the above argument. Note that for our purposes, the degrees of the polynomials appearing in the formula is the important quantity – the number of polynomials appearing is not relevant.

Proof of Theorem 2.11.

It is easy to see that the residual function $\psi (x)$ defined in (2.7) satisfies

$$ \begin{align*} \mathrm{dist}(x,M) = 0 \ \ \Longleftrightarrow \ \ \psi(x) = \sum_{j=1}^{s} |h_j(x)| + \sum_{i=1}^{r} \max\{g_i(x),0\} = 0. \end{align*} $$

The graph of $\psi (x)$ can be described using a quantifier-free $\mathcal {P}$ -formula with $\mathcal {P} \subset \mathrm {R}[X_1,\ldots ,X_n]_{\le d}$ as follows (note that we do not care about the cardinality of $\mathcal {P}$ ).

To see this, first observe that for all $x \in \mathrm {R}^n$ , and $\sigma \in \{0,1,-1\}^{[1,s]}$ if $\mathbf {sign}(h_j(x)) = \sigma (j), j \in [1,s]$ , then

$$\begin{align*}\sum_{j=1}^{s} |h_j(x)| = \sum_{j=1}^s \sigma(j) h_j(x). \end{align*}$$

Similarly, for all $x \in \mathrm {R}^n$ , and $\tau \in \{0,1,-1\}^{[1,r]}$ if $\mathbf {sign}(g_i(x)) = \tau (i), i \in [1,r]$ , then

$$\begin{align*}\sum_{i=1}^{r} \max\{g_i(x),0\} = \frac{1}{2}\sum_{i=1}^{r} \tau(i)(1 + \tau(i)) g_i(x). \end{align*}$$

It is now easy to verify that the following quantifier-free formula in $n+1$ variables:

$$ \begin{align*} \bigvee_{\substack{\sigma \in \{0,1,-1\}^{[1,s]} \\ \tau \in \{0,1,-1\}^{[1,r]}}} & \left(\bigwedge_{j=1}^{s}(\mathbf{sign}(h_j) = \sigma(j)) \wedge \bigwedge_{i=1}^{r} (\mathbf{sign}(g_i) = \tau(i))\right)\Longrightarrow \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \left(T - \sum_{j=1}^s \sigma(j) h_j - \frac{1}{2}\sum_{i=1}^{r} \tau(i)(1 + \tau(i)) g_i=0 \right) \end{align*} $$

describes the graph of $\psi $ and all polynomials occurring in it have degrees at most d.

Moreover, it follows from Lemma 5.9 that the graph of $\mathrm{dist} (\cdot ,M)$ can be defined by a quantifier-free formula involving polynomials in $n+1$ variables having degrees bounded by $d^{O(n)}$ . The first part of the theorem now follows from Theorem 2.2 after setting $f(x)= \psi (x)$ , and $g(x)=\mathrm{dist} (x,M)$ .

In case that M is finite, it is possible to derive a sharper estimate of the error bound exponent. Suppose $M = \{p_1, \ldots , p_N \} \subset \mathrm {R}^n$ . In this case, the graph of the distance function, $\mathrm{dist} (x,M)$ , is described by the following formula:

$$\begin{align*}\Theta(X,T) := (T \geq 0) \wedge \left(\bigwedge_{i=1}^N (T^2 \geq ||X - p_i||^2)\right) \wedge \left (\bigvee_{i=1}^{N} (T^2 = ||X - p_i||^2)\right). \end{align*}$$

Notice that the degrees of the polynomials appearing in the quantifier-free formula $\Theta $ are bounded by $2$ . Furthermore, the graph of the residual function $\psi $ is defined by a quantifier-free formula involving polynomials of degrees bounded by d. The second part of the theorem is now immediate from Theorem 2.2.

Proof of Corollary 2.14.

Notice that $M \cap \mathbb {S}^p_+$ can be redefined as a basic $\mathcal {Q}$ -semialgebraic set with $\mathcal {Q} \subset \mathrm {R}[X_1,\ldots ,X_{p^2}]_{\le \max \{d,p\}}$ and $\mathrm {card}(\mathcal {Q})=2^p+r-1$ ² as follows:

(5.3) $$ \begin{align} \big\{X \in \mathbb{S}^p \mid g_i(X) \le 0, \ i=1,\ldots,r, \ \det(X_{I}) \ge 0, \ \forall I \subseteq \{1,\ldots,p\}, \ I \neq \emptyset\big\}, \end{align} $$

where $X_{I}$ is a principal submatrix of X indexed by I. We also define the residual function

$$ \begin{align*} \psi(x):=\max\Big\{\mathrm{dist}(x,M),\max_{I \subseteq \{1,\ldots,p\},I \neq \emptyset} \big(\max\{-\det(X_{I}),0\}\big)\Big\}, \end{align*} $$

which is a $\mathcal {Q}'$ -semialgebraic function with $\mathcal {Q}' \subset \mathrm {R}[X_1,\ldots ,X_{p^2},Y]_{\le d^{O(p^2)}}$ ; see Lemma 5.9 and the proof of Theorem 2.11. Then by applying Theorem 2.11, Lemma 5.9 and Remark 2.13 to $M \cap \mathbb {S}^p_+$ , E and $\psi (x)$ we get

$$ \begin{align*} \mathrm{dist}(x,M \cap \mathbb{S}_+^p)^{\rho} &\le \kappa' \cdot \max\Big\{\mathrm{dist}(x,M),\max_{I \subseteq \{1,\ldots,p\},I \neq \emptyset} \big(\max\{-\det(X_{I}),0\}\big)\Big\}, \\ & \mbox{ for all } x \in E, \end{align*} $$

for some $\kappa '> 0$ and $\rho =\max \{d,p\}^{O(p^4)}$ . The rest of the proof follows from the arguments in [29]. Let $\lambda _i(X_{I})$ be the i-th smallest eigenvalue of $X_{I}$ . By the boundedness of E, there exists some positive r such that $|\lambda _i(X_{I})| \le r$ for all $i=1,\ldots ,\mathrm {card}(I)$ . Furthermore, by the interlacing property of eigenvalues of X, we have

$$ \begin{align*} \lambda_{\min}(X_{I}):=\lambda_{1}(X_{I}) \ge \lambda_{\min}(X). \end{align*} $$

If we assume, without loss of generality, that $\det (X_I) < 0$ , then we have

$$ \begin{align*} \det(X_{I}) = \prod_{i=1}^{\mathrm{card}(I)} \lambda_{i}(X_{I}) \ge r^{\mathrm{card}(I)-1} \lambda_{\min}(X_{I}) \ge r^{\mathrm{card}(I)-1} \lambda_{\min}(X). \end{align*} $$

Consequently,

$$ \begin{align*} \max\{-\det(X_{I}),0\} \le r^{\mathrm{card}(I)-1} \cdot \max\{-\lambda_{\min}(X),0\} \end{align*} $$

for every nonempty $I \subseteq \{1,\ldots ,p\}$ , which completes the proof.

5.3 Proof of Theorem 2.20

In the proof of Theorem 2.20, we need the following ingredient which is proved in [4, Theorem 2.5].

Proposition 5.12 (Quantitative cylindrical definable cell decomposition).

Fix an o-minimal expansion of the real closed field $\mathrm {R}$ . Let $\mathcal {A}$ be a definable family of subsets of $\mathrm {R}^n$ parametrized by the definable set A. Then there exist a finite set J and definable families $(\mathcal {C}_j)_{j \in J}$ of subsets of $\mathrm {R}^n$ each parametrized by $A^{N(n)}$ , where $N(n) = 2(2^n-1)$ having the following property. Suppose, $A' \subset A$ is a finite subset. Then there exists a cylindrical decomposition $\mathcal {D} = (\mathcal {D}_1,\ldots ,\mathcal {D}_n)$ of $\mathrm {R}^n$ such that for each $i, 1 \leq i \leq n$ , the set of cells of the cylindrical decomposition $(\mathcal {D}_1,\ldots ,\mathcal {D}_i)$ of $\mathrm {R}^i$ is a subset of the set of definable sets

$$\begin{align*}\{ (\mathcal{C}_{j})_{\overline{a}} \; \mid \; \overline{a} \in A^{\prime N(n)} \}. \end{align*}$$

For the rest of this section, we fix a polynomially bounded o-minimal expansion of $\mathbb {R}$ .

Proposition 5.13 (o-minimal quantitative version of Proposition 2.6.4 in [11]).

Let $\mathcal {A}$ be a definable family of subsets of $\mathbb {R}^n$ parametrized by the definable set A, and let $\mathcal {B}$ be a definable subset of $\mathbb {R}^{n+1}$ parametrized by the definable set B.

Then there exists $N = N(\mathcal {A},\mathcal {B})> 0$ having the following property. For any triple of finite sets $(A',B',B")$ with $A' \subset A, B',B" \subset B$ , a closed $(\mathcal {A},A')$ -set S, a $(\mathcal {B},B')$ -set F, $(\mathcal {B},B")$ -set G such that $F,G$ are graphs of definable functions $f:\mathbb {R}^n \rightarrow \mathbb {R}, g: \mathbb {R}^n \rightarrow \mathbb {R}$ such that $f|_S$ and $g|_{S_{f\neq 0}}$ (where $S_{f \neq 0} = \{x \in S \;\mid \; f(x) \neq 0\}$ ) are continuous, the function $f^N g|_{S_{f\neq 0}}$ extended by $0$ on $\{ x \in S \; \mid \; f(x)=0\}$ is continuous on S.

Proof. We follow closely the proof of the corresponding proposition (Proposition 5.7) in the semialgebraic case.

For each $x \in S, u \in \mathbb {R}$ , we define

$$\begin{align*}S_{x,u} = \{y \in S \;\mid\; ||y - x|| \leq 1, \ u |f(y)| = 1 \}. \end{align*}$$

The set $S_{x,u}$ is definable, closed and bounded, and we define the function

$$\begin{align*}v(x,u) = \begin{cases} 0 &\mbox{ if } A_{x,u} = \emptyset, \\ \sup\{|g(y)| \;\mid\; y \in A_{x,u}\} &\mbox{ otherwise}. \end{cases} \end{align*}$$

Clearly, $v: S \times \mathbb {R} \rightarrow \mathbb {R}$ is a definable function.

We define

$$ \begin{align*} T = \{(x,u,y,v) \mid y \in & S \wedge (||y - x||^2 - 1 \leq 0) \\ & \;\wedge\; \\ \big(((v> 0) \; \wedge \; (u v - 1 = 0)) & \vee \; ((v < 0) \; \wedge \; (u v +1 =0))\big)\\ & \;\wedge \; \\ (y,v) & \in F \}. \end{align*} $$

Notice that T is definable and for each fixed x, $T_x \subset \mathbb {R}^{n+2}$ is a $(\mathcal {C}, A' \times B')$ -set, where $\mathcal {C}$ is a definable family of subsets of $\mathbb {R}^{n+2}$ parametrized by $(A \times B)$ , and $\mathcal {C}$ depends only on the definable families $\mathcal {A},\mathcal {B}$ .

Observe also that for each $x\in A$ and $u \in \mathbb {R}$ ,

$$\begin{align*}T_{x,u} = \mathrm{graph}(f|_{S_{x,u}}). \end{align*}$$

We also define the set $L_0$ by

$$ \begin{align*} L_0 = \{(x, & u,w) \; \mid \; \forall(y,v,z) \\ (w & \geq 0) \\ & \wedge \\ \big(((x,u,y,v) \in T & \wedge (y,z) \in G) \Longrightarrow \\ ((z \geq 0) \wedge (w\geq z)) & \vee ((z \leq 0) \wedge (w \geq -z))\big) \}. \end{align*} $$

Finally, let

$$\begin{align*}L = \{(x,u,w) \; \mid \; (\forall w') (x,u,w') \in L_0 \Longrightarrow (0 \leq w \leq w') \}. \end{align*}$$

Notice that for $x \in S$ , $(x,u,w) \in L$ if and only if $w = v(x,u)$ .

Also, notice that the set $L \subset S \times \mathbb {R}^2$ is a definable set which is the complement of a projection of an $(\mathcal {D},D')$ -set $P \subset \mathbb {R}^{2n+5}$ , where $\mathcal {D}$ is a definable family of sets parametrized by $A \times A \times B \times B$ and $D' = A' \times A' \times B' \times B"$ , and $\mathcal {D}$ depends only on the definable families $\mathcal {A},\mathcal {B}$ .

We now apply Proposition 5.12 to the definable family $\mathcal {D}$ . There exist a set of definable families $(\mathcal {C}_j)_{j \in J}$ and a cylindrical decomposition $(\mathcal {D}_1,\ldots ,\mathcal {D}_{2n+5})$ of $\mathbb {R}^{2n+5}$ adapted to the set P whose cells are of the form $(\mathcal {C}_{j})_w$ with $j \in J, w \in (D')^{N(2n+5)}$ .

For $x \in S$ , there exists a unique cell, $C = (\mathcal {C}_{j})_{w}$ , $j \in J, w \in (D')^{N(2n+5)}$ , of the decomposition $\mathbb {R}^n$ containing x.

The definable functions $v(x,\cdot )$ as x varies over $(\mathcal {C}_{j})_{w}$ and w varies over $(A \times A \times B \times B)^{N(2n+5)}$ and $j \in J$ form a definable family, and using Proposition 5.2 in [40] there exists $p = p(\mathcal {A},\mathcal {B})$ such that

$$\begin{align*}|v(x,u)| \leq c(x) \cdot u^p, \end{align*}$$

for all u large enough.

Now, for each $x \in S$ , there exists a cell, $C = (\mathcal {C}_{j})_{w}$ , $j \in J, w \in (D')^{N(2n+5)}$ , of the decomposition $\mathbb {R}^n$ containing x.

This proves the proposition taking $N = p+1$ .

Theorem 5.14. Let $\mathcal {A}$ be a definable family of subsets of $\mathbb {R}^{n}$ parametrized by the definable set A, and let $\mathcal {B}$ be a definable subset of $\mathbb {R}^{n+1}$ parametrized by the definable set B. Then there exists $N = N(\mathcal {A},\mathcal {B})> 0$ having the following property. For any triple of finite sets $(A',B',B")$ with $A' \subset A, B',B" \subset B$ , a closed $(\mathcal {A},A')$ -set S, a $(\mathcal {B},B')$ -set F, $(\mathcal {B},B")$ -set G such that $F,G$ are graphs of definable functions $f:\mathbb {R}^n \rightarrow \mathbb {R}, g: \mathbb {R}^n \rightarrow \mathbb {R}$ continuous on S such that $f|_S^{-1}(0) \subset g|_S^{-1}(0)$ . Then there exists a continuous definable function $h:S \rightarrow \mathrm {R}$ such that $g|_S^N = h f|_S$ on S.

Proof. Similar to the proof of Theorem 5.8, replace semialgebraic by definable.

Proof of Theorem 2.20.

Use Theorem 5.14 with $c = \sup _{x \in S} |h(x)|$ .

6 Applications to optimization

As an illustration of the improvement one obtains by applying the improved bound on the Łojasiewicz exponent proved in Theorem 2.2 and the error bound in Theorem 2.11, we consider the following application in the theory of optimization. Clearly, Theorem 2.11 can be applied to other situations as well, where error bounds are important, for example, in the study of Hölderian continuity of the set-valued map defined by (2.6) as stated in [39, Theorem 3.1].

6.1 Binary feasibility problems

We can use Theorem 2.11 and its independence from the number of constraints to derive an error bound for a binary feasibility problem, where the feasible set is defined by

(6.1) $$ \begin{align} M=\{x \in \mathrm{R}^n \mid g_i(x) \le 0, \ h_j(x) &= 0, \ i=1,\ldots,r, \ j=1,\ldots,s, \\ x_k &\in \{0,1\}, \ k=1,\ldots,n\}, \nonumber \end{align} $$

where $g_i,h_j \in \mathrm {R}[X_1,\ldots , X_n]_{\le d}$ . The following result is a quantified version of [39, Theorem 5.6] specialized for polynomials.

Corollary 6.1. Let M be defined in (6.1), and let E be a closed and bounded $\mathcal {P}$ -semialgebraic subset of $\mathrm {R}^{n}$ with $\mathcal {P} \subset \mathrm {R}[X_1,\ldots ,X_{n}]_{\leq d}$ and $d \ge 2$ . If $M \neq \emptyset $ , then there exist $\kappa>0$ and $\rho = (O(d))^{2n+14}$ such that

$$ \begin{align*} \mathrm{dist}(x,M)^{\rho} \le \kappa \cdot \psi (x), \quad \mbox{for all } x \in E, \end{align*} $$

where

$$ \begin{align*} \psi(x) = \sqrt{\sum_{j=1}^{s} (h_j(x))^2} + \sqrt{\sum_{i=1}^{r} (\max\{g_i(x),0\})^2} +\sum_{k=1}^n \lvert x_k(1-x_k)\rvert. \end{align*} $$

Proof. Note that for every $k=1,\ldots ,n$ , the binary constraint on $x_{k}$ can be enforced by

$$ \begin{align*} x_{k}(1-x_{k}) = 0, \quad x_{k} \in \mathrm{R}. \end{align*} $$

Then M can be redefined as

(6.2) $$ \begin{align} M :=\Big\{x \in \mathrm{R}^n \mid g_i(x) \le 0, \ h_j(x) &= 0, & i&=1,\ldots,r, \ j=1,\ldots,s,\\ \nonumber x_{k}(1-x_{k}) &= 0, & k&=1,\ldots,n\Big\}, \end{align} $$

which is a finite subset of $\mathrm {R}^n$ .

Also, observe that defining

$$ \begin{align*} \widetilde{\psi}(x) = \sum_{j=1}^{s} |h_j(x)| + \sum_{i=1}^{r} \max\{g_i(x),0\} +\sum_{k=1}^n \lvert x_k(1-x_k)\rvert, \end{align*} $$

it follows from the Cauchy–Schwarz inequality that

$$\begin{align*}\widetilde{\psi}(x) \leq c \cdot \psi(x), \end{align*}$$

with $c = \max \{1,\sqrt {r},\sqrt {s}\}> 0$ .

Now, the result follows by applying the second part of Theorem 2.11 and Remark 2.13 to (6.2) and the residual function $\widetilde {\psi }(x)$ .

6.2 Convergence rate of feasible descent schemes

Error bounds are important to estimate the convergence rate of iterative algorithms in nonlinear optimization. Here, we present the convergence analysis in [38, Theorem 5], which is relevant to Theorem 2.2.

Let $\mathrm {R}=\mathbb {R}$ and $g_i,h_j$ defined in (2.6) be convex polynomials. Then the goal of a feasible descent scheme is to find stationary solutions of a polynomial $f \in \mathbb {R}[X_1,\ldots ,X_n]_{\le d}$ over a nonempty closed convex set M (assuming that $\inf _{x \in M} f> -\infty $ ), where a stationary solution is an $x \in \mathbb {R}^n$ such that

$$ \begin{align*} x - \mathrm{Proj}_M\!\big(x-\nabla f(x)\big) = 0, \end{align*} $$

in which $\mathrm{Proj} _M(\cdot )$ denotes the projection onto the convex set M. The idea of a feasible descent scheme is to generate a sequence $\{x_k\}_{k=1}^{\infty }$ of solutions by

(6.3) $$ \begin{align} x_{k+1} = \mathrm{Proj}_M\!\big(x_{k} - \alpha_k \nabla f(x_k) + e_k\big), \end{align} $$

where $\alpha _k> 0$ is the so-called step length and $e_k$ is an error vector depending on $x_k$ . If we define the set of stationary solutions as

$$ \begin{align*} S:=\Big\{x \in \mathbb{R}^n \mid x - \mathrm{Proj}_M\!\big(x-\nabla f(x)\big) = 0\Big\}, \end{align*} $$

then the following result is well known for the convergence rate of a feasible descent scheme which we specialize for the polynomial f.

Proposition 6.2 (Theorem 5 in [38]).

Suppose that S is nonempty, the gradient of f is Lipschitz continuous on M and there exists $\varepsilon> 0$ such that

$$ \begin{align*} x \in S, \ \ y \in S, \ \ f(x) \neq f(y) \Longrightarrow \|x-y\| \ge \varepsilon. \end{align*} $$

If $\liminf \alpha _k> 0$ and the sequences $\{e_k\}_{k=1}^{\infty }$ and $\{x_k\}_{k=1}^{\infty }$ generated by (6.3) satisfy

$$ \begin{align*} \|e_k\| \le \kappa_1 \|x_k - x_{k+1}\|, \ \text{for some} \ \kappa_1> 0,\\ f(x_{k+1}) - f(x_k) \le -\kappa_2 \|x_k - x_{k+1}\|^2, \ \text{for some} \ \kappa_2 > 0, \end{align*} $$

then the sequence $\{f(x_k)\}_{k=1}^{\infty }$ converges at least Q-linearly or at least sublinearly at the rate $k^{1-\rho }$ , where $\rho> 1$ is an integer satisfying

$$ \begin{align*} \mathrm{dist}(x,S)^{\rho} \le \kappa \cdot \big\|x - \mathrm{Proj}_M\!\big(x-\nabla f(x)\big)\big\| \end{align*} $$

for some $\kappa> 0$ and for all x in a compact semialgebraic subset of M.

Notice that S and $\big \|x - \mathrm{Proj} _M\!\big (x-\nabla f(x)\big )\big \|$ are both semialgebraic, and the latter is a residual function. Therefore, Remark 2.13 and Lemma 5.9 can be applied to quantify the convergence rate $k^{1-\rho }$ in terms of d and n only.

Remark 6.3. The exponent (3.6) was used to quantify the convergence rate of the cyclic projection algorithm applied to finite intersections of convex semialgebraic subsets of $\mathbb {R}^n$ [12, Theorem 4.4].

6.3 Sums of squares relaxation

A polynomial optimization problem is formally defined as the following: Given a polynomial $f \in \mathbb {R}[X_1,\ldots , X_n]_{\le d}$ , compute

(6.4) $$ \begin{align} f_{\min}^*:=\inf \big \{f(x) \mid x \in M \big\}, \end{align} $$

where M is defined in (2.6) with $\mathrm {R}=\mathbb {R}$ . We assume, without loss of generality, here that $s = 0$ in (2.6).

Unlike semidefinite optimization (see, e.g., [6]), there is no efficient interior point method for polynomial optimization. Nevertheless, tools in real algebra have laid the groundwork for developing an efficient numerical approach, where semidefinite relaxation plays a central role. Using this approach, (6.4) is approximated by a hierarchy of semidefinite relaxations, so-called sums of squares (SOS) relaxations [27, 45]; see also [28]. A SOS relaxation of order t is defined as

(6.5) $$ \begin{align} f_{\mathrm{sos}}^{*t}=\sup\{\beta \mid f-\beta \in \mathbf{\mathcal{M}}_{2t}(g_1,\ldots,g_r)\}, \end{align} $$

where

$$ \begin{align*} \mathbf{\mathcal{M}}_{2t}(g_1,\ldots,g_r)= \bigg\{u_0 - \sum_{j=1}^r u_jg_j \mid u_0,u_j \in \Sigma, \ \deg(u_0), \deg(u_jg_j) \le 2t, \ j=1,\ldots,r\bigg\} \end{align*} $$

is called the truncated quadratic module generated by $g_1,\ldots ,g_r$ and $\Sigma $ is the convex cone of SOS polynomials. It is worth noting that (6.5) is a semidefinite optimization problem of size $O(n^t)$ . Under some conditions on M (see, for example, [28, Proposition 6.2 and Theorem 6.8]), (6.5) is feasible for sufficiently large t, and $f_{\mathrm {sos}}^{*t} \to f_{\min }^*$ as $t \to \infty $ .

Recently, Baldi and Mourrain [1] provided a convergence rate for $f_{\mathrm {sos}}^{*t}$ in terms of t, in which the Łojasiewicz inequality plays a central role. The authors proved [1, Theorem 4.3], under some conditions, that there exists $c> 1$ such that

$$ \begin{align*} 0 < f_{\min}^* - f_{\mathrm{sos}}^{*t} \le c \cdot \|f\| \deg(f)^{\frac 75} t^{-\frac{1}{2.5n\rho}}, \end{align*} $$

where c depends on n, $\rho $ and $g_1,\ldots , g_r$ , $\|f\|:=\max _{x \in [-1,1]^n} |f(x)|$ and $\rho $ is the error bound exponent for the inequality

$$ \begin{align*} \mathrm{dist}(x,M)^{\rho} \le \kappa \cdot |\min\{g_1(x),\ldots,g_r(x),0\}|, \quad \text{for all} \ x\in [-1,1]^n \end{align*} $$

for some $\kappa> 0$ . Then the application of Theorem 2.11 and Remark 2.13 yields an upper bound $d^{O(n^2)}$ on $\rho $ and thus proves a lower bound on the convergence rate $t^{-\frac {1}{2.5n\rho }}$ of the SOS relaxation in terms of n and d only.

Remark 6.4. There are other applications of the Łojasiewicz inequality to polynomial optimization in the literature. For instance, it was shown in [24] that the Łojasiewicz inequality (3.2) can be used to reduce (6.4) to minimization over a ball.

7 Conclusion

In this paper, we proved a nearly tight upper bound on the Łojasiewicz exponent for semialgebraic functions over a real closed field $\mathrm {R}$ in a very general setting. Unlike the previous best-known bound in this setting due to Solernó [46], our bound is independent of the cardinalities of the semialgebraic descriptions of f, g and A. We exploited this fact to improve the best-known error bounds for polynomial and nonlinear semidefinite systems. As an abstraction of the notion of independence from the combinatorial parameters, we proved a version of Łojasiewicz inequality in polynomially bounded o-minimal structures. We proved existence of a common upper bound on the Łojasiewicz exponent for certain combinatorially defined infinite (but not necessarily definable) families of pairs of functions, which improves a prior result due to Chris Miller.

We end with a few open problems. We proved in Theorem 2.11 that the exponent $\rho = d^{O(n)}$ in the error bound with respect to a zero-dimensional semialgebraic set M, and Example 2.4 indicates that this bound is indeed tight. Without the assumption on the dimension on M, the general bound on the exponent $\rho $ in Theorem 2.11 is $d^{O(n^2)}$ . There are some indications in [22] for generating examples whose Łojasiewicz exponent is worse than Example 2.4. However, we have not been able to find any example with $\rho = d^{O(n^2)}$ , so we do not know if this bound is tight as well. It would be interesting to resolve this gap.

Another interesting question is to prove an upper bound that depends on $\dim M$ which interpolates between the zero-dimensional and the general case. More precisely, is it possible to improve the upper bound in Theorem 2.11 to $d^{O(n \cdot \dim M)}$ ?

While the emphasis in the current paper has been on proving a bound on the Łojasiewicz exponent which is independent of the combinatorial parameter, there is a special case that merits attention and in which the combinatorial parameter may play a role. It is well known [2] that the topological complexity (say measured in terms of the Betti numbers) of a real algebraic set in $\mathrm {R}^n$ defined by s quadratic equations is bounded by $n^{O(s)}$ . This bound (unlike the bounds discussed in the current paper) is polynomial in n for fixed s. One could ask if a similar bound also holds in this setting for the Łojasiewicz exponent.