Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-13T12:47:22.628Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulence measurements in the neutral ISM from Hi-21 cm emission–absorption spectra

Published online by Cambridge University Press:  17 August 2023

Atanu Koley Open the ORCID record for Atanu Koley [Opens in a new window]
Atanu Koley*
Affiliation:
Departamento de Astronomía, Universidad de Concepción, Concepción, Chile
*
Email: atanuphysics15@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the correlation between the non-thermal velocity dispersion (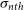$\sigma_{nth}$) and the length scale (L) in the neutral interstellar medium (ISM) using a large number of Hi gas components taken from various published Hi surveys and previous Hi studies. We notice that above the length-scale (L) of 0.40 pc, there is a power-law relationship between 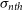$\sigma_{nth}$ and L. However, below 0.40 pc, there is a break in the power law, where 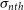$\sigma_{nth}$ is not significantly correlated with L. It has been observed from the Markov chain Monte Carlo (MCMC) method that for the dataset of L 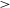$\gt$ 0.40 pc, the most probable values of intensity (A) and power-law index (p) are 1.14 and 0.55, respectively. Result of p suggests that the power law is steeper than the standard Kolmogorov law of turbulence. This is due to the dominance of clouds in the cold neutral medium. This is even more clear when we separate the clouds into two categories: one for L is 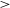$\gt$ 0.40 pc and the kinetic temperature (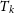$T_{k}$) is $\lt$250 K, which are in the cold neutral medium (CNM) and for other one where L is 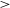$\gt$0.40 pc and 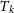$T_{k}$ is between 250 and 5 000 K, which are in the thermally unstable phase (UNM). Most probable values of A and p are 1.14 and 0.67, respectively, in the CNM phase and 1.01 and 0.52, respectively, in the UNM phase. A greater number of data points is effective for the UNM phase in constructing a more accurate estimate of A and p, since most of the clouds in the UNM phase lie below 500 K. However, from the value of p in the CNM phase, it appears that there is a significant difference from the Kolmogorov scaling, which can be attributed to a shock-dominated medium.

Keywords

ISM: atomsISM: kinematics and dynamicsISM: lines and bandsISM: structureturbulence
Type
Research Article
Information
Publications of the Astronomical Society of Australia , Volume 40 , 2023 , e046
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of the Astronomical Society of Australia

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Armstrong, J. W., Rickett, B. J. & Spangler, S. R. 1995, ApJ, 443, 209CrossRefGoogle Scholar
Audit, E. & Hennebelle, P. 2005, A&A, 433, 1CrossRefGoogle Scholar
Begum, A., et al. 2010a, ApJ, 722, 395CrossRefGoogle Scholar
Begum, A., et al. 2010b, in Astronomical Society of the Pacific Conference Series, Vol. 438, The Dynamic Interstellar Medium: A Celebration of the Canadian Galactic Plane Survey, ed. Kothes, R., Landecker, T. L., & Willis, A. G., 126 Google Scholar
Blagrave, K. et al. 2017, ApJ, 834, 126CrossRefGoogle Scholar
Braun, R. & Kanekar, N. 2005, A&A, 436, L53 CrossRefGoogle Scholar
Carroll, B. W. & Ostlie, D. A. 1996, An Introduction to Modern AstrophysicsGoogle Scholar
Choudhuri, S. & Roy, N. 2019, MNRAS, 483, 3437CrossRefGoogle Scholar
Field, G. B. 1958, Proc. IRE, 46, 240CrossRefGoogle Scholar
Field, G. B. 1965, ApJ, 142, 531CrossRefGoogle Scholar
Field, G. B., Goldsmith, D. W., & Habing, H. J. 1969, ApJ, 155, L149 CrossRefGoogle Scholar
Frisch, U. 1995, Turbulence. The legacy of A.N. KolmogorovCrossRefGoogle Scholar
Goldreich, P. & Sridhar, S. 1995, ApJ, 438, 763CrossRefGoogle Scholar
Heiles, C. & Troland, T. H. 2003a, ApJS, 145, 329CrossRefGoogle Scholar
Heiles, C. & Troland, T. H. 2003b, ApJ, 586, 1067CrossRefGoogle Scholar
Hennebelle, A. & Falgarone, E. 2012, A&ARv, 20, 55Google Scholar
Jenkins, E. B. & Tripp, T. M. 2011, ApJ, 734, 65CrossRefGoogle Scholar
Kalberla, P. M. W. & Haud, U. 2019, A&A, 627, A112CrossRefGoogle Scholar
Kalberla, P. M. W. et al., 2017, A&A, 607, A15CrossRefGoogle Scholar
Kolmogorov, A. N. 1941, Akademiia Nauk SSSR Doklady, 32, 16Google Scholar
Kowal, G. & Lazarian, A. 2007, ApJL, 666, L69 CrossRefGoogle Scholar
Larson, R. B. 1979, MNRAS, 186, 479CrossRefGoogle Scholar
Liszt, H. 2001, A&A, 371, 698CrossRefGoogle Scholar
Miville-Deschênes, M.-A. et al. 2001, A&A, 411, 109CrossRefGoogle Scholar
Mohan, R., Dwarakanath, K. S., & Srinivasan, G. 2004, JApA, 25, 143CrossRefGoogle Scholar
Murray, C. E., et al. 2015, ApJ, 804, 89CrossRefGoogle Scholar
Murray, C. E., et al. 2018, ApJS, 238, 14CrossRefGoogle Scholar
Murray, C. E., et al. 2021, ApJS, 256, 37CrossRefGoogle Scholar
Patra, N. N., Kanekar, N., Chengalur, J. N., & Roy, N. 2018, MNRAS, 479, L7 CrossRefGoogle Scholar
Roy, N., Kanekar, N., Braun, R., & Chengalur, J. N. 2013a, MNRAS, 436, 2352CrossRefGoogle Scholar
Roy, N., Kanekar, N., & Chengalur, J. N. 2013b, MNRAS, 436, 2366CrossRefGoogle Scholar
Seon, K.-i. & Kim, C.-G. 2020, ApJS, 250, 9CrossRefGoogle Scholar
Sridhar, S. & Goldreich, P. 1994, ApJ, 432, 612CrossRefGoogle Scholar
Stanimirović, S. & C., Helies 2005, ApJ, 631, 371CrossRefGoogle Scholar
Stanimirović, S., Murray, C. E., Lee, M.-Y., Heiles, C., & Miller, J. 2014, ApJ, 793, 132CrossRefGoogle Scholar
Winkel, B., et al. 2016, A&A, 585, A41 CrossRefGoogle Scholar
Wolfire, M. G., Hollenbach, D., McKee, C. F., Tielens, A. G. G. M., & Bakes, E. L. O. 1995, ApJ, 443, 152CrossRefGoogle Scholar
Wolfire, M. G., McKee, C. F., Hollenbach, D., & Tielens, A. G. G. M. 2003, ApJ, 587, 278CrossRefGoogle Scholar
Xu, S., Ji, S., & Lazarian, A. 2019, ApJ, 878, 157CrossRefGoogle Scholar