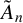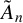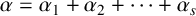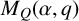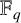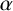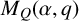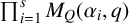CANONICAL DECOMPOSITION AND QUIVER REPRESENTATIONS OF TYPE $\tilde {A}_n$ OVER FINITE FIELDS

Abstract

Let Q be a quiver of type $\tilde {A}_n$ . Let $\alpha =\alpha _1+\alpha _2+\cdots +\alpha _s$ be the canonical decomposition. For the polynomials $M_Q(\alpha ,q)$ that count the number of isoclasses of representations of Q over ${\mathbb F}_q$ with dimension vector $\alpha $ , we obtain a precise relation between the degree of $M_Q(\alpha ,q)$ and that of $\prod _{i=1}^{s} M_Q(\alpha _i,q)$ for an arbitrary dimension vector $\alpha $ .

1 Introduction

The representations of a quiver, introduced by Gabriel [7] in the 1970s, emerge as a notion of significant interest due to a remarkable relation with Lie theory. Gabriel revealed a bijective correspondence between the set of dimension vectors of indecomposable representations of a Dynkin quiver and the root system of the corresponding semisimple Lie algebra. Kac [9] extended Gabriel’s theorem to an arbitrary quiver.

Kac’s work shows the validity of the geometric approach to classification of indecomposable representations of quivers. Consider the representation variety $R(Q,\alpha )$ associated to a fixed dimension vector $\alpha $ of a quiver Q, on which there is an algebraic group action. Then the isoclasses of representations are identified with the orbits under the action. Let $V_p$ be the representation corresponding to a point p in $R(Q,\alpha )$ . According to the Krull–Schmidt theorem, $V_p\cong \oplus V_{i,p}$ for some indecomposable representations $V_{i,p}$ . Kac proved that the set of dimension vectors $\{\mathbf {dim}\, V_{i,p}\}$ is independent of the choice of p in some dense open subset ${\mathcal U}$ in $R(Q,\alpha )$ . This leads to the notion of a canonical decomposition $\alpha =\sum \alpha _i$ (with $\mathbf {dim}\, V_{i,p}=\alpha _i$ ) and enables us to study quiver representations by a recursive method (see [5, 11]).

Let ${\mathbb F}_q$ be the finite field with q elements. Let $M_Q(\alpha ,q)$ be the number of isoclasses of representations of a quiver Q over ${\mathbb F}_q$ with a fixed dimension vector $\alpha $ . This polynomial is closely related to Kac’s conjecture (see [3, 8–10]).

We investigate the relationships between the two families of polynomials $M_Q(\alpha ,q)$ and $\prod _{i} M_Q(\alpha _i,q)$ associated with the canonical decomposition $\alpha =\alpha _1+\alpha _2+\cdots +\alpha _s$ when Q is a tame quiver of type $\tilde {A}_n$ . This allows to collect evidence relevant to questions proposed in [2, Conjecture 0.1]. The main tools are basic homological properties of module categories, especially Auslander–Reiten theory.

2 Preliminaries

In this section, we give a brief review on quiver representations and the canonical decomposition (for more details, see [1, 4]).

Let ${\mathbb F}$ be a field. Let $Q=(Q_0,Q_1)$ be a quiver with vertex set $Q_0$ and arrow set $Q_1$ . We always assume that the quiver is finite, that is, $Q_0$ and $Q_1$ are finite sets, and write $Q_0 = \{1, 2, \ldots , n\}$ . The starting and terminating vertices of an arrow $\alpha $ will be denoted by $t(\alpha )$ and $h(\alpha )$ respectively. By definition, a finite dimensional representation $V=(V_i,V_{\alpha })$ of Q consists of a set of finite dimensional vector spaces $V_i$ for all $i\in Q_0$ and of a set of linear transformations $V_\alpha : V_{t(\alpha )}\rightarrow V_{h(\alpha )}$ for all $\alpha \in Q_1$ . A representation is said to be indecomposable if it cannot be written as the direct sum of two nonzero representations. The dimension vector $\mathbf {dim}\, V$ associated with a representation V is a nonnegative integer-valued function on the vertex set $Q_0$ and so an element of ${\mathbb Z} Q_0$ . We identify ${\mathbb Z} Q_0$ with ${\mathbb Z}^n$ in what follows.

For each $\mu =(\,\mu _i)\in {\mathbb Z}^n$ , let $\mathop{\mathrm{supp}}\nolimits \mu =\{i\in Q_0\mid \mu _i\not =0\}$ be the support of $\mu $ . We say that $\mathop{\mathrm{supp}}\nolimits \mu $ is connected if the full subquiver of Q with vertex set $\mathop{\mathrm{supp}}\nolimits \mu $ is connected.

Now assume that ${\mathbb F}$ is an algebraically closed field. Fix a dimension vector $\alpha $ of Q. The representation variety associated with $\alpha $ is the affine space

$$ \begin{align*}R(Q,\alpha):=\prod\limits_{\rho:i\rightarrow j}{\mathrm{Hom}\,}({\mathbb F}^{\alpha_i},{\mathbb F}^{\alpha_j}).\end{align*} $$

Thus, each element x in $R(Q,\alpha )$ determines a representation $V_x$ of Q with dimension vector $\alpha $ . The algebraic group $GL_{\alpha }({\mathbb F}):=\prod _{i\in Q_0}GL_{\alpha _i}({\mathbb F})$ acts on $R(Q,\alpha )$ by conjugation. It is known that $GL_{\alpha }({\mathbb F})$ -orbits ${\mathcal O}_x$ correspond bijectively to isoclasses $[V_x]$ of representations of Q with dimension vector $\alpha $ .

Let Q be a quiver with n vertices and $\alpha =(\alpha _i),\beta =(\,\beta _i)\in {\mathbb Z}^n$ . The bilinear forms

$$ \begin{align*}\langle \alpha,\beta\,\rangle:=\sum_{i=1}^n\alpha_i\beta_i-\sum_{\alpha\in Q_1}\alpha_{t(\alpha)}\,\beta_{h(\alpha)}\quad\mbox{and}\quad (\alpha,\beta):=\langle \alpha,\beta\,\rangle+\langle\,\beta,\alpha\rangle\end{align*} $$

on ${\mathbb Z}^n$ are called the Euler form and the symmetric Euler form of Q, respectively.

We now recall from [9, 10] the notion of canonical decomposition of a dimension vector. Generic representations of $\alpha $ are said to have the property P if there exists a dense open subset ${\mathcal U}$ of $R(Q,\alpha )$ such that all representations parametrised by points in ${\mathcal U}$ have the property P.

Definition 2.1. The canonical decomposition of a dimension vector $\alpha $ is the sum $\alpha =\beta _1+\beta _2+\cdots +\beta _s$ provided that generic representations of $\alpha $ have indecomposable summands whose dimension vectors are given by these $\beta _i$ .

By definition, the canonical decomposition of a fixed dimension vector is unique up to reordering.

Definition 2.2. Write $\beta \hookrightarrow \alpha $ for the property that there exists a dense open subset ${\mathcal U}$ such that each representation parametrised by points in ${\mathcal U}$ of dimension vector $\alpha $ has a subrepresentation of dimension vector $\beta $ .

Given two dimension vectors $\alpha ,\beta $ of Q, denote by ${\mathrm {hom}\,}(\alpha ,\beta )$ and ${\mathrm {ext}\,}(\alpha ,\beta )$ the minimal value of the upper semi-continuous functions $\mathrm {dim}\,{\mathrm {Hom}\,}_Q(-,-)$ and $\mathrm {dim}\,{\mathrm {Ext}\,}^1_Q(-,-))$ on $R(Q,\alpha )\times R(Q,\beta )$ , respectively.

Definition 2.3. We call $\alpha $ a Schur root if $\alpha $ is the dimension vector of a representation with endormorphism ring ${\mathbb F}$ .

Theorem 2.4 [10]

The sum $\alpha =\beta _1+\beta _2+\cdots +\beta _s$ is the canonical decomposition if and only if $\beta _i$ is a Schur root and ${\mathrm {ext}\,}(\,\beta _i,\beta _j)=0$ for $i\not =j$ .

Theorem 2.5 [11]

We have ${\mathrm {ext}\,}(\alpha ,\beta )=\max _{\alpha ^{\prime }\hookrightarrow \alpha }\{-\langle \alpha ^{\prime },\beta \,\rangle \}.$

3 Main results

Throughout this section, assume that the quiver Q of type $\tilde {A}_n$ , where $n=s+t$ , has s arrows going clockwise and t arrows going anticlockwise:

We first recall some properties of module categories of tame quivers of type $\tilde {A}_n$ from [6]. Note that representations of Q are identified with left modules over the path algebra A of Q. Denote by $\Gamma (Q)$ the Auslander–Reiten quiver of A. It is known that $\Gamma (Q)$ has one preprojective component, one preinjective component and infinitely many regular tubes including two nonhomogeneous tubes ${\mathcal T}_1$ and ${\mathcal T}_2$ with ranks t and s, respectively. We say M is a preprojective, preinjective or regular module according as all indecomposable summands of M belong to the preprojective, preinjective or regular component of $\Gamma (Q)$ , respectively.

In what follows, we define by convention the partial order $<$ on the set of roots of Q by saying $\alpha <\beta $ if each component of $\alpha $ is less than or equal to that of $\beta $ . Note that $\delta =(1,1,\ldots ,1)\in {\mathbb Z}^n$ is the minimal positive imaginary root of Q.

Definition 3.1. Let Q be a quiver of type $\tilde {A_n}$ . Let $\alpha =n\delta +\gamma $ with $n\in {\mathbb N}$ and a real root $\gamma $ satisfying $0<\gamma <\delta $ .

1. (1) If $\{b_j\}_{j=0}^t\subseteq \mathop{\mathrm{supp}}\nolimits \gamma $ , then we call $\alpha $ a lower arc. If $\{a_i\}_{i=0}^s\subseteq \mathop{\mathrm{supp}}\nolimits \gamma $ , then we call $\alpha $ an upper arc.

2. (2) If $\mathop{\mathrm{supp}}\nolimits \gamma =\{a_i\}_{i=i_0}^s \cup \{b_j\}_{j=j_0}^t \; (1\leq i_0\leq s,1\leq j_0\leq t)$ , then we call $\alpha $ a right arc. If $\mathop{\mathrm{supp}}\nolimits \gamma =\{a_i\}_{i=0}^{s_0} \cup \{b_j\}_{j=0}^{t_0} \;(0\leq s_0\leq s-1,1\leq t_0\leq t-1)$ , then we call $\alpha $ a left arc.

3. (3) If $\mathop{\mathrm{supp}}\nolimits \gamma =\{a_i\}_{i=u}^v \;(0<u<v<s)$ or $\mathop{\mathrm{supp}}\nolimits \gamma =\{b_j\}_{j=u'}^{v'} \;(0<u'<v'<t)$ , then we call $\alpha $ a short arc.

Remark 3.2. An indecomposable $kQ$ -module M is preprojective or preinjective if and only if $\mathbf {dim}\, M$ is a right or a left arc, respectively. If M is an indecomposable $kQ$ -module with $\mathbf {dim}\, M$ an upper or a lower arc, then M is regular. Moreover, $\mathbf {dim}\, M$ is an upper or a lower arc if and only if M lies in ${\mathcal T}_1$ or ${\mathcal T}_2$ , respectively.

Example 3.3. Let Q be the quiver of type $\tilde {A}_5$ .

Then $\alpha _1=(1,1,0,1,1,1)$ is a lower arc and $\alpha _2=(3,3,3,2,2,3)$ is an upper arc; $\alpha _3=(3,4,4,3,4,4)$ is a right arc and $\alpha _4=(1,1,0,1,0,0)$ is a left arc; $\alpha _5=(0,1,1,0,0,0)$ and $\alpha _6=(1,1,1,2,2,1)$ are both short arcs.

For canonical decompositions of quivers of type $\tilde {A}_n$ , we follow Schofield’s inductive algorithm [11]. For more details, see [2, Examples 2.8 and 2.9], which is our case when $n=3$ and $(s,t)=(2,1)$ .

Lemma 3.4. Let $\alpha $ , $\beta $ be real roots of Q satisfying $0<\alpha ,\,\beta <\delta $ and $\alpha +\beta \geq \delta $ . Then ${\mathrm {ext}\,}(\alpha ,\beta )=0={\mathrm {ext}\,}(\,\beta ,\alpha )$ if and only if $\alpha $ and $\beta $ are a lower arc and an upper arc, respectively.

Proof. Suppose that $\alpha $ and $\beta $ are a lower arc and an upper arc, respectively. From Remark 3.2, there exist indecomposable regular modules $V,W$ with dimension vectors $\alpha ,\beta $ , which lie in ${\mathcal T}_2$ and ${\mathcal T}_1$ , respectively. It follows that

$$ \begin{align*}\mathrm{dim}\, {\mathrm{Ext}\,}_Q^1(V,W)=\mathrm{dim}\, {\mathrm{Ext}\,}_Q^1(W,V)=0.\end{align*} $$

Therefore, ${\mathrm {ext}\,}(\alpha ,\beta )=0={\mathrm {ext}\,}(\,\beta ,\alpha )$ .

Conversely, suppose that there are two real roots $\alpha , \beta <\delta $ satisfying $\alpha +\beta \geq \delta $ and ${\mathrm {ext}\,}(\alpha ,\beta )=0={\mathrm {ext}\,}(\,\beta ,\alpha )$ . We claim that $\alpha +\beta>\delta $ . Indeed if $\alpha +\beta =\delta $ , then

$$ \begin{align*}\begin{array}{lll} (\alpha,\beta)&\!\!\!\!=(\alpha,\delta-\alpha)=-(\alpha,\alpha)=-2\\ &\!\!\!\!=\langle\alpha,\beta\,\rangle+\langle\,\beta,\alpha\rangle. \end{array}\end{align*} $$

Thus, $\langle \alpha ,\beta \,\rangle <0$ (or $\langle \,\beta ,\alpha \rangle <0$ ), that is, ${\mathrm {ext}\,}(\alpha ,\beta )>0$ (or ${\mathrm {ext}\,}(\,\beta ,\alpha )>0$ ), which is a contradiction.

If $\alpha $ is the dimension vector of an indecomposable preprojective module, that is, $\alpha $ is a right arc, put

$$ \begin{align*}\mathop{\mathrm{supp}}\nolimits \alpha=\{a_i\}_{i=i_0}^s \cup \{b_j\}_{j=j_0}^t \quad (1\leq i_0\leq s,1\leq j_0\leq t).\end{align*} $$

Case 1: $\beta $ is the dimension vector of an indecomposable preprojective module. Clearly, $\alpha +\beta \ngeq \delta $ , which is a contradiction.

Case 2: $\beta $ is the dimension vector of an indecomposable preinjective module. Assume that

$$ \begin{align*}\mathop{\mathrm{supp}}\nolimits \beta=\{a_i\}_{i=0}^{s_0} \cup \{b_j\}_{j=0}^{t_0} \quad (0\leq s_0\leq s-1,1\leq t_0\leq t-1).\end{align*} $$

Thus, $s_0\geq i_0-1$ and $t_0\geq j_0-1$ . Consequently,

$$ \begin{align*}\langle\,\beta,\alpha\rangle=s_0-i_0+1+t_0-j_0+1-(s_0-(i_0-1)+1+t_0-(\,j_0-1)+1)=-2,\end{align*} $$

which implies that ${\mathrm {ext}\,}(\,\beta ,\alpha )>0$ , which is a contradiction.

Case 3: $\beta $ is the dimension vector of an indecomposable regular module. Since ${\alpha +\beta>\delta} $ and $\beta <\delta $ , it follows that $\beta $ is a lower arc or an upper arc. If $\beta $ is a lower arc, then

$$ \begin{align*}\mathop{\mathrm{supp}}\nolimits\beta=\{b_j\}_{j=0}^t \cup \{a_i\}_{i=0}^m \cup \{a_i\}_{i=n}^s \quad (0\leq m<n\leq s)\end{align*} $$

and $m\geq i_0-1$ . Consequently,

$$ \begin{align*} \langle\,\beta,\alpha\rangle & =m-i_0+1+s-n+1+t-1-j_0+1 \\ &\quad -(m-(i_0-1)+1+s-1-n+1+t-1-(\,j_0-1)+1) \\ & =-1. \end{align*} $$

This implies that ${\mathrm {ext}\,}(\,\beta ,\alpha )>0$ , contrary to the hypothesis. If $\beta $ is an upper arc, a similar argument also leads to a contradiction.

Case 4: $\alpha $ is the dimension vector of an indecomposable preinjective module. This case can be handled similarly and leads to a contradiction.

Therefore, $\alpha $ and $\beta $ are both dimension vectors of regular modules. Since $\alpha +\beta>\delta $ , it follows that there exists at least one dimension vector which is a lower arc or an upper arc. Assume that $\alpha $ is a lower arc, that is,

$$ \begin{align*}\mathop{\mathrm{supp}}\nolimits\alpha=\{b_j\}_{j=0}^t \cup \{a_i\}_{i=0}^m \cup \{a_i\}_{i=n}^s \quad (0\leq m<n\leq s).\end{align*} $$

We claim that $\beta $ is an upper arc. Indeed, on the one hand, if $\beta $ is a short arc, that is,

$$ \begin{align*}\mathop{\mathrm{supp}}\nolimits \beta=\{a_i\}_{i=u}^v \quad (0<u<v<s),\end{align*} $$

then $v\geq n-1$ and $m\geq u-1$ . Let $\beta ^{\prime }$ be a dimension vector satisfying that $0<\beta ^{\prime }<\delta $ and $\mathop{\mathrm{supp}}\nolimits \beta ^{\prime }=\{a_i\}_{i=n-1}^v.$ Thus, ${\mathrm {ext}\,}(\,\beta ^{\prime },\beta -\beta ^{\prime })=0.$ Therefore, $\beta ^{\prime }\,{\hookrightarrow}\, \beta $ and

$$ \begin{align*}\langle\,\beta^{\prime},\alpha\rangle=v-n+1-(v-(n-1)+1)=-1,\end{align*} $$

which implies that ${\mathrm {ext}\,}(\,\beta ,\alpha )>0$ , which is a contradiction. On the other hand, if $\beta $ is a lower arc, that is,

$$ \begin{align*}\mathop{\mathrm{supp}}\nolimits\beta=\{b_j\}_{j=0}^t \cup \{a_i\}_{i=0}^{m^{\prime}} \cup \{a_i\}_{i={n}^{\prime}}^s \quad (0\leq m^{\prime}<n^{\prime}\leq s),\end{align*} $$

then $m\geq n^{\prime }-1$ or $m^{\prime }\geq n-1$ . Since $\alpha +\beta \geq \delta $ and $\alpha <\delta $ , it follows that $\beta>\delta $ , which is a contradiction. In conclusion, $\alpha $ and $\beta $ are a lower arc and an upper arc, respectively.

Lemma 3.5. Assume that $\alpha $ , $\beta $ are real roots of Q such that $0<\alpha ,\beta <\delta $ and $\alpha +\beta \geq \delta $ . If ${\mathrm {ext}\,}(\alpha ,\beta )=0={\mathrm {ext}\,}(\,\beta ,\alpha )$ , then

$$ \begin{align*}{\mathrm{ext}\,}(\delta,\alpha)=0={\mathrm{ext}\,}(\alpha,\delta)\quad \text{and}\quad {\mathrm{ext}\,}(\delta,\beta)=0={\mathrm{ext}\,}(\,\beta,\delta).\end{align*} $$

Proof. According to Lemma 3.4, $\alpha ,\;\beta $ are a lower arc and an upper arc, respectively. Suppose $\alpha $ is a lower arc. Set

$$ \begin{align*}\mathop{\mathrm{supp}}\nolimits \alpha=\{b_j\}_{j=0}^t \cup \{a_i\}_{i=1}^m \cup \{a_i\}_{i=n}^{s} \quad (0\leq m<n\leq s).\end{align*} $$

It is straightforward to calculate that

$$ \begin{align*} \langle\alpha,\delta\rangle =m+s-n+t+1-(m+1+t+s-n)=0. \end{align*} $$

Applying the fact that $(\alpha ,\delta )=0$ , we get $\langle \delta ,\alpha \rangle =0$ . Let $X_{\alpha }$ be the unique indecomposable module of dimension vector $\alpha $ . Put

$$ \begin{align*} Y_{\delta}=N\oplus\bigoplus_{j=m+2}^{n-1}S_{a_j} \quad\mbox{and}\quad Y_{\delta}^{\prime}=N'\oplus \bigoplus_{j=m+1}^{n-2}S_{a_j} \end{align*} $$

for indecomposable modules $N,N'$ with

$$ \begin{align*}\mathop{\mathrm{supp}}\nolimits \mathbf{dim}\, N=\mathop{\mathrm{supp}}\nolimits \alpha\cup \{a_{m+1}\}\quad\text{and}\quad \mathop{\mathrm{supp}}\nolimits \mathbf{dim}\, N'=\mathop{\mathrm{supp}}\nolimits \alpha\cup \{a_{n-1}\},\end{align*} $$

respectively. It is easy to check that

$$ \begin{align*}{\mathrm{Hom}\,}(X_{\alpha},N)=0\quad \text{and}\quad {\mathrm{Hom}\,}(N',X_{\alpha})=0.\end{align*} $$

Hence, ${\mathrm {Hom}\,}(X_{\alpha },Y_{\delta })=0$ and ${\mathrm {Hom}\,}(Y^{\prime }_{\delta },X_{\alpha })=0$ . It follows that

$$ \begin{align*}\mathrm{dim}\,{\mathrm{Ext}\,}(X_{\alpha},Y_{\delta})=0\;\quad\text{and}\quad \mathrm{dim}\,{\mathrm{Ext}\,}(Y^{\prime}_{\delta},X_{\alpha})=0,\end{align*} $$

which implies that ${\mathrm {ext}\,}(\alpha ,\delta )=0={\mathrm {ext}\,}(\delta ,\alpha ).$ The other case is treated similarly.

Lemma 3.6. Let $\alpha _1=n_1\delta +\gamma _1$ and $\alpha _2=n_2\delta +\gamma _2$ be two dimension vectors, where $\gamma _1,\gamma _2$ are real roots satisfying $0<\gamma _1,\gamma _2<\delta $ , and $\gamma _1+\gamma _2\geq \delta $ . Suppose ${\mathrm {ext}\,}(\alpha _1,\alpha _2)=0={\mathrm {ext}\,}(\alpha _2,\alpha _1)$ . Then ${\mathrm {ext}\,}(\gamma _1,\gamma _2)=0={\mathrm {ext}\,}(\gamma _2,\gamma _1)$ .

Proof. Suppose on the contrary that ${\mathrm {ext}\,}(\gamma _1,\gamma _2)\neq 0$ or ${\mathrm {ext}\,}(\gamma _2,\gamma _1)\neq 0$ .

Case 1: $\gamma _1$ is a dimension vector of an indecomposable preprojective module.

(1) If $\gamma _2$ is a dimension vector of an indecomposable preprojective module, then we have $\gamma _1+\gamma _2\ngeq \delta $ , which is a contradiction.

(2) If $\gamma _2$ is a dimension vector of an indecomposable preinjective module, since there is no nonzero homomorphism from preinjective modules to preprojective modules, it follows that $\langle \gamma _2,\gamma _1\rangle <0$ and, by a direct calculation, $\langle \delta ,\gamma _1\rangle <0$ and $\langle \gamma _2,\delta \rangle <0$ . Therefore, $\langle \alpha _1,\alpha _2\rangle =\langle n_2\delta +\gamma _2,n_1\delta +\gamma _1\rangle =n_2\langle \delta ,\gamma _1\rangle +n_1\langle \gamma _2,\delta \rangle +\langle \gamma _2,\gamma _1\rangle <0$ , which forces ${\mathrm {ext}\,}(\alpha _2,\alpha _1)\neq 0$ , which is a contradiction.

(3) If $\gamma _2$ is a dimension vector of an indecomposable regular module, then we have ${\langle \gamma _2,\gamma _1\rangle <0}$ and $\langle \delta ,\gamma _2\rangle =0=\langle \gamma _2,\delta \rangle <0$ . This implies that

$$ \begin{align*}\langle n_2\delta+\gamma_2,n_1\delta+\gamma_1\rangle=n_2\langle\delta,\gamma_1\rangle+n_1\langle\gamma_2,\delta\rangle+\langle\gamma_2,\gamma_1\rangle<0,\end{align*} $$

so ${\mathrm {ext}\,}(\alpha _2,\alpha _1)\neq 0$ , which is a contradiction.

Case 2. $\gamma _1$ is the dimension vector of an indecomposable preinjective module. This is the case dual to Case 1.

Case 3. $\gamma _1$ , $\gamma _2$ are the dimension vectors of indecomposable regular modules. Since $\gamma _1+\gamma _2>\delta $ , at least one of $\gamma _1, \;\gamma _2$ is a lower arc or an upper arc. Assume that $\gamma _1$ is a lower arc, that is,

$$ \begin{align*}\mathop{\mathrm{supp}}\nolimits\gamma_1=\{b_j\}_{j=0}^t \cup \{a_i\}_{i=0}^m \cup \{a_i\}_{i=n}^s \quad (0\leq m<n\leq s).\end{align*} $$

If $\gamma _2$ is a short arc, we put $\mathop{\mathrm{supp}}\nolimits \gamma _2=\{\alpha _i\}_{i=u}^v\;(0<u<v<s)$ . Thus, $i_m\geq u-1, i_n\geq v-1$ . By Lemma 3.4, there exists $\gamma ^{\prime }_2 \in {\mathbb N}^n$ such that $0<\gamma ^{\prime }_2 <\delta $ and $\gamma ^{\prime }_2 \hookrightarrow \gamma _2$ . Moreover, $\langle \gamma ^{\prime }_2,\gamma _1\rangle <0 $ . Consequently, $n_2\delta +\gamma ^{\prime }_2\hookrightarrow n_2\delta +\gamma _2$ , and

$$ \begin{align*}\langle n_2\delta+\gamma^{\prime}_2,n_1\delta+\gamma_1\rangle=\langle\gamma^{\prime}_2,\gamma_1\rangle<0.\end{align*} $$

This implies that ${\mathrm {ext}\,}(\alpha _2,\alpha _1)>0$ , which is contrary to the hypothesis.

If $\gamma _2$ is a lower arc, put

$$ \begin{align*}\mathop{\mathrm{supp}}\nolimits\gamma_2=\{b_j\}_{j=0}^t \cup \{a_i\}_{i=0}^{m'} \cup \{a_i\}_{i={n}'}^s \quad (0\leq m'<n'\leq s),\end{align*} $$

so $i_m\geq n'-1$ or $m'\geq i_n-1$ .

(1) If $i_m\geq n'-1$ , then by Lemma 3.4, there exists $\gamma ^{\prime }_1\in {\mathbb N}^n$ such that $0<\gamma ^{\prime }_1<\delta $ satisfying $\gamma _1\hookrightarrow \gamma _1$ and $\langle \gamma ^{\prime }_1,\gamma _2\rangle <0 $ . Consequently, $n_1\delta +\gamma ^{\prime }_1\hookrightarrow n_1\delta +\gamma _1$ and

$$ \begin{align*}\langle n_1\delta+\gamma^{\prime}_1,n_2\delta+\gamma_2\rangle=\langle\gamma^{\prime}_1,\gamma_2\rangle<0.\end{align*} $$

Hence, ${\mathrm {ext}\,}(\alpha _1,\alpha _2)>0$ , which is a contradiction.

(2) If $m'\geq i_n-1$ , then by Lemma 3.4 again, there exists $\gamma ^{\prime }_2\in {\mathbb N}^n$ such that $0<\gamma ^{\prime }_2<\delta $ satisfying $\gamma ^{\prime }_2\hookrightarrow \gamma _2$ and $\langle \gamma _2,\gamma _1\rangle <0 $ . Thus we obtain $n_2\delta +\gamma ^{\prime }_2\hookrightarrow n_2\delta +\gamma _2$ and

$$ \begin{align*}\langle n_2\delta+\gamma^{\prime}_2,n_1\delta+\gamma_1\rangle=\langle\gamma^{\prime}_2,\gamma_1\rangle<0.\end{align*} $$

Hence, ${\mathrm {ext}\,}(\alpha _2,\alpha _1)>0$ , which is a contradiction.

If $\gamma _2$ is an upper arc, it follows from Lemma 3.4 that

$$ \begin{align*}{\mathrm{ext}\,}(\alpha_1,\alpha_2)=0={\mathrm{ext}\,}(\alpha_2,\alpha_1). \end{align*} $$

This is a contradiction. We deal with the case where $\gamma _1$ is an upper arc by a similar argument. In conclusion, we have ${\mathrm {ext}\,}(\gamma _1,\gamma _2)=0={\mathrm {ext}\,}(\gamma _2,\gamma _1),$ as desired.

Lemma 3.7. Suppose that $\alpha =n\delta +\gamma $ is the dimension vector of an indecomposable preprojective or preinjective module, where $\gamma $ is a real root satisfying $0<\gamma <\delta $ . Then ${\mathrm {ext}\,}(\delta ,\alpha )>0$ or ${\mathrm {ext}\,}(\alpha ,\delta )>0$ , respectively.

Proof. Since $\alpha $ is the dimension vector of an indecomposable preprojective module, $\alpha $ is a right arc and so $\gamma $ is a right arc. Assume that $\mathop{\mathrm{supp}}\nolimits \gamma =\{a_i\}_{i=i_0}^s \cup \{b_j\}_{j=j_0}^t\; \text {for} \;1\leq i_0\leq s \;\text {and}\;1\leq j_0\leq t.$ Therefore,

$$ \begin{align*}\langle\delta,\alpha\rangle=\langle\delta,\gamma\rangle=s-i_0+1+t-j_0-(s-i_0+1+t-j_0+1)=-1,\end{align*} $$

which implies ${\mathrm {ext}\,}(\delta ,\alpha )>0$ . The case for an indecomposable preinjective module is handled similarly. This completes the proof.

Proposition 3.8. Let $\alpha =\underbrace {\delta +\cdots +\delta }_{m}+\,\alpha _1+\cdots +\alpha _l$ be the canonical decomposition of a dimension vector $\alpha $ of Q. Let $\alpha _i=n_i\delta +\gamma _i$ with $0<\gamma _i<\delta $ for each i. Denote by $s_1,s_2$ the number of lower arcs and upper arcs, respectively, in the decomposition. Then

$$ \begin{align*}\gamma_1+\gamma_2+\cdots+\gamma_l\not \geq (\min\{s_1,s_2\}+1)\delta.\end{align*} $$

Proof. We may assume that $s_1\geq s_2$ .

Case 1: $s_1=0$ . If $m>0$ , by Theorem 2.4 and Lemma 3.7, each $\alpha _i$ is the dimension vector of a regular module. Then all $\gamma _i$ are short arcs. Clearly, $\gamma _1+\gamma _2+\cdots +\gamma _l\not \geq \delta .$ If $m=0$ , then assume that $\gamma _1,\ldots ,\gamma _{t_1}$ are right arcs, $\gamma _{t_1+1},\ldots ,\gamma _{t_1+t_2}$ are left arcs and $\gamma _{t_1+t_2+1},\ldots \gamma _{t_1+t_2+t_3}$ are short arcs. Note that $l=t_1+t_2+t_3$ . First we claim that $\gamma _1+\cdots +\gamma _{t_1+t_2}\not \geq \delta $ . Otherwise, there exist $\gamma _f \;(1\leq f\leq t_1)$ and $\gamma _g \;(t_1< g\leq t_1+t_2)$ with

$$ \begin{align*} \mathop{\mathrm{supp}}\nolimits\gamma_f&= \{a_i\}_{i=i_0}^s \cup \{b_j\}_{j=j_0}^t \quad (1\leq i_0\leq s,1\leq j_0\leq t)\\ \mathop{\mathrm{supp}}\nolimits\gamma_g&=\{a_i\}_{i=0}^{s_0} \cup \{b_j\}_{j=0}^{t_0} \quad (0\leq s_0\leq s-1,1\leq t_0\leq t-1) \end{align*} $$

satisfying $s_0\geq i_0-1$ . Thus, $\langle \gamma _g,\gamma _f\rangle <0$ . By Lemma 3.6, ${\mathrm {ext}\,}(\alpha _g,\alpha _f)>0$ , which is a contradiction. Further, we claim that $\gamma _1+\cdots +\gamma _l\not \geq \delta $ . Suppose on the contrary that $\gamma _1+\cdots +\gamma _{t_1+t_2}\not \geq \delta $ and $\gamma _1+\cdots +\gamma _l\geq \delta $ . Then there exist roots $\gamma _f \; (1\leq f\leq t_1)$ and $\gamma _h \;(t_1+t_2< h\leq ~l)$ with

$$ \begin{align*} \mathop{\mathrm{supp}}\nolimits \gamma_f&= \{a_i\}_{i=i_0}^s \cup \{b_j\}_{j=j_0}^t \quad (1\leq i_0\leq s,1\leq j_0\leq t),\\ \mathop{\mathrm{supp}}\nolimits\gamma_h&=\{a_i\}_{i=u}^{v} \quad (0<u<v<s), \end{align*} $$

for $v\geq i_0-1$ . Hence, $\langle \gamma _h,\gamma _f\rangle <0$ . Again by Lemma 3.6, ${\mathrm {ext}\,}(\alpha _h,\alpha _f)>0$ , which is a contradiction.

Case 2: $s_1\neq 0$ . Assume that $\gamma _1,\gamma _2,\ldots ,\gamma _{s_1}$ are all lower arcs and $\gamma _{s_1+1},\ldots ,\gamma _{s_1+s_2}$ are upper arcs (the case $s_2=0$ is included). We claim that $\gamma _1+\gamma _2+\cdots +\gamma _{s_1+s_2}\not \geq (\min \{s_1,s_2\}+1)\delta .$ Otherwise, there exist $\gamma _c,\gamma _d$ such that $\gamma _c+\gamma _d>\delta $ for $1\leq c,d\leq s_1+s_2$ . By Lemmas 3.4 and 3.7, ${\mathrm {ext}\,}(\alpha _c,\alpha _d)>0$ or ${\mathrm {ext}\,}(\alpha _d,\alpha _c)>0$ . This leads to a contradiction. Further, we claim that $\gamma _1+\gamma _2+\cdots +\gamma _l\not \geq (\min \{s_1,s_2\}+1)\delta .$ Suppose on the contrary that $\gamma _1+\gamma _2+\cdots +\gamma _l\geq (\min \{s_1,s_2\}+1)\delta .$ Then there exist $\gamma _c, \gamma _e$ for some $1\leq c \leq s_1$ and $s_1+s_2<e\leq l$ such that

$$ \begin{align*} \mathop{\mathrm{supp}}\nolimits \gamma_c&=\{b_j\}_{j=0}^t \cup \{a_i\}_{i=0}^{i_m} \cup \{a_i\}_{i=i_n}^s \quad (0\leq i_m<i_n\leq s),\\ \mathop{\mathrm{supp}}\nolimits \gamma_e&=\{a_i\}_{i=u}^v \quad (0<u<v<s), \end{align*} $$

for $v\geq i_n-1$ . Let $0<\gamma ^{\prime }_e<\delta $ and $\mathop{\mathrm{supp}}\nolimits \gamma ^{\prime }_e=\{a_i\}_{i=i_n-1}^v$ . Thus, $\gamma ^{\prime }_e\hookrightarrow \gamma _e$ and

$$ \begin{align*}\langle\gamma^{\prime}_e,\gamma_c\rangle=v-i_n+1-(v-(i_n-1)+1)=-1<0,\end{align*} $$

which implies ${\mathrm {ext}\,}(\gamma _e,\gamma _c)>0$ . By Lemma 3.6, ${\mathrm {ext}\,}(\alpha _{e},\alpha _{c})>0$ , which is a contradiction.

For the rest of this section, let ${\mathbb F}={\mathbb F}_q$ be the finite field with q elements. Let $M_Q(\alpha ,q)$ be the number of isoclasses of representations of a quiver Q over ${\mathbb F}$ with a fixed dimension vector $\alpha $ .

Lemma 3.9 [2]

Suppose that Q is a tame quiver and $\alpha =n_0\delta +\gamma $ is the dimension vector of Q for some $\gamma \geq 0$ and $\gamma \not \geq \delta $ . Then $\deg (M_{Q}(\alpha ,q))=n_0$ .

There is no general formula for the canonical decomposition of a fixed dimension vector of Q. To address the issue, we follow Schofield’s inductive algorithm [11], as in our previous paper [2].

Theorem 3.10. Assume that $\alpha =\underbrace {\delta +\cdots +\delta }_{m}+\,\alpha _1+\cdots +\alpha _l$ is the canonical decomposition of a dimension vector $\alpha $ of Q, where $\alpha _i \;(i=1,2,\ldots ,l)$ are all real Schur roots. Then

$$ \begin{align*}\lim_{q\rightarrow\infty}\frac{M_Q(\alpha,q)} {(M_Q(\delta,q))^{m}q^x\prod_{i=1}^l M_Q(\alpha_i,q)} =\text{constant},\end{align*} $$

where $s_1,\;s_2$ are the numbers of lower arcs and upper arcs, respectively, and $x=\min \{s_1,s_2\}$ .

Proof. Since Q is a quiver of type $\tilde {A}_n$ and $\alpha _i \;(i=1,2,\ldots ,l)$ are all real roots, it follows that $\alpha _i=n_i\delta +\gamma _i $ , where $\gamma _i $ are all real roots and $0<\gamma _i<\delta $ for $i\in \{1,\ldots ,l\}$ . Now assume that $s_1\geq s_2$ . (The case for $s_2\geq s_1$ can be handled similarly.) By Proposition 3.8,

$$ \begin{align*}\gamma_1+\gamma_2+\cdots+\gamma_l\not \geq (\min\{s_1,s_2\}+1)\delta.\end{align*} $$

Again by Lemma 3.9,

$$ \begin{align*}\deg (M_{Q}(\alpha_i,q))=n_i\quad\text{and}\quad\deg (M_{Q}(\alpha,q))=m+n_1+n_2+\cdots +n_l+\min\{s_1,s_2\}.\end{align*} $$

Therefore, $\deg (M_Q(\alpha ,q))\kern1.3pt{=}\kern1.3pt \sum _{i=1}^l \deg (M_Q(\alpha _i,q))\kern1.3pt{+}\kern1.3pt m\kern1.3pt{+}\kern1.3pt x.$ This completes the proof.

Example 3.11. As an illustration, we consider Example 3.10 in [2]. Let Q be the quiver of type $\tilde {A}_2$ :

Then the canonical decomposition of $\alpha =(2,3,3)$ is $\alpha =(0,1,0)+(2,2,3)=\alpha _1+\alpha _2$ . An elementary calculation yields

$$ \begin{align*}M_{Q}(\alpha,q)=2q^2+16q+72, \quad M_{Q}(\alpha_1,q)=1, \quad M_{Q}(\alpha_2,q)=q^2+9q+44.\end{align*} $$

Thus,

$$ \begin{align*}\lim_{q\rightarrow\infty}\frac{M_Q(\alpha,q)} {(M_Q(\alpha_1,q))M_Q(\alpha_2,q)} =2,\end{align*} $$

which is consistent with the main theorem.