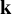1 Introduction
Inspired by persistence theory from topological data analysis (TDA) [Reference Oudot36, Reference Dey and Wang21], Kashiwara and Schapira have recently introduced the convolution distance between (derived) sheaves of
![]() $\mathbf {k}$
-vector spaces on a finite-dimensional real normed vector space [Reference Kashiwara and Schapira27]. This construction has found important applications, both in TDA – where it allows expressing stability of certain constructions with respect to noise in datasets – [Reference Berkouk and Ginot6, Reference Berkouk, Ginot and Oudot9, Reference Berkouk and Petit7, Reference Berkouk and Petit8] and in symplectic topology [Reference Asano and Ike2, Reference Asano and Ike3, Reference Guillermou and Viterbo23]. A challenging research direction, of interest to these two fields, is to associate numerical invariants to a sheaf on a vector space, which satisfy a certain form of continuity with respect to the convolution distance.
$\mathbf {k}$
-vector spaces on a finite-dimensional real normed vector space [Reference Kashiwara and Schapira27]. This construction has found important applications, both in TDA – where it allows expressing stability of certain constructions with respect to noise in datasets – [Reference Berkouk and Ginot6, Reference Berkouk, Ginot and Oudot9, Reference Berkouk and Petit7, Reference Berkouk and Petit8] and in symplectic topology [Reference Asano and Ike2, Reference Asano and Ike3, Reference Guillermou and Viterbo23]. A challenging research direction, of interest to these two fields, is to associate numerical invariants to a sheaf on a vector space, which satisfy a certain form of continuity with respect to the convolution distance.
To do so, the TDA community has been mostly using module-theoretic notions, such as the rank-invariant [Reference Carlsson and Zomorodian15, Reference Cerri, Di Fabio, Ferri, Frosini and Landi16], the Hilbert function or the graded Betti numbers [Reference Harrington, Otter, Schenck and Tillmann24, Reference Berkouk, Nielsen and Barbaresco5, Reference Oudot and Scoccola35, Reference Lesnick and Wright31]. From a sheaf-theoretic perspective, a natural numerical invariant to consider is the local Euler characteristic. It is a constructible function that exactly encodes the class of a sheaf in the Grothendieck group by a result of Kashiwara [Reference Kashiwara26]. This is usually called the sheaf-function correspondence.
The group of constructible functions is well understood and has the surprisingly nice property that the formalism of Grothendieck’s six operations descend to it through the sheaf-function correspondence [Reference Schapira39]. In particular, this allows one to introduce well-behaved transforms of constructible functions, such as the Radon or hybrid transforms [Reference Schapira, Cohen, Giusti and Mora38, Reference Baryshnikov and Ghrist4, Reference Lebovici29, Reference Kirveslahti and Mukherjee28]. Constructible functions have already been successfully applied in several domains, such as target enumeration for sensor networks, image and shape analysis [Reference Baryshnikov and Ghrist4, Reference Curry, Mukherjee and Turner20], though the question of their stability with respect to noise in the input data remains poorly understood [Reference Curry, Ghrist and Robinson19, Chapter 16]. For instance, in the context of predicting clinical outcomes in glioblastoma [Reference Crawford, Monod, Chen, Mukherjee and Rabadán18], the authors overcome numerical instability by introducing an ad-hoc smoothed version of the Euler characteristic transform (ECT) [Reference Curry, Mukherjee and Turner20], that is empirically more stable than the standard ECT, though no theoretical stability result is provided.
In this context, a natural question is to understand the stability of the sheaf-function correspondence. The convolution distance is already considered as a meaningful measurement of dissimilarity between sheaves, both in applied and pure contexts. Therefore, we propose in this work to characterize the pseudo-extended metrics on the group of constructible functions on a vector space, which are controlled in an appropriate sense by the convolution distance through the sheaf-function correspondence. Our main result (Theorem 3.11) asserts that these pseudo-metrics are almost trivial: They vanish as soon as two constructible functions have the same Euler integral.
Thanks to results by the author and F. Petit [Reference Berkouk and Petit7], we are able to transfer Theorem 3.11 in the context of persistence modules. In particular, we obtain that every
![]() $\mathrm {K}_0$
-additive invariants of compactly generated constructible persistence modules that are continuous for the interleaving distance is trivial (Theorems 4.14 and 4.15). Formulation in terms of persistence modules allows using Lesnick’s theorem on the universality of the interleaving distance [Reference Lesnick30] and to obtain that
$\mathrm {K}_0$
-additive invariants of compactly generated constructible persistence modules that are continuous for the interleaving distance is trivial (Theorems 4.14 and 4.15). Formulation in terms of persistence modules allows using Lesnick’s theorem on the universality of the interleaving distance [Reference Lesnick30] and to obtain that
![]() $\mathrm {K}_0$
-additive invariants of sublevel sets persistence modules cannot be controlled in terms of
$\mathrm {K}_0$
-additive invariants of sublevel sets persistence modules cannot be controlled in terms of
![]() $d_\infty $
distance (Corollary 4.18).
$d_\infty $
distance (Corollary 4.18).
In the final section of the paper, we provide several applications of our results to commonly used TDA constructions.
We acknowledge that similar results to Theorem 4.15 have been obtained independently by Biran, Cornea and Zhang in [Reference Biran, Cornea and Zhang10], in the specific case of
![]() $d=1$
, with the aim to study
$d=1$
, with the aim to study
![]() $\mathrm {K}_0$
-theoretical invariants of triangulated persistence categories.
$\mathrm {K}_0$
-theoretical invariants of triangulated persistence categories.
2 Sheaves and constructible functions
In this section, we introduce the necessary background and terminology on constructible sheaves and constructible functions.
2.1 Sheaf-function correspondence
Throughout this paper,
![]() $\mathbf {k}$
denotes a field. For a topological space X, we denote by
$\mathbf {k}$
denotes a field. For a topological space X, we denote by
![]() $\mathrm {Mod}(\mathbf {k}_X)$
the category of sheaves of
$\mathrm {Mod}(\mathbf {k}_X)$
the category of sheaves of
![]() $\mathbf {k}$
-vector spaces on X, and
$\mathbf {k}$
-vector spaces on X, and
![]() $\mathrm {D}^b(\mathbf {k}_X)$
its bounded derived category. Let M be a real analytic manifold. The definitions and results of this section are exposed in detail in [Reference Kashiwara, Schapira and Houzel25, Chapters 8 & 9.7].
$\mathrm {D}^b(\mathbf {k}_X)$
its bounded derived category. Let M be a real analytic manifold. The definitions and results of this section are exposed in detail in [Reference Kashiwara, Schapira and Houzel25, Chapters 8 & 9.7].
Definition 2.1. A sheaf
![]() $F \in \mathrm {Mod}(\mathbf {k}_M)$
is
$F \in \mathrm {Mod}(\mathbf {k}_M)$
is
![]() $\mathbb {R}$
-constructible (or constructible for simplicity), if there exists a locally finite covering of M by subanalytic subsets
$\mathbb {R}$
-constructible (or constructible for simplicity), if there exists a locally finite covering of M by subanalytic subsets
![]() $M = \cup _{\lambda } M_{\lambda }$
such that for all
$M = \cup _{\lambda } M_{\lambda }$
such that for all
![]() $M_{\lambda }$
and all
$M_{\lambda }$
and all
![]() $j\in \mathbb {Z}$
, the restriction
$j\in \mathbb {Z}$
, the restriction
![]() $F_{|M_{\lambda }}$
is locally constant and of finite rank.
$F_{|M_{\lambda }}$
is locally constant and of finite rank.
We denote by
![]() $\mathrm {Mod}_{\mathbb {R} c}(\mathbf {k}_M)$
the full subcategory of
$\mathrm {Mod}_{\mathbb {R} c}(\mathbf {k}_M)$
the full subcategory of
![]() $\mathrm {Mod}(\mathbf {k}_M)$
consisting of constructible sheaves and by
$\mathrm {Mod}(\mathbf {k}_M)$
consisting of constructible sheaves and by
![]() $\mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_M)$
the full subcategory of
$\mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_M)$
the full subcategory of
![]() $\mathrm {D}^b(\mathbf {k}_M)$
whose objects are sheaves
$\mathrm {D}^b(\mathbf {k}_M)$
whose objects are sheaves
![]() $F \in \mathrm {D}^b(\mathbf {k}_M)$
such that
$F \in \mathrm {D}^b(\mathbf {k}_M)$
such that
![]() $\mathrm {H}^j(F) \in \mathrm {Mod}_{\mathbb {R} c}(\mathbf {k}_M)$
for all
$\mathrm {H}^j(F) \in \mathrm {Mod}_{\mathbb {R} c}(\mathbf {k}_M)$
for all
![]() $j\in \mathbb {Z}$
. It is well known [Reference Kashiwara, Schapira and Houzel25, Th. 8.4.5] that the functor
$j\in \mathbb {Z}$
. It is well known [Reference Kashiwara, Schapira and Houzel25, Th. 8.4.5] that the functor
![]() $ \mathrm {D}^b(\mathrm {Mod}_{\mathbb {R} c}(\mathbf {k}_M))\longrightarrow \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_M) $
is an equivalence. The objects of
$ \mathrm {D}^b(\mathrm {Mod}_{\mathbb {R} c}(\mathbf {k}_M))\longrightarrow \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_M) $
is an equivalence. The objects of
![]() $\mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_M)$
are still called constructible sheaves.
$\mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_M)$
are still called constructible sheaves.
Definition 2.2. A constructible function on M is a map
![]() $\varphi : M \longrightarrow \mathbb {Z}$
such that the fibers
$\varphi : M \longrightarrow \mathbb {Z}$
such that the fibers
![]() $\varphi ^{-1}(m)$
are subanalytic subsets, and the family
$\varphi ^{-1}(m)$
are subanalytic subsets, and the family
![]() $\{\varphi ^{-1}(m)\}_{m \in \mathbb {Z}}$
is locally finite in M.
$\{\varphi ^{-1}(m)\}_{m \in \mathbb {Z}}$
is locally finite in M.
We denote by
![]() $\mathrm {CF}(M)$
the group of constructible functions on M. All the remaining results of this section are contained in [Reference Kashiwara, Schapira and Houzel25, Chapter 9.7].
$\mathrm {CF}(M)$
the group of constructible functions on M. All the remaining results of this section are contained in [Reference Kashiwara, Schapira and Houzel25, Chapter 9.7].
Theorem 2.3. Let
![]() $\varphi \in \mathrm {CF}(M)$
. There exists a locally finite family of compact contractible subanalytic subsets
$\varphi \in \mathrm {CF}(M)$
. There exists a locally finite family of compact contractible subanalytic subsets
![]() $\{X_{\lambda }\}$
such that
$\{X_{\lambda }\}$
such that
![]() $\varphi = \sum _{\lambda } C_{\lambda } \cdot 1_{X_{\lambda }}$
, with
$\varphi = \sum _{\lambda } C_{\lambda } \cdot 1_{X_{\lambda }}$
, with
![]() $C_{\lambda } \in \mathbb {Z}$
.
$C_{\lambda } \in \mathbb {Z}$
.
Proposition 2.4. Let
![]() $\varphi \in \mathrm {CF}(M)$
with compact support. For any finite sum decomposition
$\varphi \in \mathrm {CF}(M)$
with compact support. For any finite sum decomposition
![]() $\varphi =\sum _{\lambda } C_{\lambda } \cdot 1_{X_{\lambda }} $
, where the
$\varphi =\sum _{\lambda } C_{\lambda } \cdot 1_{X_{\lambda }} $
, where the
![]() $X_{\lambda }$
’s are subanalytic compact and contractible, the quantity
$X_{\lambda }$
’s are subanalytic compact and contractible, the quantity
![]() $\sum _{\lambda } C_{\lambda }$
only depends on
$\sum _{\lambda } C_{\lambda }$
only depends on
![]() $\varphi $
.
$\varphi $
.
Definition 2.5. With the above notations, one defines
![]() $\int \varphi ~\mathrm {d} \chi := \sum _{\lambda } C_{\lambda }$
.
$\int \varphi ~\mathrm {d} \chi := \sum _{\lambda } C_{\lambda }$
.
To any constructible sheaf
![]() $F \in \mathrm {D}^b_{\mathbb {R} c }(\mathbf {k}_M)$
, it is possible to associate a constructible function
$F \in \mathrm {D}^b_{\mathbb {R} c }(\mathbf {k}_M)$
, it is possible to associate a constructible function
![]() $\chi (F) \in \mathrm {CF}(M)$
, called the local Euler characteristic of F, and defined by:
$\chi (F) \in \mathrm {CF}(M)$
, called the local Euler characteristic of F, and defined by:
It is clear that for any distinguished triangle
![]() $F' \longrightarrow F \longrightarrow F" \stackrel {+1}{\longrightarrow }$
in
$F' \longrightarrow F \longrightarrow F" \stackrel {+1}{\longrightarrow }$
in
![]() $\mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_M)$
, one has
$\mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_M)$
, one has
![]() $\chi (F) = \chi (F') + \chi (F")$
. Therefore,
$\chi (F) = \chi (F') + \chi (F")$
. Therefore,
![]() $\chi $
factorizes through the Grothendieck group
$\chi $
factorizes through the Grothendieck group
![]() $\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_M))$
and there is a well-defined morphism of groups
$\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_M))$
and there is a well-defined morphism of groups
![]() $\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_M)) \longrightarrow \mathrm {CF}(M)$
mapping
$\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_M)) \longrightarrow \mathrm {CF}(M)$
mapping
![]() $[F]$
to
$[F]$
to
![]() $\chi (F)$
.
$\chi (F)$
.
Theorem 2.6 (Sheaf-function correspondence).
The morphism
![]() $\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_M)) \longrightarrow \mathrm {CF}(M)$
is an isomorphism of groups.
$\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_M)) \longrightarrow \mathrm {CF}(M)$
is an isomorphism of groups.
Remark 2.7. The proof of the above theorem in [Reference Kashiwara, Schapira and Houzel25, Theorem 9.7.1] does not make use of the characteristic
![]() $0$
hypothesis stated at the beginning of [Reference Kashiwara, Schapira and Houzel25, Chapter 9] for expository convenience and therefore extends to any field.
$0$
hypothesis stated at the beginning of [Reference Kashiwara, Schapira and Houzel25, Chapter 9] for expository convenience and therefore extends to any field.
Lemma 2.8. Let
![]() $F \in \mathrm {D}^b_{\mathbb {R} c }(\mathbf {k}_M)$
with compact support, then
$F \in \mathrm {D}^b_{\mathbb {R} c }(\mathbf {k}_M)$
with compact support, then
 $$\begin{align*}\int \chi(F) ~\mathrm{d} \chi = \chi\left(\mathrm{R} \Gamma(M; F)\right) = \sum_{i\in \mathbb{Z}}(-1)^i \mathrm{dim}_{\mathbf{k}} \left(\mathrm{H}^i(M;F)\right). \end{align*}$$
$$\begin{align*}\int \chi(F) ~\mathrm{d} \chi = \chi\left(\mathrm{R} \Gamma(M; F)\right) = \sum_{i\in \mathbb{Z}}(-1)^i \mathrm{dim}_{\mathbf{k}} \left(\mathrm{H}^i(M;F)\right). \end{align*}$$
We briefly review the construction of the direct image operation for constructible functions. Let
![]() $f : X \longrightarrow Y$
be a morphism of real analytic manifolds and
$f : X \longrightarrow Y$
be a morphism of real analytic manifolds and
![]() $\varphi \in \mathrm {CF}(X)$
such that f is proper on
$\varphi \in \mathrm {CF}(X)$
such that f is proper on
![]() $\mathrm {supp}(\varphi )$
. Then, for each
$\mathrm {supp}(\varphi )$
. Then, for each
![]() $y\in Y$
,
$y\in Y$
,
![]() $\varphi \cdot 1_{f^{-1}(y)}$
is constructible and has compact support.
$\varphi \cdot 1_{f^{-1}(y)}$
is constructible and has compact support.
Definition 2.9. Keeping the above notations, one defines the function
![]() $f_\ast \varphi : Y \longrightarrow \mathbb {Z}$
by
$f_\ast \varphi : Y \longrightarrow \mathbb {Z}$
by
Remark 2.10. With
![]() $f = a_X : X \longrightarrow \{pt\}$
, one has
$f = a_X : X \longrightarrow \{pt\}$
, one has
![]() $a_{X\ast } \varphi = (\int \varphi ~\mathrm {d} \chi ) \cdot 1_{\{pt\}} $
.
$a_{X\ast } \varphi = (\int \varphi ~\mathrm {d} \chi ) \cdot 1_{\{pt\}} $
.
Theorem 2.11. Let
![]() $\varphi \in \mathrm {CF}(X)$
and
$\varphi \in \mathrm {CF}(X)$
and
![]() $f : X \longrightarrow Y$
be a morphism of real analytic manifolds such that f is proper on
$f : X \longrightarrow Y$
be a morphism of real analytic manifolds such that f is proper on
![]() $\mathrm {supp}(\varphi )$
.
$\mathrm {supp}(\varphi )$
.
-
1. The function
 $f_\ast \varphi $
is constructible on Y.
$f_\ast \varphi $
is constructible on Y. -
2. Let
 $F \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_X)$
such that
$F \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_X)$
such that
 $\chi (F) = \varphi $
. Then
$\chi (F) = \varphi $
. Then
 $\chi (\mathrm {R} f_\ast F) = f_\ast \chi (F) = f_\ast \varphi .$
$\chi (\mathrm {R} f_\ast F) = f_\ast \chi (F) = f_\ast \varphi .$
-
3. Let
 $g : Y \longrightarrow Z$
be another morphism of real analytic manifold such that
$g : Y \longrightarrow Z$
be another morphism of real analytic manifold such that
 $g \circ f$
is proper on
$g \circ f$
is proper on
 $\mathrm {supp} (g \circ f)$
. Then
$\mathrm {supp} (g \circ f)$
. Then  $$\begin{align*}(g \circ f)_\ast \varphi = g_\ast (f_\ast \varphi).\end{align*}$$
$$\begin{align*}(g \circ f)_\ast \varphi = g_\ast (f_\ast \varphi).\end{align*}$$
2.2 Convolution distance
We consider a finite-dimensional real vector space
![]() $\mathbb {V}$
endowed with a norm
$\mathbb {V}$
endowed with a norm
![]() $\|\cdot \|$
. We equip
$\|\cdot \|$
. We equip
![]() $\mathbb {V}$
with the usual topology. Following [Reference Kashiwara and Schapira27], we briefly present the convolution distance, which is inspired from the interleaving distance between persistence modules [Reference Chazal, Cohen-Steiner, Glisse, Guibas and Oudot17]. We introduce the following notations:
$\mathbb {V}$
with the usual topology. Following [Reference Kashiwara and Schapira27], we briefly present the convolution distance, which is inspired from the interleaving distance between persistence modules [Reference Chazal, Cohen-Steiner, Glisse, Guibas and Oudot17]. We introduce the following notations:
The convolution bifunctor
![]() $- \star - \colon \mathrm {D}^b(\mathbf {k}_{\mathbb {V}})\times \mathrm {D}^b(\mathbf {k}_{\mathbb {V}}) \longrightarrow \mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
is defined as follows. For
$- \star - \colon \mathrm {D}^b(\mathbf {k}_{\mathbb {V}})\times \mathrm {D}^b(\mathbf {k}_{\mathbb {V}}) \longrightarrow \mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
is defined as follows. For
![]() $F, \; G \in \mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
, we set
$F, \; G \in \mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
, we set
For
![]() $r \geq 0$
and
$r \geq 0$
and
![]() $x\in \mathbb {V}$
, let
$x\in \mathbb {V}$
, let
![]() $B(x,r) = \{v \in \mathbb {V} \mid \|x-v\| \leq r\}$
. For
$B(x,r) = \{v \in \mathbb {V} \mid \|x-v\| \leq r\}$
. For
![]() $\varepsilon \in \mathbb {R}$
, we set
$\varepsilon \in \mathbb {R}$
, we set
 $$\begin{align*}K_{\varepsilon} := \begin{cases} \mathbf{k}_{B(0,\varepsilon)} \mathrm{~~if~~} \varepsilon \geq 0, \\ \mathbf{k}_{\mathrm{Int}(B(0,-\varepsilon))}[\mathrm{dim}(\mathbb{V})] \mathrm{~~if~~} \varepsilon < 0 \end{cases} \in \mathrm{D}^b(\mathbf{k}_{\mathbb{V}}).\end{align*}$$
$$\begin{align*}K_{\varepsilon} := \begin{cases} \mathbf{k}_{B(0,\varepsilon)} \mathrm{~~if~~} \varepsilon \geq 0, \\ \mathbf{k}_{\mathrm{Int}(B(0,-\varepsilon))}[\mathrm{dim}(\mathbb{V})] \mathrm{~~if~~} \varepsilon < 0 \end{cases} \in \mathrm{D}^b(\mathbf{k}_{\mathbb{V}}).\end{align*}$$
The following proposition is proved in [Reference Kashiwara and Schapira27].
Proposition 2.12. Let
![]() $\varepsilon , \varepsilon '\in \mathbb {R}$
and
$\varepsilon , \varepsilon '\in \mathbb {R}$
and
![]() $F \in \mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
. There are isomorphisms, functorial in F:
$F \in \mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
. There are isomorphisms, functorial in F:
If
![]() $\varepsilon \geq \varepsilon ' \geq 0 $
, there is a canonical morphism
$\varepsilon \geq \varepsilon ' \geq 0 $
, there is a canonical morphism
![]() $\chi _{\varepsilon , \varepsilon '} \colon K_{\varepsilon }\longrightarrow K_{\varepsilon '}$
in
$\chi _{\varepsilon , \varepsilon '} \colon K_{\varepsilon }\longrightarrow K_{\varepsilon '}$
in
![]() $\mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
. It induces a canonical morphism
$\mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
. It induces a canonical morphism
![]() $\chi _{\varepsilon , \varepsilon '} \star F \colon K_{\varepsilon } \star F \longrightarrow K_{\varepsilon '} \star F $
. In particular when
$\chi _{\varepsilon , \varepsilon '} \star F \colon K_{\varepsilon } \star F \longrightarrow K_{\varepsilon '} \star F $
. In particular when
![]() $\varepsilon ' = 0$
, we get
$\varepsilon ' = 0$
, we get
Following [Reference Kashiwara and Schapira27], we recall the notion of
![]() $\varepsilon $
-isomorphic sheaves.
$\varepsilon $
-isomorphic sheaves.
Definition 2.13. Let
![]() $F,G \in \mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
, and let
$F,G \in \mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
, and let
![]() $\varepsilon \geq 0$
. The sheaves F and G are
$\varepsilon \geq 0$
. The sheaves F and G are
![]() $\varepsilon $
-isomorphic if there are morphisms
$\varepsilon $
-isomorphic if there are morphisms
![]() $f : K_{\varepsilon } \star F \longrightarrow G$
and
$f : K_{\varepsilon } \star F \longrightarrow G$
and
![]() $g : K_{\varepsilon } \star G \longrightarrow F$
such that the diagrams
$g : K_{\varepsilon } \star G \longrightarrow F$
such that the diagrams

are commutative. The pair of morphisms
![]() $(f,g)$
is called a pair of
$(f,g)$
is called a pair of
![]() $\varepsilon $
-isomorphisms.
$\varepsilon $
-isomorphisms.
Definition 2.14. For
![]() $F,G \in \mathrm {D}^b(\mathbf {k}_{\mathbb {V}}) $
, their convolution distance is
$F,G \in \mathrm {D}^b(\mathbf {k}_{\mathbb {V}}) $
, their convolution distance is
Definition 2.15. A pseudo-extended metric on a set X is a map
![]() $\delta : X \times X \longrightarrow \mathbb {R}_{\geq 0}\cup \{+\infty \}$
satisfying for all
$\delta : X \times X \longrightarrow \mathbb {R}_{\geq 0}\cup \{+\infty \}$
satisfying for all
![]() $x,y,z \in X$
:
$x,y,z \in X$
:
![]() $\delta (x,y) \leq \delta (x,z) + \delta (z,y)$
.
$\delta (x,y) \leq \delta (x,z) + \delta (z,y)$
.
It is proved in [Reference Kashiwara and Schapira27] that the convolution is, indeed, a pseudo-extended metric, that is, it satisfies the triangular inequality. Having isomorphic global sections is a necessary condition for two sheaves to be at finite convolution distance, as expressed in the following proposition, which can be found as [Reference Kashiwara and Schapira27, Remark 2.5 (i)].
Proposition 2.16. Let
![]() $F,G \in \mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
such that
$F,G \in \mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
such that
![]() $d_C(F,G) < +\infty $
. Then
$d_C(F,G) < +\infty $
. Then
Moreover, it satisfies the following important stability property.
Theorem 2.17. Let
![]() $u,v : X \longrightarrow \mathbb {V}$
be continuous maps, and let
$u,v : X \longrightarrow \mathbb {V}$
be continuous maps, and let
![]() $F \in \mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
. Then,
$F \in \mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
. Then,
We will often make use of the following result, that we call the additivity of interleavings, which is a direct consequence of the additivity of the convolution functor.
Proposition 2.18 (Additivity of interleavings).
Let
![]() $(F_i)_{i \in I}$
and
$(F_i)_{i \in I}$
and
![]() $(G_j)_{j\in J}$
be two finite families of
$(G_j)_{j\in J}$
be two finite families of
![]() $\mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
. For all
$\mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
. For all
![]() $I' \subseteq I$
and
$I' \subseteq I$
and
![]() $J' \subseteq J$
of the same cardinality (eventually empty) and for all bijections
$J' \subseteq J$
of the same cardinality (eventually empty) and for all bijections
![]() $\sigma : I' \longrightarrow J'$
, one has
$\sigma : I' \longrightarrow J'$
, one has
 $$\begin{align*}d_C(\oplus_{i\in i} F_i, \oplus_{j\in J} G_j) \leq \max \left ( \max_{i \in I'} d_C(F_i, G_{\sigma(i)}), \max_{i\in I\backslash I'}d_C(F_i,0), \max_{j\in J\backslash J'}d_C(G_j,0)) \right).\end{align*}$$
$$\begin{align*}d_C(\oplus_{i\in i} F_i, \oplus_{j\in J} G_j) \leq \max \left ( \max_{i \in I'} d_C(F_i, G_{\sigma(i)}), \max_{i\in I\backslash I'}d_C(F_i,0), \max_{j\in J\backslash J'}d_C(G_j,0)) \right).\end{align*}$$
Proof. Let
![]() $I' \subseteq I$
and
$I' \subseteq I$
and
![]() $J' \subseteq J$
of the same cardinality (eventually empty), and
$J' \subseteq J$
of the same cardinality (eventually empty), and
![]() $\sigma : I' \longrightarrow J'$
a bijection. We set
$\sigma : I' \longrightarrow J'$
a bijection. We set
 $$\begin{align*}M = \max \left ( \max_{i \in I'} d_C(F_i, G_{\sigma(i)}), \max_{i\in I\backslash I'}d_C(F_i,0), \max_{j\in J\backslash J'}d_C(G_j,0)) \right).\end{align*}$$
$$\begin{align*}M = \max \left ( \max_{i \in I'} d_C(F_i, G_{\sigma(i)}), \max_{i\in I\backslash I'}d_C(F_i,0), \max_{j\in J\backslash J'}d_C(G_j,0)) \right).\end{align*}$$
If
![]() $M = + \infty $
, the inequality is true. Let us now assume that
$M = + \infty $
, the inequality is true. Let us now assume that
![]() $M < + \infty $
. Let
$M < + \infty $
. Let
![]() $\varepsilon> M$
. Then for all
$\varepsilon> M$
. Then for all
![]() $i \in I \backslash I'$
,
$i \in I \backslash I'$
,
![]() $F_i$
is
$F_i$
is
![]() $\varepsilon $
-interleaved with
$\varepsilon $
-interleaved with
![]() $0$
, so the canonical map
$0$
, so the canonical map
![]() $F_i \star K_{2\varepsilon } \longrightarrow F_i$
is zero. Similarly, for all
$F_i \star K_{2\varepsilon } \longrightarrow F_i$
is zero. Similarly, for all
![]() $j \in J\backslash J'$
,
$j \in J\backslash J'$
,
![]() $G_j$
is
$G_j$
is
![]() $\varepsilon $
-interleaved with
$\varepsilon $
-interleaved with
![]() $0$
, so the canonical map
$0$
, so the canonical map
![]() $G_j \star K_{2\varepsilon } \longrightarrow G_j$
is zero. Moreover, for all
$G_j \star K_{2\varepsilon } \longrightarrow G_j$
is zero. Moreover, for all
![]() $i \in I'$
, there exists a pair of
$i \in I'$
, there exists a pair of
![]() $\varepsilon $
-interleavings morphisms
$\varepsilon $
-interleavings morphisms
![]() $f_i : F_i \star K_{\varepsilon } \longrightarrow G_{\sigma (i)}$
and
$f_i : F_i \star K_{\varepsilon } \longrightarrow G_{\sigma (i)}$
and
![]() $g_i : G_{\sigma (i)} \star K_{\varepsilon } \longrightarrow F_i$
.
$g_i : G_{\sigma (i)} \star K_{\varepsilon } \longrightarrow F_i$
.
Since
![]() $(\oplus _{i \in I} F_i) \star K_{\varepsilon } \simeq \oplus _{i \in I} (F_i \star K_{\varepsilon })$
and
$(\oplus _{i \in I} F_i) \star K_{\varepsilon } \simeq \oplus _{i \in I} (F_i \star K_{\varepsilon })$
and
![]() $(\oplus _{j \in J} G_j) \star K_{\varepsilon } \simeq \oplus _{j \in J} (G_j \star K_{\varepsilon })$
, and these direct sums are finite, we can define
$(\oplus _{j \in J} G_j) \star K_{\varepsilon } \simeq \oplus _{j \in J} (G_j \star K_{\varepsilon })$
, and these direct sums are finite, we can define
![]() $f : \oplus _{i \in I} F_i \star K_{\varepsilon } \longrightarrow \oplus _{j \in J} G_{j}$
and
$f : \oplus _{i \in I} F_i \star K_{\varepsilon } \longrightarrow \oplus _{j \in J} G_{j}$
and
![]() $g : \oplus _{j \in J} G_j \star K_{\varepsilon } \longrightarrow \oplus _{i \in I} F_i$
uniquely by specifying
$g : \oplus _{j \in J} G_j \star K_{\varepsilon } \longrightarrow \oplus _{i \in I} F_i$
uniquely by specifying
![]() $f_{ij} \in \mathrm {Hom}(F_i \star K_{\varepsilon }, G_j)$
and
$f_{ij} \in \mathrm {Hom}(F_i \star K_{\varepsilon }, G_j)$
and
![]() $g_{ji} \in \mathrm {Hom}(G_j \star K_{\varepsilon }, F_i)$
. We set, for all
$g_{ji} \in \mathrm {Hom}(G_j \star K_{\varepsilon }, F_i)$
. We set, for all
![]() $(i,j) \in I \times J$
$(i,j) \in I \times J$
 $$\begin{align*}f_{ij} = \begin{cases} f_i ~ \mathrm{if} ~ i \in I' ~ \mathrm{and} ~ j = \sigma(i) \\ 0 ~ \mathrm{else} \end{cases} \mathrm{and} \quad g_{ji} = \begin{cases} g_i ~ \mathrm{if} ~ i \in I' ~ \mathrm{and} ~ j = \sigma(i) \\ 0 ~ \mathrm{else} \end{cases}. \end{align*}$$
$$\begin{align*}f_{ij} = \begin{cases} f_i ~ \mathrm{if} ~ i \in I' ~ \mathrm{and} ~ j = \sigma(i) \\ 0 ~ \mathrm{else} \end{cases} \mathrm{and} \quad g_{ji} = \begin{cases} g_i ~ \mathrm{if} ~ i \in I' ~ \mathrm{and} ~ j = \sigma(i) \\ 0 ~ \mathrm{else} \end{cases}. \end{align*}$$
Let us verify that
![]() $(f,g)$
is an
$(f,g)$
is an
![]() $\varepsilon $
-interleaving pair between
$\varepsilon $
-interleaving pair between
![]() $\oplus _{i\in i} F_i$
and
$\oplus _{i\in i} F_i$
and
![]() $\oplus _{j\in J} G_j$
. For all
$\oplus _{j\in J} G_j$
. For all
![]() $(i,l) \in I^2$
, one has
$(i,l) \in I^2$
, one has
 $$\begin{align*}\left (g \circ \left (f \star K_{\varepsilon} \right ) \right)_{il} = \sum_{j \in J} g_{jl} \circ (f_{ij} \star K_{\varepsilon}) = \begin{cases} \chi_{2\varepsilon,0}\star F_i ~\mathrm{if}~ i = l \\ 0 ~ \mathrm{else} \end{cases}. \end{align*}$$
$$\begin{align*}\left (g \circ \left (f \star K_{\varepsilon} \right ) \right)_{il} = \sum_{j \in J} g_{jl} \circ (f_{ij} \star K_{\varepsilon}) = \begin{cases} \chi_{2\varepsilon,0}\star F_i ~\mathrm{if}~ i = l \\ 0 ~ \mathrm{else} \end{cases}. \end{align*}$$
Therefore,
![]() $g \circ \left (f \star K_{\varepsilon } \right ) = \chi _{2\varepsilon ,0}\star F $
. A similar computation yields
$g \circ \left (f \star K_{\varepsilon } \right ) = \chi _{2\varepsilon ,0}\star F $
. A similar computation yields
![]() $f \circ \left (g \star K_{\varepsilon } \right ) = \chi _{2\varepsilon ,0}\star G$
. Thus,
$f \circ \left (g \star K_{\varepsilon } \right ) = \chi _{2\varepsilon ,0}\star G$
. Thus,
![]() $(f,g)$
is indeed an
$(f,g)$
is indeed an
![]() $\varepsilon $
-interleaving pair.
$\varepsilon $
-interleaving pair.
By taking the infimum over
![]() $\varepsilon> M$
, we get the desired inequality.
$\varepsilon> M$
, we get the desired inequality.
2.3 PL-sheaves and functions
We consider a finite-dimensional real vector space
![]() $\mathbb {V}$
endowed with a norm
$\mathbb {V}$
endowed with a norm
![]() $\|\cdot \|$
. We equip
$\|\cdot \|$
. We equip
![]() $\mathbb {V}$
with the topology induced by the norm
$\mathbb {V}$
with the topology induced by the norm
![]() $\|\cdot \|$
, and
$\|\cdot \|$
, and
![]() $\mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
with the convolution distance
$\mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
with the convolution distance
![]() $d_C$
associated to
$d_C$
associated to
![]() $\|\cdot \|$
. The notion of piecewise-linear(PL) sheaves was introduced by Kashiwara–Schapira in [Reference Kashiwara and Schapira27].
$\|\cdot \|$
. The notion of piecewise-linear(PL) sheaves was introduced by Kashiwara–Schapira in [Reference Kashiwara and Schapira27].
Definition 2.19. A convex polytope P in
![]() $\mathbb {V}$
is the intersection of a finite family of open or closed affine half-spaces.
$\mathbb {V}$
is the intersection of a finite family of open or closed affine half-spaces.
Definition 2.20. A sheaf
![]() $F \in \mathrm {D}_{\mathbb {R} c}^b(\mathbf {k}_{\mathbb {V}})$
is PL if there exists a locally finite family
$F \in \mathrm {D}_{\mathbb {R} c}^b(\mathbf {k}_{\mathbb {V}})$
is PL if there exists a locally finite family
![]() $(P_a)_{a\in A}$
of locally closed convex polytopes covering
$(P_a)_{a\in A}$
of locally closed convex polytopes covering
![]() $\mathbb {V}$
such that
$\mathbb {V}$
such that
![]() $F_{|P_a}$
is locally constant and of finite rank for all
$F_{|P_a}$
is locally constant and of finite rank for all
![]() $a\in A$
.
$a\in A$
.
We shall denote by
![]() $\mathrm {D}^b_{\mathrm {PL}}(\mathbf {k}_{\mathbb {V}})$
the full subcategory of
$\mathrm {D}^b_{\mathrm {PL}}(\mathbf {k}_{\mathbb {V}})$
the full subcategory of
![]() $\mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
consisting of PL sheaves. The two first points of the following approximation theorem are proved in [Reference Kashiwara and Schapira27], we provide a proof for three.
$\mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
consisting of PL sheaves. The two first points of the following approximation theorem are proved in [Reference Kashiwara and Schapira27], we provide a proof for three.
Theorem 2.21. Let
![]() $F \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {V}})$
and
$F \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {V}})$
and
![]() $C \in \mathbb {Z}_{\geq 0}$
such that for all
$C \in \mathbb {Z}_{\geq 0}$
such that for all
![]() $|i|> C$
, one has
$|i|> C$
, one has
![]() $\mathrm {H}^i(F) \simeq 0$
. Then for any
$\mathrm {H}^i(F) \simeq 0$
. Then for any
![]() $\varepsilon> 0$
, there exists a sheaf
$\varepsilon> 0$
, there exists a sheaf
![]() $F_{\varepsilon } \in \mathrm {D}^b_{\mathrm {PL}}(\mathbf {k}_{\mathbb {V}})$
satisfying
$F_{\varepsilon } \in \mathrm {D}^b_{\mathrm {PL}}(\mathbf {k}_{\mathbb {V}})$
satisfying
-
1.
 $d_C(F, F_{\varepsilon }) \leq \varepsilon $
,
$d_C(F, F_{\varepsilon }) \leq \varepsilon $
, -
2.
 $\mathrm {supp}(F_{\varepsilon }) \subset \mathrm {supp}(F) + B(0,\varepsilon )$
,
$\mathrm {supp}(F_{\varepsilon }) \subset \mathrm {supp}(F) + B(0,\varepsilon )$
, -
3.
 $\mathrm {H}^i(F_{\varepsilon }) \simeq 0$
, for all
$\mathrm {H}^i(F_{\varepsilon }) \simeq 0$
, for all
 $|i|> C + \mathrm {dim}(\mathbb {V}) + 1$
.
$|i|> C + \mathrm {dim}(\mathbb {V}) + 1$
.
Proof.
![]() $(1)$
and
$(1)$
and
![]() $(2)$
are [Reference Kashiwara and Schapira27, Theorem 2.11]. For
$(2)$
are [Reference Kashiwara and Schapira27, Theorem 2.11]. For
![]() $(3)$
, we have to use the construction of the proof of [Reference Kashiwara and Schapira27, Theorem 2.11]. More precisely, the authors construct a simplicial complex
$(3)$
, we have to use the construction of the proof of [Reference Kashiwara and Schapira27, Theorem 2.11]. More precisely, the authors construct a simplicial complex
![]() $(S, \Delta )$
such that there is an homeomorphism
$(S, \Delta )$
such that there is an homeomorphism
![]() $f : |S| \overset {\sim }{\longrightarrow } \mathbb {V}$
and a PL continuous map
$f : |S| \overset {\sim }{\longrightarrow } \mathbb {V}$
and a PL continuous map
![]() $g : |S| \longrightarrow \mathbb {V}$
such that
$g : |S| \longrightarrow \mathbb {V}$
such that
![]() $F \simeq \mathrm {R} f_\ast f^{-1} F $
and
$F \simeq \mathrm {R} f_\ast f^{-1} F $
and
![]() $F_{\varepsilon } \simeq \mathrm {R} g_\ast f^{-1} F$
. We conclude by observing that the flabby dimension of
$F_{\varepsilon } \simeq \mathrm {R} g_\ast f^{-1} F$
. We conclude by observing that the flabby dimension of
![]() $\mathbb {V}$
(hence of
$\mathbb {V}$
(hence of
![]() $|S|$
) is
$|S|$
) is
![]() $\dim (\mathbb {V}) + 1$
[Reference Kashiwara, Schapira and Houzel25, Exercise III.2].
$\dim (\mathbb {V}) + 1$
[Reference Kashiwara, Schapira and Houzel25, Exercise III.2].
Following [Reference Lebovici29], we introduce the PL counterpart of constructible functions.
Definition 2.22. A function
![]() $\varphi : \mathbb {V} \longrightarrow \mathbb {Z}$
is PL-constructible if there exists a locally finite covering
$\varphi : \mathbb {V} \longrightarrow \mathbb {Z}$
is PL-constructible if there exists a locally finite covering
![]() $\mathbb {V} = \bigcup _{\lambda \in A} P_{\lambda }$
by locally closed convex polytopes such that
$\mathbb {V} = \bigcup _{\lambda \in A} P_{\lambda }$
by locally closed convex polytopes such that
![]() $\varphi $
is constant on each
$\varphi $
is constant on each
![]() $P_{\lambda }$
.
$P_{\lambda }$
.
We denote by
![]() $\mathrm {CF}_{\mathrm {PL}}(\mathbb {V})$
the group of PL-constructible functions on
$\mathrm {CF}_{\mathrm {PL}}(\mathbb {V})$
the group of PL-constructible functions on
![]() $\mathbb {V}$
.
$\mathbb {V}$
.
Proposition 2.23 [Reference Lebovici29].
Any
![]() $\varphi \in \mathrm {CF}_{\mathrm {PL}}(\mathbb {V})$
with compact support can be written as a finite sum
$\varphi \in \mathrm {CF}_{\mathrm {PL}}(\mathbb {V})$
with compact support can be written as a finite sum
![]() $\varphi = \sum _{\lambda } C_{\lambda } \cdot 1_{ X_{\lambda }}$
, where
$\varphi = \sum _{\lambda } C_{\lambda } \cdot 1_{ X_{\lambda }}$
, where
![]() $X_{\lambda }$
is a compact convex polytope, and
$X_{\lambda }$
is a compact convex polytope, and
![]() $C_{\lambda } \in \mathbb {Z}$
.
$C_{\lambda } \in \mathbb {Z}$
.
3 Main result
Let
![]() $(\mathbb {V}, \| \cdot \|)$
be a finite-dimensional normed real vector space. We endow
$(\mathbb {V}, \| \cdot \|)$
be a finite-dimensional normed real vector space. We endow
![]() $\mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
with the associated convolution distance
$\mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
with the associated convolution distance
![]() $d_C$
[Reference Kashiwara and Schapira27]. Let
$d_C$
[Reference Kashiwara and Schapira27]. Let
![]() $\mathscr {C}$
be an abelian category. We denote by
$\mathscr {C}$
be an abelian category. We denote by
![]() $\mathrm {D}^b(\mathscr {C})$
its bounded derived category. Given
$\mathrm {D}^b(\mathscr {C})$
its bounded derived category. Given
![]() $a\leq b$
two integers, we also denote by
$a\leq b$
two integers, we also denote by
![]() $\mathrm {D}^{[a,b]}(\mathbf {k}_{\mathbb {V}})$
the full subcategory of
$\mathrm {D}^{[a,b]}(\mathbf {k}_{\mathbb {V}})$
the full subcategory of
![]() $\mathrm {D}^b(\mathscr {C})$
spanned by objects
$\mathrm {D}^b(\mathscr {C})$
spanned by objects
![]() $X \in \mathrm {D}^b(\mathscr {C})$
such that
$X \in \mathrm {D}^b(\mathscr {C})$
such that
![]() $\mathrm {H}^i(X)\simeq 0$
for all
$\mathrm {H}^i(X)\simeq 0$
for all
![]() $i \in \mathbb {Z} \backslash [a,b]$
.
$i \in \mathbb {Z} \backslash [a,b]$
.
Definition 3.1. A sequence of objects
![]() $(X_n)_{n \geq 0}$
of
$(X_n)_{n \geq 0}$
of
![]() $\mathrm {D}^b(\mathscr {C})$
is said to be cohomologically bounded if there exists some integers
$\mathrm {D}^b(\mathscr {C})$
is said to be cohomologically bounded if there exists some integers
![]() $a \leq b$
such that for all
$a \leq b$
such that for all
![]() $n \geq 0$
,
$n \geq 0$
,
![]() $X_n \in \mathrm {D}^{[a,b]}(\mathbf {k}_{\mathbb {V}})$
.
$X_n \in \mathrm {D}^{[a,b]}(\mathbf {k}_{\mathbb {V}})$
.
Let
![]() $\delta $
be a pseudo-extended metric on
$\delta $
be a pseudo-extended metric on
![]() $\mathrm {CF} (\mathbb {V})$
.
$\mathrm {CF} (\mathbb {V})$
.
Definition 3.2. The pseudo-extended metric
![]() $\delta $
is said to be
$\delta $
is said to be
![]() $d_C$
-dominated if for all cohomologically bounded sequences
$d_C$
-dominated if for all cohomologically bounded sequences
![]() $(F_n) \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {V}})$
of compactly supported sheaves, and
$(F_n) \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {V}})$
of compactly supported sheaves, and
![]() $F \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {V}})$
with compact support, one has
$F \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {V}})$
with compact support, one has
It shall be noted that by Proposition 2.16 and Lemma 2.8, the condition
![]() $d_C(F,G) < +\infty $
implies that
$d_C(F,G) < +\infty $
implies that
![]() $\int \chi (F) ~\mathrm {d} \chi = \int \chi (G) ~\mathrm {d} \chi $
. Our aim is to characterize all
$\int \chi (F) ~\mathrm {d} \chi = \int \chi (G) ~\mathrm {d} \chi $
. Our aim is to characterize all
![]() $d_C$
-dominated pseudo-extended metrics on
$d_C$
-dominated pseudo-extended metrics on
![]() $\mathrm {CF} (\mathbb {V})$
. This will be achieved in Theorem 3.11. In all this section,
$\mathrm {CF} (\mathbb {V})$
. This will be achieved in Theorem 3.11. In all this section,
![]() $\delta $
designates a
$\delta $
designates a
![]() $d_C$
-dominated pseudo-extended metric on
$d_C$
-dominated pseudo-extended metric on
![]() $\mathrm {CF} (\mathbb {V})$
.
$\mathrm {CF} (\mathbb {V})$
.
Our strategy is to prove that for any
![]() $\varphi \in \mathrm {CF}(\mathbb {V})$
with compact support, it is possible to concentrate the ‘mass’ of
$\varphi \in \mathrm {CF}(\mathbb {V})$
with compact support, it is possible to concentrate the ‘mass’ of
![]() $\varphi $
on one single point, that is
$\varphi $
on one single point, that is
![]() $\delta (\varphi , (\int \varphi ~\mathrm {d} \chi )\cdot 1_{\{0\}}) = 0$
. To do so, we first assume that
$\delta (\varphi , (\int \varphi ~\mathrm {d} \chi )\cdot 1_{\{0\}}) = 0$
. To do so, we first assume that
![]() $\varphi $
is PL-constructible, which allows us to use rather straightforward arguments instead of sophisticated one from subanalytic geometry. We then generalize to arbitrary stratifications thanks to Kashiwara–Schapira’s approximation Theorem 2.21.
$\varphi $
is PL-constructible, which allows us to use rather straightforward arguments instead of sophisticated one from subanalytic geometry. We then generalize to arbitrary stratifications thanks to Kashiwara–Schapira’s approximation Theorem 2.21.
In Section 3.1, we introduce the notion of
![]() $\varepsilon $
-flag, which is a nested sequence of convex compact sets. It allows us to successively concentrate the mass of an indicator PL-function onto one single point. This is our technical tool to treat the PL-case in Section 3.2, from which we deduce the general one in Section 3.3
$\varepsilon $
-flag, which is a nested sequence of convex compact sets. It allows us to successively concentrate the mass of an indicator PL-function onto one single point. This is our technical tool to treat the PL-case in Section 3.2, from which we deduce the general one in Section 3.3
3.1 Convolution distance of the difference of compact convex subsets
Recall that for
![]() $x\in \mathbb {V}$
and
$x\in \mathbb {V}$
and
![]() $\varepsilon \geq 0$
, we denote by
$\varepsilon \geq 0$
, we denote by
![]() $B(x,\varepsilon )$
the closed ball of radius
$B(x,\varepsilon )$
the closed ball of radius
![]() $\varepsilon $
centered at x.
$\varepsilon $
centered at x.
Lemma 3.3. Let
![]() $F \in \mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
with compact support, and
$F \in \mathrm {D}^b(\mathbf {k}_{\mathbb {V}})$
with compact support, and
![]() $\varepsilon \geq 0$
. If for all
$\varepsilon \geq 0$
. If for all
![]() $x \in \mathrm {supp}(F)$
one has
$x \in \mathrm {supp}(F)$
one has
![]() $\mathrm {R} \Gamma (B(x, \varepsilon ); F) \simeq 0$
, then F is
$\mathrm {R} \Gamma (B(x, \varepsilon ); F) \simeq 0$
, then F is
![]() $\frac {\varepsilon }{2}$
-isomorphic to
$\frac {\varepsilon }{2}$
-isomorphic to
![]() $0$
.
$0$
.
Proof. Let F and
![]() $\varepsilon $
be as in the statement. By definition of interleavings, it is sufficient to prove that the canonical map
$\varepsilon $
be as in the statement. By definition of interleavings, it is sufficient to prove that the canonical map
![]() $F \star K_{\varepsilon } \longrightarrow F$
is zero. Let
$F \star K_{\varepsilon } \longrightarrow F$
is zero. Let
![]() $x \in \mathbb {V}$
. If
$x \in \mathbb {V}$
. If
![]() $x \not \in \mathrm {supp}(F)$
, it is clear that the induced morphism
$x \not \in \mathrm {supp}(F)$
, it is clear that the induced morphism
![]() $(F \star K_{\varepsilon })_x \longrightarrow F_x$
is zero. Let us assume that
$(F \star K_{\varepsilon })_x \longrightarrow F_x$
is zero. Let us assume that
![]() $x \in \mathrm {supp}(F)$
. By Equation (2.12) in [Reference Petit and Schapira37], one has
$x \in \mathrm {supp}(F)$
. By Equation (2.12) in [Reference Petit and Schapira37], one has
Therefore, the morphism
![]() $(F \star K_{\varepsilon })_x \longrightarrow F_x$
is zero in every case, which implies that
$(F \star K_{\varepsilon })_x \longrightarrow F_x$
is zero in every case, which implies that
![]() $F \star K_{\varepsilon } \longrightarrow F$
is also zero.
$F \star K_{\varepsilon } \longrightarrow F$
is also zero.
Definition 3.4. Given
![]() $X \subset \mathbb {V}$
and
$X \subset \mathbb {V}$
and
![]() $\varepsilon \geq 0$
, the
$\varepsilon \geq 0$
, the
![]() $\varepsilon $
-thickening of X is defined by
$\varepsilon $
-thickening of X is defined by
Lemma 3.5. Let
![]() $X \subset Y$
be compact convex subsets of
$X \subset Y$
be compact convex subsets of
![]() $\mathbb {V}$
, and assume that there exists
$\mathbb {V}$
, and assume that there exists
![]() $\varepsilon \geq 0$
such that
$\varepsilon \geq 0$
such that
![]() $Y \subset T_{\varepsilon }(X)$
. Then
$Y \subset T_{\varepsilon }(X)$
. Then
![]() $d_C(\mathbf {k}_{Y \backslash X},0) \leq \frac {\varepsilon }{2}$
.
$d_C(\mathbf {k}_{Y \backslash X},0) \leq \frac {\varepsilon }{2}$
.
Proof. For
![]() $y\in Y$
and
$y\in Y$
and
![]() $\varepsilon '> \varepsilon $
, one has the following distinguished triangle:
$\varepsilon '> \varepsilon $
, one has the following distinguished triangle:
By hypothesis,
![]() $B(y, \varepsilon ')\cap Y \cap X$
is nonempty and convex. Since X and Y are closed convex subsets, we deduce that the map
$B(y, \varepsilon ')\cap Y \cap X$
is nonempty and convex. Since X and Y are closed convex subsets, we deduce that the map
![]() $\mathrm {R} \Gamma (B(y,\varepsilon '); \mathbf {k}_Y) \longrightarrow \mathrm {R} \Gamma (B(y,\varepsilon '); \mathbf {k}_X)$
is an isomorphism. Therefore,
$\mathrm {R} \Gamma (B(y,\varepsilon '); \mathbf {k}_Y) \longrightarrow \mathrm {R} \Gamma (B(y,\varepsilon '); \mathbf {k}_X)$
is an isomorphism. Therefore,
![]() $\mathrm {R} \Gamma (B(y,\varepsilon '); \mathbf {k}_{Y\backslash X}) \simeq 0$
, for all
$\mathrm {R} \Gamma (B(y,\varepsilon '); \mathbf {k}_{Y\backslash X}) \simeq 0$
, for all
![]() $y \in \mathrm {supp}(\mathbf {k}_{Y\backslash X}) \subset Y$
and
$y \in \mathrm {supp}(\mathbf {k}_{Y\backslash X}) \subset Y$
and
![]() $\varepsilon '> \varepsilon $
. Lemma 3.3 implies that
$\varepsilon '> \varepsilon $
. Lemma 3.3 implies that
![]() $d_C(\mathbf {k}_{Y\backslash X},0) \leq \frac {\varepsilon }{2}$
.
$d_C(\mathbf {k}_{Y\backslash X},0) \leq \frac {\varepsilon }{2}$
.
Definition 3.6. Let
![]() $\varepsilon \geq 0$
. An
$\varepsilon \geq 0$
. An
![]() $\varepsilon $
-flag is a finite sequence of nested subsets
$\varepsilon $
-flag is a finite sequence of nested subsets
![]() $X^0 \subset X^1 \subset \ldots \subset X^n$
of
$X^0 \subset X^1 \subset \ldots \subset X^n$
of
![]() $\mathbb {V}$
satisfying
$\mathbb {V}$
satisfying
-
1.
 $X^i$
is a compact convex subset of
$X^i$
is a compact convex subset of
 $\mathbb {V}$
, for all i;
$\mathbb {V}$
, for all i; -
2.
 $X^0 = \{x_0\}$
is a single point;
$X^0 = \{x_0\}$
is a single point; -
3.
 $X^i \subset T_{\varepsilon }(X^{i-1})$
for all i.
$X^i \subset T_{\varepsilon }(X^{i-1})$
for all i.
We designate these data by
![]() $X^\bullet $
.
$X^\bullet $
.
Given an
![]() $\varepsilon $
-flag
$\varepsilon $
-flag
![]() $X^\bullet = (X^i)_{i = 0\ldots n}$
, and
$X^\bullet = (X^i)_{i = 0\ldots n}$
, and ![]() , we define the spaces
, we define the spaces
![]() $\mathrm {Gr}_i(X^\bullet )$
by
$\mathrm {Gr}_i(X^\bullet )$
by
It is immediate to verify that
![]() $\mathrm {Gr}_i(X^\bullet )$
is locally closed for all
$\mathrm {Gr}_i(X^\bullet )$
is locally closed for all ![]() and that one has
and that one has
![]() $X^n = \sqcup _i \mathrm {Gr}_i(X^\bullet ).$
Moreover, we set
$X^n = \sqcup _i \mathrm {Gr}_i(X^\bullet ).$
Moreover, we set
 $$\begin{align*}S(X^\bullet) := \bigoplus_{i = 0}^n \mathbf{k}_{\mathrm{Gr}_i(X^\bullet)} \in \mathrm{D}^b_{\mathbb{R} c}(\mathbf{k}_{\mathbb{V}}).\end{align*}$$
$$\begin{align*}S(X^\bullet) := \bigoplus_{i = 0}^n \mathbf{k}_{\mathrm{Gr}_i(X^\bullet)} \in \mathrm{D}^b_{\mathbb{R} c}(\mathbf{k}_{\mathbb{V}}).\end{align*}$$
Proposition 3.7. Let
![]() $X^\bullet = (X^i)_{i = 0 \ldots n }$
be an
$X^\bullet = (X^i)_{i = 0 \ldots n }$
be an
![]() $\varepsilon $
-flag. Then one has
$\varepsilon $
-flag. Then one has
-
1.
 $\chi (S(X^\bullet )) = \chi (\mathbf {k}_{X^n})$
;
$\chi (S(X^\bullet )) = \chi (\mathbf {k}_{X^n})$
; -
2.
 $d_C(S(X^\bullet ), \mathbf {k}_{X^0} ) \leq \frac {\varepsilon }{2}$
.
$d_C(S(X^\bullet ), \mathbf {k}_{X^0} ) \leq \frac {\varepsilon }{2}$
.
Proof.
-
1. This is a direct consequence of the fact that
 $X^n = \sqcup _i \mathrm {Gr}_i(X^\bullet ).$
$X^n = \sqcup _i \mathrm {Gr}_i(X^\bullet ).$
-
2. For
 $i \geq 1$
, the definition of
$i \geq 1$
, the definition of
 $\varepsilon $
-flag implies that the pair
$\varepsilon $
-flag implies that the pair
 $(X^{i-1}, X^i)$
satisfy the hypothesis of Lemma 3.5. Therefore,
$(X^{i-1}, X^i)$
satisfy the hypothesis of Lemma 3.5. Therefore,
 $d_C(\mathbf {k}_{\mathrm {Gr}_i(X^\bullet )}, 0) \leq \frac {\varepsilon }{2}$
. By additivity of interleavings, one deduces
$d_C(\mathbf {k}_{\mathrm {Gr}_i(X^\bullet )}, 0) \leq \frac {\varepsilon }{2}$
. By additivity of interleavings, one deduces  $$ \begin{align*} d_C(S(X^\bullet), \mathbf{k}_{X^0} ) &= d_C(\mathbf{k}_{X^0} \oplus \bigoplus_{i=1}^n \mathbf{k}_{\mathrm{Gr}_i(X^\bullet)}, \mathbf{k}_{X^0}) \\ &\leq \max \left (d_C \left (\mathbf{k}_{X^0},\mathbf{k}_{X^0} \right), \max_{i = 1 \ldots n} d_C \left (\mathbf{k}_{\mathrm{Gr}_i(X^\bullet)}, 0 \right ) \right ) \quad \mathrm{(Proposition }\ 2.18)\\ &= \max_{i = 1 \ldots n} d_C(\mathbf{k}_{\mathrm{Gr}_i(X^\bullet)}, 0) \\ &\leq \frac{\varepsilon}{2}.\\[-34pt] \end{align*} $$
$$ \begin{align*} d_C(S(X^\bullet), \mathbf{k}_{X^0} ) &= d_C(\mathbf{k}_{X^0} \oplus \bigoplus_{i=1}^n \mathbf{k}_{\mathrm{Gr}_i(X^\bullet)}, \mathbf{k}_{X^0}) \\ &\leq \max \left (d_C \left (\mathbf{k}_{X^0},\mathbf{k}_{X^0} \right), \max_{i = 1 \ldots n} d_C \left (\mathbf{k}_{\mathrm{Gr}_i(X^\bullet)}, 0 \right ) \right ) \quad \mathrm{(Proposition }\ 2.18)\\ &= \max_{i = 1 \ldots n} d_C(\mathbf{k}_{\mathrm{Gr}_i(X^\bullet)}, 0) \\ &\leq \frac{\varepsilon}{2}.\\[-34pt] \end{align*} $$
3.2 PL-case
The first step of our proof is the following concentration lemma in the PL case, that we will extend later on to arbitrary stratification by density of PL-sheaves with respect to the convolution distance.
Lemma 3.8. Let
![]() $\delta $
be a
$\delta $
be a
![]() $d_C$
-dominated pseudo-extended metric on
$d_C$
-dominated pseudo-extended metric on
![]() $\mathrm {CF}(\mathbb {V})$
. Let
$\mathrm {CF}(\mathbb {V})$
. Let
![]() $\varphi \in \mathrm {CF}_{\mathrm {PL}}(\mathbb {V})$
with compact support. Therefore, there exists a finite set A, and for all
$\varphi \in \mathrm {CF}_{\mathrm {PL}}(\mathbb {V})$
with compact support. Therefore, there exists a finite set A, and for all
![]() $\lambda \in A$
, a nonempty compact subset
$\lambda \in A$
, a nonempty compact subset
![]() $X_{\lambda } \subset \mathbb {V}$
which is a convex polytope such that
$X_{\lambda } \subset \mathbb {V}$
which is a convex polytope such that
![]() $\varphi = \sum _{\lambda \in A} C_{\lambda } \cdot 1_{X_{\lambda }}$
, with
$\varphi = \sum _{\lambda \in A} C_{\lambda } \cdot 1_{X_{\lambda }}$
, with
![]() $C_{\lambda } \in \mathbb {Z}$
. For
$C_{\lambda } \in \mathbb {Z}$
. For
![]() $\lambda \in A$
, let
$\lambda \in A$
, let
![]() $x_{\lambda } \in X_{\lambda }$
. Then one has
$x_{\lambda } \in X_{\lambda }$
. Then one has
 $$\begin{align*}\delta \left (\varphi,\sum_{\lambda \in A} C_{\lambda} \cdot 1_{\{x_{\lambda}\}} \right) = 0.\end{align*}$$
$$\begin{align*}\delta \left (\varphi,\sum_{\lambda \in A} C_{\lambda} \cdot 1_{\{x_{\lambda}\}} \right) = 0.\end{align*}$$
Proof. We consider the linear deformation retraction
![]() $H_{\lambda } : X_{\lambda } \times [0,1] \longrightarrow X_{\lambda }$
from
$H_{\lambda } : X_{\lambda } \times [0,1] \longrightarrow X_{\lambda }$
from
![]() $\{x_{\lambda }\}$
to
$\{x_{\lambda }\}$
to
![]() $X_{\lambda }$
defined by
$X_{\lambda }$
defined by
We set
![]() $\ell _{\lambda } = \max \{\|x - x_{\lambda }\| \mid x \in X_{\lambda } \}$
and
$\ell _{\lambda } = \max \{\|x - x_{\lambda }\| \mid x \in X_{\lambda } \}$
and
![]() $\ell = \max _{\lambda } \ell _{\lambda }$
. Let
$\ell = \max _{\lambda } \ell _{\lambda }$
. Let
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $n = \lceil \frac {\ell }{\varepsilon }\rceil $
. We define for
$n = \lceil \frac {\ell }{\varepsilon }\rceil $
. We define for ![]() the sequence of subsets
the sequence of subsets
![]() $X_{\lambda }^i := H_{\lambda } (X_{\lambda } \times {[0, \frac {i}{n}]})$
. By construction,
$X_{\lambda }^i := H_{\lambda } (X_{\lambda } \times {[0, \frac {i}{n}]})$
. By construction,
![]() $X_{\lambda }^\bullet = (X_{\lambda }^i)_{i=0\ldots n}$
is an
$X_{\lambda }^\bullet = (X_{\lambda }^i)_{i=0\ldots n}$
is an
![]() $\varepsilon $
-flag. We depict an illustration of
$\varepsilon $
-flag. We depict an illustration of
![]() $X_{\lambda }^\bullet $
in Figure 1.
$X_{\lambda }^\bullet $
in Figure 1.
Let us define the following sheaves:
 $$\begin{align*}F_{\varepsilon} &= \bigoplus_{\lambda \in A} S(X^{\bullet}_{\lambda})^{|C_{\lambda}|}[(1-\mathrm{sgn}(C_{\lambda}))/2],\\F &= \bigoplus_{\lambda \in A} \mathbf{k}_{\{x_{\lambda}\}}^{|C_{\lambda}|}[(1-\mathrm{sgn}(C_{\lambda}))/2].\end{align*}$$
$$\begin{align*}F_{\varepsilon} &= \bigoplus_{\lambda \in A} S(X^{\bullet}_{\lambda})^{|C_{\lambda}|}[(1-\mathrm{sgn}(C_{\lambda}))/2],\\F &= \bigoplus_{\lambda \in A} \mathbf{k}_{\{x_{\lambda}\}}^{|C_{\lambda}|}[(1-\mathrm{sgn}(C_{\lambda}))/2].\end{align*}$$
Then one has
 $$ \begin{align*} \chi(F_{\varepsilon}) &= \chi \left (\bigoplus_{\lambda \in A}S(X^{\bullet}_{\lambda})^{|C_{\lambda}|}[(1-\mathrm{sgn}(C_{\lambda}))/2] \right) \\ &= \sum_{\lambda\in A} C_{\lambda} \cdot \chi(S(X^{\bullet}_{\lambda}))\\ &= \sum_{\lambda\in A} C_{\lambda} \cdot 1_{X_{\lambda}} \quad \mathrm{(Proposition}\ 3.7\mathrm{-(1))}. \\ &= \varphi. \end{align*} $$
$$ \begin{align*} \chi(F_{\varepsilon}) &= \chi \left (\bigoplus_{\lambda \in A}S(X^{\bullet}_{\lambda})^{|C_{\lambda}|}[(1-\mathrm{sgn}(C_{\lambda}))/2] \right) \\ &= \sum_{\lambda\in A} C_{\lambda} \cdot \chi(S(X^{\bullet}_{\lambda}))\\ &= \sum_{\lambda\in A} C_{\lambda} \cdot 1_{X_{\lambda}} \quad \mathrm{(Proposition}\ 3.7\mathrm{-(1))}. \\ &= \varphi. \end{align*} $$

Figure 1 Illustration of the
![]() $\varepsilon $
-flag
$\varepsilon $
-flag
![]() $X_{\lambda }^\bullet $
.
$X_{\lambda }^\bullet $
.
Similarly,
Moreover, one has by additivity of interleavings (Proposition 2.18)
 $$ \begin{align*} d_C(F_{\varepsilon},F) &\leq \max_{\lambda \in A} d_C\left (S(X^{\bullet}_{\lambda})^{|C_{\lambda}|}[(1-\mathrm{sgn}(C_{\lambda}))/2] , \mathbf{k}_{\{x_{\lambda}\}}^{|C_{\lambda}|}[(1-\mathrm{sgn}(C_{\lambda}))/2] \right) \\ &= \max_{\lambda \in A} d_C\left (S(X^{\bullet}_{\lambda}), \mathbf{k}_{\{x_{\lambda}\}} \right ) \\ &\leq \frac{\varepsilon}{2} \leq \varepsilon \quad \mathrm{(Proposition}\ 3.7\mathrm{-(2)).} \end{align*} $$
$$ \begin{align*} d_C(F_{\varepsilon},F) &\leq \max_{\lambda \in A} d_C\left (S(X^{\bullet}_{\lambda})^{|C_{\lambda}|}[(1-\mathrm{sgn}(C_{\lambda}))/2] , \mathbf{k}_{\{x_{\lambda}\}}^{|C_{\lambda}|}[(1-\mathrm{sgn}(C_{\lambda}))/2] \right) \\ &= \max_{\lambda \in A} d_C\left (S(X^{\bullet}_{\lambda}), \mathbf{k}_{\{x_{\lambda}\}} \right ) \\ &\leq \frac{\varepsilon}{2} \leq \varepsilon \quad \mathrm{(Proposition}\ 3.7\mathrm{-(2)).} \end{align*} $$
Therefore, one has for all
![]() $k\in \mathbb {Z}_{>0}$
$k\in \mathbb {Z}_{>0}$
 $$ \begin{align*} \delta\left (\varphi, \sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x_{\lambda}\}}\right ) &= \delta\left ( \chi(F), \chi(F_{\frac{1}{k}}) \right). \end{align*} $$
$$ \begin{align*} \delta\left (\varphi, \sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x_{\lambda}\}}\right ) &= \delta\left ( \chi(F), \chi(F_{\frac{1}{k}}) \right). \end{align*} $$
Since
![]() $\delta $
is
$\delta $
is
![]() $d_C$
-dominated,
$d_C$
-dominated,
![]() $(F_{\frac {1}{k}})_{k> 0}$
is a cohomologically bounded sequence of compactly supported constructible sheaves, and
$(F_{\frac {1}{k}})_{k> 0}$
is a cohomologically bounded sequence of compactly supported constructible sheaves, and
![]() $d_C(F, F_{\frac {1}{k}}) \underset {k \longrightarrow +\infty }{\longrightarrow } 0$
, we conclude that
$d_C(F, F_{\frac {1}{k}}) \underset {k \longrightarrow +\infty }{\longrightarrow } 0$
, we conclude that
 $$\begin{align*}\delta \left (\varphi, \sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x_{\lambda}\}} \right) =0.\end{align*}$$
$$\begin{align*}\delta \left (\varphi, \sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x_{\lambda}\}} \right) =0.\end{align*}$$
Proposition 3.9. Let
![]() $\delta $
be a
$\delta $
be a
![]() $d_C$
-dominated pseudo-extended metric on
$d_C$
-dominated pseudo-extended metric on
![]() $\mathrm {CF}(\mathbb {V})$
. Let
$\mathrm {CF}(\mathbb {V})$
. Let
![]() $\varphi \in \mathrm {CF}_{\mathrm {PL}}(\mathbb {V})$
with compact support, and let
$\varphi \in \mathrm {CF}_{\mathrm {PL}}(\mathbb {V})$
with compact support, and let
![]() $x \in \mathbb {V}$
. Then one has
$x \in \mathbb {V}$
. Then one has
 $$\begin{align*}\delta \left (\varphi,\left (\int \varphi ~\mathrm{d} \chi \right ) \cdot 1_{\{x\}} \right) = 0. \end{align*}$$
$$\begin{align*}\delta \left (\varphi,\left (\int \varphi ~\mathrm{d} \chi \right ) \cdot 1_{\{x\}} \right) = 0. \end{align*}$$
Proof. Given
![]() $u,v \in \mathbb {V}$
, we set
$u,v \in \mathbb {V}$
, we set
![]() $[u,v] = \{t\cdot u + (1-t)\cdot v \mid t \in [0,1]\}$
. Let us write
$[u,v] = \{t\cdot u + (1-t)\cdot v \mid t \in [0,1]\}$
. Let us write
![]() $\varphi = \sum _{\lambda \in A} C_{\lambda } \cdot 1_{X_{\lambda }}$
, with A finite,
$\varphi = \sum _{\lambda \in A} C_{\lambda } \cdot 1_{X_{\lambda }}$
, with A finite,
![]() $C_{\lambda } \in \mathbb {Z}$
and
$C_{\lambda } \in \mathbb {Z}$
and
![]() $X_{\lambda }$
compact convex polytopes. For
$X_{\lambda }$
compact convex polytopes. For
![]() $\lambda \in A$
, let
$\lambda \in A$
, let
![]() $x_{\lambda } \in X_{\lambda }$
. Then by Lemma 3.8 applied to
$x_{\lambda } \in X_{\lambda }$
. Then by Lemma 3.8 applied to
![]() $\psi = \sum _{\lambda \in A} C_{\lambda } \cdot 1_{[x_{\lambda },x]}$
, one has
$\psi = \sum _{\lambda \in A} C_{\lambda } \cdot 1_{[x_{\lambda },x]}$
, one has
 $$ \begin{align*} \delta \left (\psi, \sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x_{\lambda}\}}\right ) = 0 = \delta \left (\psi, \sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x\}}\right ). \end{align*} $$
$$ \begin{align*} \delta \left (\psi, \sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x_{\lambda}\}}\right ) = 0 = \delta \left (\psi, \sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x\}}\right ). \end{align*} $$
Therefore,
 $$\begin{align*}\delta \left (\sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x_{\lambda}\}}, \sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x\}} \right ) = 0.\end{align*}$$
$$\begin{align*}\delta \left (\sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x_{\lambda}\}}, \sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x\}} \right ) = 0.\end{align*}$$
We now apply Lemma 3.8 to
![]() $\varphi $
:
$\varphi $
:
 $$ \begin{align*} \delta \left(\varphi, \left (\int \varphi ~\mathrm{d} \chi \right ) \cdot 1_{\{x\}} \right) &= \delta \left(\varphi, \sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x\}} \right) \\ &\leq \delta \left (\varphi, \sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x_{\lambda}\}} \right) + \delta \left (\sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x_{\lambda}\}}, \sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x\}} \right) \\ &= 0.\\[-34pt] \end{align*} $$
$$ \begin{align*} \delta \left(\varphi, \left (\int \varphi ~\mathrm{d} \chi \right ) \cdot 1_{\{x\}} \right) &= \delta \left(\varphi, \sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x\}} \right) \\ &\leq \delta \left (\varphi, \sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x_{\lambda}\}} \right) + \delta \left (\sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x_{\lambda}\}}, \sum_{\lambda\in A} C_{\lambda} \cdot 1_{\{x\}} \right) \\ &= 0.\\[-34pt] \end{align*} $$
3.3 General case
In this final section, we generalize the previous results to arbitrary stratifications, by PL approximation (Theorem 2.21).
Lemma 3.10. Let
![]() $\delta $
be a
$\delta $
be a
![]() $d_C$
-dominated pseudo-extended metric on
$d_C$
-dominated pseudo-extended metric on
![]() $\mathrm {CF}(\mathbb {V})$
. Let
$\mathrm {CF}(\mathbb {V})$
. Let
![]() $\varphi \in \mathrm {CF}(\mathbb {V})$
with compact support, and let
$\varphi \in \mathrm {CF}(\mathbb {V})$
with compact support, and let
![]() $x \in \mathbb {V}$
. Then one has
$x \in \mathbb {V}$
. Then one has
 $$\begin{align*}\delta \left ( \varphi,\left ( \int \varphi ~\mathrm{d} \chi \right ) \cdot 1_{\{x\}} \right ) = 0. \end{align*}$$
$$\begin{align*}\delta \left ( \varphi,\left ( \int \varphi ~\mathrm{d} \chi \right ) \cdot 1_{\{x\}} \right ) = 0. \end{align*}$$
Proof. Let
![]() $F \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {V}})$
with compact support such that
$F \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {V}})$
with compact support such that
![]() $\varphi = \chi (F)$
. According to Theorem 2.21, for all
$\varphi = \chi (F)$
. According to Theorem 2.21, for all
![]() $n\in \mathbb {Z}_{> 0}$
, there exists
$n\in \mathbb {Z}_{> 0}$
, there exists
![]() $F_n \in \mathrm {D}^b_{\mathrm {PL}}(\mathbf {k}_{\mathbb {V}})$
such that
$F_n \in \mathrm {D}^b_{\mathrm {PL}}(\mathbf {k}_{\mathbb {V}})$
such that
![]() $d_C(F,F_n) \leq \frac {1}{n}$
,
$d_C(F,F_n) \leq \frac {1}{n}$
,
![]() $\mathrm {supp}(F_n) \subset T_{\frac {1}{n}}(\mathrm {supp}(F))$
, and the sequence
$\mathrm {supp}(F_n) \subset T_{\frac {1}{n}}(\mathrm {supp}(F))$
, and the sequence
![]() $(F_n)$
is cohomologically bounded. In particular,
$(F_n)$
is cohomologically bounded. In particular,
![]() $F_n$
has compact support for all
$F_n$
has compact support for all
![]() $n \geq 1$
. Moreover, by Proposition 2.16, one has for all
$n \geq 1$
. Moreover, by Proposition 2.16, one has for all
![]() $n \geq 1$
,
$n \geq 1$
,
Therefore,
![]() $\int \chi (F_n) ~\mathrm {d} \chi = \int \varphi ~\mathrm {d} \chi $
according to Lemma 2.8. Consequently, for all
$\int \chi (F_n) ~\mathrm {d} \chi = \int \varphi ~\mathrm {d} \chi $
according to Lemma 2.8. Consequently, for all
![]() $n>0$
$n>0$
 $$ \begin{align*}\delta \left (\varphi, \left (\int \varphi ~\mathrm{d} \chi \right ) \cdot 1_{\{x\}} \right ) &\leq \delta \left (\varphi, \chi(F_n) \right ) + \delta\left (\chi(F_n), \left (\int \varphi ~\mathrm{d} \chi \right ) \cdot 1_{\{x\}}\right) \\ &= \delta \left (\varphi, \chi(F_n) \right ) + \delta\left (\chi(F_n), \left ( \int \chi(F_n) ~\mathrm{d} \chi \right) \cdot 1_{\{x\}}\right) \\ &= \delta \left (\varphi, \chi(F_n) \right ) \quad \mathrm{(Proposition}\ 3.9) \\ &= \delta \left (\chi(F), \chi(F_n) \right ). \end{align*} $$
$$ \begin{align*}\delta \left (\varphi, \left (\int \varphi ~\mathrm{d} \chi \right ) \cdot 1_{\{x\}} \right ) &\leq \delta \left (\varphi, \chi(F_n) \right ) + \delta\left (\chi(F_n), \left (\int \varphi ~\mathrm{d} \chi \right ) \cdot 1_{\{x\}}\right) \\ &= \delta \left (\varphi, \chi(F_n) \right ) + \delta\left (\chi(F_n), \left ( \int \chi(F_n) ~\mathrm{d} \chi \right) \cdot 1_{\{x\}}\right) \\ &= \delta \left (\varphi, \chi(F_n) \right ) \quad \mathrm{(Proposition}\ 3.9) \\ &= \delta \left (\chi(F), \chi(F_n) \right ). \end{align*} $$
Since
![]() $\delta $
is
$\delta $
is
![]() $d_C$
-dominated,
$d_C$
-dominated,
![]() $(F_n)$
is a cohomologically bounded sequence of constructible compactly supported sheaves, and
$(F_n)$
is a cohomologically bounded sequence of constructible compactly supported sheaves, and
![]() $d_C(F,F_n) \underset {n \longrightarrow +\infty }{\longrightarrow } 0$
, we conclude that
$d_C(F,F_n) \underset {n \longrightarrow +\infty }{\longrightarrow } 0$
, we conclude that
 $$\begin{align*}\delta \left (\varphi, \left (\int \varphi ~\mathrm{d} \chi \right ) \cdot 1_{\{x\}} \right ) = 0.\\[-40pt] \end{align*}$$
$$\begin{align*}\delta \left (\varphi, \left (\int \varphi ~\mathrm{d} \chi \right ) \cdot 1_{\{x\}} \right ) = 0.\\[-40pt] \end{align*}$$
Theorem 3.11. Let
![]() $\delta $
be a
$\delta $
be a
![]() $d_C$
-dominated pseudo-extended metric on
$d_C$
-dominated pseudo-extended metric on
![]() $\mathrm {CF}(\mathbb {V})$
, and let
$\mathrm {CF}(\mathbb {V})$
, and let
![]() $\varphi ,\psi \in \mathrm {CF}(\mathbb {V})$
with compact supports be such that
$\varphi ,\psi \in \mathrm {CF}(\mathbb {V})$
with compact supports be such that
![]() $\int \varphi ~\mathrm {d} \chi = \int \psi ~\mathrm {d} \chi $
. Then
$\int \varphi ~\mathrm {d} \chi = \int \psi ~\mathrm {d} \chi $
. Then
Proof. By the above lemma,
 $$ \begin{align*} \delta(\varphi,\psi) &\leq \delta\left (\varphi, \left (\int \varphi ~\mathrm{d} \chi \right ) \cdot 1_{\{0\}}\right) + \delta\left (\left (\int \psi ~\mathrm{d} \chi \right ) \cdot 1_{\{0\}}, \psi\right ) \\ &= 0 \quad \mathrm{(Lemma}\ 3.10).\\[-37pt] \end{align*} $$
$$ \begin{align*} \delta(\varphi,\psi) &\leq \delta\left (\varphi, \left (\int \varphi ~\mathrm{d} \chi \right ) \cdot 1_{\{0\}}\right) + \delta\left (\left (\int \psi ~\mathrm{d} \chi \right ) \cdot 1_{\{0\}}, \psi\right ) \\ &= 0 \quad \mathrm{(Lemma}\ 3.10).\\[-37pt] \end{align*} $$
Corollary 3.12. Let
![]() $F,G \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {V}})$
with compact support such that
$F,G \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {V}})$
with compact support such that
![]() $d_C(F,G) < +\infty $
. Then
$d_C(F,G) < +\infty $
. Then
Corollary 3.13. Let X be a real analytic manifold, and let
![]() $\varphi \in \mathrm {CF}(X)$
with compact support. Also, consider
$\varphi \in \mathrm {CF}(X)$
with compact support. Also, consider
![]() $f,g : X \longrightarrow \mathbb {V}$
some morphisms of real analytic manifolds proper on
$f,g : X \longrightarrow \mathbb {V}$
some morphisms of real analytic manifolds proper on
![]() $\mathrm {supp}(\varphi )$
. Then
$\mathrm {supp}(\varphi )$
. Then
Proof. By [Reference Schapira39, Theorem 2.3],
![]() $f_\ast \varphi $
and
$f_\ast \varphi $
and
![]() $g_\ast \varphi $
are indeed constructible and have compact support by the hypothesis. Let
$g_\ast \varphi $
are indeed constructible and have compact support by the hypothesis. Let
![]() $a_X : X \longrightarrow \{\mathrm {pt}\}$
and
$a_X : X \longrightarrow \{\mathrm {pt}\}$
and
![]() $a_{\mathbb {V}} : \mathbb {V} \longrightarrow \{\mathrm {pt}\}$
be the constant maps. Then by [Reference Schapira39, Section 2], under the identification
$a_{\mathbb {V}} : \mathbb {V} \longrightarrow \{\mathrm {pt}\}$
be the constant maps. Then by [Reference Schapira39, Section 2], under the identification
![]() $\mathrm {CF}(\{pt\}) \simeq \mathbb {Z}$
, one has
$\mathrm {CF}(\{pt\}) \simeq \mathbb {Z}$
, one has
 $$ \begin{align*} \int f_\ast \varphi ~\mathrm{d} \chi &= a_{\mathbb{V} \ast}(f_\ast \varphi) \\ &= (a_{\mathbb{V}}\circ f)_{\ast} \varphi \quad \mathrm{(Theorem}\ 2.11\mathrm{-3)} \\ &= a_{X \ast} \varphi \\ &= \int \varphi ~\mathrm{d} \chi. \end{align*} $$
$$ \begin{align*} \int f_\ast \varphi ~\mathrm{d} \chi &= a_{\mathbb{V} \ast}(f_\ast \varphi) \\ &= (a_{\mathbb{V}}\circ f)_{\ast} \varphi \quad \mathrm{(Theorem}\ 2.11\mathrm{-3)} \\ &= a_{X \ast} \varphi \\ &= \int \varphi ~\mathrm{d} \chi. \end{align*} $$
Similarly,
![]() $\int g_\ast \varphi ~\mathrm {d} \chi = \int \varphi ~\mathrm {d} \chi = \int f_\ast \varphi ~\mathrm {d} \chi $
. Since both
$\int g_\ast \varphi ~\mathrm {d} \chi = \int \varphi ~\mathrm {d} \chi = \int f_\ast \varphi ~\mathrm {d} \chi $
. Since both
![]() $f_\ast \varphi $
and
$f_\ast \varphi $
and
![]() $g_\ast \varphi $
have compact support, we conclude the proof by applying Theorem 3.11.
$g_\ast \varphi $
have compact support, we conclude the proof by applying Theorem 3.11.
4 Consequences for TDA
This section is devoted to applying our main result to constructions of TDA. We start by recalling standard definitions concerning multiparameter persistence modules and review results of [Reference Berkouk and Petit7] that allows to compare the categories of persistence modules with d parameters equipped with the interleaving distance
![]() $d_I$
, and sheaves on
$d_I$
, and sheaves on
![]() $\mathbb {R}^d$
endowed with the convolution. This bridge allows transferring Corollary 3.12 to the setting of persistence and to prove that there cannot exist any nontrivial
$\mathbb {R}^d$
endowed with the convolution. This bridge allows transferring Corollary 3.12 to the setting of persistence and to prove that there cannot exist any nontrivial
![]() $d_I$
-continuous additive invariants of persistence modules. By getting into the persistent world, we are able to apply Lesnick’s universality theorem, that allows removing any occurrence of the interleaving distance in the statements. We end the section by applying our results to several common TDA construction.
$d_I$
-continuous additive invariants of persistence modules. By getting into the persistent world, we are able to apply Lesnick’s universality theorem, that allows removing any occurrence of the interleaving distance in the statements. We end the section by applying our results to several common TDA construction.
4.1 Persistence and sheaves
For a general introduction to multiparameter persistence, we refer the reader to [Reference Bakke Botnan and Lesnick11]. Let
![]() $d \geq 0$
. We equip
$d \geq 0$
. We equip
![]() $\mathbb {R}^d$
with the partial order
$\mathbb {R}^d$
with the partial order
![]() $\leq $
, defined by
$\leq $
, defined by
![]() $(x_1,\ldots ,x_d) \leq (y_1,\ldots ,y_d)$
iff
$(x_1,\ldots ,x_d) \leq (y_1,\ldots ,y_d)$
iff
![]() $x_i \leq y_i$
for all i. We denote
$x_i \leq y_i$
for all i. We denote
![]() $(\mathbb {R}^d, \leq )$
for the associated poset category. The category of persistence modules with d-parameters, denoted by
$(\mathbb {R}^d, \leq )$
for the associated poset category. The category of persistence modules with d-parameters, denoted by
![]() $\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)$
, is the category of functors
$\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)$
, is the category of functors
![]() $(\mathbb {R}^d,\leq ) \longrightarrow \operatorname {\mathrm {Mod}}(\mathbf {k})$
and natural transformations.
$(\mathbb {R}^d,\leq ) \longrightarrow \operatorname {\mathrm {Mod}}(\mathbf {k})$
and natural transformations.
Persistence modules are usually compared using the interleaving distance, which is defined as follows. Let
![]() $\varepsilon \geq 0$
and
$\varepsilon \geq 0$
and
![]() $M \in \mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)$
. The
$M \in \mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)$
. The
![]() $\varepsilon $
-shift of M is the persistence module
$\varepsilon $
-shift of M is the persistence module
![]() $M[\varepsilon ]$
defined, for
$M[\varepsilon ]$
defined, for
![]() $x \leq y \in \mathbb {R}^d$
, by
$x \leq y \in \mathbb {R}^d$
, by
This objectwise construction readily extends to an additive exact autoequivalence
![]() $\cdot [\varepsilon ] : \mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d) \to \mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)$
. The collection of linear maps
$\cdot [\varepsilon ] : \mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d) \to \mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)$
. The collection of linear maps
![]() $(M(x \leq x + (\varepsilon ,\ldots , \varepsilon )))_{x\in \mathbb {R}^d}$
induces a natural transformation
$(M(x \leq x + (\varepsilon ,\ldots , \varepsilon )))_{x\in \mathbb {R}^d}$
induces a natural transformation
![]() $M \longrightarrow M[\varepsilon ]$
, denoted
$M \longrightarrow M[\varepsilon ]$
, denoted
![]() $\tau _{\varepsilon }^M$
. An
$\tau _{\varepsilon }^M$
. An
![]() $\varepsilon $
-interleaving between two persistence modules M and N in
$\varepsilon $
-interleaving between two persistence modules M and N in
![]() $\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)$
is the data of two morphisms
$\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)$
is the data of two morphisms
![]() $f : M \longrightarrow N[\varepsilon ]$
and
$f : M \longrightarrow N[\varepsilon ]$
and
![]() $g : N \longrightarrow M[\varepsilon ]$
such that
$g : N \longrightarrow M[\varepsilon ]$
such that
![]() $g[\varepsilon ] \circ f = \tau _{2 \varepsilon }^M$
and
$g[\varepsilon ] \circ f = \tau _{2 \varepsilon }^M$
and
![]() $f[\varepsilon ] \circ g = \tau _{2 \varepsilon }^N$
. If there exists an
$f[\varepsilon ] \circ g = \tau _{2 \varepsilon }^N$
. If there exists an
![]() $\varepsilon $
-interleaving between M and N, we say that they are
$\varepsilon $
-interleaving between M and N, we say that they are
![]() $\varepsilon $
-interleaved and write
$\varepsilon $
-interleaved and write
![]() $M \sim _{\varepsilon } N$
.
$M \sim _{\varepsilon } N$
.
Definition 4.1. The interleaving distance between the persistence modules M and N in
![]() $\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)$
is the possibly infinite quantity
$\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)$
is the possibly infinite quantity
Remark 4.2.
-
1. The interleaving distance is an extended-pseudo metric on the class of objects of
 $\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)$
.
$\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)$
. -
2. By exactness of the
 $\varepsilon $
-shift functor, the interleaving distance readily extends to the bounded derived category of persistence modules
$\varepsilon $
-shift functor, the interleaving distance readily extends to the bounded derived category of persistence modules
 $\mathrm {D}^b(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
(see [Reference Berkouk and Petit7]). In the following, we will still denote it by
$\mathrm {D}^b(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
(see [Reference Berkouk and Petit7]). In the following, we will still denote it by
 $d_I$
.
$d_I$
.
We now introduce the
![]() $\gamma $
-topology after Kashiwara–Schapira [Reference Kashiwara, Schapira and Houzel25, Section 3.5], as an intermediate between the Euclidean topology and the downset (or Alexandrov) topology. Let
$\gamma $
-topology after Kashiwara–Schapira [Reference Kashiwara, Schapira and Houzel25, Section 3.5], as an intermediate between the Euclidean topology and the downset (or Alexandrov) topology. Let
![]() $\gamma = (\mathbb {R}_{\geq 0})^d$
. An open set
$\gamma = (\mathbb {R}_{\geq 0})^d$
. An open set
![]() $U \subset \mathbb {R}^d$
is
$U \subset \mathbb {R}^d$
is
![]() $\gamma $
-open if it satisfies
$\gamma $
-open if it satisfies
![]() $U + \gamma = U$
. The set of
$U + \gamma = U$
. The set of
![]() $\gamma $
-open subsets of
$\gamma $
-open subsets of
![]() $\mathbb {R}^d$
indeed forms a topology of
$\mathbb {R}^d$
indeed forms a topology of
![]() $\mathbb {R}^d$
, named the
$\mathbb {R}^d$
, named the
![]() $\gamma $
-topology. We denote the associated topological space by
$\gamma $
-topology. We denote the associated topological space by
![]() $\mathbb {R}^d_\gamma $
. The identity map
$\mathbb {R}^d_\gamma $
. The identity map
![]() $\varphi _\gamma : \mathbb {R}^d \longrightarrow \mathbb {R}^d_\gamma $
,
$\varphi _\gamma : \mathbb {R}^d \longrightarrow \mathbb {R}^d_\gamma $
,
![]() $x \mapsto x$
, is continuous, and induces an adjunction
$x \mapsto x$
, is continuous, and induces an adjunction
Following [Reference Berkouk and Petit7, Section 4.2], it is possible to define an interleaving distance on
![]() $\mathrm {D}^b(\mathbf {k}_{\mathbb {R}^d_\gamma })$
, that we write
$\mathrm {D}^b(\mathbf {k}_{\mathbb {R}^d_\gamma })$
, that we write
![]() $d_I^\gamma $
. Also, we endow
$d_I^\gamma $
. Also, we endow
![]() $\mathbb {R}^d$
with the norm
$\mathbb {R}^d$
with the norm
![]() $\|\cdot \|_\infty $
defined by
$\|\cdot \|_\infty $
defined by
![]() $\|x\|_\infty := \max _i |x_i|$
and denote by
$\|x\|_\infty := \max _i |x_i|$
and denote by
![]() $d_C$
the associated convolution distance on
$d_C$
the associated convolution distance on
![]() $\mathrm {D}^b(\mathbf {k}_{\mathbb {R}^d})$
.
$\mathrm {D}^b(\mathbf {k}_{\mathbb {R}^d})$
.
Theorem 4.3 [Reference Berkouk and Petit8].
For all
![]() $F,G \in \mathrm {D}^b(\mathbf {k}_{\mathbb {R}^d})$
, and
$F,G \in \mathrm {D}^b(\mathbf {k}_{\mathbb {R}^d})$
, and
![]() $H,I \in \mathrm {D}^b(\mathbf {k}_{\mathbb {R}^d_\gamma })$
one has
$H,I \in \mathrm {D}^b(\mathbf {k}_{\mathbb {R}^d_\gamma })$
one has
-
1.
 $ d_I^\gamma (\mathrm {R} \varphi _{\gamma \ast } F, \mathrm {R} \varphi _{\gamma \ast } G) \leq d_C(F,G)$
;
$ d_I^\gamma (\mathrm {R} \varphi _{\gamma \ast } F, \mathrm {R} \varphi _{\gamma \ast } G) \leq d_C(F,G)$
; -
2.
 $d_C (\varphi _\gamma ^{-1} H, \varphi _\gamma ^{-1} I ) =d_I^\gamma (H,I)$
.
$d_C (\varphi _\gamma ^{-1} H, \varphi _\gamma ^{-1} I ) =d_I^\gamma (H,I)$
.
Moreover, in [Reference Berkouk and Petit7], the authors introduce a pair of adjoint functors
and prove the following.
Theorem 4.4 [Reference Berkouk and Petit7].
For all
![]() $H,I \in \mathrm {D}^b(\mathbf {k}_{\mathbb {R}^d_\gamma })$
, and
$H,I \in \mathrm {D}^b(\mathbf {k}_{\mathbb {R}^d_\gamma })$
, and
![]() $M,N \in \mathrm {D}^b(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
, one has
$M,N \in \mathrm {D}^b(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
, one has
-
1.
 $d_I(\mathrm {R} \alpha _\ast H, \mathrm {R} \alpha _\ast I ) = d_I^\gamma (H,I)$
;
$d_I(\mathrm {R} \alpha _\ast H, \mathrm {R} \alpha _\ast I ) = d_I^\gamma (H,I)$
; -
2.
 $d_I^\gamma ( \alpha ^{-1}M, \alpha ^{-1} N) = d_I(M,N)$
.
$d_I^\gamma ( \alpha ^{-1}M, \alpha ^{-1} N) = d_I(M,N)$
.
Combining the above results, we obtain the following adjunction:
where the left adjoint functor is objectwise distance preserving, and the right adjoint is objectwise
![]() $1$
-Lipschitz.
$1$
-Lipschitz.
We will also need the following lemma, that was not included in [Reference Berkouk and Petit7].
Lemma 4.5. Let
![]() $M\in \mathrm {D}^b(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
, then
$M\in \mathrm {D}^b(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
, then
![]() $d_I(M, \mathrm {R} \alpha _\ast \alpha ^{-1} M) = 0$
.
$d_I(M, \mathrm {R} \alpha _\ast \alpha ^{-1} M) = 0$
.
Proof. By [Reference Berkouk and Petit7, Fact 2.10] and [Reference Berkouk and Petit7, Proposition 2.11-(i)], one has
Therefore, for any
![]() $M\in \mathrm {D}^b(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
, by Theorem 4.4-
$M\in \mathrm {D}^b(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
, by Theorem 4.4-
![]() $(1)$
, one has
$(1)$
, one has
 $$ \begin{align*} d_I(M, \mathrm{R} \alpha_\ast\alpha^{-1} M) &= d_I^\gamma(\alpha^{-1} M, \alpha^{-1} (\mathrm{R} \alpha_\ast\alpha^{-1} M)) \\ &= d_I^\gamma (\alpha^{-1} M, (\alpha^{-1} \mathrm{R} \alpha_\ast)\alpha^{-1} M)) \\ &= d_I^\gamma (\alpha^{-1} M, \alpha^{-1} M) \\ &= 0.\\[-37pt] \end{align*} $$
$$ \begin{align*} d_I(M, \mathrm{R} \alpha_\ast\alpha^{-1} M) &= d_I^\gamma(\alpha^{-1} M, \alpha^{-1} (\mathrm{R} \alpha_\ast\alpha^{-1} M)) \\ &= d_I^\gamma (\alpha^{-1} M, (\alpha^{-1} \mathrm{R} \alpha_\ast)\alpha^{-1} M)) \\ &= d_I^\gamma (\alpha^{-1} M, \alpha^{-1} M) \\ &= 0.\\[-37pt] \end{align*} $$
Definition 4.6. A persistence module
![]() $M \in \mathrm {D}^b(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
is constructible if
$M \in \mathrm {D}^b(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
is constructible if
![]() $ (\alpha \circ \varphi _\gamma )^{-1} M \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {R}^d})$
.
$ (\alpha \circ \varphi _\gamma )^{-1} M \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {R}^d})$
.
Remark 4.7. Constructibility is a rather mild finiteness condition. Indeed, standard finiteness conditions of persistence modules such as being finitely presented or finitely subanalytically encoded both imply constructibility (see [Reference Miller33]). Providing an convenient definition of constructibility for persistence modules is an open and important research direction [Reference Miller32, Reference Miller33, Reference Waas44], which is outside the scope of this paper. That is why, we simply pull back the consctructibility definition from sheaves to persistence modules.
We denote by
![]() $\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
the full subcategory of
$\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
the full subcategory of
![]() $\mathrm {D}^b(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
whose objects are constructible persistence modules. Also, we denote
$\mathrm {D}^b(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
whose objects are constructible persistence modules. Also, we denote
![]() $\mathrm {Pers}_{\mathbf {k},\mathbb {R} c}(\mathbb {R}^d)$
the intersection
$\mathrm {Pers}_{\mathbf {k},\mathbb {R} c}(\mathbb {R}^d)$
the intersection
![]() $\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)) \cap \mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)$
.
$\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)) \cap \mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)$
.
Proposition 4.8. The category
![]() $\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
is a triangulated subcategory of
$\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
is a triangulated subcategory of
![]() $\mathrm {D}^b(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
.
$\mathrm {D}^b(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
.
Proof. This is a direct consequence of
![]() $\mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {R}^d})$
being a triangulated category and
$\mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {R}^d})$
being a triangulated category and
![]() $ (\alpha \circ \varphi _\gamma )^{-1}$
being a triangulated functor.
$ (\alpha \circ \varphi _\gamma )^{-1}$
being a triangulated functor.
Definition 4.9. A constructible persistence module
![]() $M\in \mathrm {D}^b_{ }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
is compactly generated if there exists
$M\in \mathrm {D}^b_{ }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
is compactly generated if there exists
![]() $F \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {R}^d})$
compactly supported such that
$F \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {R}^d})$
compactly supported such that
![]() $ M \simeq \mathrm {R} (\alpha \circ \varphi _\gamma )_\ast F$
.
$ M \simeq \mathrm {R} (\alpha \circ \varphi _\gamma )_\ast F$
.
4.2 nonexistence of additive stable invariants of persistence modules
In this section, we identify
![]() $\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {R}^d}))$
with
$\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {R}^d}))$
with
![]() $\mathrm {CF}(\mathbb {R}^d)$
, according to the sheaf-function correspondence (Theorem 2.6). Since
$\mathrm {CF}(\mathbb {R}^d)$
, according to the sheaf-function correspondence (Theorem 2.6). Since
![]() $\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
is triangulated, its Grothendieck group is well defined. We let
$\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
is triangulated, its Grothendieck group is well defined. We let
![]() $\kappa $
be the map
$\kappa $
be the map
![]() $\mathrm {ob}(\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))) \longrightarrow \mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)))$
sending a constructible persistence module to its
$\mathrm {ob}(\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))) \longrightarrow \mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)))$
sending a constructible persistence module to its
![]() $\mathrm {K}_0$
-class.
$\mathrm {K}_0$
-class.
Definition 4.10. A pseudo-extended metric
![]() $\delta $
on
$\delta $
on
![]() $\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)))$
is said to be
$\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)))$
is said to be
![]() $d_I$
-dominated if for all cohomologically bounded sequences
$d_I$
-dominated if for all cohomologically bounded sequences
![]() $(M_n) \in \mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)) $
of compactly generated persistence modules, and
$(M_n) \in \mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)) $
of compactly generated persistence modules, and
![]() $M \in \mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
compactly generated, one has
$M \in \mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
compactly generated, one has
Any triangulated functor
![]() $T : \mathscr {C} \longrightarrow \mathscr {C}'$
between triangulated categories, induces a group morphism
$T : \mathscr {C} \longrightarrow \mathscr {C}'$
between triangulated categories, induces a group morphism
![]() $\mathrm {K}_0(\mathscr {C}) \longrightarrow \mathrm {K}_0(\mathscr {C}')$
, that, for simplicity, we keep denoting by T. Given
$\mathrm {K}_0(\mathscr {C}) \longrightarrow \mathrm {K}_0(\mathscr {C}')$
, that, for simplicity, we keep denoting by T. Given
![]() $\delta $
a pseudo-extended metric on
$\delta $
a pseudo-extended metric on
![]() $\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)))$
, we let
$\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)))$
, we let
![]() $\delta _\ast $
be the pseudo-extended metric defined on
$\delta _\ast $
be the pseudo-extended metric defined on
![]() $\mathrm {CF}(\mathbb {R}^d)$
by
$\mathrm {CF}(\mathbb {R}^d)$
by
Proposition 4.11. The pseudo-extended metric
![]() $\delta $
on
$\delta $
on
![]() $\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)))$
is
$\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)))$
is
![]() $d_I$
-dominated if and only if
$d_I$
-dominated if and only if
![]() $\delta _\ast $
is
$\delta _\ast $
is
![]() $d_C$
-dominated.
$d_C$
-dominated.
Proof. Assume that
![]() $\delta $
is
$\delta $
is
![]() $d_I$
dominated. Let
$d_I$
dominated. Let
![]() $(F_n)$
and F be compactly supported in
$(F_n)$
and F be compactly supported in
![]() $\mathrm {D}^b_{\mathbb {R} c }(\mathbf {k}_{\mathbb {R}^d})$
such that,
$\mathrm {D}^b_{\mathbb {R} c }(\mathbf {k}_{\mathbb {R}^d})$
such that,
![]() $(F_n)$
is cohomologically bounded, and
$(F_n)$
is cohomologically bounded, and
Thus, by Theorems 4.3 and 4.4,
The functor
![]() $\mathrm {R} (\alpha \circ \varphi _\gamma )_\ast $
has finite cohomological dimension [Reference Berkouk and Petit7, Proposition 3.11], thus, the sequence
$\mathrm {R} (\alpha \circ \varphi _\gamma )_\ast $
has finite cohomological dimension [Reference Berkouk and Petit7, Proposition 3.11], thus, the sequence
![]() $(\mathrm {R} (\alpha \circ \varphi _\gamma )_\ast F_n)$
is cohomologically bounded and compactly generated by definition. Since
$(\mathrm {R} (\alpha \circ \varphi _\gamma )_\ast F_n)$
is cohomologically bounded and compactly generated by definition. Since
![]() $\delta $
is
$\delta $
is
![]() $d_I$
-dominated, we deduce that
$d_I$
-dominated, we deduce that
 $$ \begin{align*} \delta(\kappa(\mathrm{R} (\alpha\circ\varphi_\gamma)_\ast F),\kappa(\mathrm{R} (\alpha\circ\varphi_\gamma)_\ast F_n)) &= \delta (\mathrm{R} (\alpha\circ\varphi_\gamma)_\ast \chi(F),\mathrm{R} (\alpha\circ\varphi_\gamma)_\ast \chi(F_n)) \\ &= \delta_\ast(\chi(F), \chi(F_n)) \underset{n \longrightarrow +\infty}{\longrightarrow} 0. \end{align*} $$
$$ \begin{align*} \delta(\kappa(\mathrm{R} (\alpha\circ\varphi_\gamma)_\ast F),\kappa(\mathrm{R} (\alpha\circ\varphi_\gamma)_\ast F_n)) &= \delta (\mathrm{R} (\alpha\circ\varphi_\gamma)_\ast \chi(F),\mathrm{R} (\alpha\circ\varphi_\gamma)_\ast \chi(F_n)) \\ &= \delta_\ast(\chi(F), \chi(F_n)) \underset{n \longrightarrow +\infty}{\longrightarrow} 0. \end{align*} $$
Therefore,
![]() $\delta _\ast $
is
$\delta _\ast $
is
![]() $d_C$
-dominated. The proof of the converse works similarly.
$d_C$
-dominated. The proof of the converse works similarly.
Corollary 4.12. Let
![]() $\delta $
be a
$\delta $
be a
![]() $d_I$
-dominated pseudo-extended metric on
$d_I$
-dominated pseudo-extended metric on
![]() $\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)))$
. Then for all
$\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)))$
. Then for all
![]() $M,N \in \mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)) $
compactly generated such that
$M,N \in \mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)) $
compactly generated such that
![]() $d_I(M,N) < +\infty $
, one has
$d_I(M,N) < +\infty $
, one has
![]() $\delta (\kappa (M), \kappa (N)) = 0$
.
$\delta (\kappa (M), \kappa (N)) = 0$
.
Proof. According to Theorem 4.3, one has
![]() $d_I(M,N) = d_C ( (\alpha \circ \varphi _\gamma )^{-1} M, (\alpha \circ \varphi _\gamma )^{-1} N) < +\infty $
. Also, since
$d_I(M,N) = d_C ( (\alpha \circ \varphi _\gamma )^{-1} M, (\alpha \circ \varphi _\gamma )^{-1} N) < +\infty $
. Also, since
![]() $\delta $
is
$\delta $
is
![]() $d_I$
-dominated,
$d_I$
-dominated,
![]() $\delta _\ast $
is
$\delta _\ast $
is
![]() $d_C$
-dominated. Therefore, by Corollary 3.12,
$d_C$
-dominated. Therefore, by Corollary 3.12,
Note that, by [Reference Kashiwara and Schapira27, Corollary 1.6],
![]() $\mathrm {R} \varphi _{\gamma \ast } \circ \varphi _\gamma ^{-1} \simeq \mathrm {id}_{\mathrm {D}^b(\mathbf {k}_{\mathbb {V}_\gamma })}$
. Therefore,
$\mathrm {R} \varphi _{\gamma \ast } \circ \varphi _\gamma ^{-1} \simeq \mathrm {id}_{\mathrm {D}^b(\mathbf {k}_{\mathbb {V}_\gamma })}$
. Therefore,
By Lemma 4.5,
![]() $d_I(M,\mathrm {R} \alpha _\ast \alpha ^{-1} M) = 0$
. Since
$d_I(M,\mathrm {R} \alpha _\ast \alpha ^{-1} M) = 0$
. Since
![]() $\delta $
is
$\delta $
is
![]() $d_I$
-dominated,
$d_I$
-dominated,
![]() $\delta (\kappa (M), \kappa (\mathrm {R} \alpha _\ast \alpha ^{-1} M)) = 0$
. Similarly,
$\delta (\kappa (M), \kappa (\mathrm {R} \alpha _\ast \alpha ^{-1} M)) = 0$
. Similarly,
![]() $\delta (\kappa (N), \kappa (\mathrm {R} \alpha _\ast \alpha ^{-1} M)) = 0$
. From Equation
$\delta (\kappa (N), \kappa (\mathrm {R} \alpha _\ast \alpha ^{-1} M)) = 0$
. From Equation
![]() $(4.3)$
, we deduce that
$(4.3)$
, we deduce that
 $$ \begin{align*} &\delta(\kappa(M), \kappa(N)) \\ &\leq \delta(\kappa(M), \kappa(\mathrm{R} \alpha_\ast \alpha^{-1} M)) + \delta(\kappa(\mathrm{R} \alpha_\ast \alpha^{-1} M), \kappa(\mathrm{R} \alpha_\ast \alpha^{-1} N)) \\ & \qquad \qquad \qquad \qquad \qquad \qquad \qquad + \delta(\kappa(\mathrm{R} \alpha_\ast \alpha^{-1} N), \kappa(N)) \\ &= 0 + 0 + 0. \\[-37pt]\end{align*} $$
$$ \begin{align*} &\delta(\kappa(M), \kappa(N)) \\ &\leq \delta(\kappa(M), \kappa(\mathrm{R} \alpha_\ast \alpha^{-1} M)) + \delta(\kappa(\mathrm{R} \alpha_\ast \alpha^{-1} M), \kappa(\mathrm{R} \alpha_\ast \alpha^{-1} N)) \\ & \qquad \qquad \qquad \qquad \qquad \qquad \qquad + \delta(\kappa(\mathrm{R} \alpha_\ast \alpha^{-1} N), \kappa(N)) \\ &= 0 + 0 + 0. \\[-37pt]\end{align*} $$
Let
![]() $(G,+)$
be an abelian group, endowed with a pseudo-extended metric
$(G,+)$
be an abelian group, endowed with a pseudo-extended metric
![]() $\delta $
. We think of G as a group of invariants of persistence modules and of
$\delta $
. We think of G as a group of invariants of persistence modules and of
![]() $\delta $
as a way of measuring dissimilarity between invariants.
$\delta $
as a way of measuring dissimilarity between invariants.
Definition 4.13. Let
![]() $\mathscr {C}$
be a triangulated category. A map
$\mathscr {C}$
be a triangulated category. A map
![]() $\lambda : \mathrm {ob}(\mathscr {C}) \longrightarrow G$
is said to be additive with respect to exact triangles if for all exact triangles
$\lambda : \mathrm {ob}(\mathscr {C}) \longrightarrow G$
is said to be additive with respect to exact triangles if for all exact triangles
![]() $X \longrightarrow Y \longrightarrow Z \stackrel {+1}{\longrightarrow }$
in
$X \longrightarrow Y \longrightarrow Z \stackrel {+1}{\longrightarrow }$
in
![]() $\mathscr {C}$
, one has,
$\mathscr {C}$
, one has,
![]() $\lambda (Y) = \lambda (X) + \lambda (Z)$
.
$\lambda (Y) = \lambda (X) + \lambda (Z)$
.
Similarly, given
![]() $\mathscr {A}$
an abelian category, a map
$\mathscr {A}$
an abelian category, a map
![]() $\lambda : \mathrm {ob}(\mathscr {A}) \longrightarrow G$
is said to be additive with respect to short exact sequences if for all short exact sequences
$\lambda : \mathrm {ob}(\mathscr {A}) \longrightarrow G$
is said to be additive with respect to short exact sequences if for all short exact sequences
![]() $0 \longrightarrow X \longrightarrow Y \longrightarrow Z \longrightarrow 0$
in
$0 \longrightarrow X \longrightarrow Y \longrightarrow Z \longrightarrow 0$
in
![]() $\mathscr {A}$
, one has
$\mathscr {A}$
, one has
![]() $\lambda (Y) = \lambda (X) + \lambda (Z)$
.
$\lambda (Y) = \lambda (X) + \lambda (Z)$
.
Theorem 4.14. Let
![]() $\lambda : \mathrm {ob}(\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))) \longrightarrow G$
be an additive map with respect to exact triangles such that for all cohomologically bounded sequence
$\lambda : \mathrm {ob}(\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))) \longrightarrow G$
be an additive map with respect to exact triangles such that for all cohomologically bounded sequence
![]() $(M_n)$
, and M, compactly generated constructible persistence modules in
$(M_n)$
, and M, compactly generated constructible persistence modules in
![]() $\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
,
$\mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
,
Then for all compactly generated constructible persistence modules
![]() $M,N \in \mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
:
$M,N \in \mathrm {D}^b_{\mathbb {R} c }(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
:
Proof. By the universal property of the Grothendieck group, there exists a unique group morphism
![]() $\Phi : \mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c}(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))) \longrightarrow G$
such that the following diagram of maps
$\Phi : \mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c}(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))) \longrightarrow G$
such that the following diagram of maps

is commutative. For
![]() $\varphi ,\psi \in \mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c}(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))) $
, define
$\varphi ,\psi \in \mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c}(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))) $
, define
![]() $\delta ^{-1}(\varphi , \psi ) := \delta (\Phi (\varphi ), \Phi (\psi )).$
It is a pseudo-extended metric on
$\delta ^{-1}(\varphi , \psi ) := \delta (\Phi (\varphi ), \Phi (\psi )).$
It is a pseudo-extended metric on
![]() $\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c}(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)))$
. Moreover,
$\mathrm {K}_0(\mathrm {D}^b_{\mathbb {R} c}(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d)))$
. Moreover,
![]() $\delta ^{-1}$
is
$\delta ^{-1}$
is
![]() $d_I$
-dominated by commutativity of the above diagram. Therefore, by Corollary 4.12, for all
$d_I$
-dominated by commutativity of the above diagram. Therefore, by Corollary 4.12, for all
![]() $M,N \in \mathrm {D}^b_{\mathbb {R} c}(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
compactly generated such that
$M,N \in \mathrm {D}^b_{\mathbb {R} c}(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
compactly generated such that
![]() $d_I(M,N) < +\infty $
, one has:
$d_I(M,N) < +\infty $
, one has:
Theorem 4.15. Let
![]() $\lambda : \mathrm {ob}(\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)) \longrightarrow G$
be an additive map with respect to short exact sequences such that for all
$\lambda : \mathrm {ob}(\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)) \longrightarrow G$
be an additive map with respect to short exact sequences such that for all
![]() $(N_n)$
and N, compactly generated constructible persistence modules in
$(N_n)$
and N, compactly generated constructible persistence modules in
![]() $\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
,
$\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
,
Also, assume that the sum map
![]() $G \times G \longrightarrow G$
and the symmetric map
$G \times G \longrightarrow G$
and the symmetric map
![]() $G \longrightarrow G$
are continuous with respect to
$G \longrightarrow G$
are continuous with respect to
![]() $\delta $
. Then, for all compactly generated constructible persistence modules
$\delta $
. Then, for all compactly generated constructible persistence modules
![]() $M,N \in \mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
,
$M,N \in \mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
,
Proof. Let
![]() $\lambda $
be as in the statement of the theorem. We extend it as a map
$\lambda $
be as in the statement of the theorem. We extend it as a map
![]() $\overline {\lambda } : \mathrm {ob}(\mathrm {D}^b_{\mathbb {R} c}(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))) \longrightarrow G$
, by
$\overline {\lambda } : \mathrm {ob}(\mathrm {D}^b_{\mathbb {R} c}(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))) \longrightarrow G$
, by
![]() $\overline {\lambda }(M) := \sum _i (-1)^i \lambda (\mathrm {H}^i(M))$
(the sum is always finite by boundedness assumption, hence well defined in G). One checks easily that
$\overline {\lambda }(M) := \sum _i (-1)^i \lambda (\mathrm {H}^i(M))$
(the sum is always finite by boundedness assumption, hence well defined in G). One checks easily that
![]() $\overline {\lambda }$
is additive with respect to exact triangles. Moreover, since the
$\overline {\lambda }$
is additive with respect to exact triangles. Moreover, since the
![]() $\varepsilon $
-shift functor is exact, the cohomological functors
$\varepsilon $
-shift functor is exact, the cohomological functors
![]() $\mathrm {H}^i$
preserve interleavings. Therefore, for
$\mathrm {H}^i$
preserve interleavings. Therefore, for
![]() $(N_n)$
and N compactly generated persistence modules in
$(N_n)$
and N compactly generated persistence modules in
![]() $\mathrm {D}^b_{\mathbb {R} c}(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
, if
$\mathrm {D}^b_{\mathbb {R} c}(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
, if
![]() $d_I(N,N_n)\underset {n \longrightarrow +\infty }{\longrightarrow } 0$
, then for all
$d_I(N,N_n)\underset {n \longrightarrow +\infty }{\longrightarrow } 0$
, then for all
![]() $i\in \mathbb {Z}$
,
$i\in \mathbb {Z}$
,
![]() $d_I(\mathrm {H}^i(N),\mathrm {H}^i(N_n))\underset {n \longrightarrow +\infty }{\longrightarrow } 0$
. Therefore, by assumptions,
$d_I(\mathrm {H}^i(N),\mathrm {H}^i(N_n))\underset {n \longrightarrow +\infty }{\longrightarrow } 0$
. Therefore, by assumptions,
Assume in addition that
![]() $(N_n)$
is cohomologically bounded, that is, there exists
$(N_n)$
is cohomologically bounded, that is, there exists
![]() $C \in \mathbb {Z}_{\geq 0}$
such that for all
$C \in \mathbb {Z}_{\geq 0}$
such that for all
![]() $n \geq 0$
,
$n \geq 0$
,
![]() $\mathrm {H}^i(N_n) \simeq 0$
whenever
$\mathrm {H}^i(N_n) \simeq 0$
whenever
![]() $|i |> C$
. We also assume without loss of generality that
$|i |> C$
. We also assume without loss of generality that
![]() $\mathrm {H}^i(N) \simeq 0$
for all
$\mathrm {H}^i(N) \simeq 0$
for all
![]() $|i |> C$
. Therefore,
$|i |> C$
. Therefore,
![]() $\overline {\lambda }(N) = \sum _{i = -C}^C (-1)^i \lambda (\mathrm {H}^i(N))$
, and for all
$\overline {\lambda }(N) = \sum _{i = -C}^C (-1)^i \lambda (\mathrm {H}^i(N))$
, and for all
![]() $n \geq 0$
,
$n \geq 0$
,
![]() $\overline {\lambda }(N_n) = \sum _{i = -C}^C (-1)^i \lambda (\mathrm {H}^i(N_n))$
. By continuity of the group operations with respect to
$\overline {\lambda }(N_n) = \sum _{i = -C}^C (-1)^i \lambda (\mathrm {H}^i(N_n))$
. By continuity of the group operations with respect to
![]() $\delta $
, one has
$\delta $
, one has
Therefore,
![]() $\overline {\lambda }$
satisfies the hypothesis of Theorem 4.14, and we can conclude for all compactly generated persistence modules
$\overline {\lambda }$
satisfies the hypothesis of Theorem 4.14, and we can conclude for all compactly generated persistence modules
![]() $M,N \in \mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
, if
$M,N \in \mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
, if
![]() $d_I(M,N)< +\infty $
, then
$d_I(M,N)< +\infty $
, then
Our effort to formulate the consequences of our main result in a purely persistent and nonderived setting, allows using the universality result proved by Lesnick in [Reference Lesnick30, Corollary 5.6], that we recall here. Given
![]() $f : X \longrightarrow \mathbb {R}^d$
, its sublevelsets filtration is the functor
$f : X \longrightarrow \mathbb {R}^d$
, its sublevelsets filtration is the functor
![]() $\mathcal {S}(f) : (\mathbb {R}^d, \leq ) \longrightarrow \textbf {Top}$
defined by
$\mathcal {S}(f) : (\mathbb {R}^d, \leq ) \longrightarrow \textbf {Top}$
defined by
![]() $\mathcal {S}(f)(x) := f^{-1} \{s \in \mathbb {R}^d \mid s \leq x\}$
, and its i-th persistence module is the functor
$\mathcal {S}(f)(x) := f^{-1} \{s \in \mathbb {R}^d \mid s \leq x\}$
, and its i-th persistence module is the functor
![]() $\mathcal {S}_i(f) :=\mathrm {H}_i(-; \mathbf {k}) \circ \mathcal {S}(f)$
, with
$\mathcal {S}_i(f) :=\mathrm {H}_i(-; \mathbf {k}) \circ \mathcal {S}(f)$
, with
![]() $\mathrm {H}_i(-; \mathbf {k})$
the i-th singular homology with coefficients in
$\mathrm {H}_i(-; \mathbf {k})$
the i-th singular homology with coefficients in
![]() $\mathbf {k}$
functor.
$\mathbf {k}$
functor.
For
![]() $f : X \longrightarrow \mathbb {R}^d$
and
$f : X \longrightarrow \mathbb {R}^d$
and
![]() $g : X \longrightarrow \mathbb {R}^d$
two continuous maps of topological space, one sets
$g : X \longrightarrow \mathbb {R}^d$
two continuous maps of topological space, one sets
where h ranges over all homeomorphisms from X to Y.
Recall that a field
![]() $\mathbf {k}$
is said to be prime if it does not contain any proper subfields; therefore, if
$\mathbf {k}$
is said to be prime if it does not contain any proper subfields; therefore, if
![]() $\mathbf {k} = \mathbb {Q} $
or
$\mathbf {k} = \mathbb {Q} $
or
![]() $\mathbb {F}_p$
, for p a prime number.
$\mathbb {F}_p$
, for p a prime number.
Theorem 4.16 [Reference Lesnick30].
Let
![]() $\mathbf {k}$
be a prime field and d be a pseudo-extended metric on
$\mathbf {k}$
be a prime field and d be a pseudo-extended metric on
![]() $\mathrm {ob}(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
such that for all maps of topological spaces
$\mathrm {ob}(\mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d))$
such that for all maps of topological spaces
![]() $f : X \longrightarrow \mathbb {R}^d$
and
$f : X \longrightarrow \mathbb {R}^d$
and
![]() $g : Y \longrightarrow \mathbb {R}^d$
, one has
$g : Y \longrightarrow \mathbb {R}^d$
, one has
Then
![]() $d \leq d_I$
.
$d \leq d_I$
.
Note that Lesnick’s proof relies on the existence of geometric lift for interleavings of persistence modules [Reference Lesnick30, Proposition 5.8], which holds without any assumption on the persistence modules. Therefore, Theorem 4.16 restricts to constructible persistence modules in the following way.
Theorem 4.17 (Universality, constructible version).
Let
![]() $\mathbf {k}$
be a prime field and d be a pseudo-extended metric on
$\mathbf {k}$
be a prime field and d be a pseudo-extended metric on
![]() $\mathrm {ob}(\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d))$
such that for all maps of topological spaces
$\mathrm {ob}(\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d))$
such that for all maps of topological spaces
![]() $f : X \longrightarrow \mathbb {R}^d$
and
$f : X \longrightarrow \mathbb {R}^d$
and
![]() $g : Y \longrightarrow \mathbb {R}^d$
such that
$g : Y \longrightarrow \mathbb {R}^d$
such that
![]() $\mathcal {S}_i(f)$
and
$\mathcal {S}_i(f)$
and
![]() $\mathcal {S}_i(g)$
are constructible, one has
$\mathcal {S}_i(g)$
are constructible, one has
Then
![]() $d \leq d_I$
.
$d \leq d_I$
.
Combining Lesnick’s universality theorem with our Theorem 4.15, we obtain the following corollary.
Corollary 4.18. Let
![]() $\lambda : \mathrm {ob}(\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)) \longrightarrow G$
be an additive map with respect to short exact sequences such that for all maps of topological spaces
$\lambda : \mathrm {ob}(\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)) \longrightarrow G$
be an additive map with respect to short exact sequences such that for all maps of topological spaces
![]() $f : X \longrightarrow \mathbb {R}^d$
and
$f : X \longrightarrow \mathbb {R}^d$
and
![]() $g : Y \longrightarrow \mathbb {R}^d$
such that
$g : Y \longrightarrow \mathbb {R}^d$
such that
![]() $\mathcal {S}_i(f)$
and
$\mathcal {S}_i(f)$
and
![]() $\mathcal {S}_i(g)$
are constructible, one has
$\mathcal {S}_i(g)$
are constructible, one has
Also, assume that the operations of G are continuous with respect to
![]() $\delta $
. Then for all compactly generated persistence modules
$\delta $
. Then for all compactly generated persistence modules
![]() $M,N \in \mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
, one has
$M,N \in \mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
, one has
4.3 Examples
In this section, we apply our results to well-known constructions that are common to TDA. We still denote by
![]() $\mathbb {V}$
a finite-dimensional real vector space endowed with a norm
$\mathbb {V}$
a finite-dimensional real vector space endowed with a norm
![]() $\|\cdot \|$
.
$\|\cdot \|$
.
4.3.1 Radon transforms
Radon transforms are a general class of transformations on constructible functions, for which there exists a well-formulated criterion of invertibility [Reference Schapira, Cohen, Giusti and Mora38]. The ECT is a particular instance of invertible Radon transform, which has found numerous applications [Reference Baryshnikov and Ghrist4, Reference Turner, Mukherjee and Boyer42, Reference Curry, Mukherjee and Turner20, Reference Crawford, Monod, Chen, Mukherjee and Rabadán18].
Let X and Y be two real analytic manifolds, and let
![]() $S \subset X \times Y$
be a locally closed subanalytic subset. Let
$S \subset X \times Y$
be a locally closed subanalytic subset. Let
![]() $q_1$
and
$q_1$
and
![]() $q_2$
be the first and second projection defined on
$q_2$
be the first and second projection defined on
![]() $X \times Y$
. We shall assume the following hypothesis:
$X \times Y$
. We shall assume the following hypothesis:
Definition 4.19. The Radon transform associated to S, is the group homomorphism
![]() $\mathscr {R}_S : \mathrm {CF}(X) \longrightarrow \mathrm {CF}(Y)$
defined by
$\mathscr {R}_S : \mathrm {CF}(X) \longrightarrow \mathrm {CF}(Y)$
defined by
Remark 4.20. When
![]() $X = \mathbb {V}$
,
$X = \mathbb {V}$
,
![]() $Y = \mathbb {S}^\ast \times \mathbb {R}$
, and
$Y = \mathbb {S}^\ast \times \mathbb {R}$
, and
![]() $S_{ECT} = \{(v, (\xi , t)) \in X \times Y \mid \xi (v) \leq t\}$
, the transform
$S_{ECT} = \{(v, (\xi , t)) \in X \times Y \mid \xi (v) \leq t\}$
, the transform
![]() $\mathscr {R}_{S_{ECT}}$
is the usual ECT. We have denoted
$\mathscr {R}_{S_{ECT}}$
is the usual ECT. We have denoted
![]() $\mathbb {S}^\ast $
the unit dual sphere of
$\mathbb {S}^\ast $
the unit dual sphere of
![]() $\mathbb {V}^\ast $
.
$\mathbb {V}^\ast $
.
Proposition 4.21. Let
![]() $X = \mathbb {V}$
, and Y be real analytic manifold, and let
$X = \mathbb {V}$
, and Y be real analytic manifold, and let
![]() $S \subset X \times Y$
satisfying hypothesis (4.4). Let
$S \subset X \times Y$
satisfying hypothesis (4.4). Let
![]() $\delta $
be a pseudo-extended distance on
$\delta $
be a pseudo-extended distance on
![]() $\mathrm {CF}(Y)$
such that
$\mathrm {CF}(Y)$
such that
![]() $\delta \circ (\mathscr {R}_S \times \mathscr {R}_S)$
is
$\delta \circ (\mathscr {R}_S \times \mathscr {R}_S)$
is
![]() $d_C$
-dominated. Then for all
$d_C$
-dominated. Then for all
![]() $\varphi ,\psi \in \mathrm {CF}(\mathbb {V})$
with compact support such that
$\varphi ,\psi \in \mathrm {CF}(\mathbb {V})$
with compact support such that
![]() $\int \varphi \mathrm {d}\chi = \int \psi \mathrm {d}\chi $
, one has
$\int \varphi \mathrm {d}\chi = \int \psi \mathrm {d}\chi $
, one has
Proof. This is a straightforward consequence of Theorem 3.11.
4.3.2 Amplitudes
In [Reference Giunti, Nolan, Otter and Waas22], the authors introduce the notion of amplitude on an abelian category
![]() $\mathscr {A}$
, as a notion of measurement of the size of objects of
$\mathscr {A}$
, as a notion of measurement of the size of objects of
![]() $\mathscr {A}$
, compatible with exact sequences.
$\mathscr {A}$
, compatible with exact sequences.
Definition 4.22. Let
![]() $\mathscr {A}$
be an abelian category. An amplitude on
$\mathscr {A}$
be an abelian category. An amplitude on
![]() $\mathscr {A}$
is a class function
$\mathscr {A}$
is a class function
![]() $\lambda : \mathrm {ob}(\mathscr {A}) \longrightarrow [0, + \infty ]$
satisfying
$\lambda : \mathrm {ob}(\mathscr {A}) \longrightarrow [0, + \infty ]$
satisfying
![]() $\lambda (0) = 0$
, and for all short exact sequence
$\lambda (0) = 0$
, and for all short exact sequence
![]() $0 \longrightarrow A \longrightarrow B \longrightarrow C \longrightarrow 0$
$0 \longrightarrow A \longrightarrow B \longrightarrow C \longrightarrow 0$
-
1.
 $\lambda (A) \leq \lambda (B)$
;
$\lambda (A) \leq \lambda (B)$
; -
2.
 $\lambda (C) \leq \lambda (B)$
;
$\lambda (C) \leq \lambda (B)$
; -
3.
 $\lambda (B) \leq \lambda (A) + \lambda (C)$
.
$\lambda (B) \leq \lambda (A) + \lambda (C)$
.
The amplitude
![]() $\lambda $
will be said to be additive if
$\lambda $
will be said to be additive if
![]() $(3)$
is an equality.
$(3)$
is an equality.
Proposition 4.23. Let
![]() $\lambda $
be an additive amplitude on
$\lambda $
be an additive amplitude on
![]() $\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
, such that for all
$\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
, such that for all
![]() $(M_n)$
and M compactly generated in
$(M_n)$
and M compactly generated in
![]() $\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
, one has
$\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
, one has
Then for all compactly generated persistence module
![]() $M, N \in \mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
such that
$M, N \in \mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
such that
![]() $d_I(M,N) < +\infty $
, one has
$d_I(M,N) < +\infty $
, one has
![]() $\lambda (M) = \lambda (N)$
.
$\lambda (M) = \lambda (N)$
.
Proof. We apply Theorem 4.15 to the additive amplitude
![]() $\lambda $
, where
$\lambda $
, where
![]() $G = (\mathbb {R},+)$
is endowed with the standard metric. Thus, for all
$G = (\mathbb {R},+)$
is endowed with the standard metric. Thus, for all
![]() $M,N \in \mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
compactly generated,
$M,N \in \mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
compactly generated,
![]() $|\lambda (M) - \lambda (N)| = 0$
.
$|\lambda (M) - \lambda (N)| = 0$
.
Corollary 4.24. Assume that
![]() $\mathbf {k}$
is a prime field, and let
$\mathbf {k}$
is a prime field, and let
![]() $\lambda : \mathrm {ob}(\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)) \longrightarrow [0,+\infty ]$
be an additive amplitude on persistence modules such that for all maps of topological spaces
$\lambda : \mathrm {ob}(\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)) \longrightarrow [0,+\infty ]$
be an additive amplitude on persistence modules such that for all maps of topological spaces
![]() $f : X \longrightarrow \mathbb {R}^d$
and
$f : X \longrightarrow \mathbb {R}^d$
and
![]() $g : Y \longrightarrow \mathbb {R}^d$
, and all
$g : Y \longrightarrow \mathbb {R}^d$
, and all
![]() $i \in \mathbb {Z}_{\geq 0}$
, if
$i \in \mathbb {Z}_{\geq 0}$
, if
![]() $\mathcal {S}_i(f)$
and
$\mathcal {S}_i(f)$
and
![]() $\mathcal {S}_i(g)$
are constructible, then
$\mathcal {S}_i(g)$
are constructible, then
Then for all compactly generated and constructible
![]() $M,N \in \mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
, one has
$M,N \in \mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
, one has
4.3.3 Additive vectorizations
It is well known that persistence modules endowed with the interleaving distance do not embed isometrically into any Hilbert space [Reference Mitra and Virk34, Theorem 4.3]. Nevertheless, since most machine learning techniques take as input elements of a vector space, it is a very common strategy to define a so-called vectorization of persistence modules, that is, a map
![]() $\Phi : \mathrm {ob}(\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)) \longrightarrow \mathbb {W}$
, where
$\Phi : \mathrm {ob}(\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)) \longrightarrow \mathbb {W}$
, where
![]() $\mathbb {W}$
is a real vector space, usually endowed with a norm
$\mathbb {W}$
is a real vector space, usually endowed with a norm
![]() $\|\cdot \|$
. To name a few, see for instance persistence landscapes [Reference Bubenik13], persistent images [Reference Adams, Emerson, Kirby, Neville, Peterson, Shipman, Chepushtanova, Hanson, Motta and Ziegelmeier1] or multiparameter persistence landscapes [Reference Vipond43].
$\|\cdot \|$
. To name a few, see for instance persistence landscapes [Reference Bubenik13], persistent images [Reference Adams, Emerson, Kirby, Neville, Peterson, Shipman, Chepushtanova, Hanson, Motta and Ziegelmeier1] or multiparameter persistence landscapes [Reference Vipond43].
Proposition 4.25. Let
![]() $\Phi : \mathrm {ob}(\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)) \longrightarrow (\mathbb {W}, \| \cdot \|)$
be an additive vectorization of persistence modules satisfying for all
$\Phi : \mathrm {ob}(\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)) \longrightarrow (\mathbb {W}, \| \cdot \|)$
be an additive vectorization of persistence modules satisfying for all
![]() $(M_n)$
and M in
$(M_n)$
and M in
![]() $\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
:
$\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)$
:
Then for all compactly generated and constructible persistence modules
![]() $M,N \in \mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d) $
, if
$M,N \in \mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d) $
, if
![]() $d_I(M,N) < +\infty $
, then
$d_I(M,N) < +\infty $
, then
![]() $\Phi (M) = \Phi (N)$
.
$\Phi (M) = \Phi (N)$
.
Proof. The proof is similar to Proposition 4.23.
Corollary 4.26. Assume that
![]() $\mathbf {k}$
is a prime field, and let
$\mathbf {k}$
is a prime field, and let
![]() $\Phi : \mathrm {ob}(\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)) \longrightarrow (\mathbb {W}, \| \cdot \|)$
be an additive vectorization of persistence modules such that for all maps of topological spaces
$\Phi : \mathrm {ob}(\mathrm {Pers}_{\mathbf {k}, \mathbb {R} c}(\mathbb {R}^d)) \longrightarrow (\mathbb {W}, \| \cdot \|)$
be an additive vectorization of persistence modules such that for all maps of topological spaces
![]() $f : X \longrightarrow \mathbb {R}^d$
and
$f : X \longrightarrow \mathbb {R}^d$
and
![]() $g : Y \longrightarrow \mathbb {R}^d$
, and all
$g : Y \longrightarrow \mathbb {R}^d$
, and all
![]() $i \in \mathbb {Z}_{\geq 0}$
such that
$i \in \mathbb {Z}_{\geq 0}$
such that
![]() $\mathcal {S}_i(f)$
and
$\mathcal {S}_i(f)$
and
![]() $\mathcal {S}_i(g)$
are constructible and compactly generated, one has
$\mathcal {S}_i(g)$
are constructible and compactly generated, one has
Then for all compactly generated and constructible persistence modules
![]() $M,N \in \mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d) $
, if
$M,N \in \mathrm {Pers}_{\mathbf {k}}(\mathbb {R}^d) $
, if
![]() $d_I(M,N) < +\infty $
, then
$d_I(M,N) < +\infty $
, then
![]() $\Phi (M) = \Phi (N)$
.
$\Phi (M) = \Phi (N)$
.
Remark 4.27. The construction
![]() $\|\Phi (\cdot )\|$
, where
$\|\Phi (\cdot )\|$
, where
![]() $\Phi $
is an additive vectorization of persistence modules, provides a very general mean of defining not necessarily additive amplitudes of persistence modules. One interpretation of Proposition 4.25 and Corollary 4.26 is that such amplitudes can never be reasonably controlled, either by the interleaving distance
$\Phi $
is an additive vectorization of persistence modules, provides a very general mean of defining not necessarily additive amplitudes of persistence modules. One interpretation of Proposition 4.25 and Corollary 4.26 is that such amplitudes can never be reasonably controlled, either by the interleaving distance
![]() $d_I$
on persistence modules nor by the infinite distance
$d_I$
on persistence modules nor by the infinite distance
![]() $d_\infty $
on functions.
$d_\infty $
on functions.
5 Discussion and further work
Our main results Theorem 3.11 and Corollary 3.12 show that any distance on the group of constructible that can be controlled by the convolution distance – in the sense of domination – vanishes as soon as two compactly supported constructible functions
![]() $\varphi ,\psi $
have the same Euler integral, a condition that is satisfied whenever there exists two sheaves
$\varphi ,\psi $
have the same Euler integral, a condition that is satisfied whenever there exists two sheaves
![]() $F,G \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {V}})$
satisfying
$F,G \in \mathrm {D}^b_{\mathbb {R} c}(\mathbf {k}_{\mathbb {V}})$
satisfying
![]() $d_C(F,G) < +\infty $
and such that
$d_C(F,G) < +\infty $
and such that
![]() $\varphi = \chi (F)$
and
$\varphi = \chi (F)$
and
![]() $\psi = \chi (G)$
. The convolution distance is usually interpreted as a
$\psi = \chi (G)$
. The convolution distance is usually interpreted as a
![]() $\ell _\infty $
type metric, because of the form of stability (Theorem 2.17) it satisfies. Our results therefore give a strong negative incentive on the possibility of a obtaining a
$\ell _\infty $
type metric, because of the form of stability (Theorem 2.17) it satisfies. Our results therefore give a strong negative incentive on the possibility of a obtaining a
![]() $\ell _\infty $
-control of the pushforward operation on constructible functions.
$\ell _\infty $
-control of the pushforward operation on constructible functions.
In terms of TDA, our result shows that additive invariants of persistence modules cannot be stable with respect to the interleaving distance. Therefore, in order to obtain well-behaved invariants, it is necessary to either loosen the additivity assumption or to consider stability with respect to other type of distances. These are both active fields of research [Reference Bubenik, Scott and Stanley14, Reference Skraba and Turner41, Reference Bakke Botnan, Oppermann, Oudot and Scoccola12], for which we hope that the present article will highlight the importance.
Schapira recently introduced the concept of constructible functions up to infinity [Reference Schapira40], that allows one to define Euler integration of constructible functions without compact support. We conjecture that Theorem 3.11 holds when replacing with compact support by constructible up to infinity, though we do not know how to adapt our
![]() $\varepsilon $
-flag technique to this setting.
$\varepsilon $
-flag technique to this setting.
Competing interests
The authors have no competing interest to declare.
Financial support
This work was supported by funds of the Laboratory for Topology and Neuroscience at EPFL.