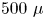Self-organization in the avalanche, quench and dissipation of a molecular ultracold plasma

Abstract

Spontaneous avalanche to plasma begins in the core of an ellipsoidal Rydberg gas of nitric oxide. Ambipolar expansion of NO$^+$ draws energy from avalanche-heated electrons. Then, cycles of long-range resonant electron transfer from Rydberg molecules to ions equalize their relative velocities. This sequence of steps gives rise to a remarkable mechanics of self-assembly, in which the kinetic energy of initially formed hot electrons and ions drives an observed separation of plasma volumes. These dynamics adiabatically sequester energy in a reservoir of mass transport, starting a process that anneals separating volumes to form an apparent glass of strongly coupled ions and electrons. Short-time electron spectroscopy provides experimental evidence for complete ionization. The long lifetime of this system, particularly its stability with respect to recombination and neutral dissociation, suggests that this transformation affords a robust state of arrested relaxation, far from thermal equilibrium. We see this most directly in the excitation spectrum of transitions to states in the initially selected Rydberg series, detected as the long-lived signal that survives a flight time of $500\ \mathrm {\mu }$s to reach an imaging detector. The initial density of electrons produced by prompt Penning ionization, which varies with the selected initial principal quantum number and density of the Rydberg gas, determines a balance between the rising density of ions and the falling density of Rydberg molecules. This Penning-regulated ion-Rydberg molecule balance appears necessary as a critical factor in achieving the long ultracold plasma lifetime to produce spectral features detected after very long delays.

Nomenclature

Greek symbol

1. Introduction

Precisely controlled conditions of laser excitation can drive cold atomic and molecular gases to form ultracold plasmas. Accessible conditions of production and evolution traverse regimes of density, $\rho$ and temperature, $T$, in which the average inter-particle potential energy, determined by the Wigner–Seitz radius, $a_{{\rm ws}} = (3/4 {\rm \pi}\rho )^{1/3}$, exceeds the thermal kinetic energy, and the coupling parameter, $\varGamma$,

(1.1)\begin{equation} \varGamma = \frac{e^2}{4 {\rm \pi}\epsilon_0 a_{{\rm ws}} k_B T}, \end{equation}

exceeds one. Under such conditions, ultracold plasmas afford isolated laboratory systems that can act as a scalable gauge of collision and transport properties under strongly coupled conditions (Deutsch, Zwicknagel & Bret 2009; Morrison, Saquet & Grant 2012; Bergeson et al. 2019). The physics of strong coupling acts to affect the dynamics of natural plasmas over a wide range of length scales (Killian et al. 2007).

Long-range correlations can steer dissipative many-body systems to transient states with an emergent dynamics in which small driving forces produce local fluctuations that trigger avalanche-like energy dissipation events. When organized to form size distributions described by power laws, such a dynamics can signal evolution to a scale-invariant critical state. This consequence, known as self-organized criticality, emerges from a superposition of local interactions that drives the system to a critical attractor irrespective of external parameters (Bak, Tang & Wiesenfeld 1987; Turcotte 1999). The process of self-organization occurs universally in coupled nonlinear systems whenever instabilities that dissipate free energy rise above some threshold and trigger avalanches.

Principles of self-organization apply to a wide variety of observations in planetary physics, solar physics, stellar physics, galactic physics and cosmology, driven globally by gravity, electromagnetic forces, particle fluxes, density gradients and subject to avalanche owing to magneto-rotational or convective instabilities, turbulence, vortex attraction, magnetic reconnection or plasma condensation (Aschwanden et al. 2018). The avalanching paradigm of self-organized criticality extends well to efforts to model and understand multiscale plasma instabilities, including transport properties near marginal stability in hot tokamak plasmas (Diamond & Hahm 1995; Hahm & Diamond 2018), as well as less complex dynamics of cold plasma double layers such as those formed in the ionosphere and unmagnetized DC discharges with electron temperatures less than 5 eV (Alex et al. 2017; Bose, Majumder & Paul 2022).

Recent experiments and theory have found signs of self-organized criticality in the off-resonant excitation of atomic Rydberg gases in the anti-blockade regime (Ding et al. 2020; Helmrich et al. 2020; Klocke et al. 2021; Brady et al. 2023). Here, exacting probes of interaction-induced line shifts and broadening together with measured size distributions of transition avalanches bear directly on the underlying physics of self-organization, supporting, for example, the development of a Langevin representation of the driven-dissipative Rydberg dynamics that connects microscopic atomic degrees of freedom to macroscopic self-organization and universality. These systems offer a tuneable environment with which to represent the dynamics in analogous natural systems.

Here, we report work on the properties of the arrested ultracold plasma state formed in a supersonic molecular beam by the spontaneous relaxation of a nitric oxide Rydberg gas, selected to occupy a single initial principal quantum number, $n_0$, in the series $nf(2)$. The laser-crossed-beam illumination geometry yields a well-defined Gaussian ellipsoidal peak density, $\rho _0$. Evidence shows that, over a correlated range of $n_0$ and $\rho _0$, all state-selected Rydberg gases evolve to form ultracold plasmas of the same average density and low internal kinetic energy. This process of self-organization appears to arise from a fundamental dynamics quenching the energy released in local avalanches that drive the system to the state of an evident attractor owing to interactions entirely within the system.

The self-organization at work in the nitric oxide ultracold plasma vastly exceeds the complexity of the driven-dissipative dipole anti-blockade. Nevertheless, much as an avalanche of dipole–dipole interactions competes with radiative decay to form a critical density of laser-driven excited potassium atoms, the molecular Rydberg gas appears to support a spontaneous flux of electron, NO$^+$ ion and Rydberg collisions that competes with neutral predissociation to shape an evolution to a consistent state of ultracold plasma. The following account details evidence assembled from a set of experiments that suggests the possibility of criticality as a factor underlying in these rate processes.

2. Experimental methods

2.1. Long flight-path molecular beam ultracold plasma imaging spectrometer

A pulsed jet of NO seeded 1:10 in helium at 5 bar enters a source chamber at 10 Hz. After 35 mm, the jet transits a 1 mm diameter skimmer to enter a differentially pumped experimental chamber. Copropagating dye laser pulses, $\omega _1$ and $\omega _2$, cross the skimmed supersonic molecular beam 150 mm further downstream, encountering a local peak density of nitric oxide of $1.6 \times 10^{14}$ cm$^{-3}$ in a Gaussian width of 3 mm ($\sigma = 1.27$ mm) at a temperature of 0.6 K measured in the longitudinal direction ($z$), with transverse ($x,y$) motion cooled to 5 mK (Schulz-Weiling et al. 2016). The 0.5 mm Gaussian width of $\omega _1$ defines a Gaussian ellipsoidal illumination volume with a 6:1 aspect ratio. Saturated steps of $\omega _1$ and $\omega _2$ excitation form a nitric oxide Rydberg gas in this volume with a consistent peak density of $5 \pm 1 \times 10^{12}$ cm$^{-3}$ ($5\ \mathrm {\mu }$m$^{-3}$). Introducing a delay between the $\omega _1$ and $\omega _2$ laser pulses quantitatively scales that initial Rydberg gas volume to smaller size.

Electron-impact avalanche to plasma begins on a nanosecond time scale in Rydberg gases produced with short $\omega _1$ and $\omega _2$ delays. A relatively small number of electrons escapes at the onset of this process. Experiments in the imaging machine sample these prompt electrons using a shielded channel electron multiplier mounted near the point of laser illumination. Correlation with the measured separation velocity of bifurcating plasma volumes indicates that relatively small fluctuations in this signal correlate with variations in the density of the initial Rydberg gas.

Within an elapsed time of $500\ \mathrm {\mu }$s after $\omega _2$, the excited volume propagates a distance of 0.7 m along the axis of the field-free experimental chamber to transit a grounded grid and reach a perpendicularly mounted Burle 75 mm dual microchannel plate phosphor-anode imaging detector, which is capacitively coupled to a transient digitizer and monitored externally by a CCD camera. Figure 1 illustrates the illumination geometry and flight path to the imaging detector.

Figure 1. Schematic illustrations showing the illumination geometries, flight path and detection set-ups in the experimental chambers of skimmed supersonic molecular beam spectrometers used to acquire long-time ultracold plasma bifurcation images under field-free conditions (a), and short-time, selective field ionization spectra (b) where the interaction region is straddled by three plates, an entrance aperture, $G_1$, and detection grids, $G_2$ and $G_3$.

2.2. Apparatus and method for selective field ionization

We propagate ultracold plasma volumes in a differentially pumped, variable flight-path apparatus for short-time measurements of selective field ionization (SFI) spectra (Saquet et al. 2011; Haenel et al. 2017). Here, as diagrammed in figure 1, copropagating pulses, $\omega _1$ and $\omega _2$, cross a skimmed supersonic molecular beam between an entrance aperture $G_1$ and grid $G_2$. A carriage, moveable in $z$, holds $G_2$ and a grid assembly, $G_3$ to which is mounted a dual multichannel plate detector. The potential difference between $G_1$ and grid $G_2$ is initially set to 0.00 V cm$^{-1}$, rigorously confirmed by detection of a test pulse of slow photoelectrons. The experiment normally operates with a $G_2$–$G_3$ potential in the range from 30 to 100 V cm$^{-1}$.

The SFI measurement begins with the application of a ramp field rising at $-0.8$ V cm$^{-1}$ ns$^{-1}$ applied to $G_1$ after a fixed delay with respect to $t=0$ defined by $\omega _2$. A transient digitizer collects the trace of the signal for conversion to a spectrum of electron binding energy. A typical experiment collects 4000 such traces for initial Rydberg gas densities varied systematically by $\omega _1$–$\omega _2$ delay to span a scale from 1 to 0.007.

Experiments in the moving grid and plasma imaging machines monitor the subsequent evolution from Rydberg gas to plasma on decidedly different time scales. Ramped electrostatic fields in the moving grid machine collect SFI spectra reflective of plasma density and distribution of electron binding energy as a function of evolution time, ranging from tens of nanoseconds to a few microseconds. The imaging machine spatially resolves the distribution of charge density in bifurcating plasma volumes after flight times of approximately $500\ \mathrm {\mu }$s.

2.3. Nitric oxide double-resonance spectroscopy and the density control of a state-selected Rydberg gas of nitric oxide

Copropagating pulses from a pair of Nd:YAG pumped dye lasers promote a double-resonant sequence of transitions to form a state-selected Rydberg gas of nitric oxide. Setting an output energy near $4\ \mathrm {\mu }$J, we tune the first laser pulse to the transition, $X {}^2\varPi _{1/2}\ N''= 1 \xrightarrow {\omega _1} A\ {}^2\varSigma ^+N'=0$. After a variable time delay, $\Delta t_{\omega _1-\omega _2}$, the second laser, 5 mJ pulse ($\omega _2$) promotes excited molecules to a selected Rydberg state. Molecules in the intermediate state, with total angular momentum neglecting electron spin, $N'=0$, can undergo second-photon transitions only to states with final $N=1$. Among these, only non-penetrating $f$ states of orbital angular momentum, $\ell =3$, built upon an NO$^+$ core with $N^+=2$ have sufficient lifetime with respect to predissociation, forming a Rydberg gas exclusively in the hydrogenic series, $n_0f(2)$.

3. Results

3.1. Resonances in the action spectrum of a persistent molecular ultracold plasma

With the $\omega _1$ dye laser tuned to prepare the $N' = 0$ rotational level of the vibrationless $A\ {}^2\varSigma ^+$ state of NO, a scan of $\omega _2$ produces an action spectrum detected in the electron signal measured after a $500\ \mathrm {\mu }$s field-free flight, when the illuminated volume travelling with the propagating beam strikes the imaging detector. Figure 2 shows a set of such $n_0f(2)$ excitation spectra recorded for $\omega _1-\omega _2$ delays chosen to yield initial average Rydberg gas densities of $5 \times 10^{12}$, $5 \times 10^{11}$ and $1.25 \times 10^{11}\ {\rm cm}^{-1}$.

Figure 2. Excitation spectrum of $\omega _2$ transitions to states in the $n_0 f (2)$ series found when integrating the long-lived ultracold plasma signal as pictured in figure 3 for the initial densities, reading from bottom to top: $5 \times 10^{12}$, $5 \times 10^{11}$ and $1.25 \times 10^{11}\ {\rm cm}^{-1}$. All scans of detected spectral intensities are plotted on the same scale: the active domains of these distributions over $n_0$ all yield approximately the same arrested density for all values of $\rho _0$. Points plotted at each principal quantum number denote relative values of the charge-transfer pair density, defined by: $\rho _{{\rm CT}} = (\rho _{{\rm NO}^+})(\rho _{{\rm NO}^*})/({\rho _{{\rm NO}^+} + \rho _{{\rm NO}^*}})$. See § 4.3.

We recorded these spectral intensities with no adjustment in the gain of the detection system. What is more, this experiment yields envelopes of comparable absolute intensity for initial Rydberg gas densities as low as $1 \times 10^{10}\ {\rm cm}^{-1}$. Thus, over a range of more than two orders of magnitude in initial density, resonant features within broad envelopes of active $n_0f(2)$ states signal long-lived plasmas of approximately equal final density. But, note how the magnitude of $n_0$ that marks the peak in the envelope of double-resonant transitions shifts to a lower value with increasing density of the initial Rydberg gas.

3.2. Plasma waveforms in space following field-free propagation

As noted above, among the $N=1$ levels accessible at a given $n_0$, only states in the $n_0f(2)$ series, converging to $N^+=2$ with orbital angular momentum, $\ell =3$ live long enough to support evolution to the long-lived state of a bifurcated ultracold plasma. Figure 3 displays a sequence of spatial distributions of plasma signal measured in the $x,y$ plane, collected following $500\ \mathrm {\mu }$s of field-free flight as the molecular NO ultracold plasma, propagating with the molecular beam in $z$, strikes the perpendicular face of a microchannel plate (MCP) imaging detector.

Figure 3. Plasma bifurcation and recoil: (left) $x,y$ images of ultracold plasma volumes produced by 6:1 aspect ratio ellipsoidal $44f(2)$ Rydberg gases after flight times of $500\ \mathrm {\mu }$s over a distance of 700 mm, for estimated initial densities of $5 \times 10^{11},\ 6.5 \times 10^{11},\ 8 \times 10^{11}$ and $1 \times 10^{12}$ cm$^{-3}$ reading from the smallest to largest separations. (right) Bifurcated traces giving pairs of replicate absolute sums of imaging detector columns in $y$ as a function of $x$ for the images pictured on the left.

Note the evidently uniform density of the $x,y$ area of each image. Each panel shows the sum of 100 single shots, selected for common initial density, as proportionately determined upstream at the point of excitation by the prompt electron signal collected on a monitor channel electron multiplier. Scaling from a maximum density of $6 \times 10^{12}\ {\rm cm}^{-1}$ at an $\omega _1-\omega _2$ delay of zero, we estimate that the initial densities represented here extend from $5 \times 10^{11}$ to $1\times 10^{12}\ {\rm cm}^{-3}$.

The same absolute colour scale applies to all contours in figure 3. The uniform appearance of these images thus signifies that all of these bifurcating volumes reach the detector with the same average Gaussian density. To estimate this density, we calibrate the imaging detector response by an experiment in which we create a Rydberg gas with a double-resonant pair of saturated $\omega _1 + \omega _2$ transitions with laser pulses configured to cross the beam approximately 6 cm from the shielded entrance to the MCP. We know the NO density in the beam at this point (Schulz-Weiling et al. 2016), and can rely on a knowledge of the short-term plasma dynamics to relate image intensity to an absolute number of electrons collected to form each 1 cm diameter lobe pictured in figure 3. Knowing the molecular beam velocity, a digital sample of the electron signal waveform at the imaging detector anode accurately determines that these invariant prolate volumes have a Gaussian depth in $z$ of 3.5 cm. From the calibrated image signal and the measured dimensions, we estimate that, after a flight of $500\ \mathrm {\mu }$s, the NO ultracold plasma relaxes to a density in the neighbourhood of $2.7\times 10^{9}\ {\rm cm}^{-3}$ or $0.0027\ \mathrm {\mu }$m$^{-3}$.

Plasmas formed over a wide range of initial conditions all yield comparable average numbers of particles in long-lived distributions that slowly expand to form very similar bifurcating volumes. The relative velocity with which these volumes separate depends sensitively on the selected initial principal quantum number, $n_0$, and initial density, $\rho _0$, but the final density and degree of expansion (signifying internal energy) remain largely invariant to these initial conditions. The right-hand frame of Figure 3 plots the integrated raw signal in $y$ and $z$ for all of the images displayed to the left, further reinforcing the conclusion that the total magnitude of the final, bifurcated plasma signal varies little with the initial density.

3.3. Selective field ionization contour maps of electron binding energy as a function of plasma evolution time

We have applied fast-rising electrostatic tramps to probe the SFI spectra of evolving plasma volumes immediately after $\omega _2$ and with delays of 150, 450 and 600 ns, as well as 1, 2 and $4\mathrm {\mu }$ in the moving grid machine, and after a field-free flight of $400\ \mathrm {\mu }$s in the imaging machine. Figure 4 shows contours of electron signal formed by linear ramps rising at 0.8 V cm$^{-1}$ ns$^{-1}$ with these selected delays after the preparation of $44f(2)$ Rydberg gases of nitric oxide. At every selected ramp-field delay, we systematically increase the $\omega _1 - \omega _2$ double-resonant excitation delay in 50 steps of 20 ns from 0 to $1\ \mathrm {\mu }$s, exponentially decreasing the intermediate state density. In each case, this procedure provides a SFI map of electron binding energy and its fluctuation, referenced in each case to the same systematically varied size of the initial Rydberg gas ellipsoid, scaled by $\omega _1 - \omega _2$ delay over a range from 1 to 0.007.

Figure 4. Contours, each displaying four thousand traces plotting the relative electron signal as a function of the amplitude of a delayed electrostatic field that rises at $0.8\ {\rm V}\ {\rm cm}^{-1}\ {\rm ns}^{-1}$, 0, 150, 450 and 600 ns, as well as 1, 2, 4 and $400\ \mathrm {\mu }$s after an $\omega _2$ pulse that forms a $44f(2)$ Rydberg gas. Traces in each panel are stacked from top to bottom in the order of the integrated electron signal. Note the substantially expanded scale that marks the rising electrostatic field applied after $400\ \mathrm {\mu }$s. Here, nearly every shot yields a signal of the same integrated amplitude that appears within the first V cm$^{-1}$ of the rising field.

At a ramp-field delay of 0 ns after $\omega _2$, we see evidence for avalanche to yield a signal of weakly bound electrons characterizing a state promptly attained by Rydberg gases of higher initial density. In smaller-scale volumes formed with slightly longer $\omega _1 - \omega _2$ delays, we observe only the signal characteristic of $44 f(2)$ Rydberg molecules, field ionizing to form NO$^+$ ions in rotational states, $N^+ =1$ and 2. Note how these signals shift to slightly higher field ionization thresholds for ramp delays of 150 ns and higher. This reflects a prompt evolution of $44 f(2)$ Rydberg molecules to states of higher orbital angular momentum as a consequence of electron collisional $\ell$-mixing. Note also the small blue wedge of low electron signal at small fields for large-scale plasmas.

At all scales of initial Rydberg gas density, fluctuating early-time SFI charge densities span two orders of magnitude. However, after a long flight time, electrons collected by SFI or as long-lived plasma images signal an invariant final charge density, independent of initial Rydberg gas density or selected principal quantum number. Thus, the final panel of figure 4 shows the SFI spectrum of bifurcated volumes after flight times of $400\ \mathrm {\mu }$s. Here, we see that a potential rising to 1 V cm$^{-1}$ or less samples the full range of electron binding energies. Whether the quasi-neutral ensemble at this point is one composed of NO Rydberg molecules with $n > 150$ or free electrons trapped by an NO$^+$ space charge (or both) remains to be determined. We argue that this progress signifies forces at work that drive a self-organization in the plasma evolution dynamics.

3.4. Self-organization in the avalanche from molecular Rydberg gas to ultracold plasma

Time-resolved SFI spectra provide a means to gauge the distribution of avalanche sizes in the evolving ultracold plasma of nitric oxide. Each of the SFI contour diagrams in figure 4 stacks the electron signal traces obtained by the application of a ramped electrostatic field to 4000 successive avalanching ensembles, diminishing in scale with increasing $\omega _1 - \omega _2$ excitation delay. Overall, they map the relative particle density distribution to the electron binding energy observed at four different evolution times following $44f(2)$ Rydberg gas preparation by $\omega _2$.

Here, we see that a ramp started immediately after $\omega _2$ yields an electron binding-energy spectrum that for the most part reflects the diabatic field ionization of a $44f(2)$ Rydberg gas, as initially prepared. Only a relatively small fraction of the SFI traces show any sign of avalanche. However, after just 150 ns, a feature owing to weakly bound electrons emerges at low field in the leading edge of the ramp. Figure 4 shows that this relative intensity waveform persists for ramp delays as long as $4\ \mathrm {\mu }$s.

The integrated electron signal for each trace observed in the SFI contour obtained for a given ramp-field delay provides a gauge of avalanche size for that ultracold plasma realization. Binning such signals as a function of their magnitude yields the distribution of this quantity for evolution times from 0 to $4\ \mathrm {\mu }$s.

Figure 5 shows the distributions obtained from the contours in figure 4 observed with zero delay and at $4\ \mathrm {\mu }$s. For very short ramp delays, this distribution has the form of a Gaussian produced by the field ionization of the initially prepared Rydberg gas (blue points in figure 5). The SFI spectrum $4\ \mathrm {\mu }$s after $\omega _2$ contains very little of this residual Rydberg contribution. Instead, the electron signal recorded in each of 4000 SFI traces fits a power law as shown by the red points on this log–log plot. After a flight time of $400\ \mathrm {\mu }$s, we see from the final SFI contour in figure 4 that this distribution collapses to form ensembles of invariant final density and very low electron binding energy.

Figure 5. Log–log plot of the distribution of avalanche size measured by the total electron signal measured in 4000 SFI spectra recorded with a ramp delay of $4\ \mathrm {\mu }$s after $\omega _2$ (red), compared with the signal produced largely by Rydberg gas at a zero ramp-field delay (blue). The distribution of early time signal, arising from the initially prepared Rydberg gas together with the beginning stage of avalanche fits a Gaussian plus a slightly attenuated step function (see text below). On the time scale of a few hundred nanoseconds, the system evolves to form a plasma with very little residual $n_0$-Rydberg population. The distribution of measured electron signal at an evolution time of $4\ \mathrm {\mu }$s conforms with a power law, described by $P(N)=N^\alpha$ with $\alpha =-1.37 \pm 0.05$.

4. Discussion

4.1. Characteristic properties of a long-lived molecular ultracold plasma of nitric oxide

For initial Rydberg gas densities, $\rho _0$, ranging from $5 \times 10^{12}$ cm$^{-3}$ ($5\ \mathrm {\mu }$m$^{-3}$) to less than $1 \times 10^{10}$ cm$^{-3}$ ($0.01\ \mathrm {\mu }$m$^{-3}$), and varying intervals of initial $n_0f(2)$, ellipsoidal ultracold plasmas of nitric oxide bifurcate to form volumes of nearly invariant density. Entrained in a molecular beam, these volumes propagate to produce compact 1 cm diameter circular projections in the $x,y$ plane of an imaging detector, with an elongation in $z$ established by the time dependence of this signal.

The figure 2 $\omega _2$ excitation spectra of this signal confirm its degree of uniformity at a glance. Here, we see the magnitude of integrated electron signal waveforms collected as a function of Rydberg gas initial principal quantum number after a field free flight of $500\ \mathrm {\mu }$s. Within systematically shifting intervals of $n_0$, analysis of digital images, such as figure 3, tells us that these resonances signal a final, arrested plasma density around $0.0027\ \mathrm {\mu }$m$^{-3}$ for all initial densities. As we see from figure 4, SFI spectra of such volumes recorded near the imaging detector signify a uniform appearance potential of 1 V cm$^{-1}$.

The velocity with which these volumes separate in $x$ depends directly on the selected initial principal quantum number of the Rydberg gas, and its initial density. However, to a remarkable degree, plasmas formed with all separation velocities exhibit virtual identical volumes. To the extent that the expansion of a plasma measures its internal energy (defined by electron binding energy and temperature), plasma volumes in every case have an invariant internal energy. These intensive measures of density and temperature suggest that the nearly 200 different initial conditions represented here all ultimately yield an ultracold molecular NO plasma in the same final state.

4.2. Dynamics of ultracold plasma bifurcation

Ultracold plasma states of the same density and internal energy form spontaneously upon avalanche of Rydberg gases with different initial densities (spanning more than two orders of magnitude) and different Rydberg electron binding energies (spanning a factor of ten). By what process does the plasma rebalance its internal energy and density to attain this evidently invariant final state?

To answer this question, we refer again to figure 3. Here, we see the equivalent integrated electron signals that define the final-state density and internal energy. We also see clear evidence that plasmas formed by Rydberg gases of different initial density deposit substantially different amounts of kinetic energy in an external reservoir associated with the recoil of plasma volumes in the laboratory. Our earliest observations of this phenomenon established that the observed velocity of separation scales linearly with the initial Rydberg gas density and selected principal quantum number (Schulz-Weiling & Grant 2016).

During the course of this avalanche and bifurcation, the plasma shows direct evidence of a composition that includes both NO$^+$ ions and NO Rydberg molecules. To form compact bifurcating volumes, some process must accelerate these heavy particles and equalize their velocity.

As the avalanche begins, Rydberg molecules release potential energy by inelastic collisions with electrons. This energized electron gas expands, creating a negative charge gradient that combines with the space charge of the affected ions and drives an ambipolar expansion of the NO$^+$ ion - free e$^-$ plasma (Sadeghi & Grant 2012; Schulz-Weiling et al. 2016). The laser-crossed beam-illumination geometry defines the excited state landscape in which this expansion takes place.

In its $y,z$ coordinate directions, the expanding ions pass through a sharp gradient of declining ion and Rydberg density determined by the narrow ($\sigma \approx 0.5$ mm) Gaussian cylinder of laser illumination. In the $x$ direction, the broader ($\sigma \approx 3$ mm) Gaussian radius of the molecular beam extends the range over which ions expanding from the centre of the Rydberg gas ellipsoid traverse a gas of excited molecules in the wings. Among possible heavy particle collisional interactions, one offers the potential of a significant effect on the plasma dynamics: resonant NO$^+$ - NO Rydberg molecule charge transfer.

A single such elementary conversion effectively transfers the velocity of an accelerated ion to a newly created Rydberg molecule, and leaves a stationary ion in its wake. This adds to the inertial mass opposing ambipolar expansion. The images in figure 3 clearly suggest that the high stopping power of a resonant Rydberg gas causes this process to recur, acting to equalize the velocities of the ions and the Rydberg molecules, and adding to the dynamics that quenches the electron energy. Intermolecular forces surely act in this process of matching velocities, which likely gives rise to spatial correlation.

Interestingly, we find no surviving ultracold plasma density propagating within the core of the illuminated ellipsoid. Here, for any scale of initial plasma ellipsoid, the system must evolve to form a peak in the density of ions and electrons centred in this core. Expansion can only broaden this distribution. However, in coupled rate equation models that adequately describe the initial dynamics of electron-impact avalanche of plasma, we can recognize ion–electron recombination processes that directly and indirectly lead to loss via neutral dissociation (Haenel & Grant 2018). The void between bifurcating volumes suggests that such processes act efficiently here to deplete the ion-rich core of the nitric oxide plasma ellipsoid, but have little effect in the domain of ion-Rydberg charge transfer at larger values of ${\pm }x$.

4.3. Spectroscopic evidence that ion-Rydberg charge transfer favours plasma stability

We associate the bifurcation that is evident in figure 3 with long-range ion-Rydberg charge-transfer collisions that act to dispose the energy of avalanche electrons to a reservoir of kinetic energy formed by separation of plasma volumes that hold NO$^+$ ions and Rydberg molecules of equalized relative velocity. This mechanics of self-assembly, which appears critical for long-term ultracold plasma stability, requires avalanche conditions of balanced ion and Rydberg density in the wings of the Gaussian ellipsoid volume of the evolving plasma.

Evidence for this appears directly in the $\omega _2$ excitation spectrum of the long-lived plasma signal shown in figure 2. Here, we see evidence, for high principal quantum numbers at the highest Rydberg gas density, that avalanche at all points but the furthest reaches of the illuminated volume proceeds at a faster rate than ambipolar expansion. Under these conditions, high Rydberg gas densities give rise to avalanche conditions that exclude the formation of a long-lived plasma state. In a similar fashion, a very low-density Rydberg gas of low principal quantum number dissociates before it can avalanche. In between, we find the balance that produces the calculated curves represented by dots in figure 2.

For any principal quantum number and Rydberg gas density, an instantaneous process at the start of the avalanche sets the relative abundance of ions and Rydberg molecules, Rydberg–Rydberg Penning ionization

(4.1)\begin{equation} {\rm NO}^*(n_0) +{\rm NO}^*(n_0)\rightarrow {\rm NO}^+ + {\rm e}^-+ {\rm N}({}^4{\rm S}) +{\rm O}({}^3{\rm P}) ,\end{equation}

where we make the reasonable assumption that, in the perturbation associated with electronic energy transfer, the Penning partner descends through a manifold of efficient predissociative crossings to neutral products. We examine this hypothesis below.

Molecular dynamics simulations suggest that Penning ionization occurs within 800 orbital periods or less in a Rydberg gas when molecules selected to have an initial quantum number, $n_0$, form within a critical intermolecular distance, $r_c = 1.8 \cdot 2 n_0^2 a_0$ (Robicheaux 2005). The relatively broad bandwidth of the pulsed dye laser that supplies $\omega _2$ excludes the development of a dipole blockade. The probability of Rydberg–Rydberg nearest neighbour distances in the illuminated volume thus conforms with an Erlang distribution (Torquato, Lu & Rubinstein 1990). We can therefore determine the density of Penning ions formed by a Rydberg gas prepared in an initial state, $n_0$, at an initial density, $\rho _0$ by integrating this distribution from a nearest neighbour distance of 0 to $r_c$

(4.2)\begin{align} \rho_{{\rm NO}^+}(\rho_0,n_0) & = \frac{1}{2} \,4 {\rm \pi}\rho_0 ^2 \int_0^{r_{c}} r^2 \exp\left({-\frac{4{\rm \pi}}{3}\rho_0 r^3}\right)\mathrm{d}r \nonumber\\ & = \frac{\rho_0}{2}\left(1-\exp\left({-\frac{4{\rm \pi}}{3}\rho_0 r_c^3}\right)\right). \end{align}

Any degree of Penning ionization via the mechanism posed by (4.1) leaves a remaining density of Rydberg molecules

(4.3)\begin{equation} \rho_{{\rm NO}^*} = \rho_0 - 2\rho_{{\rm NO}^+}. \end{equation}

Evidence suggests that the evolution from state-selected Rydberg gas to a long-lived ultracold plasma state relies on charge transfer and bifurcation. This requires a population of NO$^+$ ions and electrons balanced by NO$^*$ Rydberg molecules. We can assess conditions sufficient for the support of charge transfer by means of a simple figure of merit that we might term as a charge-transfer pair density, $\rho _{{\rm CT}}$, defined by

(4.4)\begin{equation} \rho_{{\rm CT}} = \frac{(\rho_{{\rm NO}^+})(\rho_{{\rm NO}^*})}{(\rho_{{\rm NO}^+} + \rho_{{\rm NO}^*})} .\end{equation}

Figure 2 plots values of $\rho _{{\rm CT}}$ calculated using the expressions defined by (4.2), (4.3) and (4.4) for the initial densities indicated. The striking agreement of this simple model with the experimental results affirms two important conclusions: (i) for higher principal quantum numbers at higher initial density, Penning ionization leaves few Rydberg molecules and (ii) an initial balance of Rydberg and ion populations plays a critical role in long-term plasma stability, very likely by a mechanism of charge transfer manifested in the bifurcation of plasma volumes.

4.4. Self-organized criticality as a possible determinant of the molecular ultracold plasma final state

4.4.1. SFI measures of plasma electron binding-energy composition as a function of evolution time

The SFI spectra, collected as a function of plasma evolution time, mark the varying profile of electron binding as the illuminated volume progresses from $n_0f(2)$ Rydberg gas to the invariant final plasma state. Immediately after the pulse of $\omega _2$ forms a Rydberg gas, SFI spectra measured at all initial densities (at all scales of Rydberg gas ellipsoidal size) exhibit a narrow Gaussian distribution of signal with a low appearance potential, together with a proportional yield of electrons extracted from the initially prepared Rydberg state, that appears at $n_0f(2)$ thresholds for field ionization to the $N^+=0$ and 2 rotational states of NO$^+$.

Figure 5 shows a distribution of integrated signals produced by the prompt field ionization of nitric oxide Rydberg gases measured over a range of initial densities, as pictured in the top left of figure 4. The shot-to-shot amplitude of the total SFI signal fits a distribution over 4000 measurements described by the sum of a Gaussian and a linearly attenuated step function

(4.5)\begin{equation} P(N) = A\exp\left(-\left(\frac{N-\mu}{\sigma}\right)^2\right)+ B\left[\frac{1}{1+\exp(k(h-N))}-cN\right],\end{equation}

where $N$ refers to a magnitude of electron signal extracted by an SFI field ramp, and $P(N)$ represents the number of times that the SFI trace records that signal magnitude in a 4000 shot contour of SFI spectra. The constants are $A=40$, $\mu =180$, $\sigma =80$, $B=50$, $k=0.07$, $h=60$, $c=4.6\times 10^{-4}$.

A few hundred nanoseconds after $\omega _2$, we observe a slight shift of the $N^+= 0$ and 2 features to higher fields. This directly signals the start of $\ell$-mixing collisions of free electrons with $n_0f(2)$ Rydberg states. At the same time, the distribution of the electron signal extracted by SFI widens considerably. In each of 50 successive steps of $\omega _1 - \omega _2$ delay, these SFI spectra sample avalanche sizes that vary over a range that exceeds the step of attenuation caused by the decay of the intermediate $A\ {}^2\varSigma ^+$ state by more than an order of magnitude. We find that this fluctuation in avalanche size at all selected scales of initial Rydberg gas density forms a power-law distribution in the size of the shot-by-shot extracted electron signal

(4.6)\begin{equation} P(N) = N^\alpha, \end{equation}

in which $\alpha =-1.4$. More than 50 such 4000-shot measures of plasma electron binding energy at longer evolution time yield power laws that exhibit exponents of $\alpha = -1.37\pm 0.05$.

The appearance of this power law in the extracted SFI signal size coincides with the development of a constant final plasma state. The simultaneity of these two plasma characteristics – scale-invariant fluctuations in the SFI signal giving way to invariant measures of plasma intensive variables of state – are suggestive of self-organization, perhaps to a critical state.

4.4.2. Coupled rate processes leading to an ultracold plasma state of self-organized criticality: fine-grained evolution

Double-resonant excitation forms a state-selected Gaussian ellipsoid Rydberg gas of NO. Nearest-neighbour interactions in the core of this ellipsoid form a prompt distribution of NO$^+$ ions and electrons via Penning ionization

(4.7)\begin{equation} {\rm NO}^{*}(n_0) + {\rm NO}^{*}(n_0) \longrightarrow {\rm NO}^++ {\rm e}^-+ {\rm N}({}^4{\rm S}) + {\rm O}({}^3{\rm P}). \end{equation}

We assume that the electronic relaxation associated with energy transfer from the Penning partner causes its efficient predissociation. The evident importance of a residue of Rydberg molecules in forming a long-lived plasma state, and the disappearance of this state under conditions of complete Penning ionization supports this assumption.

A realistic plasma evolves in shells of different density defined by a laser-crossed molecular beam Gaussian ellipsoid. Bifurcating plasma volumes observed in images at $500\ \mathrm {\mu }$s confirm the importance of this aspect ratio. However, the kinetic processes described below proceed in every shell.

Initiated by prompt Penning ionization, a set of electron collisional interactions govern the avalanche to plasma

(4.8)\begin{gather} {\rm NO}^{*}(n_i) + {\rm e}^- {\mathrel{\mathop{\rightleftharpoons}\limits_{k_i^{3{\rm br}} }^{k_i^{{\rm Ion}} }}} {\rm NO}^++ {\rm e}^-+ {\rm e}^-\quad \text{Ionization, three-body}\;\text{recombination}, \end{gather}

(4.9)\begin{gather}{\rm NO}^{*}(n_i) + {\rm e}^- {\mathrel{\mathop{\rightleftharpoons}\limits_{k_{ji}}^{k_{ij}}}} {\rm NO}^{*}(n_j) + {\rm e}^-\quad \text{Energy redistribution}. \end{gather}

We observe the progress of this avalanche directly in time-resolved SIF distributions of electron binding energy, such as those shown in the sequence of spectra displayed in figure 4.

Molecular rate processes lead irreversibly to neutral products, diminishing density in the evolving distributions of NO($n_i$) Rydberg molecules and NO$^+$ ions

(4.10)\begin{gather} {\rm NO}^{*}(n_i) \mathop{\longrightarrow}\limits^{k^{\text{PD}}_i} {\rm N}({}^4{\rm S}) + {\rm O}({}^3{\rm P}) \quad \text{Predissociation} \end{gather}

(4.11)\begin{gather}{\rm NO}^++ {\rm e}^- \mathop{\longrightarrow}\limits^{k^{\text{DR}}} {\rm N}({}^4{\rm S}) + {\rm O}({}^3{\rm P})\quad \text{Dissociative recombination}. \end{gather}

We directly measure global rates of plasma dissipation in experiments that monitor the density of the plasma as a function of its flight time in the molecular beam. We also see the effect of dissociative recombination in the totally depleted core as it appears in images of bifurcated plasmas recorded after $500\ \mathrm {\mu }$s.

We see evidence in the initial density dependence of $\omega _2$ excitation spectra that long-time plasma stability relies ion-Rydberg balance. The compact shape of bifurcating volumes requires a momentum matching of ions and Rydberg molecules that must involve a collisional process. This evidence points to an equilibrated channel of NO($n_i$)–NO$^+$ charge transfer

(4.12)\begin{equation} {\rm NO}^{*} + {\rm NO}^+ \mathop{\longrightarrow}\limits^{k^{\text{CT}}} {\rm NO}^++ {\rm NO}^{**} \quad \text{Charge transfer} .\end{equation}

Experiment and theory, in many cases supported by molecular dynamics simulations, establish most of the rate coefficients necessary to solve this coupled system of differential equations (Mansbach & Keck 1969; Bixon & Jortner 1996; Schneider et al. 2000; Murgu, Martin & Gallagher 2001; Pohl, Pattard & Rost 2004; Pohl, Vrinceanu & Sadeghpour 2008; Sadeghi et al. 2011). Our own simulations and experiment agree, finding an ionization avalanche that proceeds on a time scale of 10–500 nanoseconds (Saquet et al. 2011; Saquet, Morrison & Grant 2012; Haenel & Grant 2018), after which the dynamics evolves much more slowly, mainly through dissipation to neutral products. To account for the residual population of long-lived molecules detected in ultracold plasma images after $500\ \mathrm {\mu }$s, we introduce (4.12) and adjust $k^{\text {CT}}$.

Figure 6 shows the results of a typical simulation showing plasma avalanche and evolution from initial conditions of $n_0=50$ and $\rho _0=0.2\ \mathrm {\mu }$m$^{-3}$ to a quasi-steady state after 200 ns, in which the ion density has settled at $0.06\ \mathrm {\mu }$m$^{-3}$ and charge exchange has formed a distribution of high Rydberg molecules with a stabilized density of $0.02\ \mathrm {\mu }$m$^{-3}$. We collect a locus of quasi-steady state ion–electron densities in an evolving regime of bifurcation, respecting the equivalence of charged particles and high Rydberg molecules in the quasi-neutral plasma. At this point, the SFI spectrum narrows to reflect regime of very low electron binding energies, and we shift from a multichannel model of elementary rate processes to a coarse-grained kinetics of long-time evolution in the relaxing plasma.

Figure 6. (a) Simulated plasma avalanche and evolution for $n_0=50$ and $\rho _0=0.2\ \mathrm {\mu }$m$^{-3}$. (b) Locus of quasi-steady state densities found for simulations over a range of selected Rydberg gas densities from $\rho _0 = 0.05$ to $5.0\ \mathrm {\mu }$m$^{-3}$ and principal quantum numbers from $n_0=40$ to 70.

4.4.3. Coarse-grained evolution

The relatively dense state of cold ion and electrons, together with high-$\ell$ Rydberg molecules, forms a coupled (perhaps strongly coupled) array of NO$^+$ charge centres. Figure 7 classically represents a set of kinetic processes in a plasma with a density of $0.05\ \mathrm {\mu }$m$^{-3}$ divided evenly between NO$^+$ ions and electrons, associated by space charge, and long-lived NO$^{**}$ Rydberg molecules with an average principal quantum number of 80.

Figure 7. (a) Schematic illustration meant to project the three-dimensional particle distribution and rate processes in a nitric oxide ultracold plasma state with a density of $0.05\ \mathrm {\mu }$m$^{-3}$ ($a_{{\rm ws}}=1.7\ \mathrm {\mu }$m), containing Rydberg molecules with a principal quantum number of 80 ($\langle r\rangle =0.34\ \mathrm {\mu }$m). (b) Phase space of NO$^+$-e$^-$ density, $C$, versus NO$^{**}$ density, $A$, in a molecular ultracold plasma relaxation governed by the attractor formed by the coupled differential equations (4.15).

We consider rate processes in this ensemble consisting of the electron-impact ionization of Rydberg molecules and an effectively two-body recombination of associated electron–ion pairs

(4.13)\begin{equation} {\rm NO}^{**} + {\rm e}^- {\mathrel{\mathop{\rightleftharpoons}\limits_{k^{2{\rm br}}}^{k^{{\rm Ion}}}}}\;({\rm NO}^+, {\rm e}^-) + {\rm e}^- \quad \text{Ionization and recombination} \end{equation}

together with the unimolecular predissociation of electron–ion pairs

(4.14)\begin{equation} ({\rm NO}^+, {\rm e}^-) \xrightarrow[]{\gamma} {\rm N}({}^4{\rm S}) + {\rm O}({}^3{\rm P}) \quad \text{Dissociative recombination} \end{equation}

Simplifying the kinetics to represent all NO$^{**}$ molecules by a variable $A=[{\rm NO}^{**}]$, and the equivalent density of NO$^+$ ions and electrons by $C=[{\rm NO}^+] = [{\rm e}^-]$, yields the coarse-grained coupled rate equations for this scheme

(4.15)\begin{equation} \left.\begin{gathered} \frac{{\rm d}}{{\rm d} t} A ={-}k^{\rm{Ion}} AC + k^{2\text{br}} C^2 \\ \frac{{\rm d}}{{\rm d} t} C = k^{\text{Ion}} AC - k^{2\text{br}} C^2 - \gamma C . \end{gathered}\right\} \end{equation}

This set of equations features the combination of a nonlinear feedback cycle through ionization and recombination, and slow dissipation through predissociation and dissociative recombination, $\gamma C$. We assume that ionization and recombination happen on similar time scales, while dissociation is much slower, $\gamma \ll 1$, $k^{\rm Ion} \approx k^{2{\rm br}}$.

4.4.4. Self-organized criticality in the coarse-grained model

Interpreted in terms of this coarse-grained model, the short- and long-time dynamics of the nitric oxide ultracold plasma show hallmarks of self-organized criticality, the most common and evident empirical signatures of which include (Buendía et al. 2020; Helmrich et al. 2020):

1. (i) A self-assembly of the system to a steady state independent of the initial conditions within a range of initial states;

2. (ii) scale invariance of observable quantities around this steady state, indicating it to be a continuous phase transition; and

3. (iii) avalanches of activity in the steady state, initiated by fluctuations of the underlying fields that follow a power-law size distribution.

At the critical point, the correlation length scale ($\zeta$) and time scale ($\tau$) of the system diverge. Autocorrelation functions which normally follow exponential decay in the sub-critical phase become scale-invariant power laws, influencing the distribution of a wide array of other properties.

The two-phase model presented in §§ 4.4.2 and 4.4.3, encompasses these elements of self-organized criticality. Fine-grained coupled rate equations predict a rapid evolution through the ionization avalanche that brings the system from a wide set of initial conditions to a locus of paired high-$\ell$ Rydberg and (NO$^+$, e$^-$) densities that ranges from (0.0025, 0.027) to (0.25, 1.05) in $\mathrm {\mu }$m$^{-3}$ as shown in figure 6. We input these points as initial conditions for the coarse-grained model and let them evolve over time. In figure 7, we see that all phase traces rapidly converge to the same final point, corresponding to a self-assembly to a single Rydberg density and no free charged particles. The two-phase plasma model thus shows the first criterion of self-organized criticality -- self-assembly to a steady state independent of the initial conditions.

In this way, a model that accurately describes the ultracold plasma in its first few hundred nanoseconds of avalanche extends to explain its evolution to an invariant final density. This avalanche, exhibiting wide-scale fluctuations that support a power-law distribution, forms a system composed of NO$^+$ ions and free electrons plus some comparable number of NO Rydberg molecules. A combination of $\ell$-mixing and fast predissociation removes Rydberg molecules of low-$\ell$, stabilizes this population.

Any process that energizes free electrons re-mixes $\ell$ and causes Rydberg molecules to predissociate, dissipating plasma density. We have observed this effect globally in experiments that diminish plasma density by the application of weak radio-frequency fields (Wang et al. 2020). The plasma represented schematically in figure 7 mixes high-$\ell$ NO$^{**}$ Rydberg molecules with paired NO$^+$ ions and electrons. We have argued above that a coarse-grained set of long-range, low-energy interactions forms an attractor that drives this system to an invariant final state. At any point in this evolution, a fluctuation can transfer energy from a Rydberg molecule to thermally excite an electron. The consequences of this excitation depend on $\sigma$, the degree to which the effects of a fluctuation propagate, and $\zeta$, the length scale over which this propagation extends.

The initial avalanche of the state-selected Rydberg gas to plasma proceeds through a supercritical active phase, in which a relatively uniform set of intermediate-range interactions give rise to a step-function avalanche size distribution as described by (4.5). After a few hundred nanoseconds, this distribution widens considerably to fit a power law at all scales of plasma size. The scale-invariant final state of this system suggests the presence of an attractor, as defined by a simple kinetic model of the long-time evolution. This attractor evidently operates to transport the relaxation of all avalanching systems through a critical phase in which $\zeta$ diverges. We see evidence of this in SFI signal intensities modulated by plasma loss. Long-range correlations that span the full size of the plasma occur with increased probability. This property develops invariant of the plasma scale. Conversely, the proportion of domains of plasma stability scale inversely with domain size on all scales. Power-law distributions of SFI signal strengths affirm this scale invariance supporting plasma evolution constrained by conditions of self-organized criticality.

Most of the common models of self-organized criticality proposed over the years build upon conserved bulk dynamics, while including dissipation only at the boundary. This is the case for the well-studied Manna sand pile, fixed-energy sand piles and some slip-stick models (Dickman, Vespignani & Zapperi 1998; Bonachela & Munoz 2009). The present system differs fundamentally from those by incorporating bulk dissipation. Very little theoretical work has been performed in the study of SOC in non-conserving systems. The present work combines the experimental realization of such a system with an ongoing, collaborative theoretical effort to establish its properties, including its universality class and critical exponents. Further theoretical work will endeavour to connect a description of the absorbing phase transition of the system to its physical state and properties, such as density, internal energy and coupling strength.

5. Conclusions

Pulsed Nd:YAG pumped dye lasers $(\omega _1+\omega _2)$ drive a double-resonant sequence of transitions to high Rydberg states in nitric oxide seeded in a supersonic molecular beam, leading in all cases to a seemingly singular, long-lived state of molecular ultracold plasma. The absolute intensities recorded in the $\omega _2$ excitation spectrum establish that the plasma yield varies little with the initial density of the state-selected Rydberg gas or its initial principal quantum number.

Over a flight time of $500\ \mathrm {\mu }$s, this plasma propagates nearly a metre in $z$ to form images in the $x,y$ plane that bifurcate in the laser illumination axis, $x$. The characteristic velocity of this bifurcation depends both on the initial density and selected principal quantum number, but internal processes evidently quench all plasmas to form images of constant size and intensity, reflecting a final state of invariant density and internal energy, regardless of the scale or state of the initial Rydberg gas.

Delayed SFI spectra provide a measure of electron binding energy in the plasma as it evolves. As typically prepared, with an average density in the range of $10^{12}$ cm$^{-3}$ ($1\ \mathrm {\mu }$m$^{-3}$), a state-selected Rydberg gas evolves to exhibit a low-field plasma signal in 200 ns or less. Early SFI spectra show the signal formed by $n_0$ Rydberg molecules. This feature shifts to a slightly higher appearance potential owing to $\ell$-mixing collisions with free electrons that drive initially selected $n_0f(2)$ molecules to long-lived $n_0\ell (2)$ states. The peaked $n_0$ structure then disappears, and the SFI spectrum of electrons of lower binding energy fluctuates widely, conforming with a power-law distribution, $P(N)=N^\alpha$ with $\alpha =1.4$. We associate the apparent scale invariance of this distribution with the self-organization of the plasma to a steady state independent of initial conditions, within a range. Small fluctuations of the underlying fields initiate avalanches of activity altering the relative density of high Rydberg molecules and ions and electrons in the active phase. The evident scale invariance in the avalanche size distribution suggests that the attractor in this system is a critical state, which likely plays a role in the evolution to a universal long-lived molecular ultracold plasma.