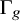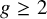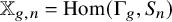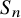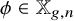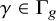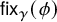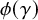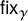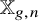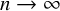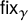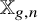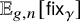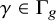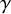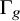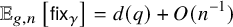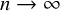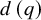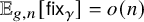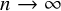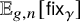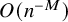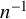1 Introduction
Let
![]() $g\geq 2$
, and let
$g\geq 2$
, and let
![]() $\Sigma _{g}$
be a closed orientable topological surface of genus g. We fix a base point
$\Sigma _{g}$
be a closed orientable topological surface of genus g. We fix a base point
![]() $o\in \Sigma _{g}$
and let
$o\in \Sigma _{g}$
and let
be the fundamental group of
![]() $\Sigma _{g}$
. Denote by
$\Sigma _{g}$
. Denote by
the representation space of all homomorphisms from
![]() $\Gamma _{g}$
to
$\Gamma _{g}$
to
![]() $S_{n}$
, where
$S_{n}$
, where
![]() $S_{n}$
is the symmetric group of permutations of
$S_{n}$
is the symmetric group of permutations of
![]() $\{1,\ldots ,n\}$
. From another point of view, the space
$\{1,\ldots ,n\}$
. From another point of view, the space
![]() $\mathbb {X}_{g,n}$
can be viewed as the space of degree-n covering maps of
$\mathbb {X}_{g,n}$
can be viewed as the space of degree-n covering maps of
![]() $\Sigma _{g}$
. Indeed, for every not-necessarily-connected degree-n covering map
$\Sigma _{g}$
. Indeed, for every not-necessarily-connected degree-n covering map
we may identify the fiber
![]() $p^{-1}\left (o\right )$
with
$p^{-1}\left (o\right )$
with
![]() $\left \{ 1,\ldots ,n\right \} $
, and the monodromy action of
$\left \{ 1,\ldots ,n\right \} $
, and the monodromy action of
![]() $\pi _{1}\left (\Sigma _{g},o\right )$
on the fiber then gives rise to a homomorphism
$\pi _{1}\left (\Sigma _{g},o\right )$
on the fiber then gives rise to a homomorphism
![]() $\phi \in \mathrm {Hom}(\Gamma _{g},S_{n})$
. This gives a one-to-one correspondence between
$\phi \in \mathrm {Hom}(\Gamma _{g},S_{n})$
. This gives a one-to-one correspondence between
![]() $\mathbb {X}_{g,n}$
and degree-n covering maps with
$\mathbb {X}_{g,n}$
and degree-n covering maps with
![]() $p^{-1}\left (o\right )=\left \{ 1,\ldots ,n\right \} $
. This correspondence is discussed in more detail in
$p^{-1}\left (o\right )=\left \{ 1,\ldots ,n\right \} $
. This correspondence is discussed in more detail in
![]() $\S \S $
2.2.
$\S \S $
2.2.
The space
![]() $\mathbb {X}_{g,n}$
was studied by Liebeck and Shalev [Reference Liebeck and ShalevLS04], who showed that a uniformly random homomorphism
$\mathbb {X}_{g,n}$
was studied by Liebeck and Shalev [Reference Liebeck and ShalevLS04], who showed that a uniformly random homomorphism
![]() $\phi \colon \Gamma _{g}\to S_{n}$
satisfies
$\phi \colon \Gamma _{g}\to S_{n}$
satisfies
![]() $\phi \left (\Gamma _{g}\right )\supseteq A_{n}$
a.a.s. (asymptotically almost surely, namely, with probability tending to
$\phi \left (\Gamma _{g}\right )\supseteq A_{n}$
a.a.s. (asymptotically almost surely, namely, with probability tending to
![]() $1$
as
$1$
as
![]() $n\to \infty $
) [Reference Liebeck and ShalevLS04, Thm. 1.12].Footnote
1
In particular the image is a.a.s. transitive, or, equivalently, the corresponding random degree-n covering space is a.a.s. connected. When
$n\to \infty $
) [Reference Liebeck and ShalevLS04, Thm. 1.12].Footnote
1
In particular the image is a.a.s. transitive, or, equivalently, the corresponding random degree-n covering space is a.a.s. connected. When
![]() $\Gamma _{g}$
is replaced by a nonabelian free group, the analogous result holds by the famous theorem of Dixon [Reference DixonDix69] that two random permutations in
$\Gamma _{g}$
is replaced by a nonabelian free group, the analogous result holds by the famous theorem of Dixon [Reference DixonDix69] that two random permutations in
![]() $S_{n}$
a.a.s. generate
$S_{n}$
a.a.s. generate
![]() $S_{n}$
or
$S_{n}$
or
![]() $A_{n}$
.
$A_{n}$
.
In the current work we address the problem of integration over the space
![]() $\mathbb {X}_{g,n}$
. Namely, our goal is to analyze the expected value
$\mathbb {X}_{g,n}$
. Namely, our goal is to analyze the expected value
![]() $\mathbb {E}_{g,n}\left [f\right ]$
of functions f on
$\mathbb {E}_{g,n}\left [f\right ]$
of functions f on
![]() $\mathbb {X}_{g,n}$
with respect to the uniform measure on
$\mathbb {X}_{g,n}$
with respect to the uniform measure on
![]() $\mathbb {X}_{g,n}$
. The functions on
$\mathbb {X}_{g,n}$
. The functions on
![]() $\mathbb {X}_{g,n}$
that we consider are natural functions that arise from loops in
$\mathbb {X}_{g,n}$
that we consider are natural functions that arise from loops in
![]() $\Sigma _{g}$
. Given an element
$\Sigma _{g}$
. Given an element
![]() $\gamma \in \Gamma _{g}$
and a character
$\gamma \in \Gamma _{g}$
and a character
![]() $\chi $
of
$\chi $
of
![]() $S_{n}$
, we let
$S_{n}$
, we let
These functions are called Wilson loops in the physics literature [Reference LabourieLab13, Def. 6.4.1]. Our focus is on the character
![]() $\mathsf {fix}$
of
$\mathsf {fix}$
of
![]() $S_{n}$
which assigns to every permutation its number of fixed points.
$S_{n}$
which assigns to every permutation its number of fixed points.
The main motivation behind this work is its relevance to the study of random covers of the closed surface
![]() $\Sigma _{g}$
. Given some
$\Sigma _{g}$
. Given some
![]() $1\ne \gamma \in \Gamma _{g}$
, consider the geodesic
$1\ne \gamma \in \Gamma _{g}$
, consider the geodesic
![]() $C_{\gamma }$
in
$C_{\gamma }$
in
![]() $\Sigma _{g}$
corresponding to the conjugacy class of
$\Sigma _{g}$
corresponding to the conjugacy class of
![]() $\gamma $
. For every homomorphism
$\gamma $
. For every homomorphism
![]() $\phi \in \mathbb {X}_{g,n}$
, the number of fixed points
$\phi \in \mathbb {X}_{g,n}$
, the number of fixed points
![]() $\mathsf {fix}_{\gamma }\left (\phi \right )$
is precisely the number of lifts of
$\mathsf {fix}_{\gamma }\left (\phi \right )$
is precisely the number of lifts of
![]() $C_{\gamma }$
to a closed geodesic in the degree-n covering corresponding to
$C_{\gamma }$
to a closed geodesic in the degree-n covering corresponding to
![]() $\phi $
. Indeed, the results of this paper are crucial ingredients in a subsequent work [Reference Magee, Naud and PuderMNP22] which gives new results on spectral gaps of random covers of a closed surface.
$\phi $
. Indeed, the results of this paper are crucial ingredients in a subsequent work [Reference Magee, Naud and PuderMNP22] which gives new results on spectral gaps of random covers of a closed surface.
Another source of motivation is the rich theory that has been discovered around similar questions when surface groups are replaced by free groups (e.g., [Reference NicaNic94, Reference Puder and ParzanchevskiPP15, Reference Magee and PuderMP19, Reference Hanany and PuderHP22] and see
![]() $\S \S $
1.2 below). Expanding this theory to other groups is challenging, as the presence of a relation between the generators presents a fundamental difficulty that is not present for free groups. Surface groups, among the best understood and best behaved one-relator groups, are a natural starting point for this quest. To overcome the difficulty brought up by the existence of a relation, we develop in this work new machinery, both in representation theory of
$\S \S $
1.2 below). Expanding this theory to other groups is challenging, as the presence of a relation between the generators presents a fundamental difficulty that is not present for free groups. Surface groups, among the best understood and best behaved one-relator groups, are a natural starting point for this quest. To overcome the difficulty brought up by the existence of a relation, we develop in this work new machinery, both in representation theory of
![]() $S_{n}$
and in combinatorial group theory.
$S_{n}$
and in combinatorial group theory.
Expected number of fixed points
Recall that the expectation
![]() $\mathbb {E}_{g,n}\left [\mathsf {fix}_{\gamma }\right ]$
is the average number of fixed points in
$\mathbb {E}_{g,n}\left [\mathsf {fix}_{\gamma }\right ]$
is the average number of fixed points in
![]() $\phi \left (\gamma \right )$
where
$\phi \left (\gamma \right )$
where
![]() $\phi \colon \Gamma _{g}\to S_{n}$
is uniformly random. Our main results are the following two theorems.
$\phi \colon \Gamma _{g}\to S_{n}$
is uniformly random. Our main results are the following two theorems.
Theorem 1.1. Fix
![]() $g\geq 2$
and
$g\geq 2$
and
![]() $\gamma \in \Gamma _{g}$
. Then there is an infinite sequence of rational numbers
$\gamma \in \Gamma _{g}$
. Then there is an infinite sequence of rational numbers
such that for any
![]() $M\in \mathbf {N}$
, as
$M\in \mathbf {N}$
, as
![]() $n\to \infty $
,
$n\to \infty $
,
 $$ \begin{align} \mathbb{E}_{g,n}\left[\mathsf{fix}_{\gamma}\right]=a_{1}\left(\gamma\right)n+a_{0}\left(\gamma\right)+\frac{a_{-1}\left(\gamma\right)}{n}+\ldots\frac{a_{-\left(M-1\right)}\left(\gamma\right)}{n^{M-1}}+O\left(\frac{1}{n^{M}}\right). \end{align} $$
$$ \begin{align} \mathbb{E}_{g,n}\left[\mathsf{fix}_{\gamma}\right]=a_{1}\left(\gamma\right)n+a_{0}\left(\gamma\right)+\frac{a_{-1}\left(\gamma\right)}{n}+\ldots\frac{a_{-\left(M-1\right)}\left(\gamma\right)}{n^{M-1}}+O\left(\frac{1}{n^{M}}\right). \end{align} $$
Theorem 1.2. If
![]() $\gamma \in \Gamma _{g}$
is not the identity, then, as
$\gamma \in \Gamma _{g}$
is not the identity, then, as
![]() $n\to \infty $
,
$n\to \infty $
,
In fact, if
![]() $q\in \mathbf {N}$
is maximal such that
$q\in \mathbf {N}$
is maximal such that
![]() $\gamma =\gamma _{0}^{~q}$
for some
$\gamma =\gamma _{0}^{~q}$
for some
![]() $\gamma _{0}\in \Gamma $
, then, as
$\gamma _{0}\in \Gamma $
, then, as
![]() $n\to \infty $
,
$n\to \infty $
,
 $$ \begin{align*} \mathbb{E}_{g,n}[\mathsf{fix}_{\gamma}] & =d(q)+O\left(\frac{1}{n}\right), \end{align*} $$
$$ \begin{align*} \mathbb{E}_{g,n}[\mathsf{fix}_{\gamma}] & =d(q)+O\left(\frac{1}{n}\right), \end{align*} $$
where
![]() $d(q)$
is the number of divisors function. In other words,
$d(q)$
is the number of divisors function. In other words,
![]() $a_{1}(\gamma )=0$
and
$a_{1}(\gamma )=0$
and
![]() $a_{0}(\gamma )=d(q)$
.
$a_{0}(\gamma )=d(q)$
.
For example, consider the element a in
![]() $\Gamma _{2}=\left \langle a,b,c,d\,\middle |\,\left [a,b\right ]\left [c,d\right ]\right \rangle $
. This element is not a proper power and so
$\Gamma _{2}=\left \langle a,b,c,d\,\middle |\,\left [a,b\right ]\left [c,d\right ]\right \rangle $
. This element is not a proper power and so
![]() $\mathbb {E}_{2,n}\left [\mathsf {fix}_{a}\right ]=1+O\left (n^{-1}\right )$
by Theorem 1.2. By Theorem 1.1, this average can be approximated to any order
$\mathbb {E}_{2,n}\left [\mathsf {fix}_{a}\right ]=1+O\left (n^{-1}\right )$
by Theorem 1.2. By Theorem 1.1, this average can be approximated to any order
![]() $n^{-M}$
by a rational function in n. In this particular case, this rational function can be computed to get for, for example,
$n^{-M}$
by a rational function in n. In this particular case, this rational function can be computed to get for, for example,
![]() $M=5$
,
$M=5$
,
 $$\begin{align*}\mathbb{E}_{2,n}\left[\mathsf{fix}_{a}\right]=1+\frac{1}{n^{2}}+\frac{2}{n^{3}}+\frac{10}{n^{4}}+O\left(\frac{1}{n^{5}}\right). \end{align*}$$
$$\begin{align*}\mathbb{E}_{2,n}\left[\mathsf{fix}_{a}\right]=1+\frac{1}{n^{2}}+\frac{2}{n^{3}}+\frac{10}{n^{4}}+O\left(\frac{1}{n^{5}}\right). \end{align*}$$
Given a finite group G, the number of homomorphisms
![]() $\Gamma _{g}\to G$
is related to the Witten zeta function of G,
$\Gamma _{g}\to G$
is related to the Witten zeta function of G,
 $$\begin{align*}\zeta^{G}\left(s\right)\stackrel{\mathrm{def}}{=}\sum_{\chi\in\mathrm{Irr}G}\chi\left(1\right)^{-s}, \end{align*}$$
$$\begin{align*}\zeta^{G}\left(s\right)\stackrel{\mathrm{def}}{=}\sum_{\chi\in\mathrm{Irr}G}\chi\left(1\right)^{-s}, \end{align*}$$
the summation being over the isomorphism classes of irreducible complex representations of G. These functions were introduced by Zagier [Reference ZagierZag94] after Witten’s work in [Reference WittenWit91]. The connection is given by
This result goes back to Hurwitz [Reference HurwitzHur02], who gave a more general formula for arbitrary Fuchsian groups (a proof in English is given in [Reference Liebeck and ShalevLS04, Prop. 3.2]). It is also sometimes called ‘Mednykh’s formula’ in the literature after [Reference MednyhkMed78]. For the case
![]() $G=S_{n}$
, the zeta function
$G=S_{n}$
, the zeta function
![]() $\zeta ^{S_{n}}$
was studied in [Reference LulovLul96, Reference Müller and PuchtaMP02, Reference Liebeck and ShalevLS04, Reference GamburdGam06]. Inter alia, these works show that, for every
$\zeta ^{S_{n}}$
was studied in [Reference LulovLul96, Reference Müller and PuchtaMP02, Reference Liebeck and ShalevLS04, Reference GamburdGam06]. Inter alia, these works show that, for every
![]() $s>0$
,
$s>0$
,
Moreover, their results yield an asymptotic expansion in n which approximates
![]() $\zeta ^{S_{n}}\left (s\right )$
as
$\zeta ^{S_{n}}\left (s\right )$
as
![]() $n\to \infty $
, in a similar manner to the one in Theorem 1.1. As such, their results can be thought of as the special case of
$n\to \infty $
, in a similar manner to the one in Theorem 1.1. As such, their results can be thought of as the special case of
![]() $\gamma =1$
of a version of Theorem 1.1. We elaborate more in
$\gamma =1$
of a version of Theorem 1.1. We elaborate more in
![]() $\S \S $
5.1.
$\S \S $
5.1.
Common fixed points of subgroups
Our proof also yields the following more general result that concerns not only elements of
![]() $\Gamma _{g}$
but also f.g. (finitely generated) subgroups. We write
$\Gamma _{g}$
but also f.g. (finitely generated) subgroups. We write
![]() $J\le _{\mathrm {f.g.}}\Gamma _{g}$
to denote a f.g. subgroup J of
$J\le _{\mathrm {f.g.}}\Gamma _{g}$
to denote a f.g. subgroup J of
![]() $\Gamma _{g}$
. Given
$\Gamma _{g}$
. Given
![]() $J\le _{\mathrm {f.g.}}\Gamma _{g}$
and
$J\le _{\mathrm {f.g.}}\Gamma _{g}$
and
![]() $\phi \in \mathbb {X}_{g,n}$
, we let
$\phi \in \mathbb {X}_{g,n}$
, we let
![]() $\mathsf {fix}_{J}\left (\phi \right )$
denote the number of elements in
$\mathsf {fix}_{J}\left (\phi \right )$
denote the number of elements in
![]() $1,\ldots ,n$
that are fixed by all permutations in
$1,\ldots ,n$
that are fixed by all permutations in
![]() $\phi \left (J\right )$
:
$\phi \left (J\right )$
:
In particular,
![]() $\mathsf {fix}_{\left \langle \gamma \right \rangle }=\mathsf {fix}_{\gamma }$
for all
$\mathsf {fix}_{\left \langle \gamma \right \rangle }=\mathsf {fix}_{\gamma }$
for all
![]() $\gamma \in \Gamma _{g}$
. For
$\gamma \in \Gamma _{g}$
. For
![]() $J\le _{\mathrm {f.g.}}\Gamma _{g}$
, we let
$J\le _{\mathrm {f.g.}}\Gamma _{g}$
, we let
denote the largest Euler characteristicFootnote
2
of a f.g. subgroup
![]() $K\le _{\mathrm {f.g.}}\Gamma _{g}$
which contains J. Note that
$K\le _{\mathrm {f.g.}}\Gamma _{g}$
which contains J. Note that
![]() $\chi \left (\Gamma _{g}\right )=2-2g\le \chi _{\max }\left (J\right )\le 1$
and that
$\chi \left (\Gamma _{g}\right )=2-2g\le \chi _{\max }\left (J\right )\le 1$
and that
![]() $\chi _{\max }\left (J\right )\ge \chi \left (J\right )$
. It is also true that
$\chi _{\max }\left (J\right )\ge \chi \left (J\right )$
. It is also true that
![]() $\chi _{\max }\left (J\right )=1$
if and only if
$\chi _{\max }\left (J\right )=1$
if and only if
![]() $J=\left \{ 1\right \} $
, and
$J=\left \{ 1\right \} $
, and
![]() $\chi _{\max }\left (J\right )\ge 0$
if and only if J is cyclic. In addition, we let
$\chi _{\max }\left (J\right )\ge 0$
if and only if J is cyclic. In addition, we let
denote the set of ‘maximal overgroups’ – f.g. subgroups achieving the maximum from equation (1.4). This set is always finite – see Corollary 2.16.
Theorem 1.3. Let
![]() $J\le _{\mathrm {f.g.}}\Gamma _{g}$
be a f.g. subgroup. Then
$J\le _{\mathrm {f.g.}}\Gamma _{g}$
be a f.g. subgroup. Then
Theorem 1.3 generalizes Theorem 1.2, as for
![]() $\gamma \ne 1$
,
$\gamma \ne 1$
,
![]() $\chi _{\max }\left (\left \langle \gamma \right \rangle \right )=0$
and
$\chi _{\max }\left (\left \langle \gamma \right \rangle \right )=0$
and
The analog of Theorem 1.1 holds too for f.g. subgroups: There is an infinite sequence of rational numbers
such that for any
![]() $M\in \mathbf {N}$
, as
$M\in \mathbf {N}$
, as
![]() $n\to \infty $
,
$n\to \infty $
,
 $$\begin{align*}\mathbb{E}_{g,n}\left[\mathsf{fix}_{J}\right]=\sum_{i=-(M-1)}^{1}a_{i}\left(J\right)n^{i}+O\left(n^{-M}\right), \end{align*}$$
$$\begin{align*}\mathbb{E}_{g,n}\left[\mathsf{fix}_{J}\right]=\sum_{i=-(M-1)}^{1}a_{i}\left(J\right)n^{i}+O\left(n^{-M}\right), \end{align*}$$
and such that
![]() $a_{1}=a_{0}=\ldots =a_{\chi _{\max }\left (J\right )+1}=0$
and
$a_{1}=a_{0}=\ldots =a_{\chi _{\max }\left (J\right )+1}=0$
and
![]() $a_{\chi _{\max }\left (J\right )}=\left |\mathfrak {MOG}\left (J\right )\right |$
.
$a_{\chi _{\max }\left (J\right )}=\left |\mathfrak {MOG}\left (J\right )\right |$
.
1.1 Related works I: Mirzakhani’s integral formulas
In [Reference MirzakhaniMir07], Mirzakhani considered a similar problem to the one in this paper. Instead of integrating over the finite space
![]() $\mathrm {Hom}(\Gamma _{g},S_{n})$
, Mirzakhani obtained formulas for the integral of geometric functions over the the moduli space
$\mathrm {Hom}(\Gamma _{g},S_{n})$
, Mirzakhani obtained formulas for the integral of geometric functions over the the moduli space
![]() $\mathcal {M}_{g}$
of complete hyperbolic surfaces of genus g, with respect to the Weil–Petersson volume form
$\mathcal {M}_{g}$
of complete hyperbolic surfaces of genus g, with respect to the Weil–Petersson volume form
![]() $d\mathrm {Vol}_{\mathrm {wp}}$
.
$d\mathrm {Vol}_{\mathrm {wp}}$
.
The geometric functions that Mirzakhani considers are very much like our Wilson loops. Given any closed curve
![]() $\gamma \in \Sigma _{g}$
, for any complete hyperbolic metric J on
$\gamma \in \Sigma _{g}$
, for any complete hyperbolic metric J on
![]() $\Sigma _{g}$
there is a unique curve isotopic to
$\Sigma _{g}$
there is a unique curve isotopic to
![]() $\gamma $
that is shortest with respect to J, and the length of this curve is called the length of
$\gamma $
that is shortest with respect to J, and the length of this curve is called the length of
![]() $\gamma $
, denoted by
$\gamma $
, denoted by
![]() $\ell _{J}([\gamma ])$
. Here,
$\ell _{J}([\gamma ])$
. Here,
![]() $[\gamma ]$
is the isotopy class of
$[\gamma ]$
is the isotopy class of
![]() $\gamma $
.
$\gamma $
.
Mirzakhani requires that
![]() $\gamma $
be simple, meaning that it does not intersect itself. This condition is not present in the current paper and can be viewed as an advantage of our work. To obtain a function on
$\gamma $
be simple, meaning that it does not intersect itself. This condition is not present in the current paper and can be viewed as an advantage of our work. To obtain a function on
![]() $\mathcal {M}_{g}$
, given a continuous function
$\mathcal {M}_{g}$
, given a continuous function
![]() $f:\mathbf {R}_{+}\to \mathbf {R}_{+}$
, Mirzakhani considers the averaged function
$f:\mathbf {R}_{+}\to \mathbf {R}_{+}$
, Mirzakhani considers the averaged function
 $$\begin{align*}f_{\gamma}(J)\stackrel{\mathrm{def}}{=}\sum_{[\gamma']\in\mathrm{MCG}(\Sigma_{g}).[\gamma]}f(\ell_{J}([\gamma'])), \end{align*}$$
$$\begin{align*}f_{\gamma}(J)\stackrel{\mathrm{def}}{=}\sum_{[\gamma']\in\mathrm{MCG}(\Sigma_{g}).[\gamma]}f(\ell_{J}([\gamma'])), \end{align*}$$
where
![]() $\mathrm {MCG}(\Sigma _{g})$
is the mapping class group of
$\mathrm {MCG}(\Sigma _{g})$
is the mapping class group of
![]() $\Sigma _{g}$
. Because of the averaging over the mapping class group,
$\Sigma _{g}$
. Because of the averaging over the mapping class group,
![]() $f_{\gamma }$
descends to a function on
$f_{\gamma }$
descends to a function on
![]() $\mathcal {M}_{g}$
. This type of averaging is not necessary in the current paper because
$\mathcal {M}_{g}$
. This type of averaging is not necessary in the current paper because
![]() $\mathbb {X}_{g,n}=\mathrm {Hom}(\Gamma _{g},S_{n})$
is already finite; here,
$\mathbb {X}_{g,n}=\mathrm {Hom}(\Gamma _{g},S_{n})$
is already finite; here,
![]() $\mathbb {X}_{g,n}$
is playing the role of the Teichmüller space and not the moduli space. In [Reference MirzakhaniMir07, Thm. 8.1], Mirzakhani gives a formula for
$\mathbb {X}_{g,n}$
is playing the role of the Teichmüller space and not the moduli space. In [Reference MirzakhaniMir07, Thm. 8.1], Mirzakhani gives a formula for
 $$\begin{align*}\int_{\mathcal{M}_{g}}f_{\gamma}\,d\mathrm{Vol}_{\mathrm{wp}} \end{align*}$$
$$\begin{align*}\int_{\mathcal{M}_{g}}f_{\gamma}\,d\mathrm{Vol}_{\mathrm{wp}} \end{align*}$$
in terms of integrating f against Weil–Petersson volumes of moduli spaces. The power of this formula is that in the same paper [Reference MirzakhaniMir07], Mirzakhani gives explicit recursive formulas for the calculations of Weil–Petersson volumes. For a more detailed discussion of these formulas, the reader should consult Wright’s survey of Mirzakhani’s work [Reference WrightWri20, §4].
1.2 Related works II: Free groups
Let
![]() $\mathrm {\mathbf {F}} _{r}$
denote a free group on r generators. For
$\mathrm {\mathbf {F}} _{r}$
denote a free group on r generators. For
![]() $\gamma \in \mathrm {\mathbf {F}} _{r}$
, the problem of integrating the Wilson loop
$\gamma \in \mathrm {\mathbf {F}} _{r}$
, the problem of integrating the Wilson loop
over
![]() $\mathrm {Hom}(\mathrm {\mathbf {F}} _{r},S_{n})$
with respect to the uniform probability measure is a basic problem that serves as a precursor to that of the current paper. As mentioned above, many of the considerations used with free groups no longer apply in the present paper. Indeed,
$\mathrm {Hom}(\mathrm {\mathbf {F}} _{r},S_{n})$
with respect to the uniform probability measure is a basic problem that serves as a precursor to that of the current paper. As mentioned above, many of the considerations used with free groups no longer apply in the present paper. Indeed,
![]() $\mathrm {Hom}(\mathrm {\mathbf {F}} _{r},S_{n})$
can be identified with
$\mathrm {Hom}(\mathrm {\mathbf {F}} _{r},S_{n})$
can be identified with
![]() $S_{n}^{r}$
and hence techniques for integrating over groups are relevant in a much more direct way than in the case of
$S_{n}^{r}$
and hence techniques for integrating over groups are relevant in a much more direct way than in the case of
![]() $\mathrm {Hom}\left (\Gamma _{g},S_{N}\right )$
.
$\mathrm {Hom}\left (\Gamma _{g},S_{N}\right )$
.
Despite being an easier problem, the theory is very rich. It was proved by Nica in [Reference NicaNic94] that the analog of Theorem 1.2 holds for
![]() $\mathbb {E}_{\mathrm {\mathbf {F}} _{r},n}[\mathsf {fix}_{\gamma }]$
. A significantly sharper result was given by Puder and Parzanchevski in [Reference Puder and ParzanchevskiPP15] where they proved that if
$\mathbb {E}_{\mathrm {\mathbf {F}} _{r},n}[\mathsf {fix}_{\gamma }]$
. A significantly sharper result was given by Puder and Parzanchevski in [Reference Puder and ParzanchevskiPP15] where they proved that if
![]() $\gamma \in \mathrm {\mathbf {F}} _{r}$
, then as
$\gamma \in \mathrm {\mathbf {F}} _{r}$
, then as
![]() $n\to \infty $
$n\to \infty $
 $$\begin{align*}\mathbb{E}_{\mathrm{\mathbf{F}} _{r},n}\left[\mathsf{fix}_{\gamma}\right]=1+\frac{c(\gamma)}{n^{\pi(\gamma)-1}}+O\left(\frac{1}{n^{\pi(\gamma)}}\right), \end{align*}$$
$$\begin{align*}\mathbb{E}_{\mathrm{\mathbf{F}} _{r},n}\left[\mathsf{fix}_{\gamma}\right]=1+\frac{c(\gamma)}{n^{\pi(\gamma)-1}}+O\left(\frac{1}{n^{\pi(\gamma)}}\right), \end{align*}$$
where
![]() $\pi (\gamma )\in \{0,\ldots ,r\}\cup \{\infty \}$
is an algebraic invariant of
$\pi (\gamma )\in \{0,\ldots ,r\}\cup \{\infty \}$
is an algebraic invariant of
![]() $\gamma $
called the primitivity rank and
$\gamma $
called the primitivity rank and
![]() $c(\gamma )\in \mathbf {N}$
is explained in terms of the enumeration of special subgroups of
$c(\gamma )\in \mathbf {N}$
is explained in terms of the enumeration of special subgroups of
![]() $\mathrm {\mathbf {F}} _{r}$
determined by
$\mathrm {\mathbf {F}} _{r}$
determined by
![]() $\gamma $
. Obtaining a similarly sharp result in the context of
$\gamma $
. Obtaining a similarly sharp result in the context of
![]() $\Gamma _{g}$
is an interesting problem that should be taken up in the future.
$\Gamma _{g}$
is an interesting problem that should be taken up in the future.
Similar Laurent series expansions for the expected value of
![]() $\chi _{\gamma }$
on
$\chi _{\gamma }$
on
![]() $\mathrm {Hom}(\mathrm {\mathbf {F}} _{r},G(n))$
have been proved to exist, and studied, when
$\mathrm {Hom}(\mathrm {\mathbf {F}} _{r},G(n))$
have been proved to exist, and studied, when
![]() $G(n)$
is one of the families of compact Lie groups
$G(n)$
is one of the families of compact Lie groups
![]() $\mathrm {U}(n),\mathrm {O}(n),\mathrm {Sp}(n)$
[Reference Magee and PuderMP19, Reference Magee and PuderMP22b], when
$\mathrm {U}(n),\mathrm {O}(n),\mathrm {Sp}(n)$
[Reference Magee and PuderMP19, Reference Magee and PuderMP22b], when
![]() $G(n)$
is a generalized symmetric group [Reference Magee and PuderMP21], and when
$G(n)$
is a generalized symmetric group [Reference Magee and PuderMP21], and when
![]() $G(n)=\mathrm {\mathrm {GL}}_{n}(\mathbb {F}_{q})$
, where
$G(n)=\mathrm {\mathrm {GL}}_{n}(\mathbb {F}_{q})$
, where
![]() $\mathbb {F}_{q}$
is a fixed finite field [Reference Ernst-West, Puder and SeidelEWPS21]. In all cases,
$\mathbb {F}_{q}$
is a fixed finite field [Reference Ernst-West, Puder and SeidelEWPS21]. In all cases,
![]() $\chi $
is taken to be a natural character. For example, when
$\chi $
is taken to be a natural character. For example, when
![]() $G(n)=\mathrm {U}(n)$
, one such
$G(n)=\mathrm {U}(n)$
, one such
![]() $\chi $
is the trace of the matrix in the group. Moreover, for
$\chi $
is the trace of the matrix in the group. Moreover, for
![]() $G(n)=\mathrm {U}(n),\mathrm {O}(n),\mathrm {Sp}(n)$
and
$G(n)=\mathrm {U}(n),\mathrm {O}(n),\mathrm {Sp}(n)$
and
![]() $\chi $
the trace, all the coefficients of the Laurent series are understood [Reference Magee and PuderMP19, Reference Magee and PuderMP22b].
$\chi $
the trace, all the coefficients of the Laurent series are understood [Reference Magee and PuderMP19, Reference Magee and PuderMP22b].
In works undertaken after the completion of this paper, the first named author has obtained analogs of Theorem 1.1 and the first part of Theorem 1.2 forFootnote
3
![]() $\mathrm {Hom}(\Gamma _{g},\mathrm {U(}n))$
and the standard matrix trace [Reference MageeMag22, Reference MageeMag21]. The methods used in (ibid.) are inspired by those of the current work.
$\mathrm {Hom}(\Gamma _{g},\mathrm {U(}n))$
and the standard matrix trace [Reference MageeMag22, Reference MageeMag21]. The methods used in (ibid.) are inspired by those of the current work.
1.3 Related works III: Noncommutative probability
Theorem 1.2 has a direct consequence in the setting of Voiculescu’s noncommutative probability theory. Following [Reference Voiculescu, Dykema and NicaVDN92, Def. 2.2.2], a
![]() $C^{*}$
-probability space is a pair
$C^{*}$
-probability space is a pair
![]() $(\mathcal {B},\tau )$
, where
$(\mathcal {B},\tau )$
, where
![]() $\mathcal {B}$
is a unital
$\mathcal {B}$
is a unital
![]() $C^{*}$
-algebra and
$C^{*}$
-algebra and
![]() $\tau $
is a stateFootnote
4
on
$\tau $
is a stateFootnote
4
on
![]() $\mathcal {B}$
. We say that a sequence
$\mathcal {B}$
. We say that a sequence
![]() $\{(\mathcal {B},\tau _{n})\}_{n=1}^{\infty }$
of
$\{(\mathcal {B},\tau _{n})\}_{n=1}^{\infty }$
of
![]() $C^{*}$
-probability spaces converges to
$C^{*}$
-probability spaces converges to
![]() $(\mathcal {B},\tau )$
if for all elements
$(\mathcal {B},\tau )$
if for all elements
![]() $b\in \mathcal {B}$
$b\in \mathcal {B}$
The functions
![]() $\tau _{n}:\Gamma _{g}\to \mathbf {R}$
defined by
$\tau _{n}:\Gamma _{g}\to \mathbf {R}$
defined by
![]() $\tau _{n}(\gamma )\stackrel {\mathrm {def}}{=} n^{-1}\mathbb {E}_{g,n}[\mathsf {fix}_{\gamma }]$
extend to states on the full group
$\tau _{n}(\gamma )\stackrel {\mathrm {def}}{=} n^{-1}\mathbb {E}_{g,n}[\mathsf {fix}_{\gamma }]$
extend to states on the full group
![]() $C^{*}$
-algebra
$C^{*}$
-algebra
![]() $C^{*}(\Gamma {}_{g})$
of
$C^{*}(\Gamma {}_{g})$
of
![]() $\Gamma _{g}$
. There is also a unique state
$\Gamma _{g}$
. There is also a unique state
![]() $\tau _{\mathrm {reg}}$
on
$\tau _{\mathrm {reg}}$
on
![]() $C^{*}(\Gamma _{g})$
that satisfies
$C^{*}(\Gamma _{g})$
that satisfies
![]() $\tau _{\mathrm {reg}}(g)=0$
for
$\tau _{\mathrm {reg}}(g)=0$
for
![]() $g\neq 1$
; we use the subscript
$g\neq 1$
; we use the subscript
![]() $\mathrm {reg}$
because the GNS representation of
$\mathrm {reg}$
because the GNS representation of
![]() $\tau _{\mathrm {reg}}$
is the left regular representation. One has the following corollary of Theorem 1.2:
$\tau _{\mathrm {reg}}$
is the left regular representation. One has the following corollary of Theorem 1.2:
Corollary 1.4. The
![]() $C^{*}$
-probability spaces
$C^{*}$
-probability spaces
![]() $(C^{*}(\Gamma _{g}),\tau _{n})$
converge to
$(C^{*}(\Gamma _{g}),\tau _{n})$
converge to
![]() $(C^{*}(\Gamma _{g}),\tau _{\mathrm {reg}})$
as
$(C^{*}(\Gamma _{g}),\tau _{\mathrm {reg}})$
as
![]() $n\to \infty $
.
$n\to \infty $
.
It is reasonable to hope that similar results can be obtained when
![]() $\Gamma _{g}$
is replaced by any residually finite one-relator group (cf.
$\Gamma _{g}$
is replaced by any residually finite one-relator group (cf.
![]() $\S \S $
1.4). We view Corollary 1.4 as an important first step in this program.
$\S \S $
1.4). We view Corollary 1.4 as an important first step in this program.
1.4 Related works IV: Residual finiteness
A f.g. discrete group
![]() $\Lambda $
is residually finite if for any nonidentity
$\Lambda $
is residually finite if for any nonidentity
![]() $\lambda \in \Lambda $
there is a finite index subgroup
$\lambda \in \Lambda $
there is a finite index subgroup
![]() $H\le \Lambda $
such that
$H\le \Lambda $
such that
![]() $\lambda \notin H$
. The residual finiteness of
$\lambda \notin H$
. The residual finiteness of
![]() $\Gamma _{g}$
has been known for a long time [Reference BaumslagBau62, Reference HempelHem72]. More recently, various quantifications of residual finiteness and of the related property of LERFFootnote
5
have been proposed by various authors [Reference Bou-RabeeBR10, Reference Lazarovich, Levit and MinskyLLM23]. Theorem 1.2 can serve as a strengthening of the residual finiteness of
$\Gamma _{g}$
has been known for a long time [Reference BaumslagBau62, Reference HempelHem72]. More recently, various quantifications of residual finiteness and of the related property of LERFFootnote
5
have been proposed by various authors [Reference Bou-RabeeBR10, Reference Lazarovich, Levit and MinskyLLM23]. Theorem 1.2 can serve as a strengthening of the residual finiteness of
![]() $\Gamma _{g}$
, as we now explain.
$\Gamma _{g}$
, as we now explain.
Note that residual finiteness of a group
![]() $\Lambda $
is equivalent to, for all
$\Lambda $
is equivalent to, for all
![]() $e\neq \lambda \in \Lambda $
, the existence of
$e\neq \lambda \in \Lambda $
, the existence of
![]() $n\in \mathbf {N}$
and
$n\in \mathbf {N}$
and
![]() $\phi \in \mathrm {Hom}(\Lambda ,S_{n})$
such that
$\phi \in \mathrm {Hom}(\Lambda ,S_{n})$
such that
![]() $\phi (\lambda )\ne 1$
. Theorem 1.2 combined with Markov’s inequality implies the following quantitative version of residual finiteness.
$\phi (\lambda )\ne 1$
. Theorem 1.2 combined with Markov’s inequality implies the following quantitative version of residual finiteness.
Corollary 1.5. Given a nonidentity element
![]() $e\ne \gamma \in \Gamma _{g}$
, for large enough n,
$e\ne \gamma \in \Gamma _{g}$
, for large enough n,
 $$ \begin{align} \frac{\left|\left\{ \phi\in\mathrm{Hom}(\Gamma_{g},S_{n})\,:\,\text{\(\phi(\gamma)\neq1\)}\right\} \right|}{|\mathrm{Hom}(\Gamma_{g},S_{n})|}\ge1-\frac{d\left(q\right)}{n}-O\left(\frac{1}{n^{2}}\right), \end{align} $$
$$ \begin{align} \frac{\left|\left\{ \phi\in\mathrm{Hom}(\Gamma_{g},S_{n})\,:\,\text{\(\phi(\gamma)\neq1\)}\right\} \right|}{|\mathrm{Hom}(\Gamma_{g},S_{n})|}\ge1-\frac{d\left(q\right)}{n}-O\left(\frac{1}{n^{2}}\right), \end{align} $$
where q and
![]() $d\left (q\right )$
are as in Theorem 1.2, and the implied constant in the big-O term depends on
$d\left (q\right )$
are as in Theorem 1.2, and the implied constant in the big-O term depends on
![]() $\gamma $
.
$\gamma $
.
In fact, the techniques of this paper can be used to show that, for example, for every
![]() $m\in \mathbb {N}$
, the expected value of
$m\in \mathbb {N}$
, the expected value of
![]() $\mathsf {fix}_{\gamma }^{~m}$
is of the form
$\mathsf {fix}_{\gamma }^{~m}$
is of the form
![]() $c\left (q\right )+O\left (n^{-1}\right )$
, where q is as in Theorem 1.2 and
$c\left (q\right )+O\left (n^{-1}\right )$
, where q is as in Theorem 1.2 and
![]() $c\left (q\right )$
is a positive integer. This would yield a probability bound similar to equation (1.5) but of the form
$c\left (q\right )$
is a positive integer. This would yield a probability bound similar to equation (1.5) but of the form
![]() $1-\frac {c\left (q\right )}{n^{m}}+O\left (n^{-m-1}\right )$
. This is done explicitly in [Reference Puder and ZimhoniPZ22, Corollary 1.8].
$1-\frac {c\left (q\right )}{n^{m}}+O\left (n^{-m-1}\right )$
. This is done explicitly in [Reference Puder and ZimhoniPZ22, Corollary 1.8].
1.5 Related works V: Benjamini–Schramm convergence
In [Reference Benjamini and SchrammBS01], Benjamini and Schramm introduced a notion of convergence of a sequence of finite graphs to a limiting graph, known now as Benjamini–Schramm convergence. This concept was extended to convergence of sequences of Riemannian manifolds in [Reference Abert, Bergeron, Biringer, Gelander, Nikolov, Raimbault and SametABB+11, Reference Abert, Bergeron, Biringer, Gelander, Nikolov, Raimbault and SametABB+17]. Theorem 1.2 has consequences for the Benjamini–Schramm convergence of random covers of Riemannian surfaces; there are various of these consequences but we present just one representative one here.Footnote 6
Corollary 1.6. Let X be a closed hyperbolic surface of genus
![]() $\geq 2$
. Then as
$\geq 2$
. Then as
![]() $n\to \infty $
, uniformly random degree-n covering spaces of X converge in the sense of Benjamini–Schramm to the hyperbolic upper half plane
$n\to \infty $
, uniformly random degree-n covering spaces of X converge in the sense of Benjamini–Schramm to the hyperbolic upper half plane
![]() $\mathbb {H}$
.
$\mathbb {H}$
.
Concretely, this means that for any
![]() $L>0$
and
$L>0$
and
![]() $\varepsilon>0$
, if
$\varepsilon>0$
, if
![]() $X_{n}$
denotes a random degree-n cover of X (as above), then a.a.s. as
$X_{n}$
denotes a random degree-n cover of X (as above), then a.a.s. as
![]() $n\to \infty $
,
$n\to \infty $
,
 $$\begin{align*}\frac{\mathrm{area}\left(X_{n}^{<L}\right)}{\mathrm{area}\left(X_{n}\right)}<\varepsilon, \end{align*}$$
$$\begin{align*}\frac{\mathrm{area}\left(X_{n}^{<L}\right)}{\mathrm{area}\left(X_{n}\right)}<\varepsilon, \end{align*}$$
where
![]() $X_{n}^{<L}$
is the points of
$X_{n}^{<L}$
is the points of
![]() $X_{n}$
with local injectivity radius
$X_{n}$
with local injectivity radius
![]() $<L$
. To see how this follows from Theorem 1.2, viewing L as a constant, any point in
$<L$
. To see how this follows from Theorem 1.2, viewing L as a constant, any point in
![]() $X_{n}^{<L}$
is in a neighborhood, with bounded area depending on L, of some simple closed geodesic of
$X_{n}^{<L}$
is in a neighborhood, with bounded area depending on L, of some simple closed geodesic of
![]() $X_{n}$
with length
$X_{n}$
with length
![]() $<2L$
[Reference BuserBus10, proof of Thm. 4.1.6]. Any such geodesic covers a closed (possibly nonprimitive) geodesic in X of length
$<2L$
[Reference BuserBus10, proof of Thm. 4.1.6]. Any such geodesic covers a closed (possibly nonprimitive) geodesic in X of length
![]() $<2L$
, and these in turn correspond to a finite list of conjugacy classes in
$<2L$
, and these in turn correspond to a finite list of conjugacy classes in
![]() $\Gamma _{g}$
. Starting with a conjugacy class
$\Gamma _{g}$
. Starting with a conjugacy class
![]() $[\gamma ]$
, the number of corresponding closed lifted geodesics in
$[\gamma ]$
, the number of corresponding closed lifted geodesics in
![]() $X_{n}$
is at most
$X_{n}$
is at most
![]() $\mathsf {fix}_{\gamma }$
. Using Markov’s inequality with Theorem 1.2 gives therefore a.a.s. that the number of simple closed geodesics of
$\mathsf {fix}_{\gamma }$
. Using Markov’s inequality with Theorem 1.2 gives therefore a.a.s. that the number of simple closed geodesics of
![]() $X_{n}$
with length
$X_{n}$
with length
![]() $<2L$
is bounded (depending on L). This means
$<2L$
is bounded (depending on L). This means
![]() $\mathrm {area}\left (X_{n}^{<L}\right )$
is bounded a.a.s. and as
$\mathrm {area}\left (X_{n}^{<L}\right )$
is bounded a.a.s. and as
![]() $\mathrm {area}\left (X_{n}\right )$
is linear in n, this completes the proof.
$\mathrm {area}\left (X_{n}\right )$
is linear in n, this completes the proof.
1.6 Structure of the proofs and the issues that arise
The reader of the paper is advised to first read this
![]() $\S $
1.6, and then
$\S $
1.6, and then
![]() $\S $
6, where all the ideas of the paper are brought together to give concise proofs of Theorems 1.1, 1.2 and 1.3, before reading the other sections.
$\S $
6, where all the ideas of the paper are brought together to give concise proofs of Theorems 1.1, 1.2 and 1.3, before reading the other sections.
There are two main ideas of the paper that we will discuss momentarily. Here, we give a ‘high-level’ account of the strategy of proving our main theorems. At times, we oversimplify definitions to be more instructive. Let us fix
![]() $g=2$
and discuss only Theorems 1.1 and 1.2. The extension of these results from cyclic groups to more general finitely generated subgroups is along the same lines. So fix
$g=2$
and discuss only Theorems 1.1 and 1.2. The extension of these results from cyclic groups to more general finitely generated subgroups is along the same lines. So fix
![]() $\gamma \in \Gamma _{2}$
.
$\gamma \in \Gamma _{2}$
.
Firstly, we view
![]() $\mathbb {X}_{n}=\mathbb {X}_{2,n}$
as a space of random coverings of a fixed genus 2 surface
$\mathbb {X}_{n}=\mathbb {X}_{2,n}$
as a space of random coverings of a fixed genus 2 surface
![]() $\Sigma _{2}$
. By fixing an octagonal fundamental domain of
$\Sigma _{2}$
. By fixing an octagonal fundamental domain of
![]() $\Sigma _{2}$
, each covering of
$\Sigma _{2}$
, each covering of
![]() $\Sigma _{2}$
is tiled by octagons. This leads us to the notion of a tiled surface, defined precisely in Definition 2.1. A tiled surface involves not just a tiling but a labeling of the edges of the tiling by generators of the fundamental group of
$\Sigma _{2}$
is tiled by octagons. This leads us to the notion of a tiled surface, defined precisely in Definition 2.1. A tiled surface involves not just a tiling but a labeling of the edges of the tiling by generators of the fundamental group of
![]() $\Sigma _{2}$
. Hence, all the main theorems can be reinterpreted in terms of random tiled surfaces that are called
$\Sigma _{2}$
. Hence, all the main theorems can be reinterpreted in terms of random tiled surfaces that are called
![]() $X_{\phi }$
for
$X_{\phi }$
for
![]() $\phi \in \mathbb {X}_{n}$
.
$\phi \in \mathbb {X}_{n}$
.
The first observation is that
![]() $\mathbb {E}_{n}\left [\mathsf {fix}_{\gamma }\right ]=\mathbb {E}_{2,n}\left [\mathsf {fix}_{\gamma }\right ]$
, the expected number of fixed points of
$\mathbb {E}_{n}\left [\mathsf {fix}_{\gamma }\right ]=\mathbb {E}_{2,n}\left [\mathsf {fix}_{\gamma }\right ]$
, the expected number of fixed points of
![]() $\gamma $
under
$\gamma $
under
![]() $\phi \in \mathbb {X}_{n}$
, is the expected number of times that we see a fixed annulus A, specified by
$\phi \in \mathbb {X}_{n}$
, is the expected number of times that we see a fixed annulus A, specified by
![]() $\gamma $
, immersed in the random tiled surface
$\gamma $
, immersed in the random tiled surface
![]() $X_{\phi }$
. This annulus A may be the ‘core surface’ corresponding to
$X_{\phi }$
. This annulus A may be the ‘core surface’ corresponding to
![]() $\left \langle \gamma \right \rangle $
– see Definition 2.6, the left part of Figure 2.3 and [Reference Magee and PuderMP22a, Lem. 5.1]. However, A needs not be embedded in
$\left \langle \gamma \right \rangle $
– see Definition 2.6, the left part of Figure 2.3 and [Reference Magee and PuderMP22a, Lem. 5.1]. However, A needs not be embedded in
![]() $X_{\phi }$
. On the other hand, it is possible to produce a finite collection
$X_{\phi }$
. On the other hand, it is possible to produce a finite collection
![]() $\mathcal {R}$
of tiled surfaces, each of which has an immersed copy of A, such that
$\mathcal {R}$
of tiled surfaces, each of which has an immersed copy of A, such that
where
![]() $\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
is the expected number of times that Y is embedded in the random
$\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
is the expected number of times that Y is embedded in the random
![]() $X_{\phi }$
.
$X_{\phi }$
.
We formalize types of collections
![]() $\mathcal {R}$
that have the above property in Definition 2.8; we call them resolutions (of A). Of course, there is a great deal of flexibility in how
$\mathcal {R}$
that have the above property in Definition 2.8; we call them resolutions (of A). Of course, there is a great deal of flexibility in how
![]() $\mathcal {R}$
is chosen; we will come back to this point shortly. The benefit to having equation (1.6) brings us to the first main idea of the paper:
$\mathcal {R}$
is chosen; we will come back to this point shortly. The benefit to having equation (1.6) brings us to the first main idea of the paper:
We have a new method of calculating
![]() $\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
, using the representation theory of symmetric groups
$\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
, using the representation theory of symmetric groups
![]() $S_{n}$
and more specifically, the approach to the representation theory of
$S_{n}$
and more specifically, the approach to the representation theory of
![]() $S_{n}$
developed by Vershik and Okounkov in [Reference Vershik and OkounkovVO96].
$S_{n}$
developed by Vershik and Okounkov in [Reference Vershik and OkounkovVO96].
This methodology is developed in
![]() $\S $
5. The necessary background on representation theory is given in
$\S $
5. The necessary background on representation theory is given in
![]() $\S $
3, and in
$\S $
3, and in
![]() $\S $
4 we prove some preliminary representation theoretic results needed for
$\S $
4 we prove some preliminary representation theoretic results needed for
![]() $\S $
5. The reader may be interested to see that Theorem 1.1 has, at its source, Proposition 4.6. See also the overview of
$\S $
5. The reader may be interested to see that Theorem 1.1 has, at its source, Proposition 4.6. See also the overview of
![]() $\S $
5 in
$\S $
5 in
![]() $\S \S $
5.1.
$\S \S $
5.1.
This new methodology to calculate
![]() $\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
is sufficient to prove Theorem 1.1. However, in the proof of Theorem 1.2, a critical issue now intervenes. We expect, based on experience with similar projects (e.g., [Reference Puder and ParzanchevskiPP15, Reference Magee and PuderMP19]) that
$\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
is sufficient to prove Theorem 1.1. However, in the proof of Theorem 1.2, a critical issue now intervenes. We expect, based on experience with similar projects (e.g., [Reference Puder and ParzanchevskiPP15, Reference Magee and PuderMP19]) that
as
![]() $n\to \infty $
. However, this cannot always be the case. For example, if, roughly speaking, it is possible to glue some octagons to Y to increase the Euler characteristic, forming
$n\to \infty $
. However, this cannot always be the case. For example, if, roughly speaking, it is possible to glue some octagons to Y to increase the Euler characteristic, forming
![]() $Y'$
, then the observation that
$Y'$
, then the observation that
![]() $\mathbb {E}_{n}^{\mathrm {emb}}(Y)\geq \mathbb {E}_{n}^{\mathrm {emb}}(Y')$
breaks equation (1.7). Then it is not unsurprising that the bounds we obtain for
$\mathbb {E}_{n}^{\mathrm {emb}}(Y)\geq \mathbb {E}_{n}^{\mathrm {emb}}(Y')$
breaks equation (1.7). Then it is not unsurprising that the bounds we obtain for
![]() $\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
do not always agree with equation (1.7).
$\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
do not always agree with equation (1.7).
On the other hand, if Y has special properties that we call boundary reduced and strongly boundary reduced, then we can get appropriate bounds on
![]() $\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
. We give the precise definitions of these properties in Definitions 2.4 and 2.5. They involve forbidding certain constellations from appearing in the boundary of Y. Even though these constellations are dictated by representation theory, forbidding them remarkably relates to natural geometric properties of Y. For example, if Y is not boundary reduced, then it is possible to add octagons to Y to decrease the number of edges in its boundary. To give some more intuition, being boundary reduced can be viewed as a discrete analog of a hyperbolic surface having geodesic boundary. This means that these properties are closely related with the problem of finding shortest representatives (with respect to word length) of elements of
$\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
. We give the precise definitions of these properties in Definitions 2.4 and 2.5. They involve forbidding certain constellations from appearing in the boundary of Y. Even though these constellations are dictated by representation theory, forbidding them remarkably relates to natural geometric properties of Y. For example, if Y is not boundary reduced, then it is possible to add octagons to Y to decrease the number of edges in its boundary. To give some more intuition, being boundary reduced can be viewed as a discrete analog of a hyperbolic surface having geodesic boundary. This means that these properties are closely related with the problem of finding shortest representatives (with respect to word length) of elements of
![]() $\Gamma _{g}$
that is addressed by Dehn’s algorithm [Reference DehnDeh12].
$\Gamma _{g}$
that is addressed by Dehn’s algorithm [Reference DehnDeh12].
If Y is boundary reduced, then we can prove (Theorem 5.10 and Proposition 5.25)
and if Y is strongly boundary reduced, we can prove (Theorem 5.10 and Proposition 5.26)
(see, again, Section 5.1 for a more detailed overview).Footnote 7 Therefore, to prove Theorem 1.2, it suffices to produce resolutions of the annulus A where we can control which elements are (strongly) boundary reduced, control their Euler characteristics and count the number of elements with maximal Euler characteristic. The design of these resolutions is the second main theme of the paper.
For any tiled surface Z, we describe an algorithm to produce finite resolutions of Z with careful control on their properties as above. This is the main topic of
![]() $\S $
2. Precisely defining the annulus A that should be used as input, as well as its generalization for noncyclic subgroups
$\S $
2. Precisely defining the annulus A that should be used as input, as well as its generalization for noncyclic subgroups
![]() $J\leq \Gamma $
, and counting the outputs of our algorithm, requires introducing the concept of a core surface of a subgroup
$J\leq \Gamma $
, and counting the outputs of our algorithm, requires introducing the concept of a core surface of a subgroup
![]() $J\leq \Gamma $
. For example, above, A should be taken to be the core surface of
$J\leq \Gamma $
. For example, above, A should be taken to be the core surface of
![]() $\langle \gamma \rangle $
. The theory of core surfaces that we develop in a companion paper [Reference Magee and PuderMP22a] is analogous to that of Stallings’ core graphs for subgroups of free groups due to Stallings [Reference StallingsSta83], and we hope that the results therein may be of independent interest.
$\langle \gamma \rangle $
. The theory of core surfaces that we develop in a companion paper [Reference Magee and PuderMP22a] is analogous to that of Stallings’ core graphs for subgroups of free groups due to Stallings [Reference StallingsSta83], and we hope that the results therein may be of independent interest.
Remark 1.7. Another perspective on the value of
![]() $\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
for arbitrary tiles surfaces is given in [Reference Puder and ZimhoniPZ22, Thm. 2.6]. Let Y be an arbitrary tiled surface,
$\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
for arbitrary tiles surfaces is given in [Reference Puder and ZimhoniPZ22, Thm. 2.6]. Let Y be an arbitrary tiled surface,
![]() $p\colon Y\to \Sigma _{g}$
the restricted covering map, and
$p\colon Y\to \Sigma _{g}$
the restricted covering map, and
![]() $\chi ^{\mathrm {grp}}\left (Y\right )$
the Euler characteristic of the subgroup
$\chi ^{\mathrm {grp}}\left (Y\right )$
the Euler characteristic of the subgroup
![]() $p_{*}\left (\pi _{1}\left (Y\right )\right )\le \pi _{1}\left (\Sigma _{g}\right )=\Gamma _{g}$
. Then
$p_{*}\left (\pi _{1}\left (Y\right )\right )\le \pi _{1}\left (\Sigma _{g}\right )=\Gamma _{g}$
. Then
where
![]() $a_{0}$
is some positive integer. This theorem heavily relies on the results of the current paper.
$a_{0}$
is some positive integer. This theorem heavily relies on the results of the current paper.
1.7 Notation
Write
![]() $\mathbf {N}$
for the natural numbers
$\mathbf {N}$
for the natural numbers
![]() $1,2,\ldots $
and so on. For
$1,2,\ldots $
and so on. For
![]() $n\in \mathbf {N}$
, we use the notation
$n\in \mathbf {N}$
, we use the notation
![]() $[n]$
for the set
$[n]$
for the set
![]() $\{1,\ldots ,n\}$
. For
$\{1,\ldots ,n\}$
. For
![]() $m\leq n$
,
$m\leq n$
,
![]() $m,n\in \mathbf {N}$
we write
$m,n\in \mathbf {N}$
we write
![]() $[m,n]$
for the set
$[m,n]$
for the set
![]() $\{m,m+1,\ldots ,n\}$
. If A and B are sets, we write
$\{m,m+1,\ldots ,n\}$
. If A and B are sets, we write
![]() $A\backslash B$
for the elements of A that are not in B. We write
$A\backslash B$
for the elements of A that are not in B. We write
![]() $(n)_{\ell }$
for the Pochhammer symbol
$(n)_{\ell }$
for the Pochhammer symbol
If V is a vector space, we write
![]() $\mathrm {End}(V)$
for the linear endomorphisms of V. If V is a unitary representation of some group, we write
$\mathrm {End}(V)$
for the linear endomorphisms of V. If V is a unitary representation of some group, we write
![]() $\check {V}$
for the dual representation. If
$\check {V}$
for the dual representation. If
![]() $P_{1},\ldots ,P_{k}$
are a series of expressions we write
$P_{1},\ldots ,P_{k}$
are a series of expressions we write
![]() $\mathbf {1}_{\left \{ P_{1},\ldots ,P_{k}\right \} }$
for a value which is 1 if all the statements
$\mathbf {1}_{\left \{ P_{1},\ldots ,P_{k}\right \} }$
for a value which is 1 if all the statements
![]() $P_{i}$
are true and
$P_{i}$
are true and
![]() $0$
else. If V is a vector space, we write
$0$
else. If V is a vector space, we write
![]() $\mathrm {Id}_{V}$
for the identity operator on that space. All integrals over finite sets are with respect to the uniform probability measure on the set. If X is a CW-complex, we write
$\mathrm {Id}_{V}$
for the identity operator on that space. All integrals over finite sets are with respect to the uniform probability measure on the set. If X is a CW-complex, we write
![]() $X^{(i)}$
for its i-skeleton. If we use the symbol
$X^{(i)}$
for its i-skeleton. If we use the symbol
![]() $\pm $
more than once in the same expression or equation, we mean that the same sign is chosen each time. If implied constants in big-O notation depend on other constants, we indicate this by adding the constants as a subscript to the O, for example,
$\pm $
more than once in the same expression or equation, we mean that the same sign is chosen each time. If implied constants in big-O notation depend on other constants, we indicate this by adding the constants as a subscript to the O, for example,
![]() $O_{\varepsilon }(f(n))$
means the implied constant depends on
$O_{\varepsilon }(f(n))$
means the implied constant depends on
![]() $\varepsilon $
. We use Vinogradov notation
$\varepsilon $
. We use Vinogradov notation
![]() $f(n)\ll g(n)$
to mean that there are constants
$f(n)\ll g(n)$
to mean that there are constants
![]() $n_{0}\ge 0$
and
$n_{0}\ge 0$
and
![]() $C_{0}>0$
such that for
$C_{0}>0$
such that for
![]() $n>n_{0}$
,
$n>n_{0}$
,
![]() $|f(n)|\leq C_{0}g(n)$
. We add subscripts to indicate dependence of the implied constants on other quantities or objects. If
$|f(n)|\leq C_{0}g(n)$
. We add subscripts to indicate dependence of the implied constants on other quantities or objects. If
![]() $a,b$
are elements of the same group, we write
$a,b$
are elements of the same group, we write
![]() $[a,b]\stackrel {\mathrm {def}}{=} aba^{-1}b^{-1}$
for their commutator.
$[a,b]\stackrel {\mathrm {def}}{=} aba^{-1}b^{-1}$
for their commutator.
2 Resolutions of core surfaces
2.1 Tiled surfaces and core surfaces
In this
![]() $\S \S $
2.1, we summarize some definitions and results from [Reference Magee and PuderMP22a].Footnote
8
$\S \S $
2.1, we summarize some definitions and results from [Reference Magee and PuderMP22a].Footnote
8
2.1.1 Tiled surfaces
Consider the construction of the surface
![]() $\Sigma _{g}$
from a
$\Sigma _{g}$
from a
![]() $4g$
-gon by identifying its edges in pairs according to the pattern
$4g$
-gon by identifying its edges in pairs according to the pattern
![]() $a_{1}b_{1}a_{1}^{-1}b_{1}^{-1}\ldots a_{g}b_{g}a_{g}^{-1}b_{g}^{-1}$
. This gives rise to a CW-structure on
$a_{1}b_{1}a_{1}^{-1}b_{1}^{-1}\ldots a_{g}b_{g}a_{g}^{-1}b_{g}^{-1}$
. This gives rise to a CW-structure on
![]() $\Sigma _{g}$
consisting of one vertex (denoted o),
$\Sigma _{g}$
consisting of one vertex (denoted o),
![]() $2g$
oriented
$2g$
oriented
![]() $1-$
cells (denoted
$1-$
cells (denoted
![]() $a_{1},b_{1},\ldots ,a_{g},b_{g}$
) and one
$a_{1},b_{1},\ldots ,a_{g},b_{g}$
) and one
![]() $2$
-cell which is the
$2$
-cell which is the
![]() $4g$
-gon glued along
$4g$
-gon glued along
![]() $4g 1$
-cells.Footnote
9
See Figure 2.1 (in our running examples with
$4g 1$
-cells.Footnote
9
See Figure 2.1 (in our running examples with
![]() $g=2$
, we denote the generators of
$g=2$
, we denote the generators of
![]() $\Gamma _{2}$
by
$\Gamma _{2}$
by
![]() $a,b,c,d$
instead of
$a,b,c,d$
instead of
![]() $a_{1},b_{1},a_{2},b_{2}$
). We identify
$a_{1},b_{1},a_{2},b_{2}$
). We identify
![]() $\Gamma _{g}$
with
$\Gamma _{g}$
with
![]() $\pi _{1}\left (\Sigma _{g},o\right )$
so that in the presentation (1.1), words in the generators
$\pi _{1}\left (\Sigma _{g},o\right )$
so that in the presentation (1.1), words in the generators
![]() $a_{1},\ldots ,b_{g}$
correspond to the homotopy class of the corresponding closed paths based at o along the
$a_{1},\ldots ,b_{g}$
correspond to the homotopy class of the corresponding closed paths based at o along the
![]() $1$
-skeleton of
$1$
-skeleton of
![]() $\Sigma _{g}$
.
$\Sigma _{g}$
.

Figure 2.1 The fixed CW-structure on
![]() $\Sigma _{2}$
.
$\Sigma _{2}$
.
Note that every covering space
![]() $p\colon \Upsilon \to \Sigma _{g}$
inherits a CW-structure from
$p\colon \Upsilon \to \Sigma _{g}$
inherits a CW-structure from
![]() $\Sigma _{g}$
: The vertices are the preimages of o, and the open
$\Sigma _{g}$
: The vertices are the preimages of o, and the open
![]() $1$
-cells (2-cells) are the connected components of the preimages of the open 1-cells (2-cells, respectively) in
$1$
-cells (2-cells) are the connected components of the preimages of the open 1-cells (2-cells, respectively) in
![]() $\Sigma _{g}$
. In particular, this is true for the universal covering space
$\Sigma _{g}$
. In particular, this is true for the universal covering space
![]() $\widetilde {\Sigma _{g}}$
of
$\widetilde {\Sigma _{g}}$
of
![]() $\Sigma _{g}$
, which we can now think of as a CW-complex. A subcomplex of a CW-complex is a subspace consisting of cells such that if some cell belongs to the subcomplex, then so do the cells of smaller dimension at its boundary.
$\Sigma _{g}$
, which we can now think of as a CW-complex. A subcomplex of a CW-complex is a subspace consisting of cells such that if some cell belongs to the subcomplex, then so do the cells of smaller dimension at its boundary.
Definition 2.1 (Tiled surface).
[Reference Magee and PuderMP22a, Def. 3.1] A tiled surface Y is a subcomplex of a (not-necessarily-connected) covering space of
![]() $\Sigma _{g}$
. In particular, a tiled surface is equipped with the restricted covering map
$\Sigma _{g}$
. In particular, a tiled surface is equipped with the restricted covering map
![]() $p\colon Y\to \Sigma _{g}$
which is an immersion. We write
$p\colon Y\to \Sigma _{g}$
which is an immersion. We write
![]() $\mathfrak {v}\left (Y\right )$
for the number of vertices of Y,
$\mathfrak {v}\left (Y\right )$
for the number of vertices of Y,
![]() $\mathfrak {e}\left (Y\right )$
for the number of edges and
$\mathfrak {e}\left (Y\right )$
for the number of edges and
![]() $\mathfrak {f}\left (Y\right )$
for the number of
$\mathfrak {f}\left (Y\right )$
for the number of
![]() $4g$
-gons.
$4g$
-gons.
Alternatively, instead of considering a tiled surface Y to be a complex equipped with a restricted covering map, one may consider Y to be a complex as above with directed and labeled edges: The directions and labels (
![]() $a_{1},b_{1},\ldots ,a_{g},b_{g}$
) are pulled back from
$a_{1},b_{1},\ldots ,a_{g},b_{g}$
) are pulled back from
![]() $\Sigma _{g}$
via p. These labels uniquely determine p as a combinatorial map between complexes. Figures 2.1 and 2.3 feature examples of tiled surfaces.
$\Sigma _{g}$
via p. These labels uniquely determine p as a combinatorial map between complexes. Figures 2.1 and 2.3 feature examples of tiled surfaces.
Note that a tiled surface is not always a surface: It may also contain vertices or edges with no
![]() $2$
-cells incident to them. However, as Y is a subcomplex of a covering space of
$2$
-cells incident to them. However, as Y is a subcomplex of a covering space of
![]() $\Sigma _{g}$
, namely, of a surface, any neighborhood of Y inside the covering is a surface, and it is sometimes beneficial to think of Y as such.
$\Sigma _{g}$
, namely, of a surface, any neighborhood of Y inside the covering is a surface, and it is sometimes beneficial to think of Y as such.
Definition 2.2 (Thick version of a tiled surface).
[Reference Magee and PuderMP22a, Def. 3.2] Given a tiled surface Y which is a subcomplex of the covering space
![]() $\Upsilon $
of
$\Upsilon $
of
![]() $\Sigma _{g}$
, adjoin to Y a small, closed, tubular neighborhood in
$\Sigma _{g}$
, adjoin to Y a small, closed, tubular neighborhood in
![]() $\Upsilon $
around every edge and a small closed disc in
$\Upsilon $
around every edge and a small closed disc in
![]() $\Upsilon $
around every vertex. The resulting closed surface, possibly with boundary, is referred to as the thick version of Y.
$\Upsilon $
around every vertex. The resulting closed surface, possibly with boundary, is referred to as the thick version of Y.
We let
![]() $\partial Y$
denote the boundary of the thick version of Y and
$\partial Y$
denote the boundary of the thick version of Y and
![]() $\mathfrak {d}\left (Y\right )$
denote the number of edges along
$\mathfrak {d}\left (Y\right )$
denote the number of edges along
![]() $\partial Y$
(so if an edge of Y does not border any
$\partial Y$
(so if an edge of Y does not border any
![]() $4g$
-gon, it is counted twice).
$4g$
-gon, it is counted twice).
In particular,
![]() $\mathfrak {d}\left (Y\right )=2\mathfrak {e}\left (Y\right )-4g\mathfrak {f}\left (Y\right )$
. We stress that we do not think of Y as a subcomplex but rather as a complex for its own sake, which happens to have the capacity to be realized as a subcomplex of a covering space of
$\mathfrak {d}\left (Y\right )=2\mathfrak {e}\left (Y\right )-4g\mathfrak {f}\left (Y\right )$
. We stress that we do not think of Y as a subcomplex but rather as a complex for its own sake, which happens to have the capacity to be realized as a subcomplex of a covering space of
![]() $\Sigma _{g}$
. See [Reference Magee and PuderMP22a, §3] for a more detailed discussion.
$\Sigma _{g}$
. See [Reference Magee and PuderMP22a, §3] for a more detailed discussion.
It is occasionally useful, for example in Section 5, to augment the tiled surface Y by adding some new half-edges. Here, formally, a half-edge is a copy of the interval
![]() $[0,\frac {1}{2})$
which is an (open) half of an edge of a covering space of
$[0,\frac {1}{2})$
which is an (open) half of an edge of a covering space of
![]() $\Sigma _{g}$
.
$\Sigma _{g}$
.
Definition 2.3 (Tiled surface with hanging half-edges).
[Reference Magee and PuderMP22a, §§3.2] Let Y be a tiled surface which is a subcomplex of the covering space
![]() $p\colon \Upsilon \to \Sigma _{g}$
. We denote by
$p\colon \Upsilon \to \Sigma _{g}$
. We denote by
![]() $Y_{+}$
the tiled surface Y together with half-edges of
$Y_{+}$
the tiled surface Y together with half-edges of
![]() $\Upsilon $
which do not belong to Y but are incident to vertices of Y. Every half-edge of
$\Upsilon $
which do not belong to Y but are incident to vertices of Y. Every half-edge of
![]() $Y_{+}$
added to Y in this manner is called a hanging half-edge. The thick version of
$Y_{+}$
added to Y in this manner is called a hanging half-edge. The thick version of
![]() $Y_{+}$
is, as above,
$Y_{+}$
is, as above,
![]() $Y_{+}$
together with a small, closed, tubular neighborhood in
$Y_{+}$
together with a small, closed, tubular neighborhood in
![]() $\Upsilon $
around every edge or hanging half-edge, and a small closed disc in
$\Upsilon $
around every edge or hanging half-edge, and a small closed disc in
![]() $\Upsilon $
around every vertex. We denote by
$\Upsilon $
around every vertex. We denote by
![]() $\partial Y_{+}$
the boundary of the think version of
$\partial Y_{+}$
the boundary of the think version of
![]() $Y_{+}$
.
$Y_{+}$
.
Note that there are exactly
![]() $4g$
half-edges incident to every vertex in
$4g$
half-edges incident to every vertex in
![]() $Y_{+}$
: Some of them originate from edges in Y and some are hanging half-edges.
$Y_{+}$
: Some of them originate from edges in Y and some are hanging half-edges.
Morphisms of tiled surfaces
If
![]() $Y_{1}$
and
$Y_{1}$
and
![]() $Y_{2}$
are tiled surfaces, a morphism from
$Y_{2}$
are tiled surfaces, a morphism from
![]() $Y_{1}$
to
$Y_{1}$
to
![]() $Y_{2}$
is a map of
$Y_{2}$
is a map of
![]() $CW$
-complexes which maps i-cells to i-cells for
$CW$
-complexes which maps i-cells to i-cells for
![]() $i=0,1,2$
and respects the directions and labels of edges. Equivalently, this is a morphism of CW-complexes which commutes with the restricted covering maps
$i=0,1,2$
and respects the directions and labels of edges. Equivalently, this is a morphism of CW-complexes which commutes with the restricted covering maps
![]() $p_{j}\colon Y_{j}\to \Sigma _{g}$
(
$p_{j}\colon Y_{j}\to \Sigma _{g}$
(
![]() $j=1,2$
). In particular, the restricted covering map from a tiled surface to
$j=1,2$
). In particular, the restricted covering map from a tiled surface to
![]() $\Sigma _{g}$
is itself a morphism of tiled surfaces. It is an easy observation that every morphism of tiled surfaces is an immersion (locally injective).
$\Sigma _{g}$
is itself a morphism of tiled surfaces. It is an easy observation that every morphism of tiled surfaces is an immersion (locally injective).
2.1.2 Blocks and chains
Some of the notions we use below are taken from [Reference Birman and SeriesBS87]. See [Reference Magee and PuderMP22a, §§3.2] for a more detailed account.
Given a covering space
![]() $\Upsilon $
of
$\Upsilon $
of
![]() $\Sigma _{g}$
, every path in the
$\Sigma _{g}$
, every path in the
![]() $1$
-skeleton
$1$
-skeleton
![]() $\Upsilon ^{\left (1\right )}$
corresponds to a word in
$\Upsilon ^{\left (1\right )}$
corresponds to a word in
![]() $\left \{ a_{1}^{\pm 1},\ldots ,b_{g}^{\pm 1}\right \} $
. A path that follows a (part of the) boundary of a
$\left \{ a_{1}^{\pm 1},\ldots ,b_{g}^{\pm 1}\right \} $
. A path that follows a (part of the) boundary of a
![]() $4g$
-gon is called a
block
. If it has length at least
$4g$
-gon is called a
block
. If it has length at least
![]() $2g+1$
it is called a
long block
, and if it has length exactly
$2g+1$
it is called a
long block
, and if it has length exactly
![]() $2g$
, it is called a
half-block
. If a (noncyclic) block of length b sits along the boundary of a
$2g$
, it is called a
half-block
. If a (noncyclic) block of length b sits along the boundary of a
![]() $4g$
-gon O, the
complement
of the block is the block of length
$4g$
-gon O, the
complement
of the block is the block of length
![]() $4g-b$
consisting of the complement set of edges along O, so the block and its complement share the same starting point and the same terminal point.
$4g-b$
consisting of the complement set of edges along O, so the block and its complement share the same starting point and the same terminal point.

Figure 2.2 A long chain of total length
![]() $17$
(blocks of sizes
$17$
(blocks of sizes
![]() $4,3,3,3,4$
, in blue) and its complement of length
$4,3,3,3,4$
, in blue) and its complement of length
![]() $15$
(in red).
$15$
(in red).
A
chain
is a path in
![]() $\Upsilon ^{\left (1\right )}$
that consists of a sequence of blocks
$\Upsilon ^{\left (1\right )}$
that consists of a sequence of blocks
![]() $b_{1},\ldots ,b_{r}$
such that if the last vertex of
$b_{1},\ldots ,b_{r}$
such that if the last vertex of
![]() $b_{i}$
and the first vertex of
$b_{i}$
and the first vertex of
![]() $b_{i+1}$
is v, there is exactly one edge incident to v between the last edge of
$b_{i+1}$
is v, there is exactly one edge incident to v between the last edge of
![]() $b_{i}$
and the first edges of
$b_{i}$
and the first edges of
![]() $b_{i+1}$
. In other words, if the
$b_{i+1}$
. In other words, if the
![]() $4g$
-gons corresponding to the blocks
$4g$
-gons corresponding to the blocks
![]() $b_{1},\ldots ,b_{r}$
are
$b_{1},\ldots ,b_{r}$
are
![]() $O_{1},\ldots ,O_{r}$
, then
$O_{1},\ldots ,O_{r}$
, then
![]() $O_{i}$
and
$O_{i}$
and
![]() $O_{i+1}$
share an edge e with an endpoint v, and
$O_{i+1}$
share an edge e with an endpoint v, and
![]() $b_{i}$
ends at v and
$b_{i}$
ends at v and
![]() $b_{i+1}$
starts at v. See Figure 2.2. A
long chain
is a chain with corresponding blocks of lengths
$b_{i+1}$
starts at v. See Figure 2.2. A
long chain
is a chain with corresponding blocks of lengths
A
half-chain
is a cyclic chain (so the corresponding path is closed) consisting of blocks each of which is of length
![]() $2g-1$
. The complement of a long chain is the chain with blocks of lengths
$2g-1$
. The complement of a long chain is the chain with blocks of lengths
![]() $2g-1,2g-1,\ldots ,2g-1$
which sits along the other side of the
$2g-1,2g-1,\ldots ,2g-1$
which sits along the other side of the
![]() $4g$
-gons bordering the long chain and with the same starting point and endpoint. Note that the complement of a long chain is shorter by two edges from the long chain (see Figure 2.2). The complement of a half-chain is defined as follows. If the half-chain sits along the boundary of the
$4g$
-gons bordering the long chain and with the same starting point and endpoint. Note that the complement of a long chain is shorter by two edges from the long chain (see Figure 2.2). The complement of a half-chain is defined as follows. If the half-chain sits along the boundary of the
![]() $4g$
-gons
$4g$
-gons
![]() $O_{1},\ldots ,O_{r}$
, its complement is the half-chain sitting along the other sides of these
$O_{1},\ldots ,O_{r}$
, its complement is the half-chain sitting along the other sides of these
![]() $4g$
-gons: A block (of length
$4g$
-gons: A block (of length
![]() $2g-1$
) of the half-chain along
$2g-1$
) of the half-chain along
![]() $O_{i}$
is replaced by the path of length
$O_{i}$
is replaced by the path of length
![]() $2g-1$
along
$2g-1$
along
![]() $O_{i}$
, with starting and terminal points one edge away from the starting and terminal points, respectively, of the block. The complement of a half-chain has the same length as the original half-chain. The left part of Figure 2.3 illustrates two complementing half-chains of length
$O_{i}$
, with starting and terminal points one edge away from the starting and terminal points, respectively, of the block. The complement of a half-chain has the same length as the original half-chain. The left part of Figure 2.3 illustrates two complementing half-chains of length
![]() $6$
each (with two octagons in between).
$6$
each (with two octagons in between).
A
boundary cycle
of Y is a cycle in
![]() $Y^{\left (1\right )}$
corresponding to an oriented boundary component of the thick version of Y (see Definition 2.2). We always choose the orientation so that there are no
$Y^{\left (1\right )}$
corresponding to an oriented boundary component of the thick version of Y (see Definition 2.2). We always choose the orientation so that there are no
![]() $4g$
-gons to the immediate left of the boundary component as it is traversed. Therefore, boundary components of Y correspond to unique cycles. Note that
$4g$
-gons to the immediate left of the boundary component as it is traversed. Therefore, boundary components of Y correspond to unique cycles. Note that
![]() $\mathfrak {d}\left (Y\right )$
is equal to the sum over boundary cycles of Y of the number of edges in each such cycle.
$\mathfrak {d}\left (Y\right )$
is equal to the sum over boundary cycles of Y of the number of edges in each such cycle.
2.1.3 Boundary reduced and strongly boundary reduced tiled surfaces
The following definitions came up from our results in representation theory in
![]() $\S $
5, but they fit perfectly with classical results in combinatorial group theory [Reference DehnDeh12] and in particular with [Reference Birman and SeriesBS87].
$\S $
5, but they fit perfectly with classical results in combinatorial group theory [Reference DehnDeh12] and in particular with [Reference Birman and SeriesBS87].
Definition 2.4 (Boundary reduced).
A tiled surface Y is boundary reduced if no boundary cycle of Y contains a long block or a long chain.
In particular, if Y is boundary reduced, then every path that reads
![]() $\left [a_{1},b_{1}\right ]\ldots \left [a_{g},b_{g}\right ]$
is not only closed, but there is also a
$\left [a_{1},b_{1}\right ]\ldots \left [a_{g},b_{g}\right ]$
is not only closed, but there is also a
![]() $4g$
-gon attached to it. We also need a stronger version of this property.
$4g$
-gon attached to it. We also need a stronger version of this property.
Definition 2.5 (Strongly boundary reduced).
A tiled surface Y is strongly boundary reduced if no boundary cycle of Y contains a half-block or is a half-chain.
Because a long block contains (at least two) half-blocks and a long chain contains (two) half-blocks, a strongly boundary reduced tiled surface is in particular boundary reduced. The relevance of the notions of being (strongly) boundary reduced is that our techniques for estimating
![]() $\mathbb {E}_{n}^{\mathrm {emb}}\left (Y\right )$
for a tiled surface Y only give the right type of estimates when Y is boundary reduced – see Proposition 5.25. If Y is strongly boundary reduced we get even better estimates – see Proposition 5.26.
$\mathbb {E}_{n}^{\mathrm {emb}}\left (Y\right )$
for a tiled surface Y only give the right type of estimates when Y is boundary reduced – see Proposition 5.25. If Y is strongly boundary reduced we get even better estimates – see Proposition 5.26.

Figure 2.3 Fix
![]() $g=2$
, and let
$g=2$
, and let
![]() $\Gamma _{2}=\left \langle a,b,c,d\,\middle |\,\left [a,b\right ]\left [c,d\right ]\right \rangle $
. On the left is the core surface
$\Gamma _{2}=\left \langle a,b,c,d\,\middle |\,\left [a,b\right ]\left [c,d\right ]\right \rangle $
. On the left is the core surface
![]() $ \mathrm {Core}\left (\left \langle aba^{-2}b^{-1}c\right \rangle \right )$
. It consists of
$ \mathrm {Core}\left (\left \langle aba^{-2}b^{-1}c\right \rangle \right )$
. It consists of
![]() $12$
vertices,
$12$
vertices,
![]() $14$
edges and two octagons and topologically it is an annulus. On the right is the core surface
$14$
edges and two octagons and topologically it is an annulus. On the right is the core surface
![]() $ \mathrm {Core}\left (\left \langle a,b\right \rangle \right )$
. It consists of four vertices, six edges and one octagon and topologically it is a genus-1 torus with one boundary component.
$ \mathrm {Core}\left (\left \langle a,b\right \rangle \right )$
. It consists of four vertices, six edges and one octagon and topologically it is a genus-1 torus with one boundary component.
Let Y be a compact tiled surface which is a subcomplex of the covering space
![]() $\Upsilon $
of
$\Upsilon $
of
![]() $\Sigma _{g}$
. In [Reference Magee and PuderMP22a, §4], we describe the ‘boundary reduced closure’
$\Sigma _{g}$
. In [Reference Magee and PuderMP22a, §4], we describe the ‘boundary reduced closure’
![]() $\mathsf {BR}\left (Y\hookrightarrow \Upsilon \right )$
of Y in
$\mathsf {BR}\left (Y\hookrightarrow \Upsilon \right )$
of Y in
![]() $\Upsilon $
which is the smallest intermediate tiled surface which is boundary reduced. By (ibid., Proposition 4.6),
$\Upsilon $
which is the smallest intermediate tiled surface which is boundary reduced. By (ibid., Proposition 4.6),
![]() $\mathsf {BR}\left (Y\hookrightarrow \Upsilon \right )$
is compact too. Likewise,
$\mathsf {BR}\left (Y\hookrightarrow \Upsilon \right )$
is compact too. Likewise,
![]() $\mathsf {SBR}\left (Y\hookrightarrow \Upsilon \right )$
, the strongly boundary reduced closure, is the smallest intermediate tiled surface which is strongly boundary reduced, but this one is not always compact. Our resolutions in Section 2.3 are based on a ‘compromise’ between these two types of closures.
$\mathsf {SBR}\left (Y\hookrightarrow \Upsilon \right )$
, the strongly boundary reduced closure, is the smallest intermediate tiled surface which is strongly boundary reduced, but this one is not always compact. Our resolutions in Section 2.3 are based on a ‘compromise’ between these two types of closures.
2.1.4 Core surfaces
Finally, let us define the main object which was introduced and analyzed in [Reference Magee and PuderMP22a], with motivation coming from the current paper. In analogy to Stallings core graphs and their role in the study of free groups and their subgroups, we introduced the notion of core surfaces which relates to subgroups of
![]() $\Gamma _{g}$
:
$\Gamma _{g}$
:
Definition 2.6 (Core surfaces).
[Reference Magee and PuderMP22a, Def. 1.1] Given a subgroup
![]() $1\ne J\le \Gamma _{g}=\pi _{1}\left (\Sigma _{g},o\right )$
, consider the covering space
$1\ne J\le \Gamma _{g}=\pi _{1}\left (\Sigma _{g},o\right )$
, consider the covering space
![]() $p\colon \Upsilon \to \Sigma _{g}$
corresponding to J, so
$p\colon \Upsilon \to \Sigma _{g}$
corresponding to J, so
![]() $\Upsilon =J\backslash \widetilde {\Sigma _{g}}$
. Define the core surface of J, denoted
$\Upsilon =J\backslash \widetilde {\Sigma _{g}}$
. Define the core surface of J, denoted
![]() $\mathrm {Core}\left (J\right )$
, as the tiled surface which is a subcomplex of
$\mathrm {Core}\left (J\right )$
, as the tiled surface which is a subcomplex of
![]() $\Upsilon $
as follows:
$\Upsilon $
as follows:
![]() $\left (i\right )$
take the union of all shortest-representative cycles in the 1-skeleton
$\left (i\right )$
take the union of all shortest-representative cycles in the 1-skeleton
![]() $\Upsilon ^{\left (1\right )}$
of every free-homotopy class of essential closed curve in
$\Upsilon ^{\left (1\right )}$
of every free-homotopy class of essential closed curve in
![]() $\Upsilon $
, and
$\Upsilon $
, and
![]() $\left (ii\right )$
add every connected component of the complement which contains finitely many
$\left (ii\right )$
add every connected component of the complement which contains finitely many
![]() $4g$
-gons.
$4g$
-gons.
For completeness define the core surface of the trivial subgroup to be the zero-dimensional tiled surface consisting of a single vertex.
Note that the quotient
![]() $\Upsilon =J\backslash \widetilde {\Sigma _{g}}$
is invariant under conjugation of J, so
$\Upsilon =J\backslash \widetilde {\Sigma _{g}}$
is invariant under conjugation of J, so
![]() $\mathrm {Core}\left (J\right )$
depends only on the conjugacy class of J in
$\mathrm {Core}\left (J\right )$
depends only on the conjugacy class of J in
![]() $\Gamma _{g}$
. Figure 2.3 gives two examples of core surfaces. As another example, if J is of finite index in
$\Gamma _{g}$
. Figure 2.3 gives two examples of core surfaces. As another example, if J is of finite index in
![]() $\Gamma $
,
$\Gamma $
,
![]() $\mathrm {Core}\left (J\right )$
is identical to
$\mathrm {Core}\left (J\right )$
is identical to
![]() $J\backslash \widetilde {\Sigma _{g}}$
and is a compact closed surface.
$J\backslash \widetilde {\Sigma _{g}}$
and is a compact closed surface.
In [Reference Magee and PuderMP22a], we give an intrinsic definition of a core surface and show there is one-to-one correspondence between core surfaces (labeled by
![]() $a_{1},\ldots ,b_{g}$
) and conjugacy classes of subgroups of
$a_{1},\ldots ,b_{g}$
) and conjugacy classes of subgroups of
![]() $\Gamma _{g}$
, we provide a ‘folding process’ to construct
$\Gamma _{g}$
, we provide a ‘folding process’ to construct
![]() $\mathrm {Core}\left (J\right )$
from a finite generating set of J (provided, of course, that J is f.g.) and prove basic properties of core surfaces. In particular,
$\mathrm {Core}\left (J\right )$
from a finite generating set of J (provided, of course, that J is f.g.) and prove basic properties of core surfaces. In particular,
![]() $\mathrm {Core}\left (J\right )$
is connected and strongly boundary reduced (ibid., Proposition 5.3), and whenever J is f.g.,
$\mathrm {Core}\left (J\right )$
is connected and strongly boundary reduced (ibid., Proposition 5.3), and whenever J is f.g.,
![]() $\mathrm {Core}\left (J\right )$
is compact (ibid, Proposition 5.8). We also show that whenever
$\mathrm {Core}\left (J\right )$
is compact (ibid, Proposition 5.8). We also show that whenever
![]() $H\le J\le \Gamma _{g}$
, the natural morphism between the corresponding covering spaces
$H\le J\le \Gamma _{g}$
, the natural morphism between the corresponding covering spaces
![]() $H\backslash \widetilde {\Sigma _{g}}\to J\backslash \widetilde {\Sigma _{g}}$
, restricts to a morphism
$H\backslash \widetilde {\Sigma _{g}}\to J\backslash \widetilde {\Sigma _{g}}$
, restricts to a morphism
![]() $\mathrm {Core}\left (H\right )\to \mathrm {Core}\left (J\right )$
.
$\mathrm {Core}\left (H\right )\to \mathrm {Core}\left (J\right )$
.
2.2 Expectations and probabilities of tiled surfaces
Correspondence between
 $ \mathrm {Hom}\left (\Gamma _{g},S_{n}\right )$
and n-sheeted covering spaces of
$ \mathrm {Hom}\left (\Gamma _{g},S_{n}\right )$
and n-sheeted covering spaces of
 $\Sigma _{g}$
$\Sigma _{g}$
Let M be a connected topological space with basepoint m. Consider n-sheeted covering spaces of M with the fiber above m labeled by
![]() $\left [n\right ]$
so that every point in the fiber has a different label. If M is ‘nice enough’, in particular if M is a surface, there is a one-to-one correspondence between these labeled n-sheeted covering spaces and the set of homomorphisms
$\left [n\right ]$
so that every point in the fiber has a different label. If M is ‘nice enough’, in particular if M is a surface, there is a one-to-one correspondence between these labeled n-sheeted covering spaces and the set of homomorphisms
![]() $\mathrm {Hom}\left (\pi _{1}\left (M,m\right ),S_{n}\right )$
(see, for instance, [Reference HatcherHat05, pp. 68-70]). If
$\mathrm {Hom}\left (\pi _{1}\left (M,m\right ),S_{n}\right )$
(see, for instance, [Reference HatcherHat05, pp. 68-70]). If
![]() $\hat {M}$
is a labeled n-sheeted covering space and
$\hat {M}$
is a labeled n-sheeted covering space and
![]() $p\colon \hat {M}\to M$
the covering map, the corresponding homomorphism
$p\colon \hat {M}\to M$
the covering map, the corresponding homomorphism
![]() $\theta \colon \pi _{1}\left (M,m\right )\to S_{n}$
is given as follows: For
$\theta \colon \pi _{1}\left (M,m\right )\to S_{n}$
is given as follows: For
![]() $h\in \pi _{1}\left (M,m\right )$
, consider
$h\in \pi _{1}\left (M,m\right )$
, consider
![]() $\gamma $
, a closed path in M, based at m, which represents h. Then
$\gamma $
, a closed path in M, based at m, which represents h. Then
![]() $\theta \left (h\right )\left (i\right )=j$
if and only if the lift of
$\theta \left (h\right )\left (i\right )=j$
if and only if the lift of
![]() $\gamma $
at the point i ends at the point j.Footnote
10
$\gamma $
at the point i ends at the point j.Footnote
10
In our case, this translates to a one-to-one correspondence between the representation space
![]() $\mathbb {X}_{g,n}=\mathrm {Hom}\left (\Gamma _{g},S_{n}\right )$
and labeled n-sheeted covering spaces of
$\mathbb {X}_{g,n}=\mathrm {Hom}\left (\Gamma _{g},S_{n}\right )$
and labeled n-sheeted covering spaces of
![]() $\Sigma _{g}$
(pointed at o). For
$\Sigma _{g}$
(pointed at o). For
![]() $\phi \colon \Gamma _{g}\to S_{n}$
, denote the corresponding covering space by
$\phi \colon \Gamma _{g}\to S_{n}$
, denote the corresponding covering space by
![]() $p_{\phi }\colon X_{\phi }\to \Sigma _{g}$
. As explained above,
$p_{\phi }\colon X_{\phi }\to \Sigma _{g}$
. As explained above,
![]() $X_{\phi }$
inherits a CW-structure from
$X_{\phi }$
inherits a CW-structure from
![]() $\Sigma _{g}$
and is, therefore, a tiled surface. The fiber above o is precisely the vertices of
$\Sigma _{g}$
and is, therefore, a tiled surface. The fiber above o is precisely the vertices of
![]() $X_{\phi }$
, and they are labeled by
$X_{\phi }$
, and they are labeled by
![]() $\left [n\right ]$
in this construction.
$\left [n\right ]$
in this construction.
Expected number of fixed points as expected number of lifts
Given a compact tiled surface Y, we are interested in the expected number of morphisms from Y to a random n-covering of
![]() $\Sigma _{g}$
, namely, in
$\Sigma _{g}$
, namely, in
where
![]() $\phi $
is sampled uniformly at random from
$\phi $
is sampled uniformly at random from
![]() $\mathbb {X}_{g,n}$
. Equivalently, this is the expected number of lifts of the restricted covering map
$\mathbb {X}_{g,n}$
. Equivalently, this is the expected number of lifts of the restricted covering map
![]() $p:Y\to \Sigma _{g}$
to the random n-covering
$p:Y\to \Sigma _{g}$
to the random n-covering
![]() $X_{\phi }$
:
$X_{\phi }$
:

Note that if Y is connected and
![]() $\phi \in \mathbb {X}_{g,n}$
, the number of morphisms
$\phi \in \mathbb {X}_{g,n}$
, the number of morphisms
![]() $Y\to X_{\phi }$
is at most n, as any vertex of Y can be lifted to one of the n vertices of
$Y\to X_{\phi }$
is at most n, as any vertex of Y can be lifted to one of the n vertices of
![]() $X_{\phi }$
, and each such lift can be extended in at most one way to a lift of the whole of Y. For suitable choices of Y,
$X_{\phi }$
, and each such lift can be extended in at most one way to a lift of the whole of Y. For suitable choices of Y,
![]() $\mathbb {E}_{n}\left (Y\right )$
is equal to the quantities
$\mathbb {E}_{n}\left (Y\right )$
is equal to the quantities
![]() $\mathbb {E}_{g,n}\left [\mathsf {fix}_{\gamma }\right ]$
and
$\mathbb {E}_{g,n}\left [\mathsf {fix}_{\gamma }\right ]$
and
![]() $\mathbb {E}_{g,n}\left [\mathsf {fix}_{J}\right ]$
that feature in our main theorems (Theorems 1.1, 1.2 and 1.3):
$\mathbb {E}_{g,n}\left [\mathsf {fix}_{J}\right ]$
that feature in our main theorems (Theorems 1.1, 1.2 and 1.3):
Lemma 2.7. Let Y be a connected tiled surface and
![]() $p\colon Y\to \Sigma _{g}$
the restricted covering map. For arbitrary vertex
$p\colon Y\to \Sigma _{g}$
the restricted covering map. For arbitrary vertex
![]() $y\in Y$
, assume that
$y\in Y$
, assume that
![]() $p_{*}\left (\pi _{1}\left (Y,y\right )\right )$
is conjugate to
$p_{*}\left (\pi _{1}\left (Y,y\right )\right )$
is conjugate to
![]() $J\le _{\mathrm {f.g.}}\Gamma _{g}$
(as a subgroup of
$J\le _{\mathrm {f.g.}}\Gamma _{g}$
(as a subgroup of
![]() $\pi _{1}\left (\Sigma _{g},o\right )=\Gamma _{g}$
). Then for all
$\pi _{1}\left (\Sigma _{g},o\right )=\Gamma _{g}$
). Then for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
In particular, for
![]() $J\le _{\mathrm {f.g.}}\Gamma _{g}$
,
$J\le _{\mathrm {f.g.}}\Gamma _{g}$
,
Proof. In fact, the equality holds at the level of the individual representation
![]() $\phi \in \mathbb {X}_{n}=\mathrm {Hom}\left (\Gamma _{g},S_{n}\right )$
: The number of morphisms
$\phi \in \mathbb {X}_{n}=\mathrm {Hom}\left (\Gamma _{g},S_{n}\right )$
: The number of morphisms
![]() $Y\to X_{\phi }$
is equal to the number of common fixed points
$Y\to X_{\phi }$
is equal to the number of common fixed points
![]() $\mathsf {fix}_{J}\left (\phi \right )$
. Indeed, because the number of common fixed points of
$\mathsf {fix}_{J}\left (\phi \right )$
. Indeed, because the number of common fixed points of
![]() $\phi \left (J\right )$
is the same as the number of fixed points of any conjugate, we may assume without loss of generality that
$\phi \left (J\right )$
is the same as the number of fixed points of any conjugate, we may assume without loss of generality that
![]() $p_{*}\left (\pi _{1}\left (Y,y\right )\right )=J$
. Now,
$p_{*}\left (\pi _{1}\left (Y,y\right )\right )=J$
. Now,
![]() $i\in \left [n\right ]$
is a common fixed point of
$i\in \left [n\right ]$
is a common fixed point of
![]() $\phi \left (J\right )$
if and only if
$\phi \left (J\right )$
if and only if
![]() $J\le \pi _{1}\left (X_{\phi },v_{i}\right )$
, where
$J\le \pi _{1}\left (X_{\phi },v_{i}\right )$
, where
![]() $v_{i}$
is the vertex of
$v_{i}$
is the vertex of
![]() $X_{\phi }$
labeled i, and
$X_{\phi }$
labeled i, and
![]() $\pi _{1}\left (X_{\phi },v_{i}\right )$
is identified with the subgroup
$\pi _{1}\left (X_{\phi },v_{i}\right )$
is identified with the subgroup
By standard facts from the theory of covering spaces [Reference HatcherHat05, Prop. 1.33 and 1.34], there is a lift of p to
![]() $X_{\phi }$
mapping the vertex y to
$X_{\phi }$
mapping the vertex y to
![]() $v_{i}$
if and only if (the image in
$v_{i}$
if and only if (the image in
![]() $\Gamma _{g}$
of)
$\Gamma _{g}$
of)
![]() $\pi _{1}\left (Y,y\right )$
is contained in (the image in
$\pi _{1}\left (Y,y\right )$
is contained in (the image in
![]() $\Gamma _{g}$
of)
$\Gamma _{g}$
of)
![]() $\pi _{1}\left (X_{\phi },v_{i}\right )$
, and this lift, if exists, is unique.
$\pi _{1}\left (X_{\phi },v_{i}\right )$
, and this lift, if exists, is unique.
The statement about core surfaces follows from the fact that (the image in
![]() $\Gamma _{g}$
of)
$\Gamma _{g}$
of)
![]() $\pi _{1}\left (\mathrm {Core}\left (J\right )\right )$
is conjugate to J [Reference Magee and PuderMP22a, Prop. 5.3].
$\pi _{1}\left (\mathrm {Core}\left (J\right )\right )$
is conjugate to J [Reference Magee and PuderMP22a, Prop. 5.3].
Another type of expectation will also feature in this work. Given a compact tiled surface Y, denote
where the expectation is over a uniformly random
![]() $\phi \in \mathbb {X}_{g,n}$
.
$\phi \in \mathbb {X}_{g,n}$
.
2.3 Resolutions
Definition 2.8 (Resolutions).
A resolution
![]() $\mathcal {\mathcal {R}}$
of a tiled surface Y is a collection of morphisms of tiled surfaces
$\mathcal {\mathcal {R}}$
of a tiled surface Y is a collection of morphisms of tiled surfaces
such that every morphism
![]() $h\colon Y\to Z$
of Y into a tiled surface Z with no boundary decomposes uniquely as
$h\colon Y\to Z$
of Y into a tiled surface Z with no boundary decomposes uniquely as
![]() $Y\stackrel {f}{\to }W_{f}\stackrel {\overline {h}}{\hookrightarrow }Z$
, where
$Y\stackrel {f}{\to }W_{f}\stackrel {\overline {h}}{\hookrightarrow }Z$
, where
![]() $f\in \mathcal {R}$
and
$f\in \mathcal {R}$
and
![]() $\overline {h}$
is an embedding.
$\overline {h}$
is an embedding.
The purpose of introducing resolutions is the following obvious lemma. Recall the notation
![]() $\mathbb {E}_{n}\left (Y\right )$
and
$\mathbb {E}_{n}\left (Y\right )$
and
![]() $\mathbb {E}_{n}^{\mathrm {emb}}\left (Y\right )$
from Section 2.2.
$\mathbb {E}_{n}^{\mathrm {emb}}\left (Y\right )$
from Section 2.2.
Lemma 2.9. If Y is a compact tiled surface and
![]() $\mathcal {R}$
is a finite resolution of Y, then
$\mathcal {R}$
is a finite resolution of Y, then
 $$ \begin{align} \mathbb{E}_{n}\left(Y\right)=\sum_{f\in\mathcal{R}}\mathbb{E}_{n}^{\mathrm{emb}}\left(W_{f}\right). \end{align} $$
$$ \begin{align} \mathbb{E}_{n}\left(Y\right)=\sum_{f\in\mathcal{R}}\mathbb{E}_{n}^{\mathrm{emb}}\left(W_{f}\right). \end{align} $$
Our main goal in the rest of this subsection is to prove the existence of a finite resolution whenever we are given a compact tiled surface Y – this is the content of Theorem 2.14 below. This resolution will consist strictly of boundary reduced tiled surfaces
![]() $W_{f}$
, and some of these will even be strongly boundary reduced. We shall make use of Theorem 2.14 mainly for Y a core surface of a finitely generated subgroup of
$W_{f}$
, and some of these will even be strongly boundary reduced. We shall make use of Theorem 2.14 mainly for Y a core surface of a finitely generated subgroup of
![]() $\Gamma $
. In this case, the resolution we construct has even nicer properties – see Proposition 2.15.
$\Gamma $
. In this case, the resolution we construct has even nicer properties – see Proposition 2.15.
Ideally, we would have liked to get a resolution where all the elements are strongly boundary reduced. Unfortunately, such a resolution does not always exist. For example, when
![]() $g=2$
and
$g=2$
and
![]() $\Gamma _{2}=\left \langle a,b,c,d\,\middle |\,\left [a,b\right ]\left [c,d\right ]\right \rangle $
, the core surface
$\Gamma _{2}=\left \langle a,b,c,d\,\middle |\,\left [a,b\right ]\left [c,d\right ]\right \rangle $
, the core surface
![]() $Y=\mathrm {Core}\left (\left \langle \left [a,b\right ]\right \rangle \right )$
does not admit such a resolution as can be inferred from [Reference Magee and PuderMP22a, Fig. 4.2].
$Y=\mathrm {Core}\left (\left \langle \left [a,b\right ]\right \rangle \right )$
does not admit such a resolution as can be inferred from [Reference Magee and PuderMP22a, Fig. 4.2].
To prove the existence of a resolution with nice properties, we first define a process which outputs a ‘compromise’ between the
![]() $\mathsf {BR}$
-closure of a tiled surface and the
$\mathsf {BR}$
-closure of a tiled surface and the
![]() $\mathsf {SBR}$
-closure, introduced in [Reference Magee and PuderMP22a, §4].
$\mathsf {SBR}$
-closure, introduced in [Reference Magee and PuderMP22a, §4].
Definition 2.10. Fix
![]() $\chi _{0}\in \mathbb {Z}$
. Assume that
$\chi _{0}\in \mathbb {Z}$
. Assume that
![]() $h\colon Y\to Z$
is a morphism between tiled surfaces where Y is compact and Z has no boundary. Let
$h\colon Y\to Z$
is a morphism between tiled surfaces where Y is compact and Z has no boundary. Let
![]() $W_{0}$
denote the h-image of Y in Z. Set
$W_{0}$
denote the h-image of Y in Z. Set
![]() $i=0$
. Perform the following algorithm we call the growing process:
$i=0$
. Perform the following algorithm we call the growing process:
-
1. If one of the following conditions holds:
-
(a)
 $W_{i}$
is strongly boundary reduced, or
$W_{i}$
is strongly boundary reduced, or -
(b)
 $W_{i}$
is boundary reduced and
$W_{i}$
is boundary reduced and
 $\chi \left (W_{i}\right )<\chi _{0}$
,
$\chi \left (W_{i}\right )<\chi _{0}$
,
terminate and return
 $h\colon Y\to W_{i}$
.
$h\colon Y\to W_{i}$
. -
-
2. Obtain
 $W_{i+1}$
from
$W_{i+1}$
from
 $W_{i}$
by adding to
$W_{i}$
by adding to
 $W_{i}$
(the closure of) every
$W_{i}$
(the closure of) every
 $4g$
-gon in
$4g$
-gon in
 $Z\setminus W_{i}$
which touches along its boundary an edge of
$Z\setminus W_{i}$
which touches along its boundary an edge of
 $\partial W_{i}$
which is part of a half-block (this includes the case of a long block), a long chain or a half-chain. Set
$\partial W_{i}$
which is part of a half-block (this includes the case of a long block), a long chain or a half-chain. Set
 $i:=i+1$
and return to item
$i:=i+1$
and return to item
 $1$
.
$1$
.
It is clear that every step of this process is deterministic. Note that if the process ends when
![]() $W_{i}$
is strongly boundary reduced, then
$W_{i}$
is strongly boundary reduced, then
![]() $W_{i}$
is the unique smallest strongly boundary reduced tiled surface inside Z containing
$W_{i}$
is the unique smallest strongly boundary reduced tiled surface inside Z containing
![]() $W_{0}$
, denoted
$W_{0}$
, denoted
![]() $\mathsf {SBR}(Y\hookrightarrow Z)$
[Reference Magee and PuderMP22a, §4]. (In general,
$\mathsf {SBR}(Y\hookrightarrow Z)$
[Reference Magee and PuderMP22a, §4]. (In general,
![]() $\mathsf {SBR}(Y\hookrightarrow Z)$
is not always compact, but in this case it is.) The growing process always terminates after finitely many steps.
$\mathsf {SBR}(Y\hookrightarrow Z)$
is not always compact, but in this case it is.) The growing process always terminates after finitely many steps.
Lemma 2.11. The process described in Definition 2.10 always terminates.
Proof. Let
![]() $\mathfrak {he}\left (W_{i}\right )$
denote the number of hanging half-edges along the boundary of
$\mathfrak {he}\left (W_{i}\right )$
denote the number of hanging half-edges along the boundary of
![]() $\left (W_{i}\right )_{+}$
, and consider the triple
$\left (W_{i}\right )_{+}$
, and consider the triple
For every i,
![]() $W_{i}$
is a compact subsurface of Z, and so the three quantities are well-defined integers. We claim that at every step in the growing process, the triple (2.2) strictly reduces with respect to the lexicographic order.
$W_{i}$
is a compact subsurface of Z, and so the three quantities are well-defined integers. We claim that at every step in the growing process, the triple (2.2) strictly reduces with respect to the lexicographic order.
Indeed, assume we do not halt after i steps, and let
![]() $O_{1},\ldots ,O_{k}$
be the list of
$O_{1},\ldots ,O_{k}$
be the list of
![]() $4g$
-gons in
$4g$
-gons in
![]() $Z\setminus W_{i}$
which are added to
$Z\setminus W_{i}$
which are added to
![]() $W_{i}$
in order to obtain
$W_{i}$
in order to obtain
![]() $W_{i+1}$
. By the choice of
$W_{i+1}$
. By the choice of
![]() $4g$
-gons, it is clear that
$4g$
-gons, it is clear that
![]() $\mathfrak {d}\left (W_{i+1}\right )\le \mathfrak {d}\left (W_{i}\right )$
. If the inequality is strict, we are done. So assume
$\mathfrak {d}\left (W_{i+1}\right )\le \mathfrak {d}\left (W_{i}\right )$
. If the inequality is strict, we are done. So assume
![]() $\mathfrak {d}\left (W_{i+1}\right )=\mathfrak {d}\left (W_{i}\right )$
. This means that
$\mathfrak {d}\left (W_{i+1}\right )=\mathfrak {d}\left (W_{i}\right )$
. This means that
![]() $\partial \left (W_{i}\right )$
contains no long blocks nor long chains, so it is boundary reduced, and that the edges in the complements in Z of the half-blocks and half-chains at
$\partial \left (W_{i}\right )$
contains no long blocks nor long chains, so it is boundary reduced, and that the edges in the complements in Z of the half-blocks and half-chains at
![]() $\partial \left (W_{i}\right )$
all belong to
$\partial \left (W_{i}\right )$
all belong to
![]() $\partial \left (W_{i+1}\right )$
. In other words, let
$\partial \left (W_{i+1}\right )$
. In other words, let
![]() $p_{1},\ldots ,p_{m}$
be these complements in Z: So
$p_{1},\ldots ,p_{m}$
be these complements in Z: So
![]() $p_{j}$
is either a half-block or a half-chain. The equality
$p_{j}$
is either a half-block or a half-chain. The equality
![]() $\mathfrak {d}\left (W_{i+1}\right )=\mathfrak {d}\left (W_{i}\right )$
means that all the edges in
$\mathfrak {d}\left (W_{i+1}\right )=\mathfrak {d}\left (W_{i}\right )$
means that all the edges in
![]() $p_{1},\ldots ,p_{m}$
belong to
$p_{1},\ldots ,p_{m}$
belong to
![]() $\partial W_{i+1}$
.
$\partial W_{i+1}$
.
It is easy to see that in this case
![]() $\chi \left (W_{i+1}\right )\le \chi \left (W_{i}\right )$
: The number of new
$\chi \left (W_{i+1}\right )\le \chi \left (W_{i}\right )$
: The number of new
![]() $4g$
-gons and vertices in
$4g$
-gons and vertices in
![]() $W_{i+1}$
at most balances the number of new edges. Let V denote the set of internal vertices in
$W_{i+1}$
at most balances the number of new edges. Let V denote the set of internal vertices in
![]() $p_{1},\ldots ,p_{m}$
(so not at their endpoints). We have strict inequality
$p_{1},\ldots ,p_{m}$
(so not at their endpoints). We have strict inequality
![]() $\chi \left (W_{i+1}\right )<\chi \left (W_{i}\right )$
if and only if some
$\chi \left (W_{i+1}\right )<\chi \left (W_{i}\right )$
if and only if some
![]() $v\in V$
belongs to
$v\in V$
belongs to
![]() $W_{i}$
or to two different complements from
$W_{i}$
or to two different complements from
![]() $p_{1},\ldots ,p_{m}$
.
$p_{1},\ldots ,p_{m}$
.
Now, assume that
![]() $\mathfrak {d}\left (W_{i+1}\right )=\mathfrak {d}\left (W_{i}\right )$
and
$\mathfrak {d}\left (W_{i+1}\right )=\mathfrak {d}\left (W_{i}\right )$
and
![]() $\chi \left (W_{i+1}\right )=\chi \left (W_{i}\right )$
. Then
$\chi \left (W_{i+1}\right )=\chi \left (W_{i}\right )$
. Then
![]() $W_{i}$
is boundary reduced and each of the complements
$W_{i}$
is boundary reduced and each of the complements
![]() $p_{1},\ldots ,p_{m}$
is a connected piece of
$p_{1},\ldots ,p_{m}$
is a connected piece of
![]() $\partial W_{i+1}$
. If
$\partial W_{i+1}$
. If
![]() $O_{j}$
touches a half-block of
$O_{j}$
touches a half-block of
![]() $\partial W_{i}$
, its annexation adds a net of
$\partial W_{i}$
, its annexation adds a net of
![]() $\left (2g-1\right )\left (4g-2\right )-2=8g\left (g-1\right )$
hanging half-edges. Every
$\left (2g-1\right )\left (4g-2\right )-2=8g\left (g-1\right )$
hanging half-edges. Every
![]() $4g$
-gon along a half-chain of
$4g$
-gon along a half-chain of
![]() $\partial W_{i}$
also adds on average a net of
$\partial W_{i}$
also adds on average a net of
![]() $8g\left (g-1\right )$
hanging half-edges. So if we add at least one
$8g\left (g-1\right )$
hanging half-edges. So if we add at least one
![]() $4g$
-gon at the
$4g$
-gon at the
![]() $\left (i+1\right )$
st step,
$\left (i+1\right )$
st step,
![]() $-\mathfrak {he}$
strictly decreases. So indeed the triple (2.2) strictly decreases lexicographically in every step.
$-\mathfrak {he}$
strictly decreases. So indeed the triple (2.2) strictly decreases lexicographically in every step.
Finally, there are at most finitely many steps in which
![]() $\mathfrak {d}\left (W_{i}\right )$
decreases because this is a nonnegative integer. So it is enough to show there cannot be infinitely many steps in which
$\mathfrak {d}\left (W_{i}\right )$
decreases because this is a nonnegative integer. So it is enough to show there cannot be infinitely many steps in which
![]() $\mathfrak {d}\left (W_{i}\right )$
is constant. If
$\mathfrak {d}\left (W_{i}\right )$
is constant. If
![]() $\mathfrak {d}\left (W_{i+1}\right )=\mathfrak {d}\left (W_{i}\right )$
, then
$\mathfrak {d}\left (W_{i+1}\right )=\mathfrak {d}\left (W_{i}\right )$
, then
![]() $W_{i}$
is boundary reduced. If
$W_{i}$
is boundary reduced. If
![]() $\chi \left (W_{i}\right )$
keeps decreasing, then eventually we hit the bound
$\chi \left (W_{i}\right )$
keeps decreasing, then eventually we hit the bound
![]() $\chi \left (W_{i}\right )<\chi _{0}$
and halt. If
$\chi \left (W_{i}\right )<\chi _{0}$
and halt. If
![]() $\mathfrak {d}\left (W_{i}\right )$
and
$\mathfrak {d}\left (W_{i}\right )$
and
![]() $\chi \left (W_{i}\right )$
are constant, then
$\chi \left (W_{i}\right )$
are constant, then
![]() $\mathfrak {he}\left (W_{i}\right )$
increases constantly, but in every tiled surface W,
$\mathfrak {he}\left (W_{i}\right )$
increases constantly, but in every tiled surface W,
![]() $\mathfrak {he}\left (W\right )\le 4g\mathfrak {d}\left (W\right )$
, so there cannot be infinitely many steps of this type too. This proves the lemma.
$\mathfrak {he}\left (W\right )\le 4g\mathfrak {d}\left (W\right )$
, so there cannot be infinitely many steps of this type too. This proves the lemma.
Lemma 2.12. There is a bound
![]() $B=B\left (Y\right )$
, independent of
$B=B\left (Y\right )$
, independent of
![]() $h\colon Y\to Z$
, such that in the entire growing process, at most
$h\colon Y\to Z$
, such that in the entire growing process, at most
![]() $B=B\left (Y\right )$
$B=B\left (Y\right )$
![]() $4g$
-gons are added to
$4g$
-gons are added to
![]() $W_{0}$
.
$W_{0}$
.
Proof. Note that every boundary edge of
![]() $W_{0}$
is necessarily an h-image of a boundary edge of Y so that
$W_{0}$
is necessarily an h-image of a boundary edge of Y so that
![]() $\mathfrak {d}\left (W_{i}\right )\le \mathfrak {d}\left (W_{0}\right )\le \mathfrak {d}\left (Y\right )$
. In every step, we add at most
$\mathfrak {d}\left (W_{i}\right )\le \mathfrak {d}\left (W_{0}\right )\le \mathfrak {d}\left (Y\right )$
. In every step, we add at most
![]() $\frac {\mathfrak {d}\left (W_{i}\right )}{2g-1}\le \frac {\mathfrak {d}\left (Y\right )}{2g-1}$
$\frac {\mathfrak {d}\left (W_{i}\right )}{2g-1}\le \frac {\mathfrak {d}\left (Y\right )}{2g-1}$
![]() $4g$
-gons. So it is enough to bound the number of steps performed in the growing process until it terminates. There are at most
$4g$
-gons. So it is enough to bound the number of steps performed in the growing process until it terminates. There are at most
![]() $\mathfrak {d}\left (Y\right )$
steps in which
$\mathfrak {d}\left (Y\right )$
steps in which
![]() $\mathfrak {d}\left (W_{i}\right )$
strictly decreasesFootnote
11
(
$\mathfrak {d}\left (W_{i}\right )$
strictly decreasesFootnote
11
(
![]() $\mathfrak {d}\left (W_{i+1}\right )<\mathfrak {d}\left (W_{i}\right )$
), so there are at most
$\mathfrak {d}\left (W_{i+1}\right )<\mathfrak {d}\left (W_{i}\right )$
), so there are at most
![]() $\mathfrak {d}\left (Y\right )+1$
possible values of
$\mathfrak {d}\left (Y\right )+1$
possible values of
![]() $\mathfrak {d}\left (W_{i}\right )$
. In steps where
$\mathfrak {d}\left (W_{i}\right )$
. In steps where
![]() $\mathfrak {d}\left (W_{i}\right )$
is unchanged,
$\mathfrak {d}\left (W_{i}\right )$
is unchanged,
![]() $W_{i}$
is boundary reduced, so by definition
$W_{i}$
is boundary reduced, so by definition
![]() $\chi \left (W_{i}\right )\ge \chi _{0}$
(otherwise, the process terminates). Let
$\chi \left (W_{i}\right )\ge \chi _{0}$
(otherwise, the process terminates). Let
![]() $\pi _{0}\left (Y\right )$
denote the number of connected components of Y. For all i,
$\pi _{0}\left (Y\right )$
denote the number of connected components of Y. For all i,
![]() $W_{i}$
is a subsurface of Z with at most
$W_{i}$
is a subsurface of Z with at most
![]() $\pi _{0}\left (Y\right )$
connected components, and by the classification of surfaces,
$\pi _{0}\left (Y\right )$
connected components, and by the classification of surfaces,
![]() $\chi \left (W_{i}\right )\le 2\pi _{0}\left (Y\right )$
. There are at most
$\chi \left (W_{i}\right )\le 2\pi _{0}\left (Y\right )$
. There are at most
![]() $2\pi _{0}\left (Y\right )-\chi _{0}$
steps with
$2\pi _{0}\left (Y\right )-\chi _{0}$
steps with
![]() $\mathfrak {d}\left (W_{i}\right )$
fixed and
$\mathfrak {d}\left (W_{i}\right )$
fixed and
![]() $\chi \left (W_{i}\right )$
strictly decreasing. Finally, when
$\chi \left (W_{i}\right )$
strictly decreasing. Finally, when
![]() $\mathfrak {d}\left (W_{i}\right )$
is constant there are at most
$\mathfrak {d}\left (W_{i}\right )$
is constant there are at most
![]() $2\pi _{0}\left (Y\right )-\chi _{0}+1$
possible values of
$2\pi _{0}\left (Y\right )-\chi _{0}+1$
possible values of
![]() $\chi \left (W_{i}\right )$
, and if
$\chi \left (W_{i}\right )$
, and if
![]() $\mathfrak {d}\left (W_{i+1}\right )=\mathfrak {d}\left (W_{i}\right )$
and
$\mathfrak {d}\left (W_{i+1}\right )=\mathfrak {d}\left (W_{i}\right )$
and
![]() $\chi \left (W_{i+1}\right )=\chi \left (W_{i}\right )$
, then
$\chi \left (W_{i+1}\right )=\chi \left (W_{i}\right )$
, then
![]() $\mathfrak {he}\left (W_{i+1}\right )\ge \mathfrak {he}\left (W_{i}\right )+8g\left (g-1\right )$
and
$\mathfrak {he}\left (W_{i+1}\right )\ge \mathfrak {he}\left (W_{i}\right )+8g\left (g-1\right )$
and
![]() $\mathfrak {he}\left (W_{i}\right )\le 4g\mathfrak {d}\left (W_{i}\right )\le 4g\mathfrak {d}\left (Y\right )$
, so there are at most
$\mathfrak {he}\left (W_{i}\right )\le 4g\mathfrak {d}\left (W_{i}\right )\le 4g\mathfrak {d}\left (Y\right )$
, so there are at most
![]() $\frac {\mathfrak {d}\left (Y\right )}{2\left (g-1\right )}$
steps with the same value of
$\frac {\mathfrak {d}\left (Y\right )}{2\left (g-1\right )}$
steps with the same value of
![]() $\mathfrak {d}\left (W_{i}\right )$
and
$\mathfrak {d}\left (W_{i}\right )$
and
![]() $\chi \left (W_{i}\right )$
. Overall there are at most
$\chi \left (W_{i}\right )$
. Overall there are at most
 $$ \begin{align} \mathfrak{d}\left(Y\right)+\left(\mathfrak{d}\left(Y\right)+1\right)\left[\left(2\pi_{0}\left(Y\right)-\chi_{0}\right)+\left(2\pi_{0}\left(Y\right)-\chi_{0}+1\right)\cdot\frac{\mathfrak{d}\left(Y\right)}{2\left(g-1\right)}\right] \end{align} $$
$$ \begin{align} \mathfrak{d}\left(Y\right)+\left(\mathfrak{d}\left(Y\right)+1\right)\left[\left(2\pi_{0}\left(Y\right)-\chi_{0}\right)+\left(2\pi_{0}\left(Y\right)-\chi_{0}+1\right)\cdot\frac{\mathfrak{d}\left(Y\right)}{2\left(g-1\right)}\right] \end{align} $$
steps in the growing process. Define
![]() $B\left (Y\right )$
to be
$B\left (Y\right )$
to be
![]() $\frac {\mathfrak {d}\left (Y\right )}{2g-1}$
times equation (2.3).
$\frac {\mathfrak {d}\left (Y\right )}{2g-1}$
times equation (2.3).
We can now define the sought-after resolution for compact tiled surfaces.
Definition 2.13. Suppose that Y is a compact tiled surface and
![]() $\chi _{0}\in \mathbb {Z}$
a fixed integer. Define the
$\chi _{0}\in \mathbb {Z}$
a fixed integer. Define the
![]() $\chi _{0}$
-resolution of Y to be the collection
$\chi _{0}$
-resolution of Y to be the collection
obtained from all possible morphisms
![]() $h\colon Y\to Z$
from Y to a tiled surface Z with no boundary via the growing process (the process applied with the parameter
$h\colon Y\to Z$
from Y to a tiled surface Z with no boundary via the growing process (the process applied with the parameter
![]() $\chi _{0}$
).
$\chi _{0}$
).
Theorem 2.14. Suppose Y is a compact tiled surface and
![]() $\chi _{0}\in \mathbb {Z}$
a fixed integer. The collection
$\chi _{0}\in \mathbb {Z}$
a fixed integer. The collection
![]() $\mathcal {R}=\mathcal {R}\left (Y,\chi _{0}\right )$
from Definition 2.13 is a finite resolution of Y which satisfies further
$\mathcal {R}=\mathcal {R}\left (Y,\chi _{0}\right )$
from Definition 2.13 is a finite resolution of Y which satisfies further
-
R1 for every
 $f\in \mathcal {R}$
, the tiled surface
$f\in \mathcal {R}$
, the tiled surface
 $W_{f}$
is compact and boundary reduced, and
$W_{f}$
is compact and boundary reduced, and -
R2 for every
 $f\in \mathcal {R}$
with
$f\in \mathcal {R}$
with
 $\chi \left (W_{f}\right )\ge \chi _{0}$
, the tiled surface
$\chi \left (W_{f}\right )\ge \chi _{0}$
, the tiled surface
 $W_{f}$
is strongly boundary reduced.
$W_{f}$
is strongly boundary reduced.
Proof. By Lemma 2.11 and the halting conditions of the growing process, it is clear that every such morphism in
![]() $\mathcal {R}$
satisfies R1 and R2. Given a morphism
$\mathcal {R}$
satisfies R1 and R2. Given a morphism
![]() $h\colon Y\to Z$
as in Definition 2.13,
$h\colon Y\to Z$
as in Definition 2.13,
![]() $h\left (Y\right )$
(also named
$h\left (Y\right )$
(also named
![]() $W_{0}$
) is a quotient of Y and therefore the number of cells in
$W_{0}$
) is a quotient of Y and therefore the number of cells in
![]() $h\left (Y\right )$
is bounded. From Lemma 2.12, we now conclude that that there is a bound on the number of cells in any
$h\left (Y\right )$
is bounded. From Lemma 2.12, we now conclude that that there is a bound on the number of cells in any
![]() $W_{f}$
with
$W_{f}$
with
![]() $f\in \mathcal {R}$
. This shows that
$f\in \mathcal {R}$
. This shows that
![]() $\mathcal {R}$
is finite as there are finitely many tiled surfaces with given bounds on the number of cells and finitely many morphisms between two given compact tiled surfaces.
$\mathcal {R}$
is finite as there are finitely many tiled surfaces with given bounds on the number of cells and finitely many morphisms between two given compact tiled surfaces.
It remains to show that
![]() $\mathcal {R}$
is a resolution. By the way it was constructed, it is clear that every morphism
$\mathcal {R}$
is a resolution. By the way it was constructed, it is clear that every morphism
![]() $h\colon Y\to Z$
with
$h\colon Y\to Z$
with
![]() $\partial Z=\emptyset $
decomposes as
$\partial Z=\emptyset $
decomposes as
and that
![]() $f\in \mathcal {R}$
. To show uniqueness, assume that h decomposes in an additional way
$f\in \mathcal {R}$
. To show uniqueness, assume that h decomposes in an additional way
where
![]() $W_{\varphi }$
is the result of the growing process for some
$W_{\varphi }$
is the result of the growing process for some
![]() $h'\colon Y\to Z'$
with
$h'\colon Y\to Z'$
with
![]() $\partial Z'=\emptyset $
. We claim that equations (2.4) and (2.5) are precisely the same decompositions of h. Indeed, the growing process defined by
$\partial Z'=\emptyset $
. We claim that equations (2.4) and (2.5) are precisely the same decompositions of h. Indeed, the growing process defined by
![]() $h'\colon Y\to Z'$
takes place entirely inside
$h'\colon Y\to Z'$
takes place entirely inside
![]() $W_{\varphi }$
and does not depend on the structure of
$W_{\varphi }$
and does not depend on the structure of
![]() $Z'\backslash W_{\varphi }$
: In the
$Z'\backslash W_{\varphi }$
: In the
![]() $\left (i+1\right )$
st step of the growing process, the decision whether or not to annex more
$\left (i+1\right )$
st step of the growing process, the decision whether or not to annex more
![]() $4g$
-gons and where depends only on the structure and boundary of
$4g$
-gons and where depends only on the structure and boundary of
![]() $W_{i}$
. Consequently, the growing process defined by the morphism
$W_{i}$
. Consequently, the growing process defined by the morphism
![]() $h'\colon Y\to Z'$
has the exact same output, in terms of the resulting element we add to
$h'\colon Y\to Z'$
has the exact same output, in terms of the resulting element we add to
![]() $\mathcal {R}$
, as the growing process defined by the composition
$\mathcal {R}$
, as the growing process defined by the composition
![]() $Y\stackrel {\varphi }{\to }W_{\varphi }\hookrightarrow Z$
. But because the growing process is deterministic, the latter is identical to the growing process defined by
$Y\stackrel {\varphi }{\to }W_{\varphi }\hookrightarrow Z$
. But because the growing process is deterministic, the latter is identical to the growing process defined by
![]() $h\colon Y\to Z$
.
$h\colon Y\to Z$
.
As mentioned above, we will use Theorem 2.14 mainly with Y being a core surface. In this case, the theorem can be strengthened as follows. Recall from Section 1 that, given
![]() $J\le _{\mathrm {f.g.}}\Gamma _{g}$
, we denote by
$J\le _{\mathrm {f.g.}}\Gamma _{g}$
, we denote by
![]() $\mathfrak {MOG}\left (J\right )$
the set of f.g. overgroups of J with maximal Euler characteristic, and by
$\mathfrak {MOG}\left (J\right )$
the set of f.g. overgroups of J with maximal Euler characteristic, and by
![]() $\chi _{\max }\left (J\right )$
this maximal Euler characteristic.
$\chi _{\max }\left (J\right )$
this maximal Euler characteristic.
Proposition 2.15 (Addendum to Theorem 2.14).
Let
![]() $J\le _{\mathrm {f.g.}}\Gamma _{g}$
, and let
$J\le _{\mathrm {f.g.}}\Gamma _{g}$
, and let
![]() $\chi _{0}\in \mathbb {Z}$
. Let
$\chi _{0}\in \mathbb {Z}$
. Let
![]() $\mathcal {R}_{J,\chi _{0}}=\left \{ f\colon \mathrm {Core}\left (J\right )\to W_{f}\right \} $
be the resolution
$\mathcal {R}_{J,\chi _{0}}=\left \{ f\colon \mathrm {Core}\left (J\right )\to W_{f}\right \} $
be the resolution
![]() $\mathcal {R}\left (\mathrm {Core}\left (J\right ),\chi _{0}\right )$
from Definition 2.13. Then
$\mathcal {R}\left (\mathrm {Core}\left (J\right ),\chi _{0}\right )$
from Definition 2.13. Then
![]() $\mathcal {R}_{J,\chi _{0}}$
satisfies further the following two properties.
$\mathcal {R}_{J,\chi _{0}}$
satisfies further the following two properties.
-
R2 For every
 $f\in \mathcal {R}_{J,\chi _{0}}$
with
$f\in \mathcal {R}_{J,\chi _{0}}$
with
 $\chi \left (W_{f}\right )\ge \chi _{0}$
, the tiled surface
$\chi \left (W_{f}\right )\ge \chi _{0}$
, the tiled surface
 $W_{f}$
is the core surface of some
$W_{f}$
is the core surface of some
 $K\le _{\mathrm {f.g.}}\Gamma _{g}$
with
$K\le _{\mathrm {f.g.}}\Gamma _{g}$
with
 $J\le K$
and f is the natural morphism between the two core surfaces (the restriction of
$J\le K$
and f is the natural morphism between the two core surfaces (the restriction of
 $J\backslash \widetilde {\Sigma _{g}}\to K\backslash \widetilde {\Sigma _{g}}$
).
$J\backslash \widetilde {\Sigma _{g}}\to K\backslash \widetilde {\Sigma _{g}}$
). -
R4 Assume that
 $\chi _{0}\le \chi _{\max }\left (J\right )$
. Then for every
$\chi _{0}\le \chi _{\max }\left (J\right )$
. Then for every
 $K\in \mathfrak {MOG}\left (J\right )$
, the natural morphism
$K\in \mathfrak {MOG}\left (J\right )$
, the natural morphism
 $\mathrm {Core}\left (J\right )\to \mathrm {Core}\left (K\right )$
belongs to
$\mathrm {Core}\left (J\right )\to \mathrm {Core}\left (K\right )$
belongs to
 $\mathcal {R}_{J,\chi _{0}}$
.
$\mathcal {R}_{J,\chi _{0}}$
.
For
![]() $K\le _{\mathrm {f.g.}}\Gamma _{g}$
, we have
$K\le _{\mathrm {f.g.}}\Gamma _{g}$
, we have
![]() $\chi \left (K\right )=\chi \left (\mathrm {Core}\left (K\right )\right )$
[Reference Magee and PuderMP22a, Prop. 5.3]. Proposition 2.15 thus shows that, as long as
$\chi \left (K\right )=\chi \left (\mathrm {Core}\left (K\right )\right )$
[Reference Magee and PuderMP22a, Prop. 5.3]. Proposition 2.15 thus shows that, as long as
![]() $\chi _{0}\le \chi _{\max }\left (J\right )$
, there is a bijection between the elements of
$\chi _{0}\le \chi _{\max }\left (J\right )$
, there is a bijection between the elements of
![]() $\mathfrak {MOG}\left (J\right )$
and the elements in the resolution with maximal Euler characteristic.
$\mathfrak {MOG}\left (J\right )$
and the elements in the resolution with maximal Euler characteristic.
Corollary 2.16. For every
![]() $J\le _{\mathrm {f.g.}}\Gamma _{g}$
, the set
$J\le _{\mathrm {f.g.}}\Gamma _{g}$
, the set
![]() $\mathfrak {MOG}\left (J\right )$
of f.g. overgroups of maximal Euler characteristic is finite.
$\mathfrak {MOG}\left (J\right )$
of f.g. overgroups of maximal Euler characteristic is finite.
Proof of Proposition 2.15.
Suppose that
![]() $f\colon \mathrm {Core}\left (J\right )\to W_{f}$
satisfies
$f\colon \mathrm {Core}\left (J\right )\to W_{f}$
satisfies
![]() $\chi \left (W_{f}\right )\ge \chi _{0}$
. In particular,
$\chi \left (W_{f}\right )\ge \chi _{0}$
. In particular,
![]() $W_{f}$
is strongly boundary reduced by R2. Let
$W_{f}$
is strongly boundary reduced by R2. Let
![]() $j\in \mathrm {Core}\left (J\right )$
be a vertex and assume without loss of generality that
$j\in \mathrm {Core}\left (J\right )$
be a vertex and assume without loss of generality that
![]() $J=p_{*}\left (\pi _{1}\left (\mathrm {Core}\left (J\right ),j\right )\right )$
(the fact that
$J=p_{*}\left (\pi _{1}\left (\mathrm {Core}\left (J\right ),j\right )\right )$
(the fact that
![]() $p_{*}\left (\pi _{1}\left (\mathrm {Core}\left (J\right ),j\right )\right )\le \pi _{1}\left (\Sigma _{g},o\right )=\Gamma _{g}$
is conjugate to J follows from [Reference Magee and PuderMP22a, Prop. 5.3 and Cor. 4.11]). Define
$p_{*}\left (\pi _{1}\left (\mathrm {Core}\left (J\right ),j\right )\right )\le \pi _{1}\left (\Sigma _{g},o\right )=\Gamma _{g}$
is conjugate to J follows from [Reference Magee and PuderMP22a, Prop. 5.3 and Cor. 4.11]). Define
![]() $K\stackrel {\mathrm {def}}{=}\pi _{1}\left (W_{f},f\left (j\right )\right )$
. As
$K\stackrel {\mathrm {def}}{=}\pi _{1}\left (W_{f},f\left (j\right )\right )$
. As
![]() $W_{f}$
is compact, K is finitely generated. Let
$W_{f}$
is compact, K is finitely generated. Let
![]() $p_{K}\colon \left (K\backslash \widetilde {\Sigma _{g}},k\right )\to \Sigma _{g}$
be the pointed covering space with
$p_{K}\colon \left (K\backslash \widetilde {\Sigma _{g}},k\right )\to \Sigma _{g}$
be the pointed covering space with
![]() $\pi _{1}\left (K\backslash \widetilde {\Sigma _{g}},k\right )=K$
. By the unique lifting property from the theory of covering spaces [Reference HatcherHat05, Prop. 1.33 and 1.34], as
$\pi _{1}\left (K\backslash \widetilde {\Sigma _{g}},k\right )=K$
. By the unique lifting property from the theory of covering spaces [Reference HatcherHat05, Prop. 1.33 and 1.34], as
![]() $W_{f}$
is connected, there is a unique lift
$W_{f}$
is connected, there is a unique lift
![]() $\alpha $
of the restricted covering map
$\alpha $
of the restricted covering map
![]() $p_{W_{f}}\colon W_{f}\to \Sigma _{g}$
to
$p_{W_{f}}\colon W_{f}\to \Sigma _{g}$
to
![]() $K\backslash \widetilde {\Sigma _{g}}$
, which maps
$K\backslash \widetilde {\Sigma _{g}}$
, which maps
![]() $f\left (j\right )$
to k. We will show that
$f\left (j\right )$
to k. We will show that
![]() $\alpha $
gives an isomorphism between
$\alpha $
gives an isomorphism between
![]() $W_{f}$
and
$W_{f}$
and
![]() $\mathrm {Core}\left (K\right )$
.
$\mathrm {Core}\left (K\right )$
.

First, we show that
![]() $\alpha \left (W_{f}\right )\subseteq \mathrm {Core}\left (K\right )$
. Recall that
$\alpha \left (W_{f}\right )\subseteq \mathrm {Core}\left (K\right )$
. Recall that
![]() $W_{f}$
is the result of the growing process for some
$W_{f}$
is the result of the growing process for some
![]() $h\colon \mathrm {Core}\left (J\right )\to Z$
with
$h\colon \mathrm {Core}\left (J\right )\to Z$
with
![]() $\partial Z=\emptyset $
. Consider
$\partial Z=\emptyset $
. Consider
![]() $W_{0}\stackrel {\mathrm {def}}{=} h\left (\mathrm {Core}\left (J\right )\right )\subseteq Z$
. Recall that
$W_{0}\stackrel {\mathrm {def}}{=} h\left (\mathrm {Core}\left (J\right )\right )\subseteq Z$
. Recall that
![]() $W_{f}=\mathsf {SBR}\left (W_{0}\hookrightarrow Z\right )$
. By the unique lifting property,
$W_{f}=\mathsf {SBR}\left (W_{0}\hookrightarrow Z\right )$
. By the unique lifting property,
![]() $\alpha \circ f$
is the natural morphism
$\alpha \circ f$
is the natural morphism
![]() $\mathrm {Core}\left (J\right )\to K\backslash \widetilde {\Sigma _{g}}$
, which, by [Reference Magee and PuderMP22a, Lem. 5.4], has an image contained in
$\mathrm {Core}\left (J\right )\to K\backslash \widetilde {\Sigma _{g}}$
, which, by [Reference Magee and PuderMP22a, Lem. 5.4], has an image contained in
![]() $\mathrm {Core}\left (K\right )$
. Hence,
$\mathrm {Core}\left (K\right )$
. Hence,
![]() $\alpha \left (W_{0}\right )\subseteq \mathrm {Core}\left (K\right )$
. As
$\alpha \left (W_{0}\right )\subseteq \mathrm {Core}\left (K\right )$
. As
![]() $\mathrm {Core}\left (K\right )$
is strongly boundary reduced [Reference Magee and PuderMP22a, Prop. 5.3], we have that
$\mathrm {Core}\left (K\right )$
is strongly boundary reduced [Reference Magee and PuderMP22a, Prop. 5.3], we have that
![]() $\mathsf {SBR}\left (\alpha \left (W_{0}\right )\hookrightarrow K\backslash \widetilde {\Sigma _{g}}\right )$
is contained in
$\mathsf {SBR}\left (\alpha \left (W_{0}\right )\hookrightarrow K\backslash \widetilde {\Sigma _{g}}\right )$
is contained in
![]() $\mathrm {Core}\left (K\right )$
. By [Reference Magee and PuderMP22a, Lem. 4.7],
$\mathrm {Core}\left (K\right )$
. By [Reference Magee and PuderMP22a, Lem. 4.7],
Now, Z is a covering space of
![]() $\Sigma _{g}$
and we may assume it is connected (because
$\Sigma _{g}$
and we may assume it is connected (because
![]() $\mathrm {Core}\left (J\right )$
is). Thus, Z is identical to
$\mathrm {Core}\left (J\right )$
is). Thus, Z is identical to
![]() $L\backslash \widetilde {\Sigma _{g}}$
for some
$L\backslash \widetilde {\Sigma _{g}}$
for some
![]() $L=\pi _{1}\left (Z,h\left (j\right )\right )$
. By property R2,
$L=\pi _{1}\left (Z,h\left (j\right )\right )$
. By property R2,
![]() $W_{f}$
is strongly boundary reduced, and so by [Reference Magee and PuderMP22a, Cor. 4.11] its embedding in Z is
$W_{f}$
is strongly boundary reduced, and so by [Reference Magee and PuderMP22a, Cor. 4.11] its embedding in Z is
![]() $\pi _{1}$
-injective. In other words,
$\pi _{1}$
-injective. In other words,
![]() $K\le L$
and, therefore, there is a morphism
$K\le L$
and, therefore, there is a morphism
![]() $m\colon \left (K\backslash \widetilde {\Sigma _{g}},k\right )\to \left (Z,f\left (j\right )\right )$
. By the unique lifting property, the composition
$m\colon \left (K\backslash \widetilde {\Sigma _{g}},k\right )\to \left (Z,f\left (j\right )\right )$
. By the unique lifting property, the composition
![]() $m\circ \alpha \colon \left (W_{f},f\left (j\right )\right )\to \left (Z,f\left (j\right )\right )$
must be identical to the embedding
$m\circ \alpha \colon \left (W_{f},f\left (j\right )\right )\to \left (Z,f\left (j\right )\right )$
must be identical to the embedding
![]() $\left (W_{f},f\left (j\right )\right )\hookrightarrow \left (Z,f\left (j\right )\right )$
and therefore
$\left (W_{f},f\left (j\right )\right )\hookrightarrow \left (Z,f\left (j\right )\right )$
and therefore
![]() $\alpha $
is injective. So
$\alpha $
is injective. So
![]() $\alpha \left (W_{f}\right )$
is a strongly boundary reduced subtiled surface of
$\alpha \left (W_{f}\right )$
is a strongly boundary reduced subtiled surface of
![]() $\mathrm {Core}\left (K\right )$
with fundamental group K. By [Reference Magee and PuderMP22a, Lem. 5.7], it follows that
$\mathrm {Core}\left (K\right )$
with fundamental group K. By [Reference Magee and PuderMP22a, Lem. 5.7], it follows that
![]() $\alpha \left (W_{f}\right )\supseteq \mathrm {Core}\left (K\right )$
. We conclude that
$\alpha \left (W_{f}\right )\supseteq \mathrm {Core}\left (K\right )$
. We conclude that
![]() $\alpha \colon W_{f}\to \mathrm {Core}\left (K\right )$
is an isomorphism, and R3 is proven.
$\alpha \colon W_{f}\to \mathrm {Core}\left (K\right )$
is an isomorphism, and R3 is proven.
To prove R4, suppose that
![]() $K\in \mathfrak {MOG}\left (J\right )$
. Let
$K\in \mathfrak {MOG}\left (J\right )$
. Let
![]() $h\colon \mathrm {Core}\left (J\right )\to K\backslash \widetilde {\Sigma _{g}}$
be the natural morphism. By the definition of the resolution
$h\colon \mathrm {Core}\left (J\right )\to K\backslash \widetilde {\Sigma _{g}}$
be the natural morphism. By the definition of the resolution
![]() $\mathcal {R}_{J}$
, the morphism h factors as
$\mathcal {R}_{J}$
, the morphism h factors as
![]() $\mathrm {Core}\left (J\right )\stackrel {f}{\to }W_{f}\stackrel {}{\hookrightarrow }K\backslash \widetilde {\Sigma _{g}}$
for some
$\mathrm {Core}\left (J\right )\stackrel {f}{\to }W_{f}\stackrel {}{\hookrightarrow }K\backslash \widetilde {\Sigma _{g}}$
for some
![]() $f\in \mathcal {R}_{J}$
. Because
$f\in \mathcal {R}_{J}$
. Because
![]() $h\left (\mathrm {Core}\left (J\right )\right )\subseteq \mathrm {Core}\left (K\right )$
(by [Reference Magee and PuderMP22a, Lem. 5.4]) and because
$h\left (\mathrm {Core}\left (J\right )\right )\subseteq \mathrm {Core}\left (K\right )$
(by [Reference Magee and PuderMP22a, Lem. 5.4]) and because
![]() $\mathrm {Core}\left (K\right )$
is strongly boundary reduced, we have
$\mathrm {Core}\left (K\right )$
is strongly boundary reduced, we have
![]() $W_{f}\subseteq \mathrm {Core}\left (K\right )$
.
$W_{f}\subseteq \mathrm {Core}\left (K\right )$
.
Let C be a connected component of the difference between the thick version of
![]() $\mathrm {Core}\left (K\right )$
and the thick version of
$\mathrm {Core}\left (K\right )$
and the thick version of
![]() $W_{f}$
. As
$W_{f}$
. As
![]() $\mathrm {Core}\left (K\right )$
is compact,
$\mathrm {Core}\left (K\right )$
is compact,
![]() $\overline {C}$
is compact. As
$\overline {C}$
is compact. As
![]() $\mathrm {Core}\left (K\right )$
is connected,
$\mathrm {Core}\left (K\right )$
is connected,
![]() $\overline {C}$
must intersect
$\overline {C}$
must intersect
![]() $\partial W_{f}$
and in particular has at least one boundary component. Since
$\partial W_{f}$
and in particular has at least one boundary component. Since
![]() $W_{f}$
is boundary reduced,
$W_{f}$
is boundary reduced,
![]() $\overline {C}$
is not homeomorphic to a disc, and so
$\overline {C}$
is not homeomorphic to a disc, and so
![]() $\chi \left (\overline {C}\right )\le 0$
. Now,
$\chi \left (\overline {C}\right )\le 0$
. Now,
the sum being over all connected components as above. We conclude that
![]() $\chi \left (W_{f}\right )\ge \chi \left (K\right )= \chi _{\max }\left (J\right )\ge \chi _{0}$
. By R2,
$\chi \left (W_{f}\right )\ge \chi \left (K\right )= \chi _{\max }\left (J\right )\ge \chi _{0}$
. By R2,
![]() $W_{f}$
is strongly boundary reduced and by R3,
$W_{f}$
is strongly boundary reduced and by R3,
![]() $W_{f}=\mathrm {Core}\left (M\right )$
for some subgroup M. But then
$W_{f}=\mathrm {Core}\left (M\right )$
for some subgroup M. But then
![]() $M\in \mathfrak {MOG}\left (J\right )$
,
$M\in \mathfrak {MOG}\left (J\right )$
,
![]() $\chi \left (\mathrm {Core}\left (M\right )\right )=\chi \left (K\right )$
, and every connected component C as above satisfies
$\chi \left (\mathrm {Core}\left (M\right )\right )=\chi \left (K\right )$
, and every connected component C as above satisfies
![]() $\chi \left (\overline {C}\right )=0$
. As
$\chi \left (\overline {C}\right )=0$
. As
![]() $\overline {C}$
has at least one boundary component, it must be an annulus. But then
$\overline {C}$
has at least one boundary component, it must be an annulus. But then
![]() $\mathrm {Core}\left (M\right )$
is a deformation retract of
$\mathrm {Core}\left (M\right )$
is a deformation retract of
![]() $\mathrm {Core}\left (K\right )$
, so
$\mathrm {Core}\left (K\right )$
, so
![]() $M=K$
up to conjugation and so
$M=K$
up to conjugation and so
![]() $W_{f}=\mathrm {Core}\left (M\right )=\mathrm {Core}\left (K\right )$
.
$W_{f}=\mathrm {Core}\left (M\right )=\mathrm {Core}\left (K\right )$
.
Corollary 2.17. Suppose
![]() $1\ne \gamma \in \Gamma _{g}$
is a nontrivial element. Let q be the maximal natural number such that
$1\ne \gamma \in \Gamma _{g}$
is a nontrivial element. Let q be the maximal natural number such that
![]() $\gamma =\gamma _{0}^{~q}$
for some
$\gamma =\gamma _{0}^{~q}$
for some
![]() $\gamma _{0}\in \Gamma _{g}$
, and
$\gamma _{0}\in \Gamma _{g}$
, and
![]() $d(q)$
the number of positive divisors of q. Then
$d(q)$
the number of positive divisors of q. Then
![]() $\mathrm {Core}\left (\left \langle \gamma \right \rangle \right )$
has a finite resolution
$\mathrm {Core}\left (\left \langle \gamma \right \rangle \right )$
has a finite resolution
![]() $\mathcal {R}_{\gamma }=\left \{ f\colon \mathrm {Core}\left (\left \langle \gamma \right \rangle \right )\to W_{f}\right \} $
with
$\mathcal {R}_{\gamma }=\left \{ f\colon \mathrm {Core}\left (\left \langle \gamma \right \rangle \right )\to W_{f}\right \} $
with
![]() $W_{f}$
boundary reduced for every
$W_{f}$
boundary reduced for every
![]() $f\in R_{\gamma }$
and with exactly
$f\in R_{\gamma }$
and with exactly
![]() $d\left (q\right )$
elements
$d\left (q\right )$
elements
![]() $f\in \mathcal {R}_{\gamma }$
with
$f\in \mathcal {R}_{\gamma }$
with
![]() $\chi \left (W_{f}\right )\ge 0$
. Moreover, these
$\chi \left (W_{f}\right )\ge 0$
. Moreover, these
![]() $d\left (q\right )$
elements are precisely
$d\left (q\right )$
elements are precisely
for
![]() $m\mid q$
, where
$m\mid q$
, where
![]() $f_{m}$
is the natural morphism between the core surfaces.
$f_{m}$
is the natural morphism between the core surfaces.
Proof. Construct
![]() $\mathcal {R}_{\gamma }=\left \{ f\colon \mathrm {Core}\left (\left \langle \gamma \right \rangle \right )\to W_{f}\right \} $
as
$\mathcal {R}_{\gamma }=\left \{ f\colon \mathrm {Core}\left (\left \langle \gamma \right \rangle \right )\to W_{f}\right \} $
as
![]() $\mathcal {R}\left (\mathrm {Core}\left (\left \langle \gamma \right \rangle \right ),0\right )$
from Definition 2.13. By Theorem 2.14 and Proposition 2.15, the elements in
$\mathcal {R}\left (\mathrm {Core}\left (\left \langle \gamma \right \rangle \right ),0\right )$
from Definition 2.13. By Theorem 2.14 and Proposition 2.15, the elements in
![]() $\mathcal {R}_{\gamma }$
with
$\mathcal {R}_{\gamma }$
with
![]() $\chi \left (W_{f}\right )=0$
are precisely the core surfaces of the subgroups in
$\chi \left (W_{f}\right )=0$
are precisely the core surfaces of the subgroups in
![]() $\mathfrak {MOG}\left (\left \langle \gamma \right \rangle \right )$
. So it only remains to show that
$\mathfrak {MOG}\left (\left \langle \gamma \right \rangle \right )$
. So it only remains to show that
![]() $\mathfrak {MOG}\left (\left \langle \gamma \right \rangle \right )$
are precisely
$\mathfrak {MOG}\left (\left \langle \gamma \right \rangle \right )$
are precisely
![]() $\left \langle \gamma _{0}^{~m}\right \rangle $
with
$\left \langle \gamma _{0}^{~m}\right \rangle $
with
![]() $m\mid q$
.
$m\mid q$
.
But f.g. subgroups
![]() $K\le \Gamma _{g}$
with
$K\le \Gamma _{g}$
with
![]() $\chi \left (K\right )=0$
are necessarily cyclic. Assume
$\chi \left (K\right )=0$
are necessarily cyclic. Assume
![]() $K=\left \langle \delta \right \rangle \in \mathfrak {MOG}\left (\left \langle \gamma \right \rangle \right )$
, so
$K=\left \langle \delta \right \rangle \in \mathfrak {MOG}\left (\left \langle \gamma \right \rangle \right )$
, so
![]() $\gamma \in \left \langle \delta \right \rangle $
, and we may assume that
$\gamma \in \left \langle \delta \right \rangle $
, and we may assume that
![]() $\gamma $
is a positive power of
$\gamma $
is a positive power of
![]() $\delta $
(otherwise switch to
$\delta $
(otherwise switch to
![]() $\delta ^{-1}$
). Every finitely generated subgroup of
$\delta ^{-1}$
). Every finitely generated subgroup of
![]() $\Gamma $
of infinite index is free (e.g., [Reference ScottSco78]), and a subgroup of finite index of
$\Gamma $
of infinite index is free (e.g., [Reference ScottSco78]), and a subgroup of finite index of
![]() $\Gamma _{g}$
is isomorphic to
$\Gamma _{g}$
is isomorphic to
![]() $\Gamma _{h}$
for some
$\Gamma _{h}$
for some
![]() $h\ge g$
and so cannot be generated by less then
$h\ge g$
and so cannot be generated by less then
![]() $2g$
elements. We conclude that the subgroup
$2g$
elements. We conclude that the subgroup
![]() $\left \langle \delta ,\gamma _{0}\right \rangle \le \Gamma $
is free. Because there is a relation
$\left \langle \delta ,\gamma _{0}\right \rangle \le \Gamma $
is free. Because there is a relation
![]() $\gamma _{0}^{~q}=\delta ^{k}$
for some
$\gamma _{0}^{~q}=\delta ^{k}$
for some
![]() $k\in \mathbb {N}$
, it must be a cyclic subgroup. By definition,
$k\in \mathbb {N}$
, it must be a cyclic subgroup. By definition,
![]() $\gamma _{0}$
is not a proper power, and so
$\gamma _{0}$
is not a proper power, and so
![]() $\delta $
must be a positive power of
$\delta $
must be a positive power of
![]() $\gamma _{0}$
, and hence
$\gamma _{0}$
, and hence
![]() $\delta =\gamma _{0}^{~m}$
for some
$\delta =\gamma _{0}^{~m}$
for some
![]() $m\mid q$
.
$m\mid q$
.
3 Background: representation theory of the symmetric group
In this section, we give background on the complex representation theory of
![]() $S_{n}$
that will be used in the sequel. We follow the Vershik–Okounkov approach to the representation theory of
$S_{n}$
that will be used in the sequel. We follow the Vershik–Okounkov approach to the representation theory of
![]() $S_{n}$
developed in [Reference Vershik and OkounkovVO96].
$S_{n}$
developed in [Reference Vershik and OkounkovVO96].
3.1 Young diagrams
A partition is a sequence
![]() $\lambda =(\lambda _{1},\lambda _{2},\ldots ,\lambda _{\ell })$
with each
$\lambda =(\lambda _{1},\lambda _{2},\ldots ,\lambda _{\ell })$
with each
![]() $\lambda _{i}\in \mathbf {N}$
and
$\lambda _{i}\in \mathbf {N}$
and
![]() $\lambda _{1}\geq \lambda _{2}\geq \cdots \geq \lambda _{\ell }$
. If
$\lambda _{1}\geq \lambda _{2}\geq \cdots \geq \lambda _{\ell }$
. If
![]() $\sum \lambda _{i}=n$
, we write this as
$\sum \lambda _{i}=n$
, we write this as
![]() $\lambda \vdash n$
. Such partitions are in one-to-one correspondence with Young diagrams (YD). A YD consists of a collection of left-aligned rows of identical square boxes, where the number of boxes in each row is nonincreasing from top to bottom. Given a partition
$\lambda \vdash n$
. Such partitions are in one-to-one correspondence with Young diagrams (YD). A YD consists of a collection of left-aligned rows of identical square boxes, where the number of boxes in each row is nonincreasing from top to bottom. Given a partition
![]() $\lambda =(\lambda _{1},\lambda _{2},\ldots ,\lambda _{\ell })$
, the corresponding YD has
$\lambda =(\lambda _{1},\lambda _{2},\ldots ,\lambda _{\ell })$
, the corresponding YD has
![]() $\ell $
rows and
$\ell $
rows and
![]() $\lambda _{i}$
boxes in the i
th row, where i increases from top to bottom. We think of partitions as YDs, and vice versa, freely throughout the sequel. If
$\lambda _{i}$
boxes in the i
th row, where i increases from top to bottom. We think of partitions as YDs, and vice versa, freely throughout the sequel. If
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
are two YDs, we say
$\mu $
are two YDs, we say
![]() $\mu \subset \lambda $
if every box of
$\mu \subset \lambda $
if every box of
![]() $\mu $
is a box of
$\mu $
is a box of
![]() $\lambda $
. We say
$\lambda $
. We say
![]() $\mu \subset _{k}\lambda $
if
$\mu \subset _{k}\lambda $
if
![]() $\mu \subset \lambda $
and
$\mu \subset \lambda $
and
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
differ by k boxes.
$\lambda $
differ by k boxes.
A skew YD (SYD) is formally a pair of YDs
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
with
$\lambda $
with
![]() $\mu \subset \lambda $
and is denoted by
$\mu \subset \lambda $
and is denoted by
![]() $\lambda /\mu $
. We also think of
$\lambda /\mu $
. We also think of
![]() $\lambda /\mu $
as a diagram consisting of the boxes of
$\lambda /\mu $
as a diagram consisting of the boxes of
![]() $\lambda $
that are not in
$\lambda $
that are not in
![]() $\mu $
. We can think of a YD
$\mu $
. We can think of a YD
![]() $\lambda $
also as a skew diagram
$\lambda $
also as a skew diagram
![]() $\lambda =\lambda /\emptyset $
, where
$\lambda =\lambda /\emptyset $
, where
![]() $\emptyset $
is the empty diagram with no boxes. Therefore, statements that we make about SYDs apply in this way also to YDs.
$\emptyset $
is the empty diagram with no boxes. Therefore, statements that we make about SYDs apply in this way also to YDs.
The size
![]() $|\lambda /\mu |$
of an SYD
$|\lambda /\mu |$
of an SYD
![]() $\lambda /\mu $
is the number of boxes that it contains, or
$\lambda /\mu $
is the number of boxes that it contains, or
![]() $\sum \lambda _{i}-\sum \mu _{i}$
. If
$\sum \lambda _{i}-\sum \mu _{i}$
. If
![]() $\square $
is a particular box appearing in an SYD, we let
$\square $
is a particular box appearing in an SYD, we let
![]() $i(\square )$
be the row number (starting at 1, counting from top to bottom) of the box and
$i(\square )$
be the row number (starting at 1, counting from top to bottom) of the box and
![]() $j(\square )$
the column number (starting at 1, counting from left to right) of the box. The content of a box
$j(\square )$
the column number (starting at 1, counting from left to right) of the box. The content of a box
![]() $\square $
in an SYD is
$\square $
in an SYD is
If
![]() $\square _{1}$
and
$\square _{1}$
and
![]() $\square _{2}$
are two boxes in an SYD, we let
$\square _{2}$
are two boxes in an SYD, we let
this is called the axial distance between
![]() $\square _{1}$
and
$\square _{1}$
and
![]() $\square _{2}$
.
$\square _{2}$
.
If
![]() $\lambda $
is a YD, we write
$\lambda $
is a YD, we write
![]() $\check {\lambda }$
for the YD obtained from
$\check {\lambda }$
for the YD obtained from
![]() $\lambda $
by swapping rows and columns, namely, by transposing. This
$\lambda $
by swapping rows and columns, namely, by transposing. This
![]() $\check {\lambda }$
is called the conjugate of
$\check {\lambda }$
is called the conjugate of
![]() $\lambda $
.
$\lambda $
.
3.2 Young tableaux
Let
![]() $\lambda /\mu $
be an SYD with
$\lambda /\mu $
be an SYD with
![]() $\lambda \vdash n$
and
$\lambda \vdash n$
and
![]() $\mu \vdash m$
. A standard Young tableau of shape
$\mu \vdash m$
. A standard Young tableau of shape
![]() $\lambda /\mu $
is a filling of the boxes of
$\lambda /\mu $
is a filling of the boxes of
![]() $\lambda /\mu $
with the numbers
$\lambda /\mu $
with the numbers
![]() $m+1,\ldots ,n$
such that
$m+1,\ldots ,n$
such that
-
• each number appears in exactly one box of
 $\lambda /\mu $
, and
$\lambda /\mu $
, and -
• the numbers in the boxes are strictly increasing from left to right and from top to bottom.
In the sequel, we will refer to standard Young tableaux simply as tableaux. For
![]() $\lambda /\mu $
an SYD, we write
$\lambda /\mu $
an SYD, we write
![]() $\mathrm {Tab}(\lambda /\mu )$
for the collection of tableaux of shape
$\mathrm {Tab}(\lambda /\mu )$
for the collection of tableaux of shape
![]() $\lambda /\mu $
. If
$\lambda /\mu $
. If
![]() $\lambda \vdash n$
,
$\lambda \vdash n$
,
![]() $T\in \mathrm {Tab}(\lambda )$
and
$T\in \mathrm {Tab}(\lambda )$
and
![]() $m\in \left [n\right ]$
, we write
$m\in \left [n\right ]$
, we write
![]() $\mu _{m}\left (T\right )$
for the YD obtained by deleting the boxes containing
$\mu _{m}\left (T\right )$
for the YD obtained by deleting the boxes containing
![]() $m+1,\ldots ,n$
from T, so
$m+1,\ldots ,n$
from T, so
![]() $\mu _{m}\left (T\right )\vdash m$
. We also write
$\mu _{m}\left (T\right )\vdash m$
. We also write
![]() $T\lvert _{\le m}\in \mathrm {Tab}\left (\mu _{m}\left (T\right )\right )$
for the tableau formed by the numbers-in-boxes of T that are
$T\lvert _{\le m}\in \mathrm {Tab}\left (\mu _{m}\left (T\right )\right )$
for the tableau formed by the numbers-in-boxes of T that are
![]() $\leq m$
, and
$\leq m$
, and
![]() $T\lvert _{>m}$
for the tableau formed by the numbers-in-boxes of T that are
$T\lvert _{>m}$
for the tableau formed by the numbers-in-boxes of T that are
![]() $>m$
. In general, the shape of
$>m$
. In general, the shape of
![]() $T\lvert _{>m}$
will be an SYD. If T is a tableau of shape
$T\lvert _{>m}$
will be an SYD. If T is a tableau of shape
![]() $\lambda /\mu $
, where
$\lambda /\mu $
, where
![]() $\lambda \vdash n$
and
$\lambda \vdash n$
and
![]() $\mu \vdash m$
, and
$\mu \vdash m$
, and
![]() $m<i\leq n$
, we write
$m<i\leq n$
, we write
![]() ${\fbox {\(i\)}}_{T}$
for the box containing i in T.
${\fbox {\(i\)}}_{T}$
for the box containing i in T.
If
![]() $\lambda \vdash n$
and
$\lambda \vdash n$
and
![]() $\mu \subset \lambda $
, then we have a concatenation between
$\mu \subset \lambda $
, then we have a concatenation between
![]() $\mathrm {Tab}(\mu )$
and
$\mathrm {Tab}(\mu )$
and
![]() $\mathrm {Tab}(\lambda /\mu )$
: If
$\mathrm {Tab}(\lambda /\mu )$
: If
![]() $T\in \mathrm {Tab}(\mu )$
and
$T\in \mathrm {Tab}(\mu )$
and
![]() $R\in \mathrm {Tab}(\lambda /\mu )$
, let
$R\in \mathrm {Tab}(\lambda /\mu )$
, let
![]() $T\sqcup R$
be the tableau obtained by adjoining R to T.
$T\sqcup R$
be the tableau obtained by adjoining R to T.
3.3 Representations of symmetric groups
The irreducible unitary representations of
![]() $S_{n}$
are parameterized, up to unitary equivalence, by YDs of size n. This correspondence between YDs and representations is denoted by
$S_{n}$
are parameterized, up to unitary equivalence, by YDs of size n. This correspondence between YDs and representations is denoted by
Each
![]() $V^{\lambda }$
is a finite-dimensional complex vector space with a unitary action of
$V^{\lambda }$
is a finite-dimensional complex vector space with a unitary action of
![]() $S_{n}$
and is also a module for the group algebra
$S_{n}$
and is also a module for the group algebra
![]() $\mathbf {C}[S_{n}]$
. Let
$\mathbf {C}[S_{n}]$
. Let
![]() $d_{\lambda }\stackrel {\mathrm {def}}{=}\dim V^{\lambda }$
. It is known that
$d_{\lambda }\stackrel {\mathrm {def}}{=}\dim V^{\lambda }$
. It is known that
![]() $d_{\lambda }=\left |\mathrm {Tab}\left (\lambda \right )\right |$
.
$d_{\lambda }=\left |\mathrm {Tab}\left (\lambda \right )\right |$
.
We now follow Vershik–Okounkov [Reference Vershik and OkounkovVO96]. The natural ordering of
![]() $[n]$
induces a filtration
$[n]$
induces a filtration
of
![]() $S_{n}$
, where
$S_{n}$
, where
![]() $S_{m}$
is the subgroup of
$S_{m}$
is the subgroup of
![]() $S_{n}$
fixing each of the numbers in
$S_{n}$
fixing each of the numbers in
![]() $\left [m+1,n\right ]$
. If W is any unitary representation of
$\left [m+1,n\right ]$
. If W is any unitary representation of
![]() $S_{n}$
, for
$S_{n}$
, for
![]() $m\in [n]$
and
$m\in [n]$
and
![]() $\mu $
a YD of size m, we write
$\mu $
a YD of size m, we write
![]() $W_{\mu }$
for the linear span in W of all elements in the image of
$W_{\mu }$
for the linear span in W of all elements in the image of
![]() $\mathrm {Hom}_{S_{m}}(V^{\mu },W)$
. In other words,
$\mathrm {Hom}_{S_{m}}(V^{\mu },W)$
. In other words,
![]() $W_{\mu }$
is the span of copies of
$W_{\mu }$
is the span of copies of
![]() $V^{\mu }$
in the restriction of W to
$V^{\mu }$
in the restriction of W to
![]() $S_{m}$
. This
$S_{m}$
. This
![]() $W_{\mu }$
is called the
$W_{\mu }$
is called the
![]() $\mu $
-isotypic subspace of W.
$\mu $
-isotypic subspace of W.
Vershik and Okounkov describe a specific orthonormal basis of
![]() $V^{\lambda }$
, called a Gelfand–Tsetlin basis, that will be useful to us here. The basis is indexed by
$V^{\lambda }$
, called a Gelfand–Tsetlin basis, that will be useful to us here. The basis is indexed by
![]() $T\in \mathrm {Tab}(\lambda )$
; each such T gives a basis vector
$T\in \mathrm {Tab}(\lambda )$
; each such T gives a basis vector
![]() $v_{T}$
. The vectors
$v_{T}$
. The vectors
![]() $v_{T}$
can be characterized up to multiplication by complex scalars of modulus
$v_{T}$
can be characterized up to multiplication by complex scalars of modulus
![]() $1$
in the following way. The intersection of subspaces
$1$
in the following way. The intersection of subspaces
is one-dimensional and contains the unit vector
![]() $v_{T}$
[Reference Vershik and OkounkovVO96,
$v_{T}$
[Reference Vershik and OkounkovVO96,
![]() $\S$
1]. One important corollary of this is that if
$\S$
1]. One important corollary of this is that if
![]() $\mu \vdash m\in [n]$
, then
$\mu \vdash m\in [n]$
, then
![]() $\left (V^{\lambda }\right )_{\mu }\neq \{0\}$
if and only if
$\left (V^{\lambda }\right )_{\mu }\neq \{0\}$
if and only if
![]() $\mu \subset \lambda $
. Also, note that if
$\mu \subset \lambda $
. Also, note that if
![]() $\mu _{1},\mu _{2}\subset \lambda , \mu _{1},\mu _{2}\vdash m\in [n]$
, and
$\mu _{1},\mu _{2}\subset \lambda , \mu _{1},\mu _{2}\vdash m\in [n]$
, and
![]() $\mu _{1}\neq \mu _{2}$
, then
$\mu _{1}\neq \mu _{2}$
, then
![]() $\left (V^{\lambda }\right )_{\mu _{1}}$
is orthogonal to
$\left (V^{\lambda }\right )_{\mu _{1}}$
is orthogonal to
![]() $\left (V^{\lambda }\right )_{\mu _{2}}$
.
$\left (V^{\lambda }\right )_{\mu _{2}}$
.
More generally, if
![]() $\lambda /\mu $
is an SYD with
$\lambda /\mu $
is an SYD with
![]() $\lambda \vdash n$
and
$\lambda \vdash n$
and
![]() $\mu \vdash m$
, then there is a skew module
$\mu \vdash m$
, then there is a skew module
![]() $V^{\lambda /\mu }$
that is a unitary representation of
$V^{\lambda /\mu }$
that is a unitary representation of
![]() $S^{\prime }_{n-m}$
where we write
$S^{\prime }_{n-m}$
where we write
![]() $S^{\prime }_{n-m}$
for the copy of
$S^{\prime }_{n-m}$
for the copy of
![]() $S_{n-m}$
in
$S_{n-m}$
in
![]() $S_{n}$
that fixes the elements
$S_{n}$
that fixes the elements
![]() $[m]$
. Formally,
$[m]$
. Formally,
where the action of
![]() $S^{\prime }_{n-m}$
is by left multiplication: for
$S^{\prime }_{n-m}$
is by left multiplication: for
![]() $\varphi \in \mathrm {Hom}_{S_{m}}\left (V^{\mu },V^{\lambda }\right )$
,
$\varphi \in \mathrm {Hom}_{S_{m}}\left (V^{\mu },V^{\lambda }\right )$
,
![]() $\tau \in S^{\prime }_{n-m}$
and
$\tau \in S^{\prime }_{n-m}$
and
![]() $v\in V^{\mu }$
,
$v\in V^{\mu }$
,
![]() $\left (\tau .\varphi \right )\left (v\right )\stackrel {\mathrm {def}}{=}\tau .\left (\varphi \left (v\right )\right )$
. This action preserves
$\left (\tau .\varphi \right )\left (v\right )\stackrel {\mathrm {def}}{=}\tau .\left (\varphi \left (v\right )\right )$
. This action preserves
![]() $V^{\lambda /\mu }$
as
$V^{\lambda /\mu }$
as
![]() $S^{\prime }_{n-m}$
is in the centralizer of
$S^{\prime }_{n-m}$
is in the centralizer of
![]() $S_{m}$
in
$S_{m}$
in
![]() $\mathbf {C}[S_{n}]$
. We write
$\mathbf {C}[S_{n}]$
. We write
![]() $d_{\lambda /\mu }$
for the dimension of
$d_{\lambda /\mu }$
for the dimension of
![]() $V^{\lambda /\mu }$
. Since
$V^{\lambda /\mu }$
. Since
![]() $d_{\lambda /\mu }$
is the multiplicity of
$d_{\lambda /\mu }$
is the multiplicity of
![]() $V^{\mu }$
in the restriction of
$V^{\mu }$
in the restriction of
![]() $V^{\lambda }$
to
$V^{\lambda }$
to
![]() $S_{m}$
, by Frobenius reciprocity, it is also the multiplicity of
$S_{m}$
, by Frobenius reciprocity, it is also the multiplicity of
![]() $V^{\lambda }$
in the induced representation
$V^{\lambda }$
in the induced representation
![]() $\mathrm {Ind}_{S_{m}}^{S_{n}}V^{\mu }$
. By calculating the dimension of
$\mathrm {Ind}_{S_{m}}^{S_{n}}V^{\mu }$
. By calculating the dimension of
![]() $\mathrm {Ind}_{S_{m}}^{S_{n}}V^{\mu }$
in two ways, we obtain the following result that will be useful later.
$\mathrm {Ind}_{S_{m}}^{S_{n}}V^{\mu }$
in two ways, we obtain the following result that will be useful later.
Lemma 3.1. Let
![]() $n\in \mathbf {N}$
,
$n\in \mathbf {N}$
,
![]() $m\in \left [n\right ]$
and
$m\in \left [n\right ]$
and
![]() $\mu \vdash m$
. Then,
$\mu \vdash m$
. Then,
 $$\begin{align*}\sum_{\lambda\vdash n\colon\mu\subset\lambda}d_{\lambda/\mu}d_{\lambda}=\frac{n!}{m!}d_{\mu}. \end{align*}$$
$$\begin{align*}\sum_{\lambda\vdash n\colon\mu\subset\lambda}d_{\lambda/\mu}d_{\lambda}=\frac{n!}{m!}d_{\mu}. \end{align*}$$
The module
![]() $V^{\lambda /\mu }$
has an orthonormal basis
$V^{\lambda /\mu }$
has an orthonormal basis
![]() $w_{T}$
indexed by
$w_{T}$
indexed by
![]() $T\in \mathrm {Tab}(\lambda /\mu )$
[Reference Vershik and OkounkovVO96, §7]. One also has the following property that we will use later [Reference Ceccherini-Silberstein, Scarabotti and TolliCSST10, Eq. (3.65)].
$T\in \mathrm {Tab}(\lambda /\mu )$
[Reference Vershik and OkounkovVO96, §7]. One also has the following property that we will use later [Reference Ceccherini-Silberstein, Scarabotti and TolliCSST10, Eq. (3.65)].
Lemma 3.2. Let
![]() $n\in \mathbf {N}$
,
$n\in \mathbf {N}$
,
![]() $m\in \left [n\right ]$
,
$m\in \left [n\right ]$
,
![]() $\lambda \vdash n$
and
$\lambda \vdash n$
and
![]() $\mu \vdash m$
and assume that
$\mu \vdash m$
and assume that
![]() $\mu \subset \lambda $
. Then the map
$\mu \subset \lambda $
. Then the map
linearly extends to an isomorphism of unitary
![]() $\left (S_{m}\times S^{\prime }_{n-m}\right )$
-representations
$\left (S_{m}\times S^{\prime }_{n-m}\right )$
-representations
![]() $V^{\mu }\otimes V^{\lambda /\mu }\cong \left (V^{\lambda }\right )_{\mu }$
.
$V^{\mu }\otimes V^{\lambda /\mu }\cong \left (V^{\lambda }\right )_{\mu }$
.
There is also an explicit formula for the action of
![]() $S^{\prime }_{n-m}$
on
$S^{\prime }_{n-m}$
on
![]() $V^{\lambda /\mu }$
. A full exposition of this formula can be found in [Reference Vershik and OkounkovVO96, §6]. Recall that
$V^{\lambda /\mu }$
. A full exposition of this formula can be found in [Reference Vershik and OkounkovVO96, §6]. Recall that
![]() $S^{\prime }_{n-m}$
is generated by the Coxeter generators
$S^{\prime }_{n-m}$
is generated by the Coxeter generators
for
![]() $m<i<n$
, where
$m<i<n$
, where
![]() $\left (i~~i+1\right )$
is our notation for a transposition switching i and
$\left (i~~i+1\right )$
is our notation for a transposition switching i and
![]() $i+1$
. Therefore, it is sufficient to describe how the
$i+1$
. Therefore, it is sufficient to describe how the
![]() $s_{i}$
act on
$s_{i}$
act on
![]() $V^{\lambda /\mu }$
. Say that T is admissible for
$V^{\lambda /\mu }$
. Say that T is admissible for
![]() $s_{i}$
if the boxes containing i and
$s_{i}$
if the boxes containing i and
![]() $i+1$
in T are neither in the same row nor the same column.
$i+1$
in T are neither in the same row nor the same column.
For
![]() $T\in \mathrm {Tab}(\lambda /\mu )$
, let
$T\in \mathrm {Tab}(\lambda /\mu )$
, let
 $$ \begin{align*} s_{i}T & =\begin{cases} T & \text{if \(T\) is not admissible for \(s_{i}\)}\\ T' & \text{if \(T\) is admissible for \(s_{i}\)}, \end{cases} \end{align*} $$
$$ \begin{align*} s_{i}T & =\begin{cases} T & \text{if \(T\) is not admissible for \(s_{i}\)}\\ T' & \text{if \(T\) is admissible for \(s_{i}\)}, \end{cases} \end{align*} $$
where
![]() $T'$
is the tableaux obtained from T by swapping i and
$T'$
is the tableaux obtained from T by swapping i and
![]() $i+1$
. The admissibility condition ensures
$i+1$
. The admissibility condition ensures
![]() $T'$
is a valid standard Young tableau. Then one has Young’s orthogonal form
$T'$
is a valid standard Young tableau. Then one has Young’s orthogonal form
 $$ \begin{align} s_{i}w_{T}=\frac{1}{\mathrm{ax}({\fbox{\(i+1\)}}_{T},{\fbox{\(i\)}}_{T})}w_{T}+\sqrt{1-\frac{1}{\mathrm{ax}({\fbox{\(i+1\)}}_{T},{\fbox{\(i\)}}_{T})^{2}}}w_{s_{i}T}. \end{align} $$
$$ \begin{align} s_{i}w_{T}=\frac{1}{\mathrm{ax}({\fbox{\(i+1\)}}_{T},{\fbox{\(i\)}}_{T})}w_{T}+\sqrt{1-\frac{1}{\mathrm{ax}({\fbox{\(i+1\)}}_{T},{\fbox{\(i\)}}_{T})^{2}}}w_{s_{i}T}. \end{align} $$
Note that as a special case of this formula, if T is not admissible for
![]() $s_{i}$
, then
$s_{i}$
, then
![]() $\mathrm {ax}({\fbox {\(i+1\)}}_{T},{\fbox {\(i\)}}_{T})=\pm 1$
and
$\mathrm {ax}({\fbox {\(i+1\)}}_{T},{\fbox {\(i\)}}_{T})=\pm 1$
and
 $$ \begin{align} s_{i}w_{T}=\frac{1}{\mathrm{ax}({\fbox{\(i+1\)}}_{T},{\fbox{\(i\)}}_{T})}w_{T}=\begin{cases} w_{T} & \mathrm{if}~i~\mathrm{and}~i+1~\mathrm{are~in~the~same~row},\\ -w_{T} & \mathrm{if}~i~\mathrm{and}~i+1~\mathrm{are~in~the~same~column.} \end{cases} \end{align} $$
$$ \begin{align} s_{i}w_{T}=\frac{1}{\mathrm{ax}({\fbox{\(i+1\)}}_{T},{\fbox{\(i\)}}_{T})}w_{T}=\begin{cases} w_{T} & \mathrm{if}~i~\mathrm{and}~i+1~\mathrm{are~in~the~same~row},\\ -w_{T} & \mathrm{if}~i~\mathrm{and}~i+1~\mathrm{are~in~the~same~column.} \end{cases} \end{align} $$
Remark 3.3. For completeness of some of our statements, we need to define the notions above also for
![]() $S_{0}$
, the symmetric group of the empty set. This is the trivial group. Whenever
$S_{0}$
, the symmetric group of the empty set. This is the trivial group. Whenever
![]() $\mu =\lambda $
, we have
$\mu =\lambda $
, we have
![]() $\mathrm {Tab}\left (\lambda /\mu \right )=\left \{ \emptyset \right \} $
, and the representation
$\mathrm {Tab}\left (\lambda /\mu \right )=\left \{ \emptyset \right \} $
, and the representation
![]() $V^{\lambda /\mu }$
is one-dimensional with basis
$V^{\lambda /\mu }$
is one-dimensional with basis
![]() $w_{T}$
, for T the empty tableau.
$w_{T}$
, for T the empty tableau.
4 Preliminary representation theoretic results
In this section, we give some preliminary results on representation theory that will be used in the rest of the paper. Although some results here seem to be novel (in particular Proposition 4.4), this section plays only a supporting role in the paper.
4.1 Commutants
Recall that if V is a finite-dimensional vector space and
![]() $\mathcal {A}$
is a subalgebra of
$\mathcal {A}$
is a subalgebra of
![]() $\mathrm {End}(V)$
, then the commutant of
$\mathrm {End}(V)$
, then the commutant of
![]() $\mathcal {A}$
in
$\mathcal {A}$
in
![]() $\mathrm {End}(V)$
is the algebra of elements
$\mathrm {End}(V)$
is the algebra of elements
![]() $b\in \mathrm {End}(V)$
such that
$b\in \mathrm {End}(V)$
such that
for all
![]() $a\in \mathcal {A}$
. For
$a\in \mathcal {A}$
. For
![]() $m\in [n]$
and
$m\in [n]$
and
![]() $\lambda \vdash n$
, let
$\lambda \vdash n$
, let
![]() $Z(\lambda ,m,n)$
denote the commutant of the image of
$Z(\lambda ,m,n)$
denote the commutant of the image of
![]() $\mathbf {C}[S_{m}]$
in
$\mathbf {C}[S_{m}]$
in
![]() $\mathrm {End}(V^{\lambda }).$
We identify
$\mathrm {End}(V^{\lambda }).$
We identify
and give
![]() $\mathrm {End}(V^{\lambda })$
the Hermitian inner product induced from
$\mathrm {End}(V^{\lambda })$
the Hermitian inner product induced from
![]() $V^{\lambda }.$
$V^{\lambda }.$
Lemma 4.1. Let
![]() $m\in [n]$
and
$m\in [n]$
and
![]() $\lambda \vdash n$
. The algebra
$\lambda \vdash n$
. The algebra
![]() $Z(\lambda ,m,n)$
has an orthonormal basis given by
$Z(\lambda ,m,n)$
has an orthonormal basis given by
 $$ \begin{align} \left\{ \mathcal{E}_{\mu,R_{1},R_{2}}^{\lambda}\stackrel{\mathrm{def}}{=}\frac{1}{\sqrt{d_{\mu}}}\sum_{T\in\mathrm{Tab}(\mu)}v_{T\sqcup R_{1}}\otimes\check{v}_{T\sqcup R_{2}}\,:\,\mu\vdash m,\,\mu\subset\lambda,\,R_{1},R_{2}\in\mathrm{Tab}(\lambda/\mu)\right\}. \end{align} $$
$$ \begin{align} \left\{ \mathcal{E}_{\mu,R_{1},R_{2}}^{\lambda}\stackrel{\mathrm{def}}{=}\frac{1}{\sqrt{d_{\mu}}}\sum_{T\in\mathrm{Tab}(\mu)}v_{T\sqcup R_{1}}\otimes\check{v}_{T\sqcup R_{2}}\,:\,\mu\vdash m,\,\mu\subset\lambda,\,R_{1},R_{2}\in\mathrm{Tab}(\lambda/\mu)\right\}. \end{align} $$
Proof. Let
![]() $\mathcal {A}\subseteq \mathrm {End}(V^{\lambda })$
be the algebra generated by the
$\mathcal {A}\subseteq \mathrm {End}(V^{\lambda })$
be the algebra generated by the
![]() $\mathcal {E}_{\mu ,R_{1},R_{2}}^{\lambda }$
(over all
$\mathcal {E}_{\mu ,R_{1},R_{2}}^{\lambda }$
(over all
![]() $\mu )$
and
$\mu )$
and
![]() $\mathcal {A}_{\mu }\subseteq \mathcal {A}$
be the algebra generated by the
$\mathcal {A}_{\mu }\subseteq \mathcal {A}$
be the algebra generated by the
![]() $\mathcal {E}_{\mu ,R_{1},R_{2}}^{\lambda }$
with a fixed value of
$\mathcal {E}_{\mu ,R_{1},R_{2}}^{\lambda }$
with a fixed value of
![]() $\mu $
. Suppose that
$\mu $
. Suppose that
![]() $Q\in \mathrm {Tab}(\lambda )$
. The formula for the action of
$Q\in \mathrm {Tab}(\lambda )$
. The formula for the action of
![]() $\mathcal {E}_{\mu ,R_{1},R_{2}}^{\lambda }$
on
$\mathcal {E}_{\mu ,R_{1},R_{2}}^{\lambda }$
on
![]() $v_{Q}$
is
$v_{Q}$
is
 $$ \begin{align} \mathcal{E}_{\mu,R_{1},R_{2}}^{\lambda}\left(v_{Q}\right)=\mathbf{1}\left\{ \mu_{m}(Q)=\mu,\,Q\lvert_{>m}=R_{2}\right\} \frac{1}{\sqrt{d_{\mu}}}v_{Q\lvert_{\le m}\sqcup R_{1}}. \end{align} $$
$$ \begin{align} \mathcal{E}_{\mu,R_{1},R_{2}}^{\lambda}\left(v_{Q}\right)=\mathbf{1}\left\{ \mu_{m}(Q)=\mu,\,Q\lvert_{>m}=R_{2}\right\} \frac{1}{\sqrt{d_{\mu}}}v_{Q\lvert_{\le m}\sqcup R_{1}}. \end{align} $$
It is clear that the
![]() $\mathcal {E}_{\mu ,R_{1},R_{2}}^{\lambda }$
are an orthonormal set of elements in
$\mathcal {E}_{\mu ,R_{1},R_{2}}^{\lambda }$
are an orthonormal set of elements in
![]() $\mathrm {End}(V^{\lambda })$
. It follows from equation (4.3) that
$\mathrm {End}(V^{\lambda })$
. It follows from equation (4.3) that
 $$\begin{align*}\mathcal{E}_{\mu_{1},R_{1},R_{2}}^{\lambda}\mathcal{E}_{\mu_{2},R_{3},R_{4}}^{\lambda}=\mathbf{1}\left\{ \mu_{1}=\mu_{2},R_{3}=R_{2}\right\} \frac{1}{\sqrt{d_{\mu_{1}}}}\mathcal{E}_{\mu_{1},R_{1},R_{4}}^{\lambda}, \end{align*}$$
$$\begin{align*}\mathcal{E}_{\mu_{1},R_{1},R_{2}}^{\lambda}\mathcal{E}_{\mu_{2},R_{3},R_{4}}^{\lambda}=\mathbf{1}\left\{ \mu_{1}=\mu_{2},R_{3}=R_{2}\right\} \frac{1}{\sqrt{d_{\mu_{1}}}}\mathcal{E}_{\mu_{1},R_{1},R_{4}}^{\lambda}, \end{align*}$$
so the
![]() $\mathcal {E}_{\mu ,R_{1},R_{2}}^{\lambda }$
are an orthonormal basis for the algebra
$\mathcal {E}_{\mu ,R_{1},R_{2}}^{\lambda }$
are an orthonormal basis for the algebra
![]() $\mathcal {A}$
, and those with a fixed
$\mathcal {A}$
, and those with a fixed
![]() $\mu $
are an orthonormal basis for
$\mu $
are an orthonormal basis for
![]() $A_{\mu }$
. Furthermore, we have
$A_{\mu }$
. Furthermore, we have
 $$\begin{align*}\mathcal{A}=\bigoplus_{\mu\subset\lambda,\mu\vdash m}\mathcal{A}_{\mu}. \end{align*}$$
$$\begin{align*}\mathcal{A}=\bigoplus_{\mu\subset\lambda,\mu\vdash m}\mathcal{A}_{\mu}. \end{align*}$$
For
![]() $\mu \vdash m$
, let
$\mu \vdash m$
, let
![]() $p_{\mu }\in \mathbf {C}[S_{m}]$
be the central idempotent projection onto the
$p_{\mu }\in \mathbf {C}[S_{m}]$
be the central idempotent projection onto the
![]() $\mu $
-isotypic component of
$\mu $
-isotypic component of
![]() $\mathbf {C}[S_{m}]$
and let
$\mathbf {C}[S_{m}]$
and let
![]() $P_{\mu }^{~\lambda }$
be the image of
$P_{\mu }^{~\lambda }$
be the image of
![]() $p_{\mu }$
in
$p_{\mu }$
in
![]() $\mathrm {End}(V^{\lambda })$
. The element
$\mathrm {End}(V^{\lambda })$
. The element
![]() $P_{\mu }^{~\lambda }$
is the orthogonal projection onto
$P_{\mu }^{~\lambda }$
is the orthogonal projection onto
![]() $\left (V^{\lambda }\right )_{\mu }$
, and
$\left (V^{\lambda }\right )_{\mu }$
, and
![]() $P_{\mu }^{~\lambda }$
is in the center of
$P_{\mu }^{~\lambda }$
is in the center of
![]() $Z(\lambda ,m,n)$
. Hence, for every
$Z(\lambda ,m,n)$
. Hence, for every
![]() $z\in Z(\lambda ,m,n)$
, we can write
$z\in Z(\lambda ,m,n)$
, we can write
 $$\begin{align*}z=\bigoplus_{\mu\vdash m,\,\mu\subset\lambda}z^{(\mu)}, \end{align*}$$
$$\begin{align*}z=\bigoplus_{\mu\vdash m,\,\mu\subset\lambda}z^{(\mu)}, \end{align*}$$
where
![]() $z^{(\mu )}\stackrel {\mathrm {def}}{=} P_{\mu }^{\lambda }zP_{\mu }^{\lambda }.$
Moreover, if we let
$z^{(\mu )}\stackrel {\mathrm {def}}{=} P_{\mu }^{\lambda }zP_{\mu }^{\lambda }.$
Moreover, if we let
![]() $\mathcal {B}_{\mu }$
be the algebra generated by the image of
$\mathcal {B}_{\mu }$
be the algebra generated by the image of
![]() $\mathbf {C}[S_{m}]$
in
$\mathbf {C}[S_{m}]$
in
![]() $\mathrm {End}(V_{\mu }^{\lambda })$
, each
$\mathrm {End}(V_{\mu }^{\lambda })$
, each
![]() $z^{(\mu )}$
must be in the commutant
$z^{(\mu )}$
must be in the commutant
![]() $\mathcal {B}^{\prime }_{\mu }$
of
$\mathcal {B}^{\prime }_{\mu }$
of
![]() $\mathcal {B}_{\mu }$
in
$\mathcal {B}_{\mu }$
in
![]() $\mathrm {End}(V_{\mu }^{\lambda }$
). On the other hand, if
$\mathrm {End}(V_{\mu }^{\lambda }$
). On the other hand, if
![]() $z=\bigoplus _{\mu \vdash m,\,\mu \subset \lambda }z^{(\mu )}$
and each
$z=\bigoplus _{\mu \vdash m,\,\mu \subset \lambda }z^{(\mu )}$
and each
![]() $z^{(\mu )}\in \mathcal {B}^{\prime }_{\mu }$
, then
$z^{(\mu )}\in \mathcal {B}^{\prime }_{\mu }$
, then
![]() $z\in Z(\lambda ,m,n)$
. This shows that
$z\in Z(\lambda ,m,n)$
. This shows that
 $$ \begin{align} Z(\lambda,m,n) & =\bigoplus_{\mu\vdash m,\,\mu\subset\lambda}\mathcal{B}^{\prime}_{\mu}. \end{align} $$
$$ \begin{align} Z(\lambda,m,n) & =\bigoplus_{\mu\vdash m,\,\mu\subset\lambda}\mathcal{B}^{\prime}_{\mu}. \end{align} $$
Since
![]() $V^{\mu }$
is an irreducible module for
$V^{\mu }$
is an irreducible module for
![]() $\mathbf {C}[S_{m}]$
, the algebra generated by
$\mathbf {C}[S_{m}]$
, the algebra generated by
![]() $\mathbf {C}[S_{m}]$
in
$\mathbf {C}[S_{m}]$
in
![]() $\mathrm {End}(V^{\mu })$
is the whole of
$\mathrm {End}(V^{\mu })$
is the whole of
![]() $\mathrm {End}(V^{\mu })$
. Hence, under the isomorphism of Lemma 3.2, the algebra
$\mathrm {End}(V^{\mu })$
. Hence, under the isomorphism of Lemma 3.2, the algebra
![]() $\mathcal {B}_{\mu }$
is identified with
$\mathcal {B}_{\mu }$
is identified with
![]() $\mathrm {End}(V^{\mu })\otimes \mathbf {C}\mathrm {Id}_{V_{\lambda /\mu }}$
. By a classical theorem, due to Tomita [Reference TomitaTom67] in the generality of von Neumann algebras,Footnote
12
the commutant of a tensor product is the tensor product of the two commutants. Therefore, still using the isomorphism of Lemma 3.2, we have
$\mathrm {End}(V^{\mu })\otimes \mathbf {C}\mathrm {Id}_{V_{\lambda /\mu }}$
. By a classical theorem, due to Tomita [Reference TomitaTom67] in the generality of von Neumann algebras,Footnote
12
the commutant of a tensor product is the tensor product of the two commutants. Therefore, still using the isomorphism of Lemma 3.2, we have
This space is the algebra
![]() $\mathcal {A}_{\mu }$
, so
$\mathcal {A}_{\mu }$
, so
![]() $\mathcal {B}^{\prime }_{\mu }=\mathcal {A}_{\mu }$
and
$\mathcal {B}^{\prime }_{\mu }=\mathcal {A}_{\mu }$
and
 $$\begin{align*}Z(\lambda,m,n)=\bigoplus_{\mu\vdash m,\,\mu\subset\lambda}\mathcal{B}^{\prime}_{\mu}=\bigoplus_{\mu\vdash m,\,\mu\subset\lambda}\mathcal{A}_{\mu}=\mathcal{A} \end{align*}$$
$$\begin{align*}Z(\lambda,m,n)=\bigoplus_{\mu\vdash m,\,\mu\subset\lambda}\mathcal{B}^{\prime}_{\mu}=\bigoplus_{\mu\vdash m,\,\mu\subset\lambda}\mathcal{A}_{\mu}=\mathcal{A} \end{align*}$$
as required.
4.2 Bounds for the dimensions of irreducible representations
In this section, we give bounds related to the dimensions of irreducible representations that we use later. We first note a very simple bound for the dimensions of irreducible representations of
![]() $S_{n}$
. For a YD, denote by
$S_{n}$
. For a YD, denote by
![]() $b_{\lambda }\stackrel {\mathrm {def}}{=}\left |\lambda \right |-\lambda _{1}$
the number of boxes outside the first row.
$b_{\lambda }\stackrel {\mathrm {def}}{=}\left |\lambda \right |-\lambda _{1}$
the number of boxes outside the first row.
Lemma 4.2. Let
![]() $\lambda \vdash n$
. Suppose that
$\lambda \vdash n$
. Suppose that
![]() $\lambda _{1}=n-b_{\lambda }\ge \frac {n}{2}$
. Then
$\lambda _{1}=n-b_{\lambda }\ge \frac {n}{2}$
. Then
 $$\begin{align*}\binom{\lambda_{1}}{b_{\lambda}}\leq d_{\lambda}\leq n^{b_{\lambda}}. \end{align*}$$
$$\begin{align*}\binom{\lambda_{1}}{b_{\lambda}}\leq d_{\lambda}\leq n^{b_{\lambda}}. \end{align*}$$
Proof. The first inequality is given by Liebeck and Shalev in [Reference Liebeck and ShalevLS04, Lem. 2.1]. To bound
![]() $d_{\lambda }$
from above, note that the standard tableaux of shape
$d_{\lambda }$
from above, note that the standard tableaux of shape
![]() $\lambda $
can be obtained by choosing which
$\lambda $
can be obtained by choosing which
![]() $\lambda _{1}$
elements of
$\lambda _{1}$
elements of
![]() $[n]$
are in the first row (of which there are at most
$[n]$
are in the first row (of which there are at most
![]() $\binom {n}{b_{\lambda }}$
choices) and choosing the remaining
$\binom {n}{b_{\lambda }}$
choices) and choosing the remaining
![]() $b_{\lambda }$
numbers’ locations outside the first row, of which there are at most
$b_{\lambda }$
numbers’ locations outside the first row, of which there are at most
![]() $b_{\lambda }!$
choices. Hence,
$b_{\lambda }!$
choices. Hence,
 $$\begin{align*}d_{\lambda}\leq b_{\lambda}!\binom{n}{b_{\lambda}}\leq n^{b_{\lambda}}.\\[-41pt] \end{align*}$$
$$\begin{align*}d_{\lambda}\leq b_{\lambda}!\binom{n}{b_{\lambda}}\leq n^{b_{\lambda}}.\\[-41pt] \end{align*}$$
Lemma 4.3. Let
![]() $\lambda \vdash n$
,
$\lambda \vdash n$
,
![]() $\nu \subset _{k}\lambda $
. If
$\nu \subset _{k}\lambda $
. If
![]() $n\ge k+2b_{\lambda }$
, then
$n\ge k+2b_{\lambda }$
, then
 $$ \begin{align} \frac{\left(n-b_{\lambda}\right)^{b_{\lambda}}}{b_{\lambda}^{~b_{\lambda}}\left(n-k\right)^{b_{\nu}}}\leq\frac{d_{\lambda}}{d_{\nu}}\leq\frac{b_{\nu}^{~b_{\nu}}n^{b_{\lambda}}}{\left(n-k-b_{\nu}\right)^{b_{\nu}}}. \end{align} $$
$$ \begin{align} \frac{\left(n-b_{\lambda}\right)^{b_{\lambda}}}{b_{\lambda}^{~b_{\lambda}}\left(n-k\right)^{b_{\nu}}}\leq\frac{d_{\lambda}}{d_{\nu}}\leq\frac{b_{\nu}^{~b_{\nu}}n^{b_{\lambda}}}{\left(n-k-b_{\nu}\right)^{b_{\nu}}}. \end{align} $$
Proof. By assumption,
![]() $n\ge k+2b_{\lambda }\ge k+2b_{\nu }$
, so
$n\ge k+2b_{\lambda }\ge k+2b_{\nu }$
, so
![]() $n-b_{\lambda }\ge \frac {n}{2}$
and
$n-b_{\lambda }\ge \frac {n}{2}$
and
![]() $n-k-b_{\nu }\ge \frac {n-k}{2}$
and Lemma 4.2 applies. The statement now follows from Lemma 4.2 together with the inequality
$n-k-b_{\nu }\ge \frac {n-k}{2}$
and Lemma 4.2 applies. The statement now follows from Lemma 4.2 together with the inequality
![]() $\binom {p}{q}\geq (\frac {p}{q})^{q}$
, holding for
$\binom {p}{q}\geq (\frac {p}{q})^{q}$
, holding for
![]() $p,q\in \mathbf {N}$
with
$p,q\in \mathbf {N}$
with
![]() $p\ge q\ge 1$
.
$p\ge q\ge 1$
.
4.3 An estimate for matrix coefficients in skew modules
Recall that the Coxeter generators of
![]() $S_{n}$
are
$S_{n}$
are
![]() $s_{i}=\left (i~~i+1\right )$
for
$s_{i}=\left (i~~i+1\right )$
for
![]() $i\in \left [n-1\right ]$
. If
$i\in \left [n-1\right ]$
. If
![]() $\tau \in S_{n}$
, we write
$\tau \in S_{n}$
, we write
![]() $\ell _{\mathrm {cox}}(\tau )$
for the minimal length of a word of Coxeter generators that equals
$\ell _{\mathrm {cox}}(\tau )$
for the minimal length of a word of Coxeter generators that equals
![]() $\tau $
. Assume that
$\tau $
. Assume that
![]() $\lambda \vdash n$
,
$\lambda \vdash n$
,
![]() $m\in \left [n\right ]$
and
$m\in \left [n\right ]$
and
![]() $\nu \vdash m$
. For
$\nu \vdash m$
. For
![]() $T\in \mathrm {Tab}\left (\lambda /\nu \right )$
, we write
$T\in \mathrm {Tab}\left (\lambda /\nu \right )$
, we write
![]() $\mathrm {top}(T)\subseteq \left [m+1,n\right ]$
for the set of elements in the top row of T (which may be empty: It is of size
$\mathrm {top}(T)\subseteq \left [m+1,n\right ]$
for the set of elements in the top row of T (which may be empty: It is of size
![]() $\lambda _{1}-\nu _{1}$
).
$\lambda _{1}-\nu _{1}$
).
For any two subsets
![]() $A,B$
of
$A,B$
of
![]() $[n]$
, we define
$[n]$
, we define
![]() $d(A,B)=\left |A\setminus B\right |$
. When restricted to subsets of
$d(A,B)=\left |A\setminus B\right |$
. When restricted to subsets of
![]() $\left [n\right ]$
with exactly p elements, for some
$\left [n\right ]$
with exactly p elements, for some
![]() $p\in \left [0,n\right ]$
, this function is a metric. Moreover, the function d is clearly invariant under
$p\in \left [0,n\right ]$
, this function is a metric. Moreover, the function d is clearly invariant under
![]() $S_{n}$
, that is, if
$S_{n}$
, that is, if
![]() $\sigma \in S_{n}$
and
$\sigma \in S_{n}$
and
![]() $A,B\subseteq \left [n\right ]$
, then
$A,B\subseteq \left [n\right ]$
, then
![]() $d\left (\sigma (A),\sigma (B)\right )=d\left (A,B\right ).$
$d\left (\sigma (A),\sigma (B)\right )=d\left (A,B\right ).$
Proposition 4.4. Suppose
![]() $m\leq n$
,
$m\leq n$
,
![]() $\lambda \vdash n$
,
$\lambda \vdash n$
,
![]() $\nu \vdash m$
and
$\nu \vdash m$
and
![]() $\nu \subset \lambda $
, and write
$\nu \subset \lambda $
, and write
![]() $k=n-m$
. If
$k=n-m$
. If
![]() $\lambda _{1}+\nu _{1}>n+k^{2}$
, then for any
$\lambda _{1}+\nu _{1}>n+k^{2}$
, then for any
![]() $T,T'\in \mathrm {Tab}(\lambda /\nu )$
and
$T,T'\in \mathrm {Tab}(\lambda /\nu )$
and
![]() $\sigma \in S^{\prime }_{k}$
we have
$\sigma \in S^{\prime }_{k}$
we have
 $$ \begin{align} \left|\langle\sigma w_{T},w_{T'}\rangle\right|\leq\left(\frac{k^{2}}{\lambda_{1}+\nu_{1}-n}\right)^{d\left(\sigma\mathrm{top}(T),\mathrm{top}(T')\right)}. \end{align} $$
$$ \begin{align} \left|\langle\sigma w_{T},w_{T'}\rangle\right|\leq\left(\frac{k^{2}}{\lambda_{1}+\nu_{1}-n}\right)^{d\left(\sigma\mathrm{top}(T),\mathrm{top}(T')\right)}. \end{align} $$
Note that if the top row of
![]() $\lambda /\nu $
is empty, namely, if
$\lambda /\nu $
is empty, namely, if
![]() $\nu _{1}=\lambda _{1}$
, then
$\nu _{1}=\lambda _{1}$
, then
![]() $\mathrm {top}\left (T\right )=\emptyset $
for every
$\mathrm {top}\left (T\right )=\emptyset $
for every
![]() $T\in \mathrm {Tab}\left (\lambda /\nu \right )$
and the upper bound in equation (4.6) is trivial:
$T\in \mathrm {Tab}\left (\lambda /\nu \right )$
and the upper bound in equation (4.6) is trivial:
![]() $\left (k^{2}/\left (\lambda _{1}+\nu _{1}-n\right )\right )^{0}=1$
. In particular, this is the case if
$\left (k^{2}/\left (\lambda _{1}+\nu _{1}-n\right )\right )^{0}=1$
. In particular, this is the case if
![]() $m=n$
, in which case
$m=n$
, in which case
![]() $k=0$
, the bound is
$k=0$
, the bound is
![]() $0^{0}=1$
and we have an action of the trivial group on a one-dimensional space spanned by
$0^{0}=1$
and we have an action of the trivial group on a one-dimensional space spanned by
![]() $w_{T}$
for T the empty tableau (see Remark 3.3).
$w_{T}$
for T the empty tableau (see Remark 3.3).
Proof. If
![]() $k=0$
the statement is trivial, so we may assume
$k=0$
the statement is trivial, so we may assume
![]() $k\ge 1$
. We prove equation (4.6) as a consequence of the following slightly stronger statement:
$k\ge 1$
. We prove equation (4.6) as a consequence of the following slightly stronger statement:
(S) If
![]() $\lambda _{1}+\nu _{1}\ge n+\ell _{\mathrm {cox}}(\sigma )$
, then for any
$\lambda _{1}+\nu _{1}\ge n+\ell _{\mathrm {cox}}(\sigma )$
, then for any
![]() $T\in \mathrm {Tab}(\lambda /\nu )$
,
$T\in \mathrm {Tab}(\lambda /\nu )$
,
![]() $A_{0}\subseteq \left [m+1,n\right ]$
of size
$A_{0}\subseteq \left [m+1,n\right ]$
of size
![]() $\lambda _{1}-\nu _{1}$
and any unit vector u in
$\lambda _{1}-\nu _{1}$
and any unit vector u in
we have
 $$ \begin{align} |\langle\sigma w_{T},u\rangle|\leq\left(\frac{\ell_{\mathrm{cox}}(\sigma)}{\nu_{1}+\lambda_{1}-n}\right)^{d(\sigma\mathrm{top}(T),A_{0})}. \end{align} $$
$$ \begin{align} |\langle\sigma w_{T},u\rangle|\leq\left(\frac{\ell_{\mathrm{cox}}(\sigma)}{\nu_{1}+\lambda_{1}-n}\right)^{d(\sigma\mathrm{top}(T),A_{0})}. \end{align} $$
The proposition follows from (S) by using the bound
![]() $\ell _{\mathrm {cox}}(\sigma )\leq k^{2}$
and setting
$\ell _{\mathrm {cox}}(\sigma )\leq k^{2}$
and setting
![]() $A_{0}=\mathrm {top}(T')$
,
$A_{0}=\mathrm {top}(T')$
,
![]() $u=w_{T'}$
.
$u=w_{T'}$
.
Let
![]() $D\stackrel {\mathrm {def}}{=} d\left (\sigma \mathrm {top}(T),A_{0}\right )$
. We prove (S) by induction on
$D\stackrel {\mathrm {def}}{=} d\left (\sigma \mathrm {top}(T),A_{0}\right )$
. We prove (S) by induction on
![]() $\ell \stackrel {\mathrm {def}}{=}\ell _{\mathrm {cox}}(\sigma )$
. The base case of the induction is
$\ell \stackrel {\mathrm {def}}{=}\ell _{\mathrm {cox}}(\sigma )$
. The base case of the induction is
![]() $\ell =0$
. Then
$\ell =0$
. Then
![]() $\sigma =\mathrm {id}$
and
$\sigma =\mathrm {id}$
and
unless
![]() $\mathrm {top}(T)=A_{0}$
, meaning
$\mathrm {top}(T)=A_{0}$
, meaning
![]() $D=0$
. On the other hand, if
$D=0$
. On the other hand, if
![]() $D=0$
, then
$D=0$
, then
 $$\begin{align*}|\langle\sigma w_{T},u\rangle|\leq1=0^{0}=\left(\frac{\ell}{\nu_{1}+\lambda_{1}-n}\right)^{D} \end{align*}$$
$$\begin{align*}|\langle\sigma w_{T},u\rangle|\leq1=0^{0}=\left(\frac{\ell}{\nu_{1}+\lambda_{1}-n}\right)^{D} \end{align*}$$
as required.
For the inductive step, for
![]() $\ell \geq 1$
we write
$\ell \geq 1$
we write
![]() $\sigma =s_{j}\sigma '$
, where
$\sigma =s_{j}\sigma '$
, where
![]() $\ell _{\mathrm {cox}}(\sigma ')=\ell -1$
and
$\ell _{\mathrm {cox}}(\sigma ')=\ell -1$
and
![]() $j\in \left [m+1,n-1\right ]$
. Two scenarios can occur.
$j\in \left [m+1,n-1\right ]$
. Two scenarios can occur.
(i) Suppose
![]() $s_{j}A_{0}=A_{0}$
. In this case, by the definition of the action of the Coxeter generators in equation (3.1),
$s_{j}A_{0}=A_{0}$
. In this case, by the definition of the action of the Coxeter generators in equation (3.1),
![]() $s_{j}u$
is a unit vector in
$s_{j}u$
is a unit vector in
![]() $W_{A_{0}}$
. Also, by the invariance of the distance function under
$W_{A_{0}}$
. Also, by the invariance of the distance function under
![]() $s_{j}$
,
$s_{j}$
,
The inductive hypothesis then yields
 $$\begin{align*}|\langle\sigma w_{T},u\rangle|=|\langle\sigma'w_{T},s_{j}u\rangle|\leq\left(\frac{\ell-1}{\nu_{1}+\lambda_{1}-n}\right)^{D}\leq\left(\frac{\ell}{\nu_{1}+\lambda_{1}-n}\right)^{D}, \end{align*}$$
$$\begin{align*}|\langle\sigma w_{T},u\rangle|=|\langle\sigma'w_{T},s_{j}u\rangle|\leq\left(\frac{\ell-1}{\nu_{1}+\lambda_{1}-n}\right)^{D}\leq\left(\frac{\ell}{\nu_{1}+\lambda_{1}-n}\right)^{D}, \end{align*}$$
as required.
(ii) Suppose otherwise that
![]() $s_{j}A_{0}\neq A_{0}$
. This means that exactly one of j and
$s_{j}A_{0}\neq A_{0}$
. This means that exactly one of j and
![]() $j+1$
are in
$j+1$
are in
![]() $A_{0}$
. We write
$A_{0}$
. We write
 $$ \begin{align} u=\sum_{T'\in\mathrm{Tab}(\lambda/\nu)\colon\mathrm{top}(T')=A_{0}}\beta_{T'}w_{T'}. \end{align} $$
$$ \begin{align} u=\sum_{T'\in\mathrm{Tab}(\lambda/\nu)\colon\mathrm{top}(T')=A_{0}}\beta_{T'}w_{T'}. \end{align} $$
For each
![]() $T'$
with
$T'$
with
![]() $\mathrm {top}(T')=A_{0}$
, we have
$\mathrm {top}(T')=A_{0}$
, we have
From equation (4.8) and the formula for the action of Coxeter generators (3.1), we can therefore write
![]() $s_{j}u=w_{1}+w_{2}$
, where
$s_{j}u=w_{1}+w_{2}$
, where
![]() $w_{1}\in W_{s_{j}A_{0}}$
and
$w_{1}\in W_{s_{j}A_{0}}$
and
![]() $w_{2}\in W_{A_{0}}$
are orthogonal vectors with
$w_{2}\in W_{A_{0}}$
are orthogonal vectors with
![]() $\|w_{1}\|\leq 1$
and
$\|w_{1}\|\leq 1$
and
![]() $\|w_{2}\|\leq (\nu _{1}+\lambda _{1}-n)^{-1}$
. Hence,
$\|w_{2}\|\leq (\nu _{1}+\lambda _{1}-n)^{-1}$
. Hence,
Note that
![]() $d(\sigma '\mathrm {top}(T),s_{j}A_{0})=d\left (\sigma \mathrm {top}(T),A_{0}\right )=D$
, so by the inductive hypothesis
$d(\sigma '\mathrm {top}(T),s_{j}A_{0})=d\left (\sigma \mathrm {top}(T),A_{0}\right )=D$
, so by the inductive hypothesis
 $$ \begin{align} |\langle\sigma w_{T},u\rangle|\leq\left(\frac{\ell-1}{\nu_{1}+\lambda_{1}-n}\right)^{D}+\frac{1}{\nu_{1}+\lambda_{1}-n}\left(\frac{\ell-1}{\nu_{1}+\lambda_{1}-n}\right)^{d(\sigma'\mathrm{top}(T),A_{0})}. \end{align} $$
$$ \begin{align} |\langle\sigma w_{T},u\rangle|\leq\left(\frac{\ell-1}{\nu_{1}+\lambda_{1}-n}\right)^{D}+\frac{1}{\nu_{1}+\lambda_{1}-n}\left(\frac{\ell-1}{\nu_{1}+\lambda_{1}-n}\right)^{d(\sigma'\mathrm{top}(T),A_{0})}. \end{align} $$
By the triangle inequality,
so using
![]() $\nu _{1}+\lambda _{1}\geq n+\ell $
we obtain from equation (4.9)
$\nu _{1}+\lambda _{1}\geq n+\ell $
we obtain from equation (4.9)
 $$ \begin{align*} |\langle\sigma w_{T},u\rangle| & \leq\left(\frac{\ell-1}{\nu_{1}+\lambda_{1}-n}\right)^{D}+\frac{1}{\nu_{1}+\lambda_{1}-n}\left(\frac{\ell-1}{\nu_{1}+\lambda_{1}-n}\right)^{D-1}\\ & =\frac{(\ell-1)^{D-1}\ell}{(\nu_{1}+\lambda_{1}-n)^{D}}\leq\left(\frac{\ell}{\nu_{1}+\lambda_{1}-n}\right)^{D}, \end{align*} $$
$$ \begin{align*} |\langle\sigma w_{T},u\rangle| & \leq\left(\frac{\ell-1}{\nu_{1}+\lambda_{1}-n}\right)^{D}+\frac{1}{\nu_{1}+\lambda_{1}-n}\left(\frac{\ell-1}{\nu_{1}+\lambda_{1}-n}\right)^{D-1}\\ & =\frac{(\ell-1)^{D-1}\ell}{(\nu_{1}+\lambda_{1}-n)^{D}}\leq\left(\frac{\ell}{\nu_{1}+\lambda_{1}-n}\right)^{D}, \end{align*} $$
as required.
4.4 Families of YDs and zeta functions
Recall from
![]() $\S $
1 that the zeta function of
$\S $
1 that the zeta function of
![]() $S_{n}$
is defined by
$S_{n}$
is defined by
 $$\begin{align*}\zeta^{S_{n}}\left(s\right)\stackrel{\mathrm{def}}{=}\sum_{\lambda\vdash n}\frac{1}{d_{\lambda}^{~s}}, \end{align*}$$
$$\begin{align*}\zeta^{S_{n}}\left(s\right)\stackrel{\mathrm{def}}{=}\sum_{\lambda\vdash n}\frac{1}{d_{\lambda}^{~s}}, \end{align*}$$
and that for
![]() $g\ge 2$
$g\ge 2$
Let
![]() $\Lambda (n,b)$
denote the collection of
$\Lambda (n,b)$
denote the collection of
![]() $\lambda \vdash n$
such that
$\lambda \vdash n$
such that
![]() $b_{\lambda }\ge b$
and
$b_{\lambda }\ge b$
and
![]() $b_{\check {\lambda }}\ge b$
. In other words,
$b_{\check {\lambda }}\ge b$
. In other words,
![]() $\Lambda (n,b)$
is the collection of YDs of size n with at least b boxes outside the first row and at least b boxes outside the first column. One has the following useful result of Liebeck and Shalev [Reference Liebeck and ShalevLS04, Prop. 2.5] and, independently, Gamburd [Reference GamburdGam06, Prop. 4.2]:
$\Lambda (n,b)$
is the collection of YDs of size n with at least b boxes outside the first row and at least b boxes outside the first column. One has the following useful result of Liebeck and Shalev [Reference Liebeck and ShalevLS04, Prop. 2.5] and, independently, Gamburd [Reference GamburdGam06, Prop. 4.2]:
Proposition 4.5. For fixed
![]() $b\geq 0$
and real
$b\geq 0$
and real
![]() $s>0$
, as
$s>0$
, as
![]() $n\to \infty $
$n\to \infty $
 $$\begin{align*}\sum_{\lambda\in\Lambda(n,b)}\frac{1}{d_{\lambda}^{~s}}=O_{b}\left(n^{-sb}\right). \end{align*}$$
$$\begin{align*}\sum_{\lambda\in\Lambda(n,b)}\frac{1}{d_{\lambda}^{~s}}=O_{b}\left(n^{-sb}\right). \end{align*}$$
The proof of Theorem 1.1 will crucially depend on certain families of YDs that interact nicely with the skew modules
![]() $V^{\lambda /\nu }$
. Given a YD
$V^{\lambda /\nu }$
. Given a YD
![]() $\lambda $
, we will write
$\lambda $
, we will write
![]() $\lambda (n)$
for the unique YD
$\lambda (n)$
for the unique YD
![]() $\lambda (n)\vdash n$
which is obtained from
$\lambda (n)\vdash n$
which is obtained from
![]() $\lambda $
by either deleting boxes from or adding boxes to the first row of
$\lambda $
by either deleting boxes from or adding boxes to the first row of
![]() $\lambda $
, if it exists. To be precise,
$\lambda $
, if it exists. To be precise,
![]() $\lambda (n)$
exists if and only if
$\lambda (n)$
exists if and only if
![]() $n\geq |\lambda |-\left (\lambda _{1}-\lambda _{2}\right )$
, interpreting
$n\geq |\lambda |-\left (\lambda _{1}-\lambda _{2}\right )$
, interpreting
![]() $\lambda _{2}=0$
if
$\lambda _{2}=0$
if
![]() $\lambda $
only has one row.
$\lambda $
only has one row.
Now, given
![]() $k\in \mathbf {N}$
, and YDs
$k\in \mathbf {N}$
, and YDs
![]() $\nu \subset _{k}\lambda $
, assume that
$\nu \subset _{k}\lambda $
, assume that
![]() $n_{1}$
and
$n_{1}$
and
![]() $n_{2}$
are large enough so that
$n_{2}$
are large enough so that
![]() $\lambda (n_{i})$
and
$\lambda (n_{i})$
and
![]() $\nu (n_{i}-k)$
both exist and so that the first row (of length
$\nu (n_{i}-k)$
both exist and so that the first row (of length
![]() $\lambda _{1}-\nu _{1}$
, which could be zero) of the SYD
$\lambda _{1}-\nu _{1}$
, which could be zero) of the SYD
![]() $\lambda \left (n_{i}\right )/\nu \left (n_{i}-k\right )$
does not border the second row, namely,
$\lambda \left (n_{i}\right )/\nu \left (n_{i}-k\right )$
does not border the second row, namely,
![]() $\nu \left (n_{i}-k\right )_{1}\ge \lambda _{2}$
. Then there is a natural way to identify
$\nu \left (n_{i}-k\right )_{1}\ge \lambda _{2}$
. Then there is a natural way to identify
![]() $\mathrm {Tab}\left (\lambda (n_{1})/\nu (n_{1}-k)\right )$
with
$\mathrm {Tab}\left (\lambda (n_{1})/\nu (n_{1}-k)\right )$
with
![]() $\mathrm {Tab}\left (\lambda (n_{2})/\nu (n_{2}-k)\right )$
by simply adding
$\mathrm {Tab}\left (\lambda (n_{2})/\nu (n_{2}-k)\right )$
by simply adding
![]() $n_{2}-n_{1}$
to all numbers in boxes of a tableau in
$n_{2}-n_{1}$
to all numbers in boxes of a tableau in
![]() $\mathrm {Tab}\left (\lambda (n_{1})/\nu (n_{1}-k)\right )$
and shifting the first row right or left as needed. If
$\mathrm {Tab}\left (\lambda (n_{1})/\nu (n_{1}-k)\right )$
and shifting the first row right or left as needed. If
![]() $\nu _{1}\ge \lambda _{2}$
and
$\nu _{1}\ge \lambda _{2}$
and
![]() $T\in \mathrm {Tab}\left (\lambda /\nu \right )$
, we write
$T\in \mathrm {Tab}\left (\lambda /\nu \right )$
, we write
![]() $T(n)$
for the resulting tableau in
$T(n)$
for the resulting tableau in
![]() $\mathrm {Tab}\left (\lambda (n)/\nu (n-k)\right )$
.
$\mathrm {Tab}\left (\lambda (n)/\nu (n-k)\right )$
.

Figure 4.1 This figure depicts two elements of a family of SYDs
![]() $\lambda (n)/\nu (n-10)$
for
$\lambda (n)/\nu (n-10)$
for
![]() $n=16$
and
$n=16$
and
![]() $n=18$
. Here, we can take
$n=18$
. Here, we can take
![]() $\lambda =(6,3,2,1)$
and
$\lambda =(6,3,2,1)$
and
![]() $\nu =(1,1)$
.
$\nu =(1,1)$
.
Given
![]() $n\in \mathbf {N}$
and
$n\in \mathbf {N}$
and
![]() $k\in \left [n\right ]$
, recall that we write
$k\in \left [n\right ]$
, recall that we write
![]() $S^{\prime }_{k}$
for the subgroup of
$S^{\prime }_{k}$
for the subgroup of
![]() $S_{n}$
that acts as the identity on
$S_{n}$
that acts as the identity on
![]() $[n-k]$
. Throughout the paper, we fix isomorphisms
$[n-k]$
. Throughout the paper, we fix isomorphisms
where we view
![]() $S_{k}\leq S_{n}$
in the usual way and
$S_{k}\leq S_{n}$
in the usual way and
 $$\begin{align*}\rho_{k}(i)=\begin{cases} i+k & \text{if \(i\in[n-k]\)}\\ i-n+k & \text{if \(i\in[n-k+1,n]\).} \end{cases} \end{align*}$$
$$\begin{align*}\rho_{k}(i)=\begin{cases} i+k & \text{if \(i\in[n-k]\)}\\ i-n+k & \text{if \(i\in[n-k+1,n]\).} \end{cases} \end{align*}$$
Using these isomorphisms allows us to identify the different subgroups
![]() $S^{\prime }_{k}$
as n varies: This will recur at several points of the sequel. It also allows us to note in the following proposition that matrix coefficients of skew modules
$S^{\prime }_{k}$
as n varies: This will recur at several points of the sequel. It also allows us to note in the following proposition that matrix coefficients of skew modules
![]() $V^{\lambda (n)/\nu (n-k)}$
are holomorphic functions of
$V^{\lambda (n)/\nu (n-k)}$
are holomorphic functions of
![]() $n^{-1}$
, for sufficiently large n. Recall that
$n^{-1}$
, for sufficiently large n. Recall that
![]() $w_{T_{i}(n)}$
are elements of the Gelfand–Tsetlin basis for
$w_{T_{i}(n)}$
are elements of the Gelfand–Tsetlin basis for
![]() $V^{\lambda (n)/\nu (n-k)}$
.
$V^{\lambda (n)/\nu (n-k)}$
.
Proposition 4.6. Let
![]() $k\in \mathbf {N}$
,
$k\in \mathbf {N}$
,
![]() $\sigma \in S_{k}$
, and
$\sigma \in S_{k}$
, and
![]() $\nu \subset _{k}\lambda $
be two YDs that differ by k boxes. Suppose that
$\nu \subset _{k}\lambda $
be two YDs that differ by k boxes. Suppose that
![]() $\nu _{1}\ge \lambda _{2}$
. Given
$\nu _{1}\ge \lambda _{2}$
. Given
![]() $T_{1},T_{2}\in \mathrm {Tab}(\lambda /\nu )$
, there is a function
$T_{1},T_{2}\in \mathrm {Tab}(\lambda /\nu )$
, there is a function
![]() $F=F_{\sigma ,\lambda ,\nu ,T_{1},T_{2}}$
that is holomorphic in the ball of radius
$F=F_{\sigma ,\lambda ,\nu ,T_{1},T_{2}}$
that is holomorphic in the ball of radius
![]() $\left |\lambda \right |{}^{-1}$
around zero, has Taylor expansion around
$\left |\lambda \right |{}^{-1}$
around zero, has Taylor expansion around
![]() $0$
with rational coefficients and such that for all
$0$
with rational coefficients and such that for all
![]() $n\geq |\lambda |$
, viewing
$n\geq |\lambda |$
, viewing
![]() $\sigma $
as an element of
$\sigma $
as an element of
![]() $S^{\prime }_{k}\leq S_{n}$
via the isomorphism (4.10),
$S^{\prime }_{k}\leq S_{n}$
via the isomorphism (4.10),
Proof. Since
![]() $V^{\lambda (n)/\nu (n-k)}$
is finite-dimensional with dimension independent of n (as long as
$V^{\lambda (n)/\nu (n-k)}$
is finite-dimensional with dimension independent of n (as long as
![]() $n\ge \left |\lambda \right |$
), it suffices to prove the result in the case that
$n\ge \left |\lambda \right |$
), it suffices to prove the result in the case that
![]() $\sigma \in S_{k}$
is a Coxeter generator
$\sigma \in S_{k}$
is a Coxeter generator
![]() $s_{i}$
with
$s_{i}$
with
![]() $i\in [k-1]$
. Interpreted as an element of
$i\in [k-1]$
. Interpreted as an element of
![]() $S^{\prime }_{k}\leq S_{n}$
via equation (4.10),
$S^{\prime }_{k}\leq S_{n}$
via equation (4.10),
![]() $\sigma $
corresponds to the Coxeter generator
$\sigma $
corresponds to the Coxeter generator
![]() $s_{i+n-k}\in S_{n}$
.
$s_{i+n-k}\in S_{n}$
.
Let a be the axial distance between
![]() $j\stackrel {\mathrm {def}}{=} i+\left |\lambda \right |-k$
and
$j\stackrel {\mathrm {def}}{=} i+\left |\lambda \right |-k$
and
![]() $j+1=i+1+\left |\lambda \right |-k$
in
$j+1=i+1+\left |\lambda \right |-k$
in
![]() $T_{1}$
. Note that
$T_{1}$
. Note that
 $$\begin{align*}\mathrm{ax}\left({\fbox{\(i+n-k\)}}_{T_{1}\left(n\right)},{\fbox{\(i+1+n-k\)}}_{T_{1}\left(n\right)}\right)=\begin{cases} a+n-\left|\lambda\right| & \mathrm{if}~j~\mathrm{in~the~first~row~of}~T_{1}~\mathrm{and}~j+1~\mathrm{not},\\ a-\left(n-\left|\lambda\right|\right) & \mathrm{if}~j+1~\mathrm{in~the~first~row~of}~T_{1}~\mathrm{and}~j~\mathrm{not},\\ a & \mathrm{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}\mathrm{ax}\left({\fbox{\(i+n-k\)}}_{T_{1}\left(n\right)},{\fbox{\(i+1+n-k\)}}_{T_{1}\left(n\right)}\right)=\begin{cases} a+n-\left|\lambda\right| & \mathrm{if}~j~\mathrm{in~the~first~row~of}~T_{1}~\mathrm{and}~j+1~\mathrm{not},\\ a-\left(n-\left|\lambda\right|\right) & \mathrm{if}~j+1~\mathrm{in~the~first~row~of}~T_{1}~\mathrm{and}~j~\mathrm{not},\\ a & \mathrm{otherwise}. \end{cases} \end{align*}$$
In the first, case
![]() $a>0$
, and in the second case,
$a>0$
, and in the second case,
![]() $a<0$
. By the description in equation (3.1) of how the Coxeter generators act,
$a<0$
. By the description in equation (3.1) of how the Coxeter generators act,
![]() $\langle s_{i+n-k}w_{T_{1}(n)},w_{T_{2}(n)}\rangle $
is therefore one of the following functions of n:
$\langle s_{i+n-k}w_{T_{1}(n)},w_{T_{2}(n)}\rangle $
is therefore one of the following functions of n:
 $$\begin{align*}0,\,\frac{1}{a-n+|\lambda|},\,\frac{1}{a+n-|\lambda|},\,\sqrt{1-\frac{1}{(a-n+|\lambda|)^{2}}},\,\sqrt{1-\frac{1}{(a+n-|\lambda|)^{2}}}. \end{align*}$$
$$\begin{align*}0,\,\frac{1}{a-n+|\lambda|},\,\frac{1}{a+n-|\lambda|},\,\sqrt{1-\frac{1}{(a-n+|\lambda|)^{2}}},\,\sqrt{1-\frac{1}{(a+n-|\lambda|)^{2}}}. \end{align*}$$
If one replaces n by
![]() $z^{-1}$
, each of these yields a holomorphic function of z when
$z^{-1}$
, each of these yields a holomorphic function of z when
![]() $|z|$
is sufficiently small.
$|z|$
is sufficiently small.
The dimensions of representations in a family
![]() $\lambda (n)$
are polynomials in n.
$\lambda (n)$
are polynomials in n.
Lemma 4.7. Given a YD
![]() $\lambda $
, consider the family of YDs
$\lambda $
, consider the family of YDs
![]() $\lambda (n)$
. There is a polynomial
$\lambda (n)$
. There is a polynomial
![]() $G=G_{\lambda }\in \mathbb {Q}\left [t\right ]$
of degree
$G=G_{\lambda }\in \mathbb {Q}\left [t\right ]$
of degree
![]() $b_{\lambda }$
with rational coefficients such that for every n such that
$b_{\lambda }$
with rational coefficients such that for every n such that
![]() $\lambda \left (n\right )$
exists,
$\lambda \left (n\right )$
exists,
Furthermore, the complex zeros of G are integers n with
![]() $n\in \left [0,\left |\lambda \right |\right ]$
, and the leading coefficient is
$n\in \left [0,\left |\lambda \right |\right ]$
, and the leading coefficient is
![]() $\frac {1}{m}$
for some integer m.
$\frac {1}{m}$
for some integer m.
For example, if
![]() $\lambda \left (n\right )=\left (n-4,3,1\right )$
, then
$\lambda \left (n\right )=\left (n-4,3,1\right )$
, then
![]() $d_{\lambda \left (n\right )}=\frac {n\left (n-1\right )\left (n-3\right )\left (n-6\right )}{8}$
for every
$d_{\lambda \left (n\right )}=\frac {n\left (n-1\right )\left (n-3\right )\left (n-6\right )}{8}$
for every
![]() $n\ge 7$
.
$n\ge 7$
.
Proof. This easily follows from the hook-length formula for the dimension
![]() $d_{\lambda }$
[Reference Frame, Robinson and ThrallFRT54].
$d_{\lambda }$
[Reference Frame, Robinson and ThrallFRT54].
Lemma 4.7 together with Proposition 4.5 have the following nice consequence for the zeta function
![]() $\zeta ^{S_{n}}$
that will be crucial in proving Theorem 1.1.
$\zeta ^{S_{n}}$
that will be crucial in proving Theorem 1.1.
Proposition 4.8. For any
![]() $s\in \mathbf {N}$
and
$s\in \mathbf {N}$
and
![]() $M\in \mathbf {N}$
, there is a polynomial
$M\in \mathbf {N}$
, there is a polynomial
![]() $P_{s,M}\in \mathbf {Z}\left [t\right ]$
with integer coefficients of degree
$P_{s,M}\in \mathbf {Z}\left [t\right ]$
with integer coefficients of degree
![]() $<M$
such that
$<M$
such that
as
![]() $n\to \infty $
. The constant coefficient of
$n\to \infty $
. The constant coefficient of
![]() $P_{s,M}$
is equal to
$P_{s,M}$
is equal to
![]() $1$
.
$1$
.
For example, for
![]() $s=2$
and
$s=2$
and
![]() $M=5$
we have
$M=5$
we have
 $$\begin{align*}\zeta^{S_{n}}\left(2\right)=2\left(1+\frac{1}{n^{2}}+\frac{2}{n^{3}}+\frac{11}{n^{4}}\right)+O\left(\frac{1}{n^{5}}\right). \end{align*}$$
$$\begin{align*}\zeta^{S_{n}}\left(2\right)=2\left(1+\frac{1}{n^{2}}+\frac{2}{n^{3}}+\frac{11}{n^{4}}\right)+O\left(\frac{1}{n^{5}}\right). \end{align*}$$
Proof. Fix
![]() $s\in \mathbf {N}$
and
$s\in \mathbf {N}$
and
![]() $M\in \mathbf {N}$
as in the statement of the proposition. Let
$M\in \mathbf {N}$
as in the statement of the proposition. Let
![]() $b=\lceil \frac {M}{s}\rceil $
. Proposition 4.5 implies that
$b=\lceil \frac {M}{s}\rceil $
. Proposition 4.5 implies that
 $$\begin{align*}\zeta^{S_{n}}\left(s\right)=\sum_{\substack{\lambda\vdash n\\ \lambda\notin\Lambda(n,b) } }\frac{1}{d_{\lambda}^{~s}}+O(n^{-M}) \end{align*}$$
$$\begin{align*}\zeta^{S_{n}}\left(s\right)=\sum_{\substack{\lambda\vdash n\\ \lambda\notin\Lambda(n,b) } }\frac{1}{d_{\lambda}^{~s}}+O(n^{-M}) \end{align*}$$
as
![]() $n\to \infty $
. The
$n\to \infty $
. The
![]() $\lambda $
in the sum above have either
$\lambda $
in the sum above have either
![]() $<b$
boxes outside their first row or
$<b$
boxes outside their first row or
![]() $<b$
boxes outside their first column. For
$<b$
boxes outside their first column. For
![]() $n>2b$
, these options are mutually exclusive. Moreover, the map
$n>2b$
, these options are mutually exclusive. Moreover, the map
![]() $\lambda \mapsto \check {\lambda }$
maps YDs of the first kind to YDs of the second kind bijectively and vice versa. Hence, if we let
$\lambda \mapsto \check {\lambda }$
maps YDs of the first kind to YDs of the second kind bijectively and vice versa. Hence, if we let
![]() $\Lambda _{b_{\lambda }<b}(n)$
be the collection of
$\Lambda _{b_{\lambda }<b}(n)$
be the collection of
![]() $\lambda \vdash n$
with
$\lambda \vdash n$
with
![]() $<b$
boxes outside their first row, then as
$<b$
boxes outside their first row, then as
![]() $n\to \infty $
,
$n\to \infty $
,
 $$ \begin{align*} \zeta^{S_{n}}\left(s\right) & =\sum_{\substack{\lambda\in\Lambda_{b_{\lambda}<b}(n)} }\left(\frac{1}{d_{\lambda}^{~s}}+\frac{1}{d_{\check{\lambda}}^{~s}}\right)+O\left(n^{-M}\right)\\ & =2\sum_{\substack{\lambda\in\Lambda_{b_{\lambda}<b}(n)} }\frac{1}{d_{\lambda}^{~s}}+O\left(n^{-M}\right). \end{align*} $$
$$ \begin{align*} \zeta^{S_{n}}\left(s\right) & =\sum_{\substack{\lambda\in\Lambda_{b_{\lambda}<b}(n)} }\left(\frac{1}{d_{\lambda}^{~s}}+\frac{1}{d_{\check{\lambda}}^{~s}}\right)+O\left(n^{-M}\right)\\ & =2\sum_{\substack{\lambda\in\Lambda_{b_{\lambda}<b}(n)} }\frac{1}{d_{\lambda}^{~s}}+O\left(n^{-M}\right). \end{align*} $$
Now, if
![]() $n>2b$
, there is a finite collection of YDs
$n>2b$
, there is a finite collection of YDs
![]() $\{\mu _{1},\ldots ,\mu _{\ell }\}$
, depending on b, with
$\{\mu _{1},\ldots ,\mu _{\ell }\}$
, depending on b, with
![]() $|\mu _{i}|<2b$
for all i, such that for each
$|\mu _{i}|<2b$
for all i, such that for each
![]() $n>2b$
$n>2b$
For each of these
![]() $\mu _{i}$
, let
$\mu _{i}$
, let
![]() $G_{\mu _{i}}$
be the polynomial provided by Lemma 4.7. No
$G_{\mu _{i}}$
be the polynomial provided by Lemma 4.7. No
![]() $G_{\mu _{i}}$
has any zero z with
$G_{\mu _{i}}$
has any zero z with
![]() $|z|>2b$
. Hence,
$|z|>2b$
. Hence,
 $$\begin{align*}\zeta^{S_{n}}\left(s\right)=2\sum_{\substack{i=1} }^{\ell}\frac{1}{\left(G_{\mu_{i}}\left(n\right)\right)^{s}}+O\left(n^{-M}\right) \end{align*}$$
$$\begin{align*}\zeta^{S_{n}}\left(s\right)=2\sum_{\substack{i=1} }^{\ell}\frac{1}{\left(G_{\mu_{i}}\left(n\right)\right)^{s}}+O\left(n^{-M}\right) \end{align*}$$
as
![]() $n\to \infty $
. Because of the special structure of
$n\to \infty $
. Because of the special structure of
![]() $G_{\mu _{i}}$
, as elaborated in Lemma 4.7,
$G_{\mu _{i}}$
, as elaborated in Lemma 4.7,
![]() $\left (G_{\mu _{i}}\left (n\right )\right )^{-1}$
is equal to a power series in
$\left (G_{\mu _{i}}\left (n\right )\right )^{-1}$
is equal to a power series in
![]() $n^{-1}$
with integer coefficients. Since
$n^{-1}$
with integer coefficients. Since
![]() $s\in \mathbf {N}$
,
$s\in \mathbf {N}$
,
![]() $\left (G_{\mu _{i}}\left (n\right )\right )^{-s}$
is too equal to a power series in
$\left (G_{\mu _{i}}\left (n\right )\right )^{-s}$
is too equal to a power series in
![]() $n^{-1}$
with integer coefficients. This proves the first statement. Because the degree of
$n^{-1}$
with integer coefficients. This proves the first statement. Because the degree of
![]() $G_{\mu _{i}}\left (n\right )$
is positive unless
$G_{\mu _{i}}\left (n\right )$
is positive unless
![]() $\mu _{i}\left (n\right )=\left (n\right )$
in which case
$\mu _{i}\left (n\right )=\left (n\right )$
in which case
![]() $G_{\mu _{i}}\left (n\right )=1$
, the constant coefficient of
$G_{\mu _{i}}\left (n\right )=1$
, the constant coefficient of
![]() $P_{s,M}$
must be
$P_{s,M}$
must be
![]() $1$
.
$1$
.
In fact, it is the following direct corollary of Proposition 4.8 that we will need.
Corollary 4.9. For any
![]() $s\in \mathbf {N}$
and
$s\in \mathbf {N}$
and
![]() $M\in \mathbf {N}$
, there is a polynomial
$M\in \mathbf {N}$
, there is a polynomial
![]() $Q_{s,M}\in \mathbf {Z}\left [t\right ]$
of degree
$Q_{s,M}\in \mathbf {Z}\left [t\right ]$
of degree
![]() $<M$
and constant coefficient
$<M$
and constant coefficient
![]() $1$
such that as
$1$
such that as
![]() $n\to \infty $
,
$n\to \infty $
,
5 The probability of an embedded tiled surface
5.1 Overview of this section
This short overview is meant to make the results of this section more transparent and to stress an analogy with known results about the zeta function of
![]() $S_{n}$
. For simplicity, we assume
$S_{n}$
. For simplicity, we assume
![]() $g=2$
throughout this Section
$g=2$
throughout this Section
![]() $\S $
5 and denote
$\S $
5 and denote
![]() $\Gamma =\Gamma _{2}=\left \langle a,b,c,d\,\middle |\,\left [a,b\right ]\left [c,d\right ]\right \rangle $
.
$\Gamma =\Gamma _{2}=\left \langle a,b,c,d\,\middle |\,\left [a,b\right ]\left [c,d\right ]\right \rangle $
.
As explained in Section
![]() $\S $
1,
$\S $
1,
 $$ \begin{align} \left|\mathbb{X}_{n}\right|=\left|\mathbb{X}_{2,n}\right|=\left(n!\right)^{3}\cdot\sum_{\lambda\vdash n}\frac{1}{d_{\lambda}^{~2}}. \end{align} $$
$$ \begin{align} \left|\mathbb{X}_{n}\right|=\left|\mathbb{X}_{2,n}\right|=\left(n!\right)^{3}\cdot\sum_{\lambda\vdash n}\frac{1}{d_{\lambda}^{~2}}. \end{align} $$
If
![]() $\left \{ \lambda \left (n\right )\right \} _{n\ge n_{0}}$
is a family of YDs obtained by extending the first row, as in Section 4.4, then
$\left \{ \lambda \left (n\right )\right \} _{n\ge n_{0}}$
is a family of YDs obtained by extending the first row, as in Section 4.4, then
![]() $d_{\lambda \left (n\right )}$
is a polynomial in n of degree
$d_{\lambda \left (n\right )}$
is a polynomial in n of degree
![]() $b_{\lambda }$
(Lemma 4.7), and so the contribution of
$b_{\lambda }$
(Lemma 4.7), and so the contribution of
![]() $\lambda \left (n\right )$
and of
$\lambda \left (n\right )$
and of
![]() $\check {\lambda \left (n\right )}$
to equation (5.1) is a rational function in n for every
$\check {\lambda \left (n\right )}$
to equation (5.1) is a rational function in n for every
![]() $n\ge n_{0}$
. Proposition 4.5 (due to [Reference Liebeck and ShalevLS04, Reference GamburdGam06]) states that up to order
$n\ge n_{0}$
. Proposition 4.5 (due to [Reference Liebeck and ShalevLS04, Reference GamburdGam06]) states that up to order
![]() $O\left (n^{-2b}\right )$
, the zeta function in equation (5.1) is determined by those families of YDs with
$O\left (n^{-2b}\right )$
, the zeta function in equation (5.1) is determined by those families of YDs with
![]() $b_{\lambda }<b$
and their transpose.
$b_{\lambda }<b$
and their transpose.
In this Section 5, we prove something analogous for
![]() $\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
, where Y is a compact tiled surface. We write
$\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
, where Y is a compact tiled surface. We write
![]() $\mathfrak {v}=\mathfrak {v}(Y)$
,
$\mathfrak {v}=\mathfrak {v}(Y)$
,
![]() $\mathfrak {e}=\mathfrak {e}(Y)$
,
$\mathfrak {e}=\mathfrak {e}(Y)$
,
![]() $\mathfrak {f}=\mathfrak {f}(Y)$
for the number of vertices, edges and octagons of Y, respectively. We will use the letter f for an element of
$\mathfrak {f}=\mathfrak {f}(Y)$
for the number of vertices, edges and octagons of Y, respectively. We will use the letter f for an element of
![]() $\{a,b,c,d\}$
and write
$\{a,b,c,d\}$
and write
![]() $\mathfrak {e}_{f}=\mathfrak {e}_{f}(Y)$
for the number of f-labeled edges of Y. The first major result is that, depending on a choice of four constant permutations
$\mathfrak {e}_{f}=\mathfrak {e}_{f}(Y)$
for the number of f-labeled edges of Y. The first major result is that, depending on a choice of four constant permutations
![]() $\sigma _{f}^{\pm },\tau _{f}^{\pm }\in S^{\prime }_{\mathfrak {v}}$
per letter (defined in Section 5.3), we have
$\sigma _{f}^{\pm },\tau _{f}^{\pm }\in S^{\prime }_{\mathfrak {v}}$
per letter (defined in Section 5.3), we have
 $$ \begin{align} \mathbb{E}_{n}^{\mathrm{emb}}\left(Y\right)=\frac{\left(n!\right)^{3}}{\left|\mathbb{X}_{n}\right|}\cdot\frac{\left(n\right)_{\mathfrak{v}}\left(n\right)_{\mathfrak{f}}}{\prod_{f}\left(n\right)_{\mathfrak{e}_{f}}}\cdot\sum_{\nu\vdash n-\mathfrak{v}}H_{Y}\left(\nu\right), \end{align} $$
$$ \begin{align} \mathbb{E}_{n}^{\mathrm{emb}}\left(Y\right)=\frac{\left(n!\right)^{3}}{\left|\mathbb{X}_{n}\right|}\cdot\frac{\left(n\right)_{\mathfrak{v}}\left(n\right)_{\mathfrak{f}}}{\prod_{f}\left(n\right)_{\mathfrak{e}_{f}}}\cdot\sum_{\nu\vdash n-\mathfrak{v}}H_{Y}\left(\nu\right), \end{align} $$
where
![]() $H_{Y}\left (\nu \right )$
is some explicit function. This follows from Theorem 5.10. Notice that as
$H_{Y}\left (\nu \right )$
is some explicit function. This follows from Theorem 5.10. Notice that as
![]() $n\to \infty $
, the first fraction in equation (5.2) is
$n\to \infty $
, the first fraction in equation (5.2) is
![]() $\frac {\left (n!\right )^{3}}{\left |\mathbb {X}_{n}\right |}=\frac {1}{2}+O\left (n^{-2}\right )$
by Proposition 4.5, and the second one is
$\frac {\left (n!\right )^{3}}{\left |\mathbb {X}_{n}\right |}=\frac {1}{2}+O\left (n^{-2}\right )$
by Proposition 4.5, and the second one is
![]() $\frac {\left (n\right )_{\mathfrak {v}}\left (n\right )_{\mathfrak {f}}}{\prod _{f}\left (n\right )_{\mathfrak {e}_{f}}}=n^{\chi \left (Y\right )}\left (1+O\left (n^{-1}\right )\right )$
. So equation (5.2) gives that
$\frac {\left (n\right )_{\mathfrak {v}}\left (n\right )_{\mathfrak {f}}}{\prod _{f}\left (n\right )_{\mathfrak {e}_{f}}}=n^{\chi \left (Y\right )}\left (1+O\left (n^{-1}\right )\right )$
. So equation (5.2) gives that
 $$ \begin{align} \mathbb{E}_{n}^{\mathrm{emb}}\left(Y\right)=\left(\frac{1}{2}+O\left(n^{-1}\right)\right)n^{\chi\left(Y\right)}\cdot\sum_{\nu\vdash n-\mathfrak{v}}H_{Y}\left(\nu\right). \end{align} $$
$$ \begin{align} \mathbb{E}_{n}^{\mathrm{emb}}\left(Y\right)=\left(\frac{1}{2}+O\left(n^{-1}\right)\right)n^{\chi\left(Y\right)}\cdot\sum_{\nu\vdash n-\mathfrak{v}}H_{Y}\left(\nu\right). \end{align} $$
Next, our analysis shows that by considering, as above, families of YDs
![]() $\left \{ \nu \left (n\right )\right \} _{n\ge n_{0}}$
, then for large enough n,
$\left \{ \nu \left (n\right )\right \} _{n\ge n_{0}}$
, then for large enough n,
![]() $H_{Y}\left (\nu \left (n\right )\right )$
is equal to a converging series
$H_{Y}\left (\nu \left (n\right )\right )$
is equal to a converging series
![]() $\sum _{j=-\infty }^{K}\beta _{j}n^{j}$
, with
$\sum _{j=-\infty }^{K}\beta _{j}n^{j}$
, with
![]() $K=K\left (Y,\nu \right )$
some integer. Section 5.8 then shows that, for any given M, there is finite set of families
$K=K\left (Y,\nu \right )$
some integer. Section 5.8 then shows that, for any given M, there is finite set of families
![]() $\nu \left (n\right )$
, with
$\nu \left (n\right )$
, with
![]() $b_{\nu }$
and
$b_{\nu }$
and
![]() $b_{\check {\nu }}$
bounded, such that all remaining summands in
$b_{\check {\nu }}$
bounded, such that all remaining summands in
![]() $\sum _{\nu \vdash n-\mathfrak {v}}H_{Y}\left (\nu \right )$
outside these families contribute jointly
$\sum _{\nu \vdash n-\mathfrak {v}}H_{Y}\left (\nu \right )$
outside these families contribute jointly
![]() $O\left (n^{-M}\right )$
– this is analogous to Proposition 4.5. Because every tiled surface admits finite resolutions as in Section 2.3, this quickly leads to the proof of Theorem 1.1 in Section 6.
$O\left (n^{-M}\right )$
– this is analogous to Proposition 4.5. Because every tiled surface admits finite resolutions as in Section 2.3, this quickly leads to the proof of Theorem 1.1 in Section 6.
In fact, the analysis so far could have been carried out with graphs (core graphs à la Stallings) rather than with tiled surfaces. The importance of tiled surfaces and, moreover, of (strongly) boundary reduced tiled surfaces, is in our ability to determine the order of magnitude of
![]() $H_{Y}\left (\nu \right )$
. Our analysis here culminates in Proposition 5.21 and Section 5.9, from which it follows that when Y is boundary reduced,
$H_{Y}\left (\nu \right )$
. Our analysis here culminates in Proposition 5.21 and Section 5.9, from which it follows that when Y is boundary reduced,
as
![]() $n\to \infty ,$
and when Y is strongly boundary reduced,
$n\to \infty ,$
and when Y is strongly boundary reduced,
 $$ \begin{align} H_{Y}\left(\nu\left(n\right)\right)=\frac{1}{d_{\nu}^{~2}}\left(1+O\left(\frac{1}{n}\right)\right). \end{align} $$
$$ \begin{align} H_{Y}\left(\nu\left(n\right)\right)=\frac{1}{d_{\nu}^{~2}}\left(1+O\left(\frac{1}{n}\right)\right). \end{align} $$
This shows that the analysis of the zeta function in equation (5.1) can be viewed as a special case of our results. Indeed, when
![]() $Y=Y_{\emptyset }$
is the empty tiled surface (which is, in particular, strongly boundary reduced), equation (5.2) together with equation (5.4) yields that
$Y=Y_{\emptyset }$
is the empty tiled surface (which is, in particular, strongly boundary reduced), equation (5.2) together with equation (5.4) yields that
 $$\begin{align*}\left|\mathbb{X}_{n}\right|=\left|\mathbb{X}_{n}\right|\cdot\mathbb{E}_{n}^{\mathrm{emb}}\left(Y_{\emptyset}\right)=\left(n!\right)^{3}\cdot\sum_{\nu\vdash n}H_{Y_{\emptyset}}\left(\nu\right)=\left(n!\right)^{3}\cdot\sum_{\nu\vdash n}\frac{1}{d_{\nu}^{~2}}\left(1+O\left(\frac{1}{n}\right)\right). \end{align*}$$
$$\begin{align*}\left|\mathbb{X}_{n}\right|=\left|\mathbb{X}_{n}\right|\cdot\mathbb{E}_{n}^{\mathrm{emb}}\left(Y_{\emptyset}\right)=\left(n!\right)^{3}\cdot\sum_{\nu\vdash n}H_{Y_{\emptyset}}\left(\nu\right)=\left(n!\right)^{3}\cdot\sum_{\nu\vdash n}\frac{1}{d_{\nu}^{~2}}\left(1+O\left(\frac{1}{n}\right)\right). \end{align*}$$
What we achieve here is the extension of this result to general strongly boundary reduced tiled surfaces, with an extra factor of
![]() $n^{\chi \left (Y\right )}$
appearing. If Y is merely boundary reduced, we obtain the same result up to multiplicative constants.
$n^{\chi \left (Y\right )}$
appearing. If Y is merely boundary reduced, we obtain the same result up to multiplicative constants.
A remark about composing permutations
A technical but important remark is due. The bijection
 $$ \begin{align*} \phi & \mapsto X_{\phi}\\ \mathrm{Hom}(\Gamma,S_{n}) & \to\{\text{degree-\(n\) covers of \(\Sigma_{2}\)} \} \end{align*} $$
$$ \begin{align*} \phi & \mapsto X_{\phi}\\ \mathrm{Hom}(\Gamma,S_{n}) & \to\{\text{degree-\(n\) covers of \(\Sigma_{2}\)} \} \end{align*} $$
described previously involves the version of
![]() $S_{n}$
where permutations are composed with the left-most permutation acting first. On the other hand, since in the rest of the paper, we work with permutations in detail and specifically with the representation theory of
$S_{n}$
where permutations are composed with the left-most permutation acting first. On the other hand, since in the rest of the paper, we work with permutations in detail and specifically with the representation theory of
![]() $S_{n}$
, it is more standard to view permutations as functions from
$S_{n}$
, it is more standard to view permutations as functions from
![]() $[n]$
to
$[n]$
to
![]() $[n]$
and hence to multiply according to composition of functions (functions acting from the left). So in the rest of the paper, permutations will be composed with the right-most permutation acting first. These two versions of
$[n]$
and hence to multiply according to composition of functions (functions acting from the left). So in the rest of the paper, permutations will be composed with the right-most permutation acting first. These two versions of
![]() $S_{n}$
are isomorphic, of course, and one isomorphism is given by
$S_{n}$
are isomorphic, of course, and one isomorphism is given by
![]() $\mathrm {inv}\colon S_{n}\to S_{n}$
defined by
$\mathrm {inv}\colon S_{n}\to S_{n}$
defined by
![]() $\sigma \mapsto \sigma ^{-1}$
.
$\sigma \mapsto \sigma ^{-1}$
.
Accordingly, by postmultiplication with
![]() $\mathrm {inv}$
, we turn a homomorphism
$\mathrm {inv}$
, we turn a homomorphism
into a homomorphism
The homomorphism
![]() $\overline {\phi }$
satisfies
$\overline {\phi }$
satisfies
![]() $\overline {\phi }\left (\gamma \right )=\phi \left (\gamma \right )^{-1}$
for every
$\overline {\phi }\left (\gamma \right )=\phi \left (\gamma \right )^{-1}$
for every
![]() $\gamma \in \Gamma _{2}$
. In particular, with composition of permutations from right to left, the four permutations
$\gamma \in \Gamma _{2}$
. In particular, with composition of permutations from right to left, the four permutations
![]() $\phi \left (a\right ),\phi \left (b\right ),\phi \left (c\right ),\phi \left (d\right )\in S_{n}$
satisfy
$\phi \left (a\right ),\phi \left (b\right ),\phi \left (c\right ),\phi \left (d\right )\in S_{n}$
satisfy
or, equivalently (taking the inverse of the resulting permutation),
This means that the word
![]() $\left [d^{-1},c^{-1}\right ]\left [b^{-1},a^{-1}\right ]$
will appear below at several points. Note that the image of
$\left [d^{-1},c^{-1}\right ]\left [b^{-1},a^{-1}\right ]$
will appear below at several points. Note that the image of
![]() $\gamma \in \Gamma $
under
$\gamma \in \Gamma $
under
![]() $\overline {\phi }$
is the inverse of
$\overline {\phi }$
is the inverse of
![]() $\phi \left (\gamma \right )$
. But since a permutation and its inverse have the same cycle-structure in
$\phi \left (\gamma \right )$
. But since a permutation and its inverse have the same cycle-structure in
![]() $S_{n}$
, this does not affect the statistics we study in this paper.
$S_{n}$
, this does not affect the statistics we study in this paper.
5.2 Tiled surfaces and cosets
We assume that Y is a compact tiled surface. In this section, we assume
![]() $n\in \mathbf {N}$
with
$n\in \mathbf {N}$
with
![]() $n\geq \mathfrak {v}$
. We fix an arbitrary bijection
$n\geq \mathfrak {v}$
. We fix an arbitrary bijection
![]() $\mathcal {J}:Y^{(0)}\to [\mathfrak {v}]$
and view
$\mathcal {J}:Y^{(0)}\to [\mathfrak {v}]$
and view
![]() $(Y,\mathcal {J})$
as fixed in this
$(Y,\mathcal {J})$
as fixed in this
![]() $\S $
5. We modify
$\S $
5. We modify
![]() $\mathcal {J}$
slightly for technical reasonsFootnote
13
by letting
$\mathcal {J}$
slightly for technical reasonsFootnote
13
by letting
Then
![]() $(Y,\mathcal {J}_{n})$
is a vertex-labeled tiled surface for each n. We are interested in the quantity
$(Y,\mathcal {J}_{n})$
is a vertex-labeled tiled surface for each n. We are interested in the quantity
![]() $\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
, but because the uniform measure on
$\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
, but because the uniform measure on
![]() $\mathbb {X}_{n}$
is invariant under conjugation by
$\mathbb {X}_{n}$
is invariant under conjugation by
![]() $S_{n}$
and
$S_{n}$
and
![]() $S_{n}$
acts transitively on ordered tuples of size
$S_{n}$
acts transitively on ordered tuples of size
![]() $\mathfrak {v}$
in
$\mathfrak {v}$
in
![]() $[n]$
, we have
$[n]$
, we have
where
(Recall from
![]() $\S \S $
2.2 that the vertices of
$\S \S $
2.2 that the vertices of
![]() $X_{\phi }$
are labeled by
$X_{\phi }$
are labeled by
![]() $[n]$
. Also, recall that an embedding
$[n]$
. Also, recall that an embedding
inducing
![]() $\mathcal {J}_{n}$
, if it exists, is unique.) Hence, we are interested in the size of the set
$\mathcal {J}_{n}$
, if it exists, is unique.) Hence, we are interested in the size of the set
![]() $\mathbb {X}_{n}(Y,\mathcal {J}_{n})$
. Henceforth, we use the map
$\mathbb {X}_{n}(Y,\mathcal {J}_{n})$
. Henceforth, we use the map
![]() $\mathcal {J}_{n}$
and the previous labelings of the vertices of
$\mathcal {J}_{n}$
and the previous labelings of the vertices of
![]() $X_{\phi }$
to identify the vertex sets of Y and
$X_{\phi }$
to identify the vertex sets of Y and
![]() $X_{\phi }$
with subsets of
$X_{\phi }$
with subsets of
![]() $\mathbf {N}$
.
$\mathbf {N}$
.
For each letter
![]() $f\in \{a,b,c,d\}$
, let
$f\in \{a,b,c,d\}$
, let
![]() $\mathcal {V}_{f}^{-}=\mathcal {V}_{f}^{-}(Y)\subset [n-\mathfrak {v}+1,n]$
be the subset of vertices of Y with outgoing f-labeled edges, and
$\mathcal {V}_{f}^{-}=\mathcal {V}_{f}^{-}(Y)\subset [n-\mathfrak {v}+1,n]$
be the subset of vertices of Y with outgoing f-labeled edges, and
![]() $\mathcal {V}_{f}^{+}\subset [n-\mathfrak {v}+1,n]$
those vertices of Y with incoming f-labeled edges. Note that
$\mathcal {V}_{f}^{+}\subset [n-\mathfrak {v}+1,n]$
those vertices of Y with incoming f-labeled edges. Note that
![]() $\mathfrak {e}_{f}=|\mathcal {V}_{f}^{\pm }|$
. We let
$\mathfrak {e}_{f}=|\mathcal {V}_{f}^{\pm }|$
. We let
![]() $G_{f}$
denote the subgroup of
$G_{f}$
denote the subgroup of
![]() $S_{n}$
that fixes
$S_{n}$
that fixes
![]() $\mathcal {V}_{f}^{-}$
and write
$\mathcal {V}_{f}^{-}$
and write
For each
![]() $f\in \{a,b,c,d\}$
, we let
$f\in \{a,b,c,d\}$
, we let
![]() $g_{f}^{0}\in S_{n}$
be a fixed element with the property that for every pair of vertices
$g_{f}^{0}\in S_{n}$
be a fixed element with the property that for every pair of vertices
![]() $i,j$
of Y (so
$i,j$
of Y (so
![]() $i,j\in [n-\mathfrak {v}+1,n]$
) with a directed f-labeled edge from i to j, we have
$i,j\in [n-\mathfrak {v}+1,n]$
) with a directed f-labeled edge from i to j, we have
![]() $g_{f}^{0}(i)=j$
. Recall the notation
$g_{f}^{0}(i)=j$
. Recall the notation
![]() $S^{\prime }_{\mathfrak {v}}$
for the subgroup of
$S^{\prime }_{\mathfrak {v}}$
for the subgroup of
![]() $S_{n}$
fixing
$S_{n}$
fixing
![]() $[n-\mathfrak {v}]$
pointwise. We choose the
$[n-\mathfrak {v}]$
pointwise. We choose the
![]() $g_{f}^{0}$
consistently for each n in the sense that
$g_{f}^{0}$
consistently for each n in the sense that
![]() $g_{f}^{0}$
is chosen when
$g_{f}^{0}$
is chosen when
![]() $n=\mathfrak {v}$
and then defined for arbitrary n by the isomorphisms
$n=\mathfrak {v}$
and then defined for arbitrary n by the isomorphisms
![]() $S_{\mathfrak {v}}\cong S^{\prime }_{\mathfrak {v}}$
given in equation (4.10). We write
$S_{\mathfrak {v}}\cong S^{\prime }_{\mathfrak {v}}$
given in equation (4.10). We write
![]() $g^{0}\stackrel {\mathrm {def}}{=}(g_{a}^{0},g_{b}^{0},g_{c}^{0},g_{d}^{0})$
. Notice that
$g^{0}\stackrel {\mathrm {def}}{=}(g_{a}^{0},g_{b}^{0},g_{c}^{0},g_{d}^{0})$
. Notice that
![]() $g_{f}^{0}(\mathcal {V}_{f}^{-})=\mathcal {V}_{f}^{+}$
.
$g_{f}^{0}(\mathcal {V}_{f}^{-})=\mathcal {V}_{f}^{+}$
.
In the rest of the paper, whenever we write an integral over a group, it is performed with respect to the uniform probability measure. Let
 $$ \begin{align} \Theta_{\lambda}\left(Y,\mathcal{J}_{n}\right)\stackrel{\mathrm{def}}{=}\int_{h_{f}\in G_{f}}\chi_{\lambda}\left(\left[\left(g_{d}^{0}h_{d}\right)^{-1},\left(g_{c}^{0}h_{c}\right)^{-1}\right]\left[\left(g_{b}^{0}h_{b}\right)^{-1},\left(g_{a}^{0}h_{a}\right)^{-1}\right]\right), \end{align} $$
$$ \begin{align} \Theta_{\lambda}\left(Y,\mathcal{J}_{n}\right)\stackrel{\mathrm{def}}{=}\int_{h_{f}\in G_{f}}\chi_{\lambda}\left(\left[\left(g_{d}^{0}h_{d}\right)^{-1},\left(g_{c}^{0}h_{c}\right)^{-1}\right]\left[\left(g_{b}^{0}h_{b}\right)^{-1},\left(g_{a}^{0}h_{a}\right)^{-1}\right]\right), \end{align} $$
where
![]() $\chi _{\lambda }$
is the character of
$\chi _{\lambda }$
is the character of
![]() $S_{n}$
corresponding to the irreducible representation
$S_{n}$
corresponding to the irreducible representation
![]() $V^{\lambda }$
. We will calculate the size of
$V^{\lambda }$
. We will calculate the size of
![]() $\mathbb {X}_{n}(Y,\mathcal {J}_{n})$
using the following result.
$\mathbb {X}_{n}(Y,\mathcal {J}_{n})$
using the following result.
Proposition 5.1. We have
 $$\begin{align*}|\mathbb{X}_{n}(Y,\mathcal{J}_{n})|=\frac{\prod_{f\in a,b,c,d}(n-\mathfrak{e}_{f})!}{n!}\sum_{\substack{\lambda\vdash n} }d_{\lambda}\Theta_{\lambda}\left(Y,\mathcal{J}_{n}\right). \end{align*}$$
$$\begin{align*}|\mathbb{X}_{n}(Y,\mathcal{J}_{n})|=\frac{\prod_{f\in a,b,c,d}(n-\mathfrak{e}_{f})!}{n!}\sum_{\substack{\lambda\vdash n} }d_{\lambda}\Theta_{\lambda}\left(Y,\mathcal{J}_{n}\right). \end{align*}$$
Proof. We begin by observing that with
![]() $g_{a}^{0},g_{b}^{0},g_{c}^{0},g_{d}^{0}$
as above, the map
$g_{a}^{0},g_{b}^{0},g_{c}^{0},g_{d}^{0}$
as above, the map
restricts to a bijection between
![]() $\mathbb {X}_{n}(Y,\mathcal {J}_{n})$
and the tuples
$\mathbb {X}_{n}(Y,\mathcal {J}_{n})$
and the tuples
![]() $(g_{a},g_{b},g_{c},g_{d})\in S_{n}^{4}$
such that both
$(g_{a},g_{b},g_{c},g_{d})\in S_{n}^{4}$
such that both
![]() $(g_{a},g_{b},g_{c},g_{d})$
is in the coset
$(g_{a},g_{b},g_{c},g_{d})$
is in the coset
![]() $(g_{a}^{0},g_{b}^{0},g_{c}^{0},g_{d}^{0})G$
and
$(g_{a}^{0},g_{b}^{0},g_{c}^{0},g_{d}^{0})G$
and
![]() $\left [g_{d}^{-1},g_{c}^{-1}\right ]\left [g_{b}^{-1},g_{a}^{-1}\right ]=1$
.
$\left [g_{d}^{-1},g_{c}^{-1}\right ]\left [g_{b}^{-1},g_{a}^{-1}\right ]=1$
.
Now, let
 $$\begin{align*}I=\int_{h_{f}\in G_{f}}\mathbf{1}\left\{ \left[\left(g_{d}^{0}h_{d}\right)^{-1},\left(g_{c}^{0}h_{c}\right)^{-1}\right]\left[\left(g_{b}^{0}h_{b}\right)^{-1},\left(g_{a}^{0}h_{a}\right)^{-1}\right]=1\right\}. \end{align*}$$
$$\begin{align*}I=\int_{h_{f}\in G_{f}}\mathbf{1}\left\{ \left[\left(g_{d}^{0}h_{d}\right)^{-1},\left(g_{c}^{0}h_{c}\right)^{-1}\right]\left[\left(g_{b}^{0}h_{b}\right)^{-1},\left(g_{a}^{0}h_{a}\right)^{-1}\right]=1\right\}. \end{align*}$$
Then it is immediate that
 $$\begin{align*}|\mathbb{X}_{n}(Y,\mathcal{J}_{n})|=|G|\cdot I=\prod_{f\in a,b,c,d}(n-\mathfrak{e}_{f})!\cdot I. \end{align*}$$
$$\begin{align*}|\mathbb{X}_{n}(Y,\mathcal{J}_{n})|=|G|\cdot I=\prod_{f\in a,b,c,d}(n-\mathfrak{e}_{f})!\cdot I. \end{align*}$$
Finally, use Schur orthogonality to write, as functions on
![]() $S_{n}$
,
$S_{n}$
,
 $$\begin{align*}\mathbf{1}\{g=1\}=\frac{1}{n!}\sum_{\lambda\vdash n}d_{\lambda}\chi_{\lambda}(g), \end{align*}$$
$$\begin{align*}\mathbf{1}\{g=1\}=\frac{1}{n!}\sum_{\lambda\vdash n}d_{\lambda}\chi_{\lambda}(g), \end{align*}$$
insert this into the definition of I and interchange summation and integration to complete the proof.
In the next sections, we will focus our attention on the quantities
![]() $\Theta _{\lambda }(Y,\mathcal {J}_{n})$
.
$\Theta _{\lambda }(Y,\mathcal {J}_{n})$
.
5.3 Construction of auxiliary permutations
In order to obtain an expression for
![]() $\Theta _{\lambda }(Y,\mathcal {J}_{n})$
that leads to good analytic estimates, we introduce further maps
$\Theta _{\lambda }(Y,\mathcal {J}_{n})$
that leads to good analytic estimates, we introduce further maps
for each
![]() $f\in \{a,b,c,d\}$
. These should be thought of as orderings of the vertices with indices from
$f\in \{a,b,c,d\}$
. These should be thought of as orderings of the vertices with indices from
![]() $[n-\mathfrak {v}+1,n]$
, other than the one fixed by
$[n-\mathfrak {v}+1,n]$
, other than the one fixed by
![]() $\mathcal {J}_{n}$
. We will first describe the construction of these maps and then note their properties.
$\mathcal {J}_{n}$
. We will first describe the construction of these maps and then note their properties.
Recall from
![]() $\S \S $
2.1 that
$\S \S $
2.1 that
![]() $Y^{(1)}$
carries the structure of a ribbon graph and this gives us a way to thicken it up to an oriented surface with boundary with an embedded copy of the graph
$Y^{(1)}$
carries the structure of a ribbon graph and this gives us a way to thicken it up to an oriented surface with boundary with an embedded copy of the graph
![]() $Y^{(1)}$
. Also recall, from
$Y^{(1)}$
. Also recall, from
![]() $\S \S $
2.1, that we constructed a larger object
$\S \S $
2.1, that we constructed a larger object
![]() $Y_{+}$
by adding extra hanging half-edges to the vertices. The one-skeleton
$Y_{+}$
by adding extra hanging half-edges to the vertices. The one-skeleton
![]() $Y_{+}^{(1)}$
also has a cyclic ordering of the half-edges (hanging or otherwise) at each vertex and so
$Y_{+}^{(1)}$
also has a cyclic ordering of the half-edges (hanging or otherwise) at each vertex and so
![]() $Y_{+}^{(1)}$
can be thickened up to a ‘cut’ ribbon graph with some half-ribbon edges. In this picture, every edge is thickened to a thin rectangle, and every hanging half-edge is thickened up to a thin half-rectangle.
$Y_{+}^{(1)}$
can be thickened up to a ‘cut’ ribbon graph with some half-ribbon edges. In this picture, every edge is thickened to a thin rectangle, and every hanging half-edge is thickened up to a thin half-rectangle.

Figure 5.1 The figure on the left shows a local picture of a vertex v in the thick version of some tiled surface with hanging half-edges
![]() $Y_{+}$
, and the correspondence between the
$Y_{+}$
, and the correspondence between the
![]() $16$
maps
$16$
maps
![]() $\sigma _{f}^{\pm },\tau _{f}^{\pm }$
and the
$\sigma _{f}^{\pm },\tau _{f}^{\pm }$
and the
![]() $16$
sides of half-edges incident to v. The figure on the right illustrates how numbering of octagons, of exposed sides of full-edges and of hanging half-edges determines the values of
$16$
sides of half-edges incident to v. The figure on the right illustrates how numbering of octagons, of exposed sides of full-edges and of hanging half-edges determines the values of
![]() $\sigma _{f}^{\pm },\tau _{f}^{\pm }$
at v. In this figure, continuous black lines mark pieces of the boundary of the thick version of
$\sigma _{f}^{\pm },\tau _{f}^{\pm }$
at v. In this figure, continuous black lines mark pieces of the boundary of the thick version of
![]() $Y_{+}$
, whereas dotted black lines mark boundary pieces of
$Y_{+}$
, whereas dotted black lines mark boundary pieces of
![]() $Y_{+}^{\left (1\right )}$
to which ocagons are glued in
$Y_{+}^{\left (1\right )}$
to which ocagons are glued in
![]() $Y_{+}$
. The vertex v in the center of the figure is incident with two octagons, numbered
$Y_{+}$
. The vertex v in the center of the figure is incident with two octagons, numbered
![]() $9$
and
$9$
and
![]() $10$
; with three hanging half-edges numbered
$10$
; with three hanging half-edges numbered
![]() $3$
(outgoing b and incoming d) and
$3$
(outgoing b and incoming d) and
![]() $4$
(incoming c) and with five half-edges belonging to full-edges, with a total of six exposed sides, the numbering of which is described in the figure. The images of this vertex under
$4$
(incoming c) and with five half-edges belonging to full-edges, with a total of six exposed sides, the numbering of which is described in the figure. The images of this vertex under
![]() $\sigma _{f}^{\pm }$
and
$\sigma _{f}^{\pm }$
and
![]() $\tau _{f}^{\pm }$
are listed in page 53.
$\tau _{f}^{\pm }$
are listed in page 53.
So every vertex of Y has eight incident half-edges (hanging or otherwise), and each of these half-edges has two sides. The
![]() $16$
maps
$16$
maps
![]() $\left \{ \sigma _{f}^{\pm },\tau _{f}^{\pm }\right \} _{f\in \left \{ a,b,c,d\right \} }$
correspond to these
$\left \{ \sigma _{f}^{\pm },\tau _{f}^{\pm }\right \} _{f\in \left \{ a,b,c,d\right \} }$
correspond to these
![]() $16$
sides of half-edges at each vertex:
$16$
sides of half-edges at each vertex:
![]() $\sigma _{f}^{-}$
and
$\sigma _{f}^{-}$
and
![]() $\tau _{f}^{-}$
correspond to the sides of the outgoing f-half-edge, while
$\tau _{f}^{-}$
correspond to the sides of the outgoing f-half-edge, while
![]() $\sigma _{f}^{+}$
and
$\sigma _{f}^{+}$
and
![]() $\tau _{f}^{+}$
correspond to the sides of the incoming f-half-edge. Finally,
$\tau _{f}^{+}$
correspond to the sides of the incoming f-half-edge. Finally,
![]() $\sigma _{f}^{\pm }$
correspond to the left side of the outgoing and incoming f-half-edges, while
$\sigma _{f}^{\pm }$
correspond to the left side of the outgoing and incoming f-half-edges, while
![]() $\tau _{f}^{\pm }$
correspond to the right side of these f-half-edges, where ‘left’ and ‘right’ here are with respect to the direction of the half-edge. (We keep our convention from
$\tau _{f}^{\pm }$
correspond to the right side of these f-half-edges, where ‘left’ and ‘right’ here are with respect to the direction of the half-edge. (We keep our convention from
![]() $\S \S $
2.1 that boundary cycles are oriented so that the object lies to the right. In particular, the boundary of an octagon is
$\S \S $
2.1 that boundary cycles are oriented so that the object lies to the right. In particular, the boundary of an octagon is
![]() $\left [a,b\right ]\left [c,d\right ]$
when followed in counterclockwise direction.) See the left-hand side of Figure 5.1.
$\left [a,b\right ]\left [c,d\right ]$
when followed in counterclockwise direction.) See the left-hand side of Figure 5.1.
The definition of
![]() $\sigma _{f}^{\pm },\tau _{f}^{\pm }$
is based on the following choices:
$\sigma _{f}^{\pm },\tau _{f}^{\pm }$
is based on the following choices:
-
• Numbering octagons: Number the
 $\mathfrak {f}$
octagons of Y by distinct elements in
$\mathfrak {f}$
octagons of Y by distinct elements in
 $[\mathfrak {v}-\mathfrak {f}+1,\mathfrak {v}]$
.
$[\mathfrak {v}-\mathfrak {f}+1,\mathfrak {v}]$
. -
• Numbering full edges at
 $\partial Y$
: For every
$\partial Y$
: For every
 $f\in \left \{ a,b,c,d\right \} $
, there are
$f\in \left \{ a,b,c,d\right \} $
, there are
 $\mathfrak {e}_{f}-\mathfrak {f}$
left-sides of full f-edges that belong to the boundary
$\mathfrak {e}_{f}-\mathfrak {f}$
left-sides of full f-edges that belong to the boundary
 $\partial Y$
(as compared with
$\partial Y$
(as compared with
 $\mathfrak {f}$
left sides of full f-edges that meet octagons of Y). Number them by distinct values in
$\mathfrak {f}$
left sides of full f-edges that meet octagons of Y). Number them by distinct values in
 $\left [\mathfrak {v}-\mathfrak {e}_{f}+1,\mathfrak {v}-\mathfrak {f}\right ]$
. Similarly, number the
$\left [\mathfrak {v}-\mathfrak {e}_{f}+1,\mathfrak {v}-\mathfrak {f}\right ]$
. Similarly, number the
 $\mathfrak {e}_{f}-\mathfrak {f}$
right sides of full f-edges belonging to
$\mathfrak {e}_{f}-\mathfrak {f}$
right sides of full f-edges belonging to
 $\partial Y$
by distinct values in the same range
$\partial Y$
by distinct values in the same range
 $\left [\mathfrak {v}-\mathfrak {e}_{f}+1,\mathfrak {v}-\mathfrak {f}\right ]$
.
$\left [\mathfrak {v}-\mathfrak {e}_{f}+1,\mathfrak {v}-\mathfrak {f}\right ]$
. -
• Numbering hanging half-edges: For each
 $f\in \{a,b,c,d\}$
, there are precisely
$f\in \{a,b,c,d\}$
, there are precisely
 $\mathfrak {v}-\mathfrak {e}_{f}$
outgoing f-labeled hanging half-edges, and we number them by distinct numbers in
$\mathfrak {v}-\mathfrak {e}_{f}$
outgoing f-labeled hanging half-edges, and we number them by distinct numbers in
 $[\mathfrak {v}-\mathfrak {e}_{f}]$
. Using the matching determined by
$[\mathfrak {v}-\mathfrak {e}_{f}]$
. Using the matching determined by
 $g_{f}^{0}$
between outgoing and incoming f-labeled hanging half-edges, the numbering we have just chosen induces a numbering also of the incoming f-labeled hanging half-edges by numbers in
$g_{f}^{0}$
between outgoing and incoming f-labeled hanging half-edges, the numbering we have just chosen induces a numbering also of the incoming f-labeled hanging half-edges by numbers in
 $[\mathfrak {v}-\mathfrak {e}_{f}]$
.
$[\mathfrak {v}-\mathfrak {e}_{f}]$
.
We now define
![]() $\sigma _{f}^{\pm }$
and
$\sigma _{f}^{\pm }$
and
![]() $\tau _{f}^{\pm }$
as follows. For every vertex v of Y and a side of an incident half-edge (hanging or otherwise), we need to determine the image of v under the permutation among
$\tau _{f}^{\pm }$
as follows. For every vertex v of Y and a side of an incident half-edge (hanging or otherwise), we need to determine the image of v under the permutation among
![]() $\sigma _{f}^{\pm },\tau _{f}^{\pm }$
corresponding to this side-of-half-edge.
$\sigma _{f}^{\pm },\tau _{f}^{\pm }$
corresponding to this side-of-half-edge.
-
• If the half-edge is part of a full-edge of Y, then
-
– if the side in question meets an octagon numbered i, we map
 $v\mapsto n-\mathfrak {v}+i$
, and
$v\mapsto n-\mathfrak {v}+i$
, and -
– if the side in question belongs to
 $\partial Y$
and the full-edge is numbered j, map
$\partial Y$
and the full-edge is numbered j, map
 $v\mapsto n-\mathfrak {v}+j$
.
$v\mapsto n-\mathfrak {v}+j$
.
-
-
• If this is a hanging half-edge numbered k, we map
 $v\mapsto n-\mathfrak {v}+k$
.
$v\mapsto n-\mathfrak {v}+k$
.
This is illustrated in the right-hand side of Figure 5.1, which shows some vertex v of some tiled surface Y, and the numbering of incident octagons, of exposed sides of full-edges and of hanging half-edges. In that case, the images of v under
![]() $\sigma _{f}^{\pm }$
and
$\sigma _{f}^{\pm }$
and
![]() $\tau _{f}^{\pm }$
are the following:
$\tau _{f}^{\pm }$
are the following:
 $$\begin{align*}\begin{array}{cccc} \sigma_{a}^{-}\left(v\right)=n-\mathfrak{v}+9 & \sigma_{b}^{-}\left(v\right)=n-\mathfrak{v}+3 & \sigma_{c}^{-}\left(v\right)=n-\mathfrak{v}+6 & \sigma_{d}^{-}\left(v\right)=n-\mathfrak{v}+4\\ \sigma_{a}^{+}\left(v\right)=n-\mathfrak{v}+7 & \sigma_{b}^{+}\left(v\right)=n-\mathfrak{v}+5 & \sigma_{c}^{+}\left(v\right)=n-\mathfrak{v}+4 & \sigma_{d}^{+}\left(v\right)=n-\mathfrak{v}+3\\ \tau_{a}^{-}\left(v\right)=n-\mathfrak{v}+10 & \tau_{b}^{-}\left(v\right)=n-\mathfrak{v}+3 & \tau_{c}^{-}\left(v\right)=n-\mathfrak{v}+5 & \tau_{d}^{-}\left(v\right)=n-\mathfrak{v}+9\\ \tau_{a}^{+}\left(v\right)=n-\mathfrak{v}+3 & \tau_{b}^{+}\left(v\right)=n-\mathfrak{v}+10 & \tau_{c}^{+}\left(v\right)=n-\mathfrak{v}+4 & \tau_{d}^{+}\left(v\right)=n-\mathfrak{v}+3. \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{cccc} \sigma_{a}^{-}\left(v\right)=n-\mathfrak{v}+9 & \sigma_{b}^{-}\left(v\right)=n-\mathfrak{v}+3 & \sigma_{c}^{-}\left(v\right)=n-\mathfrak{v}+6 & \sigma_{d}^{-}\left(v\right)=n-\mathfrak{v}+4\\ \sigma_{a}^{+}\left(v\right)=n-\mathfrak{v}+7 & \sigma_{b}^{+}\left(v\right)=n-\mathfrak{v}+5 & \sigma_{c}^{+}\left(v\right)=n-\mathfrak{v}+4 & \sigma_{d}^{+}\left(v\right)=n-\mathfrak{v}+3\\ \tau_{a}^{-}\left(v\right)=n-\mathfrak{v}+10 & \tau_{b}^{-}\left(v\right)=n-\mathfrak{v}+3 & \tau_{c}^{-}\left(v\right)=n-\mathfrak{v}+5 & \tau_{d}^{-}\left(v\right)=n-\mathfrak{v}+9\\ \tau_{a}^{+}\left(v\right)=n-\mathfrak{v}+3 & \tau_{b}^{+}\left(v\right)=n-\mathfrak{v}+10 & \tau_{c}^{+}\left(v\right)=n-\mathfrak{v}+4 & \tau_{d}^{+}\left(v\right)=n-\mathfrak{v}+3. \end{array} \end{align*}$$
The following properties of the maps we defined are all evident from the construction.
Lemma 5.2. When the vertices of Y are identified with
![]() $\left [n-\mathfrak {v}+1,n\right ]$
according to
$\left [n-\mathfrak {v}+1,n\right ]$
according to
![]() $\mathcal {J}_{n}$
, the
$\mathcal {J}_{n}$
, the
![]() $16$
maps
$16$
maps
![]() $\sigma _{f}^{+},\sigma _{f}^{-},\tau _{f}^{+},\tau _{f}^{-}$
we defined indeed belong to
$\sigma _{f}^{+},\sigma _{f}^{-},\tau _{f}^{+},\tau _{f}^{-}$
we defined indeed belong to
![]() $S^{\prime }_{\mathfrak {v}}\subset S_{n}$
. Moreover, they satisfy the following properties:
$S^{\prime }_{\mathfrak {v}}\subset S_{n}$
. Moreover, they satisfy the following properties:
-
P1 For all
 $f\in \{a,b,c,d\}$
,
$f\in \{a,b,c,d\}$
,
 $\sigma _{f}^{\pm }(\mathcal {V}_{f}^{\pm })=\tau _{f}^{\pm }(\mathcal {V}_{f}^{\pm })=[n-\mathfrak {e}_{f}+1,n]$
.
$\sigma _{f}^{\pm }(\mathcal {V}_{f}^{\pm })=\tau _{f}^{\pm }(\mathcal {V}_{f}^{\pm })=[n-\mathfrak {e}_{f}+1,n]$
. -
P2 For all
 $f\in \{a,b,c,d\}$
,
$f\in \{a,b,c,d\}$
,
 $(\sigma _{f}^{+})^{-1}\sigma _{f}^{-}=(\tau _{f}^{+})^{-1}\tau _{f}^{-}=g_{f}^{0}$
.
$(\sigma _{f}^{+})^{-1}\sigma _{f}^{-}=(\tau _{f}^{+})^{-1}\tau _{f}^{-}=g_{f}^{0}$
. -
P3 For all
 $f\in \{a,b,c,d\}$
,
$f\in \{a,b,c,d\}$
,
 $\sigma _{f}^{\pm }\lvert _{[n]\backslash \mathcal {V}_{f}^{\pm }}=\tau _{f}^{\pm }\lvert _{[n]\backslash \mathcal {V}_{f}^{\pm }}.$
$\sigma _{f}^{\pm }\lvert _{[n]\backslash \mathcal {V}_{f}^{\pm }}=\tau _{f}^{\pm }\lvert _{[n]\backslash \mathcal {V}_{f}^{\pm }}.$
-
P4 Each of the following permutations fixes every element of
 $[n-\mathfrak {f}+1,n]$
:
$[n-\mathfrak {f}+1,n]$
:  $$\begin{align*}\sigma_{b}^{-}\left(\sigma_{a}^{+}\right)^{-1},\tau_{a}^{+}\left(\sigma_{b}^{+}\right)^{-1},\tau_{b}^{+}\left(\tau_{a}^{-}\right)^{-1},\sigma_{c}^{-}\left(\tau_{b}^{-}\right)^{-1},\sigma_{d}^{-}\left(\sigma_{c}^{+}\right)^{-1},\tau_{c}^{+}\left(\sigma_{d}^{+}\right)^{-1},\tau_{d}^{+}\left(\tau_{c}^{-}\right)^{-1},\sigma_{a}^{-}\left(\tau_{d}^{-}\right)^{-1}. \end{align*}$$
$$\begin{align*}\sigma_{b}^{-}\left(\sigma_{a}^{+}\right)^{-1},\tau_{a}^{+}\left(\sigma_{b}^{+}\right)^{-1},\tau_{b}^{+}\left(\tau_{a}^{-}\right)^{-1},\sigma_{c}^{-}\left(\tau_{b}^{-}\right)^{-1},\sigma_{d}^{-}\left(\sigma_{c}^{+}\right)^{-1},\tau_{c}^{+}\left(\sigma_{d}^{+}\right)^{-1},\tau_{d}^{+}\left(\tau_{c}^{-}\right)^{-1},\sigma_{a}^{-}\left(\tau_{d}^{-}\right)^{-1}. \end{align*}$$
-
P5 The permutations
 $\sigma _{f}^{\pm },\tau _{f}^{\pm }$
are the same for each n in the sense that they change with n via the fixed isomorphisms between
$\sigma _{f}^{\pm },\tau _{f}^{\pm }$
are the same for each n in the sense that they change with n via the fixed isomorphisms between
 $S_{\mathfrak {v}}$
and
$S_{\mathfrak {v}}$
and
 $S^{\prime }_{\mathfrak {v}}\leq S_{n}$
in equation (4.10).
$S^{\prime }_{\mathfrak {v}}\leq S_{n}$
in equation (4.10).
From now on, assume that we have fixed
![]() $\sigma _{f}^{\pm },\tau _{f}^{\pm }$
with properties P1–P5. We do this once and for all for every tiled surface Y (including the choice of
$\sigma _{f}^{\pm },\tau _{f}^{\pm }$
with properties P1–P5. We do this once and for all for every tiled surface Y (including the choice of
![]() $\mathcal {J}$
).
$\mathcal {J}$
).
5.4 Integrating over cosets
We briefly review some linear algebra. Recall that
![]() $\check {V}^{\lambda }$
is the vector space of complex linear functionals on
$\check {V}^{\lambda }$
is the vector space of complex linear functionals on
![]() $V^{\lambda }$
. If
$V^{\lambda }$
. If
![]() $V^{\lambda }$
has orthonormal basis
$V^{\lambda }$
has orthonormal basis
![]() $\{v_{i}\}$
, then
$\{v_{i}\}$
, then
![]() $\check {V}^{\lambda }$
has a dual basis
$\check {V}^{\lambda }$
has a dual basis
![]() $\{\check {v}_{i}\}$
defined by
$\{\check {v}_{i}\}$
defined by
![]() $\check {v}_{i}(v)\stackrel {\mathrm {def}}{=}\langle v,v_{i}\rangle .$
Requiring the
$\check {v}_{i}(v)\stackrel {\mathrm {def}}{=}\langle v,v_{i}\rangle .$
Requiring the
![]() $\check {v_{i}}$
to be orthonormal defines a Hermitian inner product on
$\check {v_{i}}$
to be orthonormal defines a Hermitian inner product on
![]() $\check {V}^{\lambda }$
. The action of
$\check {V}^{\lambda }$
. The action of
![]() $S_{n}$
on
$S_{n}$
on
![]() $\check {V}^{\lambda }$
is by
$\check {V}^{\lambda }$
is by
![]() $g[\phi ](v)\stackrel {\mathrm {def}}{=}\phi (g^{-1}v)$
. If
$g[\phi ](v)\stackrel {\mathrm {def}}{=}\phi (g^{-1}v)$
. If
![]() $A_{ji}\stackrel {\mathrm {def}}{=}\langle gv_{i},v_{j}\rangle $
so that g acts by the matrix
$A_{ji}\stackrel {\mathrm {def}}{=}\langle gv_{i},v_{j}\rangle $
so that g acts by the matrix
![]() $A=(A_{ij})$
on
$A=(A_{ij})$
on
![]() $V^{\lambda }$
in this basis, then
$V^{\lambda }$
in this basis, then
 $$\begin{align*}g[\check{v}_{i}](v_{k})=\check{v}_{i}\left[\sum_{\ell}(A^{-1})_{\ell k}v_{\ell}\right]=\left(A^{-1}\right)_{ik}, \end{align*}$$
$$\begin{align*}g[\check{v}_{i}](v_{k})=\check{v}_{i}\left[\sum_{\ell}(A^{-1})_{\ell k}v_{\ell}\right]=\left(A^{-1}\right)_{ik}, \end{align*}$$
so
We now give some motivation for what follows. We wish to integrate the function
over a coset in
![]() $S_{n}^{4}$
. This function can clearly be written as a finite sum of finite products of matrix coefficients of the
$S_{n}^{4}$
. This function can clearly be written as a finite sum of finite products of matrix coefficients of the
![]() $g_{f}$
and
$g_{f}$
and
![]() $g_{f}^{-1}$
in
$g_{f}^{-1}$
in
![]() $V^{\lambda }$
. However, this is not the route we wish to take. Instead, following a philosophy similar to that used in the development of the Weingarten calculus (see, for example, [Reference Collins and ŚniadyCŚ06]), we aim to write this function more holistically as (what is essentially) one single matrix coefficient in one single representation. To this end, consider the vector space
$V^{\lambda }$
. However, this is not the route we wish to take. Instead, following a philosophy similar to that used in the development of the Weingarten calculus (see, for example, [Reference Collins and ŚniadyCŚ06]), we aim to write this function more holistically as (what is essentially) one single matrix coefficient in one single representation. To this end, consider the vector space
as a unitary representation of
![]() $S_{n}^{4}.$
We write an element of
$S_{n}^{4}.$
We write an element of
![]() $S_{n}^{4}$
as
$S_{n}^{4}$
as
![]() $(g_{a},g_{b},g_{c},g_{d})$
and the subscripts above indicate which coordinate acts on which factor.
$(g_{a},g_{b},g_{c},g_{d})$
and the subscripts above indicate which coordinate acts on which factor.
Let
![]() $B_{\lambda }\in \mathrm {End}(W^{\lambda })$
be defined via matrix coefficients by the formula
$B_{\lambda }\in \mathrm {End}(W^{\lambda })$
be defined via matrix coefficients by the formula
 $$ \begin{align} & \left\langle B_{\lambda}\left(v_{1}\otimes\check{v}_{2}\otimes v_{3}\otimes\check{v_{4}}\otimes v_{5}\otimes\check{v}_{6}\otimes v_{7}\otimes\check{v_{8}}\right),w_{1}\otimes\check{w}_{2}\otimes w_{3}\otimes\check{w_{4}}\otimes w_{5}\otimes\check{w}_{6}\otimes w_{7}\otimes\check{w_{8}}\right\rangle \stackrel{\mathrm{def}}{=}\nonumber \\ & ~~~~~~~~~\left\langle v_{1},w_{3}\right\rangle \left\langle v_{3},v_{2}\right\rangle \left\langle w_{2},v_{4}\right\rangle \left\langle w_{4},w_{5}\right\rangle \left\langle v_{5},w_{7}\right\rangle \left\langle v_{7},v_{6}\right\rangle \left\langle w_{6},v_{8}\right\rangle \left\langle w_{8},w_{1}\right\rangle. \end{align} $$
$$ \begin{align} & \left\langle B_{\lambda}\left(v_{1}\otimes\check{v}_{2}\otimes v_{3}\otimes\check{v_{4}}\otimes v_{5}\otimes\check{v}_{6}\otimes v_{7}\otimes\check{v_{8}}\right),w_{1}\otimes\check{w}_{2}\otimes w_{3}\otimes\check{w_{4}}\otimes w_{5}\otimes\check{w}_{6}\otimes w_{7}\otimes\check{w_{8}}\right\rangle \stackrel{\mathrm{def}}{=}\nonumber \\ & ~~~~~~~~~\left\langle v_{1},w_{3}\right\rangle \left\langle v_{3},v_{2}\right\rangle \left\langle w_{2},v_{4}\right\rangle \left\langle w_{4},w_{5}\right\rangle \left\langle v_{5},w_{7}\right\rangle \left\langle v_{7},v_{6}\right\rangle \left\langle w_{6},v_{8}\right\rangle \left\langle w_{8},w_{1}\right\rangle. \end{align} $$
Remark 5.3. One could also order the tensor factors in equation (5.8) according to the order specified by the word
![]() $\left [a,b\right ]\left [c,d\right ]$
, namely
$\left [a,b\right ]\left [c,d\right ]$
, namely
![]() $V_{a}^{\lambda }\otimes V_{b}^{\lambda }\check {\otimes V_{a}^{\lambda }}\otimes \check {V_{b}^{\lambda }}\otimes V_{c}^{\lambda }\otimes V_{d}^{\lambda }\otimes \check {V_{c}^{\lambda }}\otimes \check {V_{d}^{\lambda }}$
. In this case, the definition of
$V_{a}^{\lambda }\otimes V_{b}^{\lambda }\check {\otimes V_{a}^{\lambda }}\otimes \check {V_{b}^{\lambda }}\otimes V_{c}^{\lambda }\otimes V_{d}^{\lambda }\otimes \check {V_{c}^{\lambda }}\otimes \check {V_{d}^{\lambda }}$
. In this case, the definition of
![]() $B_{\lambda }$
would be more natural:
$B_{\lambda }$
would be more natural:
![]() $\left \langle v_{1},w_{2}\right \rangle \left \langle v_{2},v_{3}\right \rangle \left \langle w_{3},v_{4}\right \rangle \left \langle w_{4},w_{5}\right \rangle \left \langle v_{5},w_{6}\right \rangle \left \langle v_{6},v_{7}\right \rangle \left \langle w_{7},v_{8}\right \rangle \left \langle w_{8},w_{1}\right \rangle $
and easily generalizable to arbitrary words. We chose to stick with the order in equation (5.8) for ease of notation in the sequel, for example, in Lemma 5.6.
$\left \langle v_{1},w_{2}\right \rangle \left \langle v_{2},v_{3}\right \rangle \left \langle w_{3},v_{4}\right \rangle \left \langle w_{4},w_{5}\right \rangle \left \langle v_{5},w_{6}\right \rangle \left \langle v_{6},v_{7}\right \rangle \left \langle w_{7},v_{8}\right \rangle \left \langle w_{8},w_{1}\right \rangle $
and easily generalizable to arbitrary words. We chose to stick with the order in equation (5.8) for ease of notation in the sequel, for example, in Lemma 5.6.
Lemma 5.4. For any
![]() $(g_{a},g_{b},g_{c},g_{d})\in S_{n}^{4}$
, we have
$(g_{a},g_{b},g_{c},g_{d})\in S_{n}^{4}$
, we have
Proof. Let
![]() $v_{i}$
be any orthonormal basis of
$v_{i}$
be any orthonormal basis of
![]() $V^{\lambda }$
. Let
$V^{\lambda }$
. Let
![]() $a_{ji}\stackrel {\mathrm {def}}{=}\langle g_{a}v_{i},v_{j}\rangle $
be the matrix coefficients of the matrix
$a_{ji}\stackrel {\mathrm {def}}{=}\langle g_{a}v_{i},v_{j}\rangle $
be the matrix coefficients of the matrix
![]() $a=(a_{ij})$
by which g acts on
$a=(a_{ij})$
by which g acts on
![]() $V^{\lambda }$
with respect to
$V^{\lambda }$
with respect to
![]() $\{v_{i}\}$
. Similarly, define matrices
$\{v_{i}\}$
. Similarly, define matrices
![]() $b,c,d$
for
$b,c,d$
for
![]() $g_{b},g_{c},g_{d}$
in
$g_{b},g_{c},g_{d}$
in
![]() $V^{\lambda }$
. We have
$V^{\lambda }$
. We have
 $$ \begin{align*} \mathrm{tr}_{W^{\lambda}}(B_{\lambda}\circ(g_{a},g_{b},g_{c},g_{d})) & = \sum_{i_{1},\ldots,i_{8}}\langle B_{\lambda}\circ(g_{a},g_{b},g_{c},g_{d})v_{i_{1}}\otimes\check{v}_{i_{2}}\otimes v_{i_{3}}\otimes\check{v_{i_{4}}}\otimes v_{i_{5}}\otimes\check{v}_{i_{6}}\otimes v_{i_{7}}\otimes\check{v}_{i_{8}},\\ & ~~~~~~~v_{i_{1}}\otimes\check{v}_{i_{2}}\otimes v_{i_{3}}\otimes\check{v}_{i_{4}}\otimes v_{i_{5}}\otimes\check{v}_{i_{6}}\otimes v_{i_{7}}\otimes\check{v}_{i_{8}}\rangle\\ & = \sum_{\substack{i_{1},\ldots,i_{8}\\ j_{1},\ldots,j_{8} } }a_{j_{1}i_{1}}(a^{-1})_{i_{2}j_{2}}b_{j_{3}i_{3}}(b^{-1})_{i_{4}j_{4}}c_{j_{5}i_{5}}(c^{-1})_{i_{6}j_{6}}d_{j_{7}i_{7}}(d^{-1})_{i_{8}j_{8}}\cdot\\ & ~~~~~~~~~\left\langle B_{\lambda}v_{j_{1}}\otimes\check{v}_{j_{2}}\otimes v_{j_{3}}\otimes\check{v}_{j_{4}}\otimes v_{j_{5}}\otimes\check{v}_{j_{6}}\otimes v_{j_{7}}\otimes\check{v}_{j_{8}} \right.,\\ & ~~~~~~~~~~~~~~~~v_{i_{1}}\otimes\check{v}_{i_{2}}\otimes v_{i_{3}}\otimes\check{v}_{i_{4}}\otimes v_{i_{5}}\otimes\check{v}_{i_{6}}\otimes v_{i_{7}}\otimes\check{v}_{i_{8}}\rangle \end{align*} $$
$$ \begin{align*} \mathrm{tr}_{W^{\lambda}}(B_{\lambda}\circ(g_{a},g_{b},g_{c},g_{d})) & = \sum_{i_{1},\ldots,i_{8}}\langle B_{\lambda}\circ(g_{a},g_{b},g_{c},g_{d})v_{i_{1}}\otimes\check{v}_{i_{2}}\otimes v_{i_{3}}\otimes\check{v_{i_{4}}}\otimes v_{i_{5}}\otimes\check{v}_{i_{6}}\otimes v_{i_{7}}\otimes\check{v}_{i_{8}},\\ & ~~~~~~~v_{i_{1}}\otimes\check{v}_{i_{2}}\otimes v_{i_{3}}\otimes\check{v}_{i_{4}}\otimes v_{i_{5}}\otimes\check{v}_{i_{6}}\otimes v_{i_{7}}\otimes\check{v}_{i_{8}}\rangle\\ & = \sum_{\substack{i_{1},\ldots,i_{8}\\ j_{1},\ldots,j_{8} } }a_{j_{1}i_{1}}(a^{-1})_{i_{2}j_{2}}b_{j_{3}i_{3}}(b^{-1})_{i_{4}j_{4}}c_{j_{5}i_{5}}(c^{-1})_{i_{6}j_{6}}d_{j_{7}i_{7}}(d^{-1})_{i_{8}j_{8}}\cdot\\ & ~~~~~~~~~\left\langle B_{\lambda}v_{j_{1}}\otimes\check{v}_{j_{2}}\otimes v_{j_{3}}\otimes\check{v}_{j_{4}}\otimes v_{j_{5}}\otimes\check{v}_{j_{6}}\otimes v_{j_{7}}\otimes\check{v}_{j_{8}} \right.,\\ & ~~~~~~~~~~~~~~~~v_{i_{1}}\otimes\check{v}_{i_{2}}\otimes v_{i_{3}}\otimes\check{v}_{i_{4}}\otimes v_{i_{5}}\otimes\check{v}_{i_{6}}\otimes v_{i_{7}}\otimes\check{v}_{i_{8}}\rangle \end{align*} $$
which equals
 $$ \begin{align*} = & \sum_{j_{1},j_{2},j_{4},j_{5},j_{6},j_{8},i_{1},i_{4}}a_{j_{1}i_{1}}(a^{-1})_{j_{4}j_{2}}b_{j_{2}j_{1}}(b^{-1})_{i_{4}j_{4}}c_{j_{5}i_{4}}(c^{-1})_{j_{8}j_{6}}d_{j_{6}j_{5}}(d^{-1})_{i_{1}j_{8}}\\ = & \sum_{j_{1},j_{2},j_{4},j_{5},j_{6},j_{8},i_{1},i_{4}}(d^{-1})_{i_{1}j_{8}}(c^{-1})_{j_{8}j_{6}}d_{j_{6}j_{5}}c_{j_{5}i_{4}}(b^{-1})_{i_{4}j_{4}}(a^{-1})_{j_{4}j_{2}}b_{j_{2}j_{1}}a_{j_{1}i_{1}}\\ = & \chi_{\lambda}\left(\left[g_{d}^{-1},g_{c}^{-1}\right]\left[g_{b}^{-1},g_{a}^{-1}\right]\right). \end{align*} $$
$$ \begin{align*} = & \sum_{j_{1},j_{2},j_{4},j_{5},j_{6},j_{8},i_{1},i_{4}}a_{j_{1}i_{1}}(a^{-1})_{j_{4}j_{2}}b_{j_{2}j_{1}}(b^{-1})_{i_{4}j_{4}}c_{j_{5}i_{4}}(c^{-1})_{j_{8}j_{6}}d_{j_{6}j_{5}}(d^{-1})_{i_{1}j_{8}}\\ = & \sum_{j_{1},j_{2},j_{4},j_{5},j_{6},j_{8},i_{1},i_{4}}(d^{-1})_{i_{1}j_{8}}(c^{-1})_{j_{8}j_{6}}d_{j_{6}j_{5}}c_{j_{5}i_{4}}(b^{-1})_{i_{4}j_{4}}(a^{-1})_{j_{4}j_{2}}b_{j_{2}j_{1}}a_{j_{1}i_{1}}\\ = & \chi_{\lambda}\left(\left[g_{d}^{-1},g_{c}^{-1}\right]\left[g_{b}^{-1},g_{a}^{-1}\right]\right). \end{align*} $$
The third equality used equation (5.9).
Using Lemma 5.4 allows us to relate
![]() $\Theta _{\lambda }(Y,\mathcal {J}_{n})$
to orthogonal projections in the space
$\Theta _{\lambda }(Y,\mathcal {J}_{n})$
to orthogonal projections in the space
![]() $W^{\lambda }$
. For each
$W^{\lambda }$
. For each
![]() $f\in \{a,b,c,d\}$
, let
$f\in \{a,b,c,d\}$
, let
![]() $P_{f}$
be the orthogonal projection in
$P_{f}$
be the orthogonal projection in
![]() $W^{\lambda }$
onto the vectors that are invariant by
$W^{\lambda }$
onto the vectors that are invariant by
![]() $G_{f}$
. We let
$G_{f}$
. We let
![]() $Q\stackrel {\mathrm {def}}{=} P_{a}P_{b}P_{c}P_{d}.$
$Q\stackrel {\mathrm {def}}{=} P_{a}P_{b}P_{c}P_{d}.$
Lemma 5.5. We have
![]() $\Theta _{\lambda }(Y,\mathcal {J}_{n})=\mathrm {tr}_{W^{\lambda }}\left (B_{\lambda }g^{0}Q\right )$
.
$\Theta _{\lambda }(Y,\mathcal {J}_{n})=\mathrm {tr}_{W^{\lambda }}\left (B_{\lambda }g^{0}Q\right )$
.
Proof. Using Lemma 5.4, we can write
 $$ \begin{align*} \Theta_{\lambda}(Y,\mathcal{J}_{n}) & =\int_{h_{_{f}}\in G_{f}}\chi_{\lambda}\left(\left[\left(g_{d}^{0}h_{d}\right)^{-1},\left(g_{c}^{0}h_{c}\right)^{-1}\right]\left[\left(g_{b}^{0}h_{b}\right)^{-1},\left(g_{a}^{0}h_{a}\right)^{-1}\right]\right)\\ & =\mathrm{tr}_{W^{\lambda}}\left(B_{\lambda}g^{0}P_{a}P_{b}P_{c}P_{d}\right)=\mathrm{tr}_{W^{\lambda}}\left(B_{\lambda}g^{0}Q\right).\\[-41pt] \end{align*} $$
$$ \begin{align*} \Theta_{\lambda}(Y,\mathcal{J}_{n}) & =\int_{h_{_{f}}\in G_{f}}\chi_{\lambda}\left(\left[\left(g_{d}^{0}h_{d}\right)^{-1},\left(g_{c}^{0}h_{c}\right)^{-1}\right]\left[\left(g_{b}^{0}h_{b}\right)^{-1},\left(g_{a}^{0}h_{a}\right)^{-1}\right]\right)\\ & =\mathrm{tr}_{W^{\lambda}}\left(B_{\lambda}g^{0}P_{a}P_{b}P_{c}P_{d}\right)=\mathrm{tr}_{W^{\lambda}}\left(B_{\lambda}g^{0}Q\right).\\[-41pt] \end{align*} $$
Hence, we now wish to calculate
![]() $\mathrm {tr}_{W^{\lambda }}\left (B_{\lambda }g^{0}Q\right )$
. For each
$\mathrm {tr}_{W^{\lambda }}\left (B_{\lambda }g^{0}Q\right )$
. For each
![]() $f\in \{a,b,c,d\}$
and
$f\in \{a,b,c,d\}$
and
![]() $T\in \mathrm {Tab}(\lambda )$
, let
$T\in \mathrm {Tab}(\lambda )$
, let
Similarly, if
![]() $\nu \subset _{\mathfrak {v}}\lambda $
, recalling that if
$\nu \subset _{\mathfrak {v}}\lambda $
, recalling that if
![]() $T\in \mathrm {Tab}(\lambda /\nu )$
,
$T\in \mathrm {Tab}(\lambda /\nu )$
,
![]() $w_{T}$
denotes the corresponding Gelfand–Tsetlin basis element of
$w_{T}$
denotes the corresponding Gelfand–Tsetlin basis element of
![]() $V^{\lambda /\nu }$
, we define
$V^{\lambda /\nu }$
, we define
this makes sense as
![]() $\sigma _{f}^{\pm }$
and
$\sigma _{f}^{\pm }$
and
![]() $\tau _{f}^{\pm }$
are in
$\tau _{f}^{\pm }$
are in
![]() $S_{\mathfrak {v}}^{'}$
. Recalling the notation
$S_{\mathfrak {v}}^{'}$
. Recalling the notation
![]() $\mathcal {E}_{\mu ,R_{1},R_{2}}^{\lambda }$
from Lemma 4.1 (where
$\mathcal {E}_{\mu ,R_{1},R_{2}}^{\lambda }$
from Lemma 4.1 (where
![]() $\mu \subset \lambda $
), we define
$\mu \subset \lambda $
), we define
Lemma 5.6. For
![]() $\lambda \vdash n$
, the elements
$\lambda \vdash n$
, the elements
are an orthonormal basis for the G-invariant vectors in
![]() $W^{\lambda }$
.
$W^{\lambda }$
.
Proof. Consider
![]() $W^{\lambda }$
as a module for
$W^{\lambda }$
as a module for
![]() $\mathbf {G}\stackrel {\mathrm {def}}{=} S_{a}^{(1)}\times S_{a}^{(2)}\times S_{b}^{(1)}\times S_{b}^{(2)}\times S_{c}^{(1)}\times S_{c}^{(2)}\times S_{d}^{(1)}\times S_{d}^{(2)}$
, where all the
$\mathbf {G}\stackrel {\mathrm {def}}{=} S_{a}^{(1)}\times S_{a}^{(2)}\times S_{b}^{(1)}\times S_{b}^{(2)}\times S_{c}^{(1)}\times S_{c}^{(2)}\times S_{d}^{(1)}\times S_{d}^{(2)}$
, where all the
![]() $S_{f}^{(i)}$
are isomorphic copies of
$S_{f}^{(i)}$
are isomorphic copies of
![]() $S_{n}$
,
$S_{n}$
,
![]() $S_{f}^{(1)}$
acts on the
$S_{f}^{(1)}$
acts on the
![]() $V_{f}^{\lambda }$
factor and
$V_{f}^{\lambda }$
factor and
![]() $S_{f}^{(2)}$
acts on the
$S_{f}^{(2)}$
acts on the
![]() $\check {V}_{f}^{\lambda }$
factor of
$\check {V}_{f}^{\lambda }$
factor of
![]() $W^{\lambda }$
. Given subgroups
$W^{\lambda }$
. Given subgroups
![]() $H_{f}$
of
$H_{f}$
of
![]() $S_{n}$
for each
$S_{n}$
for each
![]() $f\in \{a,b,c,d\}$
, write
$f\in \{a,b,c,d\}$
, write
![]() $\Delta (H_{a},H_{b},H_{c},H_{d})$
for the subgroup consisting of tuples of the form
$\Delta (H_{a},H_{b},H_{c},H_{d})$
for the subgroup consisting of tuples of the form
![]() $(g_{a},g_{a},g_{b},g_{b},g_{c},g_{c},g_{d},g_{d})$
with each
$(g_{a},g_{a},g_{b},g_{b},g_{c},g_{c},g_{d},g_{d})$
with each
![]() $g_{f}\in H_{f}$
. The statement of Lemma 5.6 is equivalent to the statement that the set given in equation (5.12) is an orthonormal basis for the
$g_{f}\in H_{f}$
. The statement of Lemma 5.6 is equivalent to the statement that the set given in equation (5.12) is an orthonormal basis for the
![]() $\Delta (G_{a},G_{b},G_{c},G_{d})$
-invariant elements.
$\Delta (G_{a},G_{b},G_{c},G_{d})$
-invariant elements.
We have
 $$ \begin{align*} & \mathcal{E}_{\mu_{a},S_{a},T_{a}}^{\lambda,a,-}\otimes\mathcal{E}_{\mu_{b},S_{b},T_{b}}^{\lambda,b,-}\otimes\mathcal{E}_{\mu_{c},S_{c},T_{c}}^{\lambda,c,-}\otimes\mathcal{E}_{\mu_{d},S_{d},T_{d}}^{\lambda,d,-}=\\ & \left(\sigma_{a}^{-},\tau_{a}^{-},\sigma_{b}^{-},\tau_{b}^{-},\sigma_{c}^{-},\tau_{c}^{-},\sigma_{d}^{-},\tau_{d}^{-}\right)^{-1}\mathcal{E}_{\mu_{a},S_{a},T_{a}}^{\lambda}\otimes\mathcal{E}_{\mu_{b},S_{b},T_{b}}^{\lambda}\otimes\mathcal{E}_{\mu_{c},S_{c},T_{c}}^{\lambda}\otimes\mathcal{E}_{\mu_{d},S_{d},T_{d}}^{\lambda}. \end{align*} $$
$$ \begin{align*} & \mathcal{E}_{\mu_{a},S_{a},T_{a}}^{\lambda,a,-}\otimes\mathcal{E}_{\mu_{b},S_{b},T_{b}}^{\lambda,b,-}\otimes\mathcal{E}_{\mu_{c},S_{c},T_{c}}^{\lambda,c,-}\otimes\mathcal{E}_{\mu_{d},S_{d},T_{d}}^{\lambda,d,-}=\\ & \left(\sigma_{a}^{-},\tau_{a}^{-},\sigma_{b}^{-},\tau_{b}^{-},\sigma_{c}^{-},\tau_{c}^{-},\sigma_{d}^{-},\tau_{d}^{-}\right)^{-1}\mathcal{E}_{\mu_{a},S_{a},T_{a}}^{\lambda}\otimes\mathcal{E}_{\mu_{b},S_{b},T_{b}}^{\lambda}\otimes\mathcal{E}_{\mu_{c},S_{c},T_{c}}^{\lambda}\otimes\mathcal{E}_{\mu_{d},S_{d},T_{d}}^{\lambda}. \end{align*} $$
We note that
![]() $(\sigma _{a}^{-},\tau _{a}^{-},\sigma _{b}^{-},\tau _{b}^{-},\sigma _{c}^{-},\tau _{c}^{-},\sigma _{d}^{-},\tau _{d}^{-})$
acts unitarily on
$(\sigma _{a}^{-},\tau _{a}^{-},\sigma _{b}^{-},\tau _{b}^{-},\sigma _{c}^{-},\tau _{c}^{-},\sigma _{d}^{-},\tau _{d}^{-})$
acts unitarily on
![]() $W^{\lambda }$
, and by Lemma 4.1, the vectors
$W^{\lambda }$
, and by Lemma 4.1, the vectors
![]() $\mathcal {E}_{\mu _{a},S_{a},T_{a}}^{\lambda }\otimes \mathcal {E}_{\mu _{b},S_{b},T_{b}}^{\lambda }\otimes \mathcal {E}_{\mu _{c},S_{c},T_{c}}^{\lambda }\otimes \mathcal {E}_{\mu _{d},S_{d},T_{d}}^{\lambda }$
are an orthonormal basis for the
$\mathcal {E}_{\mu _{a},S_{a},T_{a}}^{\lambda }\otimes \mathcal {E}_{\mu _{b},S_{b},T_{b}}^{\lambda }\otimes \mathcal {E}_{\mu _{c},S_{c},T_{c}}^{\lambda }\otimes \mathcal {E}_{\mu _{d},S_{d},T_{d}}^{\lambda }$
are an orthonormal basis for the
![]() $\Delta (S_{n-\mathfrak {e}_{a}},S_{n-\mathfrak {e}_{b}},S_{n-\mathfrak {e}_{c}},S_{n-\mathfrak {e}_{d}})$
-invariant vectors in
$\Delta (S_{n-\mathfrak {e}_{a}},S_{n-\mathfrak {e}_{b}},S_{n-\mathfrak {e}_{c}},S_{n-\mathfrak {e}_{d}})$
-invariant vectors in
![]() $W^{\lambda }$
. Therefore, the set given in equation (5.12) is an orthonormal basis of invariant vectors for the group
$W^{\lambda }$
. Therefore, the set given in equation (5.12) is an orthonormal basis of invariant vectors for the group
It remains to prove that this group is
![]() $\Delta (G_{a},G_{b},G_{c},G_{d})$
. By property P1, this group is contained in
$\Delta (G_{a},G_{b},G_{c},G_{d})$
. By property P1, this group is contained in
![]() $G_{a}\times G_{a}\times G_{b}\times G_{b}\times G_{c}\times G_{c}\times G_{d}\times G_{d}$
. Combining this with property P3, the group displayed above is equal to
$G_{a}\times G_{a}\times G_{b}\times G_{b}\times G_{c}\times G_{c}\times G_{d}\times G_{d}$
. Combining this with property P3, the group displayed above is equal to
![]() $\Delta (G_{a},G_{b},G_{c},G_{d})$
, as required.
$\Delta (G_{a},G_{b},G_{c},G_{d})$
, as required.
Lemma 5.7. We have
Proof. This follows from property P2 together with the definitions of
![]() $\mathcal {E}_{\mu _{f},S_{f},T_{f}}^{\lambda ,f,\pm }$
in equation (5.11).
$\mathcal {E}_{\mu _{f},S_{f},T_{f}}^{\lambda ,f,\pm }$
in equation (5.11).
Proposition 5.8. Recalling the definition of
![]() $\Theta _{\lambda }(Y,\mathcal {J}_{n})$
from equation (5.7), we have
$\Theta _{\lambda }(Y,\mathcal {J}_{n})$
from equation (5.7), we have
 $$ \begin{align} \Theta_{\lambda}(Y,\mathcal{J}_{n})= & \sum_{\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda'\subset_{\mathfrak{f}}\lambda}d_{\lambda/\lambda'}d_{\nu}\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda'}\frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\left\{ \mu_{f}\right\} ,\lambda'\right), \end{align} $$
$$ \begin{align} \Theta_{\lambda}(Y,\mathcal{J}_{n})= & \sum_{\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda'\subset_{\mathfrak{f}}\lambda}d_{\lambda/\lambda'}d_{\nu}\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda'}\frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\left\{ \mu_{f}\right\} ,\lambda'\right), \end{align} $$
where
 $$ \begin{align} \Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\left\{ \mu_{f}\right\} ,\lambda'\right)\stackrel{\mathrm{def}}{=}\sum_{\begin{gathered}r_{f}^{+},r_{f}^{-}\in\mathrm{Tab}\left(\mu_{f}/\nu\right)\\ s_{f},t_{f}\in\mathrm{Tab}\left(\lambda'/\mu_{f}\right) \end{gathered} }\mathcal{M}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right) \end{align} $$
$$ \begin{align} \Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\left\{ \mu_{f}\right\} ,\lambda'\right)\stackrel{\mathrm{def}}{=}\sum_{\begin{gathered}r_{f}^{+},r_{f}^{-}\in\mathrm{Tab}\left(\mu_{f}/\nu\right)\\ s_{f},t_{f}\in\mathrm{Tab}\left(\lambda'/\mu_{f}\right) \end{gathered} }\mathcal{M}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right) \end{align} $$
and
![]() $\mathcal {M}\left (\left \{ \sigma _{f}^{\pm },\tau _{f}^{\pm },r_{f}^{\pm },s_{f},t_{f}\right \} \right )$
is the following product of matrix coefficients
$\mathcal {M}\left (\left \{ \sigma _{f}^{\pm },\tau _{f}^{\pm },r_{f}^{\pm },s_{f},t_{f}\right \} \right )$
is the following product of matrix coefficients
 $$ \begin{align} \mathcal{M}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right) & \stackrel{\mathrm{def}}{=} \left\langle \sigma_{b}^{-}\left(\sigma_{a}^{+}\right)^{-1}w_{r_{a}^{+}\sqcup s_{a}},w_{r_{b}^{-}\sqcup s{}_{b}}\right\rangle \left\langle \tau_{a}^{+}\left(\sigma_{b}^{+}\right)^{-1}w_{r_{b}^{+}\sqcup s_{b}},w_{r_{a}^{+}\sqcup t_{a}}\right\rangle \cdot\nonumber \\ & \left\langle \tau_{b}^{+}\left(\tau_{a}^{-}\right)^{-1}w_{r_{a}^{-}\sqcup t{}_{a}},w_{r_{b}^{+}\sqcup t_{b}}\right\rangle \left\langle \sigma_{c}^{-}\left(\tau_{b}^{-}\right)^{-1}w_{r_{b}^{-}\sqcup t{}_{b}},w_{r_{c}^{-}\sqcup s{}_{c}}\right\rangle \cdot\nonumber \\ & \left\langle \sigma_{d}^{-}\left(\sigma_{c}^{+}\right)^{-1}w_{r_{c}^{+}\sqcup s_{c}},w_{r_{d}^{-}\sqcup s{}_{d}}\right\rangle \left\langle \tau_{c}^{+}\left(\sigma_{d}^{+}\right)^{-1}w_{r_{d}^{+}\sqcup s_{d}},w_{r_{c}^{+}\sqcup t_{c}}\right\rangle \cdot\nonumber \\ & \left\langle \tau_{d}^{+}\left(\tau_{c}^{-}\right)^{-1}w_{r_{c}^{-}\sqcup t{}_{c}},w_{r_{d}^{+}\sqcup t_{d}}\right\rangle \left\langle \sigma_{a}^{-}\left(\tau_{d}^{-}\right)^{-1}w_{r_{d}^{-}\sqcup t{}_{d}},w_{r_{a}^{-}\sqcup s{}_{a}}\right\rangle. \end{align} $$
$$ \begin{align} \mathcal{M}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right) & \stackrel{\mathrm{def}}{=} \left\langle \sigma_{b}^{-}\left(\sigma_{a}^{+}\right)^{-1}w_{r_{a}^{+}\sqcup s_{a}},w_{r_{b}^{-}\sqcup s{}_{b}}\right\rangle \left\langle \tau_{a}^{+}\left(\sigma_{b}^{+}\right)^{-1}w_{r_{b}^{+}\sqcup s_{b}},w_{r_{a}^{+}\sqcup t_{a}}\right\rangle \cdot\nonumber \\ & \left\langle \tau_{b}^{+}\left(\tau_{a}^{-}\right)^{-1}w_{r_{a}^{-}\sqcup t{}_{a}},w_{r_{b}^{+}\sqcup t_{b}}\right\rangle \left\langle \sigma_{c}^{-}\left(\tau_{b}^{-}\right)^{-1}w_{r_{b}^{-}\sqcup t{}_{b}},w_{r_{c}^{-}\sqcup s{}_{c}}\right\rangle \cdot\nonumber \\ & \left\langle \sigma_{d}^{-}\left(\sigma_{c}^{+}\right)^{-1}w_{r_{c}^{+}\sqcup s_{c}},w_{r_{d}^{-}\sqcup s{}_{d}}\right\rangle \left\langle \tau_{c}^{+}\left(\sigma_{d}^{+}\right)^{-1}w_{r_{d}^{+}\sqcup s_{d}},w_{r_{c}^{+}\sqcup t_{c}}\right\rangle \cdot\nonumber \\ & \left\langle \tau_{d}^{+}\left(\tau_{c}^{-}\right)^{-1}w_{r_{c}^{-}\sqcup t{}_{c}},w_{r_{d}^{+}\sqcup t_{d}}\right\rangle \left\langle \sigma_{a}^{-}\left(\tau_{d}^{-}\right)^{-1}w_{r_{d}^{-}\sqcup t{}_{d}},w_{r_{a}^{-}\sqcup s{}_{a}}\right\rangle. \end{align} $$
Before proving Proposition 5.8, we say a word about the interpretation of the formula. Recall that the permutations
![]() $\sigma _{f}^{\pm }$
and
$\sigma _{f}^{\pm }$
and
![]() $\tau _{f}^{\pm }$
all belong to
$\tau _{f}^{\pm }$
all belong to
![]() $S^{\prime }_{\mathfrak {v}}\le S_{n}$
. But by property P4, the eight permutations appearing in equation (5.15) all restrict to the identity on
$S^{\prime }_{\mathfrak {v}}\le S_{n}$
. But by property P4, the eight permutations appearing in equation (5.15) all restrict to the identity on
![]() $\left [n-\mathfrak {f}+1,n\right ]$
, and so can be seen as permutations on
$\left [n-\mathfrak {f}+1,n\right ]$
, and so can be seen as permutations on
![]() $\left [n-\mathfrak {v}+1,n-\mathfrak {f}\right ]$
. For every
$\left [n-\mathfrak {v}+1,n-\mathfrak {f}\right ]$
. For every
![]() $\pi \in \left \{ \sigma _{f}^{\pm },\tau _{f}^{\pm }\right \} $
,
$\pi \in \left \{ \sigma _{f}^{\pm },\tau _{f}^{\pm }\right \} $
,
![]() $\pi ^{-1}\left (\left [n-\mathfrak {v}+1,n-\mathfrak {f}\right ]\right )$
correspond to vertices where the corresponding side-of-half-f-edge belongs either to a hanging half-edge, or to an exposed side of a full-edge. One should think of
$\pi ^{-1}\left (\left [n-\mathfrak {v}+1,n-\mathfrak {f}\right ]\right )$
correspond to vertices where the corresponding side-of-half-f-edge belongs either to a hanging half-edge, or to an exposed side of a full-edge. One should think of
![]() $r_{f}^{-}$
as the skew Young tableau consisting of indices of outgoing hanging half-edges labeled f, of
$r_{f}^{-}$
as the skew Young tableau consisting of indices of outgoing hanging half-edges labeled f, of
![]() $r_{f}^{+}$
as the tableau of incoming hanging half-edges labeled f, of
$r_{f}^{+}$
as the tableau of incoming hanging half-edges labeled f, of
![]() $s_{f}$
as the tableau of exposed left-sides of full f-edges and of
$s_{f}$
as the tableau of exposed left-sides of full f-edges and of
![]() $t_{f}$
as the tableau of exposed right-sides of full f-edges. Then indeed, for example, the indices corresponding to
$t_{f}$
as the tableau of exposed right-sides of full f-edges. Then indeed, for example, the indices corresponding to
![]() $\sigma _{f}^{-}$
are
$\sigma _{f}^{-}$
are
![]() $r_{f}^{-}\sqcup s_{f}$
, those corresponding to
$r_{f}^{-}\sqcup s_{f}$
, those corresponding to
![]() $\sigma _{f}^{+}$
are
$\sigma _{f}^{+}$
are
![]() $r_{f}^{+}\sqcup s_{f}$
, those corresponding to
$r_{f}^{+}\sqcup s_{f}$
, those corresponding to
![]() $\tau _{f}^{-}$
are
$\tau _{f}^{-}$
are
![]() $r_{f}^{-}\sqcup t_{f}$
, and those corresponding to
$r_{f}^{-}\sqcup t_{f}$
, and those corresponding to
![]() $\tau _{f}^{+}$
are
$\tau _{f}^{+}$
are
![]() $r_{f}^{+}\sqcup t_{f}$
.
$r_{f}^{+}\sqcup t_{f}$
.
Proof of Proposition 5.8.
By Lemmas 5.5, 5.6 and 5.7, we have
 $$ \begin{align} \Theta_{\lambda}\left(Y,\mathcal{J}_{n}\right) & = \mathrm{tr}_{W^{\lambda}}\left(B_{\lambda}g^{0}Q\right)\nonumber \\ & = \sum_{\begin{gathered}\mu_{f}\subset_{\mathfrak{e}_{f}}\lambda,\\ S_{f},T_{f}\in\mathrm{Tab}\left(\lambda/\mu_{f}\right) \end{gathered} }\begin{gathered}\big\langle B_{\lambda}g^{0}\left[\mathcal{E}_{\mu_{a},S_{a},T_{a}}^{\lambda,a,-}\otimes\mathcal{E}_{\mu_{b},S_{b},T_{b}}^{\lambda,b,-}\otimes\mathcal{E}_{\mu_{c},S_{c},T_{c}}^{\lambda,c,-}\otimes\mathcal{E}_{\mu_{d},S_{d},T_{d}}^{\lambda,d,-}\right],\\ \mathcal{E}_{\mu_{a},S_{a},T_{a}}^{\lambda,a,-}\otimes\mathcal{E}_{\mu_{b},S_{b},T_{b}}^{\lambda,b,-}\otimes\mathcal{E}_{\mu_{c},S_{c},T_{c}}^{\lambda,c,-}\otimes\mathcal{E}_{\mu_{d},S_{d},T_{d}}^{\lambda,d,-}\big\rangle \end{gathered} \nonumber \\ & = \sum_{\begin{gathered}\mu_{f}\subset_{\mathfrak{e}_{f}}\lambda,\\ S_{f},T_{f}\in\mathrm{Tab}\left(\lambda/\mu_{f}\right) \end{gathered} }\begin{gathered}\big\langle B_{\lambda}\left[\mathcal{E}_{\mu_{a},S_{a},T_{a}}^{\lambda,a,+}\otimes\mathcal{E}_{\mu_{b},S_{b},T_{b}}^{\lambda,b,+}\otimes\mathcal{E}_{\mu_{c},S_{c},T_{c}}^{\lambda,c,+}\otimes\mathcal{E}_{\mu_{d},S_{d},T_{d}}^{\lambda,d,+}\right],\\ \mathcal{E}_{\mu_{a},S_{a},T_{a}}^{\lambda,a,-}\otimes\mathcal{E}_{\mu_{b},S_{b},T_{b}}^{\lambda,b,-}\otimes\mathcal{E}_{\mu_{c},S_{c},T_{c}}^{\lambda,c,-}\otimes\mathcal{E}_{\mu_{d},S_{d},T_{d}}^{\lambda,d,-}\big\rangle. \end{gathered} \end{align} $$
$$ \begin{align} \Theta_{\lambda}\left(Y,\mathcal{J}_{n}\right) & = \mathrm{tr}_{W^{\lambda}}\left(B_{\lambda}g^{0}Q\right)\nonumber \\ & = \sum_{\begin{gathered}\mu_{f}\subset_{\mathfrak{e}_{f}}\lambda,\\ S_{f},T_{f}\in\mathrm{Tab}\left(\lambda/\mu_{f}\right) \end{gathered} }\begin{gathered}\big\langle B_{\lambda}g^{0}\left[\mathcal{E}_{\mu_{a},S_{a},T_{a}}^{\lambda,a,-}\otimes\mathcal{E}_{\mu_{b},S_{b},T_{b}}^{\lambda,b,-}\otimes\mathcal{E}_{\mu_{c},S_{c},T_{c}}^{\lambda,c,-}\otimes\mathcal{E}_{\mu_{d},S_{d},T_{d}}^{\lambda,d,-}\right],\\ \mathcal{E}_{\mu_{a},S_{a},T_{a}}^{\lambda,a,-}\otimes\mathcal{E}_{\mu_{b},S_{b},T_{b}}^{\lambda,b,-}\otimes\mathcal{E}_{\mu_{c},S_{c},T_{c}}^{\lambda,c,-}\otimes\mathcal{E}_{\mu_{d},S_{d},T_{d}}^{\lambda,d,-}\big\rangle \end{gathered} \nonumber \\ & = \sum_{\begin{gathered}\mu_{f}\subset_{\mathfrak{e}_{f}}\lambda,\\ S_{f},T_{f}\in\mathrm{Tab}\left(\lambda/\mu_{f}\right) \end{gathered} }\begin{gathered}\big\langle B_{\lambda}\left[\mathcal{E}_{\mu_{a},S_{a},T_{a}}^{\lambda,a,+}\otimes\mathcal{E}_{\mu_{b},S_{b},T_{b}}^{\lambda,b,+}\otimes\mathcal{E}_{\mu_{c},S_{c},T_{c}}^{\lambda,c,+}\otimes\mathcal{E}_{\mu_{d},S_{d},T_{d}}^{\lambda,d,+}\right],\\ \mathcal{E}_{\mu_{a},S_{a},T_{a}}^{\lambda,a,-}\otimes\mathcal{E}_{\mu_{b},S_{b},T_{b}}^{\lambda,b,-}\otimes\mathcal{E}_{\mu_{c},S_{c},T_{c}}^{\lambda,c,-}\otimes\mathcal{E}_{\mu_{d},S_{d},T_{d}}^{\lambda,d,-}\big\rangle. \end{gathered} \end{align} $$
Using equations (4.2), (5.9) and (5.11), we obtain
 $$ \begin{align*} & \left\langle B_{\lambda}\left[\mathcal{E}_{\mu_{a},S_{a},T_{a}}^{\lambda,a,+}\otimes\mathcal{E}_{\mu_{b},S_{b},T_{b}}^{\lambda,b,+}\otimes\mathcal{E}_{\mu_{c},S_{c},T_{c}}^{\lambda,c,+}\otimes\mathcal{E}_{\mu_{d},S_{d},T_{d}}^{\lambda,d,+}\right],\mathcal{E}_{\mu{}_{a},S_{a},T_{a}}^{\lambda,a,-}\otimes\mathcal{E}_{\mu{}_{b},S_{b},T_{b}}^{\lambda,b,-}\otimes\mathcal{E}_{\mu{}_{c},S_{c},T_{c}}^{\lambda,c,-}\otimes\mathcal{E}_{\mu{}_{d},S_{d},T_{d}}^{\lambda,d,-}\right\rangle \\= & \frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\sum_{R_{f}^{+},R_{f}^{-}\in\mathrm{Tab}\left(\mu_{f}\right)}\\ & \left\langle B_{\lambda}\left[v_{R_{a}^{+}\sqcup S_{a}}^{\sigma_{a}^{+}}\otimes\check{v}_{R_{a}^{+}\sqcup T_{a}}^{\tau_{a}^{+}}\otimes v_{R_{b}^{+}\sqcup S_{b}}^{\sigma_{b}^{+}}\otimes\check{v}_{R_{b}^{+}\sqcup T_{b}}^{\tau_{b}^{+}}\otimes v_{R_{c}^{+}\sqcup S_{c}}^{\sigma_{c}^{+}}\otimes\check{v}_{R_{c}^{+}\sqcup T_{c}}^{\tau_{c}^{+}}\otimes v_{R_{d}^{+}\sqcup S_{d}}^{\sigma_{d}^{+}}\otimes\check{v}_{R_{d}^{+}\sqcup T_{d}}^{\tau_{d}^{+}}\right]\right.,\\ & \left.~~v_{R_{a}^{-}\sqcup S_{a}}^{\sigma_{a}^{-}}\otimes\check{v}_{R_{a}^{-}\sqcup T_{a}}^{\tau_{a}^{-}}\otimes v_{R_{b}^{-}\sqcup S_{b}}^{\sigma_{b}^{-}}\otimes\check{v}_{R_{b}^{-}\sqcup T_{b}}^{\tau_{b}^{-}}\otimes v_{R_{c}^{-}\sqcup S_{c}}^{\sigma_{c}^{-}}\otimes\check{v}_{R_{c}^{-}\sqcup T_{c}}^{\tau_{c}^{-}}\otimes v_{R_{d}^{-}\sqcup S_{d}}^{\sigma_{d}^{-}}\otimes\check{v}_{R_{d}^{-}\sqcup T_{d}}^{\tau_{d}^{-}}\right\rangle \\= & \frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\sum_{R_{f}^{\pm}\in\mathrm{Tab}\left(\mu_{f}\right)}\left\langle v_{R_{a}^{+}\sqcup S_{a}}^{\sigma_{a}^{+}},v_{R_{b}^{-}\sqcup S_{b}}^{\sigma_{b}^{-}}\right\rangle \left\langle v_{R_{b}^{+}\sqcup S_{b}}^{\sigma_{b}^{+}},v_{R_{a}^{+}\sqcup T_{a}}^{\tau_{a}^{+}}\right\rangle \left\langle v_{R_{a}^{-}\sqcup T_{a}}^{\tau_{a}^{-}},v_{R_{b}^{+}\sqcup T_{b}}^{\tau_{b}^{+}}\right\rangle \cdot\\ & ~~~~~\left\langle v_{R_{b}^{-}\sqcup T_{b}}^{\tau_{b}^{-}},v_{R_{c}^{-}\sqcup S_{c}}^{\sigma_{c}^{-}}\right\rangle \left\langle v_{R_{c}^{+}\sqcup S_{c}}^{\sigma_{c}^{+}},v_{R_{d}^{-}\sqcup S_{d}}^{\sigma_{d}^{-}}\right\rangle \left\langle v_{R_{d}^{+}\sqcup S_{d}}^{\sigma_{d}^{+}},v_{R_{c}^{+}\sqcup T_{c}}^{\tau_{c}^{+}}\right\rangle \left\langle v_{R_{c}^{-}\sqcup T_{c}}^{\tau_{c}^{-}},v_{R_{d}^{+}\sqcup T_{d}}^{\tau_{d}^{+}}\right\rangle \left\langle v_{R_{d}^{-}\sqcup T_{d}}^{\tau_{d}^{-}},v_{R_{a}^{-}\sqcup S_{a}}^{\sigma_{a}^{-}}\right\rangle . \end{align*} $$
$$ \begin{align*} & \left\langle B_{\lambda}\left[\mathcal{E}_{\mu_{a},S_{a},T_{a}}^{\lambda,a,+}\otimes\mathcal{E}_{\mu_{b},S_{b},T_{b}}^{\lambda,b,+}\otimes\mathcal{E}_{\mu_{c},S_{c},T_{c}}^{\lambda,c,+}\otimes\mathcal{E}_{\mu_{d},S_{d},T_{d}}^{\lambda,d,+}\right],\mathcal{E}_{\mu{}_{a},S_{a},T_{a}}^{\lambda,a,-}\otimes\mathcal{E}_{\mu{}_{b},S_{b},T_{b}}^{\lambda,b,-}\otimes\mathcal{E}_{\mu{}_{c},S_{c},T_{c}}^{\lambda,c,-}\otimes\mathcal{E}_{\mu{}_{d},S_{d},T_{d}}^{\lambda,d,-}\right\rangle \\= & \frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\sum_{R_{f}^{+},R_{f}^{-}\in\mathrm{Tab}\left(\mu_{f}\right)}\\ & \left\langle B_{\lambda}\left[v_{R_{a}^{+}\sqcup S_{a}}^{\sigma_{a}^{+}}\otimes\check{v}_{R_{a}^{+}\sqcup T_{a}}^{\tau_{a}^{+}}\otimes v_{R_{b}^{+}\sqcup S_{b}}^{\sigma_{b}^{+}}\otimes\check{v}_{R_{b}^{+}\sqcup T_{b}}^{\tau_{b}^{+}}\otimes v_{R_{c}^{+}\sqcup S_{c}}^{\sigma_{c}^{+}}\otimes\check{v}_{R_{c}^{+}\sqcup T_{c}}^{\tau_{c}^{+}}\otimes v_{R_{d}^{+}\sqcup S_{d}}^{\sigma_{d}^{+}}\otimes\check{v}_{R_{d}^{+}\sqcup T_{d}}^{\tau_{d}^{+}}\right]\right.,\\ & \left.~~v_{R_{a}^{-}\sqcup S_{a}}^{\sigma_{a}^{-}}\otimes\check{v}_{R_{a}^{-}\sqcup T_{a}}^{\tau_{a}^{-}}\otimes v_{R_{b}^{-}\sqcup S_{b}}^{\sigma_{b}^{-}}\otimes\check{v}_{R_{b}^{-}\sqcup T_{b}}^{\tau_{b}^{-}}\otimes v_{R_{c}^{-}\sqcup S_{c}}^{\sigma_{c}^{-}}\otimes\check{v}_{R_{c}^{-}\sqcup T_{c}}^{\tau_{c}^{-}}\otimes v_{R_{d}^{-}\sqcup S_{d}}^{\sigma_{d}^{-}}\otimes\check{v}_{R_{d}^{-}\sqcup T_{d}}^{\tau_{d}^{-}}\right\rangle \\= & \frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\sum_{R_{f}^{\pm}\in\mathrm{Tab}\left(\mu_{f}\right)}\left\langle v_{R_{a}^{+}\sqcup S_{a}}^{\sigma_{a}^{+}},v_{R_{b}^{-}\sqcup S_{b}}^{\sigma_{b}^{-}}\right\rangle \left\langle v_{R_{b}^{+}\sqcup S_{b}}^{\sigma_{b}^{+}},v_{R_{a}^{+}\sqcup T_{a}}^{\tau_{a}^{+}}\right\rangle \left\langle v_{R_{a}^{-}\sqcup T_{a}}^{\tau_{a}^{-}},v_{R_{b}^{+}\sqcup T_{b}}^{\tau_{b}^{+}}\right\rangle \cdot\\ & ~~~~~\left\langle v_{R_{b}^{-}\sqcup T_{b}}^{\tau_{b}^{-}},v_{R_{c}^{-}\sqcup S_{c}}^{\sigma_{c}^{-}}\right\rangle \left\langle v_{R_{c}^{+}\sqcup S_{c}}^{\sigma_{c}^{+}},v_{R_{d}^{-}\sqcup S_{d}}^{\sigma_{d}^{-}}\right\rangle \left\langle v_{R_{d}^{+}\sqcup S_{d}}^{\sigma_{d}^{+}},v_{R_{c}^{+}\sqcup T_{c}}^{\tau_{c}^{+}}\right\rangle \left\langle v_{R_{c}^{-}\sqcup T_{c}}^{\tau_{c}^{-}},v_{R_{d}^{+}\sqcup T_{d}}^{\tau_{d}^{+}}\right\rangle \left\langle v_{R_{d}^{-}\sqcup T_{d}}^{\tau_{d}^{-}},v_{R_{a}^{-}\sqcup S_{a}}^{\sigma_{a}^{-}}\right\rangle . \end{align*} $$
Since
![]() $\sigma _{f}^{\pm },\tau _{f}^{\pm }\in S^{\prime }_{\mathfrak {v}}$
for all
$\sigma _{f}^{\pm },\tau _{f}^{\pm }\in S^{\prime }_{\mathfrak {v}}$
for all
![]() $f\in \{a,b,c,d\}$
, the only way the product of matrix coefficients above can be nonzero is if there is
$f\in \{a,b,c,d\}$
, the only way the product of matrix coefficients above can be nonzero is if there is
![]() $\nu \vdash n-\mathfrak {v}$
such that
$\nu \vdash n-\mathfrak {v}$
such that
![]() $\nu \subset \mu _{f}$
for all
$\nu \subset \mu _{f}$
for all
![]() $f\in \{a,b,c,d\}$
, and all
$f\in \{a,b,c,d\}$
, and all
![]() $R_{f}^{+}\lvert _{\le n-\mathfrak {v}}$
,
$R_{f}^{+}\lvert _{\le n-\mathfrak {v}}$
,
![]() $R_{f}^{-}\lvert _{\le n-\mathfrak {v}}$
are equal and of shape
$R_{f}^{-}\lvert _{\le n-\mathfrak {v}}$
are equal and of shape
![]() $\nu $
. Also, recall from Section 3.3 that the action of
$\nu $
. Also, recall from Section 3.3 that the action of
![]() $\sigma \in S^{\prime }_{\mathfrak {v}}$
on a tableau of shape
$\sigma \in S^{\prime }_{\mathfrak {v}}$
on a tableau of shape
![]() $\lambda \vdash n$
depends only on the boxes with numbers from
$\lambda \vdash n$
depends only on the boxes with numbers from
![]() $\left [n-\mathfrak {v}+1,n\right ]$
. This gives
$\left [n-\mathfrak {v}+1,n\right ]$
. This gives
 $$ \begin{align} & \left\langle B_{\lambda}\left[\mathcal{E}_{\mu_{a},S_{a},T_{a}}^{\lambda,a,+}\otimes\mathcal{E}_{\mu_{b},S_{b},T_{b}}^{\lambda,b,+}\otimes\mathcal{E}_{\mu_{c},S_{c},T_{c}}^{\lambda,c,+}\otimes\mathcal{E}_{\mu_{d},S_{d},T_{d}}^{\lambda,d,+}\right],\mathcal{E}_{\mu{}_{a},S_{a},T_{a}}^{\lambda,a,-}\otimes\mathcal{E}_{\mu{}_{b},S_{b},T_{b}}^{\lambda,b,-}\otimes\mathcal{E}_{\mu{}_{c},S_{c},T_{c}}^{\lambda,c,-}\otimes\mathcal{E}_{\mu{}_{d},S_{d},T_{d}}^{\lambda,d,-}\right\rangle \nonumber \\ = & \sum_{\nu\subset_{\mathfrak{v}}\lambda}\frac{d_{\nu}}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\sum_{r_{f}^{+},r_{f}^{-}\in\mathrm{Tab}\left(\mu_{f}/\nu\right)}\nonumber \\ & \left\langle w_{r_{a}^{+}\sqcup S_{a}}^{\sigma_{a}^{+}},w_{r_{b}^{-}\sqcup S_{b}}^{\sigma_{b}^{-}}\right\rangle \cdot\left\langle w_{r_{b}^{+}\sqcup S_{b}}^{\sigma_{b}^{+}},w_{r_{a}^{+}\sqcup T_{a}}^{\tau_{a}^{+}}\right\rangle \cdot\left\langle w_{r_{a}^{-}\sqcup T_{a}}^{\tau_{a}^{-}},w_{r_{b}^{+}\sqcup T_{b}}^{\tau_{b}^{+}}\right\rangle \cdot\left\langle w_{r_{b}^{-}\sqcup T_{b}}^{\tau_{b}^{-}},w_{r_{c}^{-}\sqcup S_{c}}^{\sigma_{c}^{-}}\right\rangle \cdot\nonumber \\ & \left\langle w_{r_{c}^{+}\sqcup S_{c}}^{\sigma_{c}^{+}},w_{r_{d}^{-}\sqcup S_{d}}^{\sigma_{d}^{-}}\right\rangle \cdot\left\langle w_{r_{d}^{+}\sqcup S_{d}}^{\sigma_{d}^{+}},w_{r_{c}^{+}\sqcup T_{c}}^{\tau_{c}^{+}}\right\rangle \cdot\left\langle w_{r_{c}^{-}\sqcup T_{c}}^{\tau_{c}^{-}},w_{r_{d}^{+}\sqcup T_{d}}^{\tau_{d}^{+}}\right\rangle \cdot\left\langle w_{r_{d}^{-}\sqcup T_{d}}^{\tau_{d}^{-}},w_{r_{a}^{-}\sqcup S_{a}}^{\sigma_{a}^{-}}\right\rangle. \end{align} $$
$$ \begin{align} & \left\langle B_{\lambda}\left[\mathcal{E}_{\mu_{a},S_{a},T_{a}}^{\lambda,a,+}\otimes\mathcal{E}_{\mu_{b},S_{b},T_{b}}^{\lambda,b,+}\otimes\mathcal{E}_{\mu_{c},S_{c},T_{c}}^{\lambda,c,+}\otimes\mathcal{E}_{\mu_{d},S_{d},T_{d}}^{\lambda,d,+}\right],\mathcal{E}_{\mu{}_{a},S_{a},T_{a}}^{\lambda,a,-}\otimes\mathcal{E}_{\mu{}_{b},S_{b},T_{b}}^{\lambda,b,-}\otimes\mathcal{E}_{\mu{}_{c},S_{c},T_{c}}^{\lambda,c,-}\otimes\mathcal{E}_{\mu{}_{d},S_{d},T_{d}}^{\lambda,d,-}\right\rangle \nonumber \\ = & \sum_{\nu\subset_{\mathfrak{v}}\lambda}\frac{d_{\nu}}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\sum_{r_{f}^{+},r_{f}^{-}\in\mathrm{Tab}\left(\mu_{f}/\nu\right)}\nonumber \\ & \left\langle w_{r_{a}^{+}\sqcup S_{a}}^{\sigma_{a}^{+}},w_{r_{b}^{-}\sqcup S_{b}}^{\sigma_{b}^{-}}\right\rangle \cdot\left\langle w_{r_{b}^{+}\sqcup S_{b}}^{\sigma_{b}^{+}},w_{r_{a}^{+}\sqcup T_{a}}^{\tau_{a}^{+}}\right\rangle \cdot\left\langle w_{r_{a}^{-}\sqcup T_{a}}^{\tau_{a}^{-}},w_{r_{b}^{+}\sqcup T_{b}}^{\tau_{b}^{+}}\right\rangle \cdot\left\langle w_{r_{b}^{-}\sqcup T_{b}}^{\tau_{b}^{-}},w_{r_{c}^{-}\sqcup S_{c}}^{\sigma_{c}^{-}}\right\rangle \cdot\nonumber \\ & \left\langle w_{r_{c}^{+}\sqcup S_{c}}^{\sigma_{c}^{+}},w_{r_{d}^{-}\sqcup S_{d}}^{\sigma_{d}^{-}}\right\rangle \cdot\left\langle w_{r_{d}^{+}\sqcup S_{d}}^{\sigma_{d}^{+}},w_{r_{c}^{+}\sqcup T_{c}}^{\tau_{c}^{+}}\right\rangle \cdot\left\langle w_{r_{c}^{-}\sqcup T_{c}}^{\tau_{c}^{-}},w_{r_{d}^{+}\sqcup T_{d}}^{\tau_{d}^{+}}\right\rangle \cdot\left\langle w_{r_{d}^{-}\sqcup T_{d}}^{\tau_{d}^{-}},w_{r_{a}^{-}\sqcup S_{a}}^{\sigma_{a}^{-}}\right\rangle. \end{align} $$
Putting equations (5.16) and (5.17) together yields
 $$ \begin{align*} \Theta_{\lambda}\left(Y,\mathcal{J}_{n}\right) & = \sum_{\nu\subset_{\mathfrak{v}}\lambda}d_{\nu}\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}}\lambda}\frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\sum_{r_{f}^{+},r_{f}^{-}\in\mathrm{Tab}\left(\mu_{f}/\nu\right)}\sum_{S_{f},T_{f}\in\mathrm{Tab}\left(\lambda/\mu_{f}\right)}\\ & \left\langle w_{r_{a}^{+}\sqcup S_{a}}^{\sigma_{a}^{+}},w_{r_{b}^{-}\sqcup S_{b}}^{\sigma_{b}^{-}}\right\rangle \left\langle w_{r_{b}^{+}\sqcup S_{b}}^{\sigma_{b}^{+}},w_{r_{a}^{+}\sqcup T_{a}}^{\tau_{a}^{+}}\right\rangle \left\langle w_{r_{a}^{-}\sqcup T_{a}}^{\tau_{a}^{-}},w_{r_{b}^{+}\sqcup T_{b}}^{\tau_{b}^{+}}\right\rangle \left\langle w_{r_{b}^{-}\sqcup T_{b}}^{\tau_{b}^{-}},w_{r_{c}^{-}\sqcup S_{c}}^{\sigma_{c}^{-}}\right\rangle \\ & \left\langle w_{r_{c}^{+}\sqcup S_{c}}^{\sigma_{c}^{+}},w_{r_{d}^{-}\sqcup S_{d}}^{\sigma_{d}^{-}}\right\rangle \left\langle w_{r_{d}^{+}\sqcup S_{d}}^{\sigma_{d}^{+}},w_{r_{c}^{+}\sqcup T_{c}}^{\tau_{c}^{+}}\right\rangle \left\langle w_{r_{c}^{-}\sqcup T_{c}}^{\tau_{c}^{-}},w_{r_{d}^{+}\sqcup T_{d}}^{\tau_{d}^{+}}\right\rangle \left\langle w_{r_{d}^{-}\sqcup T_{d}}^{\tau_{d}^{-}},w_{r_{a}^{-}\sqcup S_{a}}^{\sigma_{a}^{-}}\right\rangle. \end{align*} $$
$$ \begin{align*} \Theta_{\lambda}\left(Y,\mathcal{J}_{n}\right) & = \sum_{\nu\subset_{\mathfrak{v}}\lambda}d_{\nu}\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}}\lambda}\frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\sum_{r_{f}^{+},r_{f}^{-}\in\mathrm{Tab}\left(\mu_{f}/\nu\right)}\sum_{S_{f},T_{f}\in\mathrm{Tab}\left(\lambda/\mu_{f}\right)}\\ & \left\langle w_{r_{a}^{+}\sqcup S_{a}}^{\sigma_{a}^{+}},w_{r_{b}^{-}\sqcup S_{b}}^{\sigma_{b}^{-}}\right\rangle \left\langle w_{r_{b}^{+}\sqcup S_{b}}^{\sigma_{b}^{+}},w_{r_{a}^{+}\sqcup T_{a}}^{\tau_{a}^{+}}\right\rangle \left\langle w_{r_{a}^{-}\sqcup T_{a}}^{\tau_{a}^{-}},w_{r_{b}^{+}\sqcup T_{b}}^{\tau_{b}^{+}}\right\rangle \left\langle w_{r_{b}^{-}\sqcup T_{b}}^{\tau_{b}^{-}},w_{r_{c}^{-}\sqcup S_{c}}^{\sigma_{c}^{-}}\right\rangle \\ & \left\langle w_{r_{c}^{+}\sqcup S_{c}}^{\sigma_{c}^{+}},w_{r_{d}^{-}\sqcup S_{d}}^{\sigma_{d}^{-}}\right\rangle \left\langle w_{r_{d}^{+}\sqcup S_{d}}^{\sigma_{d}^{+}},w_{r_{c}^{+}\sqcup T_{c}}^{\tau_{c}^{+}}\right\rangle \left\langle w_{r_{c}^{-}\sqcup T_{c}}^{\tau_{c}^{-}},w_{r_{d}^{+}\sqcup T_{d}}^{\tau_{d}^{+}}\right\rangle \left\langle w_{r_{d}^{-}\sqcup T_{d}}^{\tau_{d}^{-}},w_{r_{a}^{-}\sqcup S_{a}}^{\sigma_{a}^{-}}\right\rangle. \end{align*} $$
Now,
![]() $\langle w_{r_{a}^{+}\sqcup S_{a}}^{\sigma _{a}^{+}},w_{r_{b}^{-}\sqcup S_{b}}^{\sigma _{b}^{-}}\rangle =\langle \sigma _{b}^{-}\left (\sigma _{a}^{+}\right )^{-1}w_{r_{a}^{+}\sqcup S_{a}},w_{r_{b}^{-}\sqcup S_{b}}\rangle $
and so on, and property P4 implies that each pair of skew Young tableaux occurring in the same matrix coefficient above have the elements
$\langle w_{r_{a}^{+}\sqcup S_{a}}^{\sigma _{a}^{+}},w_{r_{b}^{-}\sqcup S_{b}}^{\sigma _{b}^{-}}\rangle =\langle \sigma _{b}^{-}\left (\sigma _{a}^{+}\right )^{-1}w_{r_{a}^{+}\sqcup S_{a}},w_{r_{b}^{-}\sqcup S_{b}}\rangle $
and so on, and property P4 implies that each pair of skew Young tableaux occurring in the same matrix coefficient above have the elements
![]() $[n-\mathfrak {f}+1,n]$
in the same boxes, if the matrix coefficient is nonzero. This implies that if the product of matrix coefficients is nonzero then all the skew Young tableaux above have the elements
$[n-\mathfrak {f}+1,n]$
in the same boxes, if the matrix coefficient is nonzero. This implies that if the product of matrix coefficients is nonzero then all the skew Young tableaux above have the elements
![]() $[n-\mathfrak {f}+1,n]$
in the same boxes and there is
$[n-\mathfrak {f}+1,n]$
in the same boxes and there is
![]() $\lambda '\subset \lambda $
such that
$\lambda '\subset \lambda $
such that
![]() $\mu _{f}\subset _{\mathfrak {e}_{f}-\mathfrak {f}}\lambda '$
for all f. Therefore, the above is equal to
$\mu _{f}\subset _{\mathfrak {e}_{f}-\mathfrak {f}}\lambda '$
for all f. Therefore, the above is equal to
 $$ \begin{align*} \Theta_{\lambda}\left(Y,\mathcal{J}_{n}\right) & = \sum_{\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda'\subset_{\mathfrak{f}}\lambda}d_{\lambda/\lambda'}d_{\nu}\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda'}\frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\sum_{r_{f}^{+},r_{f}^{-}\in\mathrm{Tab}\left(\mu_{f}/\nu\right)}\sum_{s_{f},t_{f}\in\mathrm{Tab}\left(\lambda'/\mu_{f}\right)}\\ & \left\langle \sigma_{b}^{-}\left(\sigma_{a}^{+}\right)^{-1}w_{r_{a}^{+}\sqcup s_{a}},w_{r_{b}^{-}\sqcup s{}_{b}}\right\rangle \cdot\left\langle \tau_{a}^{+}\left(\sigma_{b}^{+}\right)^{-1}w_{r_{b}^{+}\sqcup s_{b}},w_{r_{a}^{+}\sqcup t_{a}}\right\rangle \cdot\\ & \left\langle \tau_{b}^{+}\left(\tau_{a}^{-}\right)^{-1}w_{r_{a}^{-}\sqcup t{}_{a}},w_{r_{b}^{+}\sqcup t_{b}}\right\rangle \cdot\left\langle \sigma_{c}^{-}\left(\tau_{b}^{-}\right)^{-1}w_{r_{b}^{-}\sqcup t{}_{b}},w_{r_{c}^{-}\sqcup s{}_{c}}\right\rangle \cdot\\ & \left\langle \sigma_{d}^{-}\left(\sigma_{c}^{+}\right)^{-1}w_{r_{c}^{+}\sqcup s_{c}},w_{r_{d}^{-}\sqcup s{}_{d}}\right\rangle \cdot\left\langle \tau_{c}^{+}\left(\sigma_{d}^{+}\right)^{-1}w_{r_{d}^{+}\sqcup s_{d}},w_{r_{c}^{+}\sqcup t_{c}}\right\rangle \cdot\\ & \left\langle \tau_{d}^{+}\left(\tau_{c}^{-}\right)^{-1}w_{r_{c}^{-}\sqcup t{}_{c}},w_{r_{d}^{+}\sqcup t_{d}}\right\rangle \cdot\left\langle \sigma_{a}^{-}\left(\tau_{d}^{-}\right)^{-1}w_{r_{d}^{-}\sqcup t{}_{d}},w_{r_{a}^{-}\sqcup s{}_{a}}\right\rangle. \end{align*} $$
$$ \begin{align*} \Theta_{\lambda}\left(Y,\mathcal{J}_{n}\right) & = \sum_{\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda'\subset_{\mathfrak{f}}\lambda}d_{\lambda/\lambda'}d_{\nu}\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda'}\frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\sum_{r_{f}^{+},r_{f}^{-}\in\mathrm{Tab}\left(\mu_{f}/\nu\right)}\sum_{s_{f},t_{f}\in\mathrm{Tab}\left(\lambda'/\mu_{f}\right)}\\ & \left\langle \sigma_{b}^{-}\left(\sigma_{a}^{+}\right)^{-1}w_{r_{a}^{+}\sqcup s_{a}},w_{r_{b}^{-}\sqcup s{}_{b}}\right\rangle \cdot\left\langle \tau_{a}^{+}\left(\sigma_{b}^{+}\right)^{-1}w_{r_{b}^{+}\sqcup s_{b}},w_{r_{a}^{+}\sqcup t_{a}}\right\rangle \cdot\\ & \left\langle \tau_{b}^{+}\left(\tau_{a}^{-}\right)^{-1}w_{r_{a}^{-}\sqcup t{}_{a}},w_{r_{b}^{+}\sqcup t_{b}}\right\rangle \cdot\left\langle \sigma_{c}^{-}\left(\tau_{b}^{-}\right)^{-1}w_{r_{b}^{-}\sqcup t{}_{b}},w_{r_{c}^{-}\sqcup s{}_{c}}\right\rangle \cdot\\ & \left\langle \sigma_{d}^{-}\left(\sigma_{c}^{+}\right)^{-1}w_{r_{c}^{+}\sqcup s_{c}},w_{r_{d}^{-}\sqcup s{}_{d}}\right\rangle \cdot\left\langle \tau_{c}^{+}\left(\sigma_{d}^{+}\right)^{-1}w_{r_{d}^{+}\sqcup s_{d}},w_{r_{c}^{+}\sqcup t_{c}}\right\rangle \cdot\\ & \left\langle \tau_{d}^{+}\left(\tau_{c}^{-}\right)^{-1}w_{r_{c}^{-}\sqcup t{}_{c}},w_{r_{d}^{+}\sqcup t_{d}}\right\rangle \cdot\left\langle \sigma_{a}^{-}\left(\tau_{d}^{-}\right)^{-1}w_{r_{d}^{-}\sqcup t{}_{d}},w_{r_{a}^{-}\sqcup s{}_{a}}\right\rangle. \end{align*} $$
This finishes the proof.
It is also useful to know the following.
Lemma 5.9. We have
![]() $\Upsilon _{n}\left (\left \{ \sigma _{f}^{\pm },\tau _{f}^{\pm }\right \} ,\nu ,\{\mu _{f}\},\lambda '\right )=\Upsilon _{n}\left (\left \{ \sigma _{f}^{\pm },\tau _{f}^{\pm }\right \} ,\check {\nu },\{\check {\mu }_{f}\},\check {\lambda }'\right )$
.
$\Upsilon _{n}\left (\left \{ \sigma _{f}^{\pm },\tau _{f}^{\pm }\right \} ,\nu ,\{\mu _{f}\},\lambda '\right )=\Upsilon _{n}\left (\left \{ \sigma _{f}^{\pm },\tau _{f}^{\pm }\right \} ,\check {\nu },\{\check {\mu }_{f}\},\check {\lambda }'\right )$
.
Proof. This uses that as
![]() $S_{n-\mathfrak {f}}$
modules,
$S_{n-\mathfrak {f}}$
modules,
![]() $V^{\lambda '}$
and
$V^{\lambda '}$
and
![]() $V^{\check {\lambda '}}\otimes \mathrm {sign}$
are isomorphic by the map
$V^{\check {\lambda '}}\otimes \mathrm {sign}$
are isomorphic by the map
![]() $w_{T}\mapsto w_{\check {T}}$
. This gives
$w_{T}\mapsto w_{\check {T}}$
. This gives
 $$ \begin{align*} \mathcal{M}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right)&= \mathrm{sign}\left(\sigma_{d}^{-}\left(\sigma_{c}^{+}\right)^{-1}\right)\mathrm{sign}\left(\tau_{c}^{+}\left(\sigma_{d}^{+}\right)^{-1}\right)\mathrm{sign}\left(\tau_{d}^{+}\left(\tau_{c}^{-}\right)^{-1}\right)\mathrm{sign}\left(\sigma_{a}^{-}\left(\tau_{d}^{-}\right)^{-1}\right)\\& \quad \cdot\mathrm{sign}\left(\sigma_{b}^{-}\left(\sigma_{a}^{+}\right)^{-1}\right)\mathrm{sign}\left(\tau_{a}^{+}\left(\sigma_{b}^{+}\right)^{-1}\right)\mathrm{sign}\left(\tau_{b}^{+}\left(\tau_{a}^{-}\right)^{-1}\right)\mathrm{sign}\left(\sigma_{c}^{-}\left(\tau_{b}^{-}\right)^{-1}\right)\cdot\\& \quad \cdot\mathcal{M}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},\check{r}_{f}^{\pm},\check{s}_{f},\check{t}_{f}\right\} \right)\\& = \mathcal{M}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},\check{r}_{f}^{\pm},\check{s}_{f},\check{t}_{f}\right\} \right), \end{align*} $$
$$ \begin{align*} \mathcal{M}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right)&= \mathrm{sign}\left(\sigma_{d}^{-}\left(\sigma_{c}^{+}\right)^{-1}\right)\mathrm{sign}\left(\tau_{c}^{+}\left(\sigma_{d}^{+}\right)^{-1}\right)\mathrm{sign}\left(\tau_{d}^{+}\left(\tau_{c}^{-}\right)^{-1}\right)\mathrm{sign}\left(\sigma_{a}^{-}\left(\tau_{d}^{-}\right)^{-1}\right)\\& \quad \cdot\mathrm{sign}\left(\sigma_{b}^{-}\left(\sigma_{a}^{+}\right)^{-1}\right)\mathrm{sign}\left(\tau_{a}^{+}\left(\sigma_{b}^{+}\right)^{-1}\right)\mathrm{sign}\left(\tau_{b}^{+}\left(\tau_{a}^{-}\right)^{-1}\right)\mathrm{sign}\left(\sigma_{c}^{-}\left(\tau_{b}^{-}\right)^{-1}\right)\cdot\\& \quad \cdot\mathcal{M}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},\check{r}_{f}^{\pm},\check{s}_{f},\check{t}_{f}\right\} \right)\\& = \mathcal{M}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},\check{r}_{f}^{\pm},\check{s}_{f},\check{t}_{f}\right\} \right), \end{align*} $$
where the last line used P2 to get
![]() $(\tau _{f}^{+})^{-1}\tau _{f}^{-}=(\sigma _{f}^{+})^{-1}\sigma _{f}^{-}=g_{0}^{f}$
. Using this identity gives the result.
$(\tau _{f}^{+})^{-1}\tau _{f}^{-}=(\sigma _{f}^{+})^{-1}\sigma _{f}^{-}=g_{0}^{f}$
. Using this identity gives the result.
We are now ready to give an exact expression for
![]() $\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
, which is the main result of this
$\mathbb {E}_{n}^{\mathrm {emb}}(Y)$
, which is the main result of this
![]() $\S \S $
5.4.
$\S \S $
5.4.
Theorem 5.10. For
![]() $n\geq \mathfrak {v}$
, we haveFootnote
14
$n\geq \mathfrak {v}$
, we haveFootnote
14
 $$ \begin{align} \mathbb{E}_{n}^{\mathrm{emb}}(Y)=\frac{\left(n!\right)^{3}}{\left|\mathbb{X}_{n}\right|}\cdot\frac{\left(n\right)_{\mathfrak{v}}\left(n\right)_{\mathfrak{f}}}{\prod_{f}\left(n\right)_{\mathfrak{e}_{f}}}\Xi_{n}(Y), \end{align} $$
$$ \begin{align} \mathbb{E}_{n}^{\mathrm{emb}}(Y)=\frac{\left(n!\right)^{3}}{\left|\mathbb{X}_{n}\right|}\cdot\frac{\left(n\right)_{\mathfrak{v}}\left(n\right)_{\mathfrak{f}}}{\prod_{f}\left(n\right)_{\mathfrak{e}_{f}}}\Xi_{n}(Y), \end{align} $$
where
 $$ \begin{align} \Xi_{n}(Y)\stackrel{\mathrm{def}}{=}\sum_{\substack{\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda'\vdash\,n-\mathfrak{f}} }d_{\lambda'}d_{\nu}\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda'}\frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda'\right). \end{align} $$
$$ \begin{align} \Xi_{n}(Y)\stackrel{\mathrm{def}}{=}\sum_{\substack{\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda'\vdash\,n-\mathfrak{f}} }d_{\lambda'}d_{\nu}\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda'}\frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda'\right). \end{align} $$
Remark 5.11. Although the expression (5.19) seems to depend on the choices of
![]() $\sigma _{f}^{\pm }$
etc. that we have made already, the relation (5.18) shows that it only depends on Y.
$\sigma _{f}^{\pm }$
etc. that we have made already, the relation (5.18) shows that it only depends on Y.
Proof of Theorem 5.10.
Recall from equation (5.6) that
![]() $\mathbb {E}_{n}^{\mathrm {emb}}(Y)=\frac {n!}{(n-\mathfrak {v})!}\frac {|\mathbb {X}_{n}(Y,\mathcal {J}_{n})|}{|\mathbb {X}_{n}|}$
. Combining this with Propositions 5.1 and 5.8 gives
$\mathbb {E}_{n}^{\mathrm {emb}}(Y)=\frac {n!}{(n-\mathfrak {v})!}\frac {|\mathbb {X}_{n}(Y,\mathcal {J}_{n})|}{|\mathbb {X}_{n}|}$
. Combining this with Propositions 5.1 and 5.8 gives
 $$ \begin{align*} \mathbb{E}_{n}^{\mathrm{emb}}(Y) & =\frac{\prod_{f\in a,b,c,d}(n-\mathfrak{e}_{f})!}{(n-\mathfrak{v})!\left|\mathbb{X}_{n}\right|}\sum_{\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda'\subset_{\mathfrak{f}}\lambda\vdash n}d_{\lambda}d_{\lambda/\lambda'}d_{\nu}\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda'}\frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\text{\(\Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda'\right).\)} \end{align*} $$
$$ \begin{align*} \mathbb{E}_{n}^{\mathrm{emb}}(Y) & =\frac{\prod_{f\in a,b,c,d}(n-\mathfrak{e}_{f})!}{(n-\mathfrak{v})!\left|\mathbb{X}_{n}\right|}\sum_{\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda'\subset_{\mathfrak{f}}\lambda\vdash n}d_{\lambda}d_{\lambda/\lambda'}d_{\nu}\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda'}\frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\text{\(\Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda'\right).\)} \end{align*} $$
Applying Lemma 3.1 to the summation over
![]() $\lambda ,$
for fixed
$\lambda ,$
for fixed
![]() $\lambda '$
, yields
$\lambda '$
, yields
 $$\begin{align*}\mathbb{E}_{n}^{\mathrm{emb}}(Y)=\frac{n!\prod_{f\in a,b,c,d}(n-\mathfrak{e}_{f})!}{(n-\mathfrak{v})!(n-\mathfrak{f})!\left|\mathbb{X}_{n}\right|}\sum_{\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda'\vdash\,n-\mathfrak{f}}d_{\lambda'}d_{\nu}\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda'}\frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\text{\(\Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda'\right).\)} \end{align*}$$
$$\begin{align*}\mathbb{E}_{n}^{\mathrm{emb}}(Y)=\frac{n!\prod_{f\in a,b,c,d}(n-\mathfrak{e}_{f})!}{(n-\mathfrak{v})!(n-\mathfrak{f})!\left|\mathbb{X}_{n}\right|}\sum_{\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda'\vdash\,n-\mathfrak{f}}d_{\lambda'}d_{\nu}\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda'}\frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\text{\(\Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda'\right).\)} \end{align*}$$
In view of Theorem 5.10, from now on we will not need to refer to the partition
![]() $\lambda \vdash n$
, but only to the partitions
$\lambda \vdash n$
, but only to the partitions
![]() $\nu \subset _{\mathfrak {v}-\mathfrak {e}_{f}}\mu _{f}\subset _{\mathfrak {e}_{f}-\mathfrak {f}}\lambda '\vdash n-\mathfrak {f}$
. For ease of notation, from now on we shall abuse notation and write
$\nu \subset _{\mathfrak {v}-\mathfrak {e}_{f}}\mu _{f}\subset _{\mathfrak {e}_{f}-\mathfrak {f}}\lambda '\vdash n-\mathfrak {f}$
. For ease of notation, from now on we shall abuse notation and write
![]() $\lambda $
instead of
$\lambda $
instead of
![]() $\lambda '$
.
$\lambda '$
.
Before moving on, we prove that the recently defined functions
![]() $\Upsilon _{n}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm }\},\nu ,\{\mu _{f}\},\lambda )$
are analytic functions of
$\Upsilon _{n}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm }\},\nu ,\{\mu _{f}\},\lambda )$
are analytic functions of
![]() $n^{-1}$
when
$n^{-1}$
when
![]() $\nu ,\mu _{f},\lambda $
each vary in a family of YDs. Recall the notation
$\nu ,\mu _{f},\lambda $
each vary in a family of YDs. Recall the notation
![]() $\lambda \left (n\right )$
and
$\lambda \left (n\right )$
and
![]() $T\left (n\right )$
from Section 4.4.
$T\left (n\right )$
from Section 4.4.
Lemma 5.12. Still assume that
![]() $(Y,\mathcal {J})$
,
$(Y,\mathcal {J})$
,
![]() $\sigma _{f}^{\pm }$
and
$\sigma _{f}^{\pm }$
and
![]() $\tau _{f}^{\pm }$
are all fixed in the sense of Sections 5.4 and 5.6. Suppose that we are given YDs
$\tau _{f}^{\pm }$
are all fixed in the sense of Sections 5.4 and 5.6. Suppose that we are given YDs
![]() $\nu \subset _{\mathfrak {v}-\mathfrak {f}}\lambda $
and for each
$\nu \subset _{\mathfrak {v}-\mathfrak {f}}\lambda $
and for each
![]() $f\in \{a,b,c,d\}$
a YD
$f\in \{a,b,c,d\}$
a YD
![]() $\mu _{f}$
with
$\mu _{f}$
with
There is a function
![]() $\Upsilon ^{*}\left (\nu ,\{\mu _{f}\},\lambda ,\bullet \right )$
that is holomorphic in some open disc in
$\Upsilon ^{*}\left (\nu ,\{\mu _{f}\},\lambda ,\bullet \right )$
that is holomorphic in some open disc in
![]() $\mathbf {C}$
with center
$\mathbf {C}$
with center
![]() $0$
such that for all n sufficiently large (depending on Y),
$0$
such that for all n sufficiently large (depending on Y),
![]() $\lambda (n-\mathfrak {f})$
,
$\lambda (n-\mathfrak {f})$
,
![]() $\mu _{f}(n-\mathfrak {e}_{f})$
and
$\mu _{f}(n-\mathfrak {e}_{f})$
and
![]() $\nu (n-\mathfrak {v})$
all exist and
$\nu (n-\mathfrak {v})$
all exist and
In addition, the coefficients of the Taylor series of
![]() $\kern2pt\Upsilon ^{*}\left (\nu ,\{\mu _{f}\},\lambda ,\bullet \right )$
are in
$\kern2pt\Upsilon ^{*}\left (\nu ,\{\mu _{f}\},\lambda ,\bullet \right )$
are in
![]() $\mathbf {Q}.$
$\mathbf {Q}.$
Proof. The proof relies crucially on property P5 of the permutations
![]() $\sigma _{f}^{\pm },\tau _{f}^{\pm }$
stating that they are obtained from fixed permutations in
$\sigma _{f}^{\pm },\tau _{f}^{\pm }$
stating that they are obtained from fixed permutations in
![]() $S_{\mathfrak {v}}$
. This means that each of the summands
$S_{\mathfrak {v}}$
. This means that each of the summands
of
(cf. equation (5.14)) agrees with a function of
![]() $n^{-1}$
that is holomorphic in an open disc with center
$n^{-1}$
that is holomorphic in an open disc with center
![]() $0$
and with rational coefficients of its Taylor series by Proposition 4.6. Since there are only finitely many summands in equation (5.14), this proves the lemma.
$0$
and with rational coefficients of its Taylor series by Proposition 4.6. Since there are only finitely many summands in equation (5.14), this proves the lemma.
We also give a coarse bound for the quantities
![]() $\Upsilon _{n}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm }\},\nu ,\{\mu _{f}\},\lambda )$
; this will be improved later in Proposition 5.21.
$\Upsilon _{n}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm }\},\nu ,\{\mu _{f}\},\lambda )$
; this will be improved later in Proposition 5.21.
Lemma 5.13. We have
Proof. For fixed
![]() $\nu ,\{\mu _{f}\},\lambda $
, the range of summation in equation (5.14) is parameterized
$\nu ,\{\mu _{f}\},\lambda $
, the range of summation in equation (5.14) is parameterized
![]() $1:1$
by the eight tableaux of the form
$1:1$
by the eight tableaux of the form
Also, since the matrix coefficients in equation (5.15) involve unit vectors in a unitary representation, each summand in equation (5.15) is
![]() $\leq 1$
in absolute value. Hence, the lemma follows.
$\leq 1$
in absolute value. Hence, the lemma follows.
5.5 A geometric bound for products of matrix coefficients
We continue to keep all the notations and assumptions of
![]() $\S \S $
5.4. We will show that we can give improved bounds for the product of matrix coefficients
$\S \S $
5.4. We will show that we can give improved bounds for the product of matrix coefficients
![]() $\mathcal {M}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm },r_{f}^{\pm },s_{f},t_{f}\})$
defined in equation (5.15) in terms of geometric properties of Y. Recall the definitions of the functions
$\mathcal {M}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm },r_{f}^{\pm },s_{f},t_{f}\})$
defined in equation (5.15) in terms of geometric properties of Y. Recall the definitions of the functions
![]() $\mathrm {top}$
and d from
$\mathrm {top}$
and d from
![]() $\S \S $
4.3. We define
$\S \S $
4.3. We define
 $$ \begin{align} & D_{\mathrm{top}}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right)\stackrel{\mathrm{def}}{=}\\ & ~~~d\left(\sigma_{b}^{-}\left(\sigma_{a}^{+}\right)^{-1}\mathrm{top}(r_{a}^{+}\sqcup s_{a}),\mathrm{top}(r_{b}^{-}\sqcup s{}_{b})\right)+d\left(\tau_{a}^{+}\left(\sigma_{b}^{+}\right)^{-1}\mathrm{top}(r_{b}^{+}\sqcup s_{b}),\mathrm{top}(r_{a}^{+}\sqcup t_{a})\right)+\nonumber \\ & ~~~d\left(\tau_{b}^{+}\left(\tau_{a}^{-}\right)^{-1}\mathrm{top}(r_{a}^{-}\sqcup t{}_{a}),\mathrm{top}(r_{b}^{+}\sqcup t_{b})\right)+d\left(\sigma_{c}^{-}\left(\tau_{b}^{-}\right)^{-1}\mathrm{top}(r_{b}^{-}\sqcup t{}_{b}),\mathrm{top}(r_{c}^{-}\sqcup s{}_{c})\right)+\nonumber \\ & ~~~d\left(\sigma_{d}^{-}\left(\sigma_{c}^{+}\right)^{-1}\mathrm{top}(r_{c}^{+}\sqcup s_{c}),\mathrm{top}(r_{d}^{-}\sqcup s{}_{d})\right)+d\left(\tau_{c}^{+}\left(\sigma_{d}^{+}\right)^{-1}\mathrm{top}(r_{d}^{+}\sqcup s_{d}),\mathrm{top}(r_{c}^{+}\sqcup t_{c})\right)+\nonumber \\ & ~~~d\left(\tau_{d}^{+}\left(\tau_{c}^{-}\right)^{-1}\mathrm{top}(r_{c}^{-}\sqcup t{}_{c}),\mathrm{top}(r_{d}^{+}\sqcup t_{d})\right)+d\left(\sigma_{a}^{-}\left(\tau_{d}^{-}\right)^{-1}\mathrm{top}(r_{d}^{-}\sqcup t{}_{d}),\mathrm{top}(r_{a}^{-}\sqcup s{}_{a})\right).\nonumber \end{align} $$
$$ \begin{align} & D_{\mathrm{top}}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right)\stackrel{\mathrm{def}}{=}\\ & ~~~d\left(\sigma_{b}^{-}\left(\sigma_{a}^{+}\right)^{-1}\mathrm{top}(r_{a}^{+}\sqcup s_{a}),\mathrm{top}(r_{b}^{-}\sqcup s{}_{b})\right)+d\left(\tau_{a}^{+}\left(\sigma_{b}^{+}\right)^{-1}\mathrm{top}(r_{b}^{+}\sqcup s_{b}),\mathrm{top}(r_{a}^{+}\sqcup t_{a})\right)+\nonumber \\ & ~~~d\left(\tau_{b}^{+}\left(\tau_{a}^{-}\right)^{-1}\mathrm{top}(r_{a}^{-}\sqcup t{}_{a}),\mathrm{top}(r_{b}^{+}\sqcup t_{b})\right)+d\left(\sigma_{c}^{-}\left(\tau_{b}^{-}\right)^{-1}\mathrm{top}(r_{b}^{-}\sqcup t{}_{b}),\mathrm{top}(r_{c}^{-}\sqcup s{}_{c})\right)+\nonumber \\ & ~~~d\left(\sigma_{d}^{-}\left(\sigma_{c}^{+}\right)^{-1}\mathrm{top}(r_{c}^{+}\sqcup s_{c}),\mathrm{top}(r_{d}^{-}\sqcup s{}_{d})\right)+d\left(\tau_{c}^{+}\left(\sigma_{d}^{+}\right)^{-1}\mathrm{top}(r_{d}^{+}\sqcup s_{d}),\mathrm{top}(r_{c}^{+}\sqcup t_{c})\right)+\nonumber \\ & ~~~d\left(\tau_{d}^{+}\left(\tau_{c}^{-}\right)^{-1}\mathrm{top}(r_{c}^{-}\sqcup t{}_{c}),\mathrm{top}(r_{d}^{+}\sqcup t_{d})\right)+d\left(\sigma_{a}^{-}\left(\tau_{d}^{-}\right)^{-1}\mathrm{top}(r_{d}^{-}\sqcup t{}_{d}),\mathrm{top}(r_{a}^{-}\sqcup s{}_{a})\right).\nonumber \end{align} $$
Proposition 4.4 directly implies the following result.
Lemma 5.14. If
![]() $\lambda _{1}+\nu _{1}>n-\mathfrak {f}+\left (\mathfrak {v}-\mathfrak {f}\right )^{2}$
, then
$\lambda _{1}+\nu _{1}>n-\mathfrak {f}+\left (\mathfrak {v}-\mathfrak {f}\right )^{2}$
, then
 $$\begin{align*}\left|\mathcal{M}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right)\right|\leq\left(\frac{(\mathfrak{v}-\mathfrak{f})^{2}}{\lambda_{1}+\nu_{1}-(n-\mathfrak{f})}\right)^{D_{\mathrm{top}}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right)}. \end{align*}$$
$$\begin{align*}\left|\mathcal{M}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right)\right|\leq\left(\frac{(\mathfrak{v}-\mathfrak{f})^{2}}{\lambda_{1}+\nu_{1}-(n-\mathfrak{f})}\right)^{D_{\mathrm{top}}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right)}. \end{align*}$$
Remark 5.15. If
![]() $\nu $
has a fixed bound on the number of boxes outside its first row and Y is fixed, then the hypothesis of Lemma 5.14 is satisfied for sufficiently large n.
$\nu $
has a fixed bound on the number of boxes outside its first row and Y is fixed, then the hypothesis of Lemma 5.14 is satisfied for sufficiently large n.
The quantities
![]() $D_{\mathrm {top}}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm },r_{f}^{\pm },s_{f},t_{f}\})$
have a useful interpretation in terms of the combinatorics of the boundary cycles of Y. To explain this, we construct from the data
$D_{\mathrm {top}}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm },r_{f}^{\pm },s_{f},t_{f}\})$
have a useful interpretation in terms of the combinatorics of the boundary cycles of Y. To explain this, we construct from the data
![]() $\{\sigma _{f}^{\pm },\tau _{f}^{\pm },r_{f}^{\pm },s_{f},t_{f}\}$
a labeling of the sides/half-sides of rectangles/half-rectangles in
$\{\sigma _{f}^{\pm },\tau _{f}^{\pm },r_{f}^{\pm },s_{f},t_{f}\}$
a labeling of the sides/half-sides of rectangles/half-rectangles in
![]() $Y_{+}^{(1)}$
.
$Y_{+}^{(1)}$
.
5.6 Construction of labelings of tiled surfaces from collections of tableaux
In this section, we keep all of the notation from the previous sections. In particular, we have a fixed vertex-labeled compact tiled surface
![]() $(Y,\mathcal {J}_{n})$
with
$(Y,\mathcal {J}_{n})$
with
![]() $\mathfrak {v}$
vertices,
$\mathfrak {v}$
vertices,
![]() $\mathfrak {e}_{f} f$
-labeled edges for each
$\mathfrak {e}_{f} f$
-labeled edges for each
![]() $f\in \{a,b,c,d\}$
, and
$f\in \{a,b,c,d\}$
, and
![]() $\mathfrak {f}$
octagons. We fix the data
$\mathfrak {f}$
octagons. We fix the data
 $$ \begin{align} \nu\vdash n-\mathfrak{v},\lambda\vdash n-\mathfrak{f}\nonumber \\ \nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda & \quad\forall f\in\{a,b,c,d\}\nonumber \\ r_{f}^{+},r_{f}^{-}\in\mathrm{Tab}(\mu_{f}/\nu),\,s_{f},t_{f}\in\mathrm{Tab}(\lambda/\mu_{f}) & \quad\forall f\in\{a,b,c,d\}. \end{align} $$
$$ \begin{align} \nu\vdash n-\mathfrak{v},\lambda\vdash n-\mathfrak{f}\nonumber \\ \nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda & \quad\forall f\in\{a,b,c,d\}\nonumber \\ r_{f}^{+},r_{f}^{-}\in\mathrm{Tab}(\mu_{f}/\nu),\,s_{f},t_{f}\in\mathrm{Tab}(\lambda/\mu_{f}) & \quad\forall f\in\{a,b,c,d\}. \end{align} $$
All this data uniquely determine one summand of
![]() $\Upsilon _{n}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm }\},\nu ,\{\mu _{f}\},\lambda )$
as in equation (5.15) and hence also of
$\Upsilon _{n}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm }\},\nu ,\{\mu _{f}\},\lambda )$
as in equation (5.15) and hence also of
![]() $\Xi _{n}(Y)$
as in equation (5.19).
$\Xi _{n}(Y)$
as in equation (5.19).
Recall that in
![]() $\S \S $
5.3 we constructed the maps
$\S \S $
5.3 we constructed the maps
![]() $\sigma _{f}^{\pm }$
and
$\sigma _{f}^{\pm }$
and
![]() $\tau _{f}^{\pm }$
according to numbering in
$\tau _{f}^{\pm }$
according to numbering in
![]() $\left [\mathfrak {v}-\mathfrak {f}\right ]$
of octagons, of exposed sides of full-edges and of hanging half-edges of
$\left [\mathfrak {v}-\mathfrak {f}\right ]$
of octagons, of exposed sides of full-edges and of hanging half-edges of
![]() $Y_{+}$
. By adding
$Y_{+}$
. By adding
![]() $n-\mathfrak {v},$
these numbers are in
$n-\mathfrak {v},$
these numbers are in
![]() $\left [n-\mathfrak {v}+1,n-\mathfrak {f}\right ]$
, give rise to the images of the corresponding vertices of Y through
$\left [n-\mathfrak {v}+1,n-\mathfrak {f}\right ]$
, give rise to the images of the corresponding vertices of Y through
![]() $\sigma _{f}^{\pm },\tau _{f}^{\pm }$
, and are the elements in the tableaux
$\sigma _{f}^{\pm },\tau _{f}^{\pm }$
, and are the elements in the tableaux
![]() $r_{f}^{\pm },s_{f},t_{f}$
. Given these tableaux, we assign a ‘top’ label to the hanging half-edges and exposed sides of full-edges which appear in the top row of the corresponding tableau. Namely,
$r_{f}^{\pm },s_{f},t_{f}$
. Given these tableaux, we assign a ‘top’ label to the hanging half-edges and exposed sides of full-edges which appear in the top row of the corresponding tableau. Namely,
-
• Every exposed left side (resp. right side) of an f-full-edge is labeled ‘top’ if the corresponding element in
 $s_{f}$
(resp.
$s_{f}$
(resp.
 $t_{f}$
) lies in the top row.Footnote
15
$t_{f}$
) lies in the top row.Footnote
15
-
• Every outgoing (resp. incoming) hanging f-half-edge is labeled ‘top’ if the corresponding element in
 $r_{f}^{-}$
(resp.
$r_{f}^{-}$
(resp.
 $r_{f}^{+}$
) lies in the top row.
$r_{f}^{+}$
) lies in the top row.
This labeling scheme is illustrated in Figure 5.2.

Figure 5.2 Illustration of how the tableaux
![]() $r_{f}^{-},r_{f}^{+},s_{f},t_{f}$
induce the ‘top’ labeling.
$r_{f}^{-},r_{f}^{+},s_{f},t_{f}$
induce the ‘top’ labeling.
The purpose of introducing these labelings is the following diagrammatic interpretation of
![]() $D_{\mathrm {top}}$
. We view the boundary
$D_{\mathrm {top}}$
. We view the boundary
![]() $\partial Y_{+}$
of (the thick version of)
$\partial Y_{+}$
of (the thick version of)
![]() $Y_{+}$
to consist of hanging half-edges and of exposed sides of full-edges.
$Y_{+}$
to consist of hanging half-edges and of exposed sides of full-edges.
Lemma 5.16. The quantity
![]() $D_{\mathrm {top}}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm },r_{f}^{\pm },s_{f},t_{f}\})$
is half the number of incidences between two consecutive parts of
$D_{\mathrm {top}}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm },r_{f}^{\pm },s_{f},t_{f}\})$
is half the number of incidences between two consecutive parts of
![]() $\partial Y_{+}$
among which one is labeled ‘top’ and other one is not.
$\partial Y_{+}$
among which one is labeled ‘top’ and other one is not.
Proof. This follows simply by careful consideration of the definition (5.20) of
![]() $D_{\mathrm {top}}$
, as the permutations appearing in that definition map the index of one part of
$D_{\mathrm {top}}$
, as the permutations appearing in that definition map the index of one part of
![]() $\partial Y_{+}$
to a neighboring part. For example,
$\partial Y_{+}$
to a neighboring part. For example,
![]() $\sigma _{b}^{-}\left (\sigma _{a}^{+}\right )^{-1}$
maps the index on an exposed left side of an a-full-edge to the neighboring index which either belongs to an exposed left side of a b-full-edge or to a hanging outgoing b-half-edge.
$\sigma _{b}^{-}\left (\sigma _{a}^{+}\right )^{-1}$
maps the index on an exposed left side of an a-full-edge to the neighboring index which either belongs to an exposed left side of a b-full-edge or to a hanging outgoing b-half-edge.
The reason for the factor
![]() $\frac {1}{2}$
is that for
$\frac {1}{2}$
is that for
![]() $A,B$
of the same size,
$A,B$
of the same size,
![]() $d(A,B)$
is half the size of the symmetric difference of A and B. While in the definition of
$d(A,B)$
is half the size of the symmetric difference of A and B. While in the definition of
![]() $D_{\mathrm {top}}$
we count differences
$D_{\mathrm {top}}$
we count differences
![]() $d\left (A,B\right )$
, in counting switches between ‘top’ parts to ‘nontop’ parts of
$d\left (A,B\right )$
, in counting switches between ‘top’ parts to ‘nontop’ parts of
![]() $\partial Y_{+}$
and vice versa, we refer to symmetric differences.
$\partial Y_{+}$
and vice versa, we refer to symmetric differences.
The benefit of Lemma 5.16 is that it allows us to connect the possible properties of Y being boundary reduced or strongly boundary reduced to nontrivial bounds for matrix coefficients.
A piece of
![]() $\partial Y_{+}$
is a contiguous collection of exposed sides of full-edges and of hanging half-edges. Given a piece P, we write
$\partial Y_{+}$
is a contiguous collection of exposed sides of full-edges and of hanging half-edges. Given a piece P, we write
![]() $\mathfrak {e}(P)$
for the number of exposed sides-of-full-edges in P,
$\mathfrak {e}(P)$
for the number of exposed sides-of-full-edges in P,
![]() $\mathfrak {he}(P)$
for the number of hanging half-edges in P and
$\mathfrak {he}(P)$
for the number of hanging half-edges in P and
![]() $\chi \left (P\right )$
for the Euler characteristic of P, which may by
$\chi \left (P\right )$
for the Euler characteristic of P, which may by
![]() $0$
(if P is a circle) or
$0$
(if P is a circle) or
![]() $1$
(if P is topologically a path). A piece collection
$1$
(if P is topologically a path). A piece collection
![]() $\mathcal {P}$
of
$\mathcal {P}$
of
![]() $\partial Y_{+}$
is a collection of disjoint pieces of
$\partial Y_{+}$
is a collection of disjoint pieces of
![]() $\partial Y_{+}$
(without intersection even of endpoints).
$\partial Y_{+}$
(without intersection even of endpoints).
Definition 5.17. Define
andFootnote 16
where the maximum is over all nonempty piece collections of
![]() $\partial Y_{+}$
.
$\partial Y_{+}$
.
Lemma 5.18. If Y is boundary reduced, then
If Y is strongly boundary reduced, then
Proof. Assume first that Y is boundary reduced. Recall that Y has no long blocks, so no blocks of size
![]() $>4$
and no long chains, so between every two blocks of size
$>4$
and no long chains, so between every two blocks of size
![]() $4$
in the same piece, there must be either two consecutive hanging edges or one block of size
$4$
in the same piece, there must be either two consecutive hanging edges or one block of size
![]() $\le 2$
. As a result, for every piece P of
$\le 2$
. As a result, for every piece P of
![]() $\partial Y_{+}$
that is a circle, we have
$\partial Y_{+}$
that is a circle, we have
![]() $\mathrm {Defect}(P)\leq 0$
so
$\mathrm {Defect}(P)\leq 0$
so
![]() $\mathrm {Defect}(P)-8\chi (P)\leq 0$
. For every piece P of
$\mathrm {Defect}(P)-8\chi (P)\leq 0$
. For every piece P of
![]() $\partial Y_{+}$
that is a path, we have
$\partial Y_{+}$
that is a path, we have
![]() $\mathrm {Defect}(P)\leq 4$
: This bound is attained for example when P corresponds to a block of size
$\mathrm {Defect}(P)\leq 4$
: This bound is attained for example when P corresponds to a block of size
![]() $4$
or to two consecutive blocks of size
$4$
or to two consecutive blocks of size
![]() $4$
and
$4$
and
![]() $3$
. Therefore,
$3$
. Therefore,
![]() $\mathrm {Defect}(P)-8\chi (P)\leq -4$
. Hence, all contributions to
$\mathrm {Defect}(P)-8\chi (P)\leq -4$
. Hence, all contributions to
![]() $\max \mathrm {Defect}(Y)$
are nonpositive, and we obtain equation (5.22).
$\max \mathrm {Defect}(Y)$
are nonpositive, and we obtain equation (5.22).
If Y is strongly boundary reduced, there are no blocks in
![]() $\partial Y$
of length
$\partial Y$
of length
![]() $>3$
, and so every piece P of
$>3$
, and so every piece P of
![]() $\partial Y_{+}$
which is a path that satisfies
$\partial Y_{+}$
which is a path that satisfies
![]() $\mathrm {Defect}(P)\leq 3$
and
$\mathrm {Defect}(P)\leq 3$
and
![]() $\mathrm {Defect}(P)-8\chi (P)\leq -5$
: This bound is attained when P corresponds to a chain of consecutive blocks of size
$\mathrm {Defect}(P)-8\chi (P)\leq -5$
: This bound is attained when P corresponds to a chain of consecutive blocks of size
![]() $3$
each. If P is a piece of
$3$
each. If P is a piece of
![]() $\partial Y_{+}$
that is a circle but not a cyclic chain, then there are two consecutive hanging half-edges and
$\partial Y_{+}$
that is a circle but not a cyclic chain, then there are two consecutive hanging half-edges and
![]() $\mathrm {Defect}(P)=\mathrm {Defect}(P)-\chi (P)\leq -3$
. If P is a cyclic chain, then by [Reference Magee and PuderMP22a, Lem. 3.6] it cannot have only one block of size
$\mathrm {Defect}(P)=\mathrm {Defect}(P)-\chi (P)\leq -3$
. If P is a cyclic chain, then by [Reference Magee and PuderMP22a, Lem. 3.6] it cannot have only one block of size
![]() $2$
, so
$2$
, so
![]() $\mathrm {Defect}(P)=\mathrm {Defect}(P)-\chi (P)\leq -2$
. This proves equation (5.23).
$\mathrm {Defect}(P)=\mathrm {Defect}(P)-\chi (P)\leq -2$
. This proves equation (5.23).
The following result relates the structure of the pieces of
![]() $\partial Y$
to the quantities
$\partial Y$
to the quantities
![]() $D_{\mathrm {top}}$
and
$D_{\mathrm {top}}$
and
![]() $D_{\mathrm {\mathrm {left}}}$
appearing in our previous bound (Lemma 5.14) for matrix coefficients. Given an SYD
$D_{\mathrm {\mathrm {left}}}$
appearing in our previous bound (Lemma 5.14) for matrix coefficients. Given an SYD
![]() $\lambda /\nu $
, we write
$\lambda /\nu $
, we write
![]() $b_{\lambda /\nu }$
for the number of boxes of
$b_{\lambda /\nu }$
for the number of boxes of
![]() $\lambda /\nu $
outside the first row.
$\lambda /\nu $
outside the first row.
Proposition 5.19. Suppose we are given
![]() $\nu ,\mu _{f},\lambda ,r_{f}^{\pm },s_{f},t_{f}$
as in equation (5.21). If
$\nu ,\mu _{f},\lambda ,r_{f}^{\pm },s_{f},t_{f}$
as in equation (5.21). If
![]() $b_{\lambda /\nu }>0$
, thenFootnote
17
$b_{\lambda /\nu }>0$
, thenFootnote
17
Proof. We define a collection of pieces
![]() $\mathcal {P}$
of
$\mathcal {P}$
of
![]() $\partial Y_{+}$
according to the ‘top’ labels: Pieces are contiguous segments of
$\partial Y_{+}$
according to the ‘top’ labels: Pieces are contiguous segments of
![]() $\partial Y_{+}$
(hanging half-edges or exposed sides of full edges) which are not labeled ‘top’. This collection is nonempty if and only if
$\partial Y_{+}$
(hanging half-edges or exposed sides of full edges) which are not labeled ‘top’. This collection is nonempty if and only if
![]() $b_{\lambda /\nu }>0$
, which holds by assumption. Let
$b_{\lambda /\nu }>0$
, which holds by assumption. Let
![]() $\mathcal {P}_{0}$
denote the collection of such pieces that are circles,
$\mathcal {P}_{0}$
denote the collection of such pieces that are circles,
![]() $\mathcal {P}_{1}$
denote the collection of such pieces that are paths and
$\mathcal {P}_{1}$
denote the collection of such pieces that are paths and
![]() $\mathcal {P}=\mathcal {P}_{0}\sqcup \mathcal {P}_{1}$
. It follows from Lemma 5.16 that
$\mathcal {P}=\mathcal {P}_{0}\sqcup \mathcal {P}_{1}$
. It follows from Lemma 5.16 that
Now,
![]() $b_{\lambda /\nu }=\frac {1}{8}\sum _{P\in \mathcal {P}}\left [\mathfrak {e}\left (P\right )+\mathfrak {he}\left (P\right )\right ]$
because for every
$b_{\lambda /\nu }=\frac {1}{8}\sum _{P\in \mathcal {P}}\left [\mathfrak {e}\left (P\right )+\mathfrak {he}\left (P\right )\right ]$
because for every
![]() $f\in \left \{ a,b,c,d\right \} $
, every square outside the top row of
$f\in \left \{ a,b,c,d\right \} $
, every square outside the top row of
![]() $\lambda /\nu $
corresponds either to two hanging half-edges (in case this square belongs to
$\lambda /\nu $
corresponds either to two hanging half-edges (in case this square belongs to
![]() $\mu _{f}/\nu $
) or to two exposed-sides-of-full-edges (in case this square belongs to
$\mu _{f}/\nu $
) or to two exposed-sides-of-full-edges (in case this square belongs to
![]() $\lambda /\mu _{f}$
). Similarly,
$\lambda /\mu _{f}$
). Similarly,
![]() $b_{\mu _{a}/\nu }+b_{\mu _{b}/\nu }+b_{\mu _{c}/\nu }+b_{\mu _{d}/\nu }=\frac {1}{2}\sum _{P\in \mathcal {P}}\mathfrak {he}\left (P\right )$
. Thus,
$b_{\mu _{a}/\nu }+b_{\mu _{b}/\nu }+b_{\mu _{c}/\nu }+b_{\mu _{d}/\nu }=\frac {1}{2}\sum _{P\in \mathcal {P}}\mathfrak {he}\left (P\right )$
. Thus,
 $$ \begin{align*} b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}-D_{\mathrm{top}} & =\sum_{P\in\mathcal{\mathcal{P}}}\left(\frac{1}{8}\left(\mathfrak{e}(P)+\mathfrak{he}(P)\right)-\frac{1}{2}\mathfrak{he}(P)\right)-\sum_{P\in\mathcal{P}_{1}}1\\ & =\sum_{P\in\mathcal{P}_{0}}\frac{1}{8}\mathrm{Defect}(P)+\sum_{P\in\mathcal{P}_{1}}\frac{1}{8}\left(\mathrm{Defect}(P)-8\right)\\ & =\sum_{P\in\mathcal{P}}\frac{1}{8}\left(\mathrm{Defect}(P)-8\chi(P)\right)\leq\frac{1}{8}\max\mathrm{Defect}(Y). \end{align*} $$
$$ \begin{align*} b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}-D_{\mathrm{top}} & =\sum_{P\in\mathcal{\mathcal{P}}}\left(\frac{1}{8}\left(\mathfrak{e}(P)+\mathfrak{he}(P)\right)-\frac{1}{2}\mathfrak{he}(P)\right)-\sum_{P\in\mathcal{P}_{1}}1\\ & =\sum_{P\in\mathcal{P}_{0}}\frac{1}{8}\mathrm{Defect}(P)+\sum_{P\in\mathcal{P}_{1}}\frac{1}{8}\left(\mathrm{Defect}(P)-8\right)\\ & =\sum_{P\in\mathcal{P}}\frac{1}{8}\left(\mathrm{Defect}(P)-8\chi(P)\right)\leq\frac{1}{8}\max\mathrm{Defect}(Y). \end{align*} $$
Proposition 5.20. Suppose we are given
![]() $\nu ,\mu _{f},\lambda ,r_{f}^{-},r_{f}^{+},s_{f},t_{f}$
as in equation (5.21).
$\nu ,\mu _{f},\lambda ,r_{f}^{-},r_{f}^{+},s_{f},t_{f}$
as in equation (5.21).
-
1. If Y is boundary reduced,
(5.24) $$ \begin{align} D_{\mathrm{top}}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right)\geq b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}. \end{align} $$
$$ \begin{align} D_{\mathrm{top}}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right)\geq b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}. \end{align} $$
-
2. If Y is strongly boundary reduced, then equation (5.24) becomes an equality if and only if
(5.25) $$ \begin{align} D_{\mathrm{top}}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right)=b_{\lambda/\nu}=b_{\mu_{a}/\nu}=b_{\mu_{b}/\nu}=b_{\mu_{c}/\nu}=b_{\mu_{d}/\nu}=0. \end{align} $$
$$ \begin{align} D_{\mathrm{top}}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right)=b_{\lambda/\nu}=b_{\mu_{a}/\nu}=b_{\mu_{b}/\nu}=b_{\mu_{c}/\nu}=b_{\mu_{d}/\nu}=0. \end{align} $$
Otherwise,
(5.26) $$ \begin{align} D_{\mathrm{top}}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right)\geq b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}+1. \end{align} $$
$$ \begin{align} D_{\mathrm{top}}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm},r_{f}^{\pm},s_{f},t_{f}\right\} \right)\geq b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}+1. \end{align} $$
Proof. Note that, for any Y, if
![]() $b_{\lambda /\nu }=0$
, then
$b_{\lambda /\nu }=0$
, then
![]() $D_{\mathrm {top}}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm },r_{f}^{\pm },s_{f},t_{f}\})=b_{\mu _{a}/\nu }=b_{\mu _{b}/\nu }=b_{\mu _{c}/\nu }=b_{\mu _{d}/\nu }=0$
. Otherwise, Proposition 5.19 applies, and we obtain the statement of the proposition by combining Proposition 5.19 with the inequalities (5.22) and (5.23). To obtain equation (5.26) from equation (5.23) (instead of a bound featuring
$D_{\mathrm {top}}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm },r_{f}^{\pm },s_{f},t_{f}\})=b_{\mu _{a}/\nu }=b_{\mu _{b}/\nu }=b_{\mu _{c}/\nu }=b_{\mu _{d}/\nu }=0$
. Otherwise, Proposition 5.19 applies, and we obtain the statement of the proposition by combining Proposition 5.19 with the inequalities (5.22) and (5.23). To obtain equation (5.26) from equation (5.23) (instead of a bound featuring
![]() $\frac {1}{4}$
), one uses that all
$\frac {1}{4}$
), one uses that all
![]() $b_{\bullet }$
quantities and
$b_{\bullet }$
quantities and
![]() $D_{\mathrm {top}}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm },r_{f}^{\pm },s_{f},t_{f}\})$
are integer valued.
$D_{\mathrm {top}}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm },r_{f}^{\pm },s_{f},t_{f}\})$
are integer valued.
Proposition 5.20 together with Lemma 5.16 have the following important consequence for the quantities
![]() $\Upsilon _{n}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm }\},\nu ,\{\mu _{f}\},\lambda )$
.
$\Upsilon _{n}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm }\},\nu ,\{\mu _{f}\},\lambda )$
.
Proposition 5.21. Suppose that
![]() $\nu ,\{\mu _{f}\},\lambda $
are as in equation (5.21) and that
$\nu ,\{\mu _{f}\},\lambda $
are as in equation (5.21) and that
![]() $\lambda _{1}+\nu _{1}>n-\mathfrak {f}+(\mathfrak {v}-\mathfrak {f})^{2}$
.
$\lambda _{1}+\nu _{1}>n-\mathfrak {f}+(\mathfrak {v}-\mathfrak {f})^{2}$
.
-
1. If Y is boundary reduced, then
(5.27) $$ \begin{align} \kern-10pt\left|\Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda\right)\right| & \leq\left((\mathfrak{v}-\mathfrak{f})!\right)^{8}\left(\frac{(\mathfrak{v}-\mathfrak{f})^{2}}{\nu_{1}+\lambda_{1}-(n-\mathfrak{f})}\right)^{b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}}. \end{align} $$
$$ \begin{align} \kern-10pt\left|\Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda\right)\right| & \leq\left((\mathfrak{v}-\mathfrak{f})!\right)^{8}\left(\frac{(\mathfrak{v}-\mathfrak{f})^{2}}{\nu_{1}+\lambda_{1}-(n-\mathfrak{f})}\right)^{b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}}. \end{align} $$
-
2. If Y is strongly boundary reduced and
 $b_{\text {\(\lambda /\)}\nu }>0$
, then (5.28)
$b_{\text {\(\lambda /\)}\nu }>0$
, then (5.28) $$ \begin{align} \kern-20pt\left|\Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda\right)\right|\leq\left((\mathfrak{v}-\mathfrak{f})!\right)^{8}\left(\frac{(\mathfrak{v}-\mathfrak{f})^{2}}{\nu_{1}+\lambda_{1}-(n-\mathfrak{f})}\right)^{1+b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}}. \end{align} $$
$$ \begin{align} \kern-20pt\left|\Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda\right)\right|\leq\left((\mathfrak{v}-\mathfrak{f})!\right)^{8}\left(\frac{(\mathfrak{v}-\mathfrak{f})^{2}}{\nu_{1}+\lambda_{1}-(n-\mathfrak{f})}\right)^{1+b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}}. \end{align} $$
-
3. For any Y, if
 $b_{\lambda /\nu }=0$
, then
$b_{\lambda /\nu }=0$
, then  $$\begin{align*}\Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda\right)=1. \end{align*}$$
$$\begin{align*}\Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda\right)=1. \end{align*}$$
Proof.
Part 1. Suppose that Y is boundary reduced. As argued in the proof of 5.13, there are at most
![]() $(d_{\lambda /\nu })^{8}\leq ((\mathfrak {v}-\mathfrak {f})!)^{8}$
summands in the definition (5.14) of
$(d_{\lambda /\nu })^{8}\leq ((\mathfrak {v}-\mathfrak {f})!)^{8}$
summands in the definition (5.14) of
![]() $\Upsilon _{n}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm }\},\nu ,\{\mu _{f}\},\lambda )$
. Each summand is some
$\Upsilon _{n}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm }\},\nu ,\{\mu _{f}\},\lambda )$
. Each summand is some
![]() $\mathcal {M}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm },r_{f}^{\pm },s_{f},t_{f}\})$
, so by Lemma 5.14 and Proposition 5.20 Part 1, we get that each summand of equation (5.14) has absolute value
$\mathcal {M}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm },r_{f}^{\pm },s_{f},t_{f}\})$
, so by Lemma 5.14 and Proposition 5.20 Part 1, we get that each summand of equation (5.14) has absolute value
 $$\begin{align*}\leq\left(\frac{(\mathfrak{v}-\mathfrak{f})^{2}}{\nu_{1}+\lambda_{1}-(n-\mathfrak{f})}\right)^{b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}}. \end{align*}$$
$$\begin{align*}\leq\left(\frac{(\mathfrak{v}-\mathfrak{f})^{2}}{\nu_{1}+\lambda_{1}-(n-\mathfrak{f})}\right)^{b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}}. \end{align*}$$
This proves equation (5.27).
Part 2. Suppose now that Y is strongly boundary reduced and that
![]() $b_{\lambda /\nu }>0$
. This time, Lemma 5.14 and Proposition 5.20 give that each summand of
$b_{\lambda /\nu }>0$
. This time, Lemma 5.14 and Proposition 5.20 give that each summand of
![]() $\Upsilon _{n}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm }\},\nu ,\{\mu _{f}\},\lambda )$
in equation (5.14) has absolute value
$\Upsilon _{n}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm }\},\nu ,\{\mu _{f}\},\lambda )$
in equation (5.14) has absolute value
 $$\begin{align*}\leq\left(\frac{(\mathfrak{v}-\mathfrak{f})^{2}}{\nu_{1}+\lambda_{1}-(n-\mathfrak{f})}\right)^{1+b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}}. \end{align*}$$
$$\begin{align*}\leq\left(\frac{(\mathfrak{v}-\mathfrak{f})^{2}}{\nu_{1}+\lambda_{1}-(n-\mathfrak{f})}\right)^{1+b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}}. \end{align*}$$
As in Part 1, there are
![]() $\leq ((\mathfrak {v}-\mathfrak {f})!)^{8}$
summands of equation (5.14), so this proves equation (5.28).
$\leq ((\mathfrak {v}-\mathfrak {f})!)^{8}$
summands of equation (5.14), so this proves equation (5.28).
Part 3. Suppose that
![]() $b_{\lambda /\nu }=0$
. Then there is only one possible choice for the tableaux
$b_{\lambda /\nu }=0$
. Then there is only one possible choice for the tableaux
![]() $r_{f}^{-},r_{f}^{+},s_{f},t_{f}$
in equation (5.14). Moreover,
$r_{f}^{-},r_{f}^{+},s_{f},t_{f}$
in equation (5.14). Moreover,
![]() $V^{\lambda /\nu }$
is the trivial module for the relevant copy of
$V^{\lambda /\nu }$
is the trivial module for the relevant copy of
![]() $S_{\mathfrak {v}-\mathfrak {f}}$
, hence the product of matrix coefficients appearing in equation (5.15) is equal to
$S_{\mathfrak {v}-\mathfrak {f}}$
, hence the product of matrix coefficients appearing in equation (5.15) is equal to
![]() $1$
, and
$1$
, and
![]() $\Upsilon _{n}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm }\},\nu ,\{\mu _{f}\},\lambda )=1$
.
$\Upsilon _{n}(\{\sigma _{f}^{\pm },\tau _{f}^{\pm }\},\nu ,\{\mu _{f}\},\lambda )=1$
.
5.7 Stronger bounds for matrix coefficients
In this section, we give a strengthening of Proposition 5.19 that is used in a sequel to this paper [Reference Magee, Naud and PuderMNP22]. A reader who is only interested in the current paper may skip this short
![]() $\S \S $
5.7.
$\S \S $
5.7.
Proposition 5.22. Suppose we are given YDs
![]() $\nu \vdash n-\mathfrak {v}$
,
$\nu \vdash n-\mathfrak {v}$
,
![]() $\lambda \vdash n-\mathfrak {f}$
and
$\lambda \vdash n-\mathfrak {f}$
and
![]() $\mu _{f}$
such that
$\mu _{f}$
such that
and tableaux
![]() $r_{f}^{+},r_{f}^{-}\in \mathrm {Tab}(\mu _{f}/\nu )$
and
$r_{f}^{+},r_{f}^{-}\in \mathrm {Tab}(\mu _{f}/\nu )$
and
![]() $s_{f},t_{f}\in \mathrm {Tab}(\lambda /\mu _{f})$
. Fix
$s_{f},t_{f}\in \mathrm {Tab}(\lambda /\mu _{f})$
. Fix
![]() $\varepsilon \ge 0$
, and suppose in addition that for every piece P of
$\varepsilon \ge 0$
, and suppose in addition that for every piece P of
![]() $\partial Y$
we have
$\partial Y$
we have
Then
Proof. We follow the same construction of a piece collection
![]() $\mathcal {P}$
as in the proof of Proposition 5.19. This leads to
$\mathcal {P}$
as in the proof of Proposition 5.19. This leads to
 $$ \begin{align*} b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}-D_{\mathrm{top}} & = \frac{1}{8}\sum_{P\in\mathcal{P}}\mathrm{Defect}(P)-8\chi(P)\le\frac{1}{8}\sum_{P\in\mathcal{P}}\mathrm{Defect}(P)-4\chi(P)\\ & \le -\frac{\varepsilon}{8}\sum_{P\in\mathcal{P}}\left(\mathfrak{e}(P)+\mathfrak{he}(P)\right)=-\varepsilon b_{\lambda/\nu}, \end{align*} $$
$$ \begin{align*} b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}-D_{\mathrm{top}} & = \frac{1}{8}\sum_{P\in\mathcal{P}}\mathrm{Defect}(P)-8\chi(P)\le\frac{1}{8}\sum_{P\in\mathcal{P}}\mathrm{Defect}(P)-4\chi(P)\\ & \le -\frac{\varepsilon}{8}\sum_{P\in\mathcal{P}}\left(\mathfrak{e}(P)+\mathfrak{he}(P)\right)=-\varepsilon b_{\lambda/\nu}, \end{align*} $$
as required.
5.8 Approximating
 $\Xi _{n}(Y)$
by Laurent polynomials
$\Xi _{n}(Y)$
by Laurent polynomials
In this section, we keep all the notations and assumptions of
![]() $\S \S $
5.4. We want to show that we can replace the summation over
$\S \S $
5.4. We want to show that we can replace the summation over
![]() $\nu ,\mu _{f}$
, and
$\nu ,\mu _{f}$
, and
![]() $\lambda $
given the definition of
$\lambda $
given the definition of
![]() $\Xi _{n}\left (Y\right )$
in equation (5.19) by a sum of finite size, independent of n, at the cost of a controllable error term. To state this precisely, recalling the definition of
$\Xi _{n}\left (Y\right )$
in equation (5.19) by a sum of finite size, independent of n, at the cost of a controllable error term. To state this precisely, recalling the definition of
![]() $\Lambda (n,b)$
from
$\Lambda (n,b)$
from
![]() $\S \S $
4.4, and letting
$\S \S $
4.4, and letting
![]() $b\in \mathbf {N}$
, we introduce the quantity
$b\in \mathbf {N}$
, we introduce the quantity
 $$ \begin{align} \Xi_{n}^{(b)}\left(Y\right)\stackrel{\mathrm{def}}{=}\sum_{\substack{\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda\vdash\,n-\mathfrak{f}\\ \nu\notin\Lambda(n-\mathfrak{v},b) } }d_{\lambda}d_{\nu}\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda}\frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda\right). \end{align} $$
$$ \begin{align} \Xi_{n}^{(b)}\left(Y\right)\stackrel{\mathrm{def}}{=}\sum_{\substack{\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda\vdash\,n-\mathfrak{f}\\ \nu\notin\Lambda(n-\mathfrak{v},b) } }d_{\lambda}d_{\nu}\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda}\frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\Upsilon_{n}\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda\right). \end{align} $$
In this summation, we restrict to
![]() $\nu $
that have less than b boxes either outside the first row or outside the first column. Note that whereas
$\nu $
that have less than b boxes either outside the first row or outside the first column. Note that whereas
![]() $\Xi _{n}\left (Y\right )$
does not depend on any of the choices of
$\Xi _{n}\left (Y\right )$
does not depend on any of the choices of
![]() $g^{0}$
and numberings we made in Sections 5.2 and 5.3 (see Remark 5.11),
$g^{0}$
and numberings we made in Sections 5.2 and 5.3 (see Remark 5.11),
![]() $\Xi _{n}^{\left (b\right )}\left (Y\right )$
may depend on these choices.
$\Xi _{n}^{\left (b\right )}\left (Y\right )$
may depend on these choices.
Lemma 5.23. For a fixed tiled surface Y and
![]() $b\in \mathbf {N}$
, for any vertex-ordering
$b\in \mathbf {N}$
, for any vertex-ordering
![]() $\mathcal {J}$
of Y as above, we have
$\mathcal {J}$
of Y as above, we have
as
![]() $n\to \infty $
. The implied constant depends on b,
$n\to \infty $
. The implied constant depends on b,
![]() $\mathfrak {v}$
and
$\mathfrak {v}$
and
![]() $\mathfrak {f}$
.
$\mathfrak {f}$
.
Proof. Note that
![]() $d_{\mu _{f}}\geq d_{\nu }$
, and for fixed
$d_{\mu _{f}}\geq d_{\nu }$
, and for fixed
![]() $\nu $
and
$\nu $
and
![]() $\lambda $
the number of
$\lambda $
the number of
![]() $\mu _{f}$
with
$\mu _{f}$
with
![]() $\nu \subset \mu _{f}\subset _{\mathfrak {e}_{f}-\mathfrak {f}}\lambda $
is
$\nu \subset \mu _{f}\subset _{\mathfrak {e}_{f}-\mathfrak {f}}\lambda $
is
![]() $\leq (\mathfrak {v}-\mathfrak {f})!$
(there is an injection from the collection of such
$\leq (\mathfrak {v}-\mathfrak {f})!$
(there is an injection from the collection of such
![]() $\mu _{f}$
to
$\mu _{f}$
to
![]() $\mathrm {Tab}(\lambda /\nu )$
by filling the boxes of
$\mathrm {Tab}(\lambda /\nu )$
by filling the boxes of
![]() $\mu _{f}/\nu $
with
$\mu _{f}/\nu $
with
![]() $[n-\mathfrak {v}+1,n-\mathfrak {e}_{f}]$
and the other boxes of
$[n-\mathfrak {v}+1,n-\mathfrak {e}_{f}]$
and the other boxes of
![]() $\lambda /\nu $
arbitrarily). Using these observations together with Lemma 5.13, we obtain
$\lambda /\nu $
arbitrarily). Using these observations together with Lemma 5.13, we obtain
 $$ \begin{align*} \left|\Xi_{n}(Y)-\Xi_{n}^{(b)}(Y)\right| & =\left|\sum_{\substack{\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda\vdash\,n-\mathfrak{f}\\ \nu\in\Lambda(n-\mathfrak{v},b) } }d_{\lambda}d_{\nu}\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda}\frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\Upsilon\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda\right)\right|\\ & \leq\left((\mathfrak{v}-\mathfrak{f})!\right)^{12}\sum_{\substack{\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda\vdash\,n-\mathfrak{f}\\ \nu\in\Lambda(n-\mathfrak{v},b) } }\frac{d_{\lambda}}{d_{\nu}^{3}}. \end{align*} $$
$$ \begin{align*} \left|\Xi_{n}(Y)-\Xi_{n}^{(b)}(Y)\right| & =\left|\sum_{\substack{\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda\vdash\,n-\mathfrak{f}\\ \nu\in\Lambda(n-\mathfrak{v},b) } }d_{\lambda}d_{\nu}\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda}\frac{1}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\Upsilon\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda\right)\right|\\ & \leq\left((\mathfrak{v}-\mathfrak{f})!\right)^{12}\sum_{\substack{\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda\vdash\,n-\mathfrak{f}\\ \nu\in\Lambda(n-\mathfrak{v},b) } }\frac{d_{\lambda}}{d_{\nu}^{3}}. \end{align*} $$
By Lemma 3.1, for a fixed
![]() $\nu \vdash n-\mathfrak {v}$
, we have
$\nu \vdash n-\mathfrak {v}$
, we have
 $$\begin{align*}\sum_{\lambda:\,\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda}d_{\lambda}\leq\sum_{\lambda:\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda}d_{\lambda}d_{\lambda/\nu}=\frac{(n-\mathfrak{f})!}{(n-\mathfrak{v})!}d_{\nu}. \end{align*}$$
$$\begin{align*}\sum_{\lambda:\,\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda}d_{\lambda}\leq\sum_{\lambda:\nu\subset_{\mathfrak{v}-\mathfrak{f}}\lambda}d_{\lambda}d_{\lambda/\nu}=\frac{(n-\mathfrak{f})!}{(n-\mathfrak{v})!}d_{\nu}. \end{align*}$$
Therefore, by Proposition 4.5,
 $$ \begin{align*} \left|\Xi_{n}(Y)-\Xi_{n}^{(b)}(Y)\right| & \leq\left((\mathfrak{v}-\mathfrak{f})!\right)^{12}\frac{(n-\mathfrak{f})!}{(n-\mathfrak{v})!}\sum_{\nu\in\Lambda(n-\mathfrak{v},b)}\frac{1}{d_{\nu}^{2}}\\ & =O_{b,\mathfrak{v},\mathfrak{f}}\left(n^{\mathfrak{v}-\mathfrak{f}-2b}\right).\\[-37pt] \end{align*} $$
$$ \begin{align*} \left|\Xi_{n}(Y)-\Xi_{n}^{(b)}(Y)\right| & \leq\left((\mathfrak{v}-\mathfrak{f})!\right)^{12}\frac{(n-\mathfrak{f})!}{(n-\mathfrak{v})!}\sum_{\nu\in\Lambda(n-\mathfrak{v},b)}\frac{1}{d_{\nu}^{2}}\\ & =O_{b,\mathfrak{v},\mathfrak{f}}\left(n^{\mathfrak{v}-\mathfrak{f}-2b}\right).\\[-37pt] \end{align*} $$
Proposition 5.24. For any
![]() $M\in \mathbf {N}$
, there is a Laurent polynomial
$M\in \mathbf {N}$
, there is a Laurent polynomial
![]() $\Xi _{M}^{*}(Y)\in \mathbf {Q}\left [t,t^{-1}\right ]$
such that as
$\Xi _{M}^{*}(Y)\in \mathbf {Q}\left [t,t^{-1}\right ]$
such that as
![]() $n\to \infty $
$n\to \infty $
Proof. Let
![]() $b=\left \lceil \frac {\mathfrak {v}-\mathfrak {f}+M}{2}\right \rceil $
. Then Lemma 5.23 yields that as
$b=\left \lceil \frac {\mathfrak {v}-\mathfrak {f}+M}{2}\right \rceil $
. Then Lemma 5.23 yields that as
![]() $n\to \infty $
,
$n\to \infty $
,
Similarly to the proof of Proposition 4.8, we note that for
![]() $n-\mathfrak {v}>2b$
, the collection of
$n-\mathfrak {v}>2b$
, the collection of
![]() $\nu \vdash n-\mathfrak {v}$
such that
$\nu \vdash n-\mathfrak {v}$
such that
![]() $\nu \notin \Lambda (n-\mathfrak {v},b)$
is the disjoint union of
$\nu \notin \Lambda (n-\mathfrak {v},b)$
is the disjoint union of
![]() $\Lambda _{b_{\lambda }<b}(n-\mathfrak {v})=\left \{ \nu \vdash n-\mathfrak {v}\,\middle |\,\nu _{1}>n-\mathfrak {v}-b\right \} $
and the dual partitions
$\Lambda _{b_{\lambda }<b}(n-\mathfrak {v})=\left \{ \nu \vdash n-\mathfrak {v}\,\middle |\,\nu _{1}>n-\mathfrak {v}-b\right \} $
and the dual partitions
![]() $\{\check {\nu }\,|\,\nu \in \Lambda _{b_{\lambda }<b}\left (n-\mathfrak {v}\right )\}$
. Because each
$\{\check {\nu }\,|\,\nu \in \Lambda _{b_{\lambda }<b}\left (n-\mathfrak {v}\right )\}$
. Because each
![]() $\mu _{f}$
and
$\mu _{f}$
and
![]() $\lambda $
in equation (5.29) extend
$\lambda $
in equation (5.29) extend
![]() $\nu $
by a fixed number of boxes, there is a finite number
$\nu $
by a fixed number of boxes, there is a finite number
![]() $\ell $
of tuples of YDs
$\ell $
of tuples of YDs
with
![]() $\nu ^{i}\in \Lambda _{b_{\lambda }<b}(2b)$
such that for each
$\nu ^{i}\in \Lambda _{b_{\lambda }<b}(2b)$
such that for each
![]() $1\leq i\leq \ell $
and
$1\leq i\leq \ell $
and
![]() $f\in \{a,b,c,d\}$
$f\in \{a,b,c,d\}$
Thus, equation (5.29) can be rewritten as
 $$ \begin{align*} \Xi_{n}^{(b)}(Y) & =\sum_{i=1}^{\ell}\frac{d_{\lambda^{i}(n-\mathfrak{f})}d_{\nu^{i}(n-\mathfrak{v})}}{d_{\mu_{a}^{i}(n-\mathfrak{e}_{a})}d_{\mu_{b}^{i}(n-\mathfrak{e}_{b})}d_{\mu_{c}^{i}(n-\mathfrak{e}_{c})}d_{\mu_{d}^{i}(n-\mathfrak{e}_{d})}}\cdot\left[\Upsilon\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu^{i}(n-\mathfrak{v}),\left\{ \mu_{f}^{i}(n-\mathfrak{e}_{f})\right\} ,\lambda^{i}(n-\mathfrak{f})\right)\right.\\ & ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\left.+\Upsilon\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\check{\nu^{i}(n-\mathfrak{v})},\left\{ \check{\mu_{f}^{i}(n-\mathfrak{e}_{f})}\right\} ,\check{\lambda^{i}(n-\mathfrak{f})}\right)\right]\\ & =2\sum_{i=1}^{\ell}\frac{d_{\lambda^{i}(n-\mathfrak{f})}d_{\nu^{i}(n-\mathfrak{v})}}{d_{\mu_{a}^{i}(n-\mathfrak{e}_{a})}d_{\mu_{b}^{i}(n-\mathfrak{e}_{b})}d_{\mu_{c}^{i}(n-\mathfrak{e}_{c})}d_{\mu_{d}^{i}(n-\mathfrak{e}_{d})}}\cdot\Upsilon\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu^{i}(n-\mathfrak{v}),\left\{ \mu_{f}^{i}(n-\mathfrak{e}_{f})\right\} ,\lambda^{i}(n-\mathfrak{f})\right), \end{align*} $$
$$ \begin{align*} \Xi_{n}^{(b)}(Y) & =\sum_{i=1}^{\ell}\frac{d_{\lambda^{i}(n-\mathfrak{f})}d_{\nu^{i}(n-\mathfrak{v})}}{d_{\mu_{a}^{i}(n-\mathfrak{e}_{a})}d_{\mu_{b}^{i}(n-\mathfrak{e}_{b})}d_{\mu_{c}^{i}(n-\mathfrak{e}_{c})}d_{\mu_{d}^{i}(n-\mathfrak{e}_{d})}}\cdot\left[\Upsilon\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu^{i}(n-\mathfrak{v}),\left\{ \mu_{f}^{i}(n-\mathfrak{e}_{f})\right\} ,\lambda^{i}(n-\mathfrak{f})\right)\right.\\ & ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\left.+\Upsilon\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\check{\nu^{i}(n-\mathfrak{v})},\left\{ \check{\mu_{f}^{i}(n-\mathfrak{e}_{f})}\right\} ,\check{\lambda^{i}(n-\mathfrak{f})}\right)\right]\\ & =2\sum_{i=1}^{\ell}\frac{d_{\lambda^{i}(n-\mathfrak{f})}d_{\nu^{i}(n-\mathfrak{v})}}{d_{\mu_{a}^{i}(n-\mathfrak{e}_{a})}d_{\mu_{b}^{i}(n-\mathfrak{e}_{b})}d_{\mu_{c}^{i}(n-\mathfrak{e}_{c})}d_{\mu_{d}^{i}(n-\mathfrak{e}_{d})}}\cdot\Upsilon\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu^{i}(n-\mathfrak{v}),\left\{ \mu_{f}^{i}(n-\mathfrak{e}_{f})\right\} ,\lambda^{i}(n-\mathfrak{f})\right), \end{align*} $$
where the last line used Lemma 5.9. For each i, the ratio of dimensions above agrees with a rational function
![]() $\mathcal {Q}_{i}(n)\in \mathbf {Q}(n)$
of n (at least when
$\mathcal {Q}_{i}(n)\in \mathbf {Q}(n)$
of n (at least when
![]() $n-\mathfrak {v}\geq 2b$
) by Lemma 4.7. Combining this with Lemma 5.12 gives that
$n-\mathfrak {v}\geq 2b$
) by Lemma 4.7. Combining this with Lemma 5.12 gives that
 $$\begin{align*}\Xi_{n}^{(b)}(Y)=2\sum_{i=1}^{\ell}\mathcal{Q}_{i}(n)\Upsilon^{*}\left(\nu^{i},\left\{ \mu_{f}^{i}\right\} ,\lambda^{i},n^{-1}\right) \end{align*}$$
$$\begin{align*}\Xi_{n}^{(b)}(Y)=2\sum_{i=1}^{\ell}\mathcal{Q}_{i}(n)\Upsilon^{*}\left(\nu^{i},\left\{ \mu_{f}^{i}\right\} ,\lambda^{i},n^{-1}\right) \end{align*}$$
agrees with
![]() $F(n^{-1})$
, where F is a function of a complex variable z that is meromorphic in an open disc with center
$F(n^{-1})$
, where F is a function of a complex variable z that is meromorphic in an open disc with center
![]() $0$
, and with coefficients of its Laurent series in
$0$
, and with coefficients of its Laurent series in
![]() $\mathbf {Q}$
. Hence,
$\mathbf {Q}$
. Hence,
![]() $F(n^{-1})$
itself can be approximated to order
$F(n^{-1})$
itself can be approximated to order
![]() $O(n^{-M})$
as
$O(n^{-M})$
as
![]() $n\to \infty $
by a Laurent polynomial in n with coefficients in
$n\to \infty $
by a Laurent polynomial in n with coefficients in
![]() $\mathbf {Q}$
.
$\mathbf {Q}$
.
5.9 Estimating
 $\Xi _{n}(Y)$
$\Xi _{n}(Y)$
In this
![]() $\S \S $
5.9, we give estimates for
$\S \S $
5.9, we give estimates for
![]() $\Xi _{n}(Y)$
for fixed Y which is boundary reduced or strongly boundary reduced.
$\Xi _{n}(Y)$
for fixed Y which is boundary reduced or strongly boundary reduced.
Proposition 5.25. If Y is a boundary reduced tiled surface then as
![]() $n\to \infty $
,
$n\to \infty $
,
Proof. By Proposition 5.23, there is some
![]() $b=b(Y)$
such that
$b=b(Y)$
such that
As before, let
![]() $b_{\lambda }\stackrel {\mathrm {def}}{=}\left |\lambda \right |-\lambda _{1}$
. As in the proof of Proposition 5.24, for
$b_{\lambda }\stackrel {\mathrm {def}}{=}\left |\lambda \right |-\lambda _{1}$
. As in the proof of Proposition 5.24, for
![]() $n-\mathfrak {v}>2b$
we can write
$n-\mathfrak {v}>2b$
we can write
 $$ \begin{align} \Xi_{n}^{(b)}(Y) & =2\sum_{\begin{gathered}\nu\vdash n-\mathfrak{v}~:~b_{\nu}<b\\ \nu\subset_{\mathfrak{v}-\mathfrak{e}_{f}}\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda \end{gathered} }\frac{d_{\lambda}d_{\nu}}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\Upsilon\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda\right). \end{align} $$
$$ \begin{align} \Xi_{n}^{(b)}(Y) & =2\sum_{\begin{gathered}\nu\vdash n-\mathfrak{v}~:~b_{\nu}<b\\ \nu\subset_{\mathfrak{v}-\mathfrak{e}_{f}}\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda \end{gathered} }\frac{d_{\lambda}d_{\nu}}{d_{\mu_{a}}d_{\mu_{b}}d_{\mu_{c}}d_{\mu_{d}}}\Upsilon\left(\left\{ \sigma_{f}^{\pm},\tau_{f}^{\pm}\right\} ,\nu,\{\mu_{f}\},\lambda\right). \end{align} $$
Note that in equation (5.31), each of
has
![]() $\leq \mathfrak {v}-\mathfrak {f}$
boxes outside their first row, so Lemma 4.3 implies that
$\leq \mathfrak {v}-\mathfrak {f}$
boxes outside their first row, so Lemma 4.3 implies that
(recall the notation
![]() $\ll $
from
$\ll $
from
![]() $\S \S $
1.7). Since all
$\S \S $
1.7). Since all
![]() $\lambda ,\nu $
in the sum (5.31) have a bounded number of boxes outside their first row, depending on Y, for sufficiently large n, the condition
$\lambda ,\nu $
in the sum (5.31) have a bounded number of boxes outside their first row, depending on Y, for sufficiently large n, the condition
![]() $\lambda _{1}+\nu _{1}>n-\mathfrak {f}+(\mathfrak {v}-\mathfrak {f})^{2}$
of Proposition 5.21 is met for large n. Hence, by Proposition 5.21 Part 1,
$\lambda _{1}+\nu _{1}>n-\mathfrak {f}+(\mathfrak {v}-\mathfrak {f})^{2}$
of Proposition 5.21 is met for large n. Hence, by Proposition 5.21 Part 1,
 $$ \begin{align*} \left|\Xi_{n}^{(b)}\left(Y\right)\right| & \ll_{Y}\sum_{\nu\vdash n-\mathfrak{v}~:~b_{\nu}<b}\frac{1}{d_{\nu}^{2}}\left[\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda}\left(n\cdot\frac{(\mathfrak{v}-\mathfrak{f})^{2}}{\lambda_{1}+\nu_{1}-(n-\mathfrak{f})}\right)^{b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}}\right]\\ & \ll_{Y}\sum_{\nu\vdash n-\mathfrak{v}~:~b_{\nu}<b}\frac{1}{d_{\nu}^{2}}\left[\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda}1\right]\ll_{Y}\sum_{\nu\vdash n-\mathfrak{v}~:~b_{\nu}<b}\frac{1}{d_{\nu}^{2}}\le\zeta^{S_{n-\mathfrak{v}}}\left(2\right)=2+O\left(\frac{1}{n^{2}}\right), \end{align*} $$
$$ \begin{align*} \left|\Xi_{n}^{(b)}\left(Y\right)\right| & \ll_{Y}\sum_{\nu\vdash n-\mathfrak{v}~:~b_{\nu}<b}\frac{1}{d_{\nu}^{2}}\left[\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda}\left(n\cdot\frac{(\mathfrak{v}-\mathfrak{f})^{2}}{\lambda_{1}+\nu_{1}-(n-\mathfrak{f})}\right)^{b_{\lambda/\nu}-b_{\mu_{a}/\nu}-b_{\mu_{b}/\nu}-b_{\mu_{c}/\nu}-b_{\mu_{d}/\nu}}\right]\\ & \ll_{Y}\sum_{\nu\vdash n-\mathfrak{v}~:~b_{\nu}<b}\frac{1}{d_{\nu}^{2}}\left[\sum_{\nu\subset\mu_{f}\subset_{\mathfrak{e}_{f}-\mathfrak{f}}\lambda}1\right]\ll_{Y}\sum_{\nu\vdash n-\mathfrak{v}~:~b_{\nu}<b}\frac{1}{d_{\nu}^{2}}\le\zeta^{S_{n-\mathfrak{v}}}\left(2\right)=2+O\left(\frac{1}{n^{2}}\right), \end{align*} $$
where the second asymptotic inequality follows as
![]() $n\cdot \frac {(\mathfrak {v}-\mathfrak {f})^{2}}{\lambda _{1}+\nu _{1}-(n-\mathfrak {f})}\ll 1$
uniformly over all
$n\cdot \frac {(\mathfrak {v}-\mathfrak {f})^{2}}{\lambda _{1}+\nu _{1}-(n-\mathfrak {f})}\ll 1$
uniformly over all
![]() $\nu ,\lambda $
in play and
$\nu ,\lambda $
in play and
![]() $b_{\lambda /\nu }-b_{\mu _{a}/\nu }-b_{\mu _{b}/\nu }-b_{\mu _{c}/\nu }-b_{\mu _{d}/\nu }$
is bounded from above by a constant, the third asymptotic inequality follows as the number of YDs that extend a given
$b_{\lambda /\nu }-b_{\mu _{a}/\nu }-b_{\mu _{b}/\nu }-b_{\mu _{c}/\nu }-b_{\mu _{d}/\nu }$
is bounded from above by a constant, the third asymptotic inequality follows as the number of YDs that extend a given
![]() $\nu $
by at most
$\nu $
by at most
![]() $\mathfrak {v}$
boxes is bounded independently of n, and the last asymptotic inequality follows by Proposition 4.5 with
$\mathfrak {v}$
boxes is bounded independently of n, and the last asymptotic inequality follows by Proposition 4.5 with
![]() $b=1$
.
$b=1$
.
If Y is strongly boundary reduced, then we get a finer estimate.
Proposition 5.26. If Y is a strongly boundary reduced tiled surface, then as
![]() $n\to \infty $
,
$n\to \infty $
,
Proof. We begin as in the proof of Proposition 5.25 by choosing
![]() $b(Y)$
such that
$b(Y)$
such that
![]() $\Xi _{n}(Y)=\Xi _{n}^{(b)}(Y)+O_{Y}(n^{-1})$
and equation (5.31) holds. It now suffices to prove the proposition with
$\Xi _{n}(Y)=\Xi _{n}^{(b)}(Y)+O_{Y}(n^{-1})$
and equation (5.31) holds. It now suffices to prove the proposition with
![]() $\Xi _{n}(Y)$
replaced with
$\Xi _{n}(Y)$
replaced with
![]() $\Xi _{n}^{(b)}(Y)$
.
$\Xi _{n}^{(b)}(Y)$
.
There are summands of equation (5.31) corresponding to
![]() $\lambda /\nu $
having all boxes in the first row. By Proposition 5.21 Part 3, each of these summands contributes
$\lambda /\nu $
having all boxes in the first row. By Proposition 5.21 Part 3, each of these summands contributes
![]() $2\cdot \frac {d_{\lambda }d_{\nu }}{d_{\mu _{a}}d_{\mu _{b}}d_{\mu _{c}}d_{\mu _{d}}}$
to
$2\cdot \frac {d_{\lambda }d_{\nu }}{d_{\mu _{a}}d_{\mu _{b}}d_{\mu _{c}}d_{\mu _{d}}}$
to
![]() $\Xi _{n}^{(b)}$
, but in this case
$\Xi _{n}^{(b)}$
, but in this case
![]() $\nu ,\mu _{f},\lambda $
all belong to the same family of YDs, so this contribution is
$\nu ,\mu _{f},\lambda $
all belong to the same family of YDs, so this contribution is
![]() $\frac {2}{d_{\nu }^{2}}\left (1+O\left (n^{-1}\right )\right )$
. As there is one of these summands for each
$\frac {2}{d_{\nu }^{2}}\left (1+O\left (n^{-1}\right )\right )$
. As there is one of these summands for each
![]() $\nu \vdash n-\mathfrak {v}$
with
$\nu \vdash n-\mathfrak {v}$
with
![]() $b_{\nu }<b$
, together these contribute
$b_{\nu }<b$
, together these contribute
 $$ \begin{align} 2\left(1+O\left(\frac{1}{n}\right)\right)\sum_{\nu\vdash n-\mathfrak{v}~:~b_{\nu}<b}\frac{1}{d_{\nu}^{2}}=2+O\left(\frac{1}{n}\right) \end{align} $$
$$ \begin{align} 2\left(1+O\left(\frac{1}{n}\right)\right)\sum_{\nu\vdash n-\mathfrak{v}~:~b_{\nu}<b}\frac{1}{d_{\nu}^{2}}=2+O\left(\frac{1}{n}\right) \end{align} $$
by Lemma 4.7. The constant term
![]() $2$
appearing in equation (5.34) is the main term of equation (5.33).
$2$
appearing in equation (5.34) is the main term of equation (5.33).
For any other summand of equation (5.31)
![]() $b_{\lambda /\nu }>0$
and so by Proposition 5.21 Part 2 combined with equation (5.32),
$b_{\lambda /\nu }>0$
and so by Proposition 5.21 Part 2 combined with equation (5.32),
so as argued in the proof of Proposition 5.25, the total contribution of these summands is
![]() $O_{Y}\left (n^{-1}\right )$
. Hence
$O_{Y}\left (n^{-1}\right )$
. Hence
 $$\begin{align*}\Xi_{n}^{(b)}(Y)=2+O_{Y}\left(\frac{1}{n}\right).\\[-42pt] \end{align*}$$
$$\begin{align*}\Xi_{n}^{(b)}(Y)=2+O_{Y}\left(\frac{1}{n}\right).\\[-42pt] \end{align*}$$
6 Proofs of main theorems
6.1 Proof of Theorem 1.1 and its extension to finitely generated subgroups
We give the proof when
![]() $g=2$
; the extension to other
$g=2$
; the extension to other
![]() $g\geq 2$
is clear. We are given a finitely generated subgroup
$g\geq 2$
is clear. We are given a finitely generated subgroup
![]() $J\leq \Gamma =\Gamma _{2}$
and
$J\leq \Gamma =\Gamma _{2}$
and
![]() $M\in \mathbf {N}$
and we wish to show that
$M\in \mathbf {N}$
and we wish to show that
![]() $\mathbb {E}_{n}[\mathsf {fix}_{J}]\stackrel {\mathrm {def}}{=}\mathbb {E}_{2,n}[\mathsf {fix}_{J}]$
can be approximated to order
$\mathbb {E}_{n}[\mathsf {fix}_{J}]\stackrel {\mathrm {def}}{=}\mathbb {E}_{2,n}[\mathsf {fix}_{J}]$
can be approximated to order
![]() $O(n^{-M})$
by a Laurent polynomial of n with rational coefficients. Given this, the trivial bound
$O(n^{-M})$
by a Laurent polynomial of n with rational coefficients. Given this, the trivial bound
![]() $\mathbb {E}_{n}[\mathsf {fix}_{J}]\leq n$
implies that the Laurent polynomial takes the form (1.2). The fact that the
$\mathbb {E}_{n}[\mathsf {fix}_{J}]\leq n$
implies that the Laurent polynomial takes the form (1.2). The fact that the
![]() $a_{i}(J)$
do not depend on M is clear. By setting
$a_{i}(J)$
do not depend on M is clear. By setting
![]() $J=\langle \gamma \rangle $
, we obtain Theorem 1.1 from this.
$J=\langle \gamma \rangle $
, we obtain Theorem 1.1 from this.
By Lemma 2.7, we have
Now, let
![]() $\mathcal {R}$
be any finite resolution of
$\mathcal {R}$
be any finite resolution of
![]() $\mathrm {Core}(J)$
; by Theorem 2.14 at least one exists.
$\mathrm {Core}(J)$
; by Theorem 2.14 at least one exists.
Each element of this resolution is a morphism
![]() $h:\mathrm {Core}(J)\to W_{h}$
of tiled surfaces. By Lemma 2.9,
$h:\mathrm {Core}(J)\to W_{h}$
of tiled surfaces. By Lemma 2.9,
Now, using Theorem 5.10 for each of the terms
![]() $\mathbb {E}_{n}^{\mathrm {emb}}(W_{h})$
gives
$\mathbb {E}_{n}^{\mathrm {emb}}(W_{h})$
gives
 $$\begin{align*}\mathbb{E}_{n}\left[\mathsf{fix}_{J}\right]=\frac{\left(n!\right)^{3}}{\left|\mathbb{X}_{n}\right|}\sum_{h\in\mathcal{R}}\frac{\left(n\right)_{\mathfrak{v}\left(W_{h}\right)}\left(n\right)_{\mathfrak{f}\left(W_{h}\right)}}{\prod_{f\in\{a,b,c,d\}}\left(n\right)_{\mathfrak{e}_{f}\left(W_{h}\right)}}\Xi_{n}\left(W_{h}\right), \end{align*}$$
$$\begin{align*}\mathbb{E}_{n}\left[\mathsf{fix}_{J}\right]=\frac{\left(n!\right)^{3}}{\left|\mathbb{X}_{n}\right|}\sum_{h\in\mathcal{R}}\frac{\left(n\right)_{\mathfrak{v}\left(W_{h}\right)}\left(n\right)_{\mathfrak{f}\left(W_{h}\right)}}{\prod_{f\in\{a,b,c,d\}}\left(n\right)_{\mathfrak{e}_{f}\left(W_{h}\right)}}\Xi_{n}\left(W_{h}\right), \end{align*}$$
where
![]() $\mathfrak {v}(W_{h})$
,
$\mathfrak {v}(W_{h})$
,
![]() $\mathfrak {e}_{f}(W_{h})$
and
$\mathfrak {e}_{f}(W_{h})$
and
![]() $\mathfrak {f}(W_{h})$
are the number of vertices, f-labeled edges (
$\mathfrak {f}(W_{h})$
are the number of vertices, f-labeled edges (
![]() $f\in \{a,b,c,d\}$
) and octagons, respectively, of
$f\in \{a,b,c,d\}$
) and octagons, respectively, of
![]() $W_{h}$
. Also, recall the definition of
$W_{h}$
. Also, recall the definition of
![]() $\Xi _{n}$
from Theorem 5.10. By equation (1.3),
$\Xi _{n}$
from Theorem 5.10. By equation (1.3),
![]() $\left |\mathbb {X}_{n}\right |=\left (n!\right )^{3}\cdot \zeta ^{S_{n}}\left (2\right )$
, and so
$\left |\mathbb {X}_{n}\right |=\left (n!\right )^{3}\cdot \zeta ^{S_{n}}\left (2\right )$
, and so
 $$ \begin{align} \mathbb{E}_{n}\left[\mathsf{fix}_{J}\right]=\frac{1}{\zeta^{S_{n}}(2)}\sum_{h\in\mathcal{R}}\frac{(n)_{\mathfrak{v}(W_{h})}(n)_{\mathfrak{f}(W_{h})}}{\prod_{f\in\{a,b,c,d\}}(n)_{\mathfrak{e}_{f}(W_{h})}}\Xi_{n}\left(W_{h}\right). \end{align} $$
$$ \begin{align} \mathbb{E}_{n}\left[\mathsf{fix}_{J}\right]=\frac{1}{\zeta^{S_{n}}(2)}\sum_{h\in\mathcal{R}}\frac{(n)_{\mathfrak{v}(W_{h})}(n)_{\mathfrak{f}(W_{h})}}{\prod_{f\in\{a,b,c,d\}}(n)_{\mathfrak{e}_{f}(W_{h})}}\Xi_{n}\left(W_{h}\right). \end{align} $$
Now, we note:
-
• By Corollary 4.9, there is a polynomial
 $Q_{2,M}\in \mathbf {\mathbf {Z}}[t]$
with
$Q_{2,M}\in \mathbf {\mathbf {Z}}[t]$
with
 $\frac {1}{\zeta ^{S_{n}}(2)}=\frac {1}{2}Q_{2,M}\left (n^{-1}\right )+O\left (n^{-M}\right )$
.
$\frac {1}{\zeta ^{S_{n}}(2)}=\frac {1}{2}Q_{2,M}\left (n^{-1}\right )+O\left (n^{-M}\right )$
. -
• For any fixed
 $\ell \geq 0$
, both
$\ell \geq 0$
, both
 $(n)_{\ell }$
and
$(n)_{\ell }$
and
 $(n)_{\ell }^{-1}$
agree with Laurent polynomials of n with
$(n)_{\ell }^{-1}$
agree with Laurent polynomials of n with
 $\mathbf {Q}$
-coefficients up to order
$\mathbf {Q}$
-coefficients up to order
 $O(n^{-M})$
as
$O(n^{-M})$
as
 $n\to \infty $
.
$n\to \infty $
. -
• By Proposition 5.24, there is a Laurent polynomial
 $\Xi _{M}^{*}(W_{h})\in \mathbf {Q}[t,t^{-1}]$
such that
$\Xi _{M}^{*}(W_{h})\in \mathbf {Q}[t,t^{-1}]$
such that
 $\Xi _{n}(W_{h})=\Xi _{M}^{*}(W_{h})[n]+O(n^{-M})$
as
$\Xi _{n}(W_{h})=\Xi _{M}^{*}(W_{h})[n]+O(n^{-M})$
as
 $n\to \infty $
.
$n\to \infty $
.
Hence, all terms in equation (6.2) can be approximated by Laurent polynomials of n with rational coefficients to order
![]() $O(n^{-M})$
as
$O(n^{-M})$
as
![]() $n\to \infty $
. This proves Theorem 1.1.
$n\to \infty $
. This proves Theorem 1.1.
![]() $\square $
$\square $
6.2 Proof of Theorems 1.2 and 1.3
Again, we give the proofs of Theorems 1.2 and 1.3 when
![]() $g=2$
. Given a finitely generated subgroup
$g=2$
. Given a finitely generated subgroup
![]() $J\leq \Gamma =\Gamma _{2}$
, let
$J\leq \Gamma =\Gamma _{2}$
, let
![]() $\chi _{\max }(J)$
be as in equation (1.4). We can assume J is nontrivial since Theorem 1.3 is obvious in this case (as is Theorem 1.2 when
$\chi _{\max }(J)$
be as in equation (1.4). We can assume J is nontrivial since Theorem 1.3 is obvious in this case (as is Theorem 1.2 when
![]() $\gamma $
is the identity).
$\gamma $
is the identity).
Let
![]() $\mathcal {R=\mathcal {R}}(\mathrm {Core}(J),\chi _{\max }(J))$
be the resolution of
$\mathcal {R=\mathcal {R}}(\mathrm {Core}(J),\chi _{\max }(J))$
be the resolution of
![]() $\mathrm {Core}(J)$
defined in Definition 2.13, certified to be a resolution by Theorem 2.14. Let
$\mathrm {Core}(J)$
defined in Definition 2.13, certified to be a resolution by Theorem 2.14. Let
![]() $\mathcal {R}_{\max }(\gamma )$
(resp.
$\mathcal {R}_{\max }(\gamma )$
(resp.
![]() $\mathcal {R}_{<\max }(\gamma )$
) be the morphisms
$\mathcal {R}_{<\max }(\gamma )$
) be the morphisms
![]() $h: \mathrm {Core}(J)\to W_{h}$
of
$h: \mathrm {Core}(J)\to W_{h}$
of
![]() $\mathcal {R}$
with
$\mathcal {R}$
with
![]() $\chi (W_{h})=\chi _{\max }(J)$
(resp.
$\chi (W_{h})=\chi _{\max }(J)$
(resp.
![]() $\chi (W_{h})<\chi _{\max }(J)$
), so
$\chi (W_{h})<\chi _{\max }(J)$
), so
By Theorem 2.14, all elements of
![]() $\mathcal {R}_{\max }$
are strongly boundary reduced and all elements of
$\mathcal {R}_{\max }$
are strongly boundary reduced and all elements of
![]() $\mathcal {R}$
are boundary reduced. Repeating the argument of
$\mathcal {R}$
are boundary reduced. Repeating the argument of
![]() $\S \S $
6.1 we obtain equation (6.2) again.
$\S \S $
6.1 we obtain equation (6.2) again.
Now, we observe:
-
• By Proposition 4.5 with
 $b=1$
,
$b=1$
,
 $\zeta ^{S_{n}}(2)=2+O(n^{-2})$
as
$\zeta ^{S_{n}}(2)=2+O(n^{-2})$
as
 $n\to \infty $
.
$n\to \infty $
. -
• For each
 $h:\mathrm {Core}(J)\to W_{h}\in \mathcal {R}$
, the ratio of Pochhammer symbols satisfies as
$h:\mathrm {Core}(J)\to W_{h}\in \mathcal {R}$
, the ratio of Pochhammer symbols satisfies as
 $n\to \infty $
(6.3)
$n\to \infty $
(6.3) $$ \begin{align} \frac{(n)_{\mathfrak{v}(W_{h})}(n)_{\mathfrak{f}(W_{h})}}{\prod_{f\in\{a,b,c,d\}}(n)_{\mathfrak{e}_{f}(W_{h})}}=n^{\chi\left(W_{h}\right)}+O\left(n^{\chi(W_{h})-1}\right). \end{align} $$
$$ \begin{align} \frac{(n)_{\mathfrak{v}(W_{h})}(n)_{\mathfrak{f}(W_{h})}}{\prod_{f\in\{a,b,c,d\}}(n)_{\mathfrak{e}_{f}(W_{h})}}=n^{\chi\left(W_{h}\right)}+O\left(n^{\chi(W_{h})-1}\right). \end{align} $$
-
• By Proposition 5.26, for each
 $h:\mathrm {Core}(J)\to W_{h}\in \mathcal {R}_{\max }$
we have
$h:\mathrm {Core}(J)\to W_{h}\in \mathcal {R}_{\max }$
we have
 $\Xi _{n}\left (W_{h}\right )=2+O_{W_{h}}\left (n^{-1}\right )$
.
$\Xi _{n}\left (W_{h}\right )=2+O_{W_{h}}\left (n^{-1}\right )$
. -
• By Proposition 5.25, for each
 $h:\mathrm {Core}(J)\to W_{h}\in \mathcal {R}_{<\max }$
we have
$h:\mathrm {Core}(J)\to W_{h}\in \mathcal {R}_{<\max }$
we have
 $\Xi _{n}\left (W_{h}\right )=O_{W_{h}}(1)$
.
$\Xi _{n}\left (W_{h}\right )=O_{W_{h}}(1)$
.
Hence, from equation (6.2),
 $$ \begin{align*} \mathbb{E}_{n}[\mathsf{fix}_{J}] & =\frac{1}{\zeta^{S_{n}}(2)}\left[\sum_{h\in\mathcal{R}_{\max}}n^{\chi_{\max}(J)}\left(1+O\left(n^{-1}\right)\right)\cdot\left(2+O\left(n^{-1}\right)\right)+\sum_{h\in\mathcal{R}_{<\max}}O\left(n^{\chi_{\max}(J)-1}\right)\cdot O(1)\right]\\ & =\frac{1}{2+O\left(n^{-2}\right)}\left[2\cdot\left|\mathcal{R}_{\max}\right|\cdot n^{\chi_{\max}(J)}+O\left(n^{\chi_{\max}(J)-1}\right)\right]\\ & =\left|\mathcal{R}_{\max}\right|\cdot n^{\chi_{\max}(J)}+O\left(n^{\chi_{\max}(J)-1}\right), \end{align*} $$
$$ \begin{align*} \mathbb{E}_{n}[\mathsf{fix}_{J}] & =\frac{1}{\zeta^{S_{n}}(2)}\left[\sum_{h\in\mathcal{R}_{\max}}n^{\chi_{\max}(J)}\left(1+O\left(n^{-1}\right)\right)\cdot\left(2+O\left(n^{-1}\right)\right)+\sum_{h\in\mathcal{R}_{<\max}}O\left(n^{\chi_{\max}(J)-1}\right)\cdot O(1)\right]\\ & =\frac{1}{2+O\left(n^{-2}\right)}\left[2\cdot\left|\mathcal{R}_{\max}\right|\cdot n^{\chi_{\max}(J)}+O\left(n^{\chi_{\max}(J)-1}\right)\right]\\ & =\left|\mathcal{R}_{\max}\right|\cdot n^{\chi_{\max}(J)}+O\left(n^{\chi_{\max}(J)-1}\right), \end{align*} $$
where all implied constants depend on J. By Proposition 2.15,
![]() $|\mathcal {R}_{\max }|=|\mathfrak {MOG}(J)|$
which proves Theorem 1.3.
$|\mathcal {R}_{\max }|=|\mathfrak {MOG}(J)|$
which proves Theorem 1.3.
Finally, if
![]() $J=\langle \gamma \rangle $
, and q is maximal such that
$J=\langle \gamma \rangle $
, and q is maximal such that
![]() $\gamma =\gamma _{0}^{~q}$
for some
$\gamma =\gamma _{0}^{~q}$
for some
![]() $\gamma _{0}\in \Gamma $
, then Corollary 2.17 tells us that
$\gamma _{0}\in \Gamma $
, then Corollary 2.17 tells us that
![]() $|\mathcal {R}_{\max }|=d(q)$
. This proves Theorem 1.2.
$|\mathcal {R}_{\max }|=d(q)$
. This proves Theorem 1.2.
![]() $\square $
$\square $
Acknowledgements
We thank Nir Avni, Frédéric Naud, Mark Powell and Henry Wilton for helpful discussions related to this work. The research was supported by the Israel Science Foundation: ISF grant 1071/16 of D.P. This project received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 850956 and grant agreement No 949143).
Competing interest
The authors have no competing interest to declare.