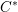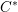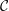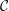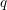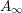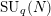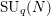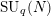1 Introduction
A locally compact group has the Howe–Moore property if for every unitary representation without invariant vectors, the matrix coefficients of the representation vanish at infinity. This property was established for connected non-compact simple Lie groups with finite center by Howe and Moore [Reference Howe and MooreHM79] and Zimmer [Reference ZimmerZim84]. Howe and Moore also showed the property for certain subgroups of simple algebraic groups over non-Archimedean local fields. Other important examples of groups with the Howe–Moore property are given in [Reference Lubotzky and MozesLM92] and [Reference Burger and MozesBM00]. The Howe–Moore property plays an essential role in the proofs of several rigidity results, most notably in Margulis’s superrigidity theorem and Mostow’s rigidity theorem. More generally, the Howe–Moore property has important applications to ergodicity and strong mixingness of actions and flows. For an overview on and a unified approach to locally compact groups with the Howe–Moore property, we refer to [Reference CiobotaruCio15] and [Reference Bader and GelanderBG17].
For Lie groups and algebraic groups over non-Archimedean local fields, we know much more than the Howe–Moore property about the asymptotic behaviour of matrix coefficients of representations. Recall that for every locally compact group
![]() $G$
, the space
$G$
, the space
![]() $\text{WAP}(G)$
of weakly almost periodic functions on
$\text{WAP}(G)$
of weakly almost periodic functions on
![]() $G$
admits a unique invariant mean. By a result of Veech [Reference VeechVee79] (see also [Reference Ellis and NerurkarEN89]), it is known that every weakly almost periodic function on a connected non-compact simple Lie group with finite center has a limit at infinity, and this limit is equal to the mean of the function. As a consequence, it follows that a very strong version of the Howe–Moore property holds for such groups: for every uniformly bounded representation on a reflexive Banach space without invariant vectors, the matrix coefficients of the representation vanish at infinity. Recently, Bader and Gelander presented an abstract and general framework for such Howe–Moore type phenomena [Reference Bader and GelanderBG17], and in particular they explain that Veech’s result also holds in the setting of connected simple algebraic groups over non-Archimedean local fields.
$G$
admits a unique invariant mean. By a result of Veech [Reference VeechVee79] (see also [Reference Ellis and NerurkarEN89]), it is known that every weakly almost periodic function on a connected non-compact simple Lie group with finite center has a limit at infinity, and this limit is equal to the mean of the function. As a consequence, it follows that a very strong version of the Howe–Moore property holds for such groups: for every uniformly bounded representation on a reflexive Banach space without invariant vectors, the matrix coefficients of the representation vanish at infinity. Recently, Bader and Gelander presented an abstract and general framework for such Howe–Moore type phenomena [Reference Bader and GelanderBG17], and in particular they explain that Veech’s result also holds in the setting of connected simple algebraic groups over non-Archimedean local fields.
In this article, we initiate the study of Howe–Moore type phenomena in the setting of quantum groups and in the setting of rigid
![]() $C^{\ast }$
-tensor categories. Unitary representations for quantum groups have been studied extensively, and recently, Popa and Vaes developed a unitary representation theory for ‘subfactor related group-like objects’ in the setting of rigid
$C^{\ast }$
-tensor categories. Unitary representations for quantum groups have been studied extensively, and recently, Popa and Vaes developed a unitary representation theory for ‘subfactor related group-like objects’ in the setting of rigid
![]() $C^{\ast }$
-tensor categories [Reference Popa and VaesPV15] (see also [Reference Neshveyev and YamashitaNY16]). Our main result is a Howe–Moore type theorem for the representation categories of
$C^{\ast }$
-tensor categories [Reference Popa and VaesPV15] (see also [Reference Neshveyev and YamashitaNY16]). Our main result is a Howe–Moore type theorem for the representation categories of
![]() $q$
-deformations of compact simple Lie groups, which are ubiquitous and historically motivating examples of compact quantum groups. The theory of compact quantum groups was initiated by Woronowicz [Reference WoronowiczWor87], and we refer to [Reference Neshveyev and TusetNT13] for a thorough account of the theory. Recall that the representation category of a compact quantum group
$q$
-deformations of compact simple Lie groups, which are ubiquitous and historically motivating examples of compact quantum groups. The theory of compact quantum groups was initiated by Woronowicz [Reference WoronowiczWor87], and we refer to [Reference Neshveyev and TusetNT13] for a thorough account of the theory. Recall that the representation category of a compact quantum group
![]() $\mathbb{G}$
is the category of finite-dimensional unitary representations of
$\mathbb{G}$
is the category of finite-dimensional unitary representations of
![]() $\mathbb{G}$
. It is a rigid
$\mathbb{G}$
. It is a rigid
![]() $C^{\ast }$
-tensor category, and, very strikingly, in the presence of a well-behaved functor into the category of finite-dimensional Hilbert spaces, there is a way to realize a rigid
$C^{\ast }$
-tensor category, and, very strikingly, in the presence of a well-behaved functor into the category of finite-dimensional Hilbert spaces, there is a way to realize a rigid
![]() $C^{\ast }$
-tensor category as the representation category of a certain compact quantum group (see e.g. [Reference Neshveyev and TusetNT13]).
$C^{\ast }$
-tensor category as the representation category of a certain compact quantum group (see e.g. [Reference Neshveyev and TusetNT13]).
Let
![]() ${\mathcal{C}}$
be a rigid
${\mathcal{C}}$
be a rigid
![]() $C^{\ast }$
-tensor category, and let
$C^{\ast }$
-tensor category, and let
![]() $\text{Irr}({\mathcal{C}})$
denote the set of equivalence classes of irreducible objects in
$\text{Irr}({\mathcal{C}})$
denote the set of equivalence classes of irreducible objects in
![]() ${\mathcal{C}}$
. Then
${\mathcal{C}}$
. Then
![]() ${\mathcal{C}}$
is said to have the Howe–Moore property if every completely positive multiplier
${\mathcal{C}}$
is said to have the Howe–Moore property if every completely positive multiplier
![]() $\unicode[STIX]{x1D714}:\text{Irr}({\mathcal{C}})\rightarrow \mathbb{C}$
has a limit at infinity (see Definition 3.1).
$\unicode[STIX]{x1D714}:\text{Irr}({\mathcal{C}})\rightarrow \mathbb{C}$
has a limit at infinity (see Definition 3.1).
Theorem A. Let
![]() $q\in (0,1]$
, and let
$q\in (0,1]$
, and let
![]() $K_{q}$
be a
$K_{q}$
be a
![]() $q$
-deformation of a connected compact simple Lie group
$q$
-deformation of a connected compact simple Lie group
![]() $K$
with trivial center. Then every completely bounded multiplier on
$K$
with trivial center. Then every completely bounded multiplier on
![]() $\operatorname{Rep}(K_{q})$
has a limit at infinity. In particular, the representation category
$\operatorname{Rep}(K_{q})$
has a limit at infinity. In particular, the representation category
![]() $\text{Rep}(K_{q})$
has the Howe–Moore property.
$\text{Rep}(K_{q})$
has the Howe–Moore property.
Another rich source of rigid
![]() $C^{\ast }$
-tensor categories is Jones’s theory of subfactors. Every inclusion
$C^{\ast }$
-tensor categories is Jones’s theory of subfactors. Every inclusion
![]() $N\subset M$
of
$N\subset M$
of
![]() $\text{II}_{1}$
-factors with finite index
$\text{II}_{1}$
-factors with finite index
![]() $[M:N]<\infty$
can be enhanced to its Jones tower
$[M:N]<\infty$
can be enhanced to its Jones tower
![]() $M_{-1}\subset M_{0}\subset M_{1}\subset M_{2}\subset \cdots \,$
of
$M_{-1}\subset M_{0}\subset M_{1}\subset M_{2}\subset \cdots \,$
of
![]() $\text{II}_{1}$
-factors, where
$\text{II}_{1}$
-factors, where
![]() $M_{-1}=N$
and
$M_{-1}=N$
and
![]() $M_{0}=M$
, satisfying
$M_{0}=M$
, satisfying
![]() $[M_{i+1}:M_{i}]=[M:N]$
for all
$[M_{i+1}:M_{i}]=[M:N]$
for all
![]() $i\geqslant 0$
and having the property that every
$i\geqslant 0$
and having the property that every
![]() $M_{i+1}$
is generated by
$M_{i+1}$
is generated by
![]() $M_{i}$
and a projection
$M_{i}$
and a projection
![]() $e_{i}$
commuting with
$e_{i}$
commuting with
![]() $M_{i-1}$
(see [Reference JonesJon83] for details). The projection
$M_{i-1}$
(see [Reference JonesJon83] for details). The projection
![]() $e_{i}$
is commonly referred to as the
$e_{i}$
is commonly referred to as the
![]() $i$
th Jones projection. The relative commutants
$i$
th Jones projection. The relative commutants
![]() $M_{i}^{\prime }\,\cap \,M_{j}$
, with
$M_{i}^{\prime }\,\cap \,M_{j}$
, with
![]() $i\leqslant j$
, of algebras in the Jones tower form a lattice of finite-dimensional
$i\leqslant j$
, of algebras in the Jones tower form a lattice of finite-dimensional
![]() $C^{\ast }$
-algebras. This lattice is called the standard invariant of
$C^{\ast }$
-algebras. This lattice is called the standard invariant of
![]() $N\subset M$
and has played a fundamental role in many aspects of subfactor theory, such as the classification of subfactors of small index (see e.g. [Reference Jones, Morrison and SnyderJMS14]). Standard invariants have been abstractly characterized in several different ways, most notably as
$N\subset M$
and has played a fundamental role in many aspects of subfactor theory, such as the classification of subfactors of small index (see e.g. [Reference Jones, Morrison and SnyderJMS14]). Standard invariants have been abstractly characterized in several different ways, most notably as
![]() $\unicode[STIX]{x1D706}$
-lattices by Popa in [Reference PopaPop95] and, more diagrammatically, as subfactor planar algebras by Jones [Reference JonesJon99]. It is a striking result due to Popa (see [Reference PopaPop95]) that every abstract
$\unicode[STIX]{x1D706}$
-lattices by Popa in [Reference PopaPop95] and, more diagrammatically, as subfactor planar algebras by Jones [Reference JonesJon99]. It is a striking result due to Popa (see [Reference PopaPop95]) that every abstract
![]() $\unicode[STIX]{x1D706}$
-lattice (and hence every subfactor planar algebra) can be realized as a concrete one coming from a subfactor
$\unicode[STIX]{x1D706}$
-lattice (and hence every subfactor planar algebra) can be realized as a concrete one coming from a subfactor
![]() $N\subset M$
of index
$N\subset M$
of index
![]() $[M:N]=\unicode[STIX]{x1D706}^{-1}$
.
$[M:N]=\unicode[STIX]{x1D706}^{-1}$
.
A central example of a standard invariant is the Temperley–Lieb–Jones standard invariant
![]() $\text{TLJ}(\unicode[STIX]{x1D706})$
. It embeds into any other standard invariant coming from a subfactor
$\text{TLJ}(\unicode[STIX]{x1D706})$
. It embeds into any other standard invariant coming from a subfactor
![]() $N\subset M$
with index
$N\subset M$
with index
![]() $[M:N]=\unicode[STIX]{x1D706}^{-1}$
, so it can be viewed as an initial object for the category of standard invariants. With the Jones tower of
$[M:N]=\unicode[STIX]{x1D706}^{-1}$
, so it can be viewed as an initial object for the category of standard invariants. With the Jones tower of
![]() $N\subset M$
, we can naturally associate a rigid
$N\subset M$
, we can naturally associate a rigid
![]() $C^{\ast }$
-tensor category
$C^{\ast }$
-tensor category
![]() ${\mathcal{C}}_{M}$
consisting of all
${\mathcal{C}}_{M}$
consisting of all
![]() $M$
-bimodules that are isomorphic to a finite direct sum of
$M$
-bimodules that are isomorphic to a finite direct sum of
![]() $M$
-subbimodules of
$M$
-subbimodules of
![]() $_{M}L^{2}(M_{i})_{M}$
, where
$_{M}L^{2}(M_{i})_{M}$
, where
![]() $i\geqslant 0$
. The tensor operation, or fusion, in this category is the Connes tensor product over
$i\geqslant 0$
. The tensor operation, or fusion, in this category is the Connes tensor product over
![]() $M$
. It is known that the category
$M$
. It is known that the category
![]() ${\mathcal{C}}_{M}$
is equivalent, as a rigid
${\mathcal{C}}_{M}$
is equivalent, as a rigid
![]() $C^{\ast }$
-tensor category, to the representation category of the compact quantum group
$C^{\ast }$
-tensor category, to the representation category of the compact quantum group
![]() $\text{PSU}_{q}(2)$
, where
$\text{PSU}_{q}(2)$
, where
![]() $q$
is the unique number
$q$
is the unique number
![]() $0<q\leqslant 1$
such that
$0<q\leqslant 1$
such that
![]() $q+1/q=\unicode[STIX]{x1D706}^{-1/2}$
(see e.g. [Reference Popa and VaesPV15]). The following result is therefore an immediate consequence of Theorem A.
$q+1/q=\unicode[STIX]{x1D706}^{-1/2}$
(see e.g. [Reference Popa and VaesPV15]). The following result is therefore an immediate consequence of Theorem A.
Corollary B. Let
![]() $N\subset M$
be an inclusion of
$N\subset M$
be an inclusion of
![]() $\text{II}_{1}$
factors with index
$\text{II}_{1}$
factors with index
![]() $[M:N]=\unicode[STIX]{x1D706}^{-1}\geqslant 4$
and Temperley–Lieb–Jones standard invariant
$[M:N]=\unicode[STIX]{x1D706}^{-1}\geqslant 4$
and Temperley–Lieb–Jones standard invariant
![]() $\text{TLJ}(\unicode[STIX]{x1D706})$
(and hence principal graph
$\text{TLJ}(\unicode[STIX]{x1D706})$
(and hence principal graph
![]() $A_{\infty }$
). The rigid
$A_{\infty }$
). The rigid
![]() $C^{\ast }$
-tensor category
$C^{\ast }$
-tensor category
![]() ${\mathcal{C}}_{M}$
of
${\mathcal{C}}_{M}$
of
![]() $M$
-bimodules associated with the Jones tower of
$M$
-bimodules associated with the Jones tower of
![]() $N\subset M$
has the Howe–Moore property.
$N\subset M$
has the Howe–Moore property.
Theorem A (and hence Corollary B) follows from a more general result (see Theorem 3.6) on the convergence of completely bounded multipliers on certain rigid
![]() $C^{\ast }$
-tensor categories. This more general result also holds for the representation categories of the free orthogonal quantum groups and for the Kazhdan–Wenzl categories. We refer to § 3 for the details.
$C^{\ast }$
-tensor categories. This more general result also holds for the representation categories of the free orthogonal quantum groups and for the Kazhdan–Wenzl categories. We refer to § 3 for the details.
Our Howe–Moore type results are the first such phenomena beyond the setting of locally compact groups. They may be useful for the study of quantum group actions. More specifically, the central Howe–Moore property (see § 3) may be of use in the setting of actions of discrete quantum groups on certain operator algebras (cf. [Reference Daws, Skalski and ViselterDSV17]). More generally, one may apply the Howe–Moore property directly in the setting of actions of rigid
![]() $C^{\ast }$
-tensor categories, which are just tensor functors from the tensor category to the category of bimodules over a von Neumann algebra (cf. [Reference PopaPop94, Reference Hayashi and YamagamiHY00, Reference MasudaMas16]).
$C^{\ast }$
-tensor categories, which are just tensor functors from the tensor category to the category of bimodules over a von Neumann algebra (cf. [Reference PopaPop94, Reference Hayashi and YamagamiHY00, Reference MasudaMas16]).
For the proof of Theorem 3.6 (and hence of Theorem A), we relate the character algebra of
![]() $K_{q}$
to the character algebra of
$K_{q}$
to the character algebra of
![]() $K$
, which can in turn be identified with the algebra of continuous functions on
$K$
, which can in turn be identified with the algebra of continuous functions on
![]() $T/W$
, where
$T/W$
, where
![]() $T$
is a maximal torus and
$T$
is a maximal torus and
![]() $W$
is the associated Weyl group. A crucial ingredient of our proof is a certain general asymptotic behaviour of the characters of highest weight representations of compact Lie groups (see Proposition 3.5).
$W$
is the associated Weyl group. A crucial ingredient of our proof is a certain general asymptotic behaviour of the characters of highest weight representations of compact Lie groups (see Proposition 3.5).
The Howe–Moore property for rigid
![]() $C^{\ast }$
-tensor categories describes certain asymptotic behaviour of completely positive multipliers. The family of completely positive multipliers on the category
$C^{\ast }$
-tensor categories describes certain asymptotic behaviour of completely positive multipliers. The family of completely positive multipliers on the category
![]() $\text{Rep}(\mathbb{G})$
(which is more restrictive than the family of completely bounded multipliers) coincides with the central states on the quantum coordinate algebra
$\text{Rep}(\mathbb{G})$
(which is more restrictive than the family of completely bounded multipliers) coincides with the central states on the quantum coordinate algebra
![]() ${\mathcal{O}}(\mathbb{G})$
, which were already investigated in [Reference De Commer, Freslon and YamashitaDCFY14]. For the most well-known examples of
${\mathcal{O}}(\mathbb{G})$
, which were already investigated in [Reference De Commer, Freslon and YamashitaDCFY14]. For the most well-known examples of
![]() $q$
-deformations, namely the quantum groups
$q$
-deformations, namely the quantum groups
![]() $\text{SU}_{q}(N)$
, where
$\text{SU}_{q}(N)$
, where
![]() $N\geqslant 2$
, it turns out that we can find an explicit characterization of the central states. To this end, we use recent work of the first-named author [Reference AranoAra17], in which the unitary representation theory of the Drinfel’d double of a
$N\geqslant 2$
, it turns out that we can find an explicit characterization of the central states. To this end, we use recent work of the first-named author [Reference AranoAra17], in which the unitary representation theory of the Drinfel’d double of a
![]() $q$
-deformation of a compact Lie group is compared with the unitary representation theory of the complexification of the compact Lie group. Indeed, we are able to relate the central states very concretely to
$q$
-deformation of a compact Lie group is compared with the unitary representation theory of the complexification of the compact Lie group. Indeed, we are able to relate the central states very concretely to
![]() $\text{SU}(N)$
-bi-invariant positive-definite functions on
$\text{SU}(N)$
-bi-invariant positive-definite functions on
![]() $\text{SL}(N,\mathbb{C})$
. Below, let
$\text{SL}(N,\mathbb{C})$
. Below, let
![]() $Q$
denote the root lattice and
$Q$
denote the root lattice and
![]() $P$
the weight lattice with respect to a fixed Cartan subalgebra (see § 2.5). Recall that a central state on
$P$
the weight lattice with respect to a fixed Cartan subalgebra (see § 2.5). Recall that a central state on
![]() ${\mathcal{O}}(\text{SU}_{q}(N))$
is uniquely determined by its restriction to a chosen set
${\mathcal{O}}(\text{SU}_{q}(N))$
is uniquely determined by its restriction to a chosen set
![]() $P_{+}$
of positive weights. Hence, we can identify the central states with maps
$P_{+}$
of positive weights. Hence, we can identify the central states with maps
![]() $\unicode[STIX]{x1D711}:P_{+}\rightarrow \mathbb{C}$
.
$\unicode[STIX]{x1D711}:P_{+}\rightarrow \mathbb{C}$
.
Theorem C. For every central state
![]() $\unicode[STIX]{x1D711}:P_{+}\rightarrow \mathbb{C}$
on
$\unicode[STIX]{x1D711}:P_{+}\rightarrow \mathbb{C}$
on
![]() $\text{SU}_{q}(N)$
, there exist
$\text{SU}_{q}(N)$
, there exist
![]() $\text{SU}(N)$
-bi-invariant positive-definite functions
$\text{SU}(N)$
-bi-invariant positive-definite functions
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D712}}$
on
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D712}}$
on
![]() $\text{SL}(N,\mathbb{C})$
such that
$\text{SL}(N,\mathbb{C})$
such that
and
where
![]() $C$
is a constant (not depending on
$C$
is a constant (not depending on
![]() $\unicode[STIX]{x1D711}$
) and
$\unicode[STIX]{x1D711}$
) and
![]() $\unicode[STIX]{x1D70C}$
is half of the sum of the positive roots.
$\unicode[STIX]{x1D70C}$
is half of the sum of the positive roots.
This explicit characterization of central states can be useful for the study of the analytic properties of the quantum groups
![]() $\text{SU}_{q}(N)$
that involve central states.
$\text{SU}_{q}(N)$
that involve central states.
The article is organized as follows. We recall some preliminaries in § 2. Theorem A is proven in § 3 and Theorem C in § 4.
2 Preliminaries
2.1 Rigid
 $C^{\ast }$
-tensor categories
$C^{\ast }$
-tensor categories
A
![]() $C^{\ast }$
-tensor category is a category that behaves similar to the category of Hilbert spaces. For the basic theory of
$C^{\ast }$
-tensor category is a category that behaves similar to the category of Hilbert spaces. For the basic theory of
![]() $C^{\ast }$
-tensor categories and the facts mentioned in this subsection, we refer to [Reference Neshveyev and TusetNT13, ch. 2].
$C^{\ast }$
-tensor categories and the facts mentioned in this subsection, we refer to [Reference Neshveyev and TusetNT13, ch. 2].
In what follows, all tensor categories will be assumed to be strict, unless explicitly mentioned otherwise. This is not a fundamental restriction, since every tensor category can be strictified.
Let
![]() ${\mathcal{C}}$
be a
${\mathcal{C}}$
be a
![]() $C^{\ast }$
-tensor category. An object
$C^{\ast }$
-tensor category. An object
![]() $\bar{u}$
in
$\bar{u}$
in
![]() ${\mathcal{C}}$
is conjugate to an object
${\mathcal{C}}$
is conjugate to an object
![]() $u$
in
$u$
in
![]() ${\mathcal{C}}$
if there are
${\mathcal{C}}$
if there are
![]() $R\in \operatorname{Mor}(\unicode[STIX]{x1D7D9},\bar{u}\,\otimes \,u)$
and
$R\in \operatorname{Mor}(\unicode[STIX]{x1D7D9},\bar{u}\,\otimes \,u)$
and
![]() $\bar{R}\in \operatorname{Mor}(\unicode[STIX]{x1D7D9},u\,\otimes \,\bar{u})$
such that
$\bar{R}\in \operatorname{Mor}(\unicode[STIX]{x1D7D9},u\,\otimes \,\bar{u})$
such that
are the identity morphisms. Conjugate objects are uniquely determined up to isomorphism. If every object has a conjugate object, then the category
![]() ${\mathcal{C}}$
is called a rigid
${\mathcal{C}}$
is called a rigid
![]() $C^{\ast }$
-tensor category.
$C^{\ast }$
-tensor category.
Let
![]() $\text{Irr}({\mathcal{C}})$
denote the set of equivalence classes of irreducible objects in
$\text{Irr}({\mathcal{C}})$
denote the set of equivalence classes of irreducible objects in
![]() ${\mathcal{C}}$
. Using the same notation as above, if
${\mathcal{C}}$
. Using the same notation as above, if
![]() $u$
is an irreducible object with a conjugate, then
$u$
is an irreducible object with a conjugate, then
![]() $d(u)=\Vert R\Vert \Vert \bar{R}\Vert$
is independent of the choice of the morphisms
$d(u)=\Vert R\Vert \Vert \bar{R}\Vert$
is independent of the choice of the morphisms
![]() $R$
and
$R$
and
![]() $\bar{R}$
. An arbitrary object
$\bar{R}$
. An arbitrary object
![]() $u$
in a rigid
$u$
in a rigid
![]() $C^{\ast }$
-tensor category is unitarily equivalent to a direct sum
$C^{\ast }$
-tensor category is unitarily equivalent to a direct sum
![]() $u\cong \bigoplus _{k}u_{k}$
of irreducible objects, and we put
$u\cong \bigoplus _{k}u_{k}$
of irreducible objects, and we put
![]() $d(u)=\sum _{k}d(u_{k})$
. The function
$d(u)=\sum _{k}d(u_{k})$
. The function
![]() $d:{\mathcal{C}}\rightarrow [0,\infty )$
defined in this way is called the intrinsic dimension of
$d:{\mathcal{C}}\rightarrow [0,\infty )$
defined in this way is called the intrinsic dimension of
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
2.2 Multipliers on rigid
 $C^{\ast }$
-tensor categories
$C^{\ast }$
-tensor categories
Multipliers on rigid
![]() $C^{\ast }$
-tensor categories were introduced by Popa and Vaes [Reference Popa and VaesPV15].
$C^{\ast }$
-tensor categories were introduced by Popa and Vaes [Reference Popa and VaesPV15].
Definition 2.1. A multiplier on a rigid
![]() $C^{\ast }$
-tensor category
$C^{\ast }$
-tensor category
![]() ${\mathcal{C}}$
is a family of linear maps
${\mathcal{C}}$
is a family of linear maps
indexed by
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in {\mathcal{C}}$
such that
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in {\mathcal{C}}$
such that
for all
![]() $\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i}\in {\mathcal{C}},X\in \operatorname{End}(\unicode[STIX]{x1D6FC}_{2}\,\otimes \,\unicode[STIX]{x1D6FD}_{1})$
and
$\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i}\in {\mathcal{C}},X\in \operatorname{End}(\unicode[STIX]{x1D6FC}_{2}\,\otimes \,\unicode[STIX]{x1D6FD}_{1})$
and
![]() $U,V\in \text{Mor}(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})\,\otimes \,\text{Mor}(\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FD}_{1})$
.
$U,V\in \text{Mor}(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})\,\otimes \,\text{Mor}(\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FD}_{1})$
.
A multiplier
![]() $(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}})$
is said to be completely positive (or a cp-multiplier) if all maps
$(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}})$
is said to be completely positive (or a cp-multiplier) if all maps
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
are completely positive. A multiplier
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
are completely positive. A multiplier
![]() $(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}})$
is said to be completely bounded (or a cb-multiplier) if all maps
$(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}})$
is said to be completely bounded (or a cb-multiplier) if all maps
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
are completely bounded and
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
are completely bounded and
![]() $\Vert \unicode[STIX]{x1D703}\Vert _{\text{cb}}=\sup _{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in {\mathcal{C}}}\Vert \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}\Vert _{\text{cb}}<\infty$
. By [Reference Popa and VaesPV15, Proposition 3.6], every multiplier corresponds uniquely to a function
$\Vert \unicode[STIX]{x1D703}\Vert _{\text{cb}}=\sup _{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in {\mathcal{C}}}\Vert \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}\Vert _{\text{cb}}<\infty$
. By [Reference Popa and VaesPV15, Proposition 3.6], every multiplier corresponds uniquely to a function
![]() $\unicode[STIX]{x1D711}:\operatorname{Irr}({\mathcal{C}})\rightarrow \mathbb{C}$
and we will often mean such a function when we speak of a multiplier.
$\unicode[STIX]{x1D711}:\operatorname{Irr}({\mathcal{C}})\rightarrow \mathbb{C}$
and we will often mean such a function when we speak of a multiplier.
2.3 The fusion algebra and admissible
 $\ast$
-representations
$\ast$
-representations
Recall that the fusion algebra
![]() $\mathbb{C}[{\mathcal{C}}]$
of a rigid
$\mathbb{C}[{\mathcal{C}}]$
of a rigid
![]() $C^{\ast }$
-tensor category
$C^{\ast }$
-tensor category
![]() ${\mathcal{C}}$
is defined as the free vector space with basis
${\mathcal{C}}$
is defined as the free vector space with basis
![]() $\operatorname{Irr}({\mathcal{C}})$
and multiplication given by
$\operatorname{Irr}({\mathcal{C}})$
and multiplication given by
In fact, the fusion algebra is a
![]() $\ast$
-algebra when equipped with the involution
$\ast$
-algebra when equipped with the involution
![]() $\unicode[STIX]{x1D6FC}^{\sharp }=\bar{\unicode[STIX]{x1D6FC}}$
.
$\unicode[STIX]{x1D6FC}^{\sharp }=\bar{\unicode[STIX]{x1D6FC}}$
.
In [Reference Popa and VaesPV15], Popa and Vaes defined the notion of admissible
![]() $\ast$
-representation of
$\ast$
-representation of
![]() $\mathbb{C}[{\mathcal{C}}]$
as a unital
$\mathbb{C}[{\mathcal{C}}]$
as a unital
![]() $\ast$
-representation
$\ast$
-representation
![]() $\unicode[STIX]{x1D6E9}:\mathbb{C}[{\mathcal{C}}]\rightarrow B({\mathcal{H}})$
such that for all
$\unicode[STIX]{x1D6E9}:\mathbb{C}[{\mathcal{C}}]\rightarrow B({\mathcal{H}})$
such that for all
![]() $\unicode[STIX]{x1D709}\in {\mathcal{H}}$
the map
$\unicode[STIX]{x1D709}\in {\mathcal{H}}$
the map
is a cp-multiplier. Moreover, they proved the existence of a universal admissible
![]() $\ast$
-representation and denoted the corresponding enveloping
$\ast$
-representation and denoted the corresponding enveloping
![]() $C^{\ast }$
-algebra of
$C^{\ast }$
-algebra of
![]() $\mathbb{C}[{\mathcal{C}}]$
by
$\mathbb{C}[{\mathcal{C}}]$
by
![]() $C_{u}({\mathcal{C}})$
.
$C_{u}({\mathcal{C}})$
.
2.4 The tube algebra
In [Reference Ghosh and JonesGJ16], the representation theory of rigid
![]() $C^{\ast }$
-tensor categories was related to Ocneanu’s tube algebra, which was introduced in [Reference OcneanuOcn94]. Let us recall the definition of the tube algebra. Let
$C^{\ast }$
-tensor categories was related to Ocneanu’s tube algebra, which was introduced in [Reference OcneanuOcn94]. Let us recall the definition of the tube algebra. Let
![]() ${\mathcal{C}}$
be a rigid
${\mathcal{C}}$
be a rigid
![]() $C^{\ast }$
-tensor category. For each equivalence class
$C^{\ast }$
-tensor category. For each equivalence class
![]() $\unicode[STIX]{x1D6FC}\in \text{Irr}({\mathcal{C}})$
, choose a representative
$\unicode[STIX]{x1D6FC}\in \text{Irr}({\mathcal{C}})$
, choose a representative
![]() $X_{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D6FC}$
, and let
$X_{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D6FC}$
, and let
![]() $X_{0}$
denote the representative of the tensor unit. Moreover, let
$X_{0}$
denote the representative of the tensor unit. Moreover, let
![]() $\unicode[STIX]{x1D6EC}$
be a countable family of equivalence classes of objects in
$\unicode[STIX]{x1D6EC}$
be a countable family of equivalence classes of objects in
![]() ${\mathcal{C}}$
with distinct representatives
${\mathcal{C}}$
with distinct representatives
![]() $Y_{\unicode[STIX]{x1D6FD}}\in \unicode[STIX]{x1D6FD}$
for every
$Y_{\unicode[STIX]{x1D6FD}}\in \unicode[STIX]{x1D6FD}$
for every
![]() $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6EC}$
. The annular algebra with weight set
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6EC}$
. The annular algebra with weight set
![]() $\unicode[STIX]{x1D6EC}$
is defined as
$\unicode[STIX]{x1D6EC}$
is defined as
The algebra
![]() ${\mathcal{A}}\unicode[STIX]{x1D6EC}$
comes equipped with the structure of an associative
${\mathcal{A}}\unicode[STIX]{x1D6EC}$
comes equipped with the structure of an associative
![]() $\ast$
-algebra. We will always assume the weight set
$\ast$
-algebra. We will always assume the weight set
![]() $\unicode[STIX]{x1D6EC}$
to be full, i.e. every irreducible object is equivalent to a subobject of some element in
$\unicode[STIX]{x1D6EC}$
to be full, i.e. every irreducible object is equivalent to a subobject of some element in
![]() $\unicode[STIX]{x1D6EC}$
. The annular algebra with weight set
$\unicode[STIX]{x1D6EC}$
. The annular algebra with weight set
![]() $\unicode[STIX]{x1D6EC}=\operatorname{Irr}({\mathcal{C}})$
is called the tube algebra of Ocneanu, and we write
$\unicode[STIX]{x1D6EC}=\operatorname{Irr}({\mathcal{C}})$
is called the tube algebra of Ocneanu, and we write
![]() ${\mathcal{A}}\unicode[STIX]{x1D6EC}={\mathcal{A}}{\mathcal{C}}$
.
${\mathcal{A}}\unicode[STIX]{x1D6EC}={\mathcal{A}}{\mathcal{C}}$
.
2.5
 $q$
-deformations of compact simple Lie groups
$q$
-deformations of compact simple Lie groups
A compact quantum group is a pair
![]() $(A,\unicode[STIX]{x1D6E5})$
consisting of a unital
$(A,\unicode[STIX]{x1D6E5})$
consisting of a unital
![]() $C^{\ast }$
-algebra
$C^{\ast }$
-algebra
![]() $A$
and a unital
$A$
and a unital
![]() $\ast$
-homomorphism
$\ast$
-homomorphism
![]() $\unicode[STIX]{x1D6E5}:A\rightarrow A\otimes A$
(comultiplication) such that
$\unicode[STIX]{x1D6E5}:A\rightarrow A\otimes A$
(comultiplication) such that
![]() $(\unicode[STIX]{x1D6E5}\otimes \text{id})\unicode[STIX]{x1D6E5}=(\text{id}\otimes \unicode[STIX]{x1D6E5})\unicode[STIX]{x1D6E5}$
and such that
$(\unicode[STIX]{x1D6E5}\otimes \text{id})\unicode[STIX]{x1D6E5}=(\text{id}\otimes \unicode[STIX]{x1D6E5})\unicode[STIX]{x1D6E5}$
and such that
![]() $\text{span}\{(A\otimes 1)\unicode[STIX]{x1D6E5}(A)\}$
and
$\text{span}\{(A\otimes 1)\unicode[STIX]{x1D6E5}(A)\}$
and
![]() $\text{span}\{(1\otimes A)\unicode[STIX]{x1D6E5}(A)\}$
are dense in
$\text{span}\{(1\otimes A)\unicode[STIX]{x1D6E5}(A)\}$
are dense in
![]() $A\otimes A$
. The tensor product
$A\otimes A$
. The tensor product
![]() $\otimes$
denotes the minimal tensor product. For a recent thorough introduction to the theory of compact quantum groups, we refer to [Reference Neshveyev and TusetNT13].
$\otimes$
denotes the minimal tensor product. For a recent thorough introduction to the theory of compact quantum groups, we refer to [Reference Neshveyev and TusetNT13].
Another class of quantum groups is the class of discrete quantum groups, which is dual to the class of compact quantum groups under an appropriate generalization of Pontryagin duality. In fact, the search for such an appropriate notion of duality was a central motivation in the early days of quantum group theory. The most general analytic framework for quantum groups is the theory of locally compact quantum groups, as introduced by Kustermans and Vaes [Reference Kustermans and VaesKV00]. It includes both the compact and discrete quantum groups and the locally compact groups, and it provides a satisfying answer to the duality question. This theory is, however, significantly more complicated.
Notable examples of compact quantum groups are the
![]() $q$
-deformations of compact Lie groups. We recall their construction below. For details, see e.g. [Reference Neshveyev and TusetNT13, §2.4] or [Reference Klimyk and SchmüdgenKS97]. Let
$q$
-deformations of compact Lie groups. We recall their construction below. For details, see e.g. [Reference Neshveyev and TusetNT13, §2.4] or [Reference Klimyk and SchmüdgenKS97]. Let
![]() $K$
be a connected simply connected compact simple Lie group. We restrict ourselves to the case of
$K$
be a connected simply connected compact simple Lie group. We restrict ourselves to the case of
![]() $K$
being simple, because we need this later. However, for the construction of
$K$
being simple, because we need this later. However, for the construction of
![]() $q$
-deformations, this is not essential. Let
$q$
-deformations, this is not essential. Let
![]() $G=K_{\mathbb{C}}$
be the complexification of
$G=K_{\mathbb{C}}$
be the complexification of
![]() $K$
. The group
$K$
. The group
![]() $G$
has an Iwasawa decomposition
$G$
has an Iwasawa decomposition
![]() $G=KAN$
. Let
$G=KAN$
. Let
![]() $\mathfrak{g}$
be the Lie algebra of
$\mathfrak{g}$
be the Lie algebra of
![]() $G$
and fix a Cartan subalgebra
$G$
and fix a Cartan subalgebra
![]() $\mathfrak{h}$
of
$\mathfrak{h}$
of
![]() $\mathfrak{g}$
. Let
$\mathfrak{g}$
. Let
![]() $\unicode[STIX]{x1D6E5}$
be the associated set of roots, let
$\unicode[STIX]{x1D6E5}$
be the associated set of roots, let
![]() $Q\subset \mathfrak{h}^{\ast }$
be the root lattice and
$Q\subset \mathfrak{h}^{\ast }$
be the root lattice and
![]() $P\subset \mathfrak{h}^{\ast }$
the weight lattice. Denote by
$P\subset \mathfrak{h}^{\ast }$
the weight lattice. Denote by
![]() $(\cdot \,,\cdot )$
the natural bilinear form on
$(\cdot \,,\cdot )$
the natural bilinear form on
![]() $\mathfrak{h}$
, which we assume to be normalized by
$\mathfrak{h}$
, which we assume to be normalized by
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC})=2$
for a short root
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC})=2$
for a short root
![]() $\unicode[STIX]{x1D6FC}$
. For each
$\unicode[STIX]{x1D6FC}$
. For each
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, define the coroot as
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, define the coroot as
![]() $\unicode[STIX]{x1D6FC}^{\vee }=2\unicode[STIX]{x1D6FC}/(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC})$
. Choose a set
$\unicode[STIX]{x1D6FC}^{\vee }=2\unicode[STIX]{x1D6FC}/(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC})$
. Choose a set
![]() $\unicode[STIX]{x1D6F1}=\{\unicode[STIX]{x1D6FC}_{i}\mid i\in I\}$
of simple roots, and let
$\unicode[STIX]{x1D6F1}=\{\unicode[STIX]{x1D6FC}_{i}\mid i\in I\}$
of simple roots, and let
![]() $\unicode[STIX]{x1D6E5}_{+}$
denote the set of positive roots,
$\unicode[STIX]{x1D6E5}_{+}$
denote the set of positive roots,
![]() $Q_{+}$
the positive elements in the root lattice and
$Q_{+}$
the positive elements in the root lattice and
![]() $P_{+}$
the positive weights. Put
$P_{+}$
the positive weights. Put
![]() $d_{i}=(\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FC}_{i})/2$
, and denote by
$d_{i}=(\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FC}_{i})/2$
, and denote by
![]() $a_{ij}=(\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FC}_{j})/d_{i}$
the entries of the Cartan matrix.
$a_{ij}=(\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FC}_{j})/d_{i}$
the entries of the Cartan matrix.
Fix
![]() $q\in (0,1)$
. Define
$q\in (0,1)$
. Define
![]() $q_{i}=q^{d_{i}}$
, and set
$q_{i}=q^{d_{i}}$
, and set
The quantized enveloping algebra
![]() $U_{q}(\mathfrak{g})$
of
$U_{q}(\mathfrak{g})$
of
![]() $\mathfrak{g}$
is the unital algebra defined by the generators
$\mathfrak{g}$
is the unital algebra defined by the generators
![]() $\{K_{i}^{\pm 1},E_{i},F_{i}\mid i\in I\}$
and the relations
$\{K_{i}^{\pm 1},E_{i},F_{i}\mid i\in I\}$
and the relations
 $$\begin{eqnarray}\displaystyle & \displaystyle K_{i}K_{i}^{-1}=K_{i}^{-1}K_{i}=1,\quad K_{i}K_{j}=K_{j}K_{i}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle K_{i}E_{j}K_{i}^{-1}=q_{i}^{a_{ij}}E_{j},\quad K_{i}F_{j}K_{i}^{-1}=q_{i}^{-a_{ij}}F_{j}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle [E_{i},F_{j}]=\unicode[STIX]{x1D6FF}_{ij}\frac{K_{i}-K_{i}^{-1}}{q_{i}-q_{i}^{-1}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\sum }_{r=0}^{1-a_{ij}}(-1)^{r}\left[\begin{array}{@{}c@{}}1-a_{ij}\\ r\end{array}\right]_{q_{i}}E_{i}^{r}E_{j}E_{i}^{1-a_{ij}-r}=0,\quad \mathop{\sum }_{r=0}^{1-a_{ij}}(-1)^{r}\left[\begin{array}{@{}c@{}}1-a_{ij}\\ r\end{array}\right]_{q_{i}}F_{i}^{r}F_{j}F_{i}^{1-a_{ij}-r}=0. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle K_{i}K_{i}^{-1}=K_{i}^{-1}K_{i}=1,\quad K_{i}K_{j}=K_{j}K_{i}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle K_{i}E_{j}K_{i}^{-1}=q_{i}^{a_{ij}}E_{j},\quad K_{i}F_{j}K_{i}^{-1}=q_{i}^{-a_{ij}}F_{j}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle [E_{i},F_{j}]=\unicode[STIX]{x1D6FF}_{ij}\frac{K_{i}-K_{i}^{-1}}{q_{i}-q_{i}^{-1}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\sum }_{r=0}^{1-a_{ij}}(-1)^{r}\left[\begin{array}{@{}c@{}}1-a_{ij}\\ r\end{array}\right]_{q_{i}}E_{i}^{r}E_{j}E_{i}^{1-a_{ij}-r}=0,\quad \mathop{\sum }_{r=0}^{1-a_{ij}}(-1)^{r}\left[\begin{array}{@{}c@{}}1-a_{ij}\\ r\end{array}\right]_{q_{i}}F_{i}^{r}F_{j}F_{i}^{1-a_{ij}-r}=0. & \displaystyle \nonumber\end{eqnarray}$$
Note that the quantized enveloping algebra is a deformation of the universal enveloping algebra of
![]() $\mathfrak{g}$
. In fact, the quantized enveloping algebra
$\mathfrak{g}$
. In fact, the quantized enveloping algebra
![]() $U_{q}(\mathfrak{g})$
can be turned into a Hopf
$U_{q}(\mathfrak{g})$
can be turned into a Hopf
![]() $\ast$
-algebra by defining a comultiplication
$\ast$
-algebra by defining a comultiplication
![]() $\hat{\unicode[STIX]{x1D6E5}}_{q}$
and involution
$\hat{\unicode[STIX]{x1D6E5}}_{q}$
and involution
![]() $^{\ast }$
by
$^{\ast }$
by
Recall that the counit
![]() $\hat{\unicode[STIX]{x1D700}}_{q}$
and the antipode
$\hat{\unicode[STIX]{x1D700}}_{q}$
and the antipode
![]() ${\hat{S}}_{q}$
are given by the formulas
${\hat{S}}_{q}$
are given by the formulas
Let
![]() $V$
be an
$V$
be an
![]() $U_{q}(\mathfrak{g})$
-module, and let
$U_{q}(\mathfrak{g})$
-module, and let
![]() $\unicode[STIX]{x1D707}\in P$
. The weight space
$\unicode[STIX]{x1D707}\in P$
. The weight space
![]() $V_{\unicode[STIX]{x1D707}}$
is defined as
$V_{\unicode[STIX]{x1D707}}$
is defined as
The module
![]() $V$
is said to be of type
$V$
is said to be of type
![]() $1$
if
$1$
if
![]() $V$
decomposes as a direct sum
$V$
decomposes as a direct sum
![]() $V=\bigoplus _{\unicode[STIX]{x1D707}\in P}V_{\unicode[STIX]{x1D707}}$
. If a vector
$V=\bigoplus _{\unicode[STIX]{x1D707}\in P}V_{\unicode[STIX]{x1D707}}$
. If a vector
![]() $v\in V$
is an element of the direct summand
$v\in V$
is an element of the direct summand
![]() $V_{\unicode[STIX]{x1D707}}$
, we sometimes refer to the weight
$V_{\unicode[STIX]{x1D707}}$
, we sometimes refer to the weight
![]() $\unicode[STIX]{x1D707}$
as
$\unicode[STIX]{x1D707}$
as
![]() $\text{wt}(v)$
.
$\text{wt}(v)$
.
For each
![]() $\unicode[STIX]{x1D706}\in P_{+}$
, there exists a uniquely determined irreducible module
$\unicode[STIX]{x1D706}\in P_{+}$
, there exists a uniquely determined irreducible module
![]() $V(\unicode[STIX]{x1D706})$
of highest weight
$V(\unicode[STIX]{x1D706})$
of highest weight
![]() $\unicode[STIX]{x1D706}$
, i.e.
$\unicode[STIX]{x1D706}$
, i.e.
![]() $V(\unicode[STIX]{x1D706})=U_{q}(\mathfrak{g})v_{\unicode[STIX]{x1D706}}$
for a non-zero vector
$V(\unicode[STIX]{x1D706})=U_{q}(\mathfrak{g})v_{\unicode[STIX]{x1D706}}$
for a non-zero vector
![]() $v_{\unicode[STIX]{x1D706}}\in V(\unicode[STIX]{x1D706})$
satisfying
$v_{\unicode[STIX]{x1D706}}\in V(\unicode[STIX]{x1D706})$
satisfying
![]() $K_{i}v_{\unicode[STIX]{x1D706}}=q_{i}^{(\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC}_{i}^{\vee })}v_{\unicode[STIX]{x1D706}}$
and
$K_{i}v_{\unicode[STIX]{x1D706}}=q_{i}^{(\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC}_{i}^{\vee })}v_{\unicode[STIX]{x1D706}}$
and
![]() $E_{i}v_{\unicode[STIX]{x1D706}}=0$
for all
$E_{i}v_{\unicode[STIX]{x1D706}}=0$
for all
![]() $i\in I$
. The module
$i\in I$
. The module
![]() $V(\unicode[STIX]{x1D706})$
is finite-dimensional and admits an invariant inner product.
$V(\unicode[STIX]{x1D706})$
is finite-dimensional and admits an invariant inner product.
For
![]() $v,w\in V_{\unicode[STIX]{x1D707}}$
, define
$v,w\in V_{\unicode[STIX]{x1D707}}$
, define
![]() $u_{vw}^{\unicode[STIX]{x1D707}}\in U_{q}(\mathfrak{g})^{\ast }$
by
$u_{vw}^{\unicode[STIX]{x1D707}}\in U_{q}(\mathfrak{g})^{\ast }$
by
![]() $(u_{vw}^{\unicode[STIX]{x1D707}},x)=(xv,w)$
. Let
$(u_{vw}^{\unicode[STIX]{x1D707}},x)=(xv,w)$
. Let
![]() ${\mathcal{O}}(K_{q})$
be the quantum coordinate algebra, i.e. the subspace of
${\mathcal{O}}(K_{q})$
be the quantum coordinate algebra, i.e. the subspace of
![]() $U_{q}(\mathfrak{g})^{\ast }$
consisting of matrix coefficients of finite-dimensional unitary modules of type 1. More precisely,
$U_{q}(\mathfrak{g})^{\ast }$
consisting of matrix coefficients of finite-dimensional unitary modules of type 1. More precisely,
The algebra
![]() ${\mathcal{O}}(K_{q})$
admits a unique Hopf
${\mathcal{O}}(K_{q})$
admits a unique Hopf
![]() $\ast$
-algebra structure that turns the pairing
$\ast$
-algebra structure that turns the pairing
![]() ${\mathcal{O}}(K_{q})\times U_{q}(\mathfrak{g})\rightarrow \mathbb{C}$
into a Hopf
${\mathcal{O}}(K_{q})\times U_{q}(\mathfrak{g})\rightarrow \mathbb{C}$
into a Hopf
![]() $\ast$
-algebra pairing. More concretely, multiplication, involution and comultiplication on
$\ast$
-algebra pairing. More concretely, multiplication, involution and comultiplication on
![]() ${\mathcal{O}}(K_{q})$
are given by the formulas
${\mathcal{O}}(K_{q})$
are given by the formulas
for
![]() $a,b\in {\mathcal{O}}(K_{q})$
and
$a,b\in {\mathcal{O}}(K_{q})$
and
![]() $x,y\in U_{q}(\mathfrak{g})$
. The universal
$x,y\in U_{q}(\mathfrak{g})$
. The universal
![]() $C^{\ast }$
-completion
$C^{\ast }$
-completion
![]() $C(K_{q})$
of the
$C(K_{q})$
of the
![]() $\ast$
-algebra
$\ast$
-algebra
![]() ${\mathcal{O}}(K_{q})$
is (the
${\mathcal{O}}(K_{q})$
is (the
![]() $C^{\ast }$
-algebra associated with) the compact quantum group
$C^{\ast }$
-algebra associated with) the compact quantum group
![]() $K_{q}$
.
$K_{q}$
.
3 The Howe–Moore property for representation categories
In this section, we prove the Howe–Moore property for the representation categories of
![]() $q$
-deformations of connected compact simple Lie groups with trivial center, i.e. Theorem A.
$q$
-deformations of connected compact simple Lie groups with trivial center, i.e. Theorem A.
Definition 3.1. A rigid
![]() $C^{\ast }$
-tensor category
$C^{\ast }$
-tensor category
![]() ${\mathcal{C}}$
is said to have the Howe–Moore property if for every completely positive multiplier
${\mathcal{C}}$
is said to have the Howe–Moore property if for every completely positive multiplier
![]() $\unicode[STIX]{x1D714}:\text{Irr}({\mathcal{C}})\rightarrow \mathbb{C}$
, we have
$\unicode[STIX]{x1D714}:\text{Irr}({\mathcal{C}})\rightarrow \mathbb{C}$
, we have
![]() $\unicode[STIX]{x1D714}\in c_{0}(\text{Irr}({\mathcal{C}}))\oplus \mathbb{C}$
.
$\unicode[STIX]{x1D714}\in c_{0}(\text{Irr}({\mathcal{C}}))\oplus \mathbb{C}$
.
In the case where
![]() ${\mathcal{C}}$
is the representation category of a compact quantum group
${\mathcal{C}}$
is the representation category of a compact quantum group
![]() $\mathbb{G}$
, it turns out that the Howe–Moore property for
$\mathbb{G}$
, it turns out that the Howe–Moore property for
![]() $\text{Rep}(\mathbb{G})$
is equivalent to a central version of the Howe–Moore property, i.e. a version of the Howe–Moore property for the central states on the quantum coordinate algebra
$\text{Rep}(\mathbb{G})$
is equivalent to a central version of the Howe–Moore property, i.e. a version of the Howe–Moore property for the central states on the quantum coordinate algebra
![]() ${\mathcal{O}}(\mathbb{G})$
of
${\mathcal{O}}(\mathbb{G})$
of
![]() $\mathbb{G}$
. This central Howe–Moore property can be viewed as a property for the dual
$\mathbb{G}$
. This central Howe–Moore property can be viewed as a property for the dual
![]() $\widehat{\mathbb{G}}$
of
$\widehat{\mathbb{G}}$
of
![]() $\mathbb{G}$
. The dual of a compact quantum group is a discrete quantum group. As indicated in § 1, the approach of structural properties of quantum groups through central versions of these properties for their duals goes back to [Reference De Commer, Freslon and YamashitaDCFY14]. It also played an important role in the work of the first-named author on property (T) in the setting of quantum groups [Reference AranoAra16].
$\mathbb{G}$
. The dual of a compact quantum group is a discrete quantum group. As indicated in § 1, the approach of structural properties of quantum groups through central versions of these properties for their duals goes back to [Reference De Commer, Freslon and YamashitaDCFY14]. It also played an important role in the work of the first-named author on property (T) in the setting of quantum groups [Reference AranoAra16].
Definition 3.2. Let
![]() $\mathbb{G}$
be a compact quantum group. The discrete quantum group
$\mathbb{G}$
be a compact quantum group. The discrete quantum group
![]() $\widehat{\mathbb{G}}$
is said to have the central Howe–Moore property if
$\widehat{\mathbb{G}}$
is said to have the central Howe–Moore property if
![]() $\unicode[STIX]{x1D714}\in c_{0}(\widehat{\mathbb{G}})\oplus \mathbb{C}$
for every central state
$\unicode[STIX]{x1D714}\in c_{0}(\widehat{\mathbb{G}})\oplus \mathbb{C}$
for every central state
![]() $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
![]() ${\mathcal{O}}(\mathbb{G})$
.
${\mathcal{O}}(\mathbb{G})$
.
The following result relates the Howe–Moore property for representation categories to the central Howe–Moore property of the duals of the underlying quantum groups. It follows immediately from the fact that completely positive multipliers on the category
![]() $\text{Rep}(\mathbb{G})$
coincide with the central states of
$\text{Rep}(\mathbb{G})$
coincide with the central states of
![]() $\mathbb{G}$
(see [Reference Popa and VaesPV15, Proposition 6.1]).
$\mathbb{G}$
(see [Reference Popa and VaesPV15, Proposition 6.1]).
Proposition 3.3. Let
![]() $\mathbb{G}$
be a compact quantum group. The representation category
$\mathbb{G}$
be a compact quantum group. The representation category
![]() $\text{Rep}(\mathbb{G})$
has the Howe–Moore property for rigid
$\text{Rep}(\mathbb{G})$
has the Howe–Moore property for rigid
![]() $C^{\ast }$
-tensor categories if and only if the dual
$C^{\ast }$
-tensor categories if and only if the dual
![]() $\widehat{\mathbb{G}}$
of
$\widehat{\mathbb{G}}$
of
![]() $\mathbb{G}$
has the central Howe–Moore property.
$\mathbb{G}$
has the central Howe–Moore property.
Let us now start working towards the proof of Theorem A.
Lemma 3.4. Let
![]() $\unicode[STIX]{x1D6E5}$
be a root system with a root subsystem
$\unicode[STIX]{x1D6E5}$
be a root system with a root subsystem
![]() $\unicode[STIX]{x1D6E5}^{0}\subset \unicode[STIX]{x1D6E5}$
. Then for all
$\unicode[STIX]{x1D6E5}^{0}\subset \unicode[STIX]{x1D6E5}$
. Then for all
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, we have the following: whenever there exists
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, we have the following: whenever there exists
![]() $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E5}\setminus \unicode[STIX]{x1D6E5}^{0}$
such that
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E5}\setminus \unicode[STIX]{x1D6E5}^{0}$
such that
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\neq 0$
, then
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\neq 0$
, then
![]() $\unicode[STIX]{x1D6FC}\in \text{span}(\unicode[STIX]{x1D6E5}\setminus \unicode[STIX]{x1D6E5}^{0})$
.
$\unicode[STIX]{x1D6FC}\in \text{span}(\unicode[STIX]{x1D6E5}\setminus \unicode[STIX]{x1D6E5}^{0})$
.
In particular, if
![]() $\unicode[STIX]{x1D6E5}$
is irreducible and
$\unicode[STIX]{x1D6E5}$
is irreducible and
![]() $\unicode[STIX]{x1D6E5}^{0}$
is a proper subsystem, then
$\unicode[STIX]{x1D6E5}^{0}$
is a proper subsystem, then
![]() $\text{span}(\unicode[STIX]{x1D6E5}\setminus \unicode[STIX]{x1D6E5}^{0})=\mathfrak{h}^{\ast }$
.
$\text{span}(\unicode[STIX]{x1D6E5}\setminus \unicode[STIX]{x1D6E5}^{0})=\mathfrak{h}^{\ast }$
.
Proof. The first assertion follows in a straightforward way from a consideration of root systems with rank
![]() $2$
. The second assertion follows from the fact that
$2$
. The second assertion follows from the fact that
![]() $\unicode[STIX]{x1D6E5}^{1}=\unicode[STIX]{x1D6E5}\cap \text{span}(\unicode[STIX]{x1D6E5}\setminus \unicode[STIX]{x1D6E5}^{0})$
and
$\unicode[STIX]{x1D6E5}^{1}=\unicode[STIX]{x1D6E5}\cap \text{span}(\unicode[STIX]{x1D6E5}\setminus \unicode[STIX]{x1D6E5}^{0})$
and
![]() $\unicode[STIX]{x1D6E5}^{2}=\unicode[STIX]{x1D6E5}\setminus \unicode[STIX]{x1D6E5}^{1}$
are root systems that are perpendicular to each other.◻
$\unicode[STIX]{x1D6E5}^{2}=\unicode[STIX]{x1D6E5}\setminus \unicode[STIX]{x1D6E5}^{1}$
are root systems that are perpendicular to each other.◻
The following result constitutes a crucial ingredient of our approach. Let
![]() $K$
be a connected compact simple Lie group (with center
$K$
be a connected compact simple Lie group (with center
![]() $Z(K)$
), and fix a Cartan subalgebra of its Lie algebra. Let
$Z(K)$
), and fix a Cartan subalgebra of its Lie algebra. Let
![]() $T$
be the associated maximal torus,
$T$
be the associated maximal torus,
![]() $\unicode[STIX]{x1D6E5}$
the set of roots (with positive part
$\unicode[STIX]{x1D6E5}$
the set of roots (with positive part
![]() $\unicode[STIX]{x1D6E5}_{+}$
) and
$\unicode[STIX]{x1D6E5}_{+}$
) and
![]() $P$
the weight lattice (with positive part
$P$
the weight lattice (with positive part
![]() $P_{+}$
). Let
$P_{+}$
). Let
![]() $\unicode[STIX]{x1D70C}=\frac{1}{2}\sum _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}}\unicode[STIX]{x1D6FC}$
. For
$\unicode[STIX]{x1D70C}=\frac{1}{2}\sum _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}}\unicode[STIX]{x1D6FC}$
. For
![]() $\unicode[STIX]{x1D706}\in P_{+}$
, the highest weight representation is denoted by
$\unicode[STIX]{x1D706}\in P_{+}$
, the highest weight representation is denoted by
![]() $V(\unicode[STIX]{x1D706})$
. The character of
$V(\unicode[STIX]{x1D706})$
. The character of
![]() $V(\unicode[STIX]{x1D706})$
is denoted by
$V(\unicode[STIX]{x1D706})$
is denoted by
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D706}}$
. We refer to § 2.5 for details on the aforementioned structures.
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D706}}$
. We refer to § 2.5 for details on the aforementioned structures.
Proposition 3.5. Let
![]() $K$
be a connected compact simple Lie group, and let
$K$
be a connected compact simple Lie group, and let
![]() $T$
,
$T$
,
![]() $P_{+}$
and
$P_{+}$
and
![]() $V(\unicode[STIX]{x1D706})$
be as above. For every
$V(\unicode[STIX]{x1D706})$
be as above. For every
![]() $t\in T\setminus Z(K)$
, we have
$t\in T\setminus Z(K)$
, we have
Proof. We use the Weyl character formula (see e.g. [Reference HelgasonHel84, Theorem V.1.7]), which computes the character
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D706}}$
of a highest weight representation
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D706}}$
of a highest weight representation
![]() $V(\unicode[STIX]{x1D706})$
of highest weight
$V(\unicode[STIX]{x1D706})$
of highest weight
![]() $\unicode[STIX]{x1D706}$
of a connected compact simple Lie group:
$\unicode[STIX]{x1D706}$
of a connected compact simple Lie group:
and the Weyl dimension formula (see e.g. [Reference HelgasonHel84, Theorem V.1.8]), which computes the dimension of the highest weight representation
![]() $V(\unicode[STIX]{x1D706})$
:
$V(\unicode[STIX]{x1D706})$
:
In the rest of this section, we will write
![]() $t=e^{H}$
and e.g.
$t=e^{H}$
and e.g.
![]() $t^{\unicode[STIX]{x1D6FC}}$
for
$t^{\unicode[STIX]{x1D6FC}}$
for
![]() $e^{\unicode[STIX]{x1D6FC}(H)}$
.
$e^{\unicode[STIX]{x1D6FC}(H)}$
.
Fix
![]() $t_{0}\in T\setminus Z(K)$
. Then
$t_{0}\in T\setminus Z(K)$
. Then
![]() $\unicode[STIX]{x1D6E5}^{0}=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\mid t_{0}^{-\unicode[STIX]{x1D6FC}}=1\}\neq \unicode[STIX]{x1D6E5}$
is a root system with positive roots
$\unicode[STIX]{x1D6E5}^{0}=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\mid t_{0}^{-\unicode[STIX]{x1D6FC}}=1\}\neq \unicode[STIX]{x1D6E5}$
is a root system with positive roots
![]() $\unicode[STIX]{x1D6E5}_{+}^{0}=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}\mid t_{0}^{-\unicode[STIX]{x1D6FC}}=1\}$
and Weyl group
$\unicode[STIX]{x1D6E5}_{+}^{0}=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}\mid t_{0}^{-\unicode[STIX]{x1D6FC}}=1\}$
and Weyl group
![]() $W_{0}=\{w\in W\mid wt_{0}=t_{0}\}$
(see [Reference KacKac90, Proposition 6.6]). Put
$W_{0}=\{w\in W\mid wt_{0}=t_{0}\}$
(see [Reference KacKac90, Proposition 6.6]). Put
![]() $\unicode[STIX]{x1D70C}_{0}=\frac{1}{2}\sum _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}^{0}}\unicode[STIX]{x1D6FC}$
. Fix representatives of
$\unicode[STIX]{x1D70C}_{0}=\frac{1}{2}\sum _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}^{0}}\unicode[STIX]{x1D6FC}$
. Fix representatives of
![]() $W_{0}\backslash W$
in
$W_{0}\backslash W$
in
![]() $W$
. Then
$W$
. Then
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D706}}(t_{0}) & = & \displaystyle \lim _{t\rightarrow t_{0}}\mathop{\sum }_{w^{\prime }\in W_{0}\backslash W}(-1)^{l(w^{\prime })}\frac{1}{t^{\unicode[STIX]{x1D70C}}\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}\setminus \unicode[STIX]{x1D6E5}_{+}^{0}}(1-t^{-\unicode[STIX]{x1D6FC}})}\frac{\mathop{\sum }_{w\in W_{0}}(-1)^{l(w)}t^{ww^{\prime }(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C})}}{\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}^{0}}(1-t^{-\unicode[STIX]{x1D6FC}})}\nonumber\\ \displaystyle & = & \displaystyle \lim _{s\rightarrow 1}\mathop{\sum }_{w^{\prime }\in W_{0}\backslash W}(-1)^{l(w^{\prime })}\frac{t_{0}^{w^{\prime }(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C})}}{t_{0}^{\unicode[STIX]{x1D70C}}s^{\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}_{0}}\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}\setminus \unicode[STIX]{x1D6E5}_{+}^{0}}(1-(t_{0}s)^{-\unicode[STIX]{x1D6FC}})}\frac{\mathop{\sum }_{w\in W_{0}}(-1)^{l(w)}s^{ww^{\prime }(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C})}}{s^{\unicode[STIX]{x1D70C}_{0}}\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}^{0}}(1-s^{-\unicode[STIX]{x1D6FC}})},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D706}}(t_{0}) & = & \displaystyle \lim _{t\rightarrow t_{0}}\mathop{\sum }_{w^{\prime }\in W_{0}\backslash W}(-1)^{l(w^{\prime })}\frac{1}{t^{\unicode[STIX]{x1D70C}}\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}\setminus \unicode[STIX]{x1D6E5}_{+}^{0}}(1-t^{-\unicode[STIX]{x1D6FC}})}\frac{\mathop{\sum }_{w\in W_{0}}(-1)^{l(w)}t^{ww^{\prime }(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C})}}{\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}^{0}}(1-t^{-\unicode[STIX]{x1D6FC}})}\nonumber\\ \displaystyle & = & \displaystyle \lim _{s\rightarrow 1}\mathop{\sum }_{w^{\prime }\in W_{0}\backslash W}(-1)^{l(w^{\prime })}\frac{t_{0}^{w^{\prime }(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C})}}{t_{0}^{\unicode[STIX]{x1D70C}}s^{\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}_{0}}\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}\setminus \unicode[STIX]{x1D6E5}_{+}^{0}}(1-(t_{0}s)^{-\unicode[STIX]{x1D6FC}})}\frac{\mathop{\sum }_{w\in W_{0}}(-1)^{l(w)}s^{ww^{\prime }(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C})}}{s^{\unicode[STIX]{x1D70C}_{0}}\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}^{0}}(1-s^{-\unicode[STIX]{x1D6FC}})},\nonumber\end{eqnarray}$$
where we have used the invariance of
![]() $t_{0}$
under the action of
$t_{0}$
under the action of
![]() $W_{0}$
in the second equality. Note that by taking the limit
$W_{0}$
in the second equality. Note that by taking the limit
![]() $s\rightarrow 1$
in the Weyl character formula for the subsystem
$s\rightarrow 1$
in the Weyl character formula for the subsystem
![]() $\unicode[STIX]{x1D6E5}^{0}$
in the same way as in the proof of the Weyl dimension formula, we obtain
$\unicode[STIX]{x1D6E5}^{0}$
in the same way as in the proof of the Weyl dimension formula, we obtain
Moreover, since
![]() $t_{0}^{\unicode[STIX]{x1D70C}}s^{\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}_{0}}\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}\setminus \unicode[STIX]{x1D6E5}_{+}^{0}}(1-(t_{0}s)^{-\unicode[STIX]{x1D6FC}})$
is non-zero whenever
$t_{0}^{\unicode[STIX]{x1D70C}}s^{\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}_{0}}\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}\setminus \unicode[STIX]{x1D6E5}_{+}^{0}}(1-(t_{0}s)^{-\unicode[STIX]{x1D6FC}})$
is non-zero whenever
![]() $s$
is sufficiently close to
$s$
is sufficiently close to
![]() $1$
, it suffices to show that for every
$1$
, it suffices to show that for every
![]() $w^{\prime }$
, we have
$w^{\prime }$
, we have
To this end, put
Then
 $$\begin{eqnarray}\frac{\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}^{0}}(w^{\prime }(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C}),\unicode[STIX]{x1D6FC})}{\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}}(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FC})}=\pm \mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}\setminus \unicode[STIX]{x1D6E5}_{+}^{w^{\prime },0}}\frac{1}{(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FC})}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}^{0}}(w^{\prime }(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C}),\unicode[STIX]{x1D6FC})}{\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}}(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FC})}=\pm \mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}\setminus \unicode[STIX]{x1D6E5}_{+}^{w^{\prime },0}}\frac{1}{(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FC})}.\end{eqnarray}$$
Note that every factor
![]() $1/(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FC})$
is at most
$1/(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FC})$
is at most
![]() $1$
. Write
$1$
. Write
![]() $\unicode[STIX]{x1D706}$
as a linear combination of
$\unicode[STIX]{x1D706}$
as a linear combination of
![]() $\unicode[STIX]{x1D71B}_{i}$
, where
$\unicode[STIX]{x1D71B}_{i}$
, where
![]() $\unicode[STIX]{x1D71B}_{i}$
is the fundamental weight, i.e.
$\unicode[STIX]{x1D71B}_{i}$
is the fundamental weight, i.e.
![]() $(\unicode[STIX]{x1D71B}_{i},\unicode[STIX]{x1D6FC}_{j}^{\vee })=\unicode[STIX]{x1D6FF}_{ij}$
. Then the maximum of the coefficients tends to infinity as
$(\unicode[STIX]{x1D71B}_{i},\unicode[STIX]{x1D6FC}_{j}^{\vee })=\unicode[STIX]{x1D6FF}_{ij}$
. Then the maximum of the coefficients tends to infinity as
![]() $\unicode[STIX]{x1D706}$
tends to infinity. Hence, we only need to show that for all
$\unicode[STIX]{x1D706}$
tends to infinity. Hence, we only need to show that for all
![]() $i\in I$
, there exists an
$i\in I$
, there exists an
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}\setminus \unicode[STIX]{x1D6E5}_{+}^{w^{\prime },0}$
such that
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}\setminus \unicode[STIX]{x1D6E5}_{+}^{w^{\prime },0}$
such that
![]() $(\unicode[STIX]{x1D71B}_{i},\unicode[STIX]{x1D6FC})\neq 0$
.
$(\unicode[STIX]{x1D71B}_{i},\unicode[STIX]{x1D6FC})\neq 0$
.
Suppose that this is not the case. Then there exists an
![]() $i\in I$
such that for all
$i\in I$
such that for all
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}\setminus \unicode[STIX]{x1D6E5}_{+}^{w^{\prime },0}$
, we have
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}\setminus \unicode[STIX]{x1D6E5}_{+}^{w^{\prime },0}$
, we have
![]() $(\unicode[STIX]{x1D71B}_{i},\unicode[STIX]{x1D6FC})=0$
. This shows that
$(\unicode[STIX]{x1D71B}_{i},\unicode[STIX]{x1D6FC})=0$
. This shows that
![]() $(w^{\prime }\unicode[STIX]{x1D71B}_{i},\unicode[STIX]{x1D6FC})=0$
for any
$(w^{\prime }\unicode[STIX]{x1D71B}_{i},\unicode[STIX]{x1D6FC})=0$
for any
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\setminus \unicode[STIX]{x1D6E5}^{0}$
. From Lemma 3.4 and the assumption that
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\setminus \unicode[STIX]{x1D6E5}^{0}$
. From Lemma 3.4 and the assumption that
![]() $K$
is simple, we obtain that
$K$
is simple, we obtain that
![]() $(w^{\prime }\unicode[STIX]{x1D71B}_{i},\unicode[STIX]{x1D6FC})=0$
for all
$(w^{\prime }\unicode[STIX]{x1D71B}_{i},\unicode[STIX]{x1D6FC})=0$
for all
![]() $\unicode[STIX]{x1D6FC}\in \text{span}(\unicode[STIX]{x1D6E5}_{+}\setminus \unicode[STIX]{x1D6E5}_{+}^{0})=\mathfrak{h}^{\ast }$
, which is a contradiction. ◻
$\unicode[STIX]{x1D6FC}\in \text{span}(\unicode[STIX]{x1D6E5}_{+}\setminus \unicode[STIX]{x1D6E5}_{+}^{0})=\mathfrak{h}^{\ast }$
, which is a contradiction. ◻
Recall that the character algebra of
![]() $C(K_{q})$
is the
$C(K_{q})$
is the
![]() $C^{\ast }$
-subalgebra of
$C^{\ast }$
-subalgebra of
![]() $C(K_{q})$
spanned by
$C(K_{q})$
spanned by
where
![]() $u_{vv}^{\unicode[STIX]{x1D706}}$
is as in § 2.5.
$u_{vv}^{\unicode[STIX]{x1D706}}$
is as in § 2.5.
Theorem 3.6. Let
![]() $K$
be a connected compact simple Lie group, and let
$K$
be a connected compact simple Lie group, and let
![]() ${\mathcal{C}}$
be a rigid
${\mathcal{C}}$
be a rigid
![]() $C^{\ast }$
-tensor category satisfying the fusion rules of
$C^{\ast }$
-tensor category satisfying the fusion rules of
![]() $K$
(i.e. the fusion ring of
$K$
(i.e. the fusion ring of
![]() ${\mathcal{C}}$
is isomorphic to the fusion ring of
${\mathcal{C}}$
is isomorphic to the fusion ring of
![]() $K$
). For every completely bounded multiplier
$K$
). For every completely bounded multiplier
![]() $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
![]() ${\mathcal{C}}$
, there exists a map
${\mathcal{C}}$
, there exists a map
![]() $c:Z(K)\rightarrow \mathbb{C}$
such that
$c:Z(K)\rightarrow \mathbb{C}$
such that
In particular, if
![]() $K$
has trivial center, then the category
$K$
has trivial center, then the category
![]() ${\mathcal{C}}$
has the Howe–Moore property.
${\mathcal{C}}$
has the Howe–Moore property.
Proof. Let
![]() $\unicode[STIX]{x1D714}:P_{+}\rightarrow \mathbb{C}$
be a completely bounded multiplier on
$\unicode[STIX]{x1D714}:P_{+}\rightarrow \mathbb{C}$
be a completely bounded multiplier on
![]() ${\mathcal{C}}$
. Then
${\mathcal{C}}$
. Then
![]() $\unicode[STIX]{x1D714}$
gives rise to a normal completely bounded map
$\unicode[STIX]{x1D714}$
gives rise to a normal completely bounded map
![]() $T:{\mathcal{A}}{\mathcal{C}}^{\prime \prime }\rightarrow {\mathcal{A}}{\mathcal{C}}^{\prime \prime }$
, where
$T:{\mathcal{A}}{\mathcal{C}}^{\prime \prime }\rightarrow {\mathcal{A}}{\mathcal{C}}^{\prime \prime }$
, where
![]() ${\mathcal{A}}{\mathcal{C}}$
is the tube algebra. We restrict
${\mathcal{A}}{\mathcal{C}}$
is the tube algebra. We restrict
![]() $T$
to the fusion algebra in order to get a completely bounded map
$T$
to the fusion algebra in order to get a completely bounded map
After composing this with the evaluation map at the neutral element in
![]() $T$
, we obtain a bounded functional
$T$
, we obtain a bounded functional
Since
![]() $\tilde{\unicode[STIX]{x1D714}}$
is a bounded functional on
$\tilde{\unicode[STIX]{x1D714}}$
is a bounded functional on
![]() $C(T/W)$
, there exists a finite measure
$C(T/W)$
, there exists a finite measure
![]() $\unicode[STIX]{x1D707}$
on
$\unicode[STIX]{x1D707}$
on
![]() $T/W$
such that
$T/W$
such that
Put
![]() $c(t)=\unicode[STIX]{x1D707}(\{t\})$
. By Proposition 3.5 and the dominated convergence theorem, we obtain that
$c(t)=\unicode[STIX]{x1D707}(\{t\})$
. By Proposition 3.5 and the dominated convergence theorem, we obtain that
Obvious examples of categories
![]() ${\mathcal{C}}$
satisfying the conditions of Theorem 3.6 are the representation categories of
${\mathcal{C}}$
satisfying the conditions of Theorem 3.6 are the representation categories of
![]() $q$
-deformations of connected compact simple Lie groups, where
$q$
-deformations of connected compact simple Lie groups, where
![]() $q\in (0,1]$
. If, moreover, the Lie group has trivial center, then the result directly implies Theorem A.
$q\in (0,1]$
. If, moreover, the Lie group has trivial center, then the result directly implies Theorem A.
Remark 3.7. It follows directly from the proof that Theorem 3.6 also holds for
![]() $\text{Rep}(\text{SU}_{q}(2))$
for
$\text{Rep}(\text{SU}_{q}(2))$
for
![]() $q\in (-1,0)$
. Since every free orthogonal quantum group
$q\in (-1,0)$
. Since every free orthogonal quantum group
![]() $O_{F}^{+}$
is monoidally equivalent to
$O_{F}^{+}$
is monoidally equivalent to
![]() $\text{SU}_{q}(2)$
(and hence has the same representation category) for some uniquely determined
$\text{SU}_{q}(2)$
(and hence has the same representation category) for some uniquely determined
![]() $q\in [-1,0)\cup (0,1]$
, the representation categories of free orthogonal quantum groups also satisfy the conditions of Theorem 3.6. Other examples of rigid
$q\in [-1,0)\cup (0,1]$
, the representation categories of free orthogonal quantum groups also satisfy the conditions of Theorem 3.6. Other examples of rigid
![]() $C^{\ast }$
-tensor categories with the same fusion ring as some connected compact simple Lie group are the Kazhdan–Wenzl categories [Reference Kazhdan and WenzlKW93] (see also [Reference JordansJor14]).
$C^{\ast }$
-tensor categories with the same fusion ring as some connected compact simple Lie group are the Kazhdan–Wenzl categories [Reference Kazhdan and WenzlKW93] (see also [Reference JordansJor14]).
4 A characterization of central states on
 $\text{SU}_{q}(N)$
$\text{SU}_{q}(N)$
Let
![]() $K$
be a connected simply connected compact simple Lie group, and take its complexification
$K$
be a connected simply connected compact simple Lie group, and take its complexification
![]() $G=K_{\mathbb{C}}$
, which has Iwasawa decomposition
$G=K_{\mathbb{C}}$
, which has Iwasawa decomposition
![]() $G=KAN$
. Let
$G=KAN$
. Let
![]() $\mathfrak{g}$
be the Lie algebra of
$\mathfrak{g}$
be the Lie algebra of
![]() $G$
, and let
$G$
, and let
![]() $\mathfrak{h}$
be a Cartan subalgebra of
$\mathfrak{h}$
be a Cartan subalgebra of
![]() $\mathfrak{g}$
. Let
$\mathfrak{g}$
. Let
![]() $K_{q}$
be a
$K_{q}$
be a
![]() $q$
-deformation of
$q$
-deformation of
![]() $K$
, where
$K$
, where
![]() $q\in (0,1)$
. Recall the following definition from [Reference AranoAra17].
$q\in (0,1)$
. Recall the following definition from [Reference AranoAra17].
Definition 4.1. We say that
![]() $\unicode[STIX]{x1D708}\in \mathfrak{h}^{\ast }$
is almost real (with respect to
$\unicode[STIX]{x1D708}\in \mathfrak{h}^{\ast }$
is almost real (with respect to
![]() $q$
) if
$q$
) if
![]() $(\text{Im}(\unicode[STIX]{x1D708}),\unicode[STIX]{x1D6FC})<2\unicode[STIX]{x1D70B}\log (q)^{-1}$
for all
$(\text{Im}(\unicode[STIX]{x1D708}),\unicode[STIX]{x1D6FC})<2\unicode[STIX]{x1D70B}\log (q)^{-1}$
for all
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
.
Recall the classification of extremal positive-definite functions of
![]() $G$
. The spherical admissible dual of
$G$
. The spherical admissible dual of
![]() $G$
is homeomorphic to
$G$
is homeomorphic to
![]() $\mathfrak{h}^{\ast }/W$
and the Berezin–Harish–Chandra formula (see [Reference HelgasonHel84, Theorem 5.7]) (with induction parameter
$\mathfrak{h}^{\ast }/W$
and the Berezin–Harish–Chandra formula (see [Reference HelgasonHel84, Theorem 5.7]) (with induction parameter
![]() $\frac{1}{2}\unicode[STIX]{x1D708}$
) asserts that the corresponding
$\frac{1}{2}\unicode[STIX]{x1D708}$
) asserts that the corresponding
![]() $K$
-bi-invariant function for
$K$
-bi-invariant function for
![]() $\unicode[STIX]{x1D708}\in \mathfrak{h}^{\ast }$
is
$\unicode[STIX]{x1D708}\in \mathfrak{h}^{\ast }$
is
where
![]() $\unicode[STIX]{x1D707}\in \mathfrak{h}_{\mathbb{R}}^{\ast }$
, the element
$\unicode[STIX]{x1D707}\in \mathfrak{h}_{\mathbb{R}}^{\ast }$
, the element
![]() $q^{\unicode[STIX]{x1D707}}$
is an element in
$q^{\unicode[STIX]{x1D707}}$
is an element in
![]() $A$
, the weight
$A$
, the weight
![]() $\unicode[STIX]{x1D70C}$
is half of the sum of the positive roots (which equals the sum of the fundamental weights), and
$\unicode[STIX]{x1D70C}$
is half of the sum of the positive roots (which equals the sum of the fundamental weights), and
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}}$
is the analytic continuation of the Weyl character formula:
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}}$
is the analytic continuation of the Weyl character formula:
Note that this formula holds for every (non-unitary) spherical principal series representation, since both sides of the equation are analytic. The unitary spherical dual (equivalently, the set of zonal spherical functions) is parametrized by
![]() $\unicode[STIX]{x1D708}\in \mathfrak{h}^{\ast }$
such that
$\unicode[STIX]{x1D708}\in \mathfrak{h}^{\ast }$
such that
![]() $\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}$
is positive-definite.
$\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}$
is positive-definite.
Recall that a central state
![]() $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
![]() $C(K_{q})$
is called extremal if
$C(K_{q})$
is called extremal if
![]() $\unicode[STIX]{x1D714}$
is a extremal point in the set of the central states. The following theorem follows from [Reference AranoAra17].
$\unicode[STIX]{x1D714}$
is a extremal point in the set of the central states. The following theorem follows from [Reference AranoAra17].
Theorem 4.2. For
![]() $q\in (0,1]$
, we have the following:
$q\in (0,1]$
, we have the following:
-
(i) the set of extremal central states on
 $K_{q}$
is parametrized by
$K_{q}$
is parametrized by
 $\unicode[STIX]{x1D708}\in \mathfrak{h}^{\ast }/2\unicode[STIX]{x1D70B}\text{i}\log (q)^{-1}Q^{\vee }\rtimes W$
such that is positive-definite;
$\unicode[STIX]{x1D708}\in \mathfrak{h}^{\ast }/2\unicode[STIX]{x1D70B}\text{i}\log (q)^{-1}Q^{\vee }\rtimes W$
such that is positive-definite; $$\begin{eqnarray}\unicode[STIX]{x1D711}_{q}^{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D706})=\frac{\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D706}}(q^{\unicode[STIX]{x1D708}})}{\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D706}}(q^{2\unicode[STIX]{x1D70C}})}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{q}^{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D706})=\frac{\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D706}}(q^{\unicode[STIX]{x1D708}})}{\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D706}}(q^{2\unicode[STIX]{x1D70C}})}\end{eqnarray}$$
-
(ii) if
 $\unicode[STIX]{x1D708}\in \mathfrak{h}^{\ast }$
is almost real, then
$\unicode[STIX]{x1D708}\in \mathfrak{h}^{\ast }$
is almost real, then
 $\unicode[STIX]{x1D711}_{q}^{\unicode[STIX]{x1D708}}$
is positive-definite if and only if
$\unicode[STIX]{x1D711}_{q}^{\unicode[STIX]{x1D708}}$
is positive-definite if and only if
 $\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}$
is;
$\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}$
is; -
(iii) if
 $K=\text{SU}(N)$
, then for all
$K=\text{SU}(N)$
, then for all
 $\unicode[STIX]{x1D708}\in \mathfrak{h}^{\ast }$
, we have
$\unicode[STIX]{x1D708}\in \mathfrak{h}^{\ast }$
, we have
 $\unicode[STIX]{x1D712}\in 2\unicode[STIX]{x1D70B}\text{i}\log (q)^{-1}P^{\vee }$
such that
$\unicode[STIX]{x1D712}\in 2\unicode[STIX]{x1D70B}\text{i}\log (q)^{-1}P^{\vee }$
such that
 $\unicode[STIX]{x1D708}-\unicode[STIX]{x1D712}$
is almost real with respect to
$\unicode[STIX]{x1D708}-\unicode[STIX]{x1D712}$
is almost real with respect to
 $q$
.
$q$
.
Proof. Recall that by [Reference De Commer, Freslon and YamashitaDCFY14, Theorem 29], the central states are in one-to-one correspondence with the
![]() $K_{q}$
-invariant states on the quantum codouble
$K_{q}$
-invariant states on the quantum codouble
![]() $C_{0}^{u}(\hat{{\mathcal{D}}}K_{q})$
, and hence unitary representations with a
$C_{0}^{u}(\hat{{\mathcal{D}}}K_{q})$
, and hence unitary representations with a
![]() $K_{q}$
-invariant vector. Then we obtain (i) from [Reference AranoAra16, Corollary 3.6], (ii) from [Reference AranoAra17, Theorem 4.9] and (iii) from [Reference AranoAra17, Lemma 2.5].◻
$K_{q}$
-invariant vector. Then we obtain (i) from [Reference AranoAra16, Corollary 3.6], (ii) from [Reference AranoAra17, Theorem 4.9] and (iii) from [Reference AranoAra17, Lemma 2.5].◻
Proposition 4.3. For
![]() $q\in (0,1]$
, we have
$q\in (0,1]$
, we have
Proof. From the Weyl character formula, it follows that
Using that
![]() $A_{\unicode[STIX]{x1D708}}(q^{\unicode[STIX]{x1D707}})=A_{\unicode[STIX]{x1D707}}(q^{\unicode[STIX]{x1D708}})$
, we compute that
$A_{\unicode[STIX]{x1D708}}(q^{\unicode[STIX]{x1D707}})=A_{\unicode[STIX]{x1D707}}(q^{\unicode[STIX]{x1D708}})$
, we compute that
Just as the Weyl character formula, the above formula should be viewed as a ‘formal’ formula, which literally holds only for generic
![]() $\unicode[STIX]{x1D708}$
. (For special
$\unicode[STIX]{x1D708}$
. (For special
![]() $\unicode[STIX]{x1D708}$
, we might get
$\unicode[STIX]{x1D708}$
, we might get
![]() $0/0$
.) Both the numerator and the denominator are analytic functions in the variable
$0/0$
.) Both the numerator and the denominator are analytic functions in the variable
![]() $\unicode[STIX]{x1D708}$
, and we take the analytic extension of the left hand side in general. Thus we can compute the zeroes of the denominator.
$\unicode[STIX]{x1D708}$
, and we take the analytic extension of the left hand side in general. Thus we can compute the zeroes of the denominator.
Proposition 4.4. For all
![]() $\unicode[STIX]{x1D708}\in \mathfrak{h}^{\ast }$
, we have
$\unicode[STIX]{x1D708}\in \mathfrak{h}^{\ast }$
, we have
![]() $\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}(q^{2\unicode[STIX]{x1D70C}})=0$
if and only if there exists
$\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}(q^{2\unicode[STIX]{x1D70C}})=0$
if and only if there exists
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}$
such that
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}$
such that
![]() $(\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}^{\vee })\in 2\unicode[STIX]{x1D70B}\text{i}\log (q_{\unicode[STIX]{x1D6FC}})^{-1}\mathbb{Z}\setminus \{0\}$
.
$(\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}^{\vee })\in 2\unicode[STIX]{x1D70B}\text{i}\log (q_{\unicode[STIX]{x1D6FC}})^{-1}\mathbb{Z}\setminus \{0\}$
.
Proof. Recall that
where we have used the Weyl dimension formula for the computation of the denominator. It follows that:
-
– the scalars
 $\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FC})$
and
$\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FC})$
and
 $A_{\unicode[STIX]{x1D70C}}(q^{2\unicode[STIX]{x1D70C}})$
are non-zero;
$A_{\unicode[STIX]{x1D70C}}(q^{2\unicode[STIX]{x1D70C}})$
are non-zero; -
– the function
 $\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}}(\frac{1}{2}\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC})$
has a zero whenever
$\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}}(\frac{1}{2}\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC})$
has a zero whenever
 $(\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC})=0$
, and each zero has order
$(\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC})=0$
, and each zero has order
 $1$
;
$1$
; -
– from the Weyl denominator formula, we obtain
which has a zero whenever $$\begin{eqnarray}A_{(1/2)\unicode[STIX]{x1D708}}(q^{2\unicode[STIX]{x1D70C}})=A_{\unicode[STIX]{x1D70C}}(q^{\unicode[STIX]{x1D708}})=q^{(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708})}\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}}(1-q^{-(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D708})}),\end{eqnarray}$$
$$\begin{eqnarray}A_{(1/2)\unicode[STIX]{x1D708}}(q^{2\unicode[STIX]{x1D70C}})=A_{\unicode[STIX]{x1D70C}}(q^{\unicode[STIX]{x1D708}})=q^{(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708})}\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{+}}(1-q^{-(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D708})}),\end{eqnarray}$$
 $(\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC})\in 2\unicode[STIX]{x1D70B}\text{i}\log (q)^{-1}\mathbb{Z}$
, and each zero has order
$(\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC})\in 2\unicode[STIX]{x1D70B}\text{i}\log (q)^{-1}\mathbb{Z}$
, and each zero has order
 $1$
.
$1$
.
Combining these, we get the desired conclusion. ◻
Corollary 4.5. Let
![]() $\unicode[STIX]{x1D708}\in \mathfrak{h}^{\ast }$
be an almost real weight such that
$\unicode[STIX]{x1D708}\in \mathfrak{h}^{\ast }$
be an almost real weight such that
![]() $\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}$
is self-adjoint. Then we have
$\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}$
is self-adjoint. Then we have
![]() $\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}(q^{2\unicode[STIX]{x1D70C}})>0$
.
$\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}(q^{2\unicode[STIX]{x1D70C}})>0$
.
Proof. Since
![]() $q^{2\unicode[STIX]{x1D70C}}$
and
$q^{2\unicode[STIX]{x1D70C}}$
and
![]() $q^{-2\unicode[STIX]{x1D70C}}$
lie in the same
$q^{-2\unicode[STIX]{x1D70C}}$
lie in the same
![]() $K$
-orbit, we know that
$K$
-orbit, we know that
![]() $\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}(q^{2\unicode[STIX]{x1D70C}})$
is real. We only need to show that the set
$\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}(q^{2\unicode[STIX]{x1D70C}})$
is real. We only need to show that the set
![]() $X$
of almost real weights
$X$
of almost real weights
![]() $\unicode[STIX]{x1D708}$
such that
$\unicode[STIX]{x1D708}$
such that
![]() $\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}$
is self-adjoint is connected. Once one shows this, since
$\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}$
is self-adjoint is connected. Once one shows this, since
![]() $\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}(q^{2\unicode[STIX]{x1D70C}})$
is non-zero, we only need to check the positivity at an arbitrary point in
$\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}(q^{2\unicode[STIX]{x1D70C}})$
is non-zero, we only need to check the positivity at an arbitrary point in
![]() $X$
, say
$X$
, say
![]() $\unicode[STIX]{x1D708}=2\unicode[STIX]{x1D70C}$
. In this case
$\unicode[STIX]{x1D708}=2\unicode[STIX]{x1D70C}$
. In this case
![]() $\unicode[STIX]{x1D711}_{1}^{2\unicode[STIX]{x1D70C}}(q^{2\unicode[STIX]{x1D70C}})=1$
, which completes the proof.
$\unicode[STIX]{x1D711}_{1}^{2\unicode[STIX]{x1D70C}}(q^{2\unicode[STIX]{x1D70C}})=1$
, which completes the proof.
To show the claim, we may assume that
![]() $\text{Re}(\unicode[STIX]{x1D708})$
is dominant, that is to say,
$\text{Re}(\unicode[STIX]{x1D708})$
is dominant, that is to say,
![]() $\text{Re}(\unicode[STIX]{x1D708})$
lies in the closure of the fundamental Weyl chamber. Note that
$\text{Re}(\unicode[STIX]{x1D708})$
lies in the closure of the fundamental Weyl chamber. Note that
![]() $\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}$
is self-adjoint if and only if there exists
$\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D708}}$
is self-adjoint if and only if there exists
![]() $w\in W$
such that
$w\in W$
such that
![]() $\unicode[STIX]{x1D708}=-w\overline{\unicode[STIX]{x1D708}}$
. Hence
$\unicode[STIX]{x1D708}=-w\overline{\unicode[STIX]{x1D708}}$
. Hence
![]() $\unicode[STIX]{x1D708}_{t}=\text{Re}(\unicode[STIX]{x1D708})+\text{i}t\,\text{Im}(\unicode[STIX]{x1D708})$
is a homotopy in
$\unicode[STIX]{x1D708}_{t}=\text{Re}(\unicode[STIX]{x1D708})+\text{i}t\,\text{Im}(\unicode[STIX]{x1D708})$
is a homotopy in
![]() $X$
that connects
$X$
that connects
![]() $\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D708}$
and
![]() $\text{Re}(\unicode[STIX]{x1D708})$
. On the other hand, the equation
$\text{Re}(\unicode[STIX]{x1D708})$
. On the other hand, the equation
![]() $\unicode[STIX]{x1D708}=-w\overline{\unicode[STIX]{x1D708}}$
shows that
$\unicode[STIX]{x1D708}=-w\overline{\unicode[STIX]{x1D708}}$
shows that
![]() $\text{Re}(\unicode[STIX]{x1D708})=-w_{0}\,\text{Re}(\unicode[STIX]{x1D708})$
, where
$\text{Re}(\unicode[STIX]{x1D708})=-w_{0}\,\text{Re}(\unicode[STIX]{x1D708})$
, where
![]() $w_{0}$
is the longest element of
$w_{0}$
is the longest element of
![]() $W$
. So the straight line connecting
$W$
. So the straight line connecting
![]() $\text{Re}(\unicode[STIX]{x1D708})$
and
$\text{Re}(\unicode[STIX]{x1D708})$
and
![]() $2\unicode[STIX]{x1D70C}$
is a homotopy in
$2\unicode[STIX]{x1D70C}$
is a homotopy in
![]() $X$
. ◻
$X$
. ◻
For
![]() $0<q\leqslant 1$
, let
$0<q\leqslant 1$
, let
![]() $Z_{q}$
be the unitary spherical dual of
$Z_{q}$
be the unitary spherical dual of
![]() $G_{q}$
inside
$G_{q}$
inside
![]() $\mathfrak{h}^{\ast }/2\unicode[STIX]{x1D70B}\text{i}\log (q)^{-1}Q^{\vee }\rtimes W$
. We make the identification
$\mathfrak{h}^{\ast }/2\unicode[STIX]{x1D70B}\text{i}\log (q)^{-1}Q^{\vee }\rtimes W$
. We make the identification
![]() $2\unicode[STIX]{x1D70B}\text{i}\log (q)^{-1}(P^{\vee }/Q^{\vee })\simeq \widehat{P/Q}$
.
$2\unicode[STIX]{x1D70B}\text{i}\log (q)^{-1}(P^{\vee }/Q^{\vee })\simeq \widehat{P/Q}$
.
Lemma 4.6. Let
![]() $K=\text{SU}(N)$
. Then we have a decomposition
$K=\text{SU}(N)$
. Then we have a decomposition
with the following properties:
-
– if
 $\unicode[STIX]{x1D708}\in Z_{q}^{\unicode[STIX]{x1D712}}$
, then
$\unicode[STIX]{x1D708}\in Z_{q}^{\unicode[STIX]{x1D712}}$
, then
 $\unicode[STIX]{x1D708}-\unicode[STIX]{x1D712}\in Z_{1}$
;
$\unicode[STIX]{x1D708}-\unicode[STIX]{x1D712}\in Z_{1}$
; -
– the function
 $\unicode[STIX]{x1D708}\mapsto 1/\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}-\unicode[STIX]{x1D712}}^{1}(q^{2\unicode[STIX]{x1D70C}})$
is positive and bounded on
$\unicode[STIX]{x1D708}\mapsto 1/\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D708}-\unicode[STIX]{x1D712}}^{1}(q^{2\unicode[STIX]{x1D70C}})$
is positive and bounded on
 $Z_{q}^{\unicode[STIX]{x1D712}}$
.
$Z_{q}^{\unicode[STIX]{x1D712}}$
.
We can now give the proof of Theorem C.
Proof of Theorem C.
Take the decomposition as in Lemma 4.6. Put
We know that
![]() $\unicode[STIX]{x1D711}$
is positive-definite if and only if there exists a finite measure
$\unicode[STIX]{x1D711}$
is positive-definite if and only if there exists a finite measure
![]() $\unicode[STIX]{x1D707}$
on the unitary spherical dual such that
$\unicode[STIX]{x1D707}$
on the unitary spherical dual such that
By putting
![]() $d\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D708})=d\unicode[STIX]{x1D707}(\unicode[STIX]{x1D708}+\unicode[STIX]{x1D712})|_{Z_{q}^{\unicode[STIX]{x1D712}}}$
, we obtain a measure on
$d\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D708})=d\unicode[STIX]{x1D707}(\unicode[STIX]{x1D708}+\unicode[STIX]{x1D712})|_{Z_{q}^{\unicode[STIX]{x1D712}}}$
, we obtain a measure on
![]() $Z_{1}$
. Defining
$Z_{1}$
. Defining
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D712}}$
as
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D712}}$
as
this gives the desired decomposition.◻
Acknowledgements
The authors thank Stefaan Vaes for valuable discussions, suggestions and remarks. The first-named author wishes to thank KU Leuven, where this research was carried out, for the invitation and hospitality.