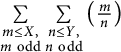1 Introduction
We study the double character sum
 $$ \begin{align} S(X,Y):=\sum_{\substack{m\leq X,\\m\mathrm{\ odd}}}\sum_{\substack{n\leq Y,\\n\mathrm{\ odd}}}\left(\frac{m}{n}\right). \end{align} $$
$$ \begin{align} S(X,Y):=\sum_{\substack{m\leq X,\\m\mathrm{\ odd}}}\sum_{\substack{n\leq Y,\\n\mathrm{\ odd}}}\left(\frac{m}{n}\right). \end{align} $$
This sum was studied by Conrey, Farmer, and Soundararajan in [Reference Chinta, Friedberg and HoffsteinCFS], where the authors give an asymptotic formula valid for all large X and Y.
If
![]() $Y=o(X/\log X)$
, then the main term of
$Y=o(X/\log X)$
, then the main term of
![]() $S(X,Y)$
comes from the terms where n is a square, and the error term can be estimated using the Pólya–Vinogradov inequality. In particular, we get that in this range,
$S(X,Y)$
comes from the terms where n is a square, and the error term can be estimated using the Pólya–Vinogradov inequality. In particular, we get that in this range,
and similarly for
![]() $X=o(Y/\log Y)$
.
$X=o(Y/\log Y)$
.
Conrey, Farmer, and Soundararajan showed that there is a transition in the behavior of
![]() $S(X,Y)$
when
$S(X,Y)$
when
![]() $X,Y$
are of similar size. In particular, they proved the following asymptotic formula, which is valid for all large
$X,Y$
are of similar size. In particular, they proved the following asymptotic formula, which is valid for all large
![]() $X,Y$
:
$X,Y$
:
where
 $$ \begin{align} C(\alpha)=\alpha+\alpha^{3/2}\frac2{\pi}\sum_{k=1}^\infty\frac1{k^2}\int_{0}^{1/\alpha}\sqrt y\sin\left(\frac{\pi k^2}{2y}\right) dy. \end{align} $$
$$ \begin{align} C(\alpha)=\alpha+\alpha^{3/2}\frac2{\pi}\sum_{k=1}^\infty\frac1{k^2}\int_{0}^{1/\alpha}\sqrt y\sin\left(\frac{\pi k^2}{2y}\right) dy. \end{align} $$
The size of the main term in this formula is
![]() $XY^{1/2}+YX^{1/2}$
, so it is always larger than the error term. The result is interesting, because
$XY^{1/2}+YX^{1/2}$
, so it is always larger than the error term. The result is interesting, because
![]() $C(\alpha )$
is a non-smooth function. For a heuristic explanation, why such functions arise in this type of problems, see the first section in [Reference PetrowPet] and the references therein.
$C(\alpha )$
is a non-smooth function. For a heuristic explanation, why such functions arise in this type of problems, see the first section in [Reference PetrowPet] and the references therein.
Conrey, Farmer, and Soundararajan also gave the following asymptotic estimates for
![]() $C(\alpha )$
:
$C(\alpha )$
:
and
To prove (1.3), Conrey, Farmer, and Soundararajan applied the Poisson summation formula and estimated the sums of Gauss sums which appeared in the computation. Similar techniques were used in the work of Gao and Zhao to compute the mean value in other families of characters, such as cubic and quartic Dirichlet characters [Reference Gao and ZhaoGZ2], and some quadratic, cubic, and quartic Hecke characters [Reference Gao and ZhaoGZ1]. Gao used similar methods to compute the mean value of the divisor function twisted by quadratic characters [Reference GaoGao].
Our approach is to rewrite
![]() $S(X,Y)$
as a double integral by using the inverse Mellin transform twice. The integral will then involve the double Dirichlet series
$S(X,Y)$
as a double integral by using the inverse Mellin transform twice. The integral will then involve the double Dirichlet series
 $$ \begin{align*}A(s,w)=\sum_{m\mathrm{\ odd}}\sum_{n\mathrm{\ odd}}\frac{\left(\frac{m}{n}\right)}{m^wn^s},\end{align*} $$
$$ \begin{align*}A(s,w)=\sum_{m\mathrm{\ odd}}\sum_{n\mathrm{\ odd}}\frac{\left(\frac{m}{n}\right)}{m^wn^s},\end{align*} $$
which was studied by Blomer [Reference BlomerBlo], who showed that it admits a meromorphic continuation to the whole
![]() $\mathbb {C}^2$
and determined the polar lines. We then shift the integrals to the left and compute the contribution of the residues. The quality of the error term depends whether we assume the truth of the Riemann Hypothesis because the zeros of
$\mathbb {C}^2$
and determined the polar lines. We then shift the integrals to the left and compute the contribution of the residues. The quality of the error term depends whether we assume the truth of the Riemann Hypothesis because the zeros of
![]() $\zeta (s)$
appear in the location of the poles of
$\zeta (s)$
appear in the location of the poles of
![]() $A(s,w)$
, and also in the contribution of the residues.
$A(s,w)$
, and also in the contribution of the residues.
An interesting feature of our proof is that the three polar lines from which our main term arises naturally correspond to the contribution of squares (the polar lines
![]() $s=1$
and
$s=1$
and
![]() $w=1$
), and the transition term where the non-smooth function appears (the polar line
$w=1$
), and the transition term where the non-smooth function appears (the polar line
![]() $s+w=3/2$
).
$s+w=3/2$
).
A more general theory of multiple Dirichlet series has been developed by Bump, Chinta, Diaconu, Friedberg, Goldfeld, Hoffstein, and others. We refer the reader interested in the theory and its applications to the expository articles [Reference Bump, Friedberg and HoffsteinBFH, Reference BumpBum, Reference Conrey, Farmer and SoundararajanCFH], the paper [Reference Diaconu, Goldfeld and HoffsteinDGH], or the book [Reference Bump, Friedberg and GoldfeldBFG].
To state our results, we first define the smooth sum
 $$ \begin{align} S(X,Y;\varphi,\psi)=\sum_{m,n\mathrm{\ odd}}\left(\frac{m}{n}\right) \varphi(m/X)\psi(n/Y), \end{align} $$
$$ \begin{align} S(X,Y;\varphi,\psi)=\sum_{m,n\mathrm{\ odd}}\left(\frac{m}{n}\right) \varphi(m/X)\psi(n/Y), \end{align} $$
where
![]() $\varphi ,\psi $
are nonnegative smooth functions supported in
$\varphi ,\psi $
are nonnegative smooth functions supported in
![]() $(0,1)$
.
$(0,1)$
.
If we denote by
![]() $\hat f$
the Mellin transform of f (see (2.7)), the main result is the following.
$\hat f$
the Mellin transform of f (see (2.7)), the main result is the following.
Theorem 1.1 Let
![]() $\varepsilon>0$
. Then for all large
$\varepsilon>0$
. Then for all large
![]() $X,Y,$
we have
$X,Y,$
we have
where
![]() $\delta =\varepsilon $
, and
$\delta =\varepsilon $
, and
 $$ \begin{align*} D(\alpha;\varphi,\psi)&=\frac{\hat\varphi(1)\hat\psi\left(\frac{1}{2}\right)\alpha^{1/2}+\hat\psi(1)\hat\varphi\left(\frac{1}{2}\right)\alpha}{2}\\ &\quad+\frac1{i\sqrt\pi }\int\limits_{(3/4)}\left(\frac{\alpha}{2\pi}\right)^s\cdot\hat\varphi\left(\frac32-s\right)\hat\psi(s)\Gamma\left( s-\frac12\right)\sin\left(\frac{\pi s}{2}\right)\zeta(2s-1)ds. \end{align*} $$
$$ \begin{align*} D(\alpha;\varphi,\psi)&=\frac{\hat\varphi(1)\hat\psi\left(\frac{1}{2}\right)\alpha^{1/2}+\hat\psi(1)\hat\varphi\left(\frac{1}{2}\right)\alpha}{2}\\ &\quad+\frac1{i\sqrt\pi }\int\limits_{(3/4)}\left(\frac{\alpha}{2\pi}\right)^s\cdot\hat\varphi\left(\frac32-s\right)\hat\psi(s)\Gamma\left( s-\frac12\right)\sin\left(\frac{\pi s}{2}\right)\zeta(2s-1)ds. \end{align*} $$
If we assume the Riemann Hypothesis, then we can take
![]() $\delta =-1/4+\varepsilon $
.
$\delta =-1/4+\varepsilon $
.
We can remove the smooth weights and obtain the following asymptotic formula for
![]() $S(X,Y)$
, which improves the error term in (1.3):
$S(X,Y)$
, which improves the error term in (1.3):
Theorem 1.2 Let
![]() $\varepsilon>0$
. Then for all large
$\varepsilon>0$
. Then for all large
![]() $X,Y$
, we have
$X,Y$
, we have
where
 $$ \begin{align} D(\alpha)=\sqrt\alpha+\alpha-\frac1{i\sqrt\pi }\int\limits_{(3/4)}\left(\frac{\alpha}{2\pi}\right)^s\cdot\frac{\Gamma\left( s-\frac32\right)\sin\left(\frac{\pi s}{2}\right)\zeta(2s-1)}{s}ds. \end{align} $$
$$ \begin{align} D(\alpha)=\sqrt\alpha+\alpha-\frac1{i\sqrt\pi }\int\limits_{(3/4)}\left(\frac{\alpha}{2\pi}\right)^s\cdot\frac{\Gamma\left( s-\frac32\right)\sin\left(\frac{\pi s}{2}\right)\zeta(2s-1)}{s}ds. \end{align} $$
We show in Section 7 that
![]() $D(\alpha )=C(\alpha )$
, so our main term agrees with that of Conrey, Farmer, and Soundararajan.
$D(\alpha )=C(\alpha )$
, so our main term agrees with that of Conrey, Farmer, and Soundararajan.
Let us also remark that a similar asymptotic can be obtained if the integers
![]() $m,n$
were restricted to lie in a congruence class modulo
$m,n$
were restricted to lie in a congruence class modulo
![]() $8$
by working with a suitable combination of the twisted double Dirichlet series, as defined in (3.3).
$8$
by working with a suitable combination of the twisted double Dirichlet series, as defined in (3.3).
2 Preliminaries and notation
Throughout the paper,
![]() $\varepsilon $
will denote a sufficiently small positive number, different at each occurrence, and all implied constants are allowed to depend on
$\varepsilon $
will denote a sufficiently small positive number, different at each occurrence, and all implied constants are allowed to depend on
![]() $\varepsilon $
.
$\varepsilon $
.
We follow the notation of [Reference BlomerBlo]. For integers
![]() $m,n$
, we denote by
$m,n$
, we denote by
![]() $\chi _m(n)$
the Kronecker symbol
$\chi _m(n)$
the Kronecker symbol
Assume that m is odd and write it as
![]() $m=m_0m_1^2$
with
$m=m_0m_1^2$
with
![]() $m_0$
squarefree. Then
$m_0$
squarefree. Then
![]() $\chi _m$
is a character of conductor
$\chi _m$
is a character of conductor
![]() $|m_0|$
if
$|m_0|$
if
![]() $m\equiv 1\mod 4$
and
$m\equiv 1\mod 4$
and
![]() $|4m_0|$
if
$|4m_0|$
if
![]() $m\equiv 3\mod 4.$
We denote by
$m\equiv 3\mod 4.$
We denote by
![]() $\psi _1,\psi _{-1},\psi _2,\psi _{-2}$
the four Dirichlet characters modulo 8 given by the Kronecker symbol
$\psi _1,\psi _{-1},\psi _2,\psi _{-2}$
the four Dirichlet characters modulo 8 given by the Kronecker symbol
![]() $\psi _j(n)=\left (\frac {j}{n}\right ).$
We also let
$\psi _j(n)=\left (\frac {j}{n}\right ).$
We also let
 $$ \begin{align*}\tilde\chi_m=\begin{cases}\chi_m,&{\text{ if }m\equiv1\ \ \mod 4,}\\\chi_{-m},&{\text{ if }m\equiv3\ \ \mod 4.}\end{cases}\end{align*} $$
$$ \begin{align*}\tilde\chi_m=\begin{cases}\chi_m,&{\text{ if }m\equiv1\ \ \mod 4,}\\\chi_{-m},&{\text{ if }m\equiv3\ \ \mod 4.}\end{cases}\end{align*} $$
With this notation, quadratic reciprocity tells us that for odd positive integers
![]() $m,n$
,
$m,n$
,
The fundamental discriminants m correspond to primitive real characters of conductor
![]() $|m|$
. In such cases, the completed L-function is
$|m|$
. In such cases, the completed L-function is
 $$ \begin{align*}\Lambda(s,\chi_{m})=\left(\frac{|m|}{\pi}\right) ^{\frac{s+a}2}\Gamma\left(\frac{s+a}{2}\right)L(s,\chi_{m}),\end{align*} $$
$$ \begin{align*}\Lambda(s,\chi_{m})=\left(\frac{|m|}{\pi}\right) ^{\frac{s+a}2}\Gamma\left(\frac{s+a}{2}\right)L(s,\chi_{m}),\end{align*} $$
where
![]() $a=0$
or
$a=0$
or
![]() $1$
depending on whether the character is even or odd, i.e., whether
$1$
depending on whether the character is even or odd, i.e., whether
![]() $\chi _m(-1)=1$
or
$\chi _m(-1)=1$
or
![]() $-1$
, and we have the functional equation
$-1$
, and we have the functional equation
All primitive real characters can be uniquely written as
![]() $\chi _{m_0}\psi _j$
for some positive odd squarefree integer
$\chi _{m_0}\psi _j$
for some positive odd squarefree integer
![]() $m_0$
and
$m_0$
and
![]() $j\in \{\pm 1,\pm 2\}$
.
$j\in \{\pm 1,\pm 2\}$
.
If m is not a fundamental discriminant, then
![]() $\chi _m$
is a character of conductor
$\chi _m$
is a character of conductor
![]() $m_0\mid 4m$
, and we have
$m_0\mid 4m$
, and we have
 $$ \begin{align} L(s,\chi_m)=L(s,\chi_{m_0})\cdot\prod_{p\mid\frac{|m|}{m_0}}\left(1-\frac{\chi_{m_0}(p)}{p^s}\right). \end{align} $$
$$ \begin{align} L(s,\chi_m)=L(s,\chi_{m_0})\cdot\prod_{p\mid\frac{|m|}{m_0}}\left(1-\frac{\chi_{m_0}(p)}{p^s}\right). \end{align} $$
A subscript
![]() $2$
of an L-function means that the Euler factor at
$2$
of an L-function means that the Euler factor at
![]() $2$
is removed, so, in particular,
$2$
is removed, so, in particular,
 $$ \begin{align} L_2(s,\chi)=\sum_{n\mathrm{\ odd}}\frac{\chi(n)}{n^s}. \end{align} $$
$$ \begin{align} L_2(s,\chi)=\sum_{n\mathrm{\ odd}}\frac{\chi(n)}{n^s}. \end{align} $$
We now record two estimates that will be used later.
The first estimate holds for any s with
![]() $\mathrm {Re}(s)\geq 1/2$
:
$\mathrm {Re}(s)\geq 1/2$
:
 $$ \begin{align} \sum_{\substack{m\leq X,\\m\mathrm{\ odd}}}|L_2(s,\chi_m\psi_j)|\ll_{\varepsilon} X^{1+\varepsilon}|s|^{\frac14+\varepsilon}. \end{align} $$
$$ \begin{align} \sum_{\substack{m\leq X,\\m\mathrm{\ odd}}}|L_2(s,\chi_m\psi_j)|\ll_{\varepsilon} X^{1+\varepsilon}|s|^{\frac14+\varepsilon}. \end{align} $$
It follows after applying Hölder’s inequality on the bound for the fourth moment, proved by Heath-Brown [Reference Heath-BrownHea, Theorem 2].
The second is conditional under RH, and it says that for any fixed
![]() $\sigma>1/2$
, we have
$\sigma>1/2$
, we have
 $$ \begin{align} \left|\frac1{\zeta(\sigma+it)}\right|\ll_\varepsilon(1+|t|)^\varepsilon. \end{align} $$
$$ \begin{align} \left|\frac1{\zeta(\sigma+it)}\right|\ll_\varepsilon(1+|t|)^\varepsilon. \end{align} $$
It follows from [Reference Carneiro and ChandeeCC, Theorem 2].
For a function
![]() $f(x)$
, we denote by
$f(x)$
, we denote by
![]() $\hat f(s)$
its Mellin transform, which is defined as
$\hat f(s)$
its Mellin transform, which is defined as
when the integral converges. If
![]() $\hat f$
is analytic in the strip
$\hat f$
is analytic in the strip
![]() $a<\mathrm {Re}(s)<b$
, then the inverse Mellin transform is given by
$a<\mathrm {Re}(s)<b$
, then the inverse Mellin transform is given by
 $$ \begin{align} f(x)=\frac1{2\pi i}\int\limits_{(c)}x^{-s}\hat f(s)ds, \end{align} $$
$$ \begin{align} f(x)=\frac1{2\pi i}\int\limits_{(c)}x^{-s}\hat f(s)ds, \end{align} $$
where the integral is over the vertical line
![]() $\mathrm {Re}(s)=c$
, and
$\mathrm {Re}(s)=c$
, and
![]() $a<c<b$
is arbitrary.
$a<c<b$
is arbitrary.
We will use the following estimate for the Gamma function, which is a consequence of Stirling’s formula: for a fixed
![]() $\sigma \in \mathbb {R}$
and
$\sigma \in \mathbb {R}$
and
![]() $|t|\geq 1$
, we have
$|t|\geq 1$
, we have
We will also use the formula
 $$ \begin{align} \frac{\Gamma\left(\frac{1-s}{2}\right)}{\Gamma\left(\frac{s}{2}\right)}=\frac{2^s\sin (\pi s/2)\Gamma(1-s)}{\sqrt\pi}. \end{align} $$
$$ \begin{align} \frac{\Gamma\left(\frac{1-s}{2}\right)}{\Gamma\left(\frac{s}{2}\right)}=\frac{2^s\sin (\pi s/2)\Gamma(1-s)}{\sqrt\pi}. \end{align} $$
We write the functional equation for the Riemann zeta function as
where
We will also use the estimate
which is true for any
![]() $\sigma \geq 1/2.$
$\sigma \geq 1/2.$
3 Outline of the proof and double Dirichlet series
Applying Mellin inversion to
![]() $S(X,Y;\varphi ,\psi )$
twice, we obtain
$S(X,Y;\varphi ,\psi )$
twice, we obtain
 $$ \begin{align} S(X,Y;\varphi,\psi)=\left(\frac{1}{2\pi i}\right)^2\int\limits_{(\sigma)}\int\limits_{(\omega)}A(s,w)X^wY^s\hat\varphi(w)\hat\psi(s)dwds, \end{align} $$
$$ \begin{align} S(X,Y;\varphi,\psi)=\left(\frac{1}{2\pi i}\right)^2\int\limits_{(\sigma)}\int\limits_{(\omega)}A(s,w)X^wY^s\hat\varphi(w)\hat\psi(s)dwds, \end{align} $$
where for
![]() $\mathrm {Re}(s)=\sigma $
and
$\mathrm {Re}(s)=\sigma $
and
![]() $\mathrm {Re}(w)=\omega $
large enough, we have the absolutely convergent double Dirichlet series
$\mathrm {Re}(w)=\omega $
large enough, we have the absolutely convergent double Dirichlet series
 $$ \begin{align} A(s,w)=\sum_{m\mathrm{\ odd}}\sum_{n\mathrm{\ odd}}\frac{\left(\frac{m}{n}\right)}{m^wn^s}=\sum_{m\mathrm{\ odd}}\frac{L_2(s,\chi_m)}{m^w}. \end{align} $$
$$ \begin{align} A(s,w)=\sum_{m\mathrm{\ odd}}\sum_{n\mathrm{\ odd}}\frac{\left(\frac{m}{n}\right)}{m^wn^s}=\sum_{m\mathrm{\ odd}}\frac{L_2(s,\chi_m)}{m^w}. \end{align} $$
We use the results of Blomer to meromorphically continue
![]() $A(s,w)$
to the whole
$A(s,w)$
to the whole
![]() $\mathbb {C}^2$
, shift the two integrals to the left and compute the contribution of the crossed polar lines.
$\mathbb {C}^2$
, shift the two integrals to the left and compute the contribution of the crossed polar lines.
We now cite and sketch the proof of Lemma 2 in [Reference BlomerBlo]. For two characters
![]() $\psi ,\psi '$
of conductor dividing
$\psi ,\psi '$
of conductor dividing
![]() $8$
, we define
$8$
, we define
 $$ \begin{align} Z(s,w;\psi,\psi'):=\zeta_2(2s+2w-1)\sum_{m,n\mathrm{\ odd}}\frac{\chi_m(n)\psi(n)\psi'(m)}{m^wn^s}, \end{align} $$
$$ \begin{align} Z(s,w;\psi,\psi'):=\zeta_2(2s+2w-1)\sum_{m,n\mathrm{\ odd}}\frac{\chi_m(n)\psi(n)\psi'(m)}{m^wn^s}, \end{align} $$
which converges absolutely if
![]() $\mathrm {Re}(s)$
and
$\mathrm {Re}(s)$
and
![]() $\mathrm {Re}(w)$
are large enough, and we let
$\mathrm {Re}(w)$
are large enough, and we let
We also denote
 $$ \begin{align*}\mathbf{Z}(s,w;\psi)=\left( \begin{array}{c} Z(s,w;\psi,\psi_1)\\ Z(s,w;\psi,\psi_{-1})\\ Z(s,w;\psi,\psi_{2})\\ Z(s,w;\psi,\psi_{-2})\\ \end{array} \right),\hspace{10pt} \mathbf{Z}(s,w)=\left( \begin{array}{c} \mathbf{Z}(s,w,\psi_1)\\ \mathbf{Z}(s,w,\psi_{-1})\\ \mathbf{Z}(s,w,\psi_{2})\\ \mathbf{Z}(s,w,\psi_{-2})\\ \end{array} \right).\end{align*} $$
$$ \begin{align*}\mathbf{Z}(s,w;\psi)=\left( \begin{array}{c} Z(s,w;\psi,\psi_1)\\ Z(s,w;\psi,\psi_{-1})\\ Z(s,w;\psi,\psi_{2})\\ Z(s,w;\psi,\psi_{-2})\\ \end{array} \right),\hspace{10pt} \mathbf{Z}(s,w)=\left( \begin{array}{c} \mathbf{Z}(s,w,\psi_1)\\ \mathbf{Z}(s,w,\psi_{-1})\\ \mathbf{Z}(s,w,\psi_{2})\\ \mathbf{Z}(s,w,\psi_{-2})\\ \end{array} \right).\end{align*} $$
Theorem 3.1 The functions
![]() $Z(s,w;\psi ,\psi ')$
have a meromorphic continuation to the whole
$Z(s,w;\psi ,\psi ')$
have a meromorphic continuation to the whole
![]() $\mathbb {C}^2$
with a polar line
$\mathbb {C}^2$
with a polar line
![]() $s+w=3/2$
. There is an additional polar line at
$s+w=3/2$
. There is an additional polar line at
![]() $s=1$
with residue
$s=1$
with residue
![]() $\mathrm {res}_{(1,w)}Z(s,w)=\zeta _2(2w)/2$
if and only if
$\mathrm {res}_{(1,w)}Z(s,w)=\zeta _2(2w)/2$
if and only if
![]() $\psi =\psi _1$
, and an additional polar line
$\psi =\psi _1$
, and an additional polar line
![]() $w=1$
with residue
$w=1$
with residue
![]() $\mathrm {res}_{(s,1)}Z(s,w)=\zeta _2(2s)/2$
if and only if
$\mathrm {res}_{(s,1)}Z(s,w)=\zeta _2(2s)/2$
if and only if
![]() $\psi '=\psi _1$
.
$\psi '=\psi _1$
.
The functions
![]() $(s-1)(w-1)(s+w-3/2)Z(s,w;\psi ,\psi ')$
are polynomially bounded in vertical strips, meaning that for fixed
$(s-1)(w-1)(s+w-3/2)Z(s,w;\psi ,\psi ')$
are polynomially bounded in vertical strips, meaning that for fixed
![]() $\mathrm {Re}(s)$
and
$\mathrm {Re}(s)$
and
![]() $\mathrm {Re}(w), (s-1)(w-1)(s+w-3/2)Z(s,w;\psi ,\psi ')$
is bounded by a polynomial in
$\mathrm {Re}(w), (s-1)(w-1)(s+w-3/2)Z(s,w;\psi ,\psi ')$
is bounded by a polynomial in
![]() $\mathrm {Im}(s),\mathrm {Im}(w)$
. The functions satisfy functional equations relating
$\mathrm {Im}(s),\mathrm {Im}(w)$
. The functions satisfy functional equations relating
![]() $\mathbf {Z}(s,w)$
with
$\mathbf {Z}(s,w)$
with
![]() $\mathbf {Z}(w,s)$
, and
$\mathbf {Z}(w,s)$
, and
![]() $\mathbf {Z}(s,w)$
with
$\mathbf {Z}(s,w)$
with
![]() $\mathbf {Z}(1-s,s+w-1/2)$
.
$\mathbf {Z}(1-s,s+w-1/2)$
.
-
(i) Blomer gives explicit
 $16\times 16$
matrices A and
$16\times 16$
matrices A and
 $B(s)$
, such that
$B(s)$
, such that
 $\mathbf {Z}(s,w)=A\cdot \mathbf {Z}(w,s)$
and
$\mathbf {Z}(s,w)=A\cdot \mathbf {Z}(w,s)$
and
 $\mathbf {Z}(s,w)=B(s)\cdot \mathbf {Z}(1-s,s+w-1/2)$
, we will use the explicit form in (5.2) to compute the residues on the polar line
$\mathbf {Z}(s,w)=B(s)\cdot \mathbf {Z}(1-s,s+w-1/2)$
, we will use the explicit form in (5.2) to compute the residues on the polar line
 $s+w=3/2$
.
$s+w=3/2$
. -
(ii) We can also iterate the two functional equations and obtain others, for example, relating
 $\mathbf {Z}(s,w)$
with
$\mathbf {Z}(s,w)$
with
 $\mathbf {Z}(1-s,1-w)$
. Blomer also gives an almost explicit form of this case.
$\mathbf {Z}(1-s,1-w)$
. Blomer also gives an almost explicit form of this case. -
(iii) For us, a polar line means that if we fix one of the variables, the resulting function of the other variable has a pole on the corresponding line with the given residue. What we state doesn’t exactly hold at the points
 $(1/2,1)$
and
$(1/2,1)$
and
 $(1,1/2)$
, where two of the polar lines intersect, but we will not need to know the exact behavior at these points.
$(1,1/2)$
, where two of the polar lines intersect, but we will not need to know the exact behavior at these points.
Proof sketch
We write the Dirichlet series for
![]() $Z(s,w;\psi ,\psi ')$
in two ways.
$Z(s,w;\psi ,\psi ')$
in two ways.
First, writing
![]() $m=m_0m_1^2$
with
$m=m_0m_1^2$
with
![]() $\mu ^2(m_0)=1$
, we have
$\mu ^2(m_0)=1$
, we have
 $$ \begin{align} \begin{aligned} Z(s,w;\psi,\psi')&=\zeta_2(2s+2w-1)\sum_{\substack{m_0\mathrm{\ odd},\\ \mu^2(m_0)=1}}\frac{L_2(s,\chi_{m_0}\psi)\psi'(m_0)}{m_0^w}\\[5pt]&\hspace{30pt}\times\sum_{m_1\mathrm{\ odd}}\frac1{m_1^{2w}}\prod_{p|m_1}\left(1-\frac{\chi_{m_0}\psi(p)}{p^s}\right)\\&=\zeta_2(2s+2w-1)\sum_{\substack{m_0\mathrm{\ odd},\\\mu^2(m_0)=1}}\frac{L_2(s,\chi_{m_0}\psi)\psi'(m_0)\zeta_2(2w)}{m_0^wL_2(s+2w,\chi_{m_0}\psi)}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} Z(s,w;\psi,\psi')&=\zeta_2(2s+2w-1)\sum_{\substack{m_0\mathrm{\ odd},\\ \mu^2(m_0)=1}}\frac{L_2(s,\chi_{m_0}\psi)\psi'(m_0)}{m_0^w}\\[5pt]&\hspace{30pt}\times\sum_{m_1\mathrm{\ odd}}\frac1{m_1^{2w}}\prod_{p|m_1}\left(1-\frac{\chi_{m_0}\psi(p)}{p^s}\right)\\&=\zeta_2(2s+2w-1)\sum_{\substack{m_0\mathrm{\ odd},\\\mu^2(m_0)=1}}\frac{L_2(s,\chi_{m_0}\psi)\psi'(m_0)\zeta_2(2w)}{m_0^wL_2(s+2w,\chi_{m_0}\psi)}. \end{aligned} \end{align} $$
If
![]() $\psi $
is nontrivial, the right-hand side converges absolutely in the region
$\psi $
is nontrivial, the right-hand side converges absolutely in the region
the second condition comes from using the functional equation in the numerator when
![]() $\mathrm {Re}(s)<1/2$
. When
$\mathrm {Re}(s)<1/2$
. When
![]() $\psi $
is the trivial character, the summand corresponding to
$\psi $
is the trivial character, the summand corresponding to
![]() $m_0=1$
is
$m_0=1$
is
![]() $\frac {\zeta _2(s)\zeta _2(2w)}{\zeta _2(s+2w)}$
, so there is a pole at
$\frac {\zeta _2(s)\zeta _2(2w)}{\zeta _2(s+2w)}$
, so there is a pole at
![]() $s=1$
with residue
$s=1$
with residue
![]() $\zeta _2(2w)/2.$
Note that the other potential polar lines coming from
$\zeta _2(2w)/2.$
Note that the other potential polar lines coming from
![]() $\frac {\zeta _2(2w)}{L_2(s+2w,\chi _{d_0}\psi )}$
are outside of the considered region.
$\frac {\zeta _2(2w)}{L_2(s+2w,\chi _{d_0}\psi )}$
are outside of the considered region.
The second way to write
![]() $Z(s,w;\psi ,\psi ')$
is by exchanging summations and using the quadratic reciprocity. We obtain
$Z(s,w;\psi ,\psi ')$
is by exchanging summations and using the quadratic reciprocity. We obtain
 $$ \begin{align}\begin{aligned} Z(s,w;\psi,\psi')&=\zeta_2(2s+2w-1)\sum_{m,n\mathrm{\ odd}}\frac{\chi_m(n)\psi(n)\psi'(m)}{m^wn^s}\\&=\zeta_2(2s+2w-1)\sum_{n\mathrm{\ odd}}\frac{L_2(w,\tilde\chi_n\psi')\psi(n)}{n^s}. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} Z(s,w;\psi,\psi')&=\zeta_2(2s+2w-1)\sum_{m,n\mathrm{\ odd}}\frac{\chi_m(n)\psi(n)\psi'(m)}{m^wn^s}\\&=\zeta_2(2s+2w-1)\sum_{n\mathrm{\ odd}}\frac{L_2(w,\tilde\chi_n\psi')\psi(n)}{n^s}. \end{aligned} \end{align} $$
We can again write
![]() $n=n_0n_1^2$
with
$n=n_0n_1^2$
with
![]() $\mu ^2(n_0)=1$
and obtain a series that is absolutely convergent in the region
$\mu ^2(n_0)=1$
and obtain a series that is absolutely convergent in the region
unless
![]() $\psi '$
is the trivial character, in which case there is a pole at
$\psi '$
is the trivial character, in which case there is a pole at
![]() $w=1$
coming from the summands when n is a square, and the residue is
$w=1$
coming from the summands when n is a square, and the residue is
![]() $\zeta _2(2s)/2.$
$\zeta _2(2s)/2.$
Note that (3.6) gives a link between
![]() $Z(s,w;\psi ,\psi ')$
and
$Z(s,w;\psi ,\psi ')$
and
![]() $Z(w,s;\psi ',\psi )$
, which gives us a functional equation relating
$Z(w,s;\psi ',\psi )$
, which gives us a functional equation relating
![]() $\mathbf {Z}(s,w)$
with
$\mathbf {Z}(s,w)$
with
![]() $\mathbf {Z}(w,s)$
. To finish the proof and obtain the meromorphic continuation to the whole
$\mathbf {Z}(w,s)$
. To finish the proof and obtain the meromorphic continuation to the whole
![]() $\mathbb {C}^2$
, we use the functional equation in the numerator of (3.5), which gives a functional equation relating
$\mathbb {C}^2$
, we use the functional equation in the numerator of (3.5), which gives a functional equation relating
![]() $\mathbf {Z}(s,w)$
and
$\mathbf {Z}(s,w)$
and
![]() $\mathbf {Z}(1-s,s+w-1/2)$
, where the change in the second coordinate comes from the conductor in the functional equation for
$\mathbf {Z}(1-s,s+w-1/2)$
, where the change in the second coordinate comes from the conductor in the functional equation for
![]() $L(s,\chi _m)$
. Notice that this change of variables interchanges
$L(s,\chi _m)$
. Notice that this change of variables interchanges
![]() $2s+2w-1$
and
$2s+2w-1$
and
![]() $2w$
, leaves
$2w$
, leaves
![]() $s+2w$
fixed, and maps the line
$s+2w$
fixed, and maps the line
![]() $w=1$
to
$w=1$
to
![]() $s+w=3/2$
, which becomes a new polar line.
$s+w=3/2$
, which becomes a new polar line.
We can iterate the two transformations coming from (3.5) and (3.6) and obtain a function meromorphic on a tube region of the form
![]() $\{(s,w):\mathrm {Re}(s)^2+\mathrm {Re}(w)^2>c\}$
for some c. During this process, we obtain some additional potential polar lines, but these will be canceled by the gamma factors coming from the functional equations. To obtain a continuation to the region
$\{(s,w):\mathrm {Re}(s)^2+\mathrm {Re}(w)^2>c\}$
for some c. During this process, we obtain some additional potential polar lines, but these will be canceled by the gamma factors coming from the functional equations. To obtain a continuation to the region
![]() $\{(s,w):\mathrm {Re}(s)^2+\mathrm {Re}(w)^2\leq c\}$
, we use Bochner’s Tube theorem from multivariable complex analysis, which states that a function that is holomorphic on a tube region can be continued to its convex hull (see [Reference BochnerBoc]).
$\{(s,w):\mathrm {Re}(s)^2+\mathrm {Re}(w)^2\leq c\}$
, we use Bochner’s Tube theorem from multivariable complex analysis, which states that a function that is holomorphic on a tube region can be continued to its convex hull (see [Reference BochnerBoc]).
The proof that the function is polynomially bounded in vertical strips is similar to the proof of Proposition 4.11 in [Reference Diaconu, Goldfeld and HoffsteinDGH].
We will also use the following estimate, which is Theorem 2 in [Reference BlomerBlo].
Theorem 3.2 For any
![]() $Y_1,Y_2\geq 1$
and characters
$Y_1,Y_2\geq 1$
and characters
![]() $\psi ,\psi '$
modulo 8, we have
$\psi ,\psi '$
modulo 8, we have
In the next two sections, we are going to shift the two integrals in (3.1) to the left and compute the contribution of the crossed polar lines. By Theorem 3.1, the polar lines of
![]() $A(s,w)=\frac {Z(s,w)}{\zeta _2(2s+2w-1)}$
are the following:
$A(s,w)=\frac {Z(s,w)}{\zeta _2(2s+2w-1)}$
are the following:
-
• The polar lines of
 $Z(s,w)$
, which give us the main term in Theorem 1.2:
$Z(s,w)$
, which give us the main term in Theorem 1.2:-
– the line
 $s=1$
with residue
$s=1$
with residue
 $\mathrm {res}_{(1,w)}A(s,w)=\frac {\zeta _2(2w)}{2\zeta _2(2w+1)}$
,
$\mathrm {res}_{(1,w)}A(s,w)=\frac {\zeta _2(2w)}{2\zeta _2(2w+1)}$
, -
– the line
 $w=1$
with residue
$w=1$
with residue
 $\mathrm {res}_{(s,1)}A(s,w)=\frac {\zeta _2(2s)}{2\zeta _2(2s+1)}$
,
$\mathrm {res}_{(s,1)}A(s,w)=\frac {\zeta _2(2s)}{2\zeta _2(2s+1)}$
, -
– the line
 $s+w=3/2$
, whose residue will be computed in Lemma 5.1.
$s+w=3/2$
, whose residue will be computed in Lemma 5.1.
-
-
• Zeros of
 $\zeta _2(2s+2w-1)=\zeta (2s+2w-1)\left (1-2^{1-2s-2w}\right )$
, which are the lines
$\zeta _2(2s+2w-1)=\zeta (2s+2w-1)\left (1-2^{1-2s-2w}\right )$
, which are the lines
 $s+w=\frac {\rho +1}{2},$
where
$s+w=\frac {\rho +1}{2},$
where
 $\rho $
is such that
$\rho $
is such that
 $\zeta (\rho )=0$
, or
$\zeta (\rho )=0$
, or
 $s+w=\frac {k\pi i}{\log 2}+\frac 12$
for some
$s+w=\frac {k\pi i}{\log 2}+\frac 12$
for some
 $k\in \mathbb {Z}$
. All these satisfy
$k\in \mathbb {Z}$
. All these satisfy
 $\mathrm {Re}(s+w)<1$
, and even
$\mathrm {Re}(s+w)<1$
, and even
 $\mathrm {Re}(s+w)\leq \frac 34$
if we assume RH.
$\mathrm {Re}(s+w)\leq \frac 34$
if we assume RH.
We will see that the main term comes from the polar lines of
![]() $Z(s,w)$
, whereas the polar lines coming from the zeros of
$Z(s,w)$
, whereas the polar lines coming from the zeros of
![]() $\zeta _2(2s+2w-1)$
determine how far to the left we will be able to shift the integrals, so they give us our error term.
$\zeta _2(2s+2w-1)$
determine how far to the left we will be able to shift the integrals, so they give us our error term.
4 Contribution of the polar lines
 $s=1$
and
$s=1$
and
 $w=1$
$w=1$
In this section, we shift the integrals to the left and compute the contribution of the polar lines
![]() $s=1$
and
$s=1$
and
![]() $w=1$
. We begin with
$w=1$
. We begin with
![]() $\sigma =2$
and
$\sigma =2$
and
![]() $\omega =2$
in (3.1), where everything converges absolutely.
$\omega =2$
in (3.1), where everything converges absolutely.
Then we move the inner integral to the line
![]() $\mathrm {Re}(w)=3/4+\varepsilon $
, so we obtain
$\mathrm {Re}(w)=3/4+\varepsilon $
, so we obtain
 $$ \begin{align}\begin{aligned} S(X,Y;\varphi,\psi)=\left( \frac1{2\pi i}\right)^2&\int\limits_{(2)}\int\limits_{(3/4+\varepsilon)}A(s,w)X^wY^s\hat \varphi(w)\hat\psi(s)dwds\\&+\frac1{2\pi i}\int\limits_{(2)}XY^s\hat\varphi(1)\hat\psi(s)\mathrm{res}_{(s,1)}A(s,w)ds. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} S(X,Y;\varphi,\psi)=\left( \frac1{2\pi i}\right)^2&\int\limits_{(2)}\int\limits_{(3/4+\varepsilon)}A(s,w)X^wY^s\hat \varphi(w)\hat\psi(s)dwds\\&+\frac1{2\pi i}\int\limits_{(2)}XY^s\hat\varphi(1)\hat\psi(s)\mathrm{res}_{(s,1)}A(s,w)ds. \end{aligned}\end{align} $$
This shift of integrals is justified by the fast decay of the Mellin transform and polynomial boundedness of
![]() $A(s,w)$
in vertical strips.
$A(s,w)$
in vertical strips.
Now we compute the second integral in (4.1), which equals
 $$ \begin{align} \frac{\hat\varphi(1)X}{2\pi i}\int\limits_{(2)}\frac{Y^s\hat\psi(s)\zeta_2(2s)}{2\zeta_2(2s+1)}ds. \end{align} $$
$$ \begin{align} \frac{\hat\varphi(1)X}{2\pi i}\int\limits_{(2)}\frac{Y^s\hat\psi(s)\zeta_2(2s)}{2\zeta_2(2s+1)}ds. \end{align} $$
We again estimate this integral using the residue theorem. The integrand has the following poles:
-
• At
 $s=1/2$
with residue
$s=1/2$
with residue  $$ \begin{align*}\frac{Y^{1/2}\hat\psi\left(\frac{1}{2}\right)}{8\zeta_2(2)}=\frac{Y^{1/2}\hat\psi\left(\frac{1}{2}\right)}{\pi^2}.\end{align*} $$
$$ \begin{align*}\frac{Y^{1/2}\hat\psi\left(\frac{1}{2}\right)}{8\zeta_2(2)}=\frac{Y^{1/2}\hat\psi\left(\frac{1}{2}\right)}{\pi^2}.\end{align*} $$
-
• Zeros of
These are at the points $$ \begin{align*}\zeta_2(2s+1)=\left(1-\frac{1}{2^{2s+1}}\right)\zeta(2s+1).\end{align*} $$
$$ \begin{align*}\zeta_2(2s+1)=\left(1-\frac{1}{2^{2s+1}}\right)\zeta(2s+1).\end{align*} $$
 $s=\frac {\rho -1}{2},$
where
$s=\frac {\rho -1}{2},$
where
 $\zeta (\rho )=0$
, and These poles have
$\zeta (\rho )=0$
, and These poles have $$ \begin{align*}s=\frac{k\pi i}{\log 2}-\frac12,\ k\in\mathbb{Z}.\end{align*} $$
$$ \begin{align*}s=\frac{k\pi i}{\log 2}-\frac12,\ k\in\mathbb{Z}.\end{align*} $$
 $\mathrm {Re}(s)<0$
and if we assume RH, they all have
$\mathrm {Re}(s)<0$
and if we assume RH, they all have
 $\mathrm {Re}(s)\leq -1/4$
.
$\mathrm {Re}(s)\leq -1/4$
.
Therefore, we have the following:
 $$ \begin{align} \begin{aligned} \frac{\hat\varphi(1)X}{2\pi i}&\int\limits_{(2)}\frac{Y^s\hat\psi(s)\zeta_2(2s)}{2\zeta_2(2s+1)}ds=\frac{\hat\varphi(1)\hat\psi\left(\frac{1}{2}\right)XY^{1/2}}{\pi^2}+\frac{\hat\varphi(1)X}{2\pi i}\int\limits_{(\delta)}\frac{Y^s\hat\psi(s)\zeta_2(2s)}{2\zeta_2(2s+1)}ds. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{\hat\varphi(1)X}{2\pi i}&\int\limits_{(2)}\frac{Y^s\hat\psi(s)\zeta_2(2s)}{2\zeta_2(2s+1)}ds=\frac{\hat\varphi(1)\hat\psi\left(\frac{1}{2}\right)XY^{1/2}}{\pi^2}+\frac{\hat\varphi(1)X}{2\pi i}\int\limits_{(\delta)}\frac{Y^s\hat\psi(s)\zeta_2(2s)}{2\zeta_2(2s+1)}ds. \end{aligned} \end{align} $$
Depending whether we assume RH or not, we take
![]() $\delta =-\frac 14+\varepsilon $
or
$\delta =-\frac 14+\varepsilon $
or
![]() $\delta =\varepsilon $
, bound the integral trivially (we use (2.6) when
$\delta =\varepsilon $
, bound the integral trivially (we use (2.6) when
![]() $\delta =-1/4+\varepsilon $
) and get
$\delta =-1/4+\varepsilon $
) and get
 $$ \begin{align} \frac{\hat\varphi(1)X}{2\pi i}\int\limits_{(2)}\frac{Y^s\hat\psi(s)\zeta_2(2s)}{2\zeta_2(2s+1)}ds=\frac{\hat\varphi(1)\hat\psi\left(\frac{1}{2}\right)XY^{1/2}}{\pi^2}+O\left( XY^{\delta}\right). \end{align} $$
$$ \begin{align} \frac{\hat\varphi(1)X}{2\pi i}\int\limits_{(2)}\frac{Y^s\hat\psi(s)\zeta_2(2s)}{2\zeta_2(2s+1)}ds=\frac{\hat\varphi(1)\hat\psi\left(\frac{1}{2}\right)XY^{1/2}}{\pi^2}+O\left( XY^{\delta}\right). \end{align} $$
Using this in (4.1), we obtain
 $$ \begin{align} \begin{aligned} S(X,Y;\varphi,\psi)=&\frac{\hat\varphi(1)\hat\psi\left(\frac{1}{2}\right)XY^{1/2}}{\pi^2}\\&+\left(\frac{1}{2\pi i}\right)^2\int\limits_{(2)}\int\limits_{(3/4+\varepsilon)}A(s,w)X^wY^s\hat\varphi(w)\hat\psi(s)dwds+O(XY^{\delta}), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} S(X,Y;\varphi,\psi)=&\frac{\hat\varphi(1)\hat\psi\left(\frac{1}{2}\right)XY^{1/2}}{\pi^2}\\&+\left(\frac{1}{2\pi i}\right)^2\int\limits_{(2)}\int\limits_{(3/4+\varepsilon)}A(s,w)X^wY^s\hat\varphi(w)\hat\psi(s)dwds+O(XY^{\delta}), \end{aligned} \end{align} $$
Note that when
![]() $\varphi =\psi =1_{[0,1]}$
, the first term is
$\varphi =\psi =1_{[0,1]}$
, the first term is
![]() $\frac {2}{\pi ^{2}}XY^{1/2}$
and corresponds to the contribution when n is a square.
$\frac {2}{\pi ^{2}}XY^{1/2}$
and corresponds to the contribution when n is a square.
Next, we exchange the integrals and shift the integral over
![]() $\mathrm {Re}(s)=2$
to
$\mathrm {Re}(s)=2$
to
![]() $\mathrm {Re}(s)=3/4$
, crossing the polar line at
$\mathrm {Re}(s)=3/4$
, crossing the polar line at
![]() $s=1$
. The computation of the residues coming from this polar line is completely analogous to the previous case, and the result is stated in the following theorem.
$s=1$
. The computation of the residues coming from this polar line is completely analogous to the previous case, and the result is stated in the following theorem.
Theorem 4.1 Let
![]() $\varepsilon>0$
. Then we have
$\varepsilon>0$
. Then we have
 $$ \begin{align}\begin{aligned} \sum_{m\mathrm{\ odd}}\sum_{n\mathrm{\ odd}}\left(\frac{m}{n}\right)\varphi\left(\frac{m}{X}\right)\psi\left(\frac{n}{Y}\right)&=\frac{\hat\varphi(1)\hat\psi\left(\frac{1}{2}\right)XY^{1/2}+\hat\psi(1)\hat\varphi\left(\frac{1}{2}\right)YX^{1/2}}{\pi^2}\\&\hspace{-100pt}+\left(\frac{1}{2\pi i}\right)^2\int\limits_{(3/4)}\int\limits_{(3/4+\varepsilon)}A(s,w)X^wY^s\hat\varphi(w)\hat\psi(s)dwds+O_\varepsilon\left( YX^\delta+XY^\delta\right), \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \sum_{m\mathrm{\ odd}}\sum_{n\mathrm{\ odd}}\left(\frac{m}{n}\right)\varphi\left(\frac{m}{X}\right)\psi\left(\frac{n}{Y}\right)&=\frac{\hat\varphi(1)\hat\psi\left(\frac{1}{2}\right)XY^{1/2}+\hat\psi(1)\hat\varphi\left(\frac{1}{2}\right)YX^{1/2}}{\pi^2}\\&\hspace{-100pt}+\left(\frac{1}{2\pi i}\right)^2\int\limits_{(3/4)}\int\limits_{(3/4+\varepsilon)}A(s,w)X^wY^s\hat\varphi(w)\hat\psi(s)dwds+O_\varepsilon\left( YX^\delta+XY^\delta\right), \end{aligned}\end{align} $$
where
![]() $\delta =\varepsilon $
. If we assume the Riemann Hypothesis, then we can take
$\delta =\varepsilon $
. If we assume the Riemann Hypothesis, then we can take
![]() $\delta =-1/4+\varepsilon $
.
$\delta =-1/4+\varepsilon $
.
5 Contribution of the polar line
 $s+w=3/2$
$s+w=3/2$
Before further shifting the integrals, we need to compute the residues on the polar line
![]() $s+w=3/2$
, which is done in the following lemma.
$s+w=3/2$
, which is done in the following lemma.
Lemma 5.1 For all
![]() $s\in \mathbb {C}$
,
$s\in \mathbb {C}$
,
 $$ \begin{align} \mathrm{res}_{\left( s,\frac32-s\right)}Z(s,w)=\frac{\sqrt\pi\sin\left(\frac{\pi s}{2}\right)\Gamma\left( s-\frac12\right)\zeta(2s-1)}{2(2\pi)^s}. \end{align} $$
$$ \begin{align} \mathrm{res}_{\left( s,\frac32-s\right)}Z(s,w)=\frac{\sqrt\pi\sin\left(\frac{\pi s}{2}\right)\Gamma\left( s-\frac12\right)\zeta(2s-1)}{2(2\pi)^s}. \end{align} $$
Proof We use the functional equation (28) in [Reference BlomerBlo], from which it follows that
 $$ \begin{align}\begin{aligned} &Z(1-u,u+v-1/2)=\frac{\pi^{-u+\frac12}\Gamma\left(\frac u2\right)}{\left( 4^{1-u}-4\right)\Gamma\left(\frac{1-u}2\right)}\cdot\Bigg(-4^uZ(u,v;\psi_1,\psi_1)\\&+\left( 4^u-2\right) Z(u,v;\psi_1,\psi_{-1})+\left( 2^u-2^{1-u}\right) \left( Z(u,v;\psi_1,\psi_2)+ Z(u,v;\psi_1,\psi_{-2})\right)\Bigg). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &Z(1-u,u+v-1/2)=\frac{\pi^{-u+\frac12}\Gamma\left(\frac u2\right)}{\left( 4^{1-u}-4\right)\Gamma\left(\frac{1-u}2\right)}\cdot\Bigg(-4^uZ(u,v;\psi_1,\psi_1)\\&+\left( 4^u-2\right) Z(u,v;\psi_1,\psi_{-1})+\left( 2^u-2^{1-u}\right) \left( Z(u,v;\psi_1,\psi_2)+ Z(u,v;\psi_1,\psi_{-2})\right)\Bigg). \end{aligned}\end{align} $$
Under the change of variables
![]() $(s,w)=(1-u,u+v-1/2)$
, the line
$(s,w)=(1-u,u+v-1/2)$
, the line
![]() $v=1$
transforms to the line
$v=1$
transforms to the line
![]() $s+w=3/2$
. Since
$s+w=3/2$
. Since
![]() $v=1$
is a polar line of
$v=1$
is a polar line of
![]() $Z(u,v;\psi ,\psi ')$
if and only if
$Z(u,v;\psi ,\psi ')$
if and only if
![]() $\psi '=\psi _1$
, the residue comes only from the first term in the parenthesis on the right-hand side of (5.2), and is given by
$\psi '=\psi _1$
, the residue comes only from the first term in the parenthesis on the right-hand side of (5.2), and is given by
 $$ \begin{align*}\mathrm{res}_{\left(1-u,u+\frac12\right)}Z(u,v;\psi_1,\psi_1)=\frac{\pi^{-u+\frac12}\Gamma\left(\frac{u}{2}\right)\left(-4^u\right)\zeta_2(2u)}{2\left(4^{1-u}-4\right)\Gamma\left(\frac{1-u}{2}\right)}=\frac{\pi^{-u+\frac12}\Gamma\left(\frac{u}{2}\right)\zeta(2u)}{2\cdot4^{1-u}\Gamma\left(\frac{1-u}{2}\right)},\end{align*} $$
$$ \begin{align*}\mathrm{res}_{\left(1-u,u+\frac12\right)}Z(u,v;\psi_1,\psi_1)=\frac{\pi^{-u+\frac12}\Gamma\left(\frac{u}{2}\right)\left(-4^u\right)\zeta_2(2u)}{2\left(4^{1-u}-4\right)\Gamma\left(\frac{1-u}{2}\right)}=\frac{\pi^{-u+\frac12}\Gamma\left(\frac{u}{2}\right)\zeta(2u)}{2\cdot4^{1-u}\Gamma\left(\frac{1-u}{2}\right)},\end{align*} $$
so we have
 $$ \begin{align*}\begin{aligned} \mathrm{res}_{\left( s,\frac32-s\right)}Z(s,w)&=\frac{\pi^{s-\frac12}\Gamma\left(\frac {1-s}2\right)\zeta(2-2s)}{2\cdot4^s\Gamma\left(\frac{s}{2}\right)}=\frac{\sqrt\pi\sin\left(\frac{\pi s}{2}\right)\Gamma\left( s-\frac12\right)\zeta(2s-1)}{2(2\pi)^s}, \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \mathrm{res}_{\left( s,\frac32-s\right)}Z(s,w)&=\frac{\pi^{s-\frac12}\Gamma\left(\frac {1-s}2\right)\zeta(2-2s)}{2\cdot4^s\Gamma\left(\frac{s}{2}\right)}=\frac{\sqrt\pi\sin\left(\frac{\pi s}{2}\right)\Gamma\left( s-\frac12\right)\zeta(2s-1)}{2(2\pi)^s}, \end{aligned}\end{align*} $$
where the last equality follows after using the functional equation for
![]() $\zeta (s)$
and the formula (2.10).
$\zeta (s)$
and the formula (2.10).
We are now ready to prove Theorem 1.1.
Proof of Theorem 1.1
We move the integral from (4.6) further to the left. According to the discussion at the end of Section 3, we know that except the line
![]() $s+w=3/2$
, the integrand has no poles with
$s+w=3/2$
, the integrand has no poles with
![]() $\mathrm {Re}(s+w)\geq 1$
, or with
$\mathrm {Re}(s+w)\geq 1$
, or with
![]() $\mathrm {Re}(s+w)>3/4$
if we assume RH. Hence we have
$\mathrm {Re}(s+w)>3/4$
if we assume RH. Hence we have
 $$ \begin{align}\begin{aligned} \left(\frac{1}{2\pi i}\right)^2&\int\limits_{(3/4)}\int\limits_{(3/4+\varepsilon)}A(s,w)X^wY^s\hat\varphi(w)\hat\psi(s)dwds\\[5pt]&= \left(\frac{1}{2\pi i}\right)^2\int\limits_{(3/4)}\int\limits_{(\delta')}A(s,w)X^wY^s\hat\varphi(w)\hat\psi(s)dwds\\[5pt]&\quad+\frac1{2\pi i}\int\limits_{(3/4)}X^{\frac32-s}Y^{s}\hat\varphi\left(\frac32-s\right)\hat\psi\left( s\right)\mathrm{res}_{\left( s,\frac32-s\right)}A(s,w)ds, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \left(\frac{1}{2\pi i}\right)^2&\int\limits_{(3/4)}\int\limits_{(3/4+\varepsilon)}A(s,w)X^wY^s\hat\varphi(w)\hat\psi(s)dwds\\[5pt]&= \left(\frac{1}{2\pi i}\right)^2\int\limits_{(3/4)}\int\limits_{(\delta')}A(s,w)X^wY^s\hat\varphi(w)\hat\psi(s)dwds\\[5pt]&\quad+\frac1{2\pi i}\int\limits_{(3/4)}X^{\frac32-s}Y^{s}\hat\varphi\left(\frac32-s\right)\hat\psi\left( s\right)\mathrm{res}_{\left( s,\frac32-s\right)}A(s,w)ds, \end{aligned}\end{align} $$
where
![]() $\delta '=1/4+\varepsilon $
, or
$\delta '=1/4+\varepsilon $
, or
![]() $\varepsilon $
under RH. Using Lemma 5.1 and (3.4), we have
$\varepsilon $
under RH. Using Lemma 5.1 and (3.4), we have
 $$ \begin{align*}\mathrm{res}_{\left( s,\frac32-s\right)}A(s,w)=\frac{\mathrm{res}_{\left( s,\frac32-s\right)}Z(s,w)}{\zeta_2(2)}=\frac{\sqrt\pi\sin\left(\frac{\pi s}{2}\right)\Gamma\left( s-\frac12\right)\zeta(2s-1)}{2\zeta_2(2)(2\pi)^s}.\end{align*} $$
$$ \begin{align*}\mathrm{res}_{\left( s,\frac32-s\right)}A(s,w)=\frac{\mathrm{res}_{\left( s,\frac32-s\right)}Z(s,w)}{\zeta_2(2)}=\frac{\sqrt\pi\sin\left(\frac{\pi s}{2}\right)\Gamma\left( s-\frac12\right)\zeta(2s-1)}{2\zeta_2(2)(2\pi)^s}.\end{align*} $$
Therefore, the second integral on the right-hand side of (5.3) is
 $$ \begin{align} \begin{aligned} \frac{2X^{\frac 32}}{i\pi^{\frac52}}\int\limits_{(3/4)}\left(\frac{Y}{2\pi X}\right)^s\hat\varphi\left(\frac32-s\right)\hat\psi(s)\Gamma\left( s-\frac12\right)\sin\left(\frac{\pi s}{2}\right)\zeta(2s-1)ds. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{2X^{\frac 32}}{i\pi^{\frac52}}\int\limits_{(3/4)}\left(\frac{Y}{2\pi X}\right)^s\hat\varphi\left(\frac32-s\right)\hat\psi(s)\Gamma\left( s-\frac12\right)\sin\left(\frac{\pi s}{2}\right)\zeta(2s-1)ds. \end{aligned} \end{align} $$
Hence, we have
 $$ \begin{align} \begin{aligned} S(X,Y;\varphi,\psi)&=\frac{\hat\varphi(1)\hat\psi\left(\frac{1}{2}\right)XY^{1/2}+\hat\psi(1)\hat\varphi\left(\frac{1}{2}\right)YX^{1/2}}{\pi^2}\\&\quad+\frac{2X^{\frac32}}{i\pi^{\frac52}}\int\limits_{(3/4)}\left(\frac{Y}{2\pi X}\right)^s\hat\varphi\left(\frac32-s\right)\hat\psi(s)\Gamma\left( s-\frac12\right)\sin\left(\frac{\pi s}{2}\right)\zeta(2s-1)ds\\&\quad+\left(\frac{1}{2\pi i}\right)^2\int\limits_{(3/4)}\int\limits_{(\delta')}A(s,w)X^wY^s\hat\varphi(w)\hat\psi(s)dwds+O\left( XY^\delta+YX^\delta\right)\\[5pt]&=\frac2{\pi^2}\cdot X^{3/2}\cdot D\left(\frac YX;\varphi,\psi\right)+O\left( XY^\delta+YX^\delta\right), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} S(X,Y;\varphi,\psi)&=\frac{\hat\varphi(1)\hat\psi\left(\frac{1}{2}\right)XY^{1/2}+\hat\psi(1)\hat\varphi\left(\frac{1}{2}\right)YX^{1/2}}{\pi^2}\\&\quad+\frac{2X^{\frac32}}{i\pi^{\frac52}}\int\limits_{(3/4)}\left(\frac{Y}{2\pi X}\right)^s\hat\varphi\left(\frac32-s\right)\hat\psi(s)\Gamma\left( s-\frac12\right)\sin\left(\frac{\pi s}{2}\right)\zeta(2s-1)ds\\&\quad+\left(\frac{1}{2\pi i}\right)^2\int\limits_{(3/4)}\int\limits_{(\delta')}A(s,w)X^wY^s\hat\varphi(w)\hat\psi(s)dwds+O\left( XY^\delta+YX^\delta\right)\\[5pt]&=\frac2{\pi^2}\cdot X^{3/2}\cdot D\left(\frac YX;\varphi,\psi\right)+O\left( XY^\delta+YX^\delta\right), \end{aligned} \end{align} $$
where the last equality follows after trivially bounding the second integral, and using
![]() $X^{\delta '}Y^{\frac 34}\ll XY^\delta +YX^\delta $
.
$X^{\delta '}Y^{\frac 34}\ll XY^\delta +YX^\delta $
.
6 Removing the smooth weights
In this section, we show how to remove the smooth weights from Theorem 1.1 and prove Theorem 1.2. We choose the weights
![]() $\varphi =\psi $
to be a smooth function which is
$\varphi =\psi $
to be a smooth function which is
![]() $1$
on the interval
$1$
on the interval
![]() $ \left [\frac 1U,1-\frac 1U\right ]$
for some U to be chosen later, and 0 outside of
$ \left [\frac 1U,1-\frac 1U\right ]$
for some U to be chosen later, and 0 outside of
![]() $(0,1)$
, and which satisfies
$(0,1)$
, and which satisfies
 $$ \begin{align} |\hat\varphi(\sigma+it)|\ll_{j,\sigma}\frac{U^{j-1}}{1+|t|^j} \end{align} $$
$$ \begin{align} |\hat\varphi(\sigma+it)|\ll_{j,\sigma}\frac{U^{j-1}}{1+|t|^j} \end{align} $$
for all
![]() $j\geq 1$
. Then using the Pólya–Vinogradov inequality (see (3.1) in [Reference Chinta, Friedberg and HoffsteinCFS]), we have
$j\geq 1$
. Then using the Pólya–Vinogradov inequality (see (3.1) in [Reference Chinta, Friedberg and HoffsteinCFS]), we have
Now we need to estimate the dependence on U of the error term in the computation of
![]() $S(X,Y;\varphi ,\psi )$
. These come from the following:
$S(X,Y;\varphi ,\psi )$
. These come from the following:
-
• The error from the polar lines
 $s=1$
and
$s=1$
and
 $w=1$
.
$w=1$
. -
• The error from the shifted integral.
-
• The difference of the main terms.
The error from the polar lines
![]() $s=1$
is
$s=1$
is
 $$ \begin{align} \ll XY^{\sigma}\left|\int_{(\delta)}\frac{\hat\psi(s)\zeta_2(2s)}{\zeta_2(2s+1)}ds\right|, \end{align} $$
$$ \begin{align} \ll XY^{\sigma}\left|\int_{(\delta)}\frac{\hat\psi(s)\zeta_2(2s)}{\zeta_2(2s+1)}ds\right|, \end{align} $$
where
![]() $\delta =\varepsilon $
, or
$\delta =\varepsilon $
, or
![]() $-1/4+\varepsilon $
, and similarly for the error from the polar line
$-1/4+\varepsilon $
, and similarly for the error from the polar line
![]() $w=1$
. We have
$w=1$
. We have
![]() $\frac {1}{\zeta _2(2\delta +2it+1)}\ll 1$
in both cases by (2.6).
$\frac {1}{\zeta _2(2\delta +2it+1)}\ll 1$
in both cases by (2.6).
We can shift the integral (6.3) to any vertical line
![]() $\mathrm {Re}(s)=\sigma $
with
$\mathrm {Re}(s)=\sigma $
with
![]() $1/4\geq \sigma \geq \delta $
, and bound the integral using the Cauchy–Schwarz inequality as
$1/4\geq \sigma \geq \delta $
, and bound the integral using the Cauchy–Schwarz inequality as
 $$ \begin{align} \begin{aligned} &\ll\int_{(\sigma)}|\hat\psi(s)\zeta(2s)|ds\\ &\ll\left(\int_{(\sigma)}\frac{|\zeta(1-2s)|^2}{(1+|s|)^{1+\varepsilon}}ds\right)^{\frac12}\left(\int_{(\sigma)}|\hat\psi(s)\chi(2s)|^2(1+|s|)^{1+\varepsilon}ds\right)^{\frac12}\\ &\ll U^{j-1}\int_{(\sigma)}(1+|s|)^{2-4\sigma-2j+\varepsilon}ds\\ &\ll U^{1/2-2\sigma+\varepsilon}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\ll\int_{(\sigma)}|\hat\psi(s)\zeta(2s)|ds\\ &\ll\left(\int_{(\sigma)}\frac{|\zeta(1-2s)|^2}{(1+|s|)^{1+\varepsilon}}ds\right)^{\frac12}\left(\int_{(\sigma)}|\hat\psi(s)\chi(2s)|^2(1+|s|)^{1+\varepsilon}ds\right)^{\frac12}\\ &\ll U^{j-1}\int_{(\sigma)}(1+|s|)^{2-4\sigma-2j+\varepsilon}ds\\ &\ll U^{1/2-2\sigma+\varepsilon}, \end{aligned} \end{align} $$
where the first integral on the second line converges by (2.13), and we took
![]() $j=3/2-2\sigma +\varepsilon .$
$j=3/2-2\sigma +\varepsilon .$
A similar computation for the polar line
![]() $w=1$
gives the same result with
$w=1$
gives the same result with
![]() $X,Y$
interchanged, so the error from these terms is
$X,Y$
interchanged, so the error from these terms is
For the error coming from the shifted integral, we need to estimate
We have
so the integral is
provided
![]() $\sigma +\omega>1+\varepsilon $
or
$\sigma +\omega>1+\varepsilon $
or
![]() $>3/4+\varepsilon $
if we assume RH. We take
$>3/4+\varepsilon $
if we assume RH. We take
![]() $\sigma =\omega =1/2+\varepsilon $
and estimate the double integral using the Cauchy–Schwarz inequality as follows:
$\sigma =\omega =1/2+\varepsilon $
and estimate the double integral using the Cauchy–Schwarz inequality as follows:
 $$ \begin{align} &\int_{(\frac12+\varepsilon)}\int_{(\frac12+\varepsilon)}\left| Z(s,w)\hat\varphi(w)\hat\psi(s)\right| dwds\nonumber\\ &\ll\left(\,\int\limits_{(\frac12+\varepsilon)}\int\limits_{(\frac12+\varepsilon)}\frac{\left| Z(s,w)\right|{}^2}{(1+|s|)^{1+\varepsilon}(1+|w|)^{1+\varepsilon}}dwds\right)^{\frac12}\nonumber \\&\quad\times\left(\,\int\limits_{(\frac12+\varepsilon)}\int\limits_{(\frac12+\varepsilon)}\left|\hat\varphi(w)\hat\psi(s)\right|{}^2(1+|s|)^{1+\varepsilon}(1+|w|)^{1+\varepsilon} dwds\right)^{\frac12}\\ &\ll U^{j_1+j_2-2}\left(\,\int\limits_{(\frac12+\varepsilon)}\int\limits_{(\frac12+\varepsilon)}(1+|s|)^{1+\varepsilon-2j_1}(1+|w|)^{1+\varepsilon-2j_2} dwds\right)^{1/2}\nonumber\\ &\ll U^{\varepsilon},\nonumber \end{align} $$
$$ \begin{align} &\int_{(\frac12+\varepsilon)}\int_{(\frac12+\varepsilon)}\left| Z(s,w)\hat\varphi(w)\hat\psi(s)\right| dwds\nonumber\\ &\ll\left(\,\int\limits_{(\frac12+\varepsilon)}\int\limits_{(\frac12+\varepsilon)}\frac{\left| Z(s,w)\right|{}^2}{(1+|s|)^{1+\varepsilon}(1+|w|)^{1+\varepsilon}}dwds\right)^{\frac12}\nonumber \\&\quad\times\left(\,\int\limits_{(\frac12+\varepsilon)}\int\limits_{(\frac12+\varepsilon)}\left|\hat\varphi(w)\hat\psi(s)\right|{}^2(1+|s|)^{1+\varepsilon}(1+|w|)^{1+\varepsilon} dwds\right)^{\frac12}\\ &\ll U^{j_1+j_2-2}\left(\,\int\limits_{(\frac12+\varepsilon)}\int\limits_{(\frac12+\varepsilon)}(1+|s|)^{1+\varepsilon-2j_1}(1+|w|)^{1+\varepsilon-2j_2} dwds\right)^{1/2}\nonumber\\ &\ll U^{\varepsilon},\nonumber \end{align} $$
where the integral on the second line converges by (3.7), and we took
![]() $j_1=j_2=1+\varepsilon .$
It follows that the error from the shifted integral is
$j_1=j_2=1+\varepsilon .$
It follows that the error from the shifted integral is
The error from the difference of the main terms is
 $$ \begin{align} \begin{aligned} E(X,Y;\varphi,\psi)&=\frac{2}{\pi^2}X^{3/2}\left( D\left(\frac YX;\varphi,\psi\right)-D\left(\frac{Y}{X}\right)\right) \\\ &\hspace{-50pt}\ll XY^{1/2}\left| \hat\varphi(1)\hat\psi(1/2)-2\right|+YX^{1/2}\left|\hat \psi(1)\hat\varphi(1/2)-2\right|\\ &\hspace{-38pt}+X^{3/2}\int_{(3/4)}\left|\left(\frac{Y}{2\pi X}\right)^s\Gamma\left( s-\frac12\right)\sin\left(\frac{\pi s}{2}\right)\zeta(2s-1)\right|\\ &\hspace{-38pt}\times\left|\hat\varphi(3/2-s)\hat\psi(s)-\frac1{s(3/2-s)}\right| ds\\ &\hspace{-50pt}\ll XY^{1/2}\left| \hat\varphi(1)\hat\psi(1/2)-2\right|+YX^{1/2}\left|\hat \psi(1)\hat\varphi(1/2)-2\right|\\ &\hspace{-38pt}+(XY)^{3/4}\int_{(3/4)}\left(1+|t|\right)^{-\frac14}\left|\zeta(2s-1)\right|\left|\hat\varphi\left(\frac32-s\right)\hat\psi(s)-\frac1{s\left(\frac32-s\right)}\right| ds. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} E(X,Y;\varphi,\psi)&=\frac{2}{\pi^2}X^{3/2}\left( D\left(\frac YX;\varphi,\psi\right)-D\left(\frac{Y}{X}\right)\right) \\\ &\hspace{-50pt}\ll XY^{1/2}\left| \hat\varphi(1)\hat\psi(1/2)-2\right|+YX^{1/2}\left|\hat \psi(1)\hat\varphi(1/2)-2\right|\\ &\hspace{-38pt}+X^{3/2}\int_{(3/4)}\left|\left(\frac{Y}{2\pi X}\right)^s\Gamma\left( s-\frac12\right)\sin\left(\frac{\pi s}{2}\right)\zeta(2s-1)\right|\\ &\hspace{-38pt}\times\left|\hat\varphi(3/2-s)\hat\psi(s)-\frac1{s(3/2-s)}\right| ds\\ &\hspace{-50pt}\ll XY^{1/2}\left| \hat\varphi(1)\hat\psi(1/2)-2\right|+YX^{1/2}\left|\hat \psi(1)\hat\varphi(1/2)-2\right|\\ &\hspace{-38pt}+(XY)^{3/4}\int_{(3/4)}\left(1+|t|\right)^{-\frac14}\left|\zeta(2s-1)\right|\left|\hat\varphi\left(\frac32-s\right)\hat\psi(s)-\frac1{s\left(\frac32-s\right)}\right| ds. \end{aligned} \end{align} $$
We estimate the Mellin transforms in the following lemma.
Lemma 6.1 For
![]() $s=\sigma +it, 0<\sigma <1$
and
$s=\sigma +it, 0<\sigma <1$
and
![]() $\varphi ,\psi $
as above, we have
$\varphi ,\psi $
as above, we have
and
 $$ \begin{align} \left|\hat\varphi(3/2-s)\hat\psi(s)-\frac1{s(3/2-s)}\right|\ll\frac{\left|\hat\varphi(3/2-s)\right|}{U^\sigma}+\frac{1}{|s|U^{3/2-\sigma}}. \end{align} $$
$$ \begin{align} \left|\hat\varphi(3/2-s)\hat\psi(s)-\frac1{s(3/2-s)}\right|\ll\frac{\left|\hat\varphi(3/2-s)\right|}{U^\sigma}+\frac{1}{|s|U^{3/2-\sigma}}. \end{align} $$
Proof For (6.12), we have
 $$ \begin{align} &\hat\varphi(1)\hat\psi(1/2)=\int_{0}^\infty \varphi(u)du\int_0^\infty\psi(v)v^{-1/2}dv\nonumber\\ &=\left(\left(\int\limits_{0}^{\frac 1U}+\int\limits_{1-\frac 1U}^{1}\right)\varphi(u)du+1-\frac2U\right)\left(\left(\int\limits_{0}^{\frac 1U}+\int\limits_{1-\frac1U}^{1}\right)\frac{\psi(v)}{\sqrt v}dv+\int\limits_{\frac1U}^{1-\frac1U}\frac{1}{\sqrt v}dv\right)\\ &=\left(1+O\left(\frac 1U\right)\right)\left( O\left(\frac1{\sqrt U}\right)+2\left(\sqrt{1-\frac{1}{U}}-\frac1{\sqrt U}\right)\right)\nonumber\\ &= 2+O\left( U^{-1/2}\right).\nonumber \end{align} $$
$$ \begin{align} &\hat\varphi(1)\hat\psi(1/2)=\int_{0}^\infty \varphi(u)du\int_0^\infty\psi(v)v^{-1/2}dv\nonumber\\ &=\left(\left(\int\limits_{0}^{\frac 1U}+\int\limits_{1-\frac 1U}^{1}\right)\varphi(u)du+1-\frac2U\right)\left(\left(\int\limits_{0}^{\frac 1U}+\int\limits_{1-\frac1U}^{1}\right)\frac{\psi(v)}{\sqrt v}dv+\int\limits_{\frac1U}^{1-\frac1U}\frac{1}{\sqrt v}dv\right)\\ &=\left(1+O\left(\frac 1U\right)\right)\left( O\left(\frac1{\sqrt U}\right)+2\left(\sqrt{1-\frac{1}{U}}-\frac1{\sqrt U}\right)\right)\nonumber\\ &= 2+O\left( U^{-1/2}\right).\nonumber \end{align} $$
For (6.13), we first use the triangle inequality to get
 $$ \begin{align} \begin{aligned} &\left|\hat\varphi(3/2-s)\hat\psi(s)-\frac1{s(3/2-s)}\right|\\ &\leq\left|\hat\varphi(3/2-s)\right|\left|\hat\psi(s)-\frac1s\right|+\left|\frac1s\right|\left|\hat\varphi(3/2-s)-\frac{1}{3/2-s}\right|. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\left|\hat\varphi(3/2-s)\hat\psi(s)-\frac1{s(3/2-s)}\right|\\ &\leq\left|\hat\varphi(3/2-s)\right|\left|\hat\psi(s)-\frac1s\right|+\left|\frac1s\right|\left|\hat\varphi(3/2-s)-\frac{1}{3/2-s}\right|. \end{aligned} \end{align} $$
Now we have
 $$ \begin{align} \begin{aligned} \left|\hat\psi(s)-\frac1s\right|&\leq\int_{0}^\infty\left|\psi(u)-1\right| u^{\sigma-1}du\\ &=\int_{0}^{\frac1U}\left|\psi(u)-1\right| u^{\sigma-1}du+\int_{1-\frac1U}^{1}\left|\psi(u)-1\right| u^{\sigma-1}du\\ &\ll \frac1{U^\sigma}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left|\hat\psi(s)-\frac1s\right|&\leq\int_{0}^\infty\left|\psi(u)-1\right| u^{\sigma-1}du\\ &=\int_{0}^{\frac1U}\left|\psi(u)-1\right| u^{\sigma-1}du+\int_{1-\frac1U}^{1}\left|\psi(u)-1\right| u^{\sigma-1}du\\ &\ll \frac1{U^\sigma}, \end{aligned} \end{align} $$
and similarly
 $$ \begin{align} \left|\hat\varphi(3/2-s)-\frac1{3/2-s}\right|\leq\int_{0}^\infty\left|\varphi(u)-1\right| u^{1/2-\sigma}du\ll\frac{1}{U^{3/2-\sigma}}.\\[-47pt]\nonumber \end{align} $$
$$ \begin{align} \left|\hat\varphi(3/2-s)-\frac1{3/2-s}\right|\leq\int_{0}^\infty\left|\varphi(u)-1\right| u^{1/2-\sigma}du\ll\frac{1}{U^{3/2-\sigma}}.\\[-47pt]\nonumber \end{align} $$
Using this Lemma in (6.11), we get
 $$ \begin{align} E(X,Y;\varphi,\psi)\ll\frac{XY^{1/2}+YX^{1/2}}{\sqrt U}+\left(\frac{XY}{U}\right)^{3/4}. \end{align} $$
$$ \begin{align} E(X,Y;\varphi,\psi)\ll\frac{XY^{1/2}+YX^{1/2}}{\sqrt U}+\left(\frac{XY}{U}\right)^{3/4}. \end{align} $$
Putting everything together, the error in both cases is
 $$ \begin{align} \frac{X^{\frac32+\varepsilon}+Y^{\frac32+\varepsilon}}{U}+\frac{XY^{\frac12}+YX^{\frac12}}{\sqrt U}+\left(\frac{XY}{U}\right)^{\frac34}+(XY^{\sigma}+YX^{\sigma})U^{\frac12-2\sigma+\varepsilon}+(XY)^{\frac12}U^{\varepsilon}, \end{align} $$
$$ \begin{align} \frac{X^{\frac32+\varepsilon}+Y^{\frac32+\varepsilon}}{U}+\frac{XY^{\frac12}+YX^{\frac12}}{\sqrt U}+\left(\frac{XY}{U}\right)^{\frac34}+(XY^{\sigma}+YX^{\sigma})U^{\frac12-2\sigma+\varepsilon}+(XY)^{\frac12}U^{\varepsilon}, \end{align} $$
where
![]() $1/4\geq \sigma \geq \delta $
. In both cases, the best choice is
$1/4\geq \sigma \geq \delta $
. In both cases, the best choice is
![]() $\sigma =1/4$
. Then we can take
$\sigma =1/4$
. Then we can take
![]() $U=\min \{X,Y\}$
and obtain the error
$U=\min \{X,Y\}$
and obtain the error
in the range
![]() $Y^{2/5}\leq X\leq Y^{5/2}.$
In the remaining range, the result follows from (1.2) and the asymptotic expansion of
$Y^{2/5}\leq X\leq Y^{5/2}.$
In the remaining range, the result follows from (1.2) and the asymptotic expansion of
![]() $C(\alpha )$
(1.5) and (1.6), together with the fact that
$C(\alpha )$
(1.5) and (1.6), together with the fact that
![]() $C(\alpha )=D(\alpha )$
as will be proved in the next section.
$C(\alpha )=D(\alpha )$
as will be proved in the next section.
7 Proving that
 $C(\alpha )=D(\alpha )$
$C(\alpha )=D(\alpha )$
In this section, we show that
![]() $C(\alpha )=D(\alpha )$
. Recall that
$C(\alpha )=D(\alpha )$
. Recall that
 $$ \begin{align} \begin{aligned} D(\alpha)=\sqrt\alpha+\alpha-\frac{2\sqrt\pi}{2\pi i}\int\limits_{(3/4)}\left(\frac{\alpha}{2\pi}\right)^s\cdot\frac{\Gamma\left( s-\frac32\right)\sin\left(\frac{\pi s}{2}\right)\zeta(2s-1)}{s}ds. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} D(\alpha)=\sqrt\alpha+\alpha-\frac{2\sqrt\pi}{2\pi i}\int\limits_{(3/4)}\left(\frac{\alpha}{2\pi}\right)^s\cdot\frac{\Gamma\left( s-\frac32\right)\sin\left(\frac{\pi s}{2}\right)\zeta(2s-1)}{s}ds. \end{aligned} \end{align} $$
We shift the integral to the left, capturing the pole at
![]() $s=\frac 12$
, which contributes
$s=\frac 12$
, which contributes
 $$ \begin{align*}2\sqrt\pi\left(\frac{\alpha}{2\pi}\right)^{1/2}\cdot\frac{-\sin(\pi/4)\zeta(0)}{1/2}=\alpha^{1/2}.\end{align*} $$
$$ \begin{align*}2\sqrt\pi\left(\frac{\alpha}{2\pi}\right)^{1/2}\cdot\frac{-\sin(\pi/4)\zeta(0)}{1/2}=\alpha^{1/2}.\end{align*} $$
The horizontal integrals vanish by (2.9) and a convexity estimate for
![]() $\zeta (s)$
, so
$\zeta (s)$
, so
 $$ \begin{align} \begin{aligned} D(\alpha)&=\alpha-\frac{2\sqrt\pi}{2\pi i}\int\limits_{(-1/4)}\left(\frac{\alpha}{2\pi}\right)^s\cdot\frac{\Gamma\left( s-\frac32\right)\sin\left(\frac{\pi s}{2}\right)\zeta(2s-1)}{s}ds\\&=\alpha-\frac{2\sqrt\pi}{2\pi i}\int\limits_{(1/4)}\alpha^{-s}\cdot\frac{(2\pi)^s\Gamma\left(-s-\frac32\right)\sin\left(\frac{\pi s}{2}\right)\zeta(-2s-1)}{s}ds. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} D(\alpha)&=\alpha-\frac{2\sqrt\pi}{2\pi i}\int\limits_{(-1/4)}\left(\frac{\alpha}{2\pi}\right)^s\cdot\frac{\Gamma\left( s-\frac32\right)\sin\left(\frac{\pi s}{2}\right)\zeta(2s-1)}{s}ds\\&=\alpha-\frac{2\sqrt\pi}{2\pi i}\int\limits_{(1/4)}\alpha^{-s}\cdot\frac{(2\pi)^s\Gamma\left(-s-\frac32\right)\sin\left(\frac{\pi s}{2}\right)\zeta(-2s-1)}{s}ds. \end{aligned} \end{align} $$
This integral is an inverse Mellin transform, so we rewrite
![]() $C(\alpha )$
using Mellin inversion. We have
$C(\alpha )$
using Mellin inversion. We have
 $$ \begin{align} \begin{aligned} C(\alpha)&=\alpha+\alpha^{3/2}\frac{2}{\pi}\sum_{k=1}^\infty\frac{1}{k^2}\int_{0}^{1/\alpha}\sqrt y\sin\left(\frac{\pi k^2}{2y}\right)dy\\&=\alpha+\frac2\pi\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\sin\left(\frac{\pi k^2\alpha}{2u}\right)du\\&=\alpha+\frac2{\pi}\cdot\frac{1}{2\pi i}\int\limits_{(c)}\alpha^{-s}\hat f(s)ds, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} C(\alpha)&=\alpha+\alpha^{3/2}\frac{2}{\pi}\sum_{k=1}^\infty\frac{1}{k^2}\int_{0}^{1/\alpha}\sqrt y\sin\left(\frac{\pi k^2}{2y}\right)dy\\&=\alpha+\frac2\pi\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\sin\left(\frac{\pi k^2\alpha}{2u}\right)du\\&=\alpha+\frac2{\pi}\cdot\frac{1}{2\pi i}\int\limits_{(c)}\alpha^{-s}\hat f(s)ds, \end{aligned} \end{align} $$
where
 $$ \begin{align} f(x)=\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\sin\left(\frac{\pi k^2 x}{2u}\right)du. \end{align} $$
$$ \begin{align} f(x)=\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\sin\left(\frac{\pi k^2 x}{2u}\right)du. \end{align} $$
For
![]() $0<\mathrm {Re}(s)<1$
, we have
$0<\mathrm {Re}(s)<1$
, we have
 $$ \begin{align} \begin{aligned} \hat f(s)&=\int_0^\infty\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\sin\left(\frac{\pi k^2 x}{2u}\right)du\ x^{s-1}dx\\&=\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\int_0^\infty \sin\left(\frac{\pi k^2 x}{2u}\right) x^{s-1}dx\ du,\end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \hat f(s)&=\int_0^\infty\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\sin\left(\frac{\pi k^2 x}{2u}\right)du\ x^{s-1}dx\\&=\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\int_0^\infty \sin\left(\frac{\pi k^2 x}{2u}\right) x^{s-1}dx\ du,\end{aligned} \end{align} $$
which isn’t obvious as the double integral doesn’t converge absolutely, but we will justify the interchange of summation and integrals in Lemma 7.1. We can now make a change of variables
![]() $y=\frac {\pi k^2x}{2u}$
and obtain
$y=\frac {\pi k^2x}{2u}$
and obtain
 $$ \begin{align} \begin{aligned} \hat f(s)&=\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\int_0^\infty \sin(y) y^{s-1}dy\ \left(\frac{2u}{\pi k^2}\right)^sdu\\&=\left(\frac{2}{\pi}\right)^s\zeta(2+2s)\int_0^1u^{s+1/2}du\int_0^\infty\sin(y)y^{s-1}dy\\&=\frac{2^s\zeta(2+2s)\Gamma(s)\sin\left(\frac{\pi s}{2}\right)}{\pi^s(s+3/2)}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \hat f(s)&=\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\int_0^\infty \sin(y) y^{s-1}dy\ \left(\frac{2u}{\pi k^2}\right)^sdu\\&=\left(\frac{2}{\pi}\right)^s\zeta(2+2s)\int_0^1u^{s+1/2}du\int_0^\infty\sin(y)y^{s-1}dy\\&=\frac{2^s\zeta(2+2s)\Gamma(s)\sin\left(\frac{\pi s}{2}\right)}{\pi^s(s+3/2)}, \end{aligned} \end{align} $$
which holds for
![]() $0<\mathrm {Re}(s)<1,$
so we can take
$0<\mathrm {Re}(s)<1,$
so we can take
![]() $c=1/4$
in (7.3). It therefore suffices to show that
$c=1/4$
in (7.3). It therefore suffices to show that
 $$ \begin{align} -2\sqrt\pi\frac{(2\pi)^s\Gamma\left(-s-\frac32\right)\sin\left(\frac{\pi s}{2}\right)\zeta(-2s-1)}{s}=\frac2\pi\cdot\frac{2^s\zeta(2+2s)\Gamma(s)\sin\left(\frac{\pi s}{2}\right)}{\pi^s(s+3/2)}. \end{align} $$
$$ \begin{align} -2\sqrt\pi\frac{(2\pi)^s\Gamma\left(-s-\frac32\right)\sin\left(\frac{\pi s}{2}\right)\zeta(-2s-1)}{s}=\frac2\pi\cdot\frac{2^s\zeta(2+2s)\Gamma(s)\sin\left(\frac{\pi s}{2}\right)}{\pi^s(s+3/2)}. \end{align} $$
The functional equation for the zeta function gives
 $$ \begin{align} \zeta(2s+2)=\pi^{2s+3/2}\cdot\frac{\Gamma\left(-s-\frac12\right)}{\Gamma(s+1)}\zeta(-2s-1), \end{align} $$
$$ \begin{align} \zeta(2s+2)=\pi^{2s+3/2}\cdot\frac{\Gamma\left(-s-\frac12\right)}{\Gamma(s+1)}\zeta(-2s-1), \end{align} $$
so using
![]() $s\Gamma (s)=\Gamma (s+1)$
and
$s\Gamma (s)=\Gamma (s+1)$
and
![]() $(-s-3/2)\Gamma (-s-3/2)=\Gamma (-s-1/2)$
gives the result.
$(-s-3/2)\Gamma (-s-3/2)=\Gamma (-s-1/2)$
gives the result.
It remains to justify the interchange of the order of summation and integrations in (7.5).
Lemma 7.1 If
![]() $0<\mathrm {Re}(s)<1$
, it holds that
$0<\mathrm {Re}(s)<1$
, it holds that
 $$ \begin{align} \begin{aligned} &\int_0^\infty\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\sin\left(\frac{\pi k^2 x}{2u}\right)du\ x^{s-1}dx\\&=\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\int_0^\infty \sin\left(\frac{\pi k^2 x}{2u}\right) x^{s-1}dx\ du. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\int_0^\infty\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\sin\left(\frac{\pi k^2 x}{2u}\right)du\ x^{s-1}dx\\&=\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\int_0^\infty \sin\left(\frac{\pi k^2 x}{2u}\right) x^{s-1}dx\ du. \end{aligned} \end{align} $$
Proof We have
 $$ \begin{align} \begin{aligned} &\int_0^\infty\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\sin\left(\frac{\pi k^2 x}{2u}\right)du\ x^{s-1}dx\\&=\lim_{A\rightarrow\infty}\int_{1/A}^A\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\sin\left(\frac{\pi k^2 x}{2u}\right)du\ x^{s-1}dx. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\int_0^\infty\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\sin\left(\frac{\pi k^2 x}{2u}\right)du\ x^{s-1}dx\\&=\lim_{A\rightarrow\infty}\int_{1/A}^A\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\sin\left(\frac{\pi k^2 x}{2u}\right)du\ x^{s-1}dx. \end{aligned} \end{align} $$
We can now interchange the integrals and summation, because
 $$ \begin{align} \begin{aligned} \sum_{k=1}^\infty\frac1{k^2}\int_0^1\int_{1/A}^A\left|\sqrt u\sin\left(\frac{\pi k^2 x}{2u}\right)x^{s-1}\right| dx\ du\ll A, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \sum_{k=1}^\infty\frac1{k^2}\int_0^1\int_{1/A}^A\left|\sqrt u\sin\left(\frac{\pi k^2 x}{2u}\right)x^{s-1}\right| dx\ du\ll A, \end{aligned} \end{align} $$
so
 $$ \begin{align} \begin{aligned} &\lim_{A\rightarrow\infty}\int_{1/A}^A\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\sin\left(\frac{\pi k^2 x}{2u}\right)du\ x^{s-1}dx\\&=\lim_{A\rightarrow\infty}\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\int_{1/A}^A\sin\left(\frac{\pi k^2 x}{2u}\right)x^{s-1}dx\ du. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\lim_{A\rightarrow\infty}\int_{1/A}^A\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\sin\left(\frac{\pi k^2 x}{2u}\right)du\ x^{s-1}dx\\&=\lim_{A\rightarrow\infty}\sum_{k=1}^\infty\frac1{k^2}\int_0^1\sqrt u\int_{1/A}^A\sin\left(\frac{\pi k^2 x}{2u}\right)x^{s-1}dx\ du. \end{aligned} \end{align} $$
To insert the limit inside the sum and integral, we use the Dominated convergence theorem with the bound
![]() $\sqrt u|\int _{1/A}^A\sin \left (\frac {\pi k^2 x}{2u}\right )x^{s-1}dx|\leq K\sqrt u$
for an absolute constant K independent of u and A in our range, which holds because
$\sqrt u|\int _{1/A}^A\sin \left (\frac {\pi k^2 x}{2u}\right )x^{s-1}dx|\leq K\sqrt u$
for an absolute constant K independent of u and A in our range, which holds because
![]() $\int _0^\infty \sin (y)y^{s-1}dy$
converges.
$\int _0^\infty \sin (y)y^{s-1}dy$
converges.
Acknowledgment
I would like to thank my supervisor Chantal David for her help and valuable comments, and David Farmer for comments on an earlier version of this paper and suggestion of the proof in Section 7. I would also like to thank the anonymous referee for many useful comments and suggestions.