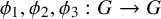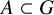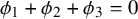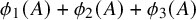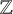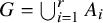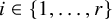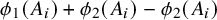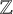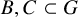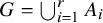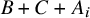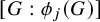1 Introduction
This paper continues the investigation set forth in [Reference Le and Lê33]. Let G be an abelian topological group. If
![]() $A, B \subset G$
, the sumset and difference set of A and B are
$A, B \subset G$
, the sumset and difference set of A and B are
![]() $A + B: = \{a + b: a \in A, b \in B \}$
and
$A + B: = \{a + b: a \in A, b \in B \}$
and
![]() $A - B:=\{a - b: a \in A, b \in B \}$
, respectively. For
$A - B:=\{a - b: a \in A, b \in B \}$
, respectively. For
![]() $a\in G$
, the translate
$a\in G$
, the translate
![]() $a+B$
is
$a+B$
is
![]() $\{a+B:b\in B\}$
. If
$\{a+B:b\in B\}$
. If
![]() $s \in {\mathbb {Z}}$
, we define
$s \in {\mathbb {Z}}$
, we define
![]() $sA:=\{sa: a \in A\}$
. A character of G is a continuous homomorphism from G to
$sA:=\{sa: a \in A\}$
. A character of G is a continuous homomorphism from G to
![]() $S^1:=\{z\in \mathbb C: |z|=1\}$
.
$S^1:=\{z\in \mathbb C: |z|=1\}$
.
Many classical results in additive combinatorics state, roughly, that sumsets are more structured than their summands. Such results often quantify the structure found in sumsets in terms of Bohr sets, which we define here. For a finite set
![]() $\Lambda $
of characters of G and a constant
$\Lambda $
of characters of G and a constant
![]() $\eta> 0$
, the set
$\eta> 0$
, the set
is called a Bohr set, a Bohr
![]() $_0$
-set or a Bohr neighborhood of
$_0$
-set or a Bohr neighborhood of
![]() $0$
in the literature. In this paper, we use mostly the first nomenclature. The set
$0$
in the literature. In this paper, we use mostly the first nomenclature. The set
![]() $B(\Lambda; \eta )$
is also called a Bohr-
$B(\Lambda; \eta )$
is also called a Bohr-
![]() $(k, \eta )$
set, where
$(k, \eta )$
set, where
![]() $k = |\Lambda |$
. We refer to
$k = |\Lambda |$
. We refer to
![]() $\eta $
as the radius and k as the rank of the Bohr set. By a translate of a Bohr set, or a Bohr neighborhood, we mean a set of the form
$\eta $
as the radius and k as the rank of the Bohr set. By a translate of a Bohr set, or a Bohr neighborhood, we mean a set of the form
![]() $a + B(\Lambda; \eta )$
for some
$a + B(\Lambda; \eta )$
for some
![]() $a \in G$
.
$a \in G$
.
After summarizing previous results in Sections 1.1 and 1.2, we state our new results in Section 1.3.
1.1 Previous results in
 ${\mathbb {Z}}$
${\mathbb {Z}}$
If
![]() $A \subset {\mathbb {Z}}$
, the upper Banach density of A is
$A \subset {\mathbb {Z}}$
, the upper Banach density of A is
The study of Bohr sets in sumsets started with the following important theorem of Bogolyubov [Reference Bogolyubov11].
Theorem A (Bogolyubov).
If
![]() $A \subset {\mathbb {Z}}$
has positive upper Banach density, then
$A \subset {\mathbb {Z}}$
has positive upper Banach density, then
![]() $A - A + A - A$
contains a Bohr set whose rank and radius depend only on
$A - A + A - A$
contains a Bohr set whose rank and radius depend only on
![]() $d^*(A)$
.
$d^*(A)$
.
While it originated from the study of almost periodic functions, Bogolyubov’s theorem is now a standard tool in additive combinatorics. It was used in Ruzsa’s proof of Freiman’s theorem [Reference Ruzsa35] and in Gowers’s proof of Szemerédi’s theorem [Reference Gowers22].
Følner [Reference Følner15] showed that the last two summands in Bogolyubov’s theorem are ‘almost’ redundant by proving that
![]() $A - A$
already contains a set of the form
$A - A$
already contains a set of the form
![]() $B\setminus E$
, where B is a Bohr set and
$B\setminus E$
, where B is a Bohr set and
![]() $d^*(E)=0$
. The exceptional set E is unavoidable: Kriz [Reference Kriz32] demonstrated that there exists a set A of positive upper Banach density for which
$d^*(E)=0$
. The exceptional set E is unavoidable: Kriz [Reference Kriz32] demonstrated that there exists a set A of positive upper Banach density for which
![]() $A - A$
contains no Bohr sets. The first author [Reference Griesmer26] showed that there is a set A having
$A - A$
contains no Bohr sets. The first author [Reference Griesmer26] showed that there is a set A having
![]() $d^*(A)>0$
such that
$d^*(A)>0$
such that
![]() $A-A$
contains no Bohr neighborhood of any integer.
$A-A$
contains no Bohr neighborhood of any integer.
Hegyvári and Ruzsa [Reference Hegyvári and Ruzsa28] generalized Bogolyubov’s theorem in a different direction, showing that there exist ‘many’
![]() $a \in {\mathbb {Z}}$
for which
$a \in {\mathbb {Z}}$
for which
![]() $A - A + A - a$
contains a Bohr set. Björklund and the first author [Reference Björklund10, Theorem 1.1] strengthened this result by providing explicit bounds on the rank and radius of such a Bohr set and generalized the result to all countable amenable discrete groups (and hence all countable discrete abelian groups).
$A - A + A - a$
contains a Bohr set. Björklund and the first author [Reference Björklund10, Theorem 1.1] strengthened this result by providing explicit bounds on the rank and radius of such a Bohr set and generalized the result to all countable amenable discrete groups (and hence all countable discrete abelian groups).
Regarding more general threefold sumsets, Bergelson and Ruzsa proved the following.
Theorem B [Reference Bergelson and Ruzsa7, Theorem 6.1].
Let
![]() $s_1, s_2, s_3$
be non-zero integers satisfying
$s_1, s_2, s_3$
be non-zero integers satisfying
![]() $s_1 +s_2+s_3 = 0$
. If
$s_1 +s_2+s_3 = 0$
. If
![]() $A \subset {\mathbb {Z}}$
has positive upper Banach density, then
$A \subset {\mathbb {Z}}$
has positive upper Banach density, then
![]() $s_1 A+s_2 A+s_3 A$
contains a Bohr set whose rank and radius depend only on
$s_1 A+s_2 A+s_3 A$
contains a Bohr set whose rank and radius depend only on
![]() $s_1, s_2, s_3$
and
$s_1, s_2, s_3$
and
![]() $d^*(A)$
.
$d^*(A)$
.
Since any Bohr set in
![]() ${\mathbb {Z}}$
must contain
${\mathbb {Z}}$
must contain
![]() $0$
, the condition
$0$
, the condition
![]() $s_1 + s_2 + s_3 = 0$
is easily seen to be necessary by taking
$s_1 + s_2 + s_3 = 0$
is easily seen to be necessary by taking
![]() $A = M {\mathbb {Z}} + 1$
for some
$A = M {\mathbb {Z}} + 1$
for some
![]() $M> |s_1| + |s_2| + |s_3|$
. In particular, one cannot expect
$M> |s_1| + |s_2| + |s_3|$
. In particular, one cannot expect
![]() $A + A - A$
to contain a Bohr set for every A of positive upper Banach density. When
$A + A - A$
to contain a Bohr set for every A of positive upper Banach density. When
![]() $(s_1, s_2, s_3) = (1, 1, -2)$
, Theorem B generalizes Theorem A since
$(s_1, s_2, s_3) = (1, 1, -2)$
, Theorem B generalizes Theorem A since
![]() $A+A-2 A \subset A+A-A-A$
.
$A+A-2 A \subset A+A-A-A$
.
While the problem of finding Bohr sets in sumsets where the summands have positive upper Banach density has attracted much attention, the analogous question concerning partitions was little studied until recently, and the situation is less well understood. The following question, popularized by Katznelson [Reference Katznelson31] and Ruzsa [Reference Ruzsa36, Chapter 5], is a well-known open problem in additive combinatorics and dynamical systems.
Question 1.1. If
![]() ${\mathbb {Z}} = \bigcup _{i=1}^r A_i$
, must one of the difference sets
${\mathbb {Z}} = \bigcup _{i=1}^r A_i$
, must one of the difference sets
![]() $A_i - A_i$
contain a Bohr set?
$A_i - A_i$
contain a Bohr set?
In terms of dynamical systems, Question 1.1 asks if every set of recurrence for minimal isometries (also known as a set of Bohr recurrence) is also a set of recurrence for minimal topological systems. See [Reference Glasscock, Koutsogiannis and Richter20] for a detailed account of the history of Question 1.1 and many equivalent formulations. See [Reference Griesmer27] for more equivalent formulations and resolution of some special cases.
Regarding three summands, the second and third authors proved the following partition analogue of Theorem B.
Theorem C [Reference Le and Lê33, Theorem 1.4].
-
(i) Let
 $s_1, s_2 \in {\mathbb {Z}} \setminus \{0\}$
. For any partition
$s_1, s_2 \in {\mathbb {Z}} \setminus \{0\}$
. For any partition
 ${\mathbb {Z}} = \bigcup _{i=1}^r A_i$
, there is an i such that
${\mathbb {Z}} = \bigcup _{i=1}^r A_i$
, there is an i such that
 $s_1 A_i + s_2 A_i - s_2 A_i$
contains a Bohr set whose rank and radius depend only on
$s_1 A_i + s_2 A_i - s_2 A_i$
contains a Bohr set whose rank and radius depend only on
 $ s_1, s_2$
and r.
$ s_1, s_2$
and r. -
(ii) For any partition
 ${\mathbb {Z}} = \bigcup _{i=1}^r A_i$
, there is an i such that
${\mathbb {Z}} = \bigcup _{i=1}^r A_i$
, there is an i such that
 $A_i - A_i + sA_i$
contains a Bohr set for any
$A_i - A_i + sA_i$
contains a Bohr set for any
 $s \in {\mathbb {Z}} \setminus \{0\}$
.
$s \in {\mathbb {Z}} \setminus \{0\}$
.
Rado’s theorem says that an equation
![]() $\sum _{j=1}^k s_j x_j = 0$
with coefficients
$\sum _{j=1}^k s_j x_j = 0$
with coefficients
![]() $s_j \in {\mathbb {Z}}\setminus \{0\}$
is partition regular over
$s_j \in {\mathbb {Z}}\setminus \{0\}$
is partition regular over
![]() ${\mathbb {Z}} \setminus \{0\}$
if and only if there exists
${\mathbb {Z}} \setminus \{0\}$
if and only if there exists
![]() $J \subset \{1, \ldots , k\}, J \neq \varnothing $
such that
$J \subset \{1, \ldots , k\}, J \neq \varnothing $
such that
![]() $\sum _{j \in J}s_j = 0$
. Combined with Theorem B, part (i) of Theorem C gives a complete characterization of tuples
$\sum _{j \in J}s_j = 0$
. Combined with Theorem B, part (i) of Theorem C gives a complete characterization of tuples
![]() $(s_1, \ldots , s_k) \in ({\mathbb {Z}} \setminus \{0\})^k$
that guarantee the existence of a Bohr set in
$(s_1, \ldots , s_k) \in ({\mathbb {Z}} \setminus \{0\})^k$
that guarantee the existence of a Bohr set in
![]() $\sum _{j=1}^k s_j A_i$
, for some i, as long as
$\sum _{j=1}^k s_j A_i$
, for some i, as long as
![]() $k \geq 3$
. They are precisely tuples satisfying Rado’s condition.Footnote
1
This characterization is a strengthening of Rado’s theorem. As the integer s in Part (ii) can be arbitrarily large, this suggests that either the answer to Question 1.1 is positive or the construction of a counterexample must be very delicate.
$k \geq 3$
. They are precisely tuples satisfying Rado’s condition.Footnote
1
This characterization is a strengthening of Rado’s theorem. As the integer s in Part (ii) can be arbitrarily large, this suggests that either the answer to Question 1.1 is positive or the construction of a counterexample must be very delicate.
1.2 Previous results in compact groups
As part of a general program, we aim to study the Bohr sets in sumsets phenomenon in more general groups. A natural setup is amenable groups, since in these groups there is a natural notion of density, and Bohr sets can also be defined.Footnote
2
A locally compact group G with left Haar measure
![]() $m_G$
is said to be amenable if there exists an invariant mean on G, that is, a linear functional
$m_G$
is said to be amenable if there exists an invariant mean on G, that is, a linear functional
![]() $\lambda $
on
$\lambda $
on
![]() $L^{\infty }(m_G)$
that is nonnegative (i.e.,
$L^{\infty }(m_G)$
that is nonnegative (i.e.,
![]() $\lambda (f) \geq 0$
if
$\lambda (f) \geq 0$
if
![]() $f \geq 0$
), of norm 1 (i.e.,
$f \geq 0$
), of norm 1 (i.e.,
![]() $\lambda (1_G)=1$
) and left-invariant (i.e.,
$\lambda (1_G)=1$
) and left-invariant (i.e.,
![]() $\lambda (f_t) = \lambda (f)$
, where
$\lambda (f_t) = \lambda (f)$
, where
![]() $f_t(x) = f(t^{-1}x))$
. If
$f_t(x) = f(t^{-1}x))$
. If
![]() $A \subset G$
is a Borel set, we can define its upper Banach density as
$A \subset G$
is a Borel set, we can define its upper Banach density as
The supremum is actually a maximum since the set of invariant means on G is weak*-compact, by the Banach-Alaoglu theorem. It is well known that all locally compact abelian groups are amenable. Følner [Reference Følner15, Reference Følner16] generalized Theorem A to discrete abelian groups, and the results of [Reference Björklund10] mentioned above apply to countable discrete amenable groups which are not necessarily abelian.
Against this backdrop, our objective in this program is threefold. First, we ask for analogues of Theorems B and C in (a subclass of) amenable groups. Second, in the context of general groups, we can replace the dilate
![]() $sA$
by
$sA$
by
![]() $\phi (A)$
, the image of A under a homomorphism
$\phi (A)$
, the image of A under a homomorphism
![]() $\phi $
. This point of view leads to a wider range of applications: we can consider linear maps on vector spaces and multiplication by an element in a ring (see Corollary 1.6 below). This broader perspective was also adopted in recent works [Reference Ackelsberg, Bergelson and Best2, Reference Ackelsberg, Bergelson and Shalom3] on Khintchine-type recurrence for actions of an abelian group. Third, we aim for uniformity in terms of rank and radius of the Bohr set in question (i.e., they are allowed to depend on
$\phi $
. This point of view leads to a wider range of applications: we can consider linear maps on vector spaces and multiplication by an element in a ring (see Corollary 1.6 below). This broader perspective was also adopted in recent works [Reference Ackelsberg, Bergelson and Best2, Reference Ackelsberg, Bergelson and Shalom3] on Khintchine-type recurrence for actions of an abelian group. Third, we aim for uniformity in terms of rank and radius of the Bohr set in question (i.e., they are allowed to depend on
![]() $d^*(A)$
and other parameters, but not A itself). This is because, in some situations, the existence of Bohr sets is straightforward (for example, an interval around 0 in
$d^*(A)$
and other parameters, but not A itself). This is because, in some situations, the existence of Bohr sets is straightforward (for example, an interval around 0 in
![]() $\mathbb {R}/{\mathbb {Z}}$
always contains a Bohr set), but obtaining uniformity is much harder.
$\mathbb {R}/{\mathbb {Z}}$
always contains a Bohr set), but obtaining uniformity is much harder.
In [Reference Le and Lê33], these objectives were achieved for compact abelian groups. Note that in this case, the only invariant mean on G is given by
![]() $m_G$
(the normalized Haar measure on G) and
$m_G$
(the normalized Haar measure on G) and
![]() $d^*(A) = m_G(A)$
. The second and third authors proved the following.
$d^*(A) = m_G(A)$
. The second and third authors proved the following.
Theorem D (Le-Lê [Reference Le and Lê33]).
Let K be a compact abelian group with normalized Haar measure
![]() $m_K$
. Let
$m_K$
. Let
![]() $\phi _1, \phi _2, \phi _3: K \to K$
be commuting continuous endomorphisms such that
$\phi _1, \phi _2, \phi _3: K \to K$
be commuting continuous endomorphisms such that
![]() $[K: \phi _j(K)] < \infty $
for each j.
$[K: \phi _j(K)] < \infty $
for each j.
-
(i) If
 $\phi _1 + \phi _2 +\phi _3=0$
and
$\phi _1 + \phi _2 +\phi _3=0$
and
 $A \subset K$
is a Borel set with
$A \subset K$
is a Borel set with
 $m_K(A)> 0$
, then
$m_K(A)> 0$
, then
 $\phi _1(A) + \phi _2(A) + \phi _3(A)$
contains a Bohr-
$\phi _1(A) + \phi _2(A) + \phi _3(A)$
contains a Bohr-
 $(k,\eta )$
set, where k and
$(k,\eta )$
set, where k and
 $\eta $
depend only on
$\eta $
depend only on
 $m_K(A)$
and
$m_K(A)$
and
 $[G: \phi _j(G)]$
.
$[G: \phi _j(G)]$
. -
(ii) If
 $K = \bigcup _{i=1}^r A_i$
is a partition of K into Borel sets, then there exists i such that
$K = \bigcup _{i=1}^r A_i$
is a partition of K into Borel sets, then there exists i such that
 $\phi _1(A_i) + \phi _2(A_i)-\phi _2(A_i)$
contains a Bohr-
$\phi _1(A_i) + \phi _2(A_i)-\phi _2(A_i)$
contains a Bohr-
 $(k,\eta )$
set, where k and
$(k,\eta )$
set, where k and
 $\eta $
depend only on r and
$\eta $
depend only on r and
 $[G: \phi _j(G)]$
.
$[G: \phi _j(G)]$
.
The finite index condition is necessary and also appears in [Reference Ackelsberg, Bergelson and Best2]. However, we do not know if the assumption that the
![]() $\phi _j$
commute can be omitted.
$\phi _j$
commute can be omitted.
1.3 New results in discrete groups
In this paper, we extend many of the preceding results to the setting of countable discrete abelian groups. Our main results are discrete analogues of Theorem D, and as such, are direct generalizations of Theorems B and C.
Theorem 1.2. Let G be a countable discrete abelian group. Let
![]() $\phi _1, \phi _2, \phi _3 : G \rightarrow G$
be commuting endomorphisms such that
$\phi _1, \phi _2, \phi _3 : G \rightarrow G$
be commuting endomorphisms such that
![]() $\phi _1 + \phi _2 +\phi _3 =0$
and
$\phi _1 + \phi _2 +\phi _3 =0$
and
![]() $[G:\phi _j(G)]$
are finite for
$[G:\phi _j(G)]$
are finite for
![]() $j \in \{1, 2, 3\}$
. Suppose
$j \in \{1, 2, 3\}$
. Suppose
![]() $A \subset G$
has positive upper Banach density, (i.e.,
$A \subset G$
has positive upper Banach density, (i.e.,
![]() $d^*(A)>0$
). Then the set
$d^*(A)>0$
). Then the set
contains a Bohr-
![]() $(k, \eta )$
set, where k and
$(k, \eta )$
set, where k and
![]() $\eta $
depend only on
$\eta $
depend only on
![]() $d^*(A)$
and the indices
$d^*(A)$
and the indices
![]() $[G: \phi _j(G)]$
.
$[G: \phi _j(G)]$
.
Remark 1.3.
-
• In the special case
 $\phi _j(x) = s_j x$
, where
$\phi _j(x) = s_j x$
, where
 $s_j \in {\mathbb {Z}} \setminus \{0\}$
, Theorem 1.2 was proven by the first author [Reference Griesmer23] without the conclusion on the uniformity of k and
$s_j \in {\mathbb {Z}} \setminus \{0\}$
, Theorem 1.2 was proven by the first author [Reference Griesmer23] without the conclusion on the uniformity of k and
 $\eta $
.
$\eta $
. -
• The conclusion of Theorem 1.2 remains valid if the
 $\phi _j$
do not necessarily commute, but one of them is an automorphism. Indeed, assume that
$\phi _j$
do not necessarily commute, but one of them is an automorphism. Indeed, assume that
 $\phi _1$
is an automorphism. We observe that Consider the endomorphisms
$\phi _1$
is an automorphism. We observe that Consider the endomorphisms $$\begin{align*}\phi_1(A) + \phi_2(A) + \phi_3(A) = \phi_1 \left(A + \phi_1^{-1} \circ \phi_2 (A) + \phi_1^{-1} \circ \phi_3 (A) \right). \end{align*}$$
$$\begin{align*}\phi_1(A) + \phi_2(A) + \phi_3(A) = \phi_1 \left(A + \phi_1^{-1} \circ \phi_2 (A) + \phi_1^{-1} \circ \phi_3 (A) \right). \end{align*}$$
 $Id$
,
$Id$
,
 $\phi _1^{-1} \circ \phi _2$
and
$\phi _1^{-1} \circ \phi _2$
and
 $\phi _1^{-1} \circ \phi _3$
. They add up to
$\phi _1^{-1} \circ \phi _3$
. They add up to
 $0$
since They also commuteFootnote 3 and have finite index images. Theorem 1.2 implies
$0$
since They also commuteFootnote 3 and have finite index images. Theorem 1.2 implies $$\begin{align*}Id + \phi_1^{-1} \circ \phi_2 + \phi_1^{-1} \circ \phi_3 = Id + \phi_1^{-1} \circ (\phi_2 + \phi_3) = Id + \phi_1^{-1} \circ (- \phi_1) = 0. \end{align*}$$
$$\begin{align*}Id + \phi_1^{-1} \circ \phi_2 + \phi_1^{-1} \circ \phi_3 = Id + \phi_1^{-1} \circ (\phi_2 + \phi_3) = Id + \phi_1^{-1} \circ (- \phi_1) = 0. \end{align*}$$
 $A + \phi _1^{-1} \circ \phi _2 (A) + \phi _1^{-1} \circ \phi _3 (A)$
contains a Bohr set, and the image of a Bohr set under an automorphism is easily seen to be a Bohr set of the same rank and radius (see Lemma 2.2).
$A + \phi _1^{-1} \circ \phi _2 (A) + \phi _1^{-1} \circ \phi _3 (A)$
contains a Bohr set, and the image of a Bohr set under an automorphism is easily seen to be a Bohr set of the same rank and radius (see Lemma 2.2).
-
• The hypothesis
 $\phi _1 + \phi _2 + \phi _3 = 0$
cannot be removed as demonstrated in the remark after Theorem B.
$\phi _1 + \phi _2 + \phi _3 = 0$
cannot be removed as demonstrated in the remark after Theorem B. -
• Similarly, the condition that each index
 $[G:\phi _j(G)]$
is finite cannot be omitted. For example, take
$[G:\phi _j(G)]$
is finite cannot be omitted. For example, take
 $G = {\mathbb {Z}}$
,
$G = {\mathbb {Z}}$
,
 $\phi _1(x) = x$
,
$\phi _1(x) = x$
,
 $\phi _2(x) = -x$
, and
$\phi _2(x) = -x$
, and
 $\phi _3(x)=0$
for
$\phi _3(x)=0$
for
 $x \in {\mathbb {Z}}$
. Then
$x \in {\mathbb {Z}}$
. Then
 $\phi _1(A) + \phi _2(A) + \phi _3(A)= A-A$
, and the Kriz example [Reference Kriz32] shows that there exists a set A of positive upper Banach density such that
$\phi _1(A) + \phi _2(A) + \phi _3(A)= A-A$
, and the Kriz example [Reference Kriz32] shows that there exists a set A of positive upper Banach density such that
 $A-A$
does not contain any Bohr set. See [Reference Griesmer23, Remark 1.6] for further discussion.
$A-A$
does not contain any Bohr set. See [Reference Griesmer23, Remark 1.6] for further discussion.
Theorem 1.4. Let G be a discrete abelian group and let
![]() $\phi _1, \phi _2: G \rightarrow G$
be commuting endomorphisms such that
$\phi _1, \phi _2: G \rightarrow G$
be commuting endomorphisms such that
![]() $[G:\phi _j(G)]$
is finite for
$[G:\phi _j(G)]$
is finite for
![]() $j \in \{1, 2\}$
. Then for every finite partition
$j \in \{1, 2\}$
. Then for every finite partition
![]() $G = \bigcup _{i=1}^r A_i$
, there exists
$G = \bigcup _{i=1}^r A_i$
, there exists
![]() $i \in \{1, \ldots , r\}$
such that
$i \in \{1, \ldots , r\}$
such that
contains a Bohr-
![]() $(k, \eta )$
set, where k and
$(k, \eta )$
set, where k and
![]() $\eta $
depend only on r and the indices
$\eta $
depend only on r and the indices
![]() $[G: \phi _j(G)]$
.
$[G: \phi _j(G)]$
.
Remark 1.5.
-
• In contrast to Theorem 1.2 and Theorem 1.7 below, Theorem 1.4 does not assume G is countable. The reason is that the former two theorems use Kronecker factors via Furstenberg’s correspondence principle, and the theory of factors requires the group to be countable. There are two ways to think of a factor of a measure preserving G-system: as a spatial map or as a G-invariant sub
 $\sigma $
-algebra. The latter can be obtained trivially from the former, but the converse is not trivial, and requires the group to be countable (in addition to the
$\sigma $
-algebra. The latter can be obtained trivially from the former, but the converse is not trivial, and requires the group to be countable (in addition to the
 $\sigma $
-algebras being separable). For instance, the method of proof of Theorem 5.15 in [Reference Furstenberg18] requires G to be countable.
$\sigma $
-algebras being separable). For instance, the method of proof of Theorem 5.15 in [Reference Furstenberg18] requires G to be countable. -
• Since Bohr sets contain
 $0$
, Theorem 1.4 implies that the equation
$0$
, Theorem 1.4 implies that the equation
 $\phi _1(x) + \phi _2(y) - \phi _2(z) = 0$
is partition regular in discrete abelian groups, that is, under any partition
$\phi _1(x) + \phi _2(y) - \phi _2(z) = 0$
is partition regular in discrete abelian groups, that is, under any partition
 $G = \bigcup _{i=1}^r A_i$
, there exists non-zero
$G = \bigcup _{i=1}^r A_i$
, there exists non-zero
 $x, y, z$
in the same class
$x, y, z$
in the same class
 $A_i$
such that
$A_i$
such that
 $\phi _1(x) + \phi _2(y) - \phi _2(z) = 0$
(to see that we can take
$\phi _1(x) + \phi _2(y) - \phi _2(z) = 0$
(to see that we can take
 $x, y, z$
to be non-zero, give 0 its own partition class).
$x, y, z$
to be non-zero, give 0 its own partition class). -
• If
 $d^*(A)>0$
, then
$d^*(A)>0$
, then
 $A + A - A$
is not guaranteed to contain a Bohr set as remarked after Theorem B. In particular, the analogous version of Theorem 1.4 for sets of positive upper Banach density is false.
$A + A - A$
is not guaranteed to contain a Bohr set as remarked after Theorem B. In particular, the analogous version of Theorem 1.4 for sets of positive upper Banach density is false. -
• The hypothesis that
 $\phi _2(G)$
has finite index in G cannot be omitted. For example, taking
$\phi _2(G)$
has finite index in G cannot be omitted. For example, taking
 $\phi _2 = 0$
and
$\phi _2 = 0$
and
 $\phi _1(x) = x$
for
$\phi _1(x) = x$
for
 $x \in G$
, the sumset in Theorem 1.4 simplifies to
$x \in G$
, the sumset in Theorem 1.4 simplifies to
 $A_i$
.
$A_i$
.The question of whether the Theorem 1.4 remains true without the assumption that
 $[G:\phi _1(G)]$
is finite is essentially Question 1.1: we may take
$[G:\phi _1(G)]$
is finite is essentially Question 1.1: we may take
 $\phi _1(x)=0$
and
$\phi _1(x)=0$
and
 $\phi _2(x)=x$
for all
$\phi _2(x)=x$
for all
 $x\in G$
, and the sumset in Theorem 1.4 simplifies to
$x\in G$
, and the sumset in Theorem 1.4 simplifies to
 $A_i-A_i$
.
$A_i-A_i$
. -
• Similar to Theorem 1.2, the hypothesis that the
 $\phi _j$
commute can be removed if one of them is an automorphism.
$\phi _j$
commute can be removed if one of them is an automorphism.
As a consequence of Theorems 1.2 and 1.4, we obtain immediately the following number field generalization of Theorems B and C. In [Reference Le and Lê33], this result was proved (at least for
![]() ${\mathbb {Z}}[i]$
) using a different argument, similar to Bogolyubov and Bergelson-Ruzsa’s proofs of Theorems A and B in
${\mathbb {Z}}[i]$
) using a different argument, similar to Bogolyubov and Bergelson-Ruzsa’s proofs of Theorems A and B in
![]() ${\mathbb {Z}}$
.
${\mathbb {Z}}$
.
Corollary 1.6. Let K be an algebraic number field of degree d and
![]() $\mathcal {O}_K$
be its ring of integers (so the additive group of
$\mathcal {O}_K$
be its ring of integers (so the additive group of
![]() $\mathcal {O}_K$
is isomorphic to
$\mathcal {O}_K$
is isomorphic to
![]() ${\mathbb {Z}}^d$
). Let
${\mathbb {Z}}^d$
). Let
![]() $s_1, s_2, s_3 \in \mathcal {O}_K \setminus \{0\}$
such that
$s_1, s_2, s_3 \in \mathcal {O}_K \setminus \{0\}$
such that
![]() $s_1+s_2+s_3=0$
.
$s_1+s_2+s_3=0$
.
-
(i) If
 $A \subset \mathcal {O}_K$
has
$A \subset \mathcal {O}_K$
has
 $d^*(A)> 0$
, then
$d^*(A)> 0$
, then
 $s_1A + s_2A + s_3A$
contains a Bohr set, whose rank and radius depend only on
$s_1A + s_2A + s_3A$
contains a Bohr set, whose rank and radius depend only on
 $d^*(A)$
and the norms of
$d^*(A)$
and the norms of
 $s_1, s_2, s_3$
.
$s_1, s_2, s_3$
. -
(ii) If
 $\mathcal {O}_K = \bigcup _{i=1}^r A_i$
, then there exists i such that
$\mathcal {O}_K = \bigcup _{i=1}^r A_i$
, then there exists i such that
 $s_1A_i + s_2A_i-s_2A_i$
contains a Bohr set, whose rank and radius depend only on r and the norms of
$s_1A_i + s_2A_i-s_2A_i$
contains a Bohr set, whose rank and radius depend only on r and the norms of
 $s_1$
and
$s_1$
and
 $s_2$
.
$s_2$
.
Bergelson, Furstenberg and Weiss [Reference Bergelson, Furstenberg and Weiss5, Corollary 1.3] showed that if
![]() $B, C \subset {\mathbb {Z}}$
have positive upper Banach density and
$B, C \subset {\mathbb {Z}}$
have positive upper Banach density and
![]() $A \subset {\mathbb {Z}}$
is syndetic, then
$A \subset {\mathbb {Z}}$
is syndetic, then
![]() $B + C + A$
contains a translate of a Bohr set. Here a set
$B + C + A$
contains a translate of a Bohr set. Here a set
![]() $A \subset {\mathbb {Z}}$
is syndetic if a collection of finitely many translates of A covers
$A \subset {\mathbb {Z}}$
is syndetic if a collection of finitely many translates of A covers
![]() ${\mathbb {Z}}$
. Our next theorem not only generalizes Bergelson-Furstenberg-Weiss’s result to countable abelian groups but also strengthens it by only assuming that A arises from an arbitrary partition. Moreover, we provide quantitative bounds on the radius and rank of the Bohr set, a feature not presented in [Reference Bergelson, Furstenberg and Weiss5].
${\mathbb {Z}}$
. Our next theorem not only generalizes Bergelson-Furstenberg-Weiss’s result to countable abelian groups but also strengthens it by only assuming that A arises from an arbitrary partition. Moreover, we provide quantitative bounds on the radius and rank of the Bohr set, a feature not presented in [Reference Bergelson, Furstenberg and Weiss5].
Theorem 1.7. Let G be a countable discrete abelian group and let
![]() $B, C \subset G$
have positive upper Banach density. Then for any partition
$B, C \subset G$
have positive upper Banach density. Then for any partition
![]() $G = \bigcup _{i=1}^r A_i$
, there is an
$G = \bigcup _{i=1}^r A_i$
, there is an
![]() $i \in \{1, \ldots , r\}$
such that
$i \in \{1, \ldots , r\}$
such that
![]() $B + C + A_i$
contains a Bohr-
$B + C + A_i$
contains a Bohr-
![]() $(k, \eta )$
set, where
$(k, \eta )$
set, where
![]() $k, \eta $
depend only on
$k, \eta $
depend only on
![]() $d^*(B), d^*(C)$
and r.
$d^*(B), d^*(C)$
and r.
We deduce Theorems 1.2, 1.4 and 1.7 from their counterparts for compact abelian groups (i.e., Theorems D and 10.1). However, the latter can be used as black boxes and the reader does not need to know their inner workings. The heavy lifting of this paper is done by correspondence principles, which state that sumsets in discrete abelian groups can be modeled by sumsets in compact abelian groups. This strategy dates back at least to Furstenberg’s correspondence principle [Reference Furstenberg17], used in his proof of Szemerédi’s theorem. However, to accommodate the three different kinds of sumsets in our results, we need three different correspondence principles. These are Proposition 6.2, Proposition 7.1 and Proposition 9.6.
Our bounds for k and
![]() $\eta $
in Theorems 1.2, 1.4 and 1.7 are transferred from and have the same quality as their compact analogues. Since the proof of Theorem D (i) relies on a regularity lemma, the bounds in Theorem 1.2 are of tower type. The proof of Theorem D(ii) relies on the Hales-Jewett theorem, so the bounds in Theorem 1.4 are extremely poor (albeit still primitive recursive). As for Theorem 1.7, we get more appealing bounds of the form
$\eta $
in Theorems 1.2, 1.4 and 1.7 are transferred from and have the same quality as their compact analogues. Since the proof of Theorem D (i) relies on a regularity lemma, the bounds in Theorem 1.2 are of tower type. The proof of Theorem D(ii) relies on the Hales-Jewett theorem, so the bounds in Theorem 1.4 are extremely poor (albeit still primitive recursive). As for Theorem 1.7, we get more appealing bounds of the form
![]() $\eta = \Omega ( d^*(B) d^*(C) r^{-1})$
and
$\eta = \Omega ( d^*(B) d^*(C) r^{-1})$
and
![]() $k = O( d^*(B)^{-2} d^*(C)^{-2} r^2)$
, though these may not be optimal (see Question 11.2).
$k = O( d^*(B)^{-2} d^*(C)^{-2} r^2)$
, though these may not be optimal (see Question 11.2).
1.4 Main ideas of the proofs
Here we outline the obstacles to proving Theorems 1.2, 1.4 and 1.7 and our strategies for overcoming them. We will use notation and terminology defined in Section 2.
Theorem 1.2 : To prove the first theorem, we find a parameterized solution to the relation
For instance, w will satisfy (2) if
Then Furstenberg’s correspondence principle is applied to show that the set of such w contains the support of the multilinear ergodic average:
where
![]() $(X, \mu , T)$
is an ergodic G-system and
$(X, \mu , T)$
is an ergodic G-system and
![]() $f: X \to [0, 1]$
is a measurable function with
$f: X \to [0, 1]$
is a measurable function with
![]() $\int _X f \, d \mu = d^*(A)$
. As shown in [Reference Ackelsberg, Bergelson and Best2], the Kronecker factor
$\int _X f \, d \mu = d^*(A)$
. As shown in [Reference Ackelsberg, Bergelson and Best2], the Kronecker factor
![]() $(Z, m_Z, R)$
is characteristic for the average in (3) and so
$(Z, m_Z, R)$
is characteristic for the average in (3) and so
where
![]() $\tilde {f}:Z\to [0,1]$
satisfies
$\tilde {f}:Z\to [0,1]$
satisfies
![]() $\int \tilde {f}\, dm_Z =\int f\, d\mu $
(see Section 2.2 for the definition of
$\int \tilde {f}\, dm_Z =\int f\, d\mu $
(see Section 2.2 for the definition of
![]() $UC-\lim $
). In order to utilize the corresponding result in compact groups [Reference Le and Lê33], we need to show that the homomorphisms
$UC-\lim $
). In order to utilize the corresponding result in compact groups [Reference Le and Lê33], we need to show that the homomorphisms
![]() $\phi _1, \phi _2, \phi _3$
induce homomorphisms
$\phi _1, \phi _2, \phi _3$
induce homomorphisms
![]() $\tilde {\phi }_j$
on Z satisfying
$\tilde {\phi }_j$
on Z satisfying
![]() $\tilde {\phi }_j \circ \tau = \tau \circ \phi _j$
, where
$\tilde {\phi }_j \circ \tau = \tau \circ \phi _j$
, where
![]() $\tau $
is a natural embedding of G in Z. This is straightforward under the additional assumption that the spectrum of
$\tau $
is a natural embedding of G in Z. This is straightforward under the additional assumption that the spectrum of
![]() $(X, \mu , T)$
(i.e., the group of eigenvalues) is closed under each
$(X, \mu , T)$
(i.e., the group of eigenvalues) is closed under each
![]() $\phi _j$
. However, the spectrum of
$\phi _j$
. However, the spectrum of
![]() $(X,\mu ,T)$
will not, in general, be closed under the
$(X,\mu ,T)$
will not, in general, be closed under the
![]() $\phi _j$
.
$\phi _j$
.
To overcome this problem, we find an ergodic extension
![]() $(Y, \nu , S)$
of
$(Y, \nu , S)$
of
![]() $(X, \mu , T)$
such that the spectrum of
$(X, \mu , T)$
such that the spectrum of
![]() $(Y,\nu ,S)$
contains a subgroup
$(Y,\nu ,S)$
contains a subgroup
![]() $\Gamma $
which extends the spectrum of
$\Gamma $
which extends the spectrum of
![]() $(X,\mu ,T)$
and is invariant under each
$(X,\mu ,T)$
and is invariant under each
![]() $\phi _j$
. After lifting f to Y, the Kronecker factor
$\phi _j$
. After lifting f to Y, the Kronecker factor
![]() $\mathbf Z$
of
$\mathbf Z$
of
![]() $\mathbf X$
can be viewed as a factor of
$\mathbf X$
can be viewed as a factor of
![]() $\mathbf Y$
and is still characteristic for the averages in (3). Thus, any extension of
$\mathbf Y$
and is still characteristic for the averages in (3). Thus, any extension of
![]() $\mathbf Z$
in
$\mathbf Z$
in
![]() $\mathbf Y$
will also be characteristic for these averages. The group rotation factor
$\mathbf Y$
will also be characteristic for these averages. The group rotation factor
![]() $\mathbf {K}$
of
$\mathbf {K}$
of
![]() $\mathbf Y$
corresponding to
$\mathbf Y$
corresponding to
![]() $\Gamma $
is such an extension of
$\Gamma $
is such an extension of
![]() $\mathbf Z$
, and this allows us to transfer the Bohr sets obtained in [Reference Le and Lê33] to G. Figure 1 demonstrates the relations among
$\mathbf Z$
, and this allows us to transfer the Bohr sets obtained in [Reference Le and Lê33] to G. Figure 1 demonstrates the relations among
![]() $\mathbf {X}, \mathbf {Y}, \mathbf {Z}$
and
$\mathbf {X}, \mathbf {Y}, \mathbf {Z}$
and
![]() $\mathbf {K}$
where
$\mathbf {K}$
where
![]() $\mathbf {Y} \to \mathbf {X}$
means
$\mathbf {Y} \to \mathbf {X}$
means
![]() $\mathbf {Y}$
is an extension of
$\mathbf {Y}$
is an extension of
![]() $\mathbf {X}$
.
$\mathbf {X}$
.

Figure 1 Relations among X, Y, Z, and K.
Theorem 1.4
: In contrast to the sumset
![]() $\phi _1(A) + \phi _2(A) + \phi _3(A)$
, a parametrized solution to
$\phi _1(A) + \phi _2(A) + \phi _3(A)$
, a parametrized solution to
![]() $\phi _2(w) \in \phi _1(A) + \phi _2(A) - \phi _2(A)$
is
$\phi _2(w) \in \phi _1(A) + \phi _2(A) - \phi _2(A)$
is
The absence of the variable u in the first function prohibits us from using Furstenberg’s correspondence principle as we do in the Proof of Theorem 1.2. Instead, we use Proposition 7.1, which models the relevant sumsets by convolutions on the Bohr compactification of G. This idea was used in [Reference Björklund10] to express
![]() $A+A-A$
in terms of convolutions on a compact group. Parts of this process also already appeared in Følner’s works [Reference Følner15, Reference Følner16].
$A+A-A$
in terms of convolutions on a compact group. Parts of this process also already appeared in Følner’s works [Reference Følner15, Reference Følner16].
Specifically, we fix an invariant mean
![]() $\nu $
on G with
$\nu $
on G with
![]() $d^*(A)=\nu (1_A)$
, and observe that the difference set
$d^*(A)=\nu (1_A)$
, and observe that the difference set
![]() $A-A$
contains the support of the convolution
$A-A$
contains the support of the convolution
![]() $1_A*_{\nu } 1_{-A}(t):= \nu (1_A 1_{A + t})$
. This convolution is easily verified to be a positive definite function on G, which can therefore be represented as a Fourier transform of a positive measure
$1_A*_{\nu } 1_{-A}(t):= \nu (1_A 1_{A + t})$
. This convolution is easily verified to be a positive definite function on G, which can therefore be represented as a Fourier transform of a positive measure
![]() $\sigma $
on
$\sigma $
on
![]() $\widehat {G}$
. The continuous part of
$\widehat {G}$
. The continuous part of
![]() $\sigma $
can be ignored, allowing us to expand
$\sigma $
can be ignored, allowing us to expand
![]() $1_A*_{\nu } 1_{-A}(t)$
as a Fourier series and express
$1_A*_{\nu } 1_{-A}(t)$
as a Fourier series and express
![]() $A+A-A$
in terms of a convolution
$A+A-A$
in terms of a convolution
![]() $h_A*h_A*h_{-A}$
on
$h_A*h_A*h_{-A}$
on
![]() $bG$
, the Bohr compactification of G.
$bG$
, the Bohr compactification of G.
To study the more complicated expression
![]() $\phi _1(A) + \phi _2(A)-\phi _2(A)$
, we need to investigate the relationship between
$\phi _1(A) + \phi _2(A)-\phi _2(A)$
, we need to investigate the relationship between
![]() $1_A*_{\nu } 1_{-A}$
and
$1_A*_{\nu } 1_{-A}$
and
![]() $1_{\phi _2(A)}*_{\nu } 1_{-\phi _2(A)}$
. This investigation leads to the introduction of Radon-Nikodym densities
$1_{\phi _2(A)}*_{\nu } 1_{-\phi _2(A)}$
. This investigation leads to the introduction of Radon-Nikodym densities
![]() $\rho _{A}^{\nu }, \rho _{\phi _2(A)}^{\nu }$
and their relationship in Section 4. After the required relationship is established, we put all ingredients together (Proposition 7.1, Corollary 4.10) and use the compact counterpart in [Reference Le and Lê33] to prove Theorem 1.4.
$\rho _{A}^{\nu }, \rho _{\phi _2(A)}^{\nu }$
and their relationship in Section 4. After the required relationship is established, we put all ingredients together (Proposition 7.1, Corollary 4.10) and use the compact counterpart in [Reference Le and Lê33] to prove Theorem 1.4.
Theorem 1.7 : This last theorem relies on two ingredients:
-
(i) an estimate for the rank and radius of a Bohr set in sumsets of the form
 $B+C+A_i$
, where
$B+C+A_i$
, where
 $B, C$
are subsets of a compact abelian group K and
$B, C$
are subsets of a compact abelian group K and
 $K= \bigcup _{i=1}^r A_i$
. We bound the rank and radius in terms of
$K= \bigcup _{i=1}^r A_i$
. We bound the rank and radius in terms of
 $m_K(B)$
,
$m_K(B)$
,
 $m_K(C)$
and r, using the pigeonhole principle and elementary estimates on Fourier coefficients.
$m_K(C)$
and r, using the pigeonhole principle and elementary estimates on Fourier coefficients. -
(ii) a correspondence principle relating the expression
 $B+C+A_i$
in a discrete abelian group to an analogous expression in a compact abelian group.
$B+C+A_i$
in a discrete abelian group to an analogous expression in a compact abelian group.
The two correspondence principles previously mentioned do not apply to the expression
![]() $B+C+A_i$
; see Remark 1.8. Instead, we use a result from [Reference Griesmer25] which exhibits piecewise Bohr structure in
$B+C+A_i$
; see Remark 1.8. Instead, we use a result from [Reference Griesmer25] which exhibits piecewise Bohr structure in
![]() $B + C$
. This allows us to relate
$B + C$
. This allows us to relate
![]() $B+C+A_i$
to a convolution
$B+C+A_i$
to a convolution
![]() $h_B*h_C*h_{A_i}$
on a compact group K, where each of these functions takes values in
$h_B*h_C*h_{A_i}$
on a compact group K, where each of these functions takes values in
![]() $[0,1]$
,
$[0,1]$
,
![]() $\int h_B\, dm_K \geq d^*(B)$
,
$\int h_B\, dm_K \geq d^*(B)$
,
![]() $\int h_C\, dm_K\geq d^*(C)$
, and
$\int h_C\, dm_K\geq d^*(C)$
, and
![]() $\sum _{i=1}^r h_{A_i}\geq 1_K$
.
$\sum _{i=1}^r h_{A_i}\geq 1_K$
.
Remark 1.8. None of the three correspondence principles outlined above subsumes the others. The sumset
![]() $\phi _1(A) + \phi _2(A) + \phi _3(A)$
with
$\phi _1(A) + \phi _2(A) + \phi _3(A)$
with
![]() $\phi _1 + \phi _2 + \phi _3 = 0$
is translation invariant (replacing A with a translate of A does not affect this sumset) and so a straightforward application of Furstenberg’s correspondence principle suffices. The second sumset
$\phi _1 + \phi _2 + \phi _3 = 0$
is translation invariant (replacing A with a translate of A does not affect this sumset) and so a straightforward application of Furstenberg’s correspondence principle suffices. The second sumset
![]() $\phi _1(A) + \phi _2(A) - \phi _2(A)$
is no longer translation invariant and hence requires a different correspondence principle. Since the last sumset
$\phi _1(A) + \phi _2(A) - \phi _2(A)$
is no longer translation invariant and hence requires a different correspondence principle. Since the last sumset
![]() $B + C + A_i$
is neither translation invariant nor has the form
$B + C + A_i$
is neither translation invariant nor has the form
![]() $A + B - B$
, we need yet another correspondence principle. Conversely, one cannot use the third principle for the first two sums since this principle does not retain the relations among the summands which are present in the fact that
$A + B - B$
, we need yet another correspondence principle. Conversely, one cannot use the third principle for the first two sums since this principle does not retain the relations among the summands which are present in the fact that
![]() $\phi _1(A), \phi _2(A), \phi _3(A)$
are images of the same set A.
$\phi _1(A), \phi _2(A), \phi _3(A)$
are images of the same set A.
1.5 Outline of the article
In Section 2, we set up notation and present some basic facts about measure preserving systems, Bohr compactifications, Kronecker factors, etc. In Section 3, we describe a general construction of homomorphisms from discrete groups into compact groups with dense image. This construction is used in the proofs of all of our results. Section 4 is devoted to transferring functions on discrete groups to compact groups, an ingredient used in the proofs of Theorems 1.4 and 1.7. After these preliminaries, Theorem 1.2 is proved in Sections 5 and 6, then Theorem 1.4 is proved in Sections 7 and 8. We prove the correspondence principle needed for Theorem 1.7 in Section 9 and establish the theorem in Section 10. Lastly, we present some open questions in Section 11.
2 Background
2.1 Notation and convention
Throughout this paper, G is a countable discrete abelian group, and K is used to denote a compact Hausdorff abelian group. We use
![]() $m_K$
to denote the unique probability Haar measure on K. The set of all continuous functions on K is denoted by
$m_K$
to denote the unique probability Haar measure on K. The set of all continuous functions on K is denoted by
![]() $C(K)$
.
$C(K)$
.
For
![]() $r \in \mathbb {N}$
, we use
$r \in \mathbb {N}$
, we use
![]() $[r]$
to denote
$[r]$
to denote
![]() $\{1, 2, \ldots , r\}$
. By the support of a function f, denoted by
$\{1, 2, \ldots , r\}$
. By the support of a function f, denoted by
![]() $\operatorname {supp} f$
, we mean
$\operatorname {supp} f$
, we mean
![]() $\{ x : f(x) \neq 0\}$
.
$\{ x : f(x) \neq 0\}$
.
2.2 Følner sequences and uniform Cesàro averages
A sequence
![]() $\mathbf {F} = (F_N)_{N \in \mathbb {N}}$
of finite subsets of G is a Følner sequence if for all
$\mathbf {F} = (F_N)_{N \in \mathbb {N}}$
of finite subsets of G is a Følner sequence if for all
![]() $g \in G$
,
$g \in G$
,
Every countable abelian group admits a Følner sequence. This is due to the fact that all discrete abelian groups are amenable, and having a Følner sequence is one of the many equivalent definitions of amenability for countable discrete groups (see [Reference Pier30]).
If
![]() $\mathbf {F}$
is a Følner sequence and
$\mathbf {F}$
is a Følner sequence and
![]() $A \subset G$
, the upper density of A with respect to
$A \subset G$
, the upper density of A with respect to
![]() $\mathbf {F}$
is
$\mathbf {F}$
is
The upper Banach density of A is
(for a proof that the definitions (1) and (5) are equivalent, see [Reference Björklund and Fish9, Proposition A.6]).
Let
![]() $u: G \to \mathbb {C}$
be a bounded sequence. We say
$u: G \to \mathbb {C}$
be a bounded sequence. We say
![]() $(u(g))_{g \in G}$
has a uniform Cesàro average if for every Følner sequence
$(u(g))_{g \in G}$
has a uniform Cesàro average if for every Følner sequence
![]() $(F_N)_{N \in \mathbb {N}}$
, the limit
$(F_N)_{N \in \mathbb {N}}$
, the limit
 $$ \begin{align*} \lim_{N \to \infty} \frac{1}{|F_N|} \sum_{n \in F_N} u(g) \end{align*} $$
$$ \begin{align*} \lim_{N \to \infty} \frac{1}{|F_N|} \sum_{n \in F_N} u(g) \end{align*} $$
exists and is independent of the choice of Følner sequence. In this case, we denote the common limit by
![]() $UC-\lim _{g \in G} u(g)$
.
$UC-\lim _{g \in G} u(g)$
.
2.3 Measure preserving systems
A measure preserving G-system (or G-system) is a quadruple
![]() $\mathbf {X} = (X, \mathcal {B}, \mu , T)$
, where
$\mathbf {X} = (X, \mathcal {B}, \mu , T)$
, where
![]() $(X, \mathcal {B}, \mu )$
is a probability space and G acts on X by transformations
$(X, \mathcal {B}, \mu )$
is a probability space and G acts on X by transformations
![]() $T_g$
which preserve
$T_g$
which preserve
![]() $\mu $
; that is,
$\mu $
; that is,
for all measurable
![]() $A \subset X$
and all
$A \subset X$
and all
![]() $g \in G$
. In this paper, all probability spaces underlying G-systems are assumed to be separable; that is,
$g \in G$
. In this paper, all probability spaces underlying G-systems are assumed to be separable; that is,
![]() $\mathcal {B}$
is countably generated modulo null sets, or equivalently,
$\mathcal {B}$
is countably generated modulo null sets, or equivalently,
![]() $L^p(X, \mathcal {B}, \mu )$
is separable for all
$L^p(X, \mathcal {B}, \mu )$
is separable for all
![]() $1\leq p < \infty $
. In particular, if X is a compact metric space,
$1\leq p < \infty $
. In particular, if X is a compact metric space,
![]() $\mathcal {B}$
is its Borel
$\mathcal {B}$
is its Borel
![]() $\sigma $
-algebra and
$\sigma $
-algebra and
![]() $\mu $
is any probability measure on
$\mu $
is any probability measure on
![]() $\mathcal {B}$
, then
$\mathcal {B}$
, then
![]() $(X, \mathcal {B}, \mu )$
is separable. When there is no danger of confusion, we will suppress the
$(X, \mathcal {B}, \mu )$
is separable. When there is no danger of confusion, we will suppress the
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal B$
and write
$\mathcal B$
and write
![]() $(X, \mu , T)$
for a G-system. We abbreviate G-systems with boldface letters:
$(X, \mu , T)$
for a G-system. We abbreviate G-systems with boldface letters:
![]() $\mathbf X=(X,\mu ,T)$
.
$\mathbf X=(X,\mu ,T)$
.
The G-system
![]() $(X, \mathcal {B}, \mu , T)$
is said to be ergodic if
$(X, \mathcal {B}, \mu , T)$
is said to be ergodic if
![]() $\mu (A \triangle T_g^{-1} A)=0$
for all
$\mu (A \triangle T_g^{-1} A)=0$
for all
![]() $g \in G$
implies
$g \in G$
implies
![]() $\mu (A) = 0$
or
$\mu (A) = 0$
or
![]() $\mu (A)=1$
.
$\mu (A)=1$
.
If
![]() $f \in L^2(\mu )$
and
$f \in L^2(\mu )$
and
![]() $g \in G$
, we write
$g \in G$
, we write
![]() $T_g f$
for
$T_g f$
for
![]() $f \circ T_g$
. This defines an action of G on
$f \circ T_g$
. This defines an action of G on
![]() $L^2(\mu )$
by unitary operators
$L^2(\mu )$
by unitary operators
![]() $T_g$
.
$T_g$
.
A G-system
![]() $\mathbf {Y} = (Y, \mathcal {D}, \nu , S)$
together with a map
$\mathbf {Y} = (Y, \mathcal {D}, \nu , S)$
together with a map
![]() $\pi : X\to Y$
defined for
$\pi : X\to Y$
defined for
![]() $\mu -$
almost every
$\mu -$
almost every
![]() $x \in X$
is a factor of
$x \in X$
is a factor of
![]() $\mathbf {X} = (X, \mathcal {B}, \mu , T)$
if
$\mathbf {X} = (X, \mathcal {B}, \mu , T)$
if
![]() $\pi _* \mu = \nu $
(i.e.
$\pi _* \mu = \nu $
(i.e.
![]() $\mu ( \pi ^{-1}(A)) = \nu (A)$
for all
$\mu ( \pi ^{-1}(A)) = \nu (A)$
for all
![]() $A \in \mathcal {D}$
) and for all
$A \in \mathcal {D}$
) and for all
![]() $g \in G$
,
$g \in G$
,
The map
![]() $\pi $
is called a factor map. The space
$\pi $
is called a factor map. The space
![]() $L^2(\nu )$
can be identified with the subspace of
$L^2(\nu )$
can be identified with the subspace of
![]() $L^2(\mu )$
consisting of functions of the form
$L^2(\mu )$
consisting of functions of the form
![]() $h \circ \pi $
, where
$h \circ \pi $
, where
![]() $h \in L^2(\nu )$
. We use
$h \in L^2(\nu )$
. We use
![]() $\mathbb {E}(\cdot |Y): L^2(\mu ) \to L^2(\nu )$
to denote the corresponding orthogonal projection. Later we abuse notation and write ‘
$\mathbb {E}(\cdot |Y): L^2(\mu ) \to L^2(\nu )$
to denote the corresponding orthogonal projection. Later we abuse notation and write ‘
![]() $\mathbf Y$
is a factor of
$\mathbf Y$
is a factor of
![]() $\mathbf X$
’ instead of ‘
$\mathbf X$
’ instead of ‘
![]() $(\mathbf Y,\pi )$
is a factor of
$(\mathbf Y,\pi )$
is a factor of
![]() $\mathbf X$
’.
$\mathbf X$
’.
For a Følner sequence
![]() $(F_N)_{N \in \mathbb {N}}$
in G, functions
$(F_N)_{N \in \mathbb {N}}$
in G, functions
![]() $f_0, \ldots , f_k \in L^{\infty }(\mu )$
and sequences
$f_0, \ldots , f_k \in L^{\infty }(\mu )$
and sequences
![]() $s_1, \ldots , s_k: G \to G$
, we say the factor
$s_1, \ldots , s_k: G \to G$
, we say the factor
![]() $\mathbf Y$
is characteristic for the average
$\mathbf Y$
is characteristic for the average
 $$\begin{align*}I := \lim_{N \to \infty} \frac{1}{|F_N|} \sum_{g \in F_N} \int_X f_0 \cdot T_{s_1(g)} f_1 \cdots T_{s_k(g)} f_k \, d \mu \end{align*}$$
$$\begin{align*}I := \lim_{N \to \infty} \frac{1}{|F_N|} \sum_{g \in F_N} \int_X f_0 \cdot T_{s_1(g)} f_1 \cdots T_{s_k(g)} f_k \, d \mu \end{align*}$$
if
 $$\begin{align*}I = \lim_{N \to \infty} \frac{1}{|F_N|} \sum_{g \in F_N} \int_Y \tilde{f}_0 \cdot T_{s_1(g)} \tilde{f}_1 \cdots T_{s_k(g)} \tilde{f}_k \, d \nu, \end{align*}$$
$$\begin{align*}I = \lim_{N \to \infty} \frac{1}{|F_N|} \sum_{g \in F_N} \int_Y \tilde{f}_0 \cdot T_{s_1(g)} \tilde{f}_1 \cdots T_{s_k(g)} \tilde{f}_k \, d \nu, \end{align*}$$
where
![]() $\tilde {f}_i = \mathbb {E}(f_i|Y)$
.
$\tilde {f}_i = \mathbb {E}(f_i|Y)$
.
Let
![]() $\widehat {G}$
denote the Pontryagin dual of G (i.e., the group of characters
$\widehat {G}$
denote the Pontryagin dual of G (i.e., the group of characters
![]() $\chi : G \to S^1$
with the operation of pointwise multiplication). A character
$\chi : G \to S^1$
with the operation of pointwise multiplication). A character
![]() $\chi \in \widehat {G}$
is called an eigenvalue of
$\chi \in \widehat {G}$
is called an eigenvalue of
![]() $\mathbf {X}$
if there exists a nonzero function
$\mathbf {X}$
if there exists a nonzero function
![]() $f \in L^2(\mu )$
such that
$f \in L^2(\mu )$
such that
![]() $T_g f = \chi (g) f$
for all
$T_g f = \chi (g) f$
for all
![]() $g \in G$
. The set of all eigenvalues for
$g \in G$
. The set of all eigenvalues for
![]() $\mathbf {X}$
forms a subgroup of
$\mathbf {X}$
forms a subgroup of
![]() $\widehat {G}$
, called the spectrum of
$\widehat {G}$
, called the spectrum of
![]() $\mathbf {X}$
and denoted by
$\mathbf {X}$
and denoted by
![]() $\mathcal {E}(\mathbf {X})$
. If
$\mathcal {E}(\mathbf {X})$
. If
![]() $\mathbf {Y}$
is a factor of
$\mathbf {Y}$
is a factor of
![]() $\mathbf {X}$
, then
$\mathbf {X}$
, then
![]() $\mathcal {E}(\mathbf {Y})$
is a subgroup of
$\mathcal {E}(\mathbf {Y})$
is a subgroup of
![]() $\mathcal {E}(\mathbf {X})$
. If
$\mathcal {E}(\mathbf {X})$
. If
![]() $\mathbf {X}$
is ergodic, then all eigenspaces are one-dimensional and mutually orthogonal (for a proof, see [Reference Walters39, Theorem 3.1]). Since
$\mathbf {X}$
is ergodic, then all eigenspaces are one-dimensional and mutually orthogonal (for a proof, see [Reference Walters39, Theorem 3.1]). Since
![]() $L^2(\mu )$
is separable,
$L^2(\mu )$
is separable,
![]() $\mathcal {E}(\mathbf {X})$
is at most countable.
$\mathcal {E}(\mathbf {X})$
is at most countable.
2.4 Kronecker factors
A group rotation G-system is a G-system
![]() $\mathbf {K} = (K, m_K, R)$
in which
$\mathbf {K} = (K, m_K, R)$
in which
-
• K is a compact metrizable abelian group with Borel
 $\sigma $
-algebra
$\sigma $
-algebra
 $\mathcal K$
, probability Haar measure
$\mathcal K$
, probability Haar measure
 $m_K$
and
$m_K$
and -
• there is a homomorphism
 $\tau : G \to K$
such
$\tau : G \to K$
such
 $R_g(z) = z + \tau (g)$
for all
$R_g(z) = z + \tau (g)$
for all
 $z \in K$
and
$z \in K$
and
 $g \in G$
.
$g \in G$
.
The group rotation
![]() $(K, m_K, R)$
is ergodic if and only if
$(K, m_K, R)$
is ergodic if and only if
![]() $\tau (G)$
is dense in K. In this case,
$\tau (G)$
is dense in K. In this case,
![]() $(K, m_K, R)$
is, in fact, uniquely ergodic (i.e.,
$(K, m_K, R)$
is, in fact, uniquely ergodic (i.e.,
![]() $m_K$
is the unique R-invariant probability measure on K) (for a proof, see [Reference Ackelsberg, Bergelson and Best2, Lemma 2.4]). Consequently, the sequence
$m_K$
is the unique R-invariant probability measure on K) (for a proof, see [Reference Ackelsberg, Bergelson and Best2, Lemma 2.4]). Consequently, the sequence
![]() $(\tau (g))_{g \in G}$
is well-distributed in K; that is, for every continuous function
$(\tau (g))_{g \in G}$
is well-distributed in K; that is, for every continuous function
![]() $h \in C(K)$
,
$h \in C(K)$
,
For an ergodic G-system
![]() $\mathbf {X}$
, its Kronecker factor
$\mathbf {X}$
, its Kronecker factor
![]() $\mathbf {K} = (K,m_K,R)$
is a factor of
$\mathbf {K} = (K,m_K,R)$
is a factor of
![]() $\mathbf {X}$
with factor map
$\mathbf {X}$
with factor map
![]() $\pi : X\to K$
such that
$\pi : X\to K$
such that
![]() $L^2(m_K)$
is spanned by the eigenfunctions of
$L^2(m_K)$
is spanned by the eigenfunctions of
![]() $\mathbf {X}$
, meaning:
$\mathbf {X}$
, meaning:
-
(i) every eigenfunction
 $f\in L^2(\mu )$
is equal
$f\in L^2(\mu )$
is equal
 $\mu $
-a.e. to
$\mu $
-a.e. to
 $\tilde {f}\circ \pi $
for some eigenfunction
$\tilde {f}\circ \pi $
for some eigenfunction
 $\tilde {f}\in L^2(m_K)$
, and
$\tilde {f}\in L^2(m_K)$
, and -
(ii) the span of the eigenfunctions of
 $\mathbf {K}$
is dense in
$\mathbf {K}$
is dense in
 $L^2(m_K)$
.
$L^2(m_K)$
.
It can be shown that
![]() $\mathbf {K}$
is the largest factor of
$\mathbf {K}$
is the largest factor of
![]() $\mathbf {X}$
that is isomorphic to an ergodic group rotation G-system. More concretely,
$\mathbf {X}$
that is isomorphic to an ergodic group rotation G-system. More concretely,
![]() $\mathbf {K} = (K, m_K, R)$
, where
$\mathbf {K} = (K, m_K, R)$
, where
![]() $K= \widehat {\mathcal {E}(\mathbf {X})}$
(see Lemma 3.3 (iii)).
$K= \widehat {\mathcal {E}(\mathbf {X})}$
(see Lemma 3.3 (iii)).
Let
![]() $(X, \mu , T)$
be an ergodic G-system with Kronecker factor
$(X, \mu , T)$
be an ergodic G-system with Kronecker factor
![]() $(K, m_K,R)$
and
$(K, m_K,R)$
and
![]() $f_1, f_2, f_3\in L^{\infty }(X)$
. It is shown in [Reference Ackelsberg, Bergelson and Best2, Theorem 3.1] that if
$f_1, f_2, f_3\in L^{\infty }(X)$
. It is shown in [Reference Ackelsberg, Bergelson and Best2, Theorem 3.1] that if
![]() $\phi , \psi : G \to G$
are homomorphisms such that
$\phi , \psi : G \to G$
are homomorphisms such that
![]() $\phi (G)$
,
$\phi (G)$
,
![]() $\psi (G)$
, and
$\psi (G)$
, and
![]() $(\psi -\phi )(G)$
each have finite index in G,
$(\psi -\phi )(G)$
each have finite index in G,
exists and is equal to
where
![]() $\tilde {f}_i=\mathbb {E}(f_i|K)$
is projection of
$\tilde {f}_i=\mathbb {E}(f_i|K)$
is projection of
![]() $f_i$
onto
$f_i$
onto
![]() $L^2(m_K)$
. In other words, the Kronecker factor is characteristic for the average in (7).
$L^2(m_K)$
. In other words, the Kronecker factor is characteristic for the average in (7).
2.5 Invariant means
If
![]() $f \in \ell ^{\infty }(G)$
and
$f \in \ell ^{\infty }(G)$
and
![]() $t \in G$
, define
$t \in G$
, define
![]() $f_t\in \ell ^{\infty }(G)$
by
$f_t\in \ell ^{\infty }(G)$
by
![]() $f_t(s) := f(s - t)$
. An invariant mean on G is a positive linear functional
$f_t(s) := f(s - t)$
. An invariant mean on G is a positive linear functional
![]() $\nu : \ell ^{\infty }(G) \to \mathbb {C}$
such that
$\nu : \ell ^{\infty }(G) \to \mathbb {C}$
such that
![]() $\nu (1_G) = 1$
and
$\nu (1_G) = 1$
and
![]() $\nu (f_t) = \nu (f)$
for every
$\nu (f_t) = \nu (f)$
for every
![]() $f \in \ell ^{\infty }(G)$
,
$f \in \ell ^{\infty }(G)$
,
![]() $t \in G$
.
$t \in G$
.
In the weak
![]() $^*$
topology on
$^*$
topology on
![]() $\ell ^{\infty }(G)^*$
, the space
$\ell ^{\infty }(G)^*$
, the space
![]() $M(G)$
of invariant means forms a compact convex set. An invariant mean
$M(G)$
of invariant means forms a compact convex set. An invariant mean
![]() $\nu $
is said to be extremal, or an extreme point, if it cannot be written as a convex linear combination of two other invariant means.
$\nu $
is said to be extremal, or an extreme point, if it cannot be written as a convex linear combination of two other invariant means.
Bauer’s maximum principle [Reference Aliprantis and Border1, 7.69] implies that if C is a compact convex subset of a locally convex Hausdorff space, then every real-valued continuous linear functional on C has a maximizer that is an extreme point. Thus, if
![]() $A \subset G$
, there is an extremal invariant mean
$A \subset G$
, there is an extremal invariant mean
![]() $\nu $
such that
$\nu $
such that
![]() $d^*(A) = \nu (1_A)$
.
$d^*(A) = \nu (1_A)$
.
Let H be a countable abelian group and
![]() $\phi : G \to H$
be a surjective homomorphism. For any invariant mean
$\phi : G \to H$
be a surjective homomorphism. For any invariant mean
![]() $\nu $
on G, the pushforward
$\nu $
on G, the pushforward
![]() $\phi _* \nu $
is an invariant mean on H and is defined by
$\phi _* \nu $
is an invariant mean on H and is defined by
for all
![]() $h \in \ell ^{\infty }(H)$
. Given
$h \in \ell ^{\infty }(H)$
. Given
![]() $f \in \ell ^{\infty }(G)$
and an invariant mean
$f \in \ell ^{\infty }(G)$
and an invariant mean
![]() $\nu $
, we sometimes write
$\nu $
, we sometimes write
![]() $\int _G f(t) \, d \nu (t)$
instead of
$\int _G f(t) \, d \nu (t)$
instead of
![]() $\nu (f)$
. If
$\nu (f)$
. If
![]() $g \in \ell ^{\infty }(G)$
, we define the ‘convolution’ of f and g with respect to
$g \in \ell ^{\infty }(G)$
, we define the ‘convolution’ of f and g with respect to
![]() $\nu $
by
$\nu $
by
In conventional notation, this could be written as
![]() $f*_{\nu } g:=\nu ((g')_t f)$
, where
$f*_{\nu } g:=\nu ((g')_t f)$
, where
![]() $g'(x):=g(-x)$
. The following lemma is a special case of [Reference Björklund and Fish9, Proposition 2.1].
$g'(x):=g(-x)$
. The following lemma is a special case of [Reference Björklund and Fish9, Proposition 2.1].
Lemma 2.1. If
![]() $\lambda $
is an extremal invariant mean on G and
$\lambda $
is an extremal invariant mean on G and
![]() $f, g \in \ell ^{\infty }(G)$
, then
$f, g \in \ell ^{\infty }(G)$
, then
for every invariant mean
![]() $\mu $
on G.
$\mu $
on G.
For completeness, we include a proof.
Proof. It suffices to prove (8) for
![]() $0 \leq f \leq 1$
. When
$0 \leq f \leq 1$
. When
![]() $\lambda (f) = 0$
or 1, it is straightforward to check (8). Suppose
$\lambda (f) = 0$
or 1, it is straightforward to check (8). Suppose
![]() $ \lambda (f) = \alpha \in (0,1)$
. Define two invariant means
$ \lambda (f) = \alpha \in (0,1)$
. Define two invariant means
![]() $\eta $
and
$\eta $
and
![]() $\eta '$
by
$\eta '$
by
Then it is easy to check that
![]() $\lambda (g) = \alpha \eta (g) + (1-\alpha ) \eta '(g)$
. Since
$\lambda (g) = \alpha \eta (g) + (1-\alpha ) \eta '(g)$
. Since
![]() $\lambda $
is extremal, we must have
$\lambda $
is extremal, we must have
![]() $\eta =\eta ' = \lambda $
, and we are done.
$\eta =\eta ' = \lambda $
, and we are done.
2.6 Bohr compactification
The Bohr compactification of G is a compact abelian group
![]() $bG$
, together with a homomorphism
$bG$
, together with a homomorphism
![]() $\tau : G \to bG$
such that
$\tau : G \to bG$
such that
![]() $\tau (G)$
is dense in
$\tau (G)$
is dense in
![]() $bG$
and every character
$bG$
and every character
![]() $\chi \in \widehat {G}$
can be written as
$\chi \in \widehat {G}$
can be written as
![]() $\chi = \chi ' \circ \tau $
, where
$\chi = \chi ' \circ \tau $
, where
![]() $\chi '$
is a continuous homomorphism from
$\chi '$
is a continuous homomorphism from
![]() $bG$
to
$bG$
to
![]() $S^1$
. The homomorphism
$S^1$
. The homomorphism
![]() $\tau $
is universal with respect to homomorphisms into compact Hausdorff groups; that is, if K is another compact Hausdorff group and
$\tau $
is universal with respect to homomorphisms into compact Hausdorff groups; that is, if K is another compact Hausdorff group and
![]() $\pi : G \to K$
is a homomorphism, then there is a unique continuous homomorphism
$\pi : G \to K$
is a homomorphism, then there is a unique continuous homomorphism
![]() $\tilde {\pi }: bG \to K$
such that
$\tilde {\pi }: bG \to K$
such that
![]() $\pi = \tilde {\pi } \circ \tau $
. The Bohr compactification also has a concrete description; it is the dual of
$\pi = \tilde {\pi } \circ \tau $
. The Bohr compactification also has a concrete description; it is the dual of
![]() $\widehat {G}$
where
$\widehat {G}$
where
![]() $\widehat {G}$
is given the discrete topology (see Section 3).
$\widehat {G}$
is given the discrete topology (see Section 3).
See [Reference Rudin34] for basic results on the Bohr compactification and [Reference Björklund and Fish9] for a recent application to sumsets.
2.7 Lemmas on Bohr sets
We document two lemmas concerning Bohr sets for later use. Similar lemmas for compact abelian groups have been proved in [Reference Le and Lê33]; the proofs for arbitrary abelian groups are identical and so we omit them.
The first lemma states that the preimage of a Bohr set is a Bohr set.
Lemma 2.2 [Reference Le and Lê33, Lemma 2.9].
Let
![]() $G, H$
be abelian groups and
$G, H$
be abelian groups and
![]() $\tau : G \to H$
be a homomorphism. If B is a Bohr-
$\tau : G \to H$
be a homomorphism. If B is a Bohr-
![]() $(k, \eta )$
set in H, then
$(k, \eta )$
set in H, then
![]() $\tau ^{-1}(B)$
is a Bohr-
$\tau ^{-1}(B)$
is a Bohr-
![]() $(k, \eta )$
set in G.
$(k, \eta )$
set in G.
The second lemma says that the image of a Bohr set under a homomorphism with finite index image is again a Bohr set.
Lemma 2.3 [Reference Le and Lê33, Lemma 2.10] and [Reference Griesmer23, Lemma 1.7].
Let G be an abelian group and
![]() $\phi : G \to G$
be an endomorphism with
$\phi : G \to G$
be an endomorphism with
![]() $[G: \phi (G)] < \infty $
. If B is a Bohr-
$[G: \phi (G)] < \infty $
. If B is a Bohr-
![]() $(k, \eta )$
set in G, then
$(k, \eta )$
set in G, then
![]() $\phi (B)$
is a Bohr-
$\phi (B)$
is a Bohr-
![]() $(k', \eta ')$
set in G, where
$(k', \eta ')$
set in G, where
![]() $k', \eta '$
depend only on k,
$k', \eta '$
depend only on k,
![]() $\eta $
, and
$\eta $
, and
![]() $[G: \phi (G)]$
.
$[G: \phi (G)]$
.
2.8 Almost periodic functions and null functions
A function on G of the form
![]() $g \mapsto \sum _{i=1}^k c_i \chi _i(g)$
, where
$g \mapsto \sum _{i=1}^k c_i \chi _i(g)$
, where
![]() $c_i \in \mathbb {C}$
and
$c_i \in \mathbb {C}$
and
![]() $\chi _i \in \widehat {G}$
, is called a trigonometric polynomial.
$\chi _i \in \widehat {G}$
, is called a trigonometric polynomial.
An
![]() $f \in \ell ^{\infty }(G)$
is called a (Bohr) almost periodic function if it is a uniform limit of a sequence of trigonometric polynomials. Alternatively, f is almost periodic if
$f \in \ell ^{\infty }(G)$
is called a (Bohr) almost periodic function if it is a uniform limit of a sequence of trigonometric polynomials. Alternatively, f is almost periodic if
![]() $f = h \circ \tau $
, where h is a continuous function on
$f = h \circ \tau $
, where h is a continuous function on
![]() $bG$
and
$bG$
and
![]() $\tau : G \to bG$
is the natural embedding. Given an almost periodic function f, a
$\tau : G \to bG$
is the natural embedding. Given an almost periodic function f, a
![]() $\chi \in \widehat {G}$
and an invariant mean
$\chi \in \widehat {G}$
and an invariant mean
![]() $\nu $
on G, we write
$\nu $
on G, we write
![]() $\hat {f}(\chi )$
for the Fourier coefficient
$\hat {f}(\chi )$
for the Fourier coefficient
![]() $\nu (f\overline {\chi })$
. It is easy to verify that for an almost periodic f,
$\nu (f\overline {\chi })$
. It is easy to verify that for an almost periodic f,
![]() $\hat {f}(\chi )$
does not depend on the choice of
$\hat {f}(\chi )$
does not depend on the choice of
![]() $\nu $
.
$\nu $
.
An
![]() $f \in \ell ^{\infty }(G)$
is called a null function if
$f \in \ell ^{\infty }(G)$
is called a null function if
![]() $\nu (|f|) = 0$
for every invariant mean
$\nu (|f|) = 0$
for every invariant mean
![]() $\nu $
on G.
$\nu $
on G.
3 Dense images of discrete groups in compact groups
This section describes a general way to construct a homomorphism
![]() $\tau :G\to K$
from a discrete abelian group G into a compact abelian group K. It also provides sufficient conditions for an endomorphism
$\tau :G\to K$
from a discrete abelian group G into a compact abelian group K. It also provides sufficient conditions for an endomorphism
![]() $\phi $
of G to induce an endomorphism
$\phi $
of G to induce an endomorphism
![]() $\tilde {\phi }$
of K. This framework provides a concrete description of the Bohr compactification of G and of the Kronecker factor of an ergodic G-system. We start with the following.
$\tilde {\phi }$
of K. This framework provides a concrete description of the Bohr compactification of G and of the Kronecker factor of an ergodic G-system. We start with the following.
Lemma 3.1. Let
![]() $\Gamma $
be a locally compact abelian group and let
$\Gamma $
be a locally compact abelian group and let
![]() $\phi :\Gamma \to \Gamma $
be a continuous endomorphism. Define an endomorphism
$\phi :\Gamma \to \Gamma $
be a continuous endomorphism. Define an endomorphism
![]() $\phi ^*:\widehat {\Gamma }\to \widehat {\Gamma }$
by
$\phi ^*:\widehat {\Gamma }\to \widehat {\Gamma }$
by
![]() $\phi ^*(\chi )=\chi \circ \phi $
. Then
$\phi ^*(\chi )=\chi \circ \phi $
. Then
-
(i)
 $\phi ^*$
is continuous.
$\phi ^*$
is continuous. -
(ii) Under the canonical identification of
 $\widehat {\widehat {\Gamma }}$
with
$\widehat {\widehat {\Gamma }}$
with
 $\Gamma $
,
$\Gamma $
,
 $(\phi ^*)^*=\phi $
.
$(\phi ^*)^*=\phi $
.
Proof. (i) By definition,
![]() $\widehat {\Gamma }$
is equipped with the topology of uniform convergence on compact subsets of
$\widehat {\Gamma }$
is equipped with the topology of uniform convergence on compact subsets of
![]() $\Gamma $
. It therefore suffices to prove that if
$\Gamma $
. It therefore suffices to prove that if
![]() $(\chi _n)_{n\in I}$
is a net of elements of
$(\chi _n)_{n\in I}$
is a net of elements of
![]() $\widehat {\Gamma }$
converging to
$\widehat {\Gamma }$
converging to
![]() $\chi \in \widehat {\Gamma }$
uniformly on compact subsets of
$\chi \in \widehat {\Gamma }$
uniformly on compact subsets of
![]() $\Gamma $
, then
$\Gamma $
, then
![]() $(\chi _n\circ \phi )_{n\in I}$
converges to
$(\chi _n\circ \phi )_{n\in I}$
converges to
![]() $\chi \circ \phi $
uniformly on compact subsets of
$\chi \circ \phi $
uniformly on compact subsets of
![]() $\Gamma $
. Continuity of
$\Gamma $
. Continuity of
![]() $\phi $
implies
$\phi $
implies
![]() $\phi (K)$
is compact for every compact
$\phi (K)$
is compact for every compact
![]() $K\subset \Gamma $
, so the assumption that
$K\subset \Gamma $
, so the assumption that
![]() $\chi _n\to \chi $
uniformly on every compact
$\chi _n\to \chi $
uniformly on every compact
![]() $K\subset \Gamma $
implies
$K\subset \Gamma $
implies
![]() $\chi _n \to \chi $
uniformly on
$\chi _n \to \chi $
uniformly on
![]() $\phi (K)$
for every compact
$\phi (K)$
for every compact
![]() $K\subset \Gamma $
. But this means
$K\subset \Gamma $
. But this means
![]() $(\chi _n \circ \phi )_{n\in I}$
converges to
$(\chi _n \circ \phi )_{n\in I}$
converges to
![]() $\chi \circ \phi $
uniformly on compact subsets of
$\chi \circ \phi $
uniformly on compact subsets of
![]() $\Gamma $
, as desired.
$\Gamma $
, as desired.
(ii) For
![]() $\gamma \in \Gamma $
, define the evaluation map
$\gamma \in \Gamma $
, define the evaluation map
![]() $e_{\gamma }(\chi ) = \chi (\gamma )$
for any
$e_{\gamma }(\chi ) = \chi (\gamma )$
for any
![]() $\chi \in \widehat {\Gamma }$
. It suffices to prove that
$\chi \in \widehat {\Gamma }$
. It suffices to prove that
meaning
![]() $(\phi ^*)^*(e_{\gamma })(\chi ) = \chi (\phi (\gamma ))$
for all
$(\phi ^*)^*(e_{\gamma })(\chi ) = \chi (\phi (\gamma ))$
for all
![]() $\chi \in \widehat {\Gamma }$
. To see this, note that
$\chi \in \widehat {\Gamma }$
. To see this, note that
![]() $\chi \mapsto (\phi ^*)^*(e_{\gamma })(\chi )$
is defined by
$\chi \mapsto (\phi ^*)^*(e_{\gamma })(\chi )$
is defined by
![]() $e_{\gamma }(\phi ^*(\chi ))=e_{\gamma }(\chi \circ \phi ).$
$e_{\gamma }(\phi ^*(\chi ))=e_{\gamma }(\chi \circ \phi ).$
We now apply Lemma 3.1 in the case where
![]() $\Gamma $
is a discrete group.
$\Gamma $
is a discrete group.
Lemma 3.2. Let
![]() $\Lambda $
be a subgroup of
$\Lambda $
be a subgroup of
![]() $\widehat {G}$
, viewed as a discrete group, so that
$\widehat {G}$
, viewed as a discrete group, so that
![]() $\widehat {\Lambda }$
is compact. For
$\widehat {\Lambda }$
is compact. For
![]() $g \in G$
, define the evaluation map
$g \in G$
, define the evaluation map
![]() $e_g (\chi ) = \chi (g)$
for
$e_g (\chi ) = \chi (g)$
for
![]() $\chi \in \widehat {G}$
. Define a homomorphism
$\chi \in \widehat {G}$
. Define a homomorphism
![]() $\tau : G\to \widehat {\Lambda }$
by
$\tau : G\to \widehat {\Lambda }$
by
![]() $\tau (g)=e_g|_{\Lambda }$
. Then
$\tau (g)=e_g|_{\Lambda }$
. Then
-
(i)
 $\tau (G)$
is dense in
$\tau (G)$
is dense in
 $\widehat {\Lambda }$
.
$\widehat {\Lambda }$
. -
(ii) Suppose
 $\phi :G\to G$
is an endomorphism such that
$\phi :G\to G$
is an endomorphism such that
 $\chi \circ \phi \in \Lambda $
for all
$\chi \circ \phi \in \Lambda $
for all
 $\chi \in \Lambda $
. Then there is a continuous endomorphism
$\chi \in \Lambda $
. Then there is a continuous endomorphism
 $\tilde {\phi }$
of
$\tilde {\phi }$
of
 $\widehat {\Lambda }$
such that
$\widehat {\Lambda }$
such that
 $\tilde {\phi }\circ \tau =\tau \circ \phi $
. Furthermore,
$\tilde {\phi }\circ \tau =\tau \circ \phi $
. Furthermore,
 $[\widehat {\Lambda }:\tilde {\phi }(\widehat {\Lambda })]\leq [G:\phi (G)]$
.
$[\widehat {\Lambda }:\tilde {\phi }(\widehat {\Lambda })]\leq [G:\phi (G)]$
.
Proof. (i) Let
![]() $\psi \in \widehat {\Lambda }$
, let
$\psi \in \widehat {\Lambda }$
, let
![]() $F = \{\chi _1,\dots ,\chi _d\} \subset \Lambda $
be finite and let
$F = \{\chi _1,\dots ,\chi _d\} \subset \Lambda $
be finite and let
![]() $\varepsilon>0$
. We will show that there is a
$\varepsilon>0$
. We will show that there is a
![]() $g\in G$
such that
$g\in G$
such that
![]() $|\psi (\chi _j)-e_g(\chi _j)|<\varepsilon $
for all
$|\psi (\chi _j)-e_g(\chi _j)|<\varepsilon $
for all
![]() $\chi _j\in F$
. Consider the subgroup
$\chi _j\in F$
. Consider the subgroup
It suffices to prove that
Assume, to get a contradiction, that (9) is false. Then there is a nontrivial character
![]() $\alpha \in \widehat {(S^{1})^d}$
which annihilates
$\alpha \in \widehat {(S^{1})^d}$
which annihilates
![]() $\overline {H}$
but does not annihilate
$\overline {H}$
but does not annihilate
![]() $\vec {t}$
. Writing
$\vec {t}$
. Writing
![]() $\alpha (x_1,\dots ,x_d)$
as
$\alpha (x_1,\dots ,x_d)$
as
![]() $x_1^{n_1} \cdots x_d^{n_d}$
, we have
$x_1^{n_1} \cdots x_d^{n_d}$
, we have
but
![]() $\psi (\chi _1)^{n_1}\cdots \psi (\chi _d)^{n_d}\neq 1$
. Since
$\psi (\chi _1)^{n_1}\cdots \psi (\chi _d)^{n_d}\neq 1$
. Since
![]() $\psi $
is a character, the latter equation means
$\psi $
is a character, the latter equation means
But (10) means that
![]() $\chi _1^{n_1}\cdots \chi _d^{n_d}$
is trivial, contradicting (11).
$\chi _1^{n_1}\cdots \chi _d^{n_d}$
is trivial, contradicting (11).
(ii) Define
![]() $\phi ':\Lambda \to \Lambda $
by
$\phi ':\Lambda \to \Lambda $
by
![]() $\phi '(\chi )=\chi \circ \phi $
. Let
$\phi '(\chi )=\chi \circ \phi $
. Let
![]() $\tilde {\phi }:=(\phi ')^*$
as in Lemma 3.1, meaning that for
$\tilde {\phi }:=(\phi ')^*$
as in Lemma 3.1, meaning that for
![]() $\psi \in \widehat {\Lambda }$
,
$\psi \in \widehat {\Lambda }$
,
![]() $\tilde {\phi }(\psi )=\psi \circ \phi '$
. By Lemma 3.1,
$\tilde {\phi }(\psi )=\psi \circ \phi '$
. By Lemma 3.1,
![]() $\tilde {\phi }$
is a continuous endomorphism. To verify that
$\tilde {\phi }$
is a continuous endomorphism. To verify that
![]() $\tilde {\phi }\circ \tau =\tau \circ \phi $
, fix
$\tilde {\phi }\circ \tau =\tau \circ \phi $
, fix
![]() $\chi \in \Lambda $
,
$\chi \in \Lambda $
,
![]() $g\in G$
and evaluate
$g\in G$
and evaluate
Thus,
![]() $\tilde {\phi }\circ \tau = \tau \circ \phi $
.
$\tilde {\phi }\circ \tau = \tau \circ \phi $
.
Now let
![]() $k=[G:\phi (G)]$
(assuming this index is finite) and let
$k=[G:\phi (G)]$
(assuming this index is finite) and let
![]() $t_j+\phi (G), j=1,\dots ,k$
be coset representatives of
$t_j+\phi (G), j=1,\dots ,k$
be coset representatives of
![]() $\phi (G)$
. The identity
$\phi (G)$
. The identity
![]() $\tilde {\phi }\circ \tau =\tau \circ \phi $
implies
$\tilde {\phi }\circ \tau =\tau \circ \phi $
implies
![]() $\tilde {\phi }(\widehat {\Lambda })$
contains
$\tilde {\phi }(\widehat {\Lambda })$
contains
![]() $\overline {\tau (\phi (G))}$
. The latter subgroup has index at most k, since the translates
$\overline {\tau (\phi (G))}$
. The latter subgroup has index at most k, since the translates
![]() $\overline {\tau (t_j+\phi (G))} = \tau (t_j)+\overline {\tau (\phi (G))}$
are closed and cover a dense subset of
$\overline {\tau (t_j+\phi (G))} = \tau (t_j)+\overline {\tau (\phi (G))}$
are closed and cover a dense subset of
![]() $\widehat {\Lambda }$
. Thus,
$\widehat {\Lambda }$
. Thus,
![]() $\tilde {\phi }(\widehat {\Lambda })$
also has index at most k.
$\tilde {\phi }(\widehat {\Lambda })$
also has index at most k.
It can be shown that all homomorphisms from G into compact groups with dense images arise from the construction in Lemma 3.2, though we do not need this fact. When
![]() $\Lambda = \widehat {G}$
with the discrete topology,
$\Lambda = \widehat {G}$
with the discrete topology,
![]() $\widehat {\Lambda }$
is the Bohr compactification
$\widehat {\Lambda }$
is the Bohr compactification
![]() $bG$
of G, which is relevant in the proof of Theorem 1.4.
$bG$
of G, which is relevant in the proof of Theorem 1.4.
In the proofs of Theorems 1.2 and 1.7, we will focus on the case where
![]() $\Lambda $
is at most countable. The relevance of countability is that, in this case,
$\Lambda $
is at most countable. The relevance of countability is that, in this case,
![]() $\widehat {\Lambda }$
is compact and metrizable. Consequently, its Borel
$\widehat {\Lambda }$
is compact and metrizable. Consequently, its Borel
![]() $\sigma $
-algebra is separable (so the theory of factors applies).
$\sigma $
-algebra is separable (so the theory of factors applies).
The group
![]() $\widehat {\Lambda }$
being abelian, we can write its group operation additively. Equipped with its normalized Haar measure
$\widehat {\Lambda }$
being abelian, we can write its group operation additively. Equipped with its normalized Haar measure
![]() $m_{\widehat {\Lambda }}$
,
$m_{\widehat {\Lambda }}$
,
![]() $\widehat {\Lambda }$
is naturally endowed with a group rotation via the G-action R given by
$\widehat {\Lambda }$
is naturally endowed with a group rotation via the G-action R given by
![]() $R_g(z) := z + \tau (g)$
for all
$R_g(z) := z + \tau (g)$
for all
![]() $z \in \widehat {\Lambda }$
and
$z \in \widehat {\Lambda }$
and
![]() $g\in G$
, where
$g\in G$
, where
![]() $\tau $
is defined in Lemma 3.2. Since
$\tau $
is defined in Lemma 3.2. Since
![]() $\tau (G)$
is dense in
$\tau (G)$
is dense in
![]() $\widehat {\Lambda }$
, this action is ergodic. We will now state some properties of these group rotations.
$\widehat {\Lambda }$
, this action is ergodic. We will now state some properties of these group rotations.
Lemma 3.3.
-
(i) For all countable subgroups
 $\Lambda $
of
$\Lambda $
of
 $\widehat {G}$
, we have
$\widehat {G}$
, we have
 $\mathcal {E}(\widehat {\Lambda }, m_{\widehat {\Lambda }}, R) = \Lambda $
. Furthermore, all the eigenvectors of R corresponding to the eigenvalue
$\mathcal {E}(\widehat {\Lambda }, m_{\widehat {\Lambda }}, R) = \Lambda $
. Furthermore, all the eigenvectors of R corresponding to the eigenvalue
 $\lambda \in \Lambda $
are constant multiples of
$\lambda \in \Lambda $
are constant multiples of
 $v_{\lambda }$
, where
$v_{\lambda }$
, where
 $v_{\lambda }(x) = x(\lambda )$
for all
$v_{\lambda }(x) = x(\lambda )$
for all
 $x \in \widehat {\Lambda }$
.
$x \in \widehat {\Lambda }$
. -
(ii) If
 $\Lambda _1 \leq \Lambda _2$
are countable subgroups of
$\Lambda _1 \leq \Lambda _2$
are countable subgroups of
 $\widehat {G}$
, then the group rotation associated with
$\widehat {G}$
, then the group rotation associated with
 $\widehat {\Lambda _1}$
is a factor of the group rotation associated with
$\widehat {\Lambda _1}$
is a factor of the group rotation associated with
 $\widehat {\Lambda _2}$
.
$\widehat {\Lambda _2}$
. -
(iii) If
 $\mathbf {X}=(X,\mu ,T)$
is an ergodic G-system and
$\mathbf {X}=(X,\mu ,T)$
is an ergodic G-system and
 $\Lambda = \mathcal {E}(\mathbf {X})$
, then
$\Lambda = \mathcal {E}(\mathbf {X})$
, then
 $(\widehat {\Lambda }, m_{\widehat {\Lambda }}, R)$
is the Kronecker factor of
$(\widehat {\Lambda }, m_{\widehat {\Lambda }}, R)$
is the Kronecker factor of
 $\mathbf {X}$
.
$\mathbf {X}$
.
Proof. (i) For
![]() $\lambda \in \Lambda $
and
$\lambda \in \Lambda $
and
![]() $x \in \widehat {\Lambda }$
, we have
$x \in \widehat {\Lambda }$
, we have
This shows that
![]() $\lambda $
is an eigenvalue of
$\lambda $
is an eigenvalue of
![]() $(\widehat {\Lambda }, m_{\widehat {\Lambda }}, R)$
and
$(\widehat {\Lambda }, m_{\widehat {\Lambda }}, R)$
and
![]() $v_{\lambda }$
is a corresponding eigenvector.
$v_{\lambda }$
is a corresponding eigenvector.
Conversely, suppose
![]() $\chi \in \widehat {G}$
and there exists non-zero
$\chi \in \widehat {G}$
and there exists non-zero
![]() $f \in L^2(\widehat {\Lambda })$
such that for all
$f \in L^2(\widehat {\Lambda })$
such that for all
![]() $g \in G$
,
$g \in G$
,
![]() $f(x + \tau (g)) = \chi (g) f(x)$
for almost all x, we need to show that
$f(x + \tau (g)) = \chi (g) f(x)$
for almost all x, we need to show that
![]() $\chi \in \Lambda $
. Since f is not zero, there exists
$\chi \in \Lambda $
. Since f is not zero, there exists
![]() $\lambda \in \Lambda $
such that
$\lambda \in \Lambda $
such that
![]() $\widehat {f}(\lambda ) \neq 0$
. Computing the Fourier coefficients of both sides, we have
$\widehat {f}(\lambda ) \neq 0$
. Computing the Fourier coefficients of both sides, we have
for any
![]() $g \in G$
. Since
$g \in G$
. Since
![]() $\widehat {f}(\lambda ) \neq 0$
, this implies that
$\widehat {f}(\lambda ) \neq 0$
, this implies that
![]() $\chi (g) = \lambda (g)$
for any
$\chi (g) = \lambda (g)$
for any
![]() $g \in G$
. Therefore,
$g \in G$
. Therefore,
![]() $\chi = \lambda \in \Lambda $
. Furthermore, this also shows that f has exactly one non-zero Fourier coefficient and
$\chi = \lambda \in \Lambda $
. Furthermore, this also shows that f has exactly one non-zero Fourier coefficient and
![]() $f = \widehat {f}(\lambda ) v_{\lambda }$
.
$f = \widehat {f}(\lambda ) v_{\lambda }$
.
(ii) Define
![]() $\pi : \widehat {\Lambda }_2 \to \widehat {\Lambda }_1$
by
$\pi : \widehat {\Lambda }_2 \to \widehat {\Lambda }_1$
by
![]() $\pi (x) = x|_{\Lambda _1}$
for all
$\pi (x) = x|_{\Lambda _1}$
for all
![]() $x \in \widehat {\Lambda }_2$
. Then
$x \in \widehat {\Lambda }_2$
. Then
![]() $\pi $
is a surjective, continuous group homomorphism. By [Reference Le and Lê33, Lemma 2.7],
$\pi $
is a surjective, continuous group homomorphism. By [Reference Le and Lê33, Lemma 2.7],
![]() $\pi $
is measure-preserving.
$\pi $
is measure-preserving.
Recall that the homomorphisms from G to
![]() $\widehat {\Lambda }_1$
and
$\widehat {\Lambda }_1$
and
![]() $\widehat {\Lambda }_2$
are
$\widehat {\Lambda }_2$
are
![]() $\tau _1 (g) = e_g|_{\Lambda _1}$
and
$\tau _1 (g) = e_g|_{\Lambda _1}$
and
![]() $\tau _2 (g) = e_g|_{\Lambda _2}$
. It is clear that
$\tau _2 (g) = e_g|_{\Lambda _2}$
. It is clear that
thus showing that
![]() $\pi $
is a factor map.
$\pi $
is a factor map.
(iii) We assume (see Section 2.3) that
![]() $L^2(\mu )$
is separable. For each
$L^2(\mu )$
is separable. For each
![]() $\lambda \in \Lambda = \mathcal {E}(\mathbf {X})$
, there is an eigenvector
$\lambda \in \Lambda = \mathcal {E}(\mathbf {X})$
, there is an eigenvector
![]() $f_{\lambda } \in L^2(\mathbf {X})$
such that
$f_{\lambda } \in L^2(\mathbf {X})$
such that
![]() $T_g f_{\lambda } = \lambda (g) f_{\lambda }$
for any
$T_g f_{\lambda } = \lambda (g) f_{\lambda }$
for any
![]() $g \in G$
. Arguing similarly to [Reference Walters39, Theorem 3.4], we may assume that
$g \in G$
. Arguing similarly to [Reference Walters39, Theorem 3.4], we may assume that
![]() $|f_{\lambda }|=1$
and
$|f_{\lambda }|=1$
and
![]() $f_{\lambda \xi } = f_{\lambda } f_{\xi }$
for any
$f_{\lambda \xi } = f_{\lambda } f_{\xi }$
for any
![]() $\lambda , \xi \in \Lambda $
. Defining
$\lambda , \xi \in \Lambda $
. Defining
![]() $V(v_{\lambda }) = f_{\lambda }$
and extending V linearly, we have an isometry
$V(v_{\lambda }) = f_{\lambda }$
and extending V linearly, we have an isometry
![]() $V: L^2(\widehat {\Lambda }) \rightarrow L^2(\mathbf {X})$
satisfying
$V: L^2(\widehat {\Lambda }) \rightarrow L^2(\mathbf {X})$
satisfying
![]() $V(fg) = V(f) V(g)$
for any
$V(fg) = V(f) V(g)$
for any
![]() $f, g \in L^2(\widehat {\Lambda })$
. By [Reference Walters39, Theorem 2.4], V induces a homomorphism of measure algebras, and therefore a factor map
$f, g \in L^2(\widehat {\Lambda })$
. By [Reference Walters39, Theorem 2.4], V induces a homomorphism of measure algebras, and therefore a factor map
![]() $\mathbf {X} \rightarrow \widehat {\Lambda }$
. Since
$\mathbf {X} \rightarrow \widehat {\Lambda }$
. Since
![]() $\mathcal {E}(\widehat {\Lambda }) = \Lambda $
, part (ii) shows that
$\mathcal {E}(\widehat {\Lambda }) = \Lambda $
, part (ii) shows that
![]() $\widehat {\Lambda }$
is the largest group rotation that is a factor of
$\widehat {\Lambda }$
is the largest group rotation that is a factor of
![]() $\mathbf {X}$
.
$\mathbf {X}$
.
4 Radon-Nikodym densities
In this section, we make no assumption on the countability (or uncountability) of G. In particular, the lemmas here will apply when G is an arbitrary discrete abelian group.
4.1 Definition of Radon-Nikodym densities
Let K be a compact abelian group and
![]() $\tau : G \to K$
be a homomorphism such that
$\tau : G \to K$
be a homomorphism such that
![]() $\tau (G)$
is dense in K. We describe a way to transfer a function
$\tau (G)$
is dense in K. We describe a way to transfer a function
![]() $f : G \to [0,1]$
to a function
$f : G \to [0,1]$
to a function
![]() $\rho : K \to [0,1]$
with the aid of invariant means. This construction follows the proof of [Reference Griesmer24, Lemma 2.5] (cf. Section 4 of [Reference Björklund10]); it will be used in the proofs of Theorems 1.4 and 1.7.
$\rho : K \to [0,1]$
with the aid of invariant means. This construction follows the proof of [Reference Griesmer24, Lemma 2.5] (cf. Section 4 of [Reference Björklund10]); it will be used in the proofs of Theorems 1.4 and 1.7.
Definition 4.1. Let
![]() $f: G \rightarrow [0,1]$
and let
$f: G \rightarrow [0,1]$
and let
![]() $\nu $
be an invariant mean on G. The Radon-Nikodym density associated with f and
$\nu $
be an invariant mean on G. The Radon-Nikodym density associated with f and
![]() $\nu $
is a Borel measurable function
$\nu $
is a Borel measurable function
![]() $\rho _{f}^{\nu }:K\to [0,1]$
satisfying
$\rho _{f}^{\nu }:K\to [0,1]$
satisfying
for every continuous
![]() $h:K\to \mathbb C$
. It is unique up to
$h:K\to \mathbb C$
. It is unique up to
![]() $m_K$
-measure
$m_K$
-measure
![]() $0$
.
$0$
.
Thus,
![]() $\rho _{f}^{\nu }$
depends on the compact group K and the map
$\rho _{f}^{\nu }$
depends on the compact group K and the map
![]() $\tau $
. When
$\tau $
. When
![]() $f=1_A$
is the characteristic function of a subset of G, we write
$f=1_A$
is the characteristic function of a subset of G, we write
![]() $\rho _{A}^{\nu }$
in place of
$\rho _{A}^{\nu }$
in place of
![]() $\rho _{1_A}^{\nu }$
to avoid nested subscripts.
$\rho _{1_A}^{\nu }$
to avoid nested subscripts.
Given an invariant mean
![]() $\nu $
on G, and
$\nu $
on G, and
![]() $f:G\to [0,1]$
, we will prove that there is a function
$f:G\to [0,1]$
, we will prove that there is a function
![]() $\rho _{f}^{\nu }$
satisfying Definition 4.1. We first observe the following.
$\rho _{f}^{\nu }$
satisfying Definition 4.1. We first observe the following.
Lemma 4.2. For all
![]() $h \in C(K)$
, we have
$h \in C(K)$
, we have
Proof. We define a linear functional L on
![]() $C(K)$
by
$C(K)$
by
By the Riesz representation theorem, there exists a regular Borel probability measure m on K such that
![]() $L(h) = \int _{K} h \, dm$
. However, for any
$L(h) = \int _{K} h \, dm$
. However, for any
![]() $g \in G$
, we have
$g \in G$
, we have
by translation invariance of
![]() $\nu $
. Since the map
$\nu $
. Since the map
![]() $x \mapsto h_x$
from K to
$x \mapsto h_x$
from K to
![]() $C(K)$
is continuous, and since
$C(K)$
is continuous, and since
![]() $\tau (G)$
is dense in K, (14) implies
$\tau (G)$
is dense in K, (14) implies
![]() $L(h_x)=L(h)$
for all
$L(h_x)=L(h)$
for all
![]() $x \in K$
. Hence, m is translation invariant. By uniqueness of the Haar measure, we have
$x \in K$
. Hence, m is translation invariant. By uniqueness of the Haar measure, we have
![]() $m=m_{K}$
, as desired.
$m=m_{K}$
, as desired.
Given
![]() $f:G\to [0,1]$
, we define a linear functional
$f:G\to [0,1]$
, we define a linear functional
![]() $\Lambda _f^{\nu }: C(K) \to \mathbb {R}$
by
$\Lambda _f^{\nu }: C(K) \to \mathbb {R}$
by
Clearly,
![]() $\Lambda _f^{\nu }$
is a positive linear functional. Thus, by the Riesz representation theorem, there exists a regular Borel measure m on K such that
$\Lambda _f^{\nu }$
is a positive linear functional. Thus, by the Riesz representation theorem, there exists a regular Borel measure m on K such that
for all
![]() $h \in C(K)$
.
$h \in C(K)$
.
Lemma 4.3. The measure m defined by (16) is absolutely continuous with respect to the Haar probability measure
![]() $m_K$
on K, and, in fact,
$m_K$
on K, and, in fact,
![]() $m(B)\leq m_K(B)$
for all Borel sets
$m(B)\leq m_K(B)$
for all Borel sets
![]() $B\subset K$
.
$B\subset K$
.
Proof. First, by (13), we have
for any
![]() $h \in C(K)$
.
$h \in C(K)$
.
Let B be any Borel set in K. By regularity of m and
![]() $m_K$
, there is an open set U, a closed set V, such that
$m_K$
, there is an open set U, a closed set V, such that
![]() $V \subset B \subset U$
,
$V \subset B \subset U$
,
![]() $m( U \setminus V ) < \epsilon $
and
$m( U \setminus V ) < \epsilon $
and
![]() $m_K( U \setminus V ) < \epsilon $
. By Urysohn’s lemma, there exists a continuous function
$m_K( U \setminus V ) < \epsilon $
. By Urysohn’s lemma, there exists a continuous function
![]() $h : K \rightarrow [0,1]$
such that
$h : K \rightarrow [0,1]$
such that
![]() $h=1$
on V and
$h=1$
on V and
![]() $h=0$
on
$h=0$
on
![]() $U^c$
. Applying (17), we have
$U^c$
. Applying (17), we have
Since
![]() $\epsilon $
is arbitrary, this implies that
$\epsilon $
is arbitrary, this implies that
![]() $m(B) \leq m_K(B)$
. Therefore, m is absolutely continuous with respect to
$m(B) \leq m_K(B)$
. Therefore, m is absolutely continuous with respect to
![]() $m_K$
.
$m_K$
.
We now prove that, for each
![]() $f:G\to [0,1]$
, there is a
$f:G\to [0,1]$
, there is a
![]() $\rho _{f}^{\nu }$
satisfying (12). Given such an f, we consider the measure m on K defined above. Since m is absolutely continuous with respect to
$\rho _{f}^{\nu }$
satisfying (12). Given such an f, we consider the measure m on K defined above. Since m is absolutely continuous with respect to
![]() $m_K$
, we may define
$m_K$
, we may define
![]() $\rho _{f}^{\nu }$
to be the Radon-Nikodym derivative of m with respect to
$\rho _{f}^{\nu }$
to be the Radon-Nikodym derivative of m with respect to
![]() $m_K$
, meaning
$m_K$
, meaning
![]() $\rho _{f}^{\nu }$
is the unique (up to
$\rho _{f}^{\nu }$
is the unique (up to
![]() $m_K$
-measure
$m_K$
-measure
![]() $0$
) function in
$0$
) function in
![]() $L^1(m_K)$
satisfying
$L^1(m_K)$
satisfying
![]() $\int h\, \rho _{f}^{\nu } \, dm_K = \int h\, dm$
for all
$\int h\, \rho _{f}^{\nu } \, dm_K = \int h\, dm$
for all
![]() $h\in C(K)$
. Then (12) follows from (15) and (16). The inequality
$h\in C(K)$
. Then (12) follows from (15) and (16). The inequality
![]() $0\leq \rho _{f}^{\nu }\leq 1 \ m_K$
-a.e. follows from the fact that
$0\leq \rho _{f}^{\nu }\leq 1 \ m_K$
-a.e. follows from the fact that
![]() $0\leq m(B)\leq m_K(B)$
for all Borel sets
$0\leq m(B)\leq m_K(B)$
for all Borel sets
![]() $B.$
$B.$
4.2 Properties of
 $\rho _{A}^{\nu }$
$\rho _{A}^{\nu }$
We will now state some properties of
![]() $\rho ^{\nu } _{f}$
when f is the characteristic function of a set. Recall that we write
$\rho ^{\nu } _{f}$
when f is the characteristic function of a set. Recall that we write
![]() $\rho _{A}^{\nu }$
in place of
$\rho _{A}^{\nu }$
in place of
![]() $\rho _{1_A}^{\nu }$
.
$\rho _{1_A}^{\nu }$
.
Lemma 4.4. Let
![]() $A \subset G$
and let
$A \subset G$
and let
![]() $\nu $
be an invariant mean on G. Then
$\nu $
be an invariant mean on G. Then
-
(i)
 $\int _K \rho _{A}^{\nu } \, d m_K = \nu (1_A)$
,
$\int _K \rho _{A}^{\nu } \, d m_K = \nu (1_A)$
, -
(ii)
 $\rho _{A}^{\nu }$
is supported on
$\rho _{A}^{\nu }$
is supported on
 $\overline {\tau (A)}$
; that is,
$\overline {\tau (A)}$
; that is,
 $\rho _{A}^{\nu } = 0 \ m_K$
-a.e. on
$\rho _{A}^{\nu } = 0 \ m_K$
-a.e. on
 $K \setminus \overline {\tau (A)}$
.
$K \setminus \overline {\tau (A)}$
.
Proof. The first claim follows from the definition of
![]() $\rho _{A}^{\nu }$
. For the second claim, let
$\rho _{A}^{\nu }$
. For the second claim, let
![]() $h: K \to \mathbb {R}_{\geq 0}$
be any continuous function that is supported on
$h: K \to \mathbb {R}_{\geq 0}$
be any continuous function that is supported on
![]() $K \setminus \overline {\tau (A)}$
. If
$K \setminus \overline {\tau (A)}$
. If
![]() $g \in A$
, then
$g \in A$
, then
![]() $\tau (g) \in \tau (A)$
will not be in the support of h. In other words,
$\tau (g) \in \tau (A)$
will not be in the support of h. In other words,
![]() $h \circ \tau \cdot 1_A(g) = 0$
for all
$h \circ \tau \cdot 1_A(g) = 0$
for all
![]() $g \in G$
, and so
$g \in G$
, and so
Suppose for a contradiction that there exists a Borel set
![]() $V \subset K \setminus \overline {\tau (A)}$
with
$V \subset K \setminus \overline {\tau (A)}$
with
![]() $m_K(V)>0$
such that
$m_K(V)>0$
such that
![]() $\rho _{A}^{\nu }>0$
on V. Since
$\rho _{A}^{\nu }>0$
on V. Since
![]() $m_K$
is regular, we may assume that V is closed. By Urysohn’s lemma, there is a continuous function
$m_K$
is regular, we may assume that V is closed. By Urysohn’s lemma, there is a continuous function
![]() $h: K \rightarrow [0,1]$
that is equal to
$h: K \rightarrow [0,1]$
that is equal to
![]() $1$
on V and
$1$
on V and
![]() $0$
on
$0$
on
![]() $\overline {\tau (A)}$
. Then (18) implies that
$\overline {\tau (A)}$
. Then (18) implies that
![]() $\int _V \rho _{A}^{\nu } dm_K = 0$
, a contradiction.
$\int _V \rho _{A}^{\nu } dm_K = 0$
, a contradiction.
Lemma 4.5. Let
![]() $G = \bigcup _{i=1}^r A_i$
be a partition of G and let
$G = \bigcup _{i=1}^r A_i$
be a partition of G and let
![]() $\nu $
be an invariant mean on G. Then
$\nu $
be an invariant mean on G. Then
 $$ \begin{align*} \sum_{i=1}^r \rho_{A_i}^{\nu} (x) = 1 \end{align*} $$
$$ \begin{align*} \sum_{i=1}^r \rho_{A_i}^{\nu} (x) = 1 \end{align*} $$
for
![]() $m_K$
-almost every x.
$m_K$
-almost every x.
Proof. Since
![]() $\sum _{i = 1}^r 1_{A_i} = 1$
, for any
$\sum _{i = 1}^r 1_{A_i} = 1$
, for any
![]() $h \in C(K)$
,
$h \in C(K)$
,
 $$\begin{align*}\int_K h \left(\sum_{i=1}^r \rho_{A_i}^{\nu} \right) \, d m_K = \sum_{i=1}^r \nu(h \circ \tau \cdot 1_{A_i}) = \nu(h \circ \tau) = \int_K h \, d m_K ,\end{align*}$$
$$\begin{align*}\int_K h \left(\sum_{i=1}^r \rho_{A_i}^{\nu} \right) \, d m_K = \sum_{i=1}^r \nu(h \circ \tau \cdot 1_{A_i}) = \nu(h \circ \tau) = \int_K h \, d m_K ,\end{align*}$$
where the last equality comes from Lemma 4.2. Since
![]() $C(K)$
is dense in
$C(K)$
is dense in
![]() $L^1(m_K)$
, this implies that
$L^1(m_K)$
, this implies that
![]() $\sum _{i=1}^r \rho _{A_i}^{\nu } = 1$
almost everywhere.
$\sum _{i=1}^r \rho _{A_i}^{\nu } = 1$
almost everywhere.
4.3 Relation between
 $\rho _{A}$
and
$\rho _{A}$
and
 $\rho _{\phi (A)}$
$\rho _{\phi (A)}$
Let
![]() $G=A_1\cup \cdots \cup A_r$
. Our proof of Theorem 1.4 relies on a correspondence principle relating
$G=A_1\cup \cdots \cup A_r$
. Our proof of Theorem 1.4 relies on a correspondence principle relating
![]() $\phi _1(A_i) + \phi _2(A_i)-\phi _2(A_i)$
to a convolution of the form
$\phi _1(A_i) + \phi _2(A_i)-\phi _2(A_i)$
to a convolution of the form
![]() $1_{\tilde {\phi }_1(B_i)}*1_{\tilde {\phi }_2(B_i)}*1_{\tilde {\phi }_2(-B_i)}$
on a compact abelian group K. To prove such a correspondence principle, we need Lemma 4.6 and Corollary 4.10, which specify the relationship between the Radon-Nikodym densities of
$1_{\tilde {\phi }_1(B_i)}*1_{\tilde {\phi }_2(B_i)}*1_{\tilde {\phi }_2(-B_i)}$
on a compact abelian group K. To prove such a correspondence principle, we need Lemma 4.6 and Corollary 4.10, which specify the relationship between the Radon-Nikodym densities of
![]() $1_A$
and
$1_A$
and
![]() $1_{\phi (A)}$
. In order to make the relevant issues apparent, the next lemma takes place in slightly greater generality than we need for our application.
$1_{\phi (A)}$
. In order to make the relevant issues apparent, the next lemma takes place in slightly greater generality than we need for our application.
Lemma 4.6. Let G and H be discrete abelian groups and let
![]() $\phi :G\to H$
be a surjective homomorphism. Let
$\phi :G\to H$
be a surjective homomorphism. Let
![]() $K_1$
,
$K_1$
,
![]() $K_2$
be compact abelian groups and
$K_2$
be compact abelian groups and
![]() $\tau _1: G\to K_1$
,
$\tau _1: G\to K_1$
,
![]() $\tau _2:H\to K_2$
be homomorphisms with dense images. Suppose
$\tau _2:H\to K_2$
be homomorphisms with dense images. Suppose
![]() $\tilde {\phi }:K_1\to K_2$
is a continuous surjective homomorphism such that
$\tilde {\phi }:K_1\to K_2$
is a continuous surjective homomorphism such that
-
(i)
 $\tilde {\phi } \circ \tau _1 = \tau _2\circ \phi $
, and
$\tilde {\phi } \circ \tau _1 = \tau _2\circ \phi $
, and -
(ii) for all
 $\chi \in \widehat {K}_1$
, if there is a
$\chi \in \widehat {K}_1$
, if there is a
 $\psi \in \widehat {H}$
such that
$\psi \in \widehat {H}$
such that
 $\chi \circ \tau _1=\psi \circ \phi $
, then there is a
$\chi \circ \tau _1=\psi \circ \phi $
, then there is a
 $\chi '\in \widehat {K}_2$
such that
$\chi '\in \widehat {K}_2$
such that
 $\psi = \chi '\circ \tau _2$
(see Figure 2).
$\psi = \chi '\circ \tau _2$
(see Figure 2).
Figure 2 Illustration of (ii).
Let
![]() $f: H\to [0,1]$
and let
$f: H\to [0,1]$
and let
![]() $\nu $
be an invariant mean on G. Let
$\nu $
be an invariant mean on G. Let
![]() $\rho _{f \circ \phi }^{\nu }: K_1 \to [0,1]$
and
$\rho _{f \circ \phi }^{\nu }: K_1 \to [0,1]$
and
![]() $\rho _f^{\phi _* \nu }: K_2 \to [0,1]$
be the associated Radon-Nikodym densities as in Definition 4.1. Then
$\rho _f^{\phi _* \nu }: K_2 \to [0,1]$
be the associated Radon-Nikodym densities as in Definition 4.1. Then
![]() $m_{K_1}$
-almost everywhere.
$m_{K_1}$
-almost everywhere.
Remark 4.7.
-
• The surjectivity of
 $\phi $
is required for
$\phi $
is required for
 $\phi _*\nu $
to be an invariant mean on H, and thus for
$\phi _*\nu $
to be an invariant mean on H, and thus for
 $\rho _f^{\phi _*\nu }$
to be defined on
$\rho _f^{\phi _*\nu }$
to be defined on
 $K_2$
.
$K_2$
. -
• The assumption (ii) is satisfied by the groups we use in the proof of Theorem 1.4; namely,
 $K_1$
will be the Bohr compactification of G,
$K_1$
will be the Bohr compactification of G,
 $K_2$
will be
$K_2$
will be
 $\tilde {\phi }(K_1)$
, which will coincide with the Bohr compactification
$\tilde {\phi }(K_1)$
, which will coincide with the Bohr compactification
 $bH$
of H, and
$bH$
of H, and
 $\tau _2:H\to K_2$
will be the usual embedding of H into
$\tau _2:H\to K_2$
will be the usual embedding of H into
 $bH$
.
$bH$
.
Proof. We will prove that
We first identify some characters of G which are orthogonal to
![]() $f\circ \phi $
.
$f\circ \phi $
.
Claim 4.8. Let
![]() $\psi \in \widehat {G}$
. Then
$\psi \in \widehat {G}$
. Then
![]() $\nu ((f\circ \phi ) \cdot \overline {\psi })=0$
unless
$\nu ((f\circ \phi ) \cdot \overline {\psi })=0$
unless
![]() $\psi =\psi '\circ \phi $
for some
$\psi =\psi '\circ \phi $
for some
![]() $\psi '\in \widehat {H}$
.
$\psi '\in \widehat {H}$
.
Similarly, if
![]() $\chi \in \widehat {K}_1$
, and
$\chi \in \widehat {K}_1$
, and
![]() $h\in L^2(m_{K_2})$
, then
$h\in L^2(m_{K_2})$
, then
![]() $\widehat {h\circ \tilde {\phi }}(\chi )=0$
unless
$\widehat {h\circ \tilde {\phi }}(\chi )=0$
unless
![]() $\chi =\chi '\circ \tilde {\phi }$
for some
$\chi =\chi '\circ \tilde {\phi }$
for some
![]() $\chi '\in \widehat {K}_2$
.
$\chi '\in \widehat {K}_2$
.
To see this, assume
![]() $\psi \in \widehat {G}$
does not have the form
$\psi \in \widehat {G}$
does not have the form
![]() $\psi '\circ \phi $
for some
$\psi '\circ \phi $
for some
![]() $\psi '\in \widehat {H}$
. Then there is a
$\psi '\in \widehat {H}$
. Then there is a
![]() $g\in \ker \phi $
such that
$g\in \ker \phi $
such that
![]() $\psi (g)\neq 1$
.Footnote
4
We then have
$\psi (g)\neq 1$
.Footnote
4
We then have
 $$ \begin{align*} \nu((f\circ \phi)\cdot \overline{\psi}) &= \nu\bigl(((f\circ \phi)\cdot \overline{\psi})_{g}\bigr)\\ &= \nu\bigl((f\circ \phi)\cdot (\overline{\psi})_{g}\bigr)\\ &= \psi(g) \nu\bigl((f\circ \phi)\cdot \overline{\psi}\bigr). \end{align*} $$
$$ \begin{align*} \nu((f\circ \phi)\cdot \overline{\psi}) &= \nu\bigl(((f\circ \phi)\cdot \overline{\psi})_{g}\bigr)\\ &= \nu\bigl((f\circ \phi)\cdot (\overline{\psi})_{g}\bigr)\\ &= \psi(g) \nu\bigl((f\circ \phi)\cdot \overline{\psi}\bigr). \end{align*} $$
So
![]() $\nu ((f\circ \phi )\cdot \overline {\psi }) = \psi (g)\nu ((f\circ \phi )\cdot \overline {\psi })$
, which means
$\nu ((f\circ \phi )\cdot \overline {\psi }) = \psi (g)\nu ((f\circ \phi )\cdot \overline {\psi })$
, which means
![]() $\widehat {f\circ \phi }(\psi )=0$
since
$\widehat {f\circ \phi }(\psi )=0$
since
![]() $\psi (g)\neq 1$
. This proves the first statement in the claim, and the second statement is proved similarly.
$\psi (g)\neq 1$
. This proves the first statement in the claim, and the second statement is proved similarly.
Claim 4.9. Let
![]() $\chi \in \widehat {K}_1$
. Then
$\chi \in \widehat {K}_1$
. Then
![]() $\widehat {\rho ^{\nu }_{f\circ \phi }}(\chi ) = 0$
unless
$\widehat {\rho ^{\nu }_{f\circ \phi }}(\chi ) = 0$
unless
![]() $\chi =\chi '\circ \tilde {\phi }$
for some
$\chi =\chi '\circ \tilde {\phi }$
for some
![]() $\chi '\in \widehat {K}_2$
.
$\chi '\in \widehat {K}_2$
.
To prove this claim, let
![]() $\chi \in \widehat {K}_1$
. Then
$\chi \in \widehat {K}_1$
. Then
By Claim 4.8, the above evaluates to
![]() $0$
unless
$0$
unless
![]() $\chi \circ \tau _1=\psi \circ \phi $
for some
$\chi \circ \tau _1=\psi \circ \phi $
for some
![]() $\psi \in \widehat {H}$
. Choosing such a
$\psi \in \widehat {H}$
. Choosing such a
![]() $\psi $
, we have
$\psi $
, we have
By assumption (ii), we may write
![]() $\psi $
as
$\psi $
as
![]() $\chi '\circ \tau _2$
for some
$\chi '\circ \tau _2$
for some
![]() $\chi '\in \widehat {K}_2$
. Then
$\chi '\in \widehat {K}_2$
. Then
![]() $\chi \circ \tau _1 = (\chi '\circ \tau _2)\circ \phi = \chi '\circ \tilde {\phi }\circ \tau _1$
. So
$\chi \circ \tau _1 = (\chi '\circ \tau _2)\circ \phi = \chi '\circ \tilde {\phi }\circ \tau _1$
. So
![]() $\chi \circ \tau _1 = \chi '\circ \tilde {\phi } \circ \tau _1$
. The denseness of
$\chi \circ \tau _1 = \chi '\circ \tilde {\phi } \circ \tau _1$
. The denseness of
![]() $\tau _1(G)$
in
$\tau _1(G)$
in
![]() $K_1$
and continuity of
$K_1$
and continuity of
![]() $\chi $
then implies
$\chi $
then implies
![]() $\chi = \chi '\circ \tilde {\phi }$
. This shows that
$\chi = \chi '\circ \tilde {\phi }$
. This shows that
![]() $\widehat {\rho ^{\nu }_{f\circ \phi }}(\chi ) = 0$
unless
$\widehat {\rho ^{\nu }_{f\circ \phi }}(\chi ) = 0$
unless
![]() $\chi =\chi '\circ \tilde {\phi }$
for some
$\chi =\chi '\circ \tilde {\phi }$
for some
![]() $\chi '\in \widehat {K}_2$
.
$\chi '\in \widehat {K}_2$
.
We now prove equation (20).
Case 1:
![]() $\chi =\chi '\circ \tilde {\phi }$
for some
$\chi =\chi '\circ \tilde {\phi }$
for some
![]() $\chi '\in \widehat {K}_2$
. Then
$\chi '\in \widehat {K}_2$
. Then
 $$ \begin{align*} \widehat{\rho_{f\circ\phi}^{\nu}}(\chi) & = \int_{K_1} \rho_{f\circ\phi}^{\nu}\, \overline{\chi}\, dm_{K_1} \\ & = \nu \left( \left( f\circ \phi \right) \cdot \left( \overline{\chi}\circ \tau_1 \right) \right) && \text{by definition of } \rho_{f\circ \phi}^{\nu}\\ & = \nu\left( (f\circ \phi) \cdot \left( \overline{\chi'\circ \tilde{\phi}}\circ \tau_1 \right) \right)\\ &= \nu\left( \left( f\circ \phi \right) \cdot \left( \overline{\chi'\circ \tau_2}\circ \phi\right) \right)\\ &= \phi_* \nu\left(f\, \cdot \overline{\chi'\circ \tau_2}\right)\\ &= \int_{K_2} \rho_f^{\phi_* \nu} \overline{\chi'}\, dm_{K_2}\\ &= \int_{K_1} \left( \rho_f^{\phi_*\nu} \circ \tilde{\phi} \right) \cdot \left( \overline{\chi'}\circ \tilde{\phi} \right)\, dm_{K_1}\\ &= \widehat{ \rho_f^{\phi_*\nu} \circ \tilde{\phi} }(\chi). \end{align*} $$
$$ \begin{align*} \widehat{\rho_{f\circ\phi}^{\nu}}(\chi) & = \int_{K_1} \rho_{f\circ\phi}^{\nu}\, \overline{\chi}\, dm_{K_1} \\ & = \nu \left( \left( f\circ \phi \right) \cdot \left( \overline{\chi}\circ \tau_1 \right) \right) && \text{by definition of } \rho_{f\circ \phi}^{\nu}\\ & = \nu\left( (f\circ \phi) \cdot \left( \overline{\chi'\circ \tilde{\phi}}\circ \tau_1 \right) \right)\\ &= \nu\left( \left( f\circ \phi \right) \cdot \left( \overline{\chi'\circ \tau_2}\circ \phi\right) \right)\\ &= \phi_* \nu\left(f\, \cdot \overline{\chi'\circ \tau_2}\right)\\ &= \int_{K_2} \rho_f^{\phi_* \nu} \overline{\chi'}\, dm_{K_2}\\ &= \int_{K_1} \left( \rho_f^{\phi_*\nu} \circ \tilde{\phi} \right) \cdot \left( \overline{\chi'}\circ \tilde{\phi} \right)\, dm_{K_1}\\ &= \widehat{ \rho_f^{\phi_*\nu} \circ \tilde{\phi} }(\chi). \end{align*} $$
Case 2:
![]() $\chi \neq \chi '\circ \tilde {\phi }$
for all
$\chi \neq \chi '\circ \tilde {\phi }$
for all
![]() $\chi '\in \widehat {K}_2$
. In this case, Claim 4.8 implies
$\chi '\in \widehat {K}_2$
. In this case, Claim 4.8 implies
![]() $\widehat {(\rho _f^{\phi _* \nu })\circ \tilde {\phi }}(\chi )=0$
, and Claim 4.9 implies
$\widehat {(\rho _f^{\phi _* \nu })\circ \tilde {\phi }}(\chi )=0$
, and Claim 4.9 implies
![]() $\widehat {\rho _{f\circ \phi }^{\nu }}(\chi )=0$
.
$\widehat {\rho _{f\circ \phi }^{\nu }}(\chi )=0$
.
Corollary 4.10. Let G be a discrete abelian group,
![]() $\nu $
an invariant mean on G and
$\nu $
an invariant mean on G and
![]() $\phi : G \to G$
an endomorphism. Let K be a compact abelian group,
$\phi : G \to G$
an endomorphism. Let K be a compact abelian group,
![]() $\tau : G \to K$
a homomorphism with dense image and
$\tau : G \to K$
a homomorphism with dense image and
![]() $\tilde {\phi }: K \to K$
an endomorphism such that
$\tilde {\phi }: K \to K$
an endomorphism such that
![]() $\tilde {\phi } \circ \tau = \tau \circ \phi $
. Assume further that for all
$\tilde {\phi } \circ \tau = \tau \circ \phi $
. Assume further that for all
![]() $\chi \in \widehat {K}$
, if there is a
$\chi \in \widehat {K}$
, if there is a
![]() $\psi \in \widehat {G}$
such that
$\psi \in \widehat {G}$
such that
![]() $\chi \circ \tau =\psi \circ \phi $
, then there is a
$\chi \circ \tau =\psi \circ \phi $
, then there is a
![]() $\chi '\in \widehat {K}$
such that
$\chi '\in \widehat {K}$
such that
![]() $\psi = \chi '\circ \tau $
. Let
$\psi = \chi '\circ \tau $
. Let
![]() $H = \phi (G)$
,
$H = \phi (G)$
,
![]() $A\subset G$
, and let
$A\subset G$
, and let
![]() $\rho _{A}^{\nu }: K \to [0, 1]$
and
$\rho _{A}^{\nu }: K \to [0, 1]$
and
![]() $\rho _{\phi (A)}^{\phi _* \nu }: \tilde {\phi }(K) \to [0, 1]$
be the associated Radon-Nikodym densities. Then
$\rho _{\phi (A)}^{\phi _* \nu }: \tilde {\phi }(K) \to [0, 1]$
be the associated Radon-Nikodym densities. Then
![]() $m_{K}$
-almost everywhere.
$m_{K}$
-almost everywhere.
Proof. Applying Lemma 4.6 for
![]() $H = \phi (G)$
and
$H = \phi (G)$
and
![]() $f = 1_{\phi (A)}: H \to [0,1]$
, we get
$f = 1_{\phi (A)}: H \to [0,1]$
, we get
Since
![]() $1_{\phi (A)} \circ \phi = 1_{\phi ^{-1}(\phi (A))} \geq 1_A$
, we have
$1_{\phi (A)} \circ \phi = 1_{\phi ^{-1}(\phi (A))} \geq 1_A$
, we have
It follows that
![]() $ \rho _{1_A}^{\nu } \leq \rho _{1_{\phi (A)}}^{\phi _* \nu } \circ \tilde {\phi }$
, meaning
$ \rho _{1_A}^{\nu } \leq \rho _{1_{\phi (A)}}^{\phi _* \nu } \circ \tilde {\phi }$
, meaning
5 Reducing correlation sequences to integrals in compact groups
The goal of this section is to show that certain averages for ergodic G-systems can be reduced to double integrals on a compact group. Lemma 5.1 establishes this for group rotations on a compact abelian group K, as long as some endomorphisms on G can be extended to all of K.
Lemma 5.1. Let K be a compact abelian group and let
![]() $\tau :G\to K$
be a homomorphism with dense image. Let
$\tau :G\to K$
be a homomorphism with dense image. Let
![]() $\phi _1, \phi _2, \phi _3: G\to G$
be endomorphisms. Suppose there are continuous endomorphisms
$\phi _1, \phi _2, \phi _3: G\to G$
be endomorphisms. Suppose there are continuous endomorphisms
![]() $\tilde {\phi }_i: K \to K$
such that
$\tilde {\phi }_i: K \to K$
such that
![]() $\tilde {\phi _i}\circ \tau = \tau \circ \phi _i$
for
$\tilde {\phi _i}\circ \tau = \tau \circ \phi _i$
for
![]() $1 \leq i \leq 3$
. Then for all bounded measurable
$1 \leq i \leq 3$
. Then for all bounded measurable
![]() $f_1, f_2, f_3 :K\to \mathbb C$
, we have
$f_1, f_2, f_3 :K\to \mathbb C$
, we have
 $$ \begin{align*} I(\vec{f}, \vec{\phi}) &:= UC-\lim_{g \in G} \int_K f_1(z+\tau(\phi_1(g)))f_2(z+\tau(\phi_2(g)))f_3(z+\tau(\phi_3(g)))\, dm_K(z) \\ &= \iint_{K^2} f_1(z+\tilde{\phi}_1(t))f_2(z+\tilde{\phi}_2(t))f_3(z+\tilde{\phi}_3(t))\, dm_K(z)\, dm_K(t). \end{align*} $$
$$ \begin{align*} I(\vec{f}, \vec{\phi}) &:= UC-\lim_{g \in G} \int_K f_1(z+\tau(\phi_1(g)))f_2(z+\tau(\phi_2(g)))f_3(z+\tau(\phi_3(g)))\, dm_K(z) \\ &= \iint_{K^2} f_1(z+\tilde{\phi}_1(t))f_2(z+\tilde{\phi}_2(t))f_3(z+\tilde{\phi}_3(t))\, dm_K(z)\, dm_K(t). \end{align*} $$
Proof. Since
![]() $I(\vec {f},\vec {\phi })$
is continuous in
$I(\vec {f},\vec {\phi })$
is continuous in
![]() $f_i$
(with respect to the
$f_i$
(with respect to the
![]() $L^2(m_K)$
-norm) and multilinear in
$L^2(m_K)$
-norm) and multilinear in
![]() $f_i$
, it suffices to prove the identity when each
$f_i$
, it suffices to prove the identity when each
![]() $f_i$
is a character
$f_i$
is a character
![]() $\chi _i$
of K. In this case, we have
$\chi _i$
of K. In this case, we have
 $$ \begin{align*} I(\chi_1,\chi_2,\chi_3,\vec{\phi})&= UC-\lim_{g \in G}\int_K \chi_1\chi_2\chi_3(z)\prod_{i=1}^3 \chi_i(\tau(\phi_i(g)))\, dm_K(z)\\ &= UC-\lim_{g \in G} \int_K \chi_1 \chi_2 \chi_3(z) \prod_{i=1}^3 \chi_i \circ \tilde{\phi}_i(\tau(g))\, dm_K(z). \end{align*} $$
$$ \begin{align*} I(\chi_1,\chi_2,\chi_3,\vec{\phi})&= UC-\lim_{g \in G}\int_K \chi_1\chi_2\chi_3(z)\prod_{i=1}^3 \chi_i(\tau(\phi_i(g)))\, dm_K(z)\\ &= UC-\lim_{g \in G} \int_K \chi_1 \chi_2 \chi_3(z) \prod_{i=1}^3 \chi_i \circ \tilde{\phi}_i(\tau(g))\, dm_K(z). \end{align*} $$
By (6), we have
 $$ \begin{align*} I(\chi_1, \chi_2, \chi_3, \vec{\phi}) &= \iint_{K^2} \chi_1 \chi_2 \chi_3(z) \prod_{i=1}^3 \chi_i \circ \tilde{\phi}_i(t) \, d m_K(z) d m_K(t) \\ &= \iint_{K^2} \prod_{i=1}^3 \chi_i(z + \tilde{\phi}_i(t)) \, d m_K(z) d m_K(t), \end{align*} $$
$$ \begin{align*} I(\chi_1, \chi_2, \chi_3, \vec{\phi}) &= \iint_{K^2} \chi_1 \chi_2 \chi_3(z) \prod_{i=1}^3 \chi_i \circ \tilde{\phi}_i(t) \, d m_K(z) d m_K(t) \\ &= \iint_{K^2} \prod_{i=1}^3 \chi_i(z + \tilde{\phi}_i(t)) \, d m_K(z) d m_K(t), \end{align*} $$
and this finishes our proof.
The next proposition deals with a general ergodic G-system
![]() $\mathbf {X}$
. The compact group in question will be an extension K of the group Z underlying Kronecker factor of
$\mathbf {X}$
. The compact group in question will be an extension K of the group Z underlying Kronecker factor of
![]() $\mathbf {X}$
, constructed to be invariant under the corresponding
$\mathbf {X}$
, constructed to be invariant under the corresponding
![]() $\tilde {\phi }_i$
, as required by Lemma 5.1.
$\tilde {\phi }_i$
, as required by Lemma 5.1.
Proposition 5.2. Given an ergodic measure preserving G-system
![]() $\mathbf X=(X,\mu , T)$
and
$\mathbf X=(X,\mu , T)$
and
![]() $f:X\to [0,1]$
, define
$f:X\to [0,1]$
, define
![]() $I:G\to \mathbb R_{\geq 0}$
by
$I:G\to \mathbb R_{\geq 0}$
by
where
![]() $\phi _2, \phi _3: G\to G$
are endomorphisms such that
$\phi _2, \phi _3: G\to G$
are endomorphisms such that
![]() $\phi _2, \phi _3, \phi _2 + \phi _3$
have finite index images in G.
$\phi _2, \phi _3, \phi _2 + \phi _3$
have finite index images in G.
Then there are a compact abelian group K, a homomorphism
![]() $\tau : G\to K$
with dense image, endomorphisms
$\tau : G\to K$
with dense image, endomorphisms
![]() $\tilde {\phi }_2, \tilde {\phi }_3:K\to K$
and
$\tilde {\phi }_2, \tilde {\phi }_3:K\to K$
and
![]() $\tilde {f}:K\to [0,1]$
with
$\tilde {f}:K\to [0,1]$
with
![]() $\int _K \tilde {f}\, dm_K = \int _X f\, d\mu $
such that for all
$\int _K \tilde {f}\, dm_K = \int _X f\, d\mu $
such that for all
![]() $w \in G$
,
$w \in G$
,
Furthermore,
![]() $[K:\tilde {\phi }_i(K)] \leq [G:\phi _i(G)]$
for each
$[K:\tilde {\phi }_i(K)] \leq [G:\phi _i(G)]$
for each
![]() $i \in \{2, 3\}$
and
$i \in \{2, 3\}$
and
![]() $[K: (\tilde {\phi }_2 + \tilde {\phi }_3)(K)] \leq [G: (\phi _2 + \phi _3)(G)]$
.
$[K: (\tilde {\phi }_2 + \tilde {\phi }_3)(K)] \leq [G: (\phi _2 + \phi _3)(G)]$
.
Proof. Let
![]() $\phi _1 = -\phi _2 - \phi _3$
. We first prove the special case of the lemma where
$\phi _1 = -\phi _2 - \phi _3$
. We first prove the special case of the lemma where
![]() $\mathcal {E}(\mathbf {X})$
is invariant under each
$\mathcal {E}(\mathbf {X})$
is invariant under each
![]() $\phi _i$
, meaning that for all eigenvalues
$\phi _i$
, meaning that for all eigenvalues
![]() $\lambda \in \mathcal {E}(\mathbf {X})$
and
$\lambda \in \mathcal {E}(\mathbf {X})$
and
![]() $i \in \{1, 2,3\}$
, we have
$i \in \{1, 2,3\}$
, we have
![]() $\lambda \circ \phi _i\in \mathcal {E}(\mathbf {X})$
. In this case, the conclusion was also observed in [Reference Ackelsberg, Bergelson and Best2, Remark 3.2]. By [Reference Ackelsberg, Bergelson and Best2, Section 3], the Kronecker factor
$\lambda \circ \phi _i\in \mathcal {E}(\mathbf {X})$
. In this case, the conclusion was also observed in [Reference Ackelsberg, Bergelson and Best2, Remark 3.2]. By [Reference Ackelsberg, Bergelson and Best2, Section 3], the Kronecker factor
![]() $(Z, m_Z, R)$
of
$(Z, m_Z, R)$
of
![]() $(X, \mu , T)$
is characteristic for the average defining
$(X, \mu , T)$
is characteristic for the average defining
![]() $I(w).$
Let
$I(w).$
Let
![]() $\tau : G \to Z$
be the canonical projection. We can therefore replace f with
$\tau : G \to Z$
be the canonical projection. We can therefore replace f with
![]() $\tilde {f} := \mathbb {E}(f|Z)$
without changing
$\tilde {f} := \mathbb {E}(f|Z)$
without changing
![]() $I(w)$
:
$I(w)$
:
 $$ \begin{align} I(w)&= UC-\lim_{g \in G} \int_Z \tilde{f} \cdot R_{\phi_3(g)}\tilde{f} \cdot R_{w-\phi_2(g)}\tilde{f}\, dm_Z \nonumber\\ &= UC-\lim_{g \in G} \int_Z \tilde{f}(z)\tilde{f}(z+\tau(\phi_3(g)))\tilde{f}(z+\tau(w-\phi_2(g)))\, dm_Z(z). \end{align} $$
$$ \begin{align} I(w)&= UC-\lim_{g \in G} \int_Z \tilde{f} \cdot R_{\phi_3(g)}\tilde{f} \cdot R_{w-\phi_2(g)}\tilde{f}\, dm_Z \nonumber\\ &= UC-\lim_{g \in G} \int_Z \tilde{f}(z)\tilde{f}(z+\tau(\phi_3(g)))\tilde{f}(z+\tau(w-\phi_2(g)))\, dm_Z(z). \end{align} $$
In view of Lemma 3.2, let
![]() $\tilde {\phi }_i:Z\to Z$
be continuous endomorphisms satisfying
$\tilde {\phi }_i:Z\to Z$
be continuous endomorphisms satisfying
![]() $\tau \circ \phi _i=\tilde {\phi }_i\circ \tau $
. Applying this identity to (22), we have
$\tau \circ \phi _i=\tilde {\phi }_i\circ \tau $
. Applying this identity to (22), we have
By Lemma 5.1, we can rewrite the previous line as
Taking
![]() $K = Z$
, we prove the proposition in this special case.
$K = Z$
, we prove the proposition in this special case.
For the general case, let
![]() $\Lambda $
be the smallest subgroup of
$\Lambda $
be the smallest subgroup of
![]() $\widehat {G}$
that contains
$\widehat {G}$
that contains
![]() $\mathcal {E}(\mathbf {X})$
and is closed under each
$\mathcal {E}(\mathbf {X})$
and is closed under each
![]() $\phi _i^*$
. Since
$\phi _i^*$
. Since
![]() $\mathcal {E}(\mathbf {X})$
is countable, it is easy to see that
$\mathcal {E}(\mathbf {X})$
is countable, it is easy to see that
![]() $\Lambda $
is countable. Let
$\Lambda $
is countable. Let
![]() $\mathbf {K} = (\widehat {\Lambda }, m_{\widehat {\Lambda }}, R)$
be the group rotation on
$\mathbf {K} = (\widehat {\Lambda }, m_{\widehat {\Lambda }}, R)$
be the group rotation on
![]() $\widehat {\Lambda }$
described in Lemma 3.3. By part (i) of Lemma 3.3, we have
$\widehat {\Lambda }$
described in Lemma 3.3. By part (i) of Lemma 3.3, we have
![]() $\mathcal {E}(\mathbf {K}) = \Lambda $
. Since
$\mathcal {E}(\mathbf {K}) = \Lambda $
. Since
![]() $\mathcal {E}(\mathbf {Z}) = \mathcal {E}(\mathbf {X}) \subset \Lambda $
, part (ii) of Lemma 3.3 implies that
$\mathcal {E}(\mathbf {Z}) = \mathcal {E}(\mathbf {X}) \subset \Lambda $
, part (ii) of Lemma 3.3 implies that
![]() $\mathbf {Z}$
is a factor of
$\mathbf {Z}$
is a factor of
![]() $\mathbf {K}$
.
$\mathbf {K}$
.
We now fix an ergodic G-system
![]() $\mathbf {Y} = (Y, \nu , S)$
that is a common extension of
$\mathbf {Y} = (Y, \nu , S)$
that is a common extension of
![]() $\mathbf {X}$
and
$\mathbf {X}$
and
![]() $\mathbf {K}$
. For example, we can take
$\mathbf {K}$
. For example, we can take
![]() $\mathbf {Y} = (X \times K, \nu , T \times R)$
to be an ergodic joining of
$\mathbf {Y} = (X \times K, \nu , T \times R)$
to be an ergodic joining of
![]() $\mathbf X$
and
$\mathbf X$
and
![]() $\mathbf K$
. (For details about joinings and the existence of ergodic joinings, see Glasner [Reference Glasner19, Section 6] or de la Rue [Reference de la Rue and Meyers14, Section 3.1].)
$\mathbf K$
. (For details about joinings and the existence of ergodic joinings, see Glasner [Reference Glasner19, Section 6] or de la Rue [Reference de la Rue and Meyers14, Section 3.1].)
Writing
![]() $\pi : Y\to X$
for the factor map, we define
$\pi : Y\to X$
for the factor map, we define
![]() $f': Y \to \mathbb [0,1]$
to satisfy
$f': Y \to \mathbb [0,1]$
to satisfy
![]() $f':= f\circ \pi $
and
$f':= f\circ \pi $
and
Since
![]() $f'$
is a lift from f on X, it is obvious that
$f'$
is a lift from f on X, it is obvious that
![]() $I' = I$
and the Kronecker factor
$I' = I$
and the Kronecker factor
![]() $\mathbf {Z}$
of
$\mathbf {Z}$
of
![]() $\mathbf {X}$
is characteristic for the averages
$\mathbf {X}$
is characteristic for the averages
![]() $I'(w)$
. Thus, any factor of
$I'(w)$
. Thus, any factor of
![]() $\mathbf {Y}$
between
$\mathbf {Y}$
between
![]() $\mathbf {Y}$
and
$\mathbf {Y}$
and
![]() $\mathbf {Z}$
is also characteristic for
$\mathbf {Z}$
is also characteristic for
![]() $I'(w)$
. In particular,
$I'(w)$
. In particular,
![]() $\mathbf {K}$
is characteristic for
$\mathbf {K}$
is characteristic for
![]() $I'(w)$
. Now applying an argument similar to the first part of the proof to the factor
$I'(w)$
. Now applying an argument similar to the first part of the proof to the factor
![]() $\mathbf {K}$
of
$\mathbf {K}$
of
![]() $\mathbf {Y}$
and the function
$\mathbf {Y}$
and the function
![]() $f'$
, we obtain the compact group
$f'$
, we obtain the compact group
![]() $K = \widehat {\Lambda }$
, the function
$K = \widehat {\Lambda }$
, the function
![]() $\tilde {f} = \mathbb {E}(f'| K)$
and endomorphisms
$\tilde {f} = \mathbb {E}(f'| K)$
and endomorphisms
![]() $\tilde {\phi }_i$
satisfying (21). Finally, we have
$\tilde {\phi }_i$
satisfying (21). Finally, we have
![]() $[K:\tilde {\phi }_i(K)] \leq [G:\phi _i(G)]$
for each
$[K:\tilde {\phi }_i(K)] \leq [G:\phi _i(G)]$
for each
![]() $i \in \{1, 2, 3\}$
by Lemma 3.2 (ii).
$i \in \{1, 2, 3\}$
by Lemma 3.2 (ii).
6 First correspondence principle and Bohr sets in
 $\phi _1(A) + \phi _2(A) + \phi _3(A)$
$\phi _1(A) + \phi _2(A) + \phi _3(A)$
Proposition 6.1. Let G be a countable abelian group. Let
![]() $\phi _1, \phi _2, \phi _3: G \to G$
be commuting endomorphisms with finite index images such that
$\phi _1, \phi _2, \phi _3: G \to G$
be commuting endomorphisms with finite index images such that
![]() $\phi _1 + \phi _2 + \phi _3 = 0$
. Let
$\phi _1 + \phi _2 + \phi _3 = 0$
. Let
![]() $(X, \mu , T)$
be an ergodic G-system and
$(X, \mu , T)$
be an ergodic G-system and
![]() $f: X \to [0, 1]$
with
$f: X \to [0, 1]$
with
![]() $\int _X f = \delta> 0$
. Define the function
$\int _X f = \delta> 0$
. Define the function
![]() $I: G \to [0,1]$
by
$I: G \to [0,1]$
by
Then
![]() $\operatorname {supp}(I)$
contains a Bohr-
$\operatorname {supp}(I)$
contains a Bohr-
![]() $(k, \eta )$
set, where
$(k, \eta )$
set, where
![]() $k, \eta $
depend only on
$k, \eta $
depend only on
![]() $\delta $
and the indices of
$\delta $
and the indices of
![]() $\phi _i(G)$
in G.
$\phi _i(G)$
in G.
Proof. By Proposition 5.2, there exist a compact abelian group K with Haar measure
![]() $m_K$
, a homomorphism
$m_K$
, a homomorphism
![]() $\tau : G\to K$
with dense image, and endomorphisms
$\tau : G\to K$
with dense image, and endomorphisms
![]() $\tilde {\phi }_i:K\to K$
and
$\tilde {\phi }_i:K\to K$
and
![]() $\tilde {f}:K\to [0,1]$
with
$\tilde {f}:K\to [0,1]$
with
![]() $\int _K \tilde {f}\, dm_K=\int _X f\, d\mu = \delta $
such that
$\int _K \tilde {f}\, dm_K=\int _X f\, d\mu = \delta $
such that
Furthermore,
![]() $[K:\tilde {\phi }_i(K)] \leq [G:\phi _i(G)]$
for each i. Now define
$[K:\tilde {\phi }_i(K)] \leq [G:\phi _i(G)]$
for each i. Now define
![]() $I': K \to [0, 1]$
by
$I': K \to [0, 1]$
by
By change of variable
![]() $z \mapsto z + \tilde {\phi }_2(t)$
and using
$z \mapsto z + \tilde {\phi }_2(t)$
and using
![]() $\phi _2 + \phi _3 = - \phi _1$
, we obtain
$\phi _2 + \phi _3 = - \phi _1$
, we obtain
Applying [Reference Le and Lê33, Proposition 4.3], it follows that
![]() $\operatorname {supp}(I')$
contains a Bohr-
$\operatorname {supp}(I')$
contains a Bohr-
![]() $(k, \eta )$
set B in K, where
$(k, \eta )$
set B in K, where
![]() $k, \eta $
depends only on
$k, \eta $
depends only on
![]() $\delta $
and the indices
$\delta $
and the indices
![]() $[K:\tilde {\phi }_i(K)]$
. It is easy to see that
$[K:\tilde {\phi }_i(K)]$
. It is easy to see that
![]() $\operatorname {supp}(I)$
contains
$\operatorname {supp}(I)$
contains
![]() $\tau ^{-1}(B)$
. Moreover, Lemma 2.2 implies that
$\tau ^{-1}(B)$
. Moreover, Lemma 2.2 implies that
![]() $\tau ^{-1}(B)$
contains a Bohr-
$\tau ^{-1}(B)$
contains a Bohr-
![]() $(k, \eta )$
set in G, completing the proof.
$(k, \eta )$
set in G, completing the proof.
Proposition 6.2 (First correspondence principle).
Let G be a countable abelian group and
![]() $A \subset G$
with
$A \subset G$
with
![]() $d^*(A) = \delta> 0$
. Let
$d^*(A) = \delta> 0$
. Let
![]() $\phi _1, \phi _2, \phi _3$
be commuting endomorphisms of G with finite index image such that
$\phi _1, \phi _2, \phi _3$
be commuting endomorphisms of G with finite index image such that
![]() $\phi _1 + \phi _2 + \phi _3 = 0$
. Then there is an ergodic G-system
$\phi _1 + \phi _2 + \phi _3 = 0$
. Then there is an ergodic G-system
![]() $\mathbf {X} := (X, \mu , T)$
and a function
$\mathbf {X} := (X, \mu , T)$
and a function
![]() $f: X \to [0, 1]$
with
$f: X \to [0, 1]$
with
![]() $\int _X f \, d\mu = d^*(A)$
such that the function
$\int _X f \, d\mu = d^*(A)$
such that the function
![]() $I: G \to [0,1]$
defined by
$I: G \to [0,1]$
defined by
satisfies
![]() $\phi _3(\operatorname {supp} I) \subset \phi _1(A) + \phi _2(A) + \phi _3(A)$
.
$\phi _3(\operatorname {supp} I) \subset \phi _1(A) + \phi _2(A) + \phi _3(A)$
.
Proof. By Furstenberg’s correspondence principle (for example, see [Reference Bergelson and Moragues6, Theorem 2.8]), there exists an ergodic G-system
![]() $(X, \mu , T)$
and a measurable set
$(X, \mu , T)$
and a measurable set
![]() $E \subset X$
with
$E \subset X$
with
![]() $\mu (E) = d^*(A)$
such that for all
$\mu (E) = d^*(A)$
such that for all
![]() $w_1, w_2 \in G$
,
$w_1, w_2 \in G$
,
Letting
![]() $f = 1_E$
,
$f = 1_E$
,
![]() $w_1 = \phi _3(g)$
and
$w_1 = \phi _3(g)$
and
![]() $w_2 = w - \phi _2(g)$
, we deduce that for all w and
$w_2 = w - \phi _2(g)$
, we deduce that for all w and
![]() $g \in G$
,
$g \in G$
,
It follows that if
![]() $w \in \operatorname {supp}(I)$
, then there are
$w \in \operatorname {supp}(I)$
, then there are
![]() $h \in A$
and
$h \in A$
and
![]() $g \in G$
such that h,
$g \in G$
such that h,
![]() $h + \phi _3(g)$
, and
$h + \phi _3(g)$
, and
![]() $h + w - \phi _2(g)$
all belong to A. Therefore,
$h + w - \phi _2(g)$
all belong to A. Therefore,
and this finishes our proof. Note that in (23), we use the fact that
![]() $\phi _2 \circ \phi _3 = \phi _3 \circ \phi _2$
.
$\phi _2 \circ \phi _3 = \phi _3 \circ \phi _2$
.
We are ready to prove Theorem 1.2.
Proof of Theorem 1.2.
By Proposition 6.2, there exists an ergodic G-system
![]() $(X, \mu , T)$
and
$(X, \mu , T)$
and
![]() $f: X \to [0,1]$
with
$f: X \to [0,1]$
with
![]() $\int _X f = d^*(A)$
such that
$\int _X f = d^*(A)$
such that
has
![]() $\phi _3(\operatorname {supp}(I)) \subset \phi _1(A) + \phi _2(A) + \phi _3(A)$
.
$\phi _3(\operatorname {supp}(I)) \subset \phi _1(A) + \phi _2(A) + \phi _3(A)$
.
In view of Proposition 6.1,
![]() $\operatorname {supp}(I)$
contains a Bohr-
$\operatorname {supp}(I)$
contains a Bohr-
![]() $(k, \eta )$
set where
$(k, \eta )$
set where
![]() $k, \eta $
only depends on
$k, \eta $
only depends on
![]() $\delta $
and the indices of
$\delta $
and the indices of
![]() $\phi _i(G)$
in G. Lemma 2.3 then implies that
$\phi _i(G)$
in G. Lemma 2.3 then implies that
![]() $\phi _3(\operatorname {supp}(I))$
contains a Bohr-
$\phi _3(\operatorname {supp}(I))$
contains a Bohr-
![]() $(k', \eta ')$
set where
$(k', \eta ')$
set where
![]() $k', \eta '$
depends only on
$k', \eta '$
depends only on
![]() $\delta $
and the indices mentioned above.
$\delta $
and the indices mentioned above.
7 Second correspondence principle
In this section, we establish the second correspondence principle Proposition 7.1, which is used in the proof of Theorem 1.4. This can be thought of as a special case of Propositions 3.1 and 3.2 of [Reference Björklund10]. Here we write
![]() $bG$
for the Bohr compactification of G.
$bG$
for the Bohr compactification of G.
Proposition 7.1 (Second correspondence principle).
Let
![]() $K = bG$
and let
$K = bG$
and let
![]() $\tau : G \to K$
be the natural embedding. Let
$\tau : G \to K$
be the natural embedding. Let
![]() $A, B \subset G$
and let
$A, B \subset G$
and let
![]() $\nu , \lambda $
be two invariant means on G where
$\nu , \lambda $
be two invariant means on G where
![]() $\lambda $
is extremal. Then
$\lambda $
is extremal. Then
![]() $A + B - B$
contains
$A + B - B$
contains
![]() $\tau ^{-1}(\operatorname {supp} (\rho _{A}^{\nu } * \rho _{B}^{\lambda } * \rho _{-B}^{\lambda }))$
.
$\tau ^{-1}(\operatorname {supp} (\rho _{A}^{\nu } * \rho _{B}^{\lambda } * \rho _{-B}^{\lambda }))$
.
Proof. By Lemma 4.4, the Radon-Nikodym density
![]() $\rho _{A}^{\nu }$
is supported on
$\rho _{A}^{\nu }$
is supported on
![]() $\overline {\tau (A)}$
. Therefore, the convolution
$\overline {\tau (A)}$
. Therefore, the convolution
![]() $\rho _{A}^{\nu } * \rho _{B}^{\lambda }$
, which is defined as
$\rho _{A}^{\nu } * \rho _{B}^{\lambda }$
, which is defined as
is supported on
![]() $\overline {\tau (A)} + \overline {\tau (B)} = \overline {\tau (A + B)}$
. Similarly,
$\overline {\tau (A)} + \overline {\tau (B)} = \overline {\tau (A + B)}$
. Similarly,
![]() $\rho _{A}^{\nu } * \rho _{B}^{\lambda } * \rho _{-B}^{\lambda }$
is supported on
$\rho _{A}^{\nu } * \rho _{B}^{\lambda } * \rho _{-B}^{\lambda }$
is supported on
![]() $\overline {\tau (A + B - B)}$
. This, however, is weaker than the conclusion of Proposition 7.1 and is insufficient for our purpose.
$\overline {\tau (A + B - B)}$
. This, however, is weaker than the conclusion of Proposition 7.1 and is insufficient for our purpose.
Define
![]() $\phi , \theta : G \to [0, 1]$
by
$\phi , \theta : G \to [0, 1]$
by
and
We can see that
![]() $\theta $
is supported on
$\theta $
is supported on
![]() $A + B - B$
. It remains to show that
$A + B - B$
. It remains to show that
![]() $\theta = (\rho _{A}^{\nu } * \rho _{B}^{\lambda } * \rho _{-B}^{\lambda }) \circ \tau $
.
$\theta = (\rho _{A}^{\nu } * \rho _{B}^{\lambda } * \rho _{-B}^{\lambda }) \circ \tau $
.
Claim 7.2.
![]() $\phi = \eta + \psi $
, where
$\phi = \eta + \psi $
, where
![]() $\psi $
is a null function and
$\psi $
is a null function and
![]() $\eta := (\rho _{B}^{\lambda } * \rho _{-B}^{\lambda }) \circ \tau $
.
$\eta := (\rho _{B}^{\lambda } * \rho _{-B}^{\lambda }) \circ \tau $
.
Proof of claim.
One can verify that
![]() $\phi $
is positive definite by writing
$\phi $
is positive definite by writing
![]() $\sum _{g,h\in G} c_g\overline {c}_h \phi (g-h)$
as
$\sum _{g,h\in G} c_g\overline {c}_h \phi (g-h)$
as
![]() $\int _G (\sum _{g} c_g1_B(x-g))\overline {\sum _{h} c_h 1_{B}(x-h)}\, d\lambda (x)= \int _G \bigl |\sum _{g} 1_B(x-g)\bigr |^2\, d\lambda (x)$
for a finite collection of coefficients
$\int _G (\sum _{g} c_g1_B(x-g))\overline {\sum _{h} c_h 1_{B}(x-h)}\, d\lambda (x)= \int _G \bigl |\sum _{g} 1_B(x-g)\bigr |^2\, d\lambda (x)$
for a finite collection of coefficients
![]() $c_g\in \mathbb C$
. Therefore, by the Bochner-Herglotz Theorem,
$c_g\in \mathbb C$
. Therefore, by the Bochner-Herglotz Theorem,
![]() $\phi $
is the Fourier transform of a positive measure
$\phi $
is the Fourier transform of a positive measure
![]() $\sigma $
on
$\sigma $
on
![]() $\widehat {G}$
. Decomposing
$\widehat {G}$
. Decomposing
![]() $\sigma = \sigma _{d} + \sigma _{c}$
, where
$\sigma = \sigma _{d} + \sigma _{c}$
, where
![]() $\sigma _{d}$
is the discrete component of
$\sigma _{d}$
is the discrete component of
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma _{c}$
is the continuous part, we have
$\sigma _{c}$
is the continuous part, we have
Since
![]() $\sigma _d$
has only countably many atoms,
$\sigma _d$
has only countably many atoms,
![]() $\hat {\sigma }_{d}$
is an almost periodic function. However, by Wiener’s lemma (see [Reference Godement21, Théorème 16(2)]),
$\hat {\sigma }_{d}$
is an almost periodic function. However, by Wiener’s lemma (see [Reference Godement21, Théorème 16(2)]),
![]() $\int _G |\hat {\sigma }_{c}|^2 \, d \mu = 0$
for all invariant means
$\int _G |\hat {\sigma }_{c}|^2 \, d \mu = 0$
for all invariant means
![]() $\mu $
on G.
$\mu $
on G.
Now we will prove that
![]() $\hat {\sigma }_d=\eta $
. We first show that
$\hat {\sigma }_d=\eta $
. We first show that
![]() $\hat {\sigma }_d$
and
$\hat {\sigma }_d$
and
![]() $\eta $
are almost periodic functions defined by Fourier series on G with absolutely summable coefficients. To see this for
$\eta $
are almost periodic functions defined by Fourier series on G with absolutely summable coefficients. To see this for
![]() $\hat {\sigma }_d$
, we write
$\hat {\sigma }_d$
, we write
![]() $\hat {\sigma }_d = \sum _{\chi \in \widehat {G}} \sigma (\{\chi \}) \chi $
, where
$\hat {\sigma }_d = \sum _{\chi \in \widehat {G}} \sigma (\{\chi \}) \chi $
, where
![]() $\sum _{\chi \in \widehat {G}} \sigma (\{\chi \})$
is a convergent sum of nonnegative values. For
$\sum _{\chi \in \widehat {G}} \sigma (\{\chi \})$
is a convergent sum of nonnegative values. For
![]() $\eta $
, note that both
$\eta $
, note that both
![]() $\rho _{B}^{\lambda }$
and
$\rho _{B}^{\lambda }$
and
![]() $\rho _{-B}^{\lambda }$
are in
$\rho _{-B}^{\lambda }$
are in
![]() $L^2(m_K)$
. Thus, their Fourier coefficients are square-summable, and the Fourier coefficents of
$L^2(m_K)$
. Thus, their Fourier coefficients are square-summable, and the Fourier coefficents of
![]() $\rho _B^{\lambda }*\rho _{-B}^{\lambda }$
are absolutely summable. To prove that
$\rho _B^{\lambda }*\rho _{-B}^{\lambda }$
are absolutely summable. To prove that
![]() $\hat {\sigma }_d=\eta $
, it therefore suffices to prove that
$\hat {\sigma }_d=\eta $
, it therefore suffices to prove that
![]() $\hat {\sigma }_d$
and
$\hat {\sigma }_d$
and
![]() $\eta $
have the same Fourier coefficients. This is the same as showing that
$\eta $
have the same Fourier coefficients. This is the same as showing that
![]() $\phi $
and
$\phi $
and
![]() $\eta $
have the same Fourier coefficients, as the Fourier coefficients of
$\eta $
have the same Fourier coefficients, as the Fourier coefficients of
![]() $\hat {\sigma }_c$
are all
$\hat {\sigma }_c$
are all
![]() $0$
(since
$0$
(since
![]() $\hat {\sigma }_c$
is a null function). So we verify that
$\hat {\sigma }_c$
is a null function). So we verify that
for every invariant mean
![]() $\mu $
on G and every character
$\mu $
on G and every character
![]() $\chi \in \widehat {G}$
. Fix the invariant mean
$\chi \in \widehat {G}$
. Fix the invariant mean
![]() $\mu $
, characters
$\mu $
, characters
![]() $\chi \in \widehat {G}$
and
$\chi \in \widehat {G}$
and
![]() $\chi ' \in \widehat {K}$
such that
$\chi ' \in \widehat {K}$
such that
![]() $\chi = \chi ' \circ \tau $
. We then have
$\chi = \chi ' \circ \tau $
. We then have
 $$ \begin{align*} \mu(\phi \overline{\chi}) &= \iint_{G^2} 1_B(t) 1_{-B}(s - t) \overline{\chi(s)} \, d \lambda(t) d \mu(s) \\ &=\iint_{G^2} (1_B \cdot \overline{\chi})(t) \cdot (1_{-B} \cdot \overline{\chi})(s - t) \, d \lambda(t) d \mu(s) \\ &= \lambda(1_B \cdot \overline{\chi}) \lambda(1_{-B} \cdot \overline{\chi}) \;\;\; \text{(by Lemma 2.1)}\\ &= \int_K \rho_{B}^{\lambda} \overline{\chi'} \, d m_K \cdot \int_K \rho_{-B}^{\lambda} \overline{\chi'} \, d m_K \;\;\; (\text{by definitions of } \rho_{B}^{\lambda} \text{ and } \rho_{-B}^{\lambda}) \\ &= \widehat{\rho_{B}^{\lambda}}(\chi') \cdot \widehat{\rho_{-B}^{\lambda}}(\chi')\\ &= \widehat{\rho_{B}^{\lambda} * \rho_{-B}^{\lambda}}(\chi') \\ &= \int_K (\rho_{B}^{\lambda} * \rho_{-B}^{\lambda}) \cdot \overline{\chi'} \, d m_K \\ &= \mu(\eta \overline{\chi}) \;\; \; (\text{by the definition of } \eta \text{ and Lemma 4.2}).\\[-36pt] \end{align*} $$
$$ \begin{align*} \mu(\phi \overline{\chi}) &= \iint_{G^2} 1_B(t) 1_{-B}(s - t) \overline{\chi(s)} \, d \lambda(t) d \mu(s) \\ &=\iint_{G^2} (1_B \cdot \overline{\chi})(t) \cdot (1_{-B} \cdot \overline{\chi})(s - t) \, d \lambda(t) d \mu(s) \\ &= \lambda(1_B \cdot \overline{\chi}) \lambda(1_{-B} \cdot \overline{\chi}) \;\;\; \text{(by Lemma 2.1)}\\ &= \int_K \rho_{B}^{\lambda} \overline{\chi'} \, d m_K \cdot \int_K \rho_{-B}^{\lambda} \overline{\chi'} \, d m_K \;\;\; (\text{by definitions of } \rho_{B}^{\lambda} \text{ and } \rho_{-B}^{\lambda}) \\ &= \widehat{\rho_{B}^{\lambda}}(\chi') \cdot \widehat{\rho_{-B}^{\lambda}}(\chi')\\ &= \widehat{\rho_{B}^{\lambda} * \rho_{-B}^{\lambda}}(\chi') \\ &= \int_K (\rho_{B}^{\lambda} * \rho_{-B}^{\lambda}) \cdot \overline{\chi'} \, d m_K \\ &= \mu(\eta \overline{\chi}) \;\; \; (\text{by the definition of } \eta \text{ and Lemma 4.2}).\\[-36pt] \end{align*} $$
We are ready to prove
![]() $\theta = (\rho _{A}^{\nu } * \rho _{B}^{\lambda } * \rho _{-B}^{\lambda }) \circ \tau $
. Indeed, by Claim 7.2,
$\theta = (\rho _{A}^{\nu } * \rho _{B}^{\lambda } * \rho _{-B}^{\lambda }) \circ \tau $
. Indeed, by Claim 7.2,
where
![]() $\psi $
is a null function and
$\psi $
is a null function and
![]() $\eta =(\rho _{B}^{\lambda } * \rho _{-B}^{\lambda } )\circ \tau $
. For all
$\eta =(\rho _{B}^{\lambda } * \rho _{-B}^{\lambda } )\circ \tau $
. For all
![]() $t \in G$
, we have
$t \in G$
, we have
Moreover, since
![]() $\eta $
is a Fourier series with absolutely summable coefficients,
$\eta $
is a Fourier series with absolutely summable coefficients,
![]() $1_A *_{\nu } \eta $
is as well. It follows that
$1_A *_{\nu } \eta $
is as well. It follows that
![]() $\theta $
is almost periodic. Therefore, to show
$\theta $
is almost periodic. Therefore, to show
![]() $\theta = (\rho _{A}^{\nu } * \rho _{B}^{\lambda } * \rho _{-B}^{\lambda }) \circ \tau $
, it suffices to check that
$\theta = (\rho _{A}^{\nu } * \rho _{B}^{\lambda } * \rho _{-B}^{\lambda }) \circ \tau $
, it suffices to check that
![]() $\theta $
and
$\theta $
and
![]() $(\rho _{A}^{\nu } * \rho _{B}^{\lambda } * \rho _{-B}^{\lambda }) \circ \tau $
have the same Fourier coefficients. We omit the computations as they are nearly identical to the proof of Claim 7.2.
$(\rho _{A}^{\nu } * \rho _{B}^{\lambda } * \rho _{-B}^{\lambda }) \circ \tau $
have the same Fourier coefficients. We omit the computations as they are nearly identical to the proof of Claim 7.2.
8 Bohr sets in
 $\phi _1(A_i) + \phi _2(A_i) - \phi _2(A_i)$
$\phi _1(A_i) + \phi _2(A_i) - \phi _2(A_i)$
In this section, we prove Theorem 1.4, which says that
![]() $\phi _1(A_i) + \phi _2(A_i) - \phi _2(A_i)$
contains a Bohr set for some
$\phi _1(A_i) + \phi _2(A_i) - \phi _2(A_i)$
contains a Bohr set for some
![]() $A_i$
in any partition
$A_i$
in any partition
![]() $G = \bigcup _{i=1}^r A_i$
. Since the proof is technical and uses cumbersome notation, we first sketch the main idea. Fix an invariant mean
$G = \bigcup _{i=1}^r A_i$
. Since the proof is technical and uses cumbersome notation, we first sketch the main idea. Fix an invariant mean
![]() $\nu $
on G. The pushforwards
$\nu $
on G. The pushforwards
![]() $\phi _{1, *} \nu $
and
$\phi _{1, *} \nu $
and
![]() $\phi _{2, *} \nu $
are invariant means on
$\phi _{2, *} \nu $
are invariant means on
![]() $H_1 = \phi _1(G)$
and
$H_1 = \phi _1(G)$
and
![]() $H_2 = \phi _2(G)$
, respectively. Since
$H_2 = \phi _2(G)$
, respectively. Since
![]() $H_1, H_2$
are only subgroups of G, in order to apply the correspondence principle (Proposition 7.1), we need to extend
$H_1, H_2$
are only subgroups of G, in order to apply the correspondence principle (Proposition 7.1), we need to extend
![]() $\phi _{1, *} \nu $
and
$\phi _{1, *} \nu $
and
![]() $\phi _{2, *} \nu $
to means
$\phi _{2, *} \nu $
to means
![]() $\nu _1$
and
$\nu _1$
and
![]() $\nu _2$
on G. Furthermore,
$\nu _2$
on G. Furthermore,
![]() $\nu $
can be chosen in such a way that
$\nu $
can be chosen in such a way that
![]() $\nu _2$
is extremal. Having found such extensions, Proposition 7.1 implies that
$\nu _2$
is extremal. Having found such extensions, Proposition 7.1 implies that
![]() $\phi _1(A_i) + \phi _2(A_i) - \phi _2(A_i)$
contains the preimage of the support of
$\phi _1(A_i) + \phi _2(A_i) - \phi _2(A_i)$
contains the preimage of the support of
which, in turn, contains a Bohr set for some
![]() $i \in [r]$
thanks to Corollary 4.10 and the corresponding partition result in compact groups (Theorem D (ii)) from [Reference Le and Lê33].
$i \in [r]$
thanks to Corollary 4.10 and the corresponding partition result in compact groups (Theorem D (ii)) from [Reference Le and Lê33].
The precise result we need from [Reference Le and Lê33] is the following.
Proposition 8.1 [Reference Le and Lê33, Proposition 3.4].
Let K be a compact abelian group and
![]() $\tilde {\phi _1}, \tilde {\phi _2}$
be commuting continuous endomorphisms on K with finite index images. Suppose
$\tilde {\phi _1}, \tilde {\phi _2}$
be commuting continuous endomorphisms on K with finite index images. Suppose
![]() $\rho _1, \ldots , \rho _r: K \to [0,1]$
are measurable functions such that
$\rho _1, \ldots , \rho _r: K \to [0,1]$
are measurable functions such that
![]() $\sum _{i=1}^r \rho _i \geq 1$
almost everywhere. For
$\sum _{i=1}^r \rho _i \geq 1$
almost everywhere. For
![]() $w \in G$
, define
$w \in G$
, define
Then there are
![]() $k, \eta>0$
depending only on
$k, \eta>0$
depending only on
![]() $[K:\tilde {\phi _1}(K)], [K:\tilde {\phi _2}(K)]$
and r such that for some
$[K:\tilde {\phi _1}(K)], [K:\tilde {\phi _2}(K)]$
and r such that for some
![]() $i \in [r]$
, the support of
$i \in [r]$
, the support of
![]() $R_i$
contains a Bohr-
$R_i$
contains a Bohr-
![]() $(k,\eta )$
set.
$(k,\eta )$
set.
We turn to the details. The following lemma helps us extend an invariant mean on
![]() $H = \phi (G)$
to a mean on G by thinking of
$H = \phi (G)$
to a mean on G by thinking of
![]() $\ell ^{\infty }(H)$
as embedded into
$\ell ^{\infty }(H)$
as embedded into
![]() $\ell ^{\infty }(G)$
through the pullback map
$\ell ^{\infty }(G)$
through the pullback map
![]() $\phi ^*$
.
$\phi ^*$
.
Lemma 8.2. Let G and H be discrete abelian groups and
![]() $\phi :G \to H$
be a surjective homomorphism. Then for every invariant mean
$\phi :G \to H$
be a surjective homomorphism. Then for every invariant mean
![]() $\mu $
on H, there exists an invariant mean
$\mu $
on H, there exists an invariant mean
![]() $\nu $
on G such that
$\nu $
on G such that
![]() $\phi _* \nu = \mu $
.
$\phi _* \nu = \mu $
.
Proof. First, we observe that if
![]() $\nu $
is a linear functional on
$\nu $
is a linear functional on
![]() $\ell ^{\infty }_{\mathbb {R}}(G)$
and
$\ell ^{\infty }_{\mathbb {R}}(G)$
and
![]() $\nu (1_G) = 1$
, then
$\nu (1_G) = 1$
, then
![]() $\nu $
is positive if and only if
$\nu $
is positive if and only if
![]() $\nu (f) \geq p(f):= \inf _{x \in G} f(x)$
for all
$\nu (f) \geq p(f):= \inf _{x \in G} f(x)$
for all
![]() $f \in \ell ^{\infty }_{\mathbb {R}}(G)$
. Clearly p is a concave function.
$f \in \ell ^{\infty }_{\mathbb {R}}(G)$
. Clearly p is a concave function.
Let V be the vector subspace of
![]() $\ell _{\mathbb {R}}^{\infty }(G)$
consisting of functions of the form
$\ell _{\mathbb {R}}^{\infty }(G)$
consisting of functions of the form
![]() $h \circ \phi $
for some
$h \circ \phi $
for some
![]() $h \in \ell _{\mathbb {R}}^{\infty }(H)$
. If
$h \in \ell _{\mathbb {R}}^{\infty }(H)$
. If
![]() $f \in V$
, then by surjectivity of
$f \in V$
, then by surjectivity of
![]() $\phi $
, there is a unique
$\phi $
, there is a unique
![]() $h \in \ell _{\mathbb {R}}^{\infty }(H)$
such that
$h \in \ell _{\mathbb {R}}^{\infty }(H)$
such that
![]() $f = h \circ \phi $
. We have
$f = h \circ \phi $
. We have
 $$ \begin{align*} \mu(h) &\geq \inf_{y \in H} h(y) \qquad (\text{since } \mu \text{ is an invariant mean on } H) \\ & = \inf_{x \in G} h(\phi(x)) = p(f) \qquad (\text{since } \phi \text{ is surjective}). \end{align*} $$
$$ \begin{align*} \mu(h) &\geq \inf_{y \in H} h(y) \qquad (\text{since } \mu \text{ is an invariant mean on } H) \\ & = \inf_{x \in G} h(\phi(x)) = p(f) \qquad (\text{since } \phi \text{ is surjective}). \end{align*} $$
By the Hahn-Banach theorem, the linear functional
![]() $f \mapsto \mu (h)$
on V can be extended to a linear functional
$f \mapsto \mu (h)$
on V can be extended to a linear functional
![]() $\lambda $
on
$\lambda $
on
![]() $\ell _{\mathbb {R}}^{\infty }(G)$
such that
$\ell _{\mathbb {R}}^{\infty }(G)$
such that
![]() $\lambda (f) \geq p(f)$
for any
$\lambda (f) \geq p(f)$
for any
![]() $f \in \ell _{\mathbb {R}}^{\infty }(G)$
. In particular,
$f \in \ell _{\mathbb {R}}^{\infty }(G)$
. In particular,
![]() $\lambda $
is positive and
$\lambda $
is positive and
![]() $\lambda (1_G) = \lambda (1_H \circ \phi ) = \mu (1_H) = 1$
. We now show that
$\lambda (1_G) = \lambda (1_H \circ \phi ) = \mu (1_H) = 1$
. We now show that
![]() $\lambda $
can be further refined to become G-invariant.
$\lambda $
can be further refined to become G-invariant.
We let
![]() $\eta $
be an invariant mean on G and define
$\eta $
be an invariant mean on G and define
for all
![]() $f \in \ell _{\mathbb {R}}^{\infty }(G)$
. Then
$f \in \ell _{\mathbb {R}}^{\infty }(G)$
. Then
![]() $\nu (f_g) = \nu (f)$
for all
$\nu (f_g) = \nu (f)$
for all
![]() $g \in G$
since
$g \in G$
since
![]() $\eta $
is translation invariant. The positivity of
$\eta $
is translation invariant. The positivity of
![]() $\nu $
follows from the positivity of
$\nu $
follows from the positivity of
![]() $\lambda $
and
$\lambda $
and
![]() $\eta $
. If
$\eta $
. If
![]() $f = h \circ \phi \in V$
, then
$f = h \circ \phi \in V$
, then
![]() $\lambda (f_g) = \mu (h_{\phi (g)}) = \mu (h)$
for all
$\lambda (f_g) = \mu (h_{\phi (g)}) = \mu (h)$
for all
![]() $g \in G$
, so
$g \in G$
, so
![]() $\nu (f) = \mu (h)$
. The lemma now follows since an invariant mean is completely determined by its values on real-valued functions.
$\nu (f) = \mu (h)$
. The lemma now follows since an invariant mean is completely determined by its values on real-valued functions.
If H happens to be a subgroup of G, then another way to extend a mean on H to a mean on G is to consider
![]() $\ell ^{\infty }(H)$
as a subset of
$\ell ^{\infty }(H)$
as a subset of
![]() $\ell ^{\infty }(G)$
consisting of functions supported on H. This is the content of the next lemma.
$\ell ^{\infty }(G)$
consisting of functions supported on H. This is the content of the next lemma.
Lemma 8.3. Let H be a subgroup of G of index
![]() $k \in \mathbb {N}$
and let
$k \in \mathbb {N}$
and let
![]() $\mu $
be an invariant mean on H. There exists a unique invariant mean
$\mu $
be an invariant mean on H. There exists a unique invariant mean
![]() $\nu $
on G such that
$\nu $
on G such that
for every
![]() $f \in \ell ^{\infty }(G)$
supported on H. Furthermore, if
$f \in \ell ^{\infty }(G)$
supported on H. Furthermore, if
![]() $\mu $
is extremal, then
$\mu $
is extremal, then
![]() $\nu $
is also extremal.
$\nu $
is also extremal.
Proof. Let
![]() $H - g_i$
for
$H - g_i$
for
![]() $0 \leq i \leq k - 1$
be the cosets of H in G with
$0 \leq i \leq k - 1$
be the cosets of H in G with
![]() $g_0 = 0$
. We first show that an invariant mean
$g_0 = 0$
. We first show that an invariant mean
![]() $\nu $
satisfying the conclusion of the lemma must be unique. For a function f supported on
$\nu $
satisfying the conclusion of the lemma must be unique. For a function f supported on
![]() $H - g_i$
, the function
$H - g_i$
, the function
![]() $f_{g_i}$
given by
$f_{g_i}$
given by
![]() $x \mapsto f(x - g_i)$
is supported on H. Therefore, in this case, since
$x \mapsto f(x - g_i)$
is supported on H. Therefore, in this case, since
![]() $\nu $
is G-invariant, we must have
$\nu $
is G-invariant, we must have
For an arbitrary
![]() $f \in \ell ^{\infty }(G)$
, define
$f \in \ell ^{\infty }(G)$
, define
![]() $f^i = f \cdot 1_{H - g_i}$
. Since
$f^i = f \cdot 1_{H - g_i}$
. Since
![]() $f = \sum _{i=0}^{k-1} f^i$
, from the previous paragraph, we must have
$f = \sum _{i=0}^{k-1} f^i$
, from the previous paragraph, we must have
 $$ \begin{align} \nu(f) = \sum_{i=0}^{k-1} \nu(f^i) = \frac{1}{k} \sum_{i=0}^{k-1} \mu((f^i)_{g_i}). \end{align} $$
$$ \begin{align} \nu(f) = \sum_{i=0}^{k-1} \nu(f^i) = \frac{1}{k} \sum_{i=0}^{k-1} \mu((f^i)_{g_i}). \end{align} $$
This equation uniquely defines
![]() $\nu $
.
$\nu $
.
It is easy to see that
![]() $\nu $
as defined in (26) is a linear functional on
$\nu $
as defined in (26) is a linear functional on
![]() $\ell ^{\infty }(G)$
with
$\ell ^{\infty }(G)$
with
![]() $\nu (1_G) = 1$
. To show
$\nu (1_G) = 1$
. To show
![]() $\nu $
is G-invariant, we consider arbitrary
$\nu $
is G-invariant, we consider arbitrary
![]() $g \in G$
and
$g \in G$
and
![]() $f \in \ell ^{\infty }(G)$
. By the linearity of
$f \in \ell ^{\infty }(G)$
. By the linearity of
![]() $\nu $
and (25),
$\nu $
and (25),
 $$ \begin{align} \nu(f_g) = \sum_{i=0}^{k-1} \nu((f^i)_g) = \frac{1}{k} \sum_{i=0}^{k-1} \mu(((f^i)_g)_{g_{j(i)}}) = \frac{1}{k} \sum_{i=0}^{k-1} \mu(((f^i)_{g+g_{j(i)}}). \end{align} $$
$$ \begin{align} \nu(f_g) = \sum_{i=0}^{k-1} \nu((f^i)_g) = \frac{1}{k} \sum_{i=0}^{k-1} \mu(((f^i)_g)_{g_{j(i)}}) = \frac{1}{k} \sum_{i=0}^{k-1} \mu(((f^i)_{g+g_{j(i)}}). \end{align} $$
where
![]() $j(i) \in \{0, \ldots , k-1\}$
is such that
$j(i) \in \{0, \ldots , k-1\}$
is such that
![]() $-g_i + g + g_{j(i)} \in H$
. For
$-g_i + g + g_{j(i)} \in H$
. For
![]() $i \in \{0, \ldots , k - 1\}$
, let
$i \in \{0, \ldots , k - 1\}$
, let
![]() $h = -g_i + g + g_{j(i)}$
. Since
$h = -g_i + g + g_{j(i)}$
. Since
![]() $\mu $
is H-invariant,
$\mu $
is H-invariant,
Relations (26), (27) and (28) give
![]() $\nu (f_g) = \nu (f)$
, and so
$\nu (f_g) = \nu (f)$
, and so
![]() $\nu $
is G-invariant.
$\nu $
is G-invariant.
Suppose
![]() $\mu $
is extremal. To show that
$\mu $
is extremal. To show that
![]() $\nu $
is extremal, suppose
$\nu $
is extremal, suppose
![]() $\nu = \alpha \nu _1 + (1 - \alpha ) \nu _2$
, where
$\nu = \alpha \nu _1 + (1 - \alpha ) \nu _2$
, where
![]() $\nu _1$
and
$\nu _1$
and
![]() $\nu _2$
are means on G and
$\nu _2$
are means on G and
![]() $0 < \alpha < 1$
. Restricting to
$0 < \alpha < 1$
. Restricting to
![]() $S := \{f \in \ell ^{\infty }(G): f \text { is supported on } H\}$
, we get
$S := \{f \in \ell ^{\infty }(G): f \text { is supported on } H\}$
, we get
Since
![]() $\mu $
is extremal, it must be that
$\mu $
is extremal, it must be that
![]() $\nu _1|_S = \nu _2|_S = \mu /k$
. Due to the uniqueness of the extension of
$\nu _1|_S = \nu _2|_S = \mu /k$
. Due to the uniqueness of the extension of
![]() $\mu $
from H to G, we deduce that
$\mu $
from H to G, we deduce that
![]() $\nu _1 = \nu _2 = \nu $
. Therefore,
$\nu _1 = \nu _2 = \nu $
. Therefore,
![]() $\nu $
is extremal.
$\nu $
is extremal.
The next lemma shows that if H is a subgroup of G with finite index, then the Radon-Nikodym density associated with the mean
![]() $\mu $
on H and the one associated with its extension on G are the same.
$\mu $
on H and the one associated with its extension on G are the same.
Lemma 8.4. Let H be a subgroup of G of index
![]() $k \in \mathbb {N}$
. Let K be a compact abelian group and
$k \in \mathbb {N}$
. Let K be a compact abelian group and
![]() $\tau : G \to K$
be a homomorphism with dense image and
$\tau : G \to K$
be a homomorphism with dense image and
![]() $K_H = \overline {\tau (H)}$
. Let
$K_H = \overline {\tau (H)}$
. Let
![]() $B \subset H$
and
$B \subset H$
and
![]() $\mu $
be an invariant mean on H. Let
$\mu $
be an invariant mean on H. Let
![]() $\nu $
be the extension of
$\nu $
be the extension of
![]() $\mu $
to G as stated in Lemma 8.3. Suppose
$\mu $
to G as stated in Lemma 8.3. Suppose
![]() $\rho _{B}^{\nu }: K \to [0, 1]$
and
$\rho _{B}^{\nu }: K \to [0, 1]$
and
![]() $\rho _{B}^{\mu }: K_H \to [0, 1]$
are the associated Radon-Nikodym densities. By identifying
$\rho _{B}^{\mu }: K_H \to [0, 1]$
are the associated Radon-Nikodym densities. By identifying
![]() $\rho _{B}^{\mu }$
with its extension to
$\rho _{B}^{\mu }$
with its extension to
![]() $0$
outside of
$0$
outside of
![]() $K_H$
, we have
$K_H$
, we have
![]() $m_K$
-almost everywhere.
$m_K$
-almost everywhere.
Proof. As in the proof of Lemma 8.3, let
![]() $H - g_i$
for
$H - g_i$
for
![]() $0 \leq i \leq k -1 $
be the cosets of H in G with
$0 \leq i \leq k -1 $
be the cosets of H in G with
![]() $g_0 = 0$
. Since
$g_0 = 0$
. Since
![]() $B \subset H$
, according to Lemma 4.4, both
$B \subset H$
, according to Lemma 4.4, both
![]() $\rho _{B}^{\nu }$
and
$\rho _{B}^{\nu }$
and
![]() $\rho _{B}^{\mu }$
are supported on
$\rho _{B}^{\mu }$
are supported on
![]() $K_H$
. From (26), for
$K_H$
. From (26), for
![]() $h \in C(K)$
,
$h \in C(K)$
,
 $$ \begin{align} \nu(h \circ \tau \cdot 1_B) = \frac{1}{k} \sum_{i=0}^{k-1} \mu((h \circ \tau \cdot 1_B \cdot 1_{H-g_i})_{g_i}). \end{align} $$
$$ \begin{align} \nu(h \circ \tau \cdot 1_B) = \frac{1}{k} \sum_{i=0}^{k-1} \mu((h \circ \tau \cdot 1_B \cdot 1_{H-g_i})_{g_i}). \end{align} $$
Since
![]() $1_B$
is supported on H,
$1_B$
is supported on H,
Therefore, the right-hand side of (29) is equal to
which is equal to
It follows that
Since when restricting to
![]() $K_H$
, the measure
$K_H$
, the measure
![]() $m_K$
is equal to
$m_K$
is equal to
![]() $\frac {1}{k} m_{K_H}$
, we deduce that
$\frac {1}{k} m_{K_H}$
, we deduce that
![]() $\rho _{B}^{\nu } = \rho _{B}^{\mu }$
.
$\rho _{B}^{\nu } = \rho _{B}^{\mu }$
.
We are ready to prove Theorem 1.4. Our proof will use Corollary 4.10, applied in the case where
![]() $K_1=bG$
,
$K_1=bG$
,
![]() $K_2=\tilde {\phi }(bG)$
(where
$K_2=\tilde {\phi }(bG)$
(where
![]() $\tilde {\phi }$
is given by Lemma 3.2(ii)), and
$\tilde {\phi }$
is given by Lemma 3.2(ii)), and
![]() $\tau _1=\tau _2=\tau =$
the canonical embedding of G into
$\tau _1=\tau _2=\tau =$
the canonical embedding of G into
![]() $bG$
. In order to verify that the hypotheses of Corollary 4.10 are satisfied, we want to know that every character
$bG$
. In order to verify that the hypotheses of Corollary 4.10 are satisfied, we want to know that every character
![]() $\psi $
of
$\psi $
of
![]() $\phi (G)$
can be written in the form
$\phi (G)$
can be written in the form
![]() $\chi ' \circ \tau $
, where
$\chi ' \circ \tau $
, where
![]() $\chi '$
is a character of
$\chi '$
is a character of
![]() $\tilde {\phi }(bG)$
. This is the case, as every
$\tilde {\phi }(bG)$
. This is the case, as every
![]() $\psi \in \widehat {\phi (G)}$
can be extended to a character
$\psi \in \widehat {\phi (G)}$
can be extended to a character
![]() $\psi _0\in \widehat {G}$
and
$\psi _0\in \widehat {G}$
and
![]() $\psi _0= \chi _0\circ \tau $
for some
$\psi _0= \chi _0\circ \tau $
for some
![]() $\chi _0 \in \widehat {bG}$
. Let
$\chi _0 \in \widehat {bG}$
. Let
![]() $\chi ':=\chi _0|_{\tilde {\phi }(bG)}$
. We claim that
$\chi ':=\chi _0|_{\tilde {\phi }(bG)}$
. We claim that
![]() $\chi '\circ \tau = \psi $
. To see this, note that
$\chi '\circ \tau = \psi $
. To see this, note that
![]() $\chi _0\circ \tau = \psi _0$
, so
$\chi _0\circ \tau = \psi _0$
, so
![]() $(\chi _0\circ \tau )|_{\phi (G)}=\psi _0|_{\phi (G)}=\psi $
. Finally, note that
$(\chi _0\circ \tau )|_{\phi (G)}=\psi _0|_{\phi (G)}=\psi $
. Finally, note that
![]() $\tau (\phi (G))\subset \tilde {\phi }(bG)$
since
$\tau (\phi (G))\subset \tilde {\phi }(bG)$
since
![]() $\tilde {\phi }\circ \tau = \tau \circ \phi $
. Thus,
$\tilde {\phi }\circ \tau = \tau \circ \phi $
. Thus,
![]() $(\chi _0\circ \tau )|_{\phi (G)}=\chi '\circ \tau $
.
$(\chi _0\circ \tau )|_{\phi (G)}=\chi '\circ \tau $
.
Proof of Theorem 1.4.
Let
![]() $H_1 = \phi _1(G)$
and
$H_1 = \phi _1(G)$
and
![]() $H_2 = \phi _2(G)$
. Let
$H_2 = \phi _2(G)$
. Let
![]() $\mu $
be an extremal invariant mean on
$\mu $
be an extremal invariant mean on
![]() $H_2$
. By Lemma 8.2, there exists an invariant mean
$H_2$
. By Lemma 8.2, there exists an invariant mean
![]() $\nu $
on G such that the pushforward
$\nu $
on G such that the pushforward
![]() $\phi _{2, *} \nu $
is equal to
$\phi _{2, *} \nu $
is equal to
![]() $\mu $
. In view of Lemma 8.3,
$\mu $
. In view of Lemma 8.3,
![]() $\phi _{1,*} \nu $
can be extended canonically from
$\phi _{1,*} \nu $
can be extended canonically from
![]() $H_1$
to a mean
$H_1$
to a mean
![]() $\nu _1$
on G such that
$\nu _1$
on G such that
for every
![]() $f \in \ell ^{\infty }(G)$
supported on
$f \in \ell ^{\infty }(G)$
supported on
![]() $H_1$
. Likewise, extend
$H_1$
. Likewise, extend
![]() $\mu = \phi _{2,*} \nu $
from
$\mu = \phi _{2,*} \nu $
from
![]() $H_2$
to a mean
$H_2$
to a mean
![]() $\nu _2$
on G. Since
$\nu _2$
on G. Since
![]() $\mu $
is extremal,
$\mu $
is extremal,
![]() $\nu _2$
is extremal; however,
$\nu _2$
is extremal; however,
![]() $\nu _1$
may not be extremal.
$\nu _1$
may not be extremal.
Let
![]() $A \subset G$
,
$A \subset G$
,
![]() $K = bG$
and
$K = bG$
and
![]() $\tau : G \to K$
be the natural embedding. By Proposition 7.1 and because
$\tau : G \to K$
be the natural embedding. By Proposition 7.1 and because
![]() $\nu _2$
is extremal, the sumset
$\nu _2$
is extremal, the sumset
![]() $\phi _1(A) + \phi _2(A) - \phi _2(A)$
contains
$\phi _1(A) + \phi _2(A) - \phi _2(A)$
contains
In light of Lemma 8.4,
where we identify
![]() $\rho _{\phi _j(A)}^{\phi _{j,*} \nu }$
with its extension to
$\rho _{\phi _j(A)}^{\phi _{j,*} \nu }$
with its extension to
![]() $0$
outside of
$0$
outside of
![]() $\phi _j(K)$
. It follows that
$\phi _j(K)$
. It follows that
![]() $\phi _1(A) + \phi _2(A) - \phi _2(A)$
contains
$\phi _1(A) + \phi _2(A) - \phi _2(A)$
contains
For
![]() $j \in \{1, 2\}$
, let
$j \in \{1, 2\}$
, let
![]() $\tilde {\phi }_j: K \to K$
be a continuous homomorphism such that
$\tilde {\phi }_j: K \to K$
be a continuous homomorphism such that
![]() $\tilde {\phi }_j \circ \tau = \tau \circ \phi _j$
. Then
$\tilde {\phi }_j \circ \tau = \tau \circ \phi _j$
. Then
![]() $\tilde {\phi }_1 \circ \tilde {\phi }_2 \circ \tau = \tau \circ \phi _1 \circ \phi _2 = \tau \circ \phi _2 \circ \phi _1 = \tilde {\phi }_2 \circ \tilde {\phi }_1 \circ \tau $
. It follows that
$\tilde {\phi }_1 \circ \tilde {\phi }_2 \circ \tau = \tau \circ \phi _1 \circ \phi _2 = \tau \circ \phi _2 \circ \phi _1 = \tilde {\phi }_2 \circ \tilde {\phi }_1 \circ \tau $
. It follows that
![]() $\tilde {\phi }_1$
and
$\tilde {\phi }_1$
and
![]() $ \tilde {\phi }_2$
commute since
$ \tilde {\phi }_2$
commute since
![]() $\tau (G)$
is dense in K. By Lemma 3.2,
$\tau (G)$
is dense in K. By Lemma 3.2,
![]() $[K: \tilde {\phi }_j(K)] \leq [G: \phi _j(G)]$
is finite.
$[K: \tilde {\phi }_j(K)] \leq [G: \phi _j(G)]$
is finite.
For ease of notation, we write
Note that
![]() $f, g, h$
are nonnegative.
$f, g, h$
are nonnegative.
Claim 8.5. The support of
![]() $f * g * h$
contains the support of
$f * g * h$
contains the support of
![]() $S: K \to [0, 1]$
defined by
$S: K \to [0, 1]$
defined by
Proof of Claim.
Note that by [Reference Le and Lê33, Lemma 2.6],
![]() $\tilde {\phi _1} \circ \tilde {\phi _2} (K)$
has finite index in K. We recall [Reference Le and Lê33, Lemma 2.8], which says that if f is a nonnegative function on a compact abelian group K,
$\tilde {\phi _1} \circ \tilde {\phi _2} (K)$
has finite index in K. We recall [Reference Le and Lê33, Lemma 2.8], which says that if f is a nonnegative function on a compact abelian group K,
![]() $\phi $
is a continuous endomorphism on K and
$\phi $
is a continuous endomorphism on K and
![]() $m = [K: \phi (K)] < \infty $
, then
$m = [K: \phi (K)] < \infty $
, then
By two applications of this fact, we have
 $$ \begin{align*} S(w) & \leq [K:\tilde{\phi_2}(K)] \iint_{K^2} f(\tilde{\phi_1} \circ \tilde{\phi_2}(v)) \cdot g(w + u) \cdot h(- u - \tilde{\phi_2} \circ \tilde{\phi_1}(v)) \ d m_K(u) d m_K(v) \\ &\leq [K:\tilde{\phi_2}(K)] \cdot [K: \tilde{\phi_1} \circ \tilde{\phi_2}(K)] \iint_{K^2} f(v) \cdot g(w + u) \cdot h(- u - v) \ d m_K(u) d m_K(v) \\ & = [K:\tilde{\phi_2}(K)] \cdot [K: \tilde{\phi_1} \circ \tilde{\phi_2}(K)] \cdot f*g*h(w), \end{align*} $$
$$ \begin{align*} S(w) & \leq [K:\tilde{\phi_2}(K)] \iint_{K^2} f(\tilde{\phi_1} \circ \tilde{\phi_2}(v)) \cdot g(w + u) \cdot h(- u - \tilde{\phi_2} \circ \tilde{\phi_1}(v)) \ d m_K(u) d m_K(v) \\ &\leq [K:\tilde{\phi_2}(K)] \cdot [K: \tilde{\phi_1} \circ \tilde{\phi_2}(K)] \iint_{K^2} f(v) \cdot g(w + u) \cdot h(- u - v) \ d m_K(u) d m_K(v) \\ & = [K:\tilde{\phi_2}(K)] \cdot [K: \tilde{\phi_1} \circ \tilde{\phi_2}(K)] \cdot f*g*h(w), \end{align*} $$
thus proving the claim.
By Corollary 4.10, we have
and
Therefore,
for all
![]() $w \in K$
, where
$w \in K$
, where
Combining (30)-(33), we get that for all
![]() $A \subset G$
, the sumset
$A \subset G$
, the sumset
![]() $\phi _1(A) + \phi _2(A) - \phi _2(A)$
contains
$\phi _1(A) + \phi _2(A) - \phi _2(A)$
contains
![]() $\tau ^{-1}(\tilde {\phi }_2(\operatorname {supp} R_{A}))$
.
$\tau ^{-1}(\tilde {\phi }_2(\operatorname {supp} R_{A}))$
.
As a consequence, we have for each partition
![]() $G = \bigcup _{i=1}^r A_i$
and each
$G = \bigcup _{i=1}^r A_i$
and each
![]() $i \in [r]$
,
$i \in [r]$
,
By Corollary 4.5,
![]() $\sum _{i=1}^r \rho _{A_i}^{\nu } = 1$
almost everywhere. Therefore, in view of Proposition 8.1, for some
$\sum _{i=1}^r \rho _{A_i}^{\nu } = 1$
almost everywhere. Therefore, in view of Proposition 8.1, for some
![]() $i \in [r]$
, the support of
$i \in [r]$
, the support of
![]() $R_{A_i}$
contains a Bohr-
$R_{A_i}$
contains a Bohr-
![]() $(k, \eta )$
set
$(k, \eta )$
set
![]() $B \subset K$
, where
$B \subset K$
, where
![]() $k, \eta $
depend only on r and the indices
$k, \eta $
depend only on r and the indices
![]() $[K:\tilde {\phi }_1(K)], [K:\tilde {\phi }_2(K)]$
.
$[K:\tilde {\phi }_1(K)], [K:\tilde {\phi }_2(K)]$
.
By Lemma 2.3,
![]() $\tilde {\phi }_2(B)$
is a Bohr-
$\tilde {\phi }_2(B)$
is a Bohr-
![]() $(k', \eta ')$
set where
$(k', \eta ')$
set where
![]() $k', \eta '$
depend only on
$k', \eta '$
depend only on
![]() $k, \eta $
and
$k, \eta $
and
![]() $[K:\tilde {\phi }_2(K)]$
. Lemma 2.2 then implies that
$[K:\tilde {\phi }_2(K)]$
. Lemma 2.2 then implies that
![]() $\tau ^{-1}(\tilde {\phi }_2(B))$
contains a Bohr-
$\tau ^{-1}(\tilde {\phi }_2(B))$
contains a Bohr-
![]() $(k', \eta ')$
set and our proof finishes.
$(k', \eta ')$
set and our proof finishes.
9 Third correspondence principle
In this section, we derive a correspondence principle for
![]() $B + C + A_i$
. Assuming only that the summands
$B + C + A_i$
. Assuming only that the summands
![]() $A, B, C$
have positive upper Banach density, we cannot guarantee that
$A, B, C$
have positive upper Banach density, we cannot guarantee that
![]() $A+B+C$
is a Bohr set, a translate of a Bohr set or even that
$A+B+C$
is a Bohr set, a translate of a Bohr set or even that
![]() $A+B+C$
is syndetic.Footnote
5
Under the stronger assumption that A and B have positive upper Banach density and that C is syndetic, [Reference Bergelson, Furstenberg and Weiss5] proves (for the ambient group
$A+B+C$
is syndetic.Footnote
5
Under the stronger assumption that A and B have positive upper Banach density and that C is syndetic, [Reference Bergelson, Furstenberg and Weiss5] proves (for the ambient group
![]() $\mathbb Z$
) that
$\mathbb Z$
) that
![]() $A+B+C$
contains a translate of a Bohr set. Our Theorem 1.7 has a similar, but weaker, hypothesis: partitioning G as
$A+B+C$
contains a translate of a Bohr set. Our Theorem 1.7 has a similar, but weaker, hypothesis: partitioning G as
![]() $A_1\cup \cdots \cup A_r$
, it is possible that none of the
$A_1\cup \cdots \cup A_r$
, it is possible that none of the
![]() $A_i$
are syndetic. Of course, one of the
$A_i$
are syndetic. Of course, one of the
![]() $A_i$
must be piecewise syndetic ([Reference Braun12], [Reference Hindman and Strauss29]).
$A_i$
must be piecewise syndetic ([Reference Braun12], [Reference Hindman and Strauss29]).
Proposition 9.6 says that when
![]() $A, B, C\subset G$
with
$A, B, C\subset G$
with
![]() $d^*(B), d^*(C)>0$
, the sumset
$d^*(B), d^*(C)>0$
, the sumset
![]() $B+C+A$
can be modeled by a convolution
$B+C+A$
can be modeled by a convolution
![]() $h_B*h_C*h_A$
on a compact group K, where
$h_B*h_C*h_A$
on a compact group K, where
![]() $\int h_B\, dm_K \geq d^*(B)$
and
$\int h_B\, dm_K \geq d^*(B)$
and
![]() $\int h_C\, dm_K\geq d^*(C)$
. In this correspondence principle, the hypothesis
$\int h_C\, dm_K\geq d^*(C)$
. In this correspondence principle, the hypothesis
![]() $d^*(A)>0$
is not strong enough to guarantee that
$d^*(A)>0$
is not strong enough to guarantee that
![]() $h_A$
is nonzero. However, assuming that
$h_A$
is nonzero. However, assuming that
![]() $G=A_1\cup \cdots \cup A_r$
, we will be able to conclude that
$G=A_1\cup \cdots \cup A_r$
, we will be able to conclude that
![]() $\sum _{i=1}^r h_{A_i} \geq 1$
almost everywhere and this suffices to give a useful bound on the
$\sum _{i=1}^r h_{A_i} \geq 1$
almost everywhere and this suffices to give a useful bound on the
![]() $h_B * h_C * h_{A_i}(0)$
for some
$h_B * h_C * h_{A_i}(0)$
for some
![]() $i \in [r]$
.
$i \in [r]$
.
Definition 9.1. Let
![]() $A,B\subset G$
. We write
$A,B\subset G$
. We write
![]() $A\prec B$
if for all finite subsets
$A\prec B$
if for all finite subsets
![]() $A'\subset A$
, there exists
$A'\subset A$
, there exists
![]() $t\in G$
such that
$t\in G$
such that
![]() $A'+t\subset B$
. In this case, we say that A is finitely embeddable in B.
$A'+t\subset B$
. In this case, we say that A is finitely embeddable in B.
The following lemma is implicit in [Reference Griesmer25] and, to some extent, in [Reference Griesmer24]. A similar statement for amenable groups can be obtained from Propositions 1.10 and 1.11 in [Reference Björklund and Fish8].
Lemma 9.2. Let
![]() $B, C \subset G$
. There exist a compact abelian group K, a homomorphism
$B, C \subset G$
. There exist a compact abelian group K, a homomorphism
![]() $\tau : G \to K$
for which
$\tau : G \to K$
for which
![]() $\tau (G)$
is dense in K, functions
$\tau (G)$
is dense in K, functions
![]() $h_B, h_C: K \to [0, 1]$
such that
$h_B, h_C: K \to [0, 1]$
such that
-
(i)
 $\int _K h_B \, d m_K = d^*(B)$
and
$\int _K h_B \, d m_K = d^*(B)$
and
 $\int _K h_C \, d m_K = d^*(C)$
, and
$\int _K h_C \, d m_K = d^*(C)$
, and -
(ii)
 $\{g \in G: h_B * h_C(\tau (g))> 0\} \prec B+C$
.
$\{g \in G: h_B * h_C(\tau (g))> 0\} \prec B+C$
.
Remark 9.3. Readers familiar with Furstenberg’s correspondence principle and Kronecker factors may appreciate the following additional detail: to obtain the group K, one may apply the Furstenberg correspondence principle to find ergodic measure preserving systems
![]() $\mathbf X_B=(X_B,\mu _B,T_B)$
and
$\mathbf X_B=(X_B,\mu _B,T_B)$
and
![]() $\mathbf X_C=(X_C,\mu _C,T_C)$
modeling B and C, with corresponding Kronecker factors
$\mathbf X_C=(X_C,\mu _C,T_C)$
modeling B and C, with corresponding Kronecker factors
![]() $\mathbf K_B=(K_B,m_{K_B},R_B)$
and
$\mathbf K_B=(K_B,m_{K_B},R_B)$
and
![]() $\mathbf K_C=(K_C,m_{K_C},R_C)$
. The groups
$\mathbf K_C=(K_C,m_{K_C},R_C)$
. The groups
![]() $K_B$
and
$K_B$
and
![]() $K_C$
are the respective duals of the eigenvalue groups
$K_C$
are the respective duals of the eigenvalue groups
![]() $\mathcal E(\mathbf X_B)$
and
$\mathcal E(\mathbf X_B)$
and
![]() $\mathcal E(\mathbf X_C)$
of
$\mathcal E(\mathbf X_C)$
of
![]() $\mathbf X_B$
and
$\mathbf X_B$
and
![]() $\mathbf X_C$
(as described by Lemma 3.3). The group K may be realized as the phase space of the maximal common factor of
$\mathbf X_C$
(as described by Lemma 3.3). The group K may be realized as the phase space of the maximal common factor of
![]() $\mathbf K_B$
and
$\mathbf K_B$
and
![]() $\mathbf K_C$
, or, equivalently, as the dual of
$\mathbf K_C$
, or, equivalently, as the dual of
![]() $\mathcal E(\mathbf X_B)\cap \mathcal E(\mathbf X_C)$
.
$\mathcal E(\mathbf X_B)\cap \mathcal E(\mathbf X_C)$
.
Proof. By [Reference Griesmer25, Lemma 2.8], there is an ergodic measure preserving G-system
![]() $(X,\mu ,T)$
, where X is a compact metric space, and a clopen set
$(X,\mu ,T)$
, where X is a compact metric space, and a clopen set
![]() $O_C\subset X$
with
$O_C\subset X$
with
![]() $\mu (O_C)=d^*(C)$
such that for all
$\mu (O_C)=d^*(C)$
such that for all
![]() $x\in X$
,
$x\in X$
,
By [Reference Griesmer25, Lemma 4.1], there is a group rotation factor
![]() $(K, m_K,R)$
of
$(K, m_K,R)$
of
![]() $(X,\mu ,T)$
with factor map
$(X,\mu ,T)$
with factor map
![]() $\pi :X\to K$
and a homomorphism
$\pi :X\to K$
and a homomorphism
![]() $\tau : G \to K$
with dense image such that
$\tau : G \to K$
with dense image such that
where
![]() $J := \operatorname {supp} (f_B * f_C)$
for some functions
$J := \operatorname {supp} (f_B * f_C)$
for some functions
![]() $f_B, f_C:K\to [0,1]$
with
$f_B, f_C:K\to [0,1]$
with
![]() $\int _K f_B\, dm_K = d^*(B)$
and
$\int _K f_B\, dm_K = d^*(B)$
and
![]() $\int _K f_C \, dm_K=d^*(C)$
.
$\int _K f_C \, dm_K=d^*(C)$
.
Note that for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x \in X$
,
$x \in X$
,
![]() $R_g \pi (x) = \pi (T_g x)$
. Therefore, if
$R_g \pi (x) = \pi (T_g x)$
. Therefore, if
![]() $R_g (\pi (x)) \in J$
, then
$R_g (\pi (x)) \in J$
, then
![]() $T_g x \in \pi ^{-1}(J)$
. Thus, from (35), for
$T_g x \in \pi ^{-1}(J)$
. Thus, from (35), for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x\in X$
, we have
$x\in X$
, we have
Fix such an x. Then,
The relation (34) then implies
![]() $\{g \in G: f_B*f_C(\pi (x)+\tau (g))>0\} \prec B+C$
. By defining functions
$\{g \in G: f_B*f_C(\pi (x)+\tau (g))>0\} \prec B+C$
. By defining functions
![]() $h_B, h_C$
as
$h_B, h_C$
as
![]() $h_B(t) := f_B(t + \pi (x))$
and
$h_B(t) := f_B(t + \pi (x))$
and
![]() $h_C = f_C$
, we obtain our conclusion.
$h_C = f_C$
, we obtain our conclusion.
Lemma 9.4. Let K be a compact metrizable abelian group and
![]() $\tau :G\to K$
be a homomorphism with dense image. Let
$\tau :G\to K$
be a homomorphism with dense image. Let
![]() $h: K\to [0,1]$
be continuous and let
$h: K\to [0,1]$
be continuous and let
![]() $A_h:=\{g \in G:h(\tau (g))>0\}$
. If
$A_h:=\{g \in G:h(\tau (g))>0\}$
. If
![]() $A_h\prec D$
, then there is a translate
$A_h\prec D$
, then there is a translate
![]() $h'$
of h and an invariant mean
$h'$
of h and an invariant mean
![]() $\lambda $
on G such that
$\lambda $
on G such that
for all
![]() $q: G\to [0,1]$
.
$q: G\to [0,1]$
.
Proof. Let
![]() $(F_N)_{N\in \mathbb N}$
be a Følner sequence for G. Since
$(F_N)_{N\in \mathbb N}$
be a Følner sequence for G. Since
![]() $F_N\cap A_h\subset A_h$
and
$F_N\cap A_h\subset A_h$
and
![]() $A_h\prec D$
, we may choose, for each
$A_h\prec D$
, we may choose, for each
![]() $N\in \mathbb N$
, a
$N\in \mathbb N$
, a
![]() $t_N\in G$
so that
$t_N\in G$
so that
![]() $(F_N\cap A_h)+t_N\subset D$
. Note that
$(F_N\cap A_h)+t_N\subset D$
. Note that
![]() $(F_N+t_N)_{N \in \mathbb {N}}$
is also a Følner sequence. Passing to a subsequence if necessary, we assume
$(F_N+t_N)_{N \in \mathbb {N}}$
is also a Følner sequence. Passing to a subsequence if necessary, we assume
![]() $\tau (t_N)$
converges to a point
$\tau (t_N)$
converges to a point
![]() $k_0$
in K. Let
$k_0$
in K. Let
![]() $h'(k) = h(k-k_0)$
for
$h'(k) = h(k-k_0)$
for
![]() $k \in K$
, so that
$k \in K$
, so that
![]() $h(k-\tau (t_N))$
converges uniformly to
$h(k-\tau (t_N))$
converges uniformly to
![]() $h'(k)$
.
$h'(k)$
.
Define a sequence of functions
![]() $p_N: F_N+t_N\to [0,1]$
by
$p_N: F_N+t_N\to [0,1]$
by
![]() $p_N(g+t_N)=h(\tau (g))$
. Since
$p_N(g+t_N)=h(\tau (g))$
. Since
![]() $h(\tau (g))=0$
for each
$h(\tau (g))=0$
for each
![]() $g\in (F_N\setminus A_h)$
, and
$g\in (F_N\setminus A_h)$
, and
![]() $F_N\cap A_h + t_N\subset D$
, we have
$F_N\cap A_h + t_N\subset D$
, we have
![]() $1_D(g)\geq p_N(g)$
for all
$1_D(g)\geq p_N(g)$
for all
![]() $g\in F_N+t_N$
.
$g\in F_N+t_N$
.
For each
![]() $N\in \mathbb N$
and each
$N\in \mathbb N$
and each
![]() $q:G\to [0,1]$
, we have
$q:G\to [0,1]$
, we have
 $$ \begin{align} \begin{aligned} \frac{1}{|F_N|}\sum_{g\in F_N+t_N} 1_D(g)q(t-g) &\geq \frac{1}{|F_N|}\sum_{g\in F_N+t_N} p_N(g) q(t-g)\\ &= \frac{1}{|F_N|}\sum_{g\in F_N+t_N} h(\tau(g)-\tau(t_N))q(t-g). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{1}{|F_N|}\sum_{g\in F_N+t_N} 1_D(g)q(t-g) &\geq \frac{1}{|F_N|}\sum_{g\in F_N+t_N} p_N(g) q(t-g)\\ &= \frac{1}{|F_N|}\sum_{g\in F_N+t_N} h(\tau(g)-\tau(t_N))q(t-g). \end{aligned} \end{align} $$
For each N, let
![]() $\lambda _N$
be the linear functional on
$\lambda _N$
be the linear functional on
![]() $\ell ^{\infty }(G)$
defined by
$\ell ^{\infty }(G)$
defined by
![]() $\lambda _N(f):=\frac {1}{|F_N|}\sum _{g\in F_N + t_N} f(g)$
. Let
$\lambda _N(f):=\frac {1}{|F_N|}\sum _{g\in F_N + t_N} f(g)$
. Let
![]() $\lambda $
be a linear functional on
$\lambda $
be a linear functional on
![]() $\ell ^{\infty }(G)$
that is a weak
$\ell ^{\infty }(G)$
that is a weak
![]() $^*$
limit point of the sequence
$^*$
limit point of the sequence
![]() $\lambda _N$
(meaning that for all
$\lambda _N$
(meaning that for all
![]() $f\in \ell ^{\infty }(G)$
, all
$f\in \ell ^{\infty }(G)$
, all
![]() $\varepsilon>0$
, and all
$\varepsilon>0$
, and all
![]() $M\in \mathbb N$
, there is an
$M\in \mathbb N$
, there is an
![]() $N>M$
such that
$N>M$
such that
![]() $|\lambda (f)-\lambda _N(f)|<\varepsilon $
). In other words,
$|\lambda (f)-\lambda _N(f)|<\varepsilon $
). In other words,
![]() $\lambda \in \bigcap _{M=1}^{\infty } \overline {\{\lambda _N: N>M\}}.$
$\lambda \in \bigcap _{M=1}^{\infty } \overline {\{\lambda _N: N>M\}}.$
Since
![]() $h(k-\tau (t_N))$
converges uniformly in N to
$h(k-\tau (t_N))$
converges uniformly in N to
![]() $h(k-k_0)=h'(k)$
, (36) implies
$h(k-k_0)=h'(k)$
, (36) implies
![]() $1_D*_{\lambda }q(t) \geq h'\circ \tau *_{\lambda } q(t)$
for all
$1_D*_{\lambda }q(t) \geq h'\circ \tau *_{\lambda } q(t)$
for all
![]() $t\in G$
.
$t\in G$
.
Lemma 9.5. Let K be a compact abelian group and
![]() $\tau :G\to K$
be homomorphism with dense image. Let
$\tau :G\to K$
be homomorphism with dense image. Let
![]() $h: K\to [0,1]$
be a continuous function and
$h: K\to [0,1]$
be a continuous function and
![]() $\lambda $
be an invariant mean on G. Then for every
$\lambda $
be an invariant mean on G. Then for every
![]() $A \subset G$
,
$A \subset G$
,
where
![]() $\rho _{A}^{\lambda }$
is defined in Definition 4.1.
$\rho _{A}^{\lambda }$
is defined in Definition 4.1.
Proof. Approximating h by trigonometric polynomials, it suffices to prove the statement for the special case where h is a trigonometric polynomial. By linearity, we may assume
![]() $h=\chi \in \widehat {K}$
. For such
$h=\chi \in \widehat {K}$
. For such
![]() $\chi $
, we have
$\chi $
, we have
 $$ \begin{align*} (\chi\circ \tau)*_{\lambda} 1_{A}(g) &:= \int_G \chi \circ \tau(x) \cdot 1_{A}(g-x)\, d\lambda(x)\\&= \int_G \chi \circ \tau(g+x) 1_{A}(-x)\, d\lambda(x)\\&= \chi\circ \tau(g) \int_G \chi \circ \tau(x) \cdot 1_{A}(-x)\, d\lambda(x)\\&= \chi\circ \tau(g) \int_G \chi\circ \tau \cdot 1_{-A}\, d\lambda\\&= \chi\circ \tau(g) \int_K \chi \cdot \rho_{-A}^{\lambda}\, dm_K. \end{align*} $$
$$ \begin{align*} (\chi\circ \tau)*_{\lambda} 1_{A}(g) &:= \int_G \chi \circ \tau(x) \cdot 1_{A}(g-x)\, d\lambda(x)\\&= \int_G \chi \circ \tau(g+x) 1_{A}(-x)\, d\lambda(x)\\&= \chi\circ \tau(g) \int_G \chi \circ \tau(x) \cdot 1_{A}(-x)\, d\lambda(x)\\&= \chi\circ \tau(g) \int_G \chi\circ \tau \cdot 1_{-A}\, d\lambda\\&= \chi\circ \tau(g) \int_K \chi \cdot \rho_{-A}^{\lambda}\, dm_K. \end{align*} $$
Computing
![]() $\chi *\rho _{A}^{\lambda }(t)$
for
$\chi *\rho _{A}^{\lambda }(t)$
for
![]() $t\in K$
, we get
$t\in K$
, we get
 $$ \begin{align*} \chi*\rho_{A}^{\lambda}(t) &= \int_K \chi(z)\rho_{A}^{\lambda}(t-z)\, dm_K(z) \\ &= \int_K \chi(z+t) \rho_{A}^{\lambda}(-z)\, dm_K(z)\\ &= \chi(t) \int_K \chi(z) \rho_{-A}^{\lambda}(z)\, dm_K(z)\\ &= \chi(t) \int_K \chi \cdot \rho_{-A}^{\lambda}\, dm_K. \end{align*} $$
$$ \begin{align*} \chi*\rho_{A}^{\lambda}(t) &= \int_K \chi(z)\rho_{A}^{\lambda}(t-z)\, dm_K(z) \\ &= \int_K \chi(z+t) \rho_{A}^{\lambda}(-z)\, dm_K(z)\\ &= \chi(t) \int_K \chi(z) \rho_{-A}^{\lambda}(z)\, dm_K(z)\\ &= \chi(t) \int_K \chi \cdot \rho_{-A}^{\lambda}\, dm_K. \end{align*} $$
Substituting
![]() $\tau (g)$
for t, we get
$\tau (g)$
for t, we get
completing the proof.
Combining Lemmas 9.2, 9.4 and 9.5, we have a proposition which serves as a correspondence principle for
![]() $B + C + A_i$
.
$B + C + A_i$
.
Proposition 9.6 (Third correspondence principle).
Let
![]() $B, C \subset G$
. There exist a compact abelian group K, a homomorphism
$B, C \subset G$
. There exist a compact abelian group K, a homomorphism
![]() $\tau : G \to K$
with dense image, measurable functions
$\tau : G \to K$
with dense image, measurable functions
![]() $h_B, h_C: K \to [0, 1]$
and an invariant mean
$h_B, h_C: K \to [0, 1]$
and an invariant mean
![]() $\lambda $
on G such that
$\lambda $
on G such that
-
(i)
 $\int _K h_B \, d m_K = d^*(B)$
and
$\int _K h_B \, d m_K = d^*(B)$
and
 $\int _K h_C \, d m_K = d^*(C)$
,
$\int _K h_C \, d m_K = d^*(C)$
, -
(ii) for all
 $A \subset G$
,
$A \subset G$
,  $$\begin{align*}B + C + A \supset \tau^{-1} (\operatorname{supp}( h_B * h_C * \rho_{A}^{\lambda})). \end{align*}$$
$$\begin{align*}B + C + A \supset \tau^{-1} (\operatorname{supp}( h_B * h_C * \rho_{A}^{\lambda})). \end{align*}$$
Remark 9.7. The invariant mean
![]() $\lambda $
depends on B and C; it may not realize the upper Banach density of A. In particular, it is possible that
$\lambda $
depends on B and C; it may not realize the upper Banach density of A. In particular, it is possible that
![]() $\lambda (A) = 0$
while
$\lambda (A) = 0$
while
![]() $d^*(A)> 0$
.
$d^*(A)> 0$
.
Proof. In view of Lemma 9.2, there are a compact abelian group K, homomorphism
![]() $\tau : G \to K$
with dense image, measurable functions
$\tau : G \to K$
with dense image, measurable functions
![]() $h_B, h_C:K\to [0,1]$
with
$h_B, h_C:K\to [0,1]$
with
![]() $\int h_B\, dm_K = d^*(B)$
,
$\int h_B\, dm_K = d^*(B)$
,
![]() $\int h_C\, dm_K=d^*(C)$
such that
$\int h_C\, dm_K=d^*(C)$
such that
We now apply Lemma 9.4 with
![]() $h_B*h_C$
in place of h: there is an invariant mean
$h_B*h_C$
in place of h: there is an invariant mean
![]() $\lambda $
on G such that
$\lambda $
on G such that
where
![]() $h'$
is a translate of
$h'$
is a translate of
![]() $h_B*h_C$
.
$h_B*h_C$
.
By Lemma 9.5,
Note that
![]() $B + C + A$
contains the support of
$B + C + A$
contains the support of
![]() $1_{B + C} *_{\lambda } 1_A$
and
$1_{B + C} *_{\lambda } 1_A$
and
![]() $h'$
can be written as
$h'$
can be written as
![]() $h_B' * h_C$
, where
$h_B' * h_C$
, where
![]() $h_B'$
is a translate of
$h_B'$
is a translate of
![]() $h_B$
. Therefore, (37) and (38) imply
$h_B$
. Therefore, (37) and (38) imply
and this proves our proposition.
10 Bohr sets in
 $B + C + A_i$
$B + C + A_i$
The next proposition establishes the existence of Bohr sets in
![]() $B + C + A_i$
in compact abelian groups.
$B + C + A_i$
in compact abelian groups.
Proposition 10.1. Let
![]() $\delta _1, \delta _2>0$
and
$\delta _1, \delta _2>0$
and
![]() $r\in \mathbb N$
. There are constants
$r\in \mathbb N$
. There are constants
![]() $\eta>0$
and
$\eta>0$
and
![]() $k\in \mathbb N$
such that the following holds. Let K be a compact abelian group with probability Haar measure
$k\in \mathbb N$
such that the following holds. Let K be a compact abelian group with probability Haar measure
![]() $m_K$
and let
$m_K$
and let
![]() $f, g: K \to [0, 1]$
be measurable functions such that
$f, g: K \to [0, 1]$
be measurable functions such that
![]() $\int _K f \, d m_K \geq \delta _1$
and
$\int _K f \, d m_K \geq \delta _1$
and
![]() $\int _K g \, d m_K \geq \delta _2$
. For
$\int _K g \, d m_K \geq \delta _2$
. For
![]() $i \in [r]$
, let
$i \in [r]$
, let
![]() $h_i: K \to [0, 1]$
be measurable functions such that
$h_i: K \to [0, 1]$
be measurable functions such that
![]() $\sum _{i=1}^r h_i = 1 \ m_K$
-almost everywhere. Then for some
$\sum _{i=1}^r h_i = 1 \ m_K$
-almost everywhere. Then for some
![]() $i \in [r]$
, the support of
$i \in [r]$
, the support of
![]() $f * g * h_i$
contains a Bohr-
$f * g * h_i$
contains a Bohr-
![]() $(k,\eta )$
set.
$(k,\eta )$
set.
Proof. The proof is similar to an argument used in [Reference Le and Lê33] (Part I of this series). Since
![]() $\sum _{i=1}^r h_i=1$
almost everywhere, we have
$\sum _{i=1}^r h_i=1$
almost everywhere, we have
 $$\begin{align*}f*g* \left(\sum_{i=1}^r h_i \right)(x) = f * g * 1_K (x) = \int_K f \, d m_K \cdot \int_K g \, d m_K \geq \delta_1 \delta_2 \end{align*}$$
$$\begin{align*}f*g* \left(\sum_{i=1}^r h_i \right)(x) = f * g * 1_K (x) = \int_K f \, d m_K \cdot \int_K g \, d m_K \geq \delta_1 \delta_2 \end{align*}$$
for all
![]() $x \in K$
. Therefore, by the pigeonhole principle, there exists
$x \in K$
. Therefore, by the pigeonhole principle, there exists
![]() $i \in [r]$
such that
$i \in [r]$
such that
![]() $f*g*h_i(0) \geq \delta _1 \delta _2/r.$
$f*g*h_i(0) \geq \delta _1 \delta _2/r.$
By [Reference Le and Lê33, Lemma 2.12], we have
 $$ \begin{align*} \left| f*g*h_i(t) - f*g*h_i(0) \right| & = \left| \iint_{K^2} (g(x)-g_t(x)) f(y) h_i(-x-y) \, dm_K(x) dm_K(y) \right| \\ & \leq \| \widehat{g} - \widehat{g_t} \|_{\infty} \|f\|_2 \| h_i\|_2 \\ & \leq \| \widehat{g} - \widehat{g_t} \|_{\infty}, \end{align*} $$
$$ \begin{align*} \left| f*g*h_i(t) - f*g*h_i(0) \right| & = \left| \iint_{K^2} (g(x)-g_t(x)) f(y) h_i(-x-y) \, dm_K(x) dm_K(y) \right| \\ & \leq \| \widehat{g} - \widehat{g_t} \|_{\infty} \|f\|_2 \| h_i\|_2 \\ & \leq \| \widehat{g} - \widehat{g_t} \|_{\infty}, \end{align*} $$
where
![]() $g_t(x) = g(t+x)$
. Hence,
$g_t(x) = g(t+x)$
. Hence,
![]() $f*g*h_i(t)> \frac {\delta _1 \delta _2}{2r}$
whenever
$f*g*h_i(t)> \frac {\delta _1 \delta _2}{2r}$
whenever
![]() $\| \widehat {g} - \widehat {g_t} \|_{\infty } < \frac {\delta _1 \delta _2}{2r}$
. By [Reference Le and Lê33, Lemma 2.1], the set of those t contains a Bohr-
$\| \widehat {g} - \widehat {g_t} \|_{\infty } < \frac {\delta _1 \delta _2}{2r}$
. By [Reference Le and Lê33, Lemma 2.1], the set of those t contains a Bohr-
![]() $(k, \frac {\delta _1 \delta _2}{2r})$
set B with
$(k, \frac {\delta _1 \delta _2}{2r})$
set B with
![]() $k \leq \frac {16r^2}{(\delta _1 \delta _2)^2}$
.
$k \leq \frac {16r^2}{(\delta _1 \delta _2)^2}$
.
We are ready to prove Theorem 1.7.
Proof of Theorem 1.7.
By Proposition 9.6, there exist a compact abelian group K, a homomorphism
![]() $\tau : G \to K$
with dense image, measurable functions
$\tau : G \to K$
with dense image, measurable functions
![]() $h_B, h_C: K \to [0, 1]$
and an invariant mean
$h_B, h_C: K \to [0, 1]$
and an invariant mean
![]() $\lambda $
on G such that
$\lambda $
on G such that
-
(i)
 $\int _K h_B \, d m_K = d^*(B)$
and
$\int _K h_B \, d m_K = d^*(B)$
and
 $\int _K h_C \, d m_K = d^*(C)$
,
$\int _K h_C \, d m_K = d^*(C)$
, -
(ii) for all
 $i \in [r]$
,
$i \in [r]$
,
 $B + C + A_i \supset \tau ^{-1} (\operatorname {supp}( h_B * h_C * \rho _{A_i}^{\lambda })).$
$B + C + A_i \supset \tau ^{-1} (\operatorname {supp}( h_B * h_C * \rho _{A_i}^{\lambda })).$
In light of Corollary 4.5,
![]() $\sum _{i=1}^r \rho _{A_i}^{\lambda } = 1$
almost everywhere. Therefore, by Proposition 10.1, there exist k and
$\sum _{i=1}^r \rho _{A_i}^{\lambda } = 1$
almost everywhere. Therefore, by Proposition 10.1, there exist k and
![]() $\eta $
depending only on
$\eta $
depending only on
![]() $\delta $
and r such that the support of
$\delta $
and r such that the support of
![]() $h_B * h_C * \rho _{A_i}^{\lambda }$
contains a Bohr-
$h_B * h_C * \rho _{A_i}^{\lambda }$
contains a Bohr-
![]() $(k, \eta )$
set in K for some
$(k, \eta )$
set in K for some
![]() $i \in [r]$
. Lemma 2.2 then implies that
$i \in [r]$
. Lemma 2.2 then implies that
![]() $B + C + A_i$
contains a Bohr-
$B + C + A_i$
contains a Bohr-
![]() $(k, \eta )$
set in G.
$(k, \eta )$
set in G.
Remark 10.2. The proof of Theorem 1.7 follows a general phenomenon: if
![]() $D \subset G$
is a piecewise Bohr set, then for any partition
$D \subset G$
is a piecewise Bohr set, then for any partition
![]() $G = \bigcup _{i=1}^r A_i$
, there is an
$G = \bigcup _{i=1}^r A_i$
, there is an
![]() $i \in [r]$
such that
$i \in [r]$
such that
![]() $D + A_i$
contains a Bohr set. However, if we did not know that D has the form
$D + A_i$
contains a Bohr set. However, if we did not know that D has the form
![]() $B + C$
, it is impossible to give any quantitative bounds on the rank and radius of the Bohr set in
$B + C$
, it is impossible to give any quantitative bounds on the rank and radius of the Bohr set in
![]() $D + A_i$
. This necessitates the presence of triple sum
$D + A_i$
. This necessitates the presence of triple sum
![]() $B + C + A_i$
in Theorem 1.7.
$B + C + A_i$
in Theorem 1.7.
11 Open questions
In the proofs of Theorems 1.2 and 1.4, the assumption that
![]() $\phi _1, \phi _2, \phi _3$
commute is used to provide a parameterized solution to the relation
$\phi _1, \phi _2, \phi _3$
commute is used to provide a parameterized solution to the relation
![]() $w \in \phi _1(A) + \phi _2(A) + \phi _3(A)$
. This concern raises the following question.
$w \in \phi _1(A) + \phi _2(A) + \phi _3(A)$
. This concern raises the following question.
The Bohr sets in Proposition 10.1 and Theorem 1.7 have the same rank k and radius
![]() $\eta $
. Proposition 10.1 gives
$\eta $
. Proposition 10.1 gives
![]() $k \ll \alpha ^{-6}$
and
$k \ll \alpha ^{-6}$
and
![]() $\eta \gg \alpha ^3$
, where
$\eta \gg \alpha ^3$
, where
![]() $\alpha = (\delta _1 \delta _2 r^{-1})^{1/3}$
. If we are only interested in translates of Bohr sets (i.e., Bohr neighborhoods of some element), then better bounds are available. A result of Sanders [Reference Sanders37, Theorem 2.4] implies that there exists i such that
$\alpha = (\delta _1 \delta _2 r^{-1})^{1/3}$
. If we are only interested in translates of Bohr sets (i.e., Bohr neighborhoods of some element), then better bounds are available. A result of Sanders [Reference Sanders37, Theorem 2.4] implies that there exists i such that
![]() $B+C+A_i$
contains a translate of a Bohr-
$B+C+A_i$
contains a translate of a Bohr-
![]() $(k,\eta )$
set with
$(k,\eta )$
set with
![]() $k \ll \alpha ^{-1}$
and
$k \ll \alpha ^{-1}$
and
![]() $\eta \geq \exp \left ( - c \alpha ^{-1} \log \alpha ^{-1} \right )$
, for some absolute constant c. We ask the following.
$\eta \geq \exp \left ( - c \alpha ^{-1} \log \alpha ^{-1} \right )$
, for some absolute constant c. We ask the following.
Question 11.2. Is it possible to improve on k and/or
![]() $\eta $
in Theorem 1.7? Can we take
$\eta $
in Theorem 1.7? Can we take
![]() $k \ll \alpha ^{-1}$
?
$k \ll \alpha ^{-1}$
?
In the spirit of Ruzsa and Hegyvári’s result [Reference Hegyvári and Ruzsa28] on Bohr sets in
![]() $A+A-A-a$
mentioned in the introduction, we ask whether the Bohr set in Theorem 1.7 can be given by a fixed element of C. More precisely, we ask the following question.
$A+A-A-a$
mentioned in the introduction, we ask whether the Bohr set in Theorem 1.7 can be given by a fixed element of C. More precisely, we ask the following question.
Question 11.3. If
![]() $B, C \subset G$
with
$B, C \subset G$
with
![]() $d^*(B), d^*(C)>0$
and
$d^*(B), d^*(C)>0$
and
![]() $G = \bigcup _{i=1}^r A_i$
, must there exist
$G = \bigcup _{i=1}^r A_i$
, must there exist
![]() $c \in C$
and
$c \in C$
and
![]() $i \in [r]$
such that
$i \in [r]$
such that
![]() $B+c+A_i$
contains a Bohr set?
$B+c+A_i$
contains a Bohr set?
The proof of Theorem 1.7 uses the fact that
![]() $D := B + C$
is a piecewise Bohr set to deduce the Bohr structure in
$D := B + C$
is a piecewise Bohr set to deduce the Bohr structure in
![]() $D + A_i$
. It is natural to ask besides piecewise Bohr, what other conditions on D guarantee the existence of a Bohr set in
$D + A_i$
. It is natural to ask besides piecewise Bohr, what other conditions on D guarantee the existence of a Bohr set in
![]() $D + A_i$
.
$D + A_i$
.
Question 11.4. What is a sufficient condition on
![]() $D \subset G$
so that for any partition
$D \subset G$
so that for any partition
![]() $G= \bigcup _{i=1}^r A_i$
, there is
$G= \bigcup _{i=1}^r A_i$
, there is
![]() $i \in [r]$
such that
$i \in [r]$
such that
![]() $D+A_i$
is a Bohr set (or a translate of a Bohr set)? In particular, does the assumption that D is piecewise syndetic or
$D+A_i$
is a Bohr set (or a translate of a Bohr set)? In particular, does the assumption that D is piecewise syndetic or
![]() $d^*(D)>0$
suffice? What if
$d^*(D)>0$
suffice? What if
![]() $G = {\mathbb {Z}}$
and
$G = {\mathbb {Z}}$
and
![]() $D = \mathbb {P}$
(the set of primes) or
$D = \mathbb {P}$
(the set of primes) or
![]() $D = \{n^2: n \in \mathbb {N}\}$
?
$D = \{n^2: n \in \mathbb {N}\}$
?
Our Theorem 1.2 generalizes Theorem B in two ways: replacing the ambient group
![]() $\mathbb Z$
with an arbitrary countable abelian group and replacing the endomorphisms
$\mathbb Z$
with an arbitrary countable abelian group and replacing the endomorphisms
![]() $g\mapsto s_ig$
with commuting endomorphisms having finite index image. The main result of [Reference Griesmer23] generalizes Theorem B in a different way: the endomorphisms still have the form
$g\mapsto s_ig$
with commuting endomorphisms having finite index image. The main result of [Reference Griesmer23] generalizes Theorem B in a different way: the endomorphisms still have the form
![]() $g\mapsto s_i g$
, but more summands are considered. The following conjecture is a natural joint generalization of these results.
$g\mapsto s_i g$
, but more summands are considered. The following conjecture is a natural joint generalization of these results.
Conjecture 11.5. Let G be a (not necessarily countable) abelian group, let
![]() $d\geq 3$
, let
$d\geq 3$
, let
![]() $\phi _1,\dots , \phi _d$
be endomorphisms of G such that
$\phi _1,\dots , \phi _d$
be endomorphisms of G such that
![]() $[G:\phi _j(G)]<\infty $
for each j, and such that
$[G:\phi _j(G)]<\infty $
for each j, and such that
![]() $\phi _1+\cdots +\phi _d=0$
. Then for all
$\phi _1+\cdots +\phi _d=0$
. Then for all
![]() $A\subset G$
with
$A\subset G$
with
![]() $d^*(A)>0$
, the sumset
$d^*(A)>0$
, the sumset
![]() $\phi _1(A)+\cdots + \phi _d(A)$
contains a Bohr set with rank and radius depending only on
$\phi _1(A)+\cdots + \phi _d(A)$
contains a Bohr set with rank and radius depending only on
![]() $d^*(A)$
and the indices
$d^*(A)$
and the indices
![]() $[G:\phi _j(G)]$
.
$[G:\phi _j(G)]$
.
Defining endomorphism
![]() $\psi : G \to G$
by
$\psi : G \to G$
by
![]() $\psi (g) := \sum _{j=3}^d \phi _j(g)$
. Then
$\psi (g) := \sum _{j=3}^d \phi _j(g)$
. Then
![]() $\phi _1 + \phi _2 + \psi = 0$
and
$\phi _1 + \phi _2 + \psi = 0$
and
 $$\begin{align*}\sum_{j=1}^d \phi_j(A) \supset \phi_1(A) + \phi_2(A) + \psi(A). \end{align*}$$
$$\begin{align*}\sum_{j=1}^d \phi_j(A) \supset \phi_1(A) + \phi_2(A) + \psi(A). \end{align*}$$
Therefore, if
![]() $[G:\psi (G)]$
is finite, then Conjecture 11.5 immediately follows from Theorem 1.2. However, it is not true in general that
$[G:\psi (G)]$
is finite, then Conjecture 11.5 immediately follows from Theorem 1.2. However, it is not true in general that
![]() $\psi (G)$
has finite index (for example, take
$\psi (G)$
has finite index (for example, take
![]() $d = 4$
,
$d = 4$
,
![]() $\phi _3 = - \phi _4$
), and so Conjecture 11.5 is genuinely interesting. It may be necessary to impose some additional hypotheses on the
$\phi _3 = - \phi _4$
), and so Conjecture 11.5 is genuinely interesting. It may be necessary to impose some additional hypotheses on the
![]() $\phi _j$
; see [Reference Griesmer23, Section 4] for more discussion.
$\phi _j$
; see [Reference Griesmer23, Section 4] for more discussion.
Along the same lines, we have the following conjecture for partition that extends Theorem 1.4.
Conjecture 11.6. Let G be a (not necessarily countable) abelian group, let
![]() $d\geq 3$
and let
$d\geq 3$
and let
![]() $\phi _1,\dots , \phi _d$
be endomorphisms of G such that
$\phi _1,\dots , \phi _d$
be endomorphisms of G such that
![]() $[G:\phi _j(G)]<\infty $
for each j. Suppose
$[G:\phi _j(G)]<\infty $
for each j. Suppose
![]() $\sum _{j \in S} \phi _j = 0$
for some non-empty subset
$\sum _{j \in S} \phi _j = 0$
for some non-empty subset
![]() $S \subset [d]$
. Then for every finite partition
$S \subset [d]$
. Then for every finite partition
![]() $G = \bigcup _{i=1}^r A_i$
, there exists
$G = \bigcup _{i=1}^r A_i$
, there exists
![]() $i \in [r]$
such that
$i \in [r]$
such that
![]() $\sum _{j=1}^d \phi _j(A_i)$
contains a Bohr-
$\sum _{j=1}^d \phi _j(A_i)$
contains a Bohr-
![]() $(k, \eta )$
set, where k and
$(k, \eta )$
set, where k and
![]() $\eta $
depend only on r and the indices
$\eta $
depend only on r and the indices
![]() $[G: \phi _j(G)]$
.
$[G: \phi _j(G)]$
.
Acknowledgements
We thank the anonymous referee for carefully reading the manuscript, pointing out some oversights and providing many suggestions which help improve the presentation of the paper. The third author is partially supported by NSF Grant DMS-2246921.
Competing Interest
The authors have no conflicts of interest to declare.
Financial Support
The third author is partially supported by NSF Grant DMS-2246921.