1. Introduction
Growth of high quality single crystals is of primary importance for the development of homoepitaxial techniques for optoelectronic applications. The high pressure solution method is at present the most reliable way to obtain GaN crystals of size up to 15 mm.
In the growth of GaN from nitrogen dissolved in Ga under high pressure of nitrogen two main growth habits are observed: plate-like and needle-like Reference Elwell, Feigelson, Simkins and Tiller[1] Reference Grzegory and Krukowski[2] Reference Yamane, Shimada, Sekiguchi and DiSalvo[3] Reference Grzegory, Jun and Krukowski[4]. There are a few kinds of plate-like habits. They differ from each other by the pyramidal faces. Among needle-like habits there are also a few kinds which differ from each other by the pyramidal faces and the tips of the needles which may be sharp or blunt. There are also observed habits which are something between the plate and needle. Looking at such transient habits, the question arises whether a transformation from plate-like to needle-like habit is possible.
The aim of this study is to analyze the growth process of both types of GaN single crystals. The attempt to answer the above question is the main subject of this paper.
The computer program SHAPE v. 4.1.1. Reference Dowty[5] was chosen as a tool for the graphical presentation of morphologies and sections of GaN crystals (crystal class 6mm, a = 3.1892Å, c = 5.1850Å) and for presentation of the analytically predicted transitions between different habits.
2. Method of Crystal Growth
The observed GaN single crystals were grown from a metallic solution of nitrogen in liquid Ga under high pressure of nitrogen (close to 15 kbar) and high temperature (close to 1500 °C) Reference Grzegory and Krukowski[2] Reference Grzegory, Jun and Krukowski[4]. In this method GaN single crystals are grown on the sides of the crucible in the cold end zone. The supersaturation is determined from the temperature difference leading to a difference in nitrogen solubility Reference Grzegory and Krukowski[2] Reference Grzegory, Jun and Krukowski[4].
3. The Observed GaN Single Crystal Habits
Generally, GaN single crystal habits we observe may be divided into two kinds. The first one is the plate-like habit (Figure 1a). The second kind is the needle-like habit (Figure 1b). Sometimes, unusual star-like needles were observed.

Figure 1a. The exemplary GaN needle-like and plate-like single crystal habits.

Figure 1b. The exemplary GaN needle-like single crystal habits Reference Grzegory and Krukowski[2].
Generally, it is possible to divide the observed plate-like habits into four types which are shown schematically in Figure 2. They differ from each other by the pyramidal faces. We observed platelet habits without any pyramidal faces - Figure 2a. We also observed platelet habits with {10

Figure 2. The observed GaN plate-like single crystal habits and their longitudinal sections; habits: a) without pyramidal faces, b) with pyramidal faces {10
Generally, we observed three types of needle-like GaN single crystal habits: needle-like habits with {10
Generally, plate-like crystals are characterized by much more stable growth. The morphological instabilities of plate-like crystals are mostly related to the edge instability. On the other hand the needle-like crystals frequently show twins or more pronounced instabilities, such as star-shapes. This is related to the characterized growth regimes: it is known that plate-like crystals are observed for lower supersaturations and needle-like for higher supersaturations.
As it is seen in Figure 1b some of the crystals are in the shape of plate, some of them are in the shape of needle and the shape of some of them is something between plate-like and needle-like. That is why it is supposed that it may happen that at first the habits are plate-like. During the growth process the crystals become bigger and some of them remain of the platelet shape but some of them change shape from plate-like to needle-like.
4. Theoretical Analysis of the Observed GaN Single Crystal Habits
4.1 Method of analysis
In order to investigate how the plate-like or needle-like GaN single crystals grow, it is necessary to take a closer look at the longitudinal sections along each of the habits (cf. Figure 2). All sections of crystals shown in this paper present the growth bands corresponding to subsequently growing layers, often observed in real crystals. Each layer corresponds to the position of a given face at equal time intervals. It means that the growth bands allow the investigation of the growth history of crystals Reference Görnert, Voigt and Kaldis[6]. Therefore, the sections illustrate growth histories of exemplary GaN single crystals. If we assume that the layer of a given face grows with constant rate, the distances between the growth bands are proportional to growth rates of individual faces. The same layer, but of some other face, grows with constant rate too, but these two constant rates do not have to be the same. It means that the distance between growth bands is not the same for different faces.
In all cases considered in this paper the growth begins from a two-dimensional seed. The (000
In order to explain these different crystal habits let us analyze the critical growth rate RA crit , defined as the normal growth rate of face Aat which the edge lA/C created by faces Aand C preserves its size Reference Szurgot and Prywer[7] Reference Szurgot[8]. It was derived in Reference Prywer[9] that the critical growth rate RA crit may be expressed by the formula:
where: RB , RC and RD are the normal growth rates of individual faces B, C and D respectively. These faces B, C and D are surrounding faces of the edge lA/C . Their growth rates, RB , RC and RD , are assumed to be constant not during the whole growth process, but only during the growth of a single layer of crystal. A layer of crystal may be defined as the distance between one growth band and another as described above. The angles α, β, γ are the angles between vectors normal to the pairs of faces: A/B, A/C, A/D, respectively. The angles ψ 1, ψ 2 are the complements of angles between appropriate edges of face A Reference Prywer[9]. If the face A grows with normal growth rate RA greater than RA crit , then the size of lA/C decreases. In the case where the growth rate RA is smaller than RA crit the edge size increases. For some faces, (for example all faces without parallel edges or pentagonal faces) the critical growth rate for a given edge is simultaneously the critical growth rate for the whole face Reference Prywer[10]. This means that for such cases not only a given edge but also the whole face may change or preserve its size.
The above formula is applied in this paper to GaN single crystals. It yields critical growth rates for different edges and faces which correspond to decreases in the size of some faces and to increases in the size of other faces. The values obtained for these critical growth rates make it possible to analyze the changes in habits of growing GaN crystals.
4.2 Transformation from plate-like into needle-like GaN single crystal habits
In order to investigate how these plate-like or needle-like crystals grow, let us take a closer look at one chosen habit, for example the one shown in Figure 3a and Figure 3b. The section (Figure 3b) shows the growth bands which illustrate an exemplary growth history and the transition from plate-like to needle-like GaN single crystal habit. The growth begins from a two-dimensional seed. The two-dimensional seed grows and a plate-like three-dimensional crystal appears. Up to the m 3 growth band (Figure 2b) the relative growth rates R {10

Figure 3a. The observed GaN needle-like single crystal habits with pyramidal faces {10

Figure 3b. The longitudinal section of GaN single crystal habit shown in Figure 3a, with pyramidal faces {10
It is possible to apply Equation (1) to GaN single crystals and evaluate the relative growth rate
Similarly, as it was done for the (0001) face, it is also possible to evaluate
Let us take a closer look at the habit at the m 9 growth band. It is seen that at this stage of growth the crystal is plate-like. The relative growth rates R (0001)/R {10
Generally, it is seen that the plate-like GaN single crystals grow when the relative growth rate R (0001)/R {10
For some crystals, pyramids are formed with {10

Figure 4. Two kinds of the observed GaN needle-like single crystal habits and their longitudinal sections; habits: a) with pyramidal faces {10
In the case considered above it is assumed that all faces belonging to a given set {10
Sometimes, star-like GaN crystal habits were observed - Figure 5. In this figure well developed {10

Figure 5. The exemplary star-like GaN single crystal habit Reference Grzegory and Krukowski[2].
On the basis of the above analysis and the exemplary longitudinal sections of GaN single crystal habits, the conclusion may be drawn that the transition from the plate-like to needle-like habit is possible and it can occur in a stable way. The transformation from the plate-like into the needle-like habit in the case of the {10
5. Conclusions
Our considerations allow us to draw the following conclusions:
-
1. GaN growth habits depend on the relative growth rates; the transition from plate-like to needle-like habits may occur without loss of morphological stability.
-
2. The transformation from plate-like to needle-like habit, in the case when the pyramid is created by the set of the {10
1} faces, is caused by the increase in the relative growth rate R (0001)/R {10 1} above the evaluated value 2.13 and simultaneous decrease in the relative growth rate R {10
1} above the evaluated value 2.13 and simultaneous decrease in the relative growth rate R {10 0} /R {10
0} /R {10 1} below the value 1.13.
1} below the value 1.13.
-
3. When the pyramid is created by the set of {10
2} faces, the transformation from plate-like to needle-like habit is caused by the increase in the relative growth rate R (0001)/R {10 2} above the evaluated value 1.37 and the simultaneous decrease in relative growth rate R {10
2} above the evaluated value 1.37 and the simultaneous decrease in relative growth rate R {10 0} /R {10
0} /R {10 2} below the value 1.46.
2} below the value 1.46.
-
4. GaN star-like crystals result from unstable morphologically growth rate.
-
5. The relative change of the growth rates occurs via the kinetic mechanism and depends on the orientation of the growing face. The change of the mechanism can lead to growth of three-dimensional GaN crystals.

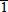 ) and {10
) and {10



