1. Introduction
The European Alps were characterised by multiple extensive glaciations (Ehlers and Gibbard, Reference Ehlers and Gibbard2008) during the late Quaternary following glacial cycles of the Milankovitch theory. Our understanding of the most recent and most extensive glaciations is largely based on geomorphological evidence left on the landscape, such as moraines, erratic boulders, trimlines or drumlins (Kelly and others, Reference Kelly, Buoncristiani and Schlüchter2004; Bini and others, Reference Bini2009; Preusser and others, Reference Preusser, Graf, Keller, Krayss and Schlüchter2011; Palacios and others, Reference Palacios, Hughes, Ruiz and Andrés2021). In contrast, most of the geological traces related to earlier or less extensive glaciations were destroyed by subsequent glacier readvances. This is the reason why the Last Glacial Maximum (LGM, ~24′000 years BP in the Alps) and the deglaciation until the Holocene are the best constrained time periods during the late Quaternary (Ivy-Ochs, Reference Ivy-Ochs2015; Ivy-Ochs and others, Reference Ivy-Ochs, Monegato and Reitner2022). In fact, the extent of the Alpine Ice Field (AIF) is reasonably well defined in the Alpine forelands due to abundant moraines (Jäckli, Reference Jäckli1962; Van Husen, Reference Van Husen1987; Bini and others, Reference Bini2009; Ehlers and others, Reference Ehlers, Gibbard and Hughes2011). Still, there are higher uncertainties in the timing of glacier advances (Kamleitner and others, Reference Kamleitner2022, Fig. 1), although cosmogenic nuclide dating has greatly improved our ability to assign an age to mapped features (e.g., Gosse and Phillips, Reference Gosse and Phillips2001; Ivy-Ochs and Kober, Reference Ivy-Ochs and Kober2008; Balco, Reference Balco2011).
The European Alps are probably the place with the largest number of individual studies with precise mapping and dating of 15–20 lobes of the AIF (Wirsig and others, Reference Wirsig, Zasadni, Christl, Akçar and Ivy-Ochs2016, Fig. 5). Recent contributions have refined our knowledge by providing better time constraints, identifying multiphase LGM advances, as well as other maxima based on exposure age estimates of erratic boulders and other dating techniques (e.g. Graf and others, Reference Graf2015, and references therein). These findings suggest that the Alpine glaciers during Marine Isotopic Stage 4 (MIS4, 71–59 ka BP) were generally less extensive than during the LGM. In the eastern Alps, there is no evidence of the presence of glaciers in the main Alpine valleys (van Husen, Reference van Husen2004), while in the western Alps an important glaciation reached the lowlands during MIS4 (e.g. Schlüchter, Reference Schlüchter1991). There are some hints that glacier extents larger than at the LGM may have occurred in the western Alps (e.g. the Lyon lobe Gribenski and others, Reference Gribenski2021 or the Reuss Glacier Gaar and others, Reference Gaar, Graf and Preusser2019). In the eastern Alps, the LGM appears to be the period with the maximal extent of glaciers, for example, in the Inn Valley (Spötl and others, Reference Spötl, Reimer, Starnberger and Reimer2013).
In recent years, numerical models that simulate the interaction between the thermodynamics of the ice and the climate-induced mass balance proved to be very valuable tools to deepen our understanding of glacial states from physical principles (Mey and others, Reference Mey2016; Jouvet and others, Reference Jouvet, Seguinot, Ivy-Ochs and Funk2017; Cohen and others, Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018; Seguinot and others, Reference Seguinot2018; Imhof and others, Reference Imhof2019; Višnjević and others, Reference Višnjević, Herman and Prasicek2020; Imhof, Reference Imhof2021). Among them, Seguinot and others (Reference Seguinot2018) simulated the evolution of the AIF at a resolution of 1 km during the entire last glacial cycle. The simulation suggests that the Alpine glaciers advanced several times on the foreland during this period. However, the uncertainty in climate forcing, which controls mass balance, and thus glacier extent, limits the scope of the results. Indeed, all of these studies – with the exception of Imhof (Reference Imhof2021) – apply a distortion of today's climate to mimic paleo conditions, while several proxies (Florineth and Schlüchter, Reference Florineth and Schlüchter2000; Luetscher and others, Reference Luetscher2015; Monegato and others, Reference Monegato, Scardia, Hajdas, Rizzini and Piccin2017) suggest a dramatically different precipitation pattern over the Alps during the LGM (dominated by southerly atmospheric circulation) compared to today (dominated by westerly circulation). This may explain biases between model results and observations such as a too extensive glaciation in the east and a too weak extension of glaciers in the west (Seguinot and others, Reference Seguinot2018), and the incorrect ice flow distribution between the Soloturn and Lyon lobes, as witnessed by trajectories of erratic boulders from the south Valais (Jouvet and others, Reference Jouvet, Seguinot, Ivy-Ochs and Funk2017).
Our current knowledge of the climate of glacial periods mainly relies on reconstructions from proxy records such as ice cores, speleothems, sediment cores, etc. For the midlatitudes of the northern hemisphere, pollen data are used mainly to generate reconstructions of temperature and precipitation (Bartlein and others, Reference Bartlein2011; Cleator and others, Reference Cleator, Harrison, Nichols, Prentice and Roulstone2020; Davis and others, Reference Davis, Fasel, Kaplan, Russo and Burke2022). For the LGM, these reconstructions indicate that the European climate was fundamentally different compared to the present-day (Mix and others, Reference Mix, Bard and Schneider2001). The temperatures were lower, with summer differences up to 6–12°C and winter ones up to 10–17 °C (Wu and others, Reference Wu, Guiot, Brewer and Guo2007). Furthermore, reconstructed precipitation indicates that the LGM was probably dryer than today, but the amplitude of this reduction is rather uncertain. Indirect evidence of changes in atmospheric circulation during the LGM from the major loess deposits found across Europe (Antoine and others, Reference Antoine2009; Obreht and others, Reference Obreht2019) and from several independent proxy-based studies of LGM precipitation (Florineth and Schlüchter, Reference Florineth and Schlüchter2000; Luetscher and others, Reference Luetscher2015; Monegato and others, Reference Monegato, Scardia, Hajdas, Rizzini and Piccin2017), suggest that LGM precipitation was mainly controlled by south-westerly flow, whereas today's precipitation is advected from the west-northwest direction (Fig. 1).
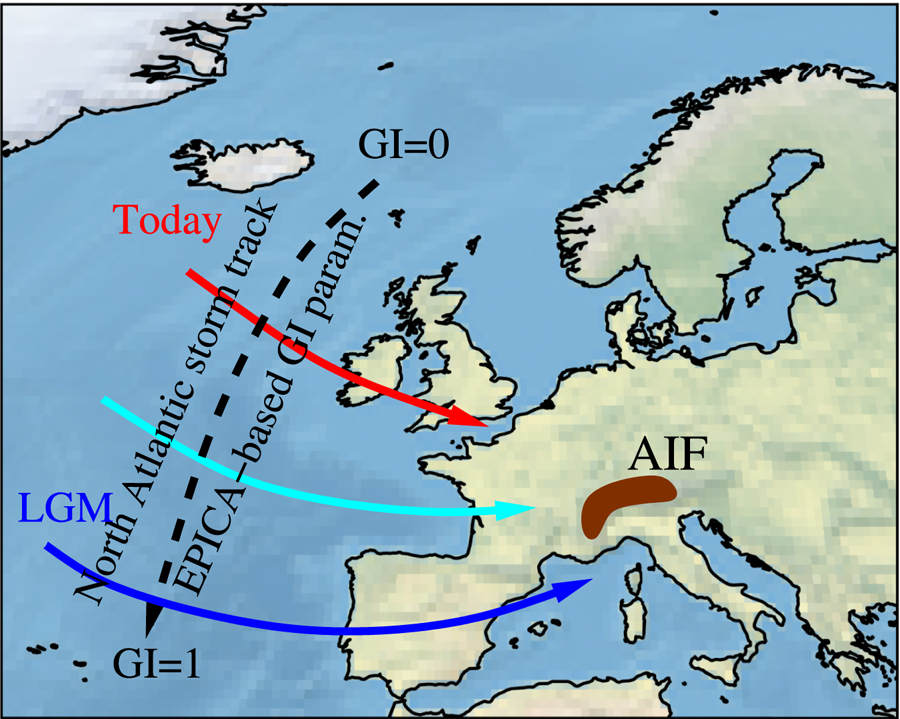
Figure 1. The North-Atlantic storm track and the resulting moisture advection towards and across the Alps were probably shifted southwards at the LGM compared to present-day conditions. The glacial index parametrisation used in this study can be seen as a control of the North-Atlantic storm track: the moisture is mostly advected towards the north west of the Alps when GI is close to zero to mimic present-day situation, while the moisture advection is shifted southwards when GI is close to one to mimic the LGM situation.
Physically consistent climate models complement our understanding of the relevant processes governing the climate of glacial periods by filling existing gaps of spatial coverage and temporal resolution of proxy data (Raible and others, Reference Raible, Pinto, Ludwig and Messmer2021). Additionally, models constitute a powerful tool for testing plausible physical hypotheses for the interpretation of evidence from proxies (Russo and others, Reference Russo, Fallah, Ludwig, Karremann and Raible2022). Hence, the global LGM is one of the key periods selected by the Paleo Modelling Intercomparison Projects (Kageyama and others, Reference Kageyama2021). Models helped identify atmospheric circulation changes during the LGM (Kutzbach and Geuetter, Reference Kutzbach and Geuetter1986; Dong and Valdes, Reference Dong and Valdes1998; Kageyama and others, Reference Kageyama, Valdes, Ramstein, Hewitt and Wyputta1999; Hofer and others, Reference Hofer, Raible, Dehnert and Kuhlemann2012b, Reference Hofer, Raible, Dehnert and Kuhlemann2012a; Merz and others, Reference Merz, Raible and Woollings2015; Lofverstrom and others, Reference Lofverstrom, Caballero, Nilsson and Messori2016). For example, Merz and others (Reference Merz, Raible and Woollings2015) provided evidence that the stationary wave activity is enhanced southeast of the Northern Hemisphere Ice Sheet (NHIS) during glacial periods. The consequential southward shift of the storm track and the jet stream (Fig. 1), strongly affects the precipitation pattern over the north Atlantic and Europe (e.g., Hofer and others, Reference Hofer, Raible, Dehnert and Kuhlemann2012b; Lofverstrom and others, Reference Lofverstrom, Caballero, Nilsson and Messori2016; Roberts and others, Reference Roberts, Li and Valdes2019).
Yet, these global modelling approaches allow to resolve processes at relatively coarse resolutions, between 100 and 200 km. This is a strong limitation, in particular over complex terrain such as the Alps. To increase resolution, global climate model simulations are statistically (Latombe and others, Reference Latombe2018) or dynamically downscaled (Prömmel and others, Reference Prömmel, Cubasch and Kaspar2013; Fallah and others, Reference Fallah, Sodoudi and Cubasch2016; Russo and Cubasch, Reference Russo and Cubasch2016; Ludwig and others, Reference Ludwig, Pinto, Raible and Shao2017; Fallah and others, Reference Fallah2018; Russo and others, Reference Russo, Fallah, Ludwig, Karremann and Raible2022). Del Gobbo and others (Reference Del Gobbo, Colucci, Monegato, Žebre and Giorgi2023) used a regional climate model (RCM) to reconstruct the equilibrium line altitude (ELA) of glaciers in the Alps at the LGM. They found consistent results with geologically based glacier extent reconstructions, demonstrating the potential of climate modelling, especially the patterns of paleo precipitation which play an important role in the distribution of ice. However, this study had two limitations: (i) The low resolution of the climate model (12 km) can hardly resolve the mountain orography in the Alpine environment, (ii) their ELA-based glacier reconstruction lacks essential transient and dynamical aspects of the climate–glacier interactions. Recently, a convection-permitting regional climate was applied to realistically represent precipitation-related processes over the Alps, during glacial periods such as the LGM and MIS4 (Velasquez and others, Reference Velasquez, Messmer and Raible2020, Reference Velasquez, Kaplan, Messmer, Ludwig and Raible2021, Reference Velasquez, Messmer and Raible2022; Russo and others, Reference Russo2023). These new achievements in climate modelling enable us to provide physically consistent high-resolution boundary conditions for glacier modelling over the Alps.
In this paper, we attempt to overcome the two aforementioned limitations, and present a reconstruction of the AIF over the last 120 000 years by combining state-of-the-art, high-resolution (2 km), RCM obtained with the Weather Research and Forecasting Model (WRF, Powers and others (Reference Powers2017)), and glacier modelling with the Parallel Ice Sheet Model (PISM). Our study follows the work of Seguinot and others (Reference Seguinot2018) and Imhof (Reference Imhof2021), but uses a modelled paleoclimate instead of a distortion of present-day climate for forcing the AIF mass balance in PISM. This new approach yields an improved match between LGM-related characteristics, such as maximal extent, ice flow and ice thickness, with field evidence observations.
The outline of this paper is as follows. First, we describe the climate and glacier models. Then we present the new AIF for the last glaciation cycle and compare the simulation with documented geological field evidence. Finally, we discuss the implications of our new findings for our knowledge of the AIF.
2. Models
To simulate the AIF over paleo-time scales with a resolution that allows to capture the complex topography of the alpine mountain range, we first target a series of climate states by combining global Earth System (ESM) and Regional Climate Models (RCM) following an approach already applied by Velasquez and others (Reference Velasquez, Messmer and Raible2020, Reference Velasquez, Kaplan, Messmer, Ludwig and Raible2021, Reference Velasquez, Messmer and Raible2022). Then, we generate a transient climate using a Glacial Index (GI) approach. Finally, we use the transient climate to force the Parallel Ice Sheet Model (PISM). These four key steps are illustrated in Figure 2.

Figure 2. Model chain implemented in the study.
2.1. Earth System Model (ESM)
The Community Earth System Model (CESM, version 1.2 Hurrell and others, Reference Hurrell2013) is used to perform simulations for key periods (referred as ‘states’) during the late Quaternary. We use the fully coupled version of the model with a coarser resolution of ~$2^\circ$![]() in the atmosphere and $1^\circ$
in the atmosphere and $1^\circ$![]() in the ocean. The original LGM state is derived from a 1500-year-long simulation (Zhu and others, Reference Zhu2017). This was extended an additional 150 years and then subsequent sensitivity simulations are run to reach a quasi-equilibrium state (this takes ~400 years depending on the climate state and the initial conditions used). Then we repeat the simulation using only the atmospheric and land model components, with an increased horizontal resolution of $0.9^\circ \times 1.2^\circ$
in the ocean. The original LGM state is derived from a 1500-year-long simulation (Zhu and others, Reference Zhu2017). This was extended an additional 150 years and then subsequent sensitivity simulations are run to reach a quasi-equilibrium state (this takes ~400 years depending on the climate state and the initial conditions used). Then we repeat the simulation using only the atmospheric and land model components, with an increased horizontal resolution of $0.9^\circ \times 1.2^\circ$![]() , using prescribed time-varying sea surface temperatures and sea-ice distributions obtained from the fully coupled simulation. This strategy is applied to the Pre-Industrial (PI) period, the global LGM (~21 ka) and the MIS4 (~65 ka) (Buzan and others, Reference Buzan, Russo, Kim and Raible2023). Throughout the paper, the LGM climate state refers implicitly to the global LGM (~21 ka) while the LGM in the Alps (i.e. the timing of maximum glaciation) refers to ~24 ka. The climate forcing of the states consists of changes in orbital parameters, concentration of greenhouse gases and prescribed reconstructed NHIS configurations for LGM and MIS4. As studies have shown that the NHIS plays an important role in shaping the climate of Europe during glacial periods (Merz and others, Reference Merz, Raible and Woollings2015), we perform a set of sensitivity simulations for each of the LGM and MIS4 glacial states, scaling the height of the NHIS (Fig. 1 in Buzan and others, Reference Buzan, Russo, Kim and Raible2023) by 66, 100 and 125% of the reconstruction of Peltier and others (Reference Peltier, Argus and Drummond2015). Indeed, Batchelor and others (Reference Batchelor2019) estimates that the ice heights are up to 125% (MIS6) and down to 67% (MIS8/MIS4), therefore, our three simulations cover a physical range of uncertainty. Thus, in total, we have seven global model simulations available. Further technical details on the global simulations performed are presented in Buzan and others (Reference Buzan, Russo, Kim and Raible2023).
, using prescribed time-varying sea surface temperatures and sea-ice distributions obtained from the fully coupled simulation. This strategy is applied to the Pre-Industrial (PI) period, the global LGM (~21 ka) and the MIS4 (~65 ka) (Buzan and others, Reference Buzan, Russo, Kim and Raible2023). Throughout the paper, the LGM climate state refers implicitly to the global LGM (~21 ka) while the LGM in the Alps (i.e. the timing of maximum glaciation) refers to ~24 ka. The climate forcing of the states consists of changes in orbital parameters, concentration of greenhouse gases and prescribed reconstructed NHIS configurations for LGM and MIS4. As studies have shown that the NHIS plays an important role in shaping the climate of Europe during glacial periods (Merz and others, Reference Merz, Raible and Woollings2015), we perform a set of sensitivity simulations for each of the LGM and MIS4 glacial states, scaling the height of the NHIS (Fig. 1 in Buzan and others, Reference Buzan, Russo, Kim and Raible2023) by 66, 100 and 125% of the reconstruction of Peltier and others (Reference Peltier, Argus and Drummond2015). Indeed, Batchelor and others (Reference Batchelor2019) estimates that the ice heights are up to 125% (MIS6) and down to 67% (MIS8/MIS4), therefore, our three simulations cover a physical range of uncertainty. Thus, in total, we have seven global model simulations available. Further technical details on the global simulations performed are presented in Buzan and others (Reference Buzan, Russo, Kim and Raible2023).
2.2. Regional Climate Model (RCM)
The ESM simulations are the basis for the second step in the model chain (Fig. 2), the dynamical downscaling. For this purpose, we use the Weather Research and Forecasting model (WRF, version 3.8.1) (Skamarock and others, Reference Skamarock2008; Powers and others, Reference Powers2017). The model uses four two-way nested domains, with a spatial resolution going from 54 km over Europe, down to 2 km over the Alps. In the two innermost domains, the convection parametrisation is switched off, leading to a more realistic simulation of precipitation (Ban and others, Reference Ban, Schmidli and Schär2014; Messmer and others, Reference Messmer, Gómez-Navarro and Raible2017; Velasquez and others, Reference Velasquez, Messmer and Raible2020). For the different glacial periods, the RCM requires information on the top surface elevation (the AIF) at the time of the considered state, which is not available a priori as this is what we intend to model. Instead, we use as ice surface topography input for the model over the Alpine region, the LGM ice surface topography derived from an earlier modelling work, for all states except for the PI for which the present-day surface topography is taken. Similarly, we use the maximum top surface elevation of the Fennoscandian ice sheet from 24 to 18 ka BP from the dataset of Peltier and others (Reference Peltier, Argus and Drummond2015) to force the RCM at a continental scale. Each of the seven simulations is performed for 10 years in order to obtain mean values necessary for the subsequent glacier modelling with PISM. More details on the parametrisations used, the necessary model developments to make the model usable for paleo applications and the assessment of model performances against proxy reconstructions are presented in Russo and others (Reference Russo2023).
In summary, the climate model chain provides physically consistent high-resolution (2 km) values of temperature and precipitation fields at daily timescales over 10 years for each targeted climate state (PI, LGM, MIS4). Because such a high temporal resolution is not needed for glacier modelling, we calculate, for each period, decadal monthly averages of daily values of temperature and precipitation. To keep the annual and daily variability of the original temperature data, we additionally estimate the monthly standard deviation of the mean daily temperatures. Note that the temperature fields always refer to the surface topography given as input to the RCM, which is the same for all states except for the PI. To simulate the temperature when the modelled surface deviates from the reference one, we apply a vertical and linear lapse correction, the lapse rate being estimated from the RCM outputs to 6 and 5.74 °C km−1 for the PI and LGM/MIS4 states, respectively.
2.3. Glacial index approach
To extend the climate data between the states, we adopt a GI approach (e.g. Sutter and others, Reference Sutter2019). For this purpose, we define a function GI that maps time t to a scalar with two extreme states: one state with almost no ice over the Alps corresponding to GI=0 and one maximum state in terms of glacier extent corresponding GI=1. The climate CL consists of a set of variables: mean temperature, temperature variability, mean precipitation and lapse rate,
and is assumed to be a linear combination:
where the two climate states
correspond to GI=0 and GI=1, respectively. Here, we associate the Pre-Industrial (PI) climate state with GI=0:
and MIS4 and LGM with GI=1 as follows:
Last, the GI function is built by linearly rescaling a climate proxy signal in such a way that GI is close to 1 at the LGM and close to 0 at the PI. The chosen procedure is used to build the AIF consistently with geomorphological evidence (especially in the building phase of the LGM) but can, of course, not reproduce the full timing and complexity of the last glacial cycle climate. Despite its distance to the AIF, we mainly used here the Antarctic EPICA temperature anomaly signal (Jouzel and others, Reference Jouzel2007), which is available for the last 800 000 years, because it yields the best match with geological evidence and a realistic global timing of the maximum glacier extent among the three signals tested. These include EPICA, the Greenland NGRIP signal (Seierstad and others, Reference Seierstad2014) and a local pollen-based signal (rescaled linearly from the principal component of the pollen data) from Bergsee, southern Germany (Duprat-Oualid and others, Reference Duprat-Oualid2017). For sensitivity analysis, we also show results obtained with the Bergsee signal, which is available from 45 to 15 ka BP. The two resulting GI functions are shown in Figure 3, top panel. Note that we, in fact, rescaled the EPICA signal to slightly negative GI values (~−0.25) at the PI to correct for an overestimation of modelled ice volumes during the Holocene obtained when rescaling the GI to zero. We mainly attribute this bias to (i) an inadequacy of the model resolution (2 km) to resolve Holocene/present-day small-scale glaciers (the tongue of the largest present-day glacier being narrower than one pixel resolution, leading to underestimated ice flow, and thus artificial ice accumulation), (ii) biases in PI modelled climate and (iii) inappropriate melt parameters. Due to (i), we refrain from analysing the results of our model during the Holocene.

Figure 3. Time evolution of the glacial index based on the EPICA (continuous line) and Bergsee (dashed line) signals for climate forcing (continuous line, panel a), and resulting modelled evolution of the entire glaciated area and ice volume (panel b) during the last glacial cycle (based on EPICA).
2.4. Parallel Ice Sheet Model (PISM)
We use the Parallel Ice Sheet Model (PISM, Bueler and Brown, Reference Bueler and Brown2009; Winkelmann and others, Reference Winkelmann2011) (version 2.0.2), which jointly models the ice thickness evolution, the ice thermodynamics, the surface mass balance, and the deformation of the lithosphere given initial conditions (Fig. 4). The four model components of PISM are described in turn.
1. To model the dynamical motion of ice, PISM uses a linear combination of low order approximations (Bueler and Brown, Reference Bueler and Brown2009), namely the shallow ice approximation (SIA) for the vertical shear and the shallow shelf approximation (SSA) for the longitudinal ice extension. This hybrid approach is a trade-off between mechanical accuracy and computational cost that permits to simulate long time scales. In the SSA, the basal velocity and the basal shear stress are related non-linearly with the Mohr–Coulomb sliding law (Cuffey and Paterson, Reference Cuffey and Paterson2010). This law is parameterised by the yield stress, i.e. the product of the till friction angle and the effective pressure in the till, which is determined by the weight of the ice column minus the modelled pressure of water in the till derived from a simple subglacial hydrology model (Khroulev and the PISM Authors, Reference Khroulev2022).
2. PISM is a polythermal model, i.e. it solves jointly the ice dynamics together with the ice temperature field in three dimensions using an enthalpy formulation (Aschwanden and others, Reference Aschwanden, Bueler, Khroulev and Blatter2012). The ice enthalpy (or the temperature and the water content) impacts both the ice softness, as well as the basal motion. Additionally, the dynamics of ice influences the evolution of the enthalpy field. The enthalpy equation is constrained by the mean air temperature at the glacier surface (given by the climate forcing) and by a spatially variable geothermal heat flux at the glacier base (here we use the data of Goutorbe and others (Reference Goutorbe, Poort, Lucazeau and Raillard2011)).
3. PISM uses a combined snow accumulation/positive degree-day (PDD) model (cf. Hock, Reference Hock2003) to compute the surface mass balance from temperature and precipitation fields. On the one hand, surface accumulation is equal to solid precipitation when temperature is below 0$^\circ$
 C, and decreases to zero linearly between 0 and 2$^\circ$
C, and decreases to zero linearly between 0 and 2$^\circ$ C. On the other hand, the surface ablation is computed proportionally to the number of PDD. The PDD integral is numerically approximated using week-long sub-intervals based on Calov and Greve (Reference Calov and Greve2005), with PDD proportionality factors of f i = 8×C mm $^\circ$
C. On the other hand, the surface ablation is computed proportionally to the number of PDD. The PDD integral is numerically approximated using week-long sub-intervals based on Calov and Greve (Reference Calov and Greve2005), with PDD proportionality factors of f i = 8×C mm $^\circ$ C−1 day−1 for ice, and f s = 3×C mm $^\circ$
C−1 day−1 for ice, and f s = 3×C mm $^\circ$ C−1 day−1 for snow, where C is a tuning parameter. Note that a fraction (60%) of the melt is assumed to refreeze. These values coincide with the ones of the EISMINT intercomparison experiments for Greenland (MacAyeal, Reference MacAyeal1997) when C = 1. Note that PDD parameters are not well constrained and may vary substantially: C ∈ [0.5, 2] encompasses most values measured in Greenland (e.g. Braithwaite, Reference Braithwaite1995; Braithwaite and Zhang, Reference Braithwaite and Zhang2000), and the values used by Heyman and others (Reference Heyman, Heyman, Fickert and Harbor2013) to model LGM surface mass balance in central Europe. Therefore, the parameter C is used to tune the modelled maximum extent to the LGM maximum observed extent.
C−1 day−1 for snow, where C is a tuning parameter. Note that a fraction (60%) of the melt is assumed to refreeze. These values coincide with the ones of the EISMINT intercomparison experiments for Greenland (MacAyeal, Reference MacAyeal1997) when C = 1. Note that PDD parameters are not well constrained and may vary substantially: C ∈ [0.5, 2] encompasses most values measured in Greenland (e.g. Braithwaite, Reference Braithwaite1995; Braithwaite and Zhang, Reference Braithwaite and Zhang2000), and the values used by Heyman and others (Reference Heyman, Heyman, Fickert and Harbor2013) to model LGM surface mass balance in central Europe. Therefore, the parameter C is used to tune the modelled maximum extent to the LGM maximum observed extent.4. PISM includes an Earth deformation model based on Lingle and Clark (Reference Lingle and Clark1985) and Bueler and others (Reference Bueler, Lingle and Kallen-Brown2007), which combines a layered elastic spherical Earth with a viscous half-space overlain by an elastic plate lithosphere.

Figure 4. Flowchart of PISM model components.
For climate forcing, several possible scenarios are available based on (i) the choice of the height of the NHIS, 66 100 or 125% of the height of the NHIS where 100% is the height of the NHIS computed by Zhu and others (Reference Zhu2017), and (ii) the climate proxy signal for the GI method (EPICA available over the entire last glacial period or Bergsee available from 45 to 15 ka BP, Fig. 3). In this paper, we focus mainly on one simulation obtained using NHIS 66% and the EPICA climate signal, since this combination gives the best geological reconstruction of the glacial extent at the LGM both temporally and spatially. However, the sensitivity of the different climate forcings is tested in additional simulations. Also, the sensitivity to the thermal component of the ice dynamical model is investigated.
To simulate the evolution of the AIF, we build an initial basal topography using the publicly available NASA Shuttle Radar Topographic Mission (SRTM, http://srtm.csi.cgiar.org/) Digital Elevation Model (DEM), re-sampled at 2 km resolution, and remove major lakes (e.g. Lake Constance and Lake Zurich) and present day glaciers (Farinotti and others, Reference Farinotti2019). The simulation is initialised with ice-free conditions at 120 ka BP. Note that the modelling results are not affected by the initialisation procedure, as the response time of the AIF does not exceed a few millennia. The melt control parameter, C, is calibrated such that the glacial maximum area best fits the reconstructed value given by Ehlers and others (Reference Ehlers, Gibbard and Hughes2011). The settings in PISM for the thermodynamical and bed deformation models are identical to the ones of Seguinot and others (Reference Seguinot2018) and Mey and others (Reference Mey2016), respectively.
3. Results and discussion
In this section, we first discuss the results of the modelled climate states. Then we analyse the modelled glacier fluctuations and the timing of the global maxima before conducting a regional analysis of several glacier lobes of the AIF, comparing modelled outcomes with geological reconstructions. We then analyse the ice thickness and flow within the Rhone catchment and discuss the findings against field evidence. Sensitivity analyses are reported to assess the influence of key climatic and non-climatic model parameters. Lastly, we compare our results with previous modelling studies, and discuss the benefits of coupled climate and glacier modelling for paleo-glacier reconstruction in the Alps. As our model was primarily designed to match LGM evidence, our analysis focusses primarily on maximum states, and to a lesser extent the intermediate states. As explained before, our model resolution (2 km) is not suitable for modelling glacier extent during the Holocene. Therefore, this period is excluded from the analysis.
3.1. PI, LGM and MIS4 climate states
Figure 5 shows the modelled PI and LGM NHIS 66% climate states summer temperature and winter precipitation, two first-order control variables of the surface mass balance of a glacier. Simulated LGM climate conditions are substantially colder (by 12.5°C in summer, 12°C annually) on average compared to the PI period. Note that the temperature difference includes the important change in surface elevation: at the LGM, the surface topography is substantially higher than at PI due to the presence of the AIF, which amplifies the temperature decrease by several degrees. As expected, the precipitation pattern at the LGM differs substantially from PI and indicates overall drier conditions, on average about 17% in winter and 21% annually.

Figure 5. Summer temperature (panels a1–c1) and winter precipitation (panels a2–c2) of the modelled PI (panels a) and LGM (panels b) over the Alps. Panels c show the difference between LGM and PI.
Figure 6 shows the difference between LGM and MIS4 for summer temperature and winter precipitation. We find that the MIS4 is slightly warmer (~2.5°C in summer, ~0.5°C annually) than the LGM, especially in the southern Alps, while it is slightly drier (~15% in winter, $\sim 5\%$![]() annually) than the LGM, especially in the northern part of the Alps.
annually) than the LGM, especially in the northern part of the Alps.

Figure 6. Difference between summer temperature (panel a) and winter precipitation (panel b) of the modelled climate values between MIS4 and LGM.
Lastly, Figure 7 shows the variations between the climate variables obtained under the scaling assumptions of NHIS 66% and NHIS 100%. A NHIS 100% leads to warmer temperatures (~0.6°C in summer, ~1.2°C annually) and less precipitation ($\sim 22\%$![]() in winter, $\sim 2\%$
in winter, $\sim 2\%$![]() annually) compared to 66% NHIS. The precipitation pattern is also affected by the NHIS scaling parameter: the 100% NHIS climate has more precipitation south of the Alps compared to 66% as expected since the 66% NHIS can be seen as an intermediate state between PI (no NHIS) and 100%. Note that we find (not shown) that changing from a 100% to a 125% NHIS has only a minor impact on the climatic conditions modelled in the Alps. Comparison of climate model outputs with recently available pollen-based reconstructions (Davis and others, Reference Davis, Fasel, Kaplan, Russo and Burke2022) is performed by Russo and others (Reference Russo2023).
annually) compared to 66% NHIS. The precipitation pattern is also affected by the NHIS scaling parameter: the 100% NHIS climate has more precipitation south of the Alps compared to 66% as expected since the 66% NHIS can be seen as an intermediate state between PI (no NHIS) and 100%. Note that we find (not shown) that changing from a 100% to a 125% NHIS has only a minor impact on the climatic conditions modelled in the Alps. Comparison of climate model outputs with recently available pollen-based reconstructions (Davis and others, Reference Davis, Fasel, Kaplan, Russo and Burke2022) is performed by Russo and others (Reference Russo2023).

Figure 7. Difference between summer temperature (panel a) and winter precipitation (panel b) of the modelled climate values between LGM NHIS 66% and LGM NHIS 100%.
3.2. Compatibility climate/glaciation
When tuning melt parameters in the iceflow model to reproduce the geomorphologically reconstructed glacier outlines (Fig. 8), we find that only a minor (C = 1.1) adjustment was needed, i.e. the melt parameters needed to be increased by only 10% from the values of the EISMINT intercomparison experiments (MacAyeal, Reference MacAyeal1997), which are standard mean values from the literature. Furthermore, the maximum extent of the east-west glaciers modelled matches (Fig. 8) the geomorphological reconstruction of Ehlers and others (Reference Ehlers, Gibbard and Hughes2011) fairly well. This result supports the adequacy of the chain of data and models (Fig. 4) and the minor adjustment of the PDD parameter C shows the general compatibility of the climate and glacier models.
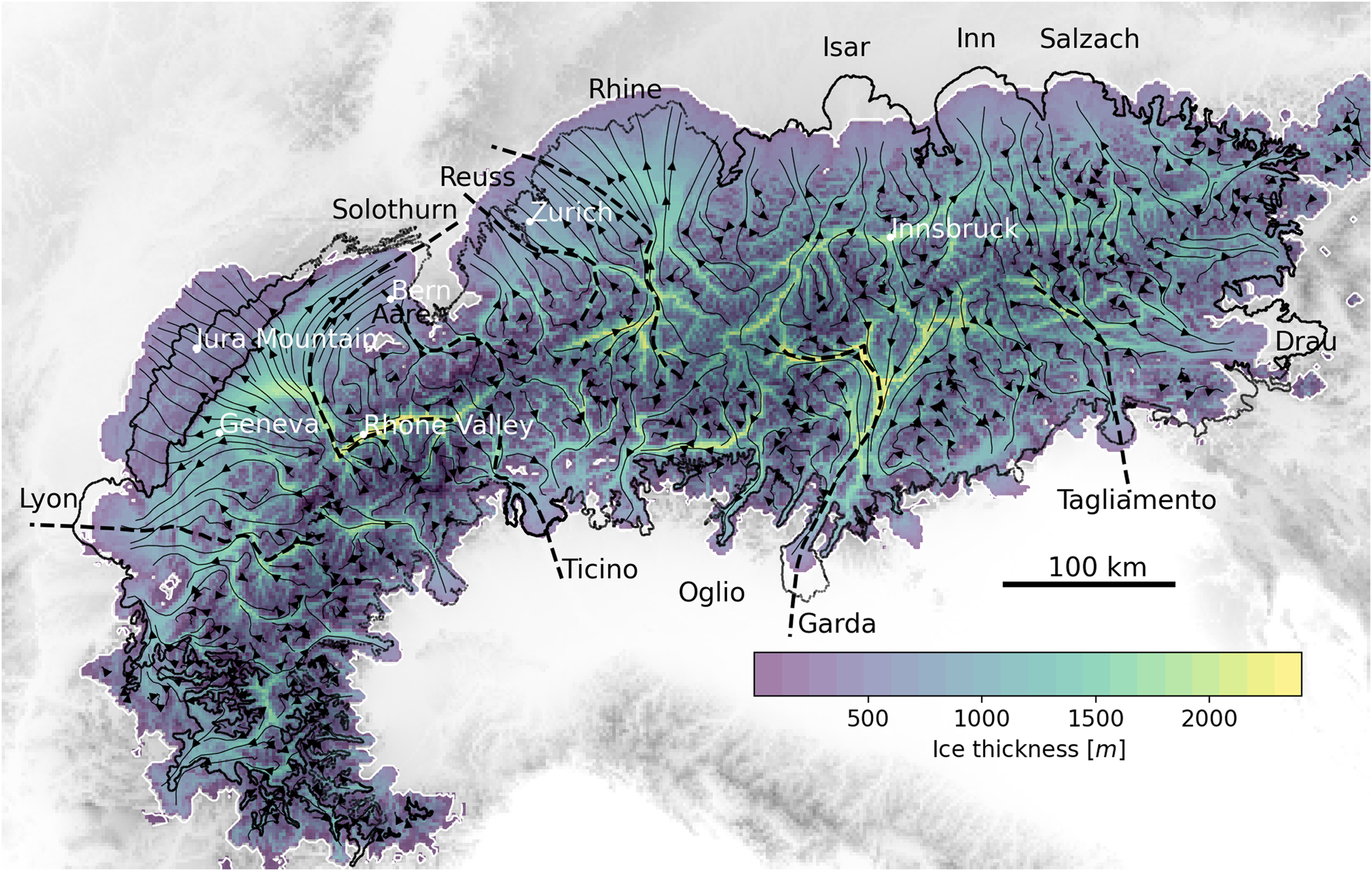
Figure 8. Maximum modelled ice thickness and modelled streamlines computed from the surface ice flow at the maximum state (thin lines). For comparison purposes, the reconstructed LGM outline (modified after Ehlers and others (Reference Ehlers, Gibbard and Hughes2011)) is shown with a solid line. The dashed lines correspond to flowlines along which the time evolution of individual glaciers is monitored in Figure 9.

Figure 9. Transient advance and retreat of Rhone (Lyon and Solothurn lobes), Rhine, Garda, Reuss, Aare, Ticino-Toce and Tagliamento glaciers from 80 to 10 ka BP along the flowline drawn in Figure 8 compared to field data. Field data from Roattino and others (Reference Roattino2023), Ivy-Ochs and others (Reference Ivy-Ochs, Schäfer, Kubik, Synal and Schlüchter2004), Kamleitner and others (Reference Kamleitner2023), Monegato and others (Reference Monegato, Scardia, Hajdas, Rizzini and Piccin2017), Kamleitner and others (Reference Kamleitner2023), Wüthrich and others (Reference Wüthrich2018), Kamleitner and others (Reference Kamleitner2022) and Monegato and others (Reference Monegato2007), respectively.
3.3. Glacier fluctuations and timing of maxima
Similarly to Seguinot and others (Reference Seguinot2018), our simulation suggests that the size and extent of the AIF fluctuated during the last glacial cycle with many advance and retreat phases onto the Alpine foreland (Fig. 9) and two distinct periods of extensive glaciations: a first maximum occurs during MIS4 reaching a maximum ice volume of ~67 × 103 km3 at ~68 ka; a second maximum occurs during LGM reaching a maximum ice volume of ~88 × 103 km3 and a glaciated area of ~167 × 103 km2 at ~25 ka (Fig. 3). Most glaciers reached their maximum thicknesses close to the LGM (between 30 and 20 ka, Fig. 10), and the largest glaciers were significantly smaller during MIS4 compared to the LGM (Fig. 11).

Figure 10. Modelled age of maximum ice thickness from 30 to 20 ka BP. The solid line shows the LGM outline modified after Ehlers and others (Reference Ehlers, Gibbard and Hughes2011).

Figure 11. Modelled maximum extent during MIS4 compared to the one of MIS2. The solid black line shows the LGM outline modified after Ehlers and others (Reference Ehlers, Gibbard and Hughes2011) while the blue and the orange lines show the maximum extent during LGM and MIS4, respectively.
Fluctuations are clearly controlled by the size of the catchments and the resulting inertia of each glacier (Figs 9 and 12). The largest glacier located in the western Alps, the Rhone Glacier and its two lobes, the Lyon and Solothurn lobes, shows a single, long and late advance (~23 ka) into the foreland. On the contrary, the medium-sized Rhine Glacier exhibits multiple, shorter and slightly earlier (~24 ka) maxima. This situation is even more pronounced with other smaller glaciers in the east and in the south of the Alps (e.g. Ticino-Toce, Tagliamento).

Figure 12. Transient evolution of the Central Alpine glacier systems around the LGM. The magnitude of the surface ice speed and the trajectory of erratic boulders from Valais are shown. The symbols ★, ▲ and ■ represent markers seeded at Mont Blanc, Val de Bagnes and Val d'Arolla, respectively. The solid line shows the LGM outline modified after Ehlers and others (Reference Ehlers, Gibbard and Hughes2011).
3.4. Individual glacier lobes
In this section, we analyse glaciers individually starting with the Rhine Glacier and looping around the Alps counterclockwise (Fig. 8).
3.4.1. Rhine Glacier
Our simulation shows that the Rhine Glacier may have advanced multiple times into the foreland during MIS4 and LGM (about 10 times in total, Fig. 9). Despite an overshoot of at most 15 km at LGM (Figs 8 and 9), the modelled LGM and post-LGM periods are well in line with spatio-temporal reconstruction based on geomorphological mapping and cosmogenic nuclide, luminescence and radiocarbon ages for the different ice-marginal positions (Preusser and others, Reference Preusser, Blei, Graf and Schlüchter2007; Kamleitner and others, Reference Kamleitner2023). In particular, Figure 9 shows that the double maximum and the post-LGM deglaciation are well reproduced by the model. Geomorphologically, the former is seen as the Schaffhausen and Stein am Rhein stadial moraine complexes, dated 26–22 and 20.6 ± 1.7 ka, respectively (Kamleitner and others, Reference Kamleitner2023).
3.4.2. Reuss Glacier
According to luminescence ages from Gaar and others (Reference Gaar, Graf and Preusser2019), Reuss Glacier reached its maximum extent around 24/25 ± 2 ka. In total, four stadials have been identified (Untertannwald, Mellingen, Stetten, Bremgarten) with clear signs of glacier readvances for Mellingen and Bremgarten stadials (Kamleitner and others, Reference Kamleitner2023). 10Be exposure ages suggest abandonment of the Reuss LGM maximum position was underway by 22 ± 1 ka (Reber and others, Reference Reber2014; Kamleitner and others, Reference Kamleitner2023). The Bremgarten stadial moraines were built after 20.8 ± 1.3 ka (Kamleitner and others, Reference Kamleitner2023). The model gives a two-phase LGM advance (Fig. 9) in the right order (the largest is the earliest) and remarkably similar timing (~26 and ~21 ka), although the first slightly overshoots the end position (by ~10 km, Fig. 8). Furthermore, our model shows another substantial (but less extensive) glaciation of the Reuss Glacier during MIS4, which is in line with the findings of Gaar and others (Reference Gaar, Graf and Preusser2019).
3.4.3. Aare Glacier
Aare Glacier was a tributary to the Solothurn lobe of the Rhone Glacier during the LGM climax (see the following section). Our model indicates that both glaciers were connected from 24.5 to 23.1 ka. Wüthrich and others (Reference Wüthrich2018) dated a stabilisation of the Aare Glacier to 20.7 ± 2.2 ka (Gurten stadial). The lack of evidence of a frontal position suggests that the Aare Glacier was still connected to the Rhone Glacier at that time. A frontal moraine complex in the city of Bern points to a readvance, which Wüthrich and others (Reference Wüthrich2018) dated to 19.0 ± 2 ka. In light of the uncertainties of the dating, the readvance to the Bern stadial position may correspond to the advance seen in the model at 20.5 ka (Figs 9 and 12).
3.4.4. Rhone Glacier, Solothurn lobe
During the LGM, the northern branch of the Rhone Glacier flowed to the north east, forming the Solothurn lobe (Jäckli, Reference Jäckli1962; Bini and others, Reference Bini2009), which merged with the Aare Glacier. Figure 9 shows a single major modelled advance of the Solothurn lobe of the Rhone Glacier with a maximum at 23 ka at a position, which matches the reconstructed lobe of Ehlers and others (Reference Ehlers, Gibbard and Hughes2011) (with an undershoot of ~15 km, Figs 8 and 12). This result is in good agreement with the cosmogenic 10Be exposure dating of erratics at Steinhof, which shows that the maximum was likely reached at 24 ± 2 ka (Ivy-Ochs and others, Reference Ivy-Ochs, Schäfer, Kubik, Synal and Schlüchter2004; Ivy-Ochs, Reference Ivy-Ochs2015). In contrast, the modelled Solothurn lobe of the Rhone Glacier is found to have been much smaller during MIS4 (Fig. 11).
3.4.5. Jura Mountains
Glacial records in the Jura Mountains, including boulder deposition elevation (Graf and others, Reference Graf2015), suggest that the mountain range was not covered by ice from the Rhone Glacier, but instead hosted its own ice cap during the LGM (Buoncristiani and Campy, Reference Buoncristiani and Campy2011). This hypothesis is supported by our modelling results. Indeed, our model shows that the climate forcing allows for such an independent ice cap to form and remain in the Jura Mountains (Fig. 12). The modelled extent, however, exceeds observations in the West. At the LGM, the Jura Mountains with its ice cap constituted a significant obstacle for the ice originating from the Rhone Valley and contributed to split the ice flow coming from the Rhone Valley into two lobes, the Solothurn and Lyon lobes, and prevented the Rhone Glacier from covering the Jura Mountains (Jouvet and others, Reference Jouvet, Seguinot, Ivy-Ochs and Funk2017).
3.4.6. Rhone Glacier, Lyon lobe
The modelled LGM extent of the Lyon lobe of the Rhone Glacier shows a single advance with a maximum at about 23.5 ka (Fig. 9), which slightly undershoots the maximum outline from Ehlers and others (Reference Ehlers, Gibbard and Hughes2011) (Fig. 8). Therefore, we do not reproduce the two-phase advance scenario suggested by recent surface exposure datings of Roattino and others (Reference Roattino2023). Timing of the LGM maximum advance, however, matches field evidence well. The front of the Lyon lobe was found to fluctuate at or close to the LGM maximum position between ~24 − 21 ka (Roattino and others, Reference Roattino2023). A glacier re-advance was dated to 19 ± 1 ka (Roattino and others, Reference Roattino2023). Furthermore, our simulation supports (streamlines in Fig. 8) the hypothesis that the Lyon lobe was fed mainly from the French/Savoyan Alps (Coutterand and others, Reference Coutterand, Schoeneich and Nicoud2009) and not from the Rhone Valley, as evidenced by the absence of boulder lithologies from that region. Lastly, our simulation indicates that LGM was clearly more extensive than MIS4 in this region (Fig. 11), which seems to contradict the two major late Pleistocene glaciations in the western Alpine foreland, during MIS 4 (75–60 ka) and late MIS 3 (40–30 ka) revealed by luminescence dating (Gribenski and others, Reference Gribenski2021).
3.4.7. South-western Alps
Our model overshoots the maximum outlines documented by Ehlers and others (Reference Ehlers, Gibbard and Hughes2011) in the South West Alps. We find several reasons that may explain this discrepancy: (i) the model resolution (2 km) is too poor to resolve the complex topography of this region and the relatively small glacier catchments, (ii) the climate model overestimates precipitation in this region, as evident from a comparison against available pollen-based reconstructions (Davis and others, Reference Davis, Fasel, Kaplan, Russo and Burke2022; Russo and others, Reference Russo, Fallah, Ludwig, Karremann and Raible2022), (iii) the outlines given by Ehlers and others (Reference Ehlers, Gibbard and Hughes2011) correspond to a more recent maximum than the LGM, which occurred around 24 ka in the Maritime Alps, as shown by exposure dates from the Stura and Gesso valleys Ribolini and others (Reference Ribolini, Spagnolo, Cyr and Federici2022). Note that Višnjević and others (Reference Višnjević, Herman and Prasicek2020) have already evidenced that the outlines of this region correspond to very high ELAs in comparison to the rest of the Alps, questioning the timing of these outlines.
3.4.8. Ticino-Toce, Oglio, Garda and Tagliamento lobes
Analysis and dating of moraines have revealed incredibly synchronous LGM maxima of Southern Alpine glacier systems. The Dora Riparia Glacier reached its LGM maximum extent in the Rivoli-Avigliana end moraine system at 24.0 ± 1.5 ka (Ivy-Ochs and others, Reference Ivy-Ochs2018). A major glacier re-advance was reconstructed at 19.6 ± 0.9 ka (Ivy-Ochs and others, Reference Ivy-Ochs2018). The Ticino-Toce Glacier fluctuated at or close to its LGM maximum position from ca. 25 ± 1 ka to ca. 20 ka ± 1ka (Kamleitner and others, Reference Kamleitner2022). A late LGM readvance was dated 19.7 ± 1.1 ka (Kamleitner and others, Reference Kamleitner2022) and 19 ± 1 ka (Braakhekke and others, Reference Braakhekke2020), in Verbano and Orta lobes, respectively. Reaching of the LGM maximum extent in the Oglio Glacier system was constrained to 26.4–25.3 ka cal BP (Ravazzi and others, Reference Ravazzi, Badino, Marsetti, Patera and Reimer2012). A two-phased LGM maximum at 25.0–24.2 and 23.3–23.1 ka cal BP was found for the Garda lobe (Adige-Sarca Glacier, Monegato and others, Reference Monegato, Scardia, Hajdas, Rizzini and Piccin2017). Tagliamento glacier reached its biggest extent at 28.0–24.5 ka cal BP, with a re-advance to nearly the same position at 23.2–22.8 ka cal BP (Monegato and others, Reference Monegato2007). Furthermore, the aforementioned studies evidenced the collapse and clear-up of the valley floors relatively quickly after the last re-advance, namely between 19 and 17.2 ka.
Figure 9 shows the evolution of three of the four lobes and compares them with the space-time positions of the glacier margin documented by Kamleitner and others (Reference Kamleitner2022) and Monegato and others (Reference Monegato, Scardia, Hajdas, Rizzini and Piccin2017, Reference Monegato2007). Our model shows a good fit for the Tagliamento and the Ticino-Toce lobes (Fig. 8), but the Garda Glacier is too small (by ~15 km). The two-phase advance of the Tagliamento Glacier is generally well captured; however, the timings of these two events differ slightly (within the uncertainty range) from those documented. In contrast, the Garda lobe is found to be fairly stable close to LGM. Lastly, the rapid collapse of the lobes is in general well reproduced by the model; however, it occurs ~15 ka, i.e. a few millennia after the timing given in the references.
3.4.9. Eastern Alps
Although the easternmost Alps have well-mapped maximum ice margins (Van Husen, Reference Van Husen1987; Ehlers and Gibbard, Reference Ehlers and Gibbard2008) there exist very little quantitative age constraints to reconstruct the spatio-temporal evolution of glaciers in this region of the Alps (Wölfler and others, Reference Wölfler, Hampel, Dielforder, Hetzel and Glotzbach2021). With the exception of the southern lobe (Drau Glacier, Schmidt and others, Reference Schmidt, Weckström, Lauterbach, Tessadri and Huber2012), whose extent is underestimated (by ~40 km), our modelled maximum ice extent reproduces the mapped ice margins well (Fig. 8).
3.4.10. Salzach, Inn and Isar lobes
In the north east of the Alps, the model roughly reproduces the Salzach lobe, underestimates the Inn lobe, and largely underestimates the Isar lobe (by ~40 km) as mapped by Van Husen (Reference Van Husen1987) (compiled by Ehlers and Gibbard, Reference Ehlers and Gibbard2008). This suggests that our modelled LGM climate may have underestimated precipitation or overestimated temperature in the catchment of the Inn and Isar lobes. In addition, the model shows uniform glacier extents on the northern foreland, while the geological reconstruction shows three well-distinct lobes. This may be due to the fact that the basal topography used in the model (the present-day surface topography) includes sediment layers that may have been absent at the LGM. Lastly, our model indicates that the maximum was reached at ~26 ka BP (Fig. 10).
3.5. Ice thickness and flow pattern around the Rhone catchment
The Rhone Glacier basin contains several well-documented geomorphological findings related to the last glaciation that allow us to assess our modelling results in terms of ice flow patterns and ice thickness. We now describe in turn the compatibility of our model results with erratic boulders, trimlines and erosional features of transfluences.
First, by integrating the modelled transient ice flow velocities, we reconstruct the transport and deposition of erratic boulders. Figure 12 shows the modelled trajectories of boulders originating from the southern Rhone Valley and Mont Blanc as in Jouvet and others (Reference Jouvet, Seguinot, Ivy-Ochs and Funk2017). The results show that a large number of these modelled erratic boulders are deposited in the Solothurn lobe during the retreating stage (Fig. 12, bottom panels), consistent with the lithology characteristics of the boulders found in this region (e.g. Burkard and Spring, Reference Burkard and Spring2004; Graf and others, Reference Graf2015).
Second, trimlines in the Alps were mostly interpreted as a marker of the maximum elevation of the ice surface (e.g. Florineth and Schlüchter, Reference Florineth and Schlüchter2000; Kelly and others, Reference Kelly, Buoncristiani and Schlüchter2004; Bini and others, Reference Bini2009) and therefore should coincide with the maximum vertical extent of our model. However, comparing the maximum modelled ice thickness to the trimlines of the Rhone Valley documented by Kelly and others (Reference Kelly, Buoncristiani and Schlüchter2004) reveals a bias: the modelled maximum ice surface is overestimated by ~387 m on average (Fig. 13), which is approximately 50% of the ice thickness in this region. This bias may be the result of simplification (SIA) in the PISM iceflow model (Imhof and others, Reference Imhof2019) and too poor spatial resolution: 2 km does not resolve the complex topography of high mountain summits and cannot represent the steep ridges on which trimlines are observed. As a result, the ice accumulates over the highest model grid cells without being evacuated due to cold-based slow motion and gentle slopes caused by averaging. This in turn may cause the ice thickness to be overestimated in the highest regions. The hypothesis that the timelines reflect the warm-cold base transition rather than the maximum surface elevation is another reason that may explain the discrepancy (Cohen and others, Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018; Seguinot and others, Reference Seguinot2018).

Figure 13. Modelled maximum ice surface (corrected for the depression of the bedrock) versus observed trimline elevations in the Rhone Valley by Kelly and others (Reference Kelly, Buoncristiani and Schlüchter2004) (Fig. 14). The modelled ice thickness is overestimated by 387 m on average compared to trimlines.

Figure 14. Modelled maximum ice thickness in the Rhone catchment. Continuous lines indicate the streamlines computed from the surface ice flow at the maximum state. The two transfluences (Simplon and Brünig) are shown with black dots. The black crosses correspond to places where trimlines have been documented in the Rhone Valley by Kelly and others (Reference Kelly, Buoncristiani and Schlüchter2004).
Finally, despite an overestimation of the ice thickness, our simulation depicts the AIF as a network of glaciers whose flow is mainly controlled by the basal topography. The modelled ice flow field at the border of the Rhone catchment shows clear transfluences (Fig. 14). This includes the southward transfluence across the Simplon Pass into the Toce Glacier catchment and the transfluence across Brünig Pass from the Aare catchment (right tributary of the Rhone glacier) to the Reuss glacier system (Jäckli, Reference Jäckli1962; Kelly and others, Reference Kelly, Buoncristiani and Schlüchter2004; Bini and others, Reference Bini2009).
3.6. Sensitivity to model parameters
In this section, we present the results of three additional model runs to assess the influence of important parameters on our model results.
3.6.1. Influence of the size of the NHIS
We model the AIF during the last glacial cycle using climate forcing based on the assumption of 100% NHIS (instead of 66%) to measure the influence of this parameter. To maintain a similar ice extent at the LGM, the melting parameter is tuned to C = 0.9 (Fig. 15, top panel). There are, however, notable local discrepancies between glacier lobes: the 100% NHIS climate forcing produces more extensive glaciers in the south with some notable overshoots (e.g. Ticino-Toce), and less extensive glaciers in the north resulting in several good matches (e.g. Solothurn and Rhine lobes), and some undershoots (e.g. lobes in the northeast). This result is in line with the difference between the precipitation patterns of the two forcings (Fig. 7).

Figure 15. Modelled maximum extent during LGM using NHIS 100% (panel a) and Bergsee signal (panel b) compared to the reference simulation that uses 66% NHIS and EPICA. The solid black line shows the reconstructed LGM outline modified after Ehlers and others (Reference Ehlers, Gibbard and Hughes2011), the blue shows the reference simulation while the orange line shows the NHIS 100% (panel a) and Bergsee signal (panel b) simulations, respectively.
3.6.2. Influence of the climate signal
We have performed simulations with different climate signals including EPICA (Jouzel and others, Reference Jouzel2007), NGRIP (Seierstad and others, Reference Seierstad2014) and the local pollen-based signal from Bergsee, Southern Germany (Duprat-Oualid and others, Reference Duprat-Oualid2017), which correlates relatively well with NGRIP in terms of variability, to drive the glacial index transient climate. An important difference between the EPICA and Bergsee signals is that the glacial index prior to the LGM is generally smaller, i.e. the length of the time period with a GI close to one is shorter (Fig. 3) for the Bergsee signal. As a result, we notice in general very minor or no differences with the EPICA simulation except for the Rhone Glacier, which is largely underestimated (Fig. 15, bottom panel). This experiment shows that the considerable size of the Rhone Glacier at LGM is the result of prolonged cold conditions in the climate forcing, and that the duration these conditions prevail is an essential parameter that must be considered to model the transient evolution of the AIF in agreement with the known LGM glacier footprints. This additional sensitivity experiment highlights the dependence to the chosen climate signal, and the limitation of our GI approach to reproduce glacier states different from LGM in the absence of tuning data.
3.6.3. Importance of modelling the ice thermo-mechanics
In a last sensitivity model experiment, we run the isothermal version of PISM by switching off the thermal component of the model. Figure 16 compares the fluctuations of the Rhine Glacier using these two settings: (i) the polythermal reference version discussed in this paper and (ii) the isothermal version. The polythermal model shows many more fluctuations than the isothermal model, indicating that the amplification of glacier fluctuations is the direct consequence of feedback mechanisms in the thermo-mechanics of ice. When glacier ice temperature is modelled, cooling causes successively a thick glacier lobe to form, temperate basal conditions to occur due to thermal isolation, downwasting of ice due to enhanced sliding and evacuation of ice to the ablation zone leading to glacier retreat. In contrast, the AIF clearly shows much fewer fluctuations (only long-term climate-induced ones) when switching off the thermal component of the model. In summary, this model experiment shows that the frequent glacier oscillations displayed by the model are partly non-climatic as the EPICA climate signal chosen to drive the glacial index is relatively smooth (Fig. 3). In fact, they are the consequence of positive feedback mechanisms between the basal ice temperature, the basal sliding and the ice thickness. This shows that while climate is the main driver that leads to major glaciations, non-climatic internal glacier thermomechanics may play an equally important role in explaining the dynamical behaviour of glaciers.

Figure 16. Transient advance and retreat of the Rhine Glacier (as in Fig. 9) using a polythermal model (panel a), and using an isothermal model (switching off the ice temperature, panel b).
3.7. Importance of climate modelling
The benefit of modelling the climate of glacial states can be illustrated by comparing our simulation at the LGM to the one of Seguinot and others (Reference Seguinot2018), who used the same ice-flow model (at 1 km) but with a paleoclimate based on a distortion of today's climate driven by the EPICA signal. While there exist important discrepancies (100 km eastward shift) between the LGM ice margin mapped from geomorphological evidence and the one predicted by Seguinot and others (Reference Seguinot2018), our new model (and independently of the assumption on the NHIS height) mostly resolves this discrepancy (Fig. 17), especially in the Western lobes (Lyon and Solothurn) and in the eastern Alps. This result shows that the modelled precipitation pattern, which features notably more precipitation in the western Alps at the LGM (Fig. 5), is a key factor to reproduce the AIF ice cover consistent with moraine-based reconstructions. As a corollary, our results demonstrate the importance of the shift of the westerlies in the building-up of the AIF (Fig. 1).

Figure 17. Comparison of the maximum ice extent modelled by Seguinot and others (Reference Seguinot2018) and in the present study. The solid black line shows the reconstructed LGM outline modified after Ehlers and others (Reference Ehlers, Gibbard and Hughes2011), the blue shows our reference simulation while the orange line shows the one of Seguinot and others (Reference Seguinot2018).
Another important difference between modelled and geological evidence is the ice thickness in the Rhone Valley: our simulation overestimates the ice thickness by 387 m on average using trimlines as reference of the maximum elevation of the ice surface (Fig. 13). This is about 60% less than the ice thickness overestimate of Seguinot and others (Reference Seguinot2018). The difference between the two models is presumably due to temperature differences in the climate forcing: our forcing causes smaller cold basal areas. This, in turn, increases basal motion and ice fluxes and thus contributes to thinning the ice at high elevations. The modelled climate forcing used in this study, therefore, contributes to reducing the mismatch between the modelled maximum surface elevation and the trimlines. The remaining discrepancy, which is still significant, is mainly attributed to the horizontal resolution of the model (2 km), which cannot capture complex three-dimensional topography, and possibly to simplification in modelled ice physics (Imhof and others, Reference Imhof2019). Despite the thinner AIF, the model reproduces two major transfluences at the Simplon and Brünnig passes well (Fig. 14).
Tracking the trajectory of erratic boulders in the Soloturn lobe near the LGM is important for evaluating the model against field evidence (Jouvet and others, Reference Jouvet, Seguinot, Ivy-Ochs and Funk2017). Indeed, many erratics with lithologies characteristic of southern Valais and Mont Blanc were found in the northern Solothurn lobe (e.g. Burkard and Spring, Reference Burkard and Spring2004; Graf and others, Reference Graf2015; Jouvet and others, Reference Jouvet, Seguinot, Ivy-Ochs and Funk2017), demonstrating that the boulders must have been diverted across the centreline of the Rhone Valley (Kelly and others, Reference Kelly, Buoncristiani and Schlüchter2004) during the LGM. Previous modelling studies showed that this boulder diversion is highly conditioned to the distribution of precipitation in the Alps (Jouvet and others, Reference Jouvet, Seguinot, Ivy-Ochs and Funk2017) or transient effects on climate forcing (Imhof, Reference Imhof2021). In our simulation, the modelled erratic boulders from the southern Valais are first transported towards Geneva during the first advance phase when the Solothurn lobe is relatively small (Fig. 12, top panels). Then, when the Soloturn lobe grows until it reaches its maximum, a clear switch from east-south to northwest occurs in the dominant ice flow direction causing boulders to be diverted (Fig. 12, bottom panels). The diversion, which is maintained during the entire deglaciation of the Rhone Glacier, is consistent with today's distribution of erratic boulders.
3.8. Importance of transient glacier modelling
Beside climate modelling, our results also illustrate the importance of using a physical and time evolving glacier model to reproduce the AIF dynamics and its transient behaviour:
• Modelling the climate and the resulting glacier response in a transient way is essential to capture glacier volumes and inertia (Fig. 15, bottom panel), glacier fluctuations (Fig. 16) and the timing of maxima (Fig. 9).
• Accounting for the ice dynamics is essential to reproduce the ice flow pattern revealed by erratic boulders or erosional features, as well as the inertia of glaciers of various sizes and the resulting timing of maxima (Fig. 12).
• Modelling the thermomechanics of ice and the feedback between basal conditions and climate forcing is important to reproduce glacier fluctuations revealed by moraine mapping and dating (Figs 9 and 16).
These results justify our choice of using a multiphysics model such as PISM, but also highlight the limitations of simpler models (e.g. Del Gobbo and others, Reference Del Gobbo, Colucci, Monegato, Žebre and Giorgi2023) that do not consider ice dynamics or transient glacier evolution, and thus cannot capture these features.
4. Conclusions
In this work, we have simulated the climatic conditions and the resulting glacier evolution in the European Alps over the last glacial cycle at a high spatial resolution (2 km) by coupling for the first time a climate model to an ice-flow model. Only minor adjustments of the melting parameters (on the order of 10%) were needed to model the AIF consistently with geomorphological reconstructions demonstrating the coherence of both the climate and glacier models. Our study allows us to simultaneously overcome shortcomings of previous studies in terms of paleoclimate forcing (Seguinot and others, Reference Seguinot2018) and glacier modelling (Višnjević and others, Reference Višnjević, Herman and Prasicek2020; Del Gobbo and others, Reference Del Gobbo, Colucci, Monegato, Žebre and Giorgi2023). Comparisons with field evidence in terms of maximum horizontal and vertical glacier extents, as well as in terms of ice dynamics, show that the model reproduces LGM-related field observations: (1) the moraine-based maximum extents are well reproduced with only minor regional exceptions; (2) the trajectory of erratic boulders in the Rhone Valley is consistent with observations at the Solothurn lobe; (3) the trimline-based vertical maximum ice surface elevation in the Rhone Valley is reproduced with a limited bias leading to a moderate overestimation of the ice thickness; (4) two transfluences from the Rhone/Aare catchment documented by glacial erosion features are well reproduced by the model. Our results remain limited by uncertainties in climate and glacier modelling and spatial resolution. Indeed, the EPICA signal together with the climate states is not meant to represent the full timing and complexity of the last glacial paleoclimate in the Alps revealed by proxy records (e.g. Duprat-Oualid and others, Reference Duprat-Oualid2017; Luetscher and others, Reference Luetscher2015), but is used to build the AIF consistently with geomorphological evidence during glacial maxima. Therefore, our modelled results related to intermediate states and the Holocene must be interpreted with caution. Furthermore, the 2 km model grid cell is too coarse to model small-scale glaciers during the Holocene and capture complex glacial reliefs through the entire simulation period. This probably partly explains the overestimation of the ice thickness.
Difficulties to constrain different model parameters may affect our modelling results: for instance, we found that climate modelling results are sensitive to the assumption on the height of the NHIS. We tuned the mass-balance melt parameters to match the LGM glacier extent, as they are among the least constrained parameters (and are expected to vary spatially to account for different sources of melt). Another tuning strategy (e.g. through climate GI variables) with different mass-balance parameters could modify the glacier response to climate, especially between small and large lobes. Examples of model parameters that exert a first-order control of the ice flow, and therefore may influence the dynamic response of the AIF to climate forcing are the till friction angle in the Mohr–Coulomb sliding law and parameters of the subglacial hydrology model.
Similarly to Del Gobbo and others (Reference Del Gobbo, Colucci, Monegato, Žebre and Giorgi2023), our climate model results demonstrate the importance of climate to force paleo glacier models to reproduce the precipitation pattern and ice geometry consistent with the geomorphologically reconstructed distribution of LGM glaciers in the Alps. The LGM precipitation pattern is found to be different from that prevailing in modern times (Fig. 5) probably due to significant changes in global atmospheric circulation between glacial and interglacial periods (Fig. 1). Our results show that a consistent precipitation pattern is necessary but not sufficient to reproduce key observed features. Including both transient climate and the thermomechanics of glacier evolution were found equally important to capture the ice flow patterns as well as the spatiotemporal fluctuations of glaciers, which strongly vary according to the size of glacier basins. In that perspective, key aspects to be improved are the modelling of a truly transient climate to better represent the entire glacial cycle, overcome the shortcomings of the GI approach and reduce the uncertainty due to the choice of the climate signal. Transient high-resolution downscaling of temperature and precipitation data during deglaciation (from LGM to the Holocene) proposed by Karger and others (Reference Karger, Nobis, Normand, Graham and Zimmermann2023) is a promising approach to address this issue.
Achieving subkilometre spatial resolution is another essential aspect that must be investigated in future work to resolve ice fluxes in the rugged topography of the Alps and the resulting ice thickness, which remain subject to biases between geomorphological and modelled-based reconstructions. We also noticed that high resolution is crucial for handling interglacial states such as during the Holocene. Unfortunately, modelling the entire Alps at subkilometre spatial resolution is prohibitively expensive with physical traditional glacier models. In that perspective, a new modelling approach (Jouvet and Cordonnier, Reference Jouvet and Cordonnier2023) based on deep learning emulation and Graphical Processing Units offers a promising perspective to overcome the computational bottleneck and achieve a spatial resolution that is suitable for describing the complex topography of the Alpine mountains.
Data
The glacier evolution modelling results are freely available at https://doi.org/10.5281/zenodo.8270674.
Acknowledgements
This research was funded by the National Cooperative for the Disposal of Radioactive Waste (NAGRA), and the Swiss National Science Foundation (SNSF, project 200021–162444). Climate simulations were performed on the supercomputing architecture of the Swiss National Supercomputing Centre (CSCS). Guillaume Jouvet thank Andreas Vieli and Martin Funk for their support and inspiring discussions, the PISM developing team (Constantine Khroulev, Andy Aschwanden, Ed Bueler) for support, Natacha Gribenski for insipring Figure 1, Fanny Duprat Oualid and Damien Rius for giving access to the data of the Bergsee signal.
Author contributions
The ice flow modelling was performed by Guillaume Jouvet with the help of Denis Cohen. The climate modelling was performed by Emmanuele Russo, Jonathan Buzan and Christoph Raible. Guillaume Jouvet analysed the glacier modelling results with support from Sarah Kamleitner and Susan Ivy-Ochs for comparison with geomorphological and dating evidence. Guillaume Jouvet wrote the paper with inputs from all coauthors. The research of this paper was conceived as part of EIDER project led by Guillaume Jouvet, Denis Cohen, Urs Fischer and Angela Landgraf.




















