Introduction
Fedchenko glacier in the Pamir, Tajikistan, is one of the largest mountain glaciers in the world, with a total length of ~72 km. The elevation ranges from 2900 m at the terminus to ~5400 m in the highest basins, while the highest peak in the drainage basin, the Peak Revolution or Koh-i Abu Ali Sino, reaches 6940 m a.s.l. Fedchenko is by far the largest glacier in the Pamir, consisting of several small tributary basins in the accumulation zone and a valley-glacier-type tongue, which is fully covered by supraglacial debris for the last 7 km. Its equilibrium-line altitude (ELA) is situated at ~4700–4800 m (Reference Dolgushin and OsipovaDolgushin and Osipova, 1989; personal observations), and earlier studies found a total glacier area of 649 km2 (Reference Dolgushin and OsipovaDolgushin and Osipova, 1989). The glacier was discovered in 1878 by V.F. Oshanin (Reference RegensburgerRegensburger, 1963), and the joint Russian–German expedition of 1928 recognized its actual size (Reference Gorbunov, Dorofeyev and ScherbakovGorbunov and others, 1929; Reference FinsterwalderFinsterwalder, 1932). As a result of this expedition the first accurate map of the glacier was produced at a scale of 1: 50 000, based on terrestrial photogrammetry. A wealth of information about the glacier system, including geological surveys and meteorological and glaciological observations, resulted from the extensive fieldwork in 1928. Based on these results, new investigations were started in 1958 by the Academy of Sciences of the Uzbek Republic in the Soviet Union. A new map was produced, which allowed the investigation of glacier changes within the intervening 30 years, albeit this map does not cover the region of the main glacier above 5000 m (Reference RegensburgerRegensburger, 1963; NKGG, 1964).
The total ice-covered area in the entire Pamir is estimated at 12 078 km2 (Reference Dolgushin and OsipovaDolgushin and Osipova, 1989), while the central Pamir, the largest glaciated region in Tajikistan, has a glacier cover of 2473 km2 (Reference SchetinnikovSchetinnikov, 1998). Fedchenko glacier represents 26% of this glacier area. The drainage basin covers 1537 km2 and feeds the Muksu river, a tributary of the Vakhsh and thus the Amudarya rivers.
Fedchenko glacier showed only a small area change between the two historical investigations, where the tongue retreated ~400 m and lost ~1.66 km2 in area (Reference RegensburgerRegensburger, 1963), i.e. <0.25% of the total glacier area in the 30 years. This small change is not significant with respect to the total glacier area, but it is a directly observed significant change of the tongue. During the same period the glacier snout lost ~40 m in thickness, while above 4000 m the elevation change was insignificant. These observations indicate that the major part of the glacier was close to equilibrium during the middle of the last century. Only the lowermost part (i.e. the last ~20 km of the tongue) experienced a significant mass loss.
Seismic and gravimetric investigations in 1958 resulted in ice thicknesses of ~700–800 m at 4750–4850 m elevation, while the tongue area was ~200–250 m thick (Reference Berzon, Pak, Yakovlev and LeontievBerzon and others, 1961). The volume was estimated to be ~124 km3 (Reference SchetinnikovSchetinnikov, 1998). The surface velocity observations showed maximum horizontal displacements of 0.5–0.7 m d–1 in the middle of the glacier.
Compared with the minor geometrical changes of Fedchenko glacier, large changes are shown by smaller glaciers in the eastern Pamir during different time periods. The observed area decrease of 19% between 1978 and 2001 was attributed to an increase in summer temperatures, while an observed moderate increase in precipitation could not compensate this mass loss (Reference Khromova, Osipova, Tsvetkov, Dyurgerov and BarryKhromova and others, 2006). Available meteorological data from Gorbunov station at ~4200 m a.s.l. close to the margin of Fedchenko glacier (see Fig. 1 for location) show no significant long-term trend of mean summer air temperature in the period 1938–90 (0.0051°C a–1), while precipitation increased slightly during the same period (in total 7.1 mm a–1) (Reference Glazirin and KodamaGlazirin and Kodama, 2003). For this period the mean annual and summer air temperatures were –6.98ºC and 2.48ºC, respectively.

Fig. 1. Map of Fedchenko glacier. The background shows a Landsat 7 ETM image from 24 August 2000. The profile numbers of the glacier velocity measurements in 1958 are given.
Our new assessment of the available historical data, in combination with field data from 2009 and recent remote-sensing information, documents and analyses the changes and temporal variability of Fedchenko glacier during the past eight decades. Surface information (slope and velocities) in combination with our field measurements are used to calculate ice flux and glacier volume. These data allow us to compare balance fluxes with accumulation measurements and to verify earlier volume estimates.
Data and Methods
Historical mapping
The main sources of information about the former glacier conditions are the two maps produced after the expeditions in 1928 and 1958. The accompanying literature provided valuable details about ice velocity and glacier geometry (Reference FinsterwalderFinsterwalder, 1932; Reference Berzon, Pak, Yakovlev and LeontievBerzon and others, 1961; NKGG, 1964). In 1928, a region of 15 000 km2 was covered by a detailed photogrammetric survey (234 image pairs), resulting in two maps of the Fedchenko–Tanimas region (north and south) at a scale of 1: 50 000 (Reference Brunner, Brunner and WelschBrunner, 1999). In 1958, again two maps at the same scale were produced from 58 image pairs, mostly taken at the old baselines, covering the glacier up to 5000 m elevation (NKGG, 1964). Photogrammetric surveys of several cross profiles at different times also provided glacier surface velocities. Both map series are based on the same local geodetic system, defined by astronomical measurements during the 1928 expedition (NKGG, 1964). The original maps have been scanned and orthorectified according to their original projection. Based on the regular coordinate grid for the adjustment, the orthorectified digital maps show only small horizontal location errors compared with the original maps (<25 m, or 0.5 mm in map scale). The elevation contours and glacier boundaries were then digitized from the scanned maps. The contour thickness is ~0.2 mm in map scale, and the exact digitizing of the contours introduces a mean error of ~10 m in location, which is probably on the same order as the original location error of the photogrammetric survey (Reference Haggrén, Mayer, Nuikka, Braun, Rentsch and PeipeHaggrén and others, 2007). Owing to the dense contour interval of 25 m, and even 12.5 m in some flat glacier areas, a kriging algorithm showed the best interpolation results for the final digital elevation model (DEM). The contours derived from this DEM match the original contours of the scanned map versions. Therefore the location error of the derived DEMs is on the order of 35 m.
For the altitude, the digitizing process does not introduce an additional error on the glacier areas. The uncertainty in elevation due to the location error depends on the slope of the terrain. Reference FinsterwalderFinsterwalder (1932) reports a mean elevation error of ~9.2 m, which should also be valid for the maps of 1958.
The velocity measurements by photogrammetric methods in 1928 and 1958 are concentrated on three regions (Fig. 1, profiles 1–7): (1) the lower part of the glacier tongue (~3200 m elevation), (2) the region at, and upstream of, Gorbunov station (4000–4300 m elevation) and (3) close to Tanimas pass (4550 m, only in 1958). In 1928 the profiles upstream of Gorbunov station (profiles 3 and 4) were observed between 18 and 22 August, and the profile close to the terminus (profile 1) in mid-September (Reference FinsterwalderFinsterwalder, 1932). In 1958 the upper profiles were measured in a period around 20 August, and the lower profile at the beginning of August. The estimated error of these measurements is in the range of centimetres per day, depending on the observation interval and the distance from the baseline (NKGG, 1964). After the establishment of Gorbunov station in 1935, continuous velocity measurements were carried out along a stake profile across the nearby glacier (4000 m a.s.l.) until 1981 (Reference Kamnyanskiy and ChertanovKamnyanskiy and Chertanov, 1988). Monthly values of the maximum velocity are available for analysis.
Seismic and gravity measurements on the lower and middle part of the glacier in 1958 and 1959 provide information about ice thickness on several profiles (Reference Berzon, Pack and YakovlevBerzon and others, 1960; Reference SchulzSchulz, 1962). Unfortunately the results are without accurate location information and the vertical scale is imprecise. However, it can be concluded that the ice thickness reaches ~300–400 m at the lower tongue (up to a surface elevation of ~3900 m), while the middle and upper part of the glacier (4200–5200 m elevation) is thick, with ice thicknesses of >700 m and probably up to 1000 m.
Field measurements
In summer 2009 an international expedition within the framework of the Central Asian Deep Ice-coring Project (CADIP) carried out a number of investigations on the middle and upper part of Fedchenko glacier from 8 to 28 August. Apart from climatological investigations, this expedition was aimed at:
mapping the glacier surface elevation with kinematic GPS for comparison with the earlier surveys,
determining the ice thickness by ground-penetrating radar (GPR)
obtaining surface velocities as ground truth for ice flux estimates.
For the GPS observations, TOPCON GB1000 two-frequency receivers were used, while for the kinematic profiles downstream of Gorbunov station an Ashtech Promark L1 receiver was used as rover. Four reference locations were established in order to provide short baselines for the kinematic processing and also to relate the elevation base to the elevation system of the historical maps. Close to Gorbunov station a new benchmark was established on a rock outcrop 135 m south of the station at 4219 m a.s.l. (Fig. 1). In addition, the coordinates of a reference point from 1928 and 1958 (map elevation 4143 m) were determined by differential GPS (DGPS). At the base camp (elevation 4923 m) two rocky spurs at both sides of the glacier were used as reference locations. Based on these benchmarks we related the measured kinematic profiles to modern DEMs and to the historical surveys.
The surface elevation of the glacier was determined along kinematic GPS profiles (~73 km in total) in the region of Gorbunov station and in the accumulation zone between 4640 m (near Tanimas) and 5400 m elevation (Figs 1 and 2). In addition, the positions of two stakes fixed in the ice close to Gorbunov station and the base camp have been determined repeatedly by DGPS.

Fig. 2. Map of the upper part of Fedchenko glacier including the measured GPS (dashed dark grey) and GPR (bright grey) lines. The background shows a Landsat image from 24 August 2000 with 100 m contours derived from the SRTM DEM.
The local DGPS network was connected to the reference station Kitab (IGS (International GNSS (global navigation satellite systems) Service) station KIT3) for calculating baselines to our local reference positions with observation periods of several days each. In addition, the coordinates of our reference network were processed by the Precise Point Positioning service of the Jet Propulsion Laboratory (http://apps.gdgps.net). The mean error of the results is in both cases within 2–3 cm. Based on this local reference network, both the kinematic and static surveys have been processed. The local baselines are <20 km long and the accuracy of the processed DGPS positions is on the order of millimetres, while the point positions of the kinematic profiles show accuracies of 4–5 cm for the profiles upstream of Gorbunov station and 5–10 cm for the profiles downstream, which were measured with the L1 system. The total horizontal and vertical error of the determined GPS positions is <20 cm. For the static observations of the surface displacement the accuracy is on the order of 2 cm.
In the accumulation area of Fedchenko glacier a low-frequency pulse radar with resistivity-loaded dipole antennas up to 40 m in length (10–20 MHz) was used for measuring the ice thickness. Two profiles were located close to the base camp, crossing the glacier more or less perpendicular to the flow direction. A longer profile in the upper accumulation basin consists of one cross profile and a longitudinal section along the central part of the glacier (Fig. 2). The shot positions, 2.0–4.5 m from each other, were recorded with a single-frequency handheld GPS. The vertical resolution of the radar data is usually estimated as one-quarter of the wavelength (e.g. Reference Brandt, Kohler and LüthjeBrandt and others, 2008). Thus for a wave velocity of 1.68 108 m s–1 for ice, the maximum resolution would be 4.2 m, while for snow (velocity 2.24 108 m s–1; Reference Eisen, Nixdorf, Wilhelms and MillerEisen and others, 2002) it is 5.6 m. The total error also includes picking errors of the ice– bedrock reflection (~2 ns or 4.2 m) and a depth-dependent component due to variations in the wave velocity (assumed velocity uncertainty of 5% results in an error of 40 m for 800 m of ice, reducing to zero for very shallow ice). The total vertical error therefore varies between 50 m for the deepest parts and 10 m for thin ice.
Remote-sensing information
Remote-sensing data and derived products (Table 1) were used to compile the modern conditions of the glacier, including glacier boundaries, surface elevation and surface velocities.
Table 1. Overview of the remote-sensing dataset used in this study

Landsat 7 Enhanced Thematic Mapper Plus (ETM+) imagery from 24 August 2000 (Table 1) was used for mapping the glacier extent and surface features on the glacier, and as the reference for the spatial analysis. This image was chosen because it was taken closest to the Shuttle Radar Topography Mission (SRTM) in February 2000 (Reference FarrFarr and others, 2007). The historical maps were co-registered on this image for investigating the area changes. In addition, an image from the Corona mission (acquisition date 8 August 1968) was integrated for improving the temporal coverage of glacier changes in the tongue area. More recent information was retrieved from a Satellite Pour l’Observation de la Terre (SPOT) scene from 2007 and an additional Landsat 7 scene from 2 August 2011.
The SRTM DEM of 2000 (Reference Rabus, Eineder, Roth and BamlerRabus and others, 2003; Reference Jarvis, Reuter, Nelson and GuevaraJarvis and others, 2008) acts as the baseline for investigations of elevation and volume changes. The data are integrated in our Fedchenko GIS and checked for a potential elevation-dependent bias (Reference Nuth and Ka¨a¨bNuth and Ka¨a¨b, 2011) which was not significant up to 5400 m and only affects steep glacierized slopes in the highest accumulation basins of the glacier. The DGPS measurements on stable rock outcrops, as well as trigonometrical points in flat ice-free areas of the 1928 map, were used to test the consistency of the elevation data. The difference is on the order of 10–15 m and thus in the same order as the map accuracy. The C-band (5.3 GHz) SRTM penetration depth in firn and snow could not be evaluated with the method described in Reference Gardelle, Berthier and ArnaudGardelle and others (2012) because no SRTM-X-band (9.65 GHz) coverage is available for Fedchenko glacier. The authors determined the C-band penetration depth in the accumulation area of Karakoram glaciers to be 2–3 m at 5400 m elevation. This value should be similar in the Pamir because of a comparable annual temperature range at this altitude.
Data from the TerraSAR-X satellite mission (Reference Werninghaus and BuckreussWerninghaus and Buckreuss, 2010) operating an X-band synthetic aperture radar (SAR) instrument (Table 1) were used to 30 m (panchromatic 15 m) SPOT 12 October 2007 10 m (panchromatic 5 m) Landsat 7 ETM+ 2 August 2011 3 m in ground range and azimuth 30 m (panchromatic 15 m) determine the surface velocity field of the glacier. For this purpose we used TerraSAR-X 11 day repeat-pass data pairs from August/September 2009 and March 2010. The high resolution of the TerraSAR-X data (below 3 m) allows us to obtain the two-dimensional velocity field of Fedchenko glacier using the amplitude correlation method. The algorithm was applied to enhanced ellipsoid corrected and spatially enhanced level 1b (EEC SE L1b) products with a pixel spacing of 1.25 m and a number of looks slightly above 1 (Reference Breit, Fritz, Balss, Lachaise, Niedermeier and VonavkaBreit and others, 2010). Generally the backscattering over ice and snow decorrelates over 11 days, but cross-correlation of amplitude images is feasible if conservative surface features (drainage patterns, crevasses, etc.) provide the required contrast. The overall absolute accuracy of the method depends on orbital errors and the stability of surface features. Mean accuracies of 0.05 m d–1 in ground range can be achieved, while the accuracy of the individual motion vector is determined by the correlation coefficient (Reference Floricioiu, Eineder, Rott, Yague-Martinez and NaglerFloricioiu and others, 2009).
Ice thickness reconstruction
A physical relationship exists between ice thickness, surface slope, ice velocity and the rheological properties of the glacier ice. However, the full formulation of this relation, considering the nonlinear flow law of ice, and the Stokes equations for ice flow including specific boundary conditions, is complicated. For large parts of the glacier the driving stress is compensated by the basal shear stress, which is in many cases the major stress component in the force balance (Reference PatersonPaterson, 1994). Longitudinal stresses are only of importance close to ice divides, very flat glacier parts or the margins. Therefore we assume that the simplified approach of a balance between driving stress and basal shear stress will also provide a reasonable estimate of the glacier conditions for most parts. The relation between the shear stress τ zx , the ice thickness h and the surface slope α is then given by
With ρ the density of ice and g the acceleration due to gravity.
The flow law (Reference GlenGlen, 1955) provides the required relation between shear stresses τ
zx
and strain rates ![]() , respectively the velocity gradients
, respectively the velocity gradients ![]() with the flow factor A and the flow exponent n:
with the flow factor A and the flow exponent n:

neglecting all other stress components.
The following derivation of the ice thickness is according to Hooke (2005, p. 81–82) for deriving the velocity distribution in a uniform glacier slab. Combining Eqns (1) and (2), rearranging the terms and assuming the vertical gradient of the horizontal velocity u is large compared with the horizontal gradient of the vertical velocity w, will result in an equation for the horizontal ice velocity in dependence of the ice depth z:
The bascal velocity ub = u(h) then is

An expression for the ice thickness is then

This formulation is only valid for an infinitely wide slab. Geometry considerations suggest that a shape factor of ~0.5 in the denominator of the second root should be used for semicircular valley glaciers (Reference HookeHooke, 2005).
Results
Our analysis and interpretation of the data are restricted to the main Fedchenko glacier trunk. Bivouac glacier, a former left-hand tributary to the Fedchenko glacier tongue, today is more or less stagnant and not contributing ice mass to Fedchenko glacier. The glacier mapping based on the remote-sensing imagery described above resulted in the following glacier areas (2011) and is also displayed in Figure 1:
Fedchenko glacier: 579.9 km2
Bivouac glacier: 164.7 km2
Total area: 744.6 km2
Fedchenko main trunk: 213.3 km2.
The main trunk is used for calculation of fluxes and ice thicknesses, neglecting the tributary glaciers and including only the uppermost accumulation basin above 5200 m. Adopting the mean ELA from earlier investigations and our own observations (~4800 m a.s.l.), the ablation area is 210.5 km2 and the accumulation–area ratio (AAR) is ~64%.
Area changes
Comparison of the historical maps with the remote-sensing imagery shows that considerable variations of the glacier area only occurred at its terminus and along the lowermost 20 km of the glacier tongue, where its width was reduced by ~150 m on average. The area reduction at the glacier tongue did not occur in a continuous way. The 30 year period 1928– 58 shows the largest mean rate of change (Table 2). In the 1960s and between 2000 and 2007 the area loss rates are small (0.014 and 0.010 km2 a–1, respectively), while during 1968–2000 the loss rate increased more than twofold. From 2007 to 2011 the changes are within the uncertainty of the boundary delineation on the Landsat image. Consequently, the mean area change from 2000 to 2011 results in a loss rate of 0.006 km2 a–1. Some minor area changes also occur in the upper part of the glacier, but these changes are not homogeneous and in total are well within the mapping error range. The total area change for the entire observation with period is –2.91 ± 0.3km2, or about –0.5% of the total glacier area. With respect to the main trunk of Fedchenko glacier, this represents a change of –1.4%.
Table 2. Area changes and change rates of the lower glacier between 1928 and 2007

Elevation changes
For debris-covered glaciers the surface elevation change and thus the volume change is a much better indicator for climate-related glacier reactions than area fluctuations. The surface elevation differences between the two historical maps have been investigated (NKGG, 1964; Reference FranzFranz, 2001). However, our carefully digitized maps allow a much more detailed analysis of these changes and also in a spatially distributed way. The SRTM elevation model and our measurements in 2009 allow us to extend this change analysis to the recent past. The elevation offsets between the intrinsic elevation system of the maps and the local GPS reference system (World Geodetic System 1984 ellipsoidal elevation (WGS84)) were 32.4 m at the lower point and 31.7 m at the higher points. The difference between these two offsets is well within the combined uncertainty of the elevation measurements, and the map-derived DEMs were corrected by the mean of the detected offsets.
The analysis of the elevation changes shows that there are no large lateral deviations and the main changes are observed along the glacier. Therefore the elevation changes are only discussed along the central flowline, although they are also valid across the glacier. The results are presented in Figures 3 and 4, displaying the total changes and the change rates per year, respectively.

Fig. 3. Elevation changes and elevation along the central flowline at Fedchenko glacier between 1928 and 2000 (2009). The surface data are derived from the maps (1928, 1958), SRTM data and GPS data from measurements in 2009 (see Fig. 1).

Fig. 4. Rates of elevation change and elevation along the central flowline at Fedchenko glacier between 1928 and 2000 (2009). The surface data are derived from the maps (1928, 1958), SRTM data and GPS data from measurements in 2009 (see Fig. 1).
The elevation changes vary considerably through time and with the largest values close to the terminus (Fig. 3). In the first period (1928–58), the lowering reduces continuously from 35 m at the terminus to zero 28 km upstream. In the second observation period (1958–2000), elevation changes are similar along the first 12 km (–28 m compared with –30 m in the first period). However, the lowering extends all the way to the ELA (57 km). The large opposing fluctuations in the two periods between 50 and 57 km might be due to problems with long observation distances during the 1958 survey. Upstream of 58 km (4900 m a.s.l.) the surface lowering increases again towards the highest parts of the glacier (only observed for 1928–2000), reaching a maximum of 35 m in the upper accumulation basin (68 km, 5200 m a.s.l.). During the first 30 years the surface lost ~1.0 m a–1 along the lowermost 12 km, while in the second period the mean lowering was 0.7 m a–1 along the first 20 km and thereafter reduces gradually towards zero close to the ELA (Fig. 4). Considering the entire period, the surface lowering at 30 km from the glacier terminus increases from 0.03 to 0.42 m a–1 and further to 0.85 m a–1 during the three observation periods, while a few kilometres further upstream the surface lowering increases before 2000, but reduces afterwards. Close to the equilibrium line, surface changes are generally small. Above 5000 m, however, a large change from negative to positive rates is observed before and after 2000.
Volume changes
The area-distributed elevation changes can be used to calculate the volume change for 1928–2000 (Table 3). Here we concentrate on the main trunk of the glacier, including only the main glacial valley and the uppermost accumulation basin above 5200 m, because we also have ground-truth elevation data for this part. In this area the glacier surface is flat and the elevation models are most accurate. Nevertheless, changes in the tributary basins should be similar to those determined on the main glacier. At the lowermost glacier tongue (2900–3100 m a.s.l.), the volume changes are near constant over the entire time period. Further upstream the volume change in the second period gradually increases towards the equilibrium line compared with the earlier period. Between 3900 and 4800 m elevation there was almost no change in the first period, while during the second period a considerable volume loss can be observed. Therefore we assume that also in the accumulation area the change occurred only after 1958 (–1.1 ± 1.6 km3). The mean total volume loss is ~5.1 ± 3.9 km3. Below 4850 m elevation (the approximate ablation zone) the total loss amounts to 4.0 ± 2.4 km3 compared with ~3.0 ± 2.4 km3 between 1958 and 2000. Therefore 75% of the volume change in the ablation zone occurred during the 42 year period in the second half of the 20th century, while only 25% was lost in the 30 years before. On the main glacier trunk, 1.0 km3 of glacier volume was lost between 1928 and 1958, while the remaining 4.1 km3 (80.4%) disappeared in the period 1958–2000.
Table 3. Ice-volume changes on the main glacier trunk for the different observation periods and for 100 m elevation bands

Ice thickness
The seismic and gravity measurements carried out during the International Geophysical Year (Reference Berzon, Pack and YakovlevBerzon and others, 1960; Reference SchulzSchulz, 1962) only cover the lower and central part of the glacier up to ~4800 m a.s.l. Unfortunately these data are not well documented, so only the general characterization of the ice thickness for this region can be adopted.
Our measurements close to the base camp and in the upper accumulation basin in 2009 covered parts of the glacier where no information was previously available (profiles FT3/FT4 and 1–2–3–4 in Fig. 2). The radargrams show a strong signal of the bedrock reflection and only some internal structure in the ice. The ice thickness could be clearly determined along the profiles. The cross profile at 4950 m (base camp) shows a typical valley shape, with the maximum thickness of ~780 ± 50 m almost in the centre of the glacier. The slopes to both sides are smooth, with a mean inclination of 358. The vertical cross section of the glacier along the radio-echo sounding (RES) profile is 1.05 ± 0.1 km2. The second cross profile just above the base camp shows very similar ice thicknesses, which indicates that the glacier bed is flat in this area.
The highest cross profile is ~800 m downstream of Jasgulem pass (Fig. 5, part 1–2) in the upper accumulation basin. Here the valley is not symmetrical. The western part is clearly less steep with some steps along the slope. The valley bottom is flat, before the terrain rises steeply towards the ridge that splits the accumulation basin. Along this profile the glacier has a similar width to that at the base camp, while the maximum ice thickness is _514_40m and the cross-sectional area is 0.86_0.07km2. Towards the centre of the upper accumulation basin the ice thickness increases slightly to 550_ 40m (Fig. 5, part 3–4). Here the glacier bed is also flat, but shows undulations of 50m magnitude. Considering the geometry of the upper accumulation basin, where different sub-basins join to form the main trunk of Fedchenko glacier, and the fact that the centre of this junction also shows the lowest surface slopes, it can be assumed that the maximum ice thickness will not significantly exceed the observed maximum of 550m above 5200ma.s.l. in this region. Between this junction of the accumulation basins and the base camp the ice thickness increases by ~230 m along a distance of 9 km, while the surface elevation decreases by ~250 m. This indicates that the mean slope of the glacier bed is approximately twice the slope of the glacier surface on this part of the glacier.
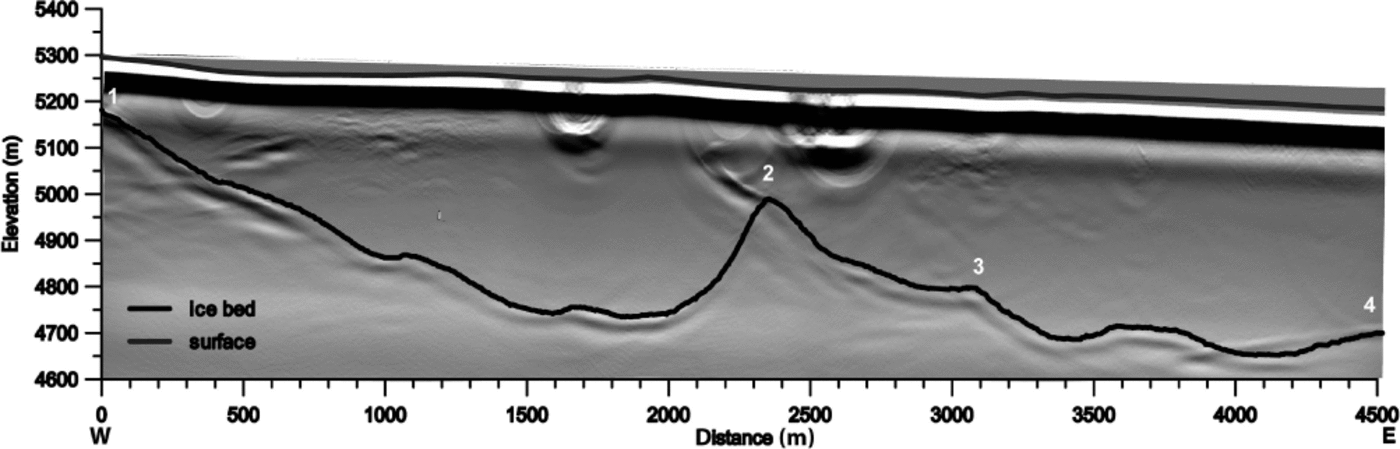
Fig. 5. Ice bed and surface data from the GPR and GPS measurements in the upper basin of Fedchenko glacier. The numbers mark the positions of the break points in the profile (see Fig. 2). The migrated GPR data are displayed in the background.
Surface velocity
The analysis of the DGPS measurements provides short-term surface velocities for the two stakes, in the vicinity of Gorbunov station and at the base camp of 2009. At the lower stake the displacement was 68.0 ± 1.3 cm d–1 (248 ± 5 m a–1), while at the upper stake the mean daily displacement was 69.9 ± 0.6 cm (255 ± 2 m a–1). At the lower stake the observations were carried out during 3 days (18–20 August), while the upper stake was observed for 7 days (22–29 August). It is very likely that a contribution from basal sliding during the summer months influences at least the velocities at the lower stake.
The 11 day repeat-pass acquisitions of TerraSAR-X data in August/September 2009 (Fig. 6) and March 2010 allowed us to obtain surface displacement fields for the largest part of the glacier, while in some areas on the glacier the SAR signal decorrelated. This occurred in particular on tributary glaciers and in steeper basins. Gaps on the main glacier exist downstream of the Tanimas pass (4600 m a.s.l.) and in the vicinity of the base camp. On ice-free areas the mean velocity is well below the amplitude correlation accuracy. The TerraSAR-X velocities agree well with our local GPS measurements at the lower stake (242 ± 18 m a–1 compared with 248 5 m a–1 from DGPS). Therefore we assume that the spatially distributed velocities realistically represent the true surface velocities for the observed dates. In March 2010 the TerraSAR-X velocities are ~20% higher in the ELA region, while the velocities above 5100 m are almost identical to the results from September 2009.

Fig. 6. Surface velocity map of Fedchenko glacier from TerraSAR-X data in August/September 2009. Areas on the main trunk with no velocity information are indicated by grey boxes. Contours are displayed every 500 m
The overall pattern (Fig. 6) of the velocities in autumn 2009 indicates two regions with generally higher velocities, from 4600 to 5000 m elevation and from 3600 to 4250 m elevation. In most other areas the surface velocity is <200 m a–1.
The historical measurements on the lower part of the glacier tongue (profiles 1 and 2) show displacements on the order of 70–110 m a–1. Profile 3 close to Gorbunov station shows displacements of >290 m a–1 in 1958 and 10% lower values in 1928 (NKGG, 1964). The maximum displacements at profile 4, 6.5 km upstream of Gorbunov station, were 175 m a–1 in 1928, very similar to the measurements in 1958. The 45 year time series of monthly velocity observations at profile 3 (Reference Kamnyanskiy and ChertanovKamnyanskiy and Chertanov, 1988) allows the analysis of intra-annual velocity variations (Fig. 7). The interannual variations of the monthly data are usually within 14% of the absolute value, with no long-term trend. The standard deviation of the interannual variability (4.8) is smaller than the mean standard deviation for the monthly variability (7.6). A remarkable deviation from the mean velocity cycle occurs between 1954 and 1957, when the velocities increase to an absolute maximum of 431 m a–1 (118 cm d–1) in July 1954 (long- term mean value of 310 m a–1 (85 cm d–1)). The velocities remain on a high level until June 1956.

Fig. 7. Monthly velocities measured at the centre of a cross profile close to Gorbunov station at 4000 m a.s.l. during the period 1936–81 (Reference Kamnyanskiy and ChertanovKamnyanskiy and Chertanov, 1988). The monthly velocities for the individual years are shown in light grey, and the monthly mean velocities for the entire period in bold and symbols. The diamonds show the velocity measurements at the stake and from TerraSAR-X imagery in August/September 2009 and March 2010, including the error range (vertical bars).
The annual velocity variation shows a very characteristic shape, with the maximum in June and a sharp decline from July to minimum velocities in October. Ice velocities increase again during the autumn and remain at an intermediate level from January until April.
Ice thickness and flux estimates for the main glacier tongue
We used a simplified approach for deriving ice thicknesses from surface information to estimate ice flux and glacier volume. We calculated a shape factor for Eqn (5) from the ice thickness cross profile at base camp. The result is almost exactly 0.5. Therefore the theoretical value for semicircular valley shapes (Reference HookeHooke, 2005) is used for the entire glacier trunk. The surface slope was interpolated over a horizontal distance of 2 km (equivalent to more than two ice thicknesses everywhere), in order to remove small-scale surface undulations originating from surface processes (Reference HookeHooke, 2005, p. 81).
The influence of basal sliding
The surface velocities were determined at the end of the ablation season. It is likely that they contain some contribution from basal sliding. We can infer the role of basal sliding at an old velocity profile close to Gorbunov station (Fig. 7). Here the long-term annual mean velocity is 263 m a–1 (±30 m a–1) and the seasonal variability is +55 m a–1 (+21%) to –44 m a–1 (–17%). Velocities at the end of August are ~19 m a–1 (7%) lower than the annual mean velocity, with a slightly higher standard deviation (±39 m a–1). The velocity minimum in October indicates that basal sliding plays only a small role at the end of the ablation season. The mean velocity decrease between the end of August and October is 26 m a–1 (±36 m a–1) and represents the contribution of basal sliding to the surface velocity in August (10%). Meltwater production decreases with elevation and so does the influence of basal sliding on the surface velocity.
The sensitivity of Eqn (5) is investigated with respect to variations of the two input variables surface velocity and surface slope (for n = 3). The typical slope of Fedchenko glacier is ~2º (±1º). Thus the last part of Eqn (5), sin-0: 75 α comes to 12.4 (9.1 and 20.8 for 38 and 18, respectively). The contribution of the velocity term is 5.13% for the October (deformation) velocity of 219 m a–1. At the end of August (244 m a–1) the resulting factor comes to 5.27%. With mean surface slope of 2º and flow factor A = 4 10–24 s–1 Pa–3, the ice thickness is 582 m, varying up to 598 m (+2.8%) for the higher velocities at the end of August. Based on the observed velocity variations (Fig. 6), the potential error in calculated ice thicknesses due to the estimation of the deformation velocity from the surface velocity is <10% at Gorbunov station and decreases with increasing altitude. A correct determination of the interpolated surface slope is crucial for the resulting ice thickness. For surface slopes <1.0º the resulting ice thicknesses are not realistic. Unfortunately this is the case for the base camp region and thus the ice thickness profile cannot be used for model calibration.
The SRTM surface elevations and the velocities based on the TerraSAR-X imagery are used to calculate ice thicknesses for the entire main glacier. We use a cross profile at 4800 m a.s.l. to demonstrate the uncertainty included in this analysis by calculating ice thicknesses for different parameter sets (Table 4): for temperate conditions (A = 6.8 × 10–24 s–1 Pa–3), slightly cold ice (A = 2.4 × 10–24 s–1 Pa–3) (Reference PatersonPaterson, 1994) and including the uncertainty of the velocity from the remote-sensing analysis (±18 m a–1) and from the basal sliding contribution (10%). The results show that the variations due to the uncertainties in the potential contribution of basal sliding are small. The largest effect is due to the ice temperature and thus the flow factor.
Table 4. Parameter test for the calculation of ice thicknesses according to Eqn (5). Ice thicknesses are calculated for two different temperature conditions (temperate and –28C), including the uncertainty in the velocity determination (±18 m a–1) and the potential influence of basal sliding (±10%)

Results from the 1958 expedition indicate a maximum ice thickness of ~1000 m in this region. A comparison of our derived and measured ice thicknesses in the upper accumulation area (at profile 2–3–4) shows good agreement when using the flow factor for temperate conditions. Therefore the flow parameter for temperate conditions is used for the flux calculation at 4800 m altitude. This represents roughly the flux at the equilibrium line. With a mean cross section of 1.874 ± 0.145 km2 and the derived surface velocity, the ice flux is 0.23 ± 0.05 km3 a–1. This corresponds to 1.21 ± 0.26 m of ice, or 1.10 ± 0.23 m of water distributed over the upstream area of 189.4 km2.
Calculated ice thicknesses on the central flowline increase to ~300 m thickness within the first 6 km from the snout and remain for the major part of the lower glacier tongue in the range 400–500 m. Thicker ice is found above 4500 m, and maximum ice thicknesses reach >1000 m just below the equilibrium line. The upper basin shows a rather steep headwall, where the ice thickness reduces from >700 m to <100 m within just 10 km. The volume of the main trunk of the glacier is calculated to be 78.6 ± 18 km3. With the assumption that the slope of the SRTM elevation model is correct in the tributary basins, and interpolating the gaps in the TerraSAR-X velocity model, the volume of the entire glacier is 123.4 ± 28 km3. This extension of the analysis to the entire glacier is justified, because the main tributaries to the total glacier volume show a similar distribution of surface slopes to that on the main trunk. The result is almost identical to earlier estimates (Reference SchetinnikovSchetinnikov, 1998; 124 km3).
Discussion
Area changes
The highest rates of area change occurred during the first observation period (1928–58). Continuous ice melt during summer probably increased the debris thickness on the tongue, which subsequently protected this area more effectively from melting. The reaction of the glacier tongue is typical for debris-covered glaciers, where the accumulated debris obstructs a direct relationship between the surface energy balance and ice melt. Thus a stagnant debris-covered terminus does not necessarily indicate balanced conditions. Compared with the total area of 580 km2, the area change of the glacier tongue of –2.91 km2 (~0.5%) is small. Compared with smaller glaciers east of Fedchenko glacier, which show an area reduction of almost 20% from 1978 to 2001 (Reference Khromova, Osipova, Tsvetkov, Dyurgerov and BarryKhromova and others, 2006), Fedchenko glacier is surprisingly stable.
Elevation changes
The surface elevation change of the glacier during the entire observation period can be characterized as described below.
The lower glacier area shows continuous surface lowering, with a trend to lower values in more recent times. This trend fits the observations of the area changes, and might be explained by an increase of the debris cover thickness on this part of the glacier. Upstream of the debris-covered part, the lowering rates increase. Above 4050 m elevation and up to the equilibrium line, the observed surface lowering has occurred almost entirely since 1958. In the accumulation area the surface lowering increases again with increasing elevation, showing maximum losses in the upper basin. Even though the lack of information in 1958 does not allow resolution of the timing of the elevation change, it seems reasonable to assume that the major part of the elevation change occurred after 1958. The large surface lowering in the higher accumulation basin could have several causes:
The accumulation pattern changed to drier conditions, creating an imbalance between accumulation and discharge.
The compaction of the firn layers intensified because of increasing summer air temperatures.
For the past decade the GPS elevations are almost identical to the SRTM data close to the equilibrium line. However, further up-glacier the difference between the GPS elevations and the SRTM elevation model increases to ~+7 m in the upper accumulation basin. Because this increase is more or less continuous from the equilibrium line into the area of dry snow, we argue that this difference might be due to the increasing penetration of the C-band signal (Reference Gardelle, Berthier and ArnaudGardelle and others, 2012) in the snow cover and not to an elevation change signal. Consequently the elevation reductions in the observation period 1928 (1958) to 2000 should be corrected, leading to elevation differences of up to 10 m closer to the equilibrium line and ~25 m in the upper accumulation basin. These values correspond to an elevation change rate of –0.24 to –0.60 m a–1 over the 42 year period 1958–2000.
Velocity changes
The long-term velocity observations at the Gorbunov cross profile (Reference Kamnyanskiy and ChertanovKamnyanskiy and Chertanov, 1988) show no trend, indicating a stable dynamic situation. Therefore the volume loss in the upper part of the glacier after 1958 must be related to an increase in ice melt or a decrease in accumulation. The observed and derived velocities in 2009 and 2010 are about the same as the observations in the earlier years. In 2009 they also show the characteristic decline towards the end of August. The high velocities in March 2010, however, are higher than the observations in earlier years.
The annual velocity pattern may be explained by the development of the subglacial drainage system during the summer. High meltwater fluxes lead to an increase of subglacial drainage, while the evolution of the drainage system lags behind. The increase of subglacial water pressure increases the sliding velocity (e.g. Reference Bartholomaus, Anderson and AndersonBartholomaus and others, 2008). The reduction of surface melt during August coincides with the establishment of an efficient drainage system. Therefore the subglacial water pressure reduces, as does the sliding velocity. During the winter months the subglacial drainage system adapts to the water supply by creep, and the pressure rises again, which stimulates the basal sliding.
With otherwise stable conditions, the reduction of ice thickness would result in lower ice velocities. For the observed ice thickness reduction of 33 m at the centre of the Gorbunov cross profile and the calculated ice thickness of 480 m, the deformation velocity is 174 m a–1, according to Eqn (5). This is in the lower range of the observed velocities in October. The velocity signal from a reduction in ice thickness is therefore still within the long-term observed velocity variations.
Volume changes and state of the glacier
The volume loss of >5 km3 on the main glacier trunk over the period of 81 years relates to an initial volume of 83.6 km3 in 1928 and is therefore 6.0% (1%). If we assume as an upper boundary that half the volume loss in the accumulation area can be attributed to firn compaction, the total mass loss is 4.14 km3 w.e. or 0.05 km3 w.e. a–1. As a rough estimate for a mean annual ablation period of 100 days, the mean daily run-off would be enhanced by 510 × 103 m3 d–1 or 5.9 m3 s–1 (616 × 103 m3 d–1 (7.1 m3 s–1) for no additional firn compaction). This corresponds to a mean imbalance ablation across the ablation area of 0.0024 m w.e. d–1. This is small compared with mean daily melt rates on glaciers in general. The AAR of more than 60% indicates near-balanced glacier conditions, despite the observed losses during the past eight decades. The calculated ice flux of 0.23 ± 0.05 km3 a–1 close to the equilibrium line results in a realistic balance accumulation of 1.10±0.23 m w.e. Reference AizenAizen and others (2009) found accumulation rates of 1.38 and 2.09 m w.e. a–1 based on two firn cores in the upper accumulation basin. Given that the measurements of Reference AizenAizen and others (2009) were carried out at elevations of 5206 and 5365 m in the upper accumulation zone, our mean balance accumulation rate seems reasonable.
Conclusions
Fedchenko glacier and its tributaries comprise one of the largest glacier systems outside the polar regions. Unlike other large glaciers and observed glacier changes in the vicinity, the area decrease has been low over the past eight decades. This cannot be attributed entirely to a less expressed climatic signal in the central Pamir region, but is mainly connected to the debris-covered tongue of the glacier. For example, similar small area changes can be observed for the strongly debris-covered Baltoro glacier in the Karakoram (Reference Mayer, Lambrecht, Belò, Smiraglia and DiolaiutiMayer and others, 2006). The total elevation reduction of ~70 m in 72 years (1928–2000) on the lower glacier tongue demonstrates the continuous negative mass balance of this part of the glacier. Despite the small glacier area changes, the four decades after 1958 show a threefold higher volume loss of the glacier below 4800 m (~ELA) than during the 30 years before. This demonstrates that, especially for glaciers with debris-covered tongues, the glacier length variation provides no suitable information about the climate-related glacier reaction. The relative volume loss of 6.0% of the initial ice volume on the main trunk of the glacier during eight decades, where 4.9% was lost during the last five decades, is not correlated to the observed area change of 1.4% over the same region.
Above 3900 m elevation (~22 km from the terminus) almost the entire volume loss occurred after 1958, and a more or less continuous reduction of elevation change with altitude was observed from the glacier terminus up to this elevation in the period 1928–58. In the second half of the 20th century the increased melt also reached the higher parts of the glacier, while at least part of the signal in the accumulation area may also be attributed to a compaction of the firn layer due to increasing summer temperatures. The ice velocities in the ablation area do not show a clear reaction to these elevation changes. Measured velocities are within the range of the long-term velocity variation at the Gorbunov cross profile. However, the seasonal velocity distribution indicates a continuous adaptation of the basal drainage system to the meltwater availability. The run-off increase due to non-equilibrium ice melt is small compared with the mean run-off during the ablation season.
Acknowledgements
Support from the US National Science Foundation (NSF grants ATM-0754479 and ATM-0754644), NASA (grant NNX08L68G) and the Arbeitsgemeinschaft für vergleichende Hochgebirgsforschung is gratefully acknowledged. The University of Innsbruck, Austria, and the Central Asian Institute for Applied Geosciences in Bishkek generously supported the fieldwork. V. Denisov, A. and TopAsia Travel Co. assisted with organization of the 2009 expedition to Fedchenko glacier. The TerraSAR-X data were made available by DLR through science proposal HYD0396.













